XIII
Zeno: Paradox and Progression

(a) Sprightly running

Zeno’s four arguments against motion are known to us from Aristotle’s discussion of them in Physics Z. The Greek commentators on Aristotle for once fail us: they do not reproduce any of Zeno’s own words, and with one trivial exception they provide us with no information we cannot glean from Aristotle’s text. The paradoxes were famous in antiquity, and they influenced philosophers other than Aristotle: it is odd, as well as unfortunate, that our knowledge of them is virtually confined to the brief and polemical reports in the Physics.¹

Z 9 contains Aristotle’s main discussion: the section begins thus:

There are four arguments of Zeno’s about motion which provide difficulties for their solvers—first, the one about a thing’s not moving because what is travelling must arrive at the half-way point before the end (we have discussed this earlier)…(182: Phys 239b9–14=A 25=19 L).

I shall refer to this first paradox as the Dichotomy; it is also called the Stadium, but I reserve that title for the fourth paradox.²

Aristotle’s earlier discussion of the Dichotomy appears in Z 2:

That is why Zeno’s argument assumes a falsehood—that one cannot pass through an unlimited number of things or touch an unlimited number of things individually in a limited time. For both length and time—and, in general, whatever is continuous—are called unlimited in two ways: either by division or as to their extremes. Now one cannot touch things unlimited in respect of quantity in a limited time, but one can so touch things unlimited by division—for the time itself is unlimited in this way. Hence it is in an unlimited and not in a limited time that, as it turns out, one traverses the unlimited, and one touches the unlimited things in unlimited and not in limited times (183: Phys 233a21–31=A25=19L).

From this critical appraisal, and the half-line of description in Z 9, we must reconstruct the Dichotomy.

Suppose that in a finite period of time T, a body b traverses a finite distance AB. Then at some instant within T b will ‘touch’ a1, the mid-point of AB; and at some later instant, again within T, b will ‘touch’ a2, the mid-point between a1 and B; and so on: in general, for any ai there is a point aj, mid-way between ai and B, which b will ‘touch’ at some instant within T. Thus within T b will ‘touch’ infinitely many points along AB; but that is impossible: hence b cannot traverse AB in T. And, in general, locomotion is impossible.

The exposition requires three preliminary comments. First, it interprets the Dichotomy in terms of a division which may be drawn thus:

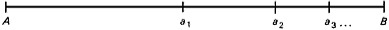
Aristotle’s commentators prefer a different diagram:

Thus: ‘Before reaching B, b must touch the midpoint a1 of AB; and before reaching a1, b must touch the midpoint a2 of Aa1…’. Aristotle, I think, had the first diagram in mind;³ and I rest on his authority. But it is to be observed that there is no interesting logical difference between the two ways of expounding the paradox. Many commentators suppose that, with the first diagram, Zeno attempts to show that no moving body can ever complete its journey: it can never take the last step to B, since there is no last step. With the second diagram, they say, Zeno shows, more strikingly, that no body can ever start its journey: it can never take its first step, since there is no first step to take. But that distinction is unimportant: with either diagram, Zeno means to show that no body can traverse a finite distance in a finite time—in other words, that no body can move. The first diagram does not allow travellers to begin but not end their journeys; for every journey begun is eo ipso a journey ended.

Second, we may wonder what is meant by ‘touch’ (haptesthai) in Aristotle’s exposition, and why Zeno should think that moving bodies must ‘touch’ points in their travel. Some sources compare ‘touching’ to counting: b, they say, can no more ‘touch’ each at inside AB than he can count each ai as he passes it; and some scholars have supposed that Zeno’s original traveller went on a mental rather than a physical journey: b cannot run through AB in his mind, for he cannot, so to speak, give his mind in turn to each of the points in AB. ‘Touching’, on this view, is a sort of mental stopping: the physical runner ‘touches’ ai in so far as, on passing ai, he stops mentally and says to himself: ‘This is a_i’.⁴

That interpretation is surely not Zenonian: Aristotle explicitly distinguishes between Zeno’s paradox and the argument which requires the traveller to count the halfway points on his journey (Phys 263a6–11); and it is clear that the counting version was a vulgarization of Zeno’s argument. ‘Touching’ in Zeno is what it sounds like: physical contact. Let us idealize the example: suppose b to be a perfect cube travelling along the straight path AB; and represent each ai by a line across AB parallel to the front edge of b. Then b touches ai if and only if ai lies on the same plane as the front surface of b. Clearly, then, if b is to traverse AB, it must, in this sense, touch successively every ai inside AB.

Third, we must be on our guard against the wiles of infinitude: in the paradox of ‘large and small’ Zeno falsely claimed an infinite regress; here does Zeno really show that b has infinitely many ais to touch? It is easy to show that he does: the successive ais are constructed by dichotomy: if AB=1, then Aa1=½, a1a2=¼, a2a3 =1/8, and in general · Thus the ais can be put in one-one correspondence with the powers of 2; hence they can be put in one-one correspondence with the natural numbers, and they are infinitely numerous.

Were he to travel from A to B, b would perform infinitely many tasks: there are infinitely many ais between A and B, each of which b must touch; there are infinitely many distinct propositions of the form ‘b touches ai’, and if b reaches B every one of these propositions has been made true. Thus Zeno thinks to establish:

(1) If anything moves, it performs infinitely many tasks. Since he holds it to be a truism that:

(2) Nothing can perform infinitely many tasks, he concludes that nothing moves. Unless we are to follow Zeno into his immobile world, we must reject either (1) or (2). Philosophical controversy has settled about (2); but I shall begin my discussion with a few thoughts on (1).

Some philosophers reject (1): in running from A to B, they say, b does not have to undertake, successively, infinitely many tasks; his run from A to B is not composed of an infinite sequence of progressively shorter runs. He performs one run, takes a hundred strides, feels fifty heart-beats, and so on; but he does not do or undergo an infinity of anything.

As an exercise in pure pedantry there is something to be said for that objection; for it is indeed mildly odd to call each of b’s successive moves to the next ai a ‘run’ or a ‘task’. Yet the point is merely verbal: Zeno himself does not use the terminology; and if b need not perform infinitely many tasks, that does not show that he has not got infinitely many ais to touch, infinitely many points to pass, infinitely many subsections of AB to traverse. The claim that b’s operations are not ‘tasks’, or are only ‘tasks’ in a Pickwickian sense, is boring.⁵

Proponents of the boring claim sometimes mean to deny (1) outright; but sometimes they offer a slightly subtler suggestion: b’s move from A to B, they suggest, is a single run, a century of paces, half a century of heart-beats, etc. To get from A to B requires the performance of many finite sets of tasks. Now, they continue, we can describe b’s journey in terms of an infinite succession of tasks; but that does not show (1) to be true: the performances required of a locomotor can indeed be described in terms of infinity, but for all that they are finite performances.

I set down this view because I have frequently heard it; but I dismiss it shortly: if any piece of locomotion can be truly described as the successive performance of an infinity of operations, then (1) is true. There are no two ways about it: either the description does not apply, or else it does apply and (1) is true; you cannot allow the description and brush aside the infinity it imports.

A more interesting objection to (1) can be formulated: (1) is true only if space is continuous or infinitely divisible; for it rests upon the assumption that any stretch of space, AB, contains infinitely many spatial points, ai. That assumption, which I adverted to in the previous chapter (above, pp. 245–6), is not examined in our ancient texts; and those philosophers who do examine it usually accept it on insufficient grounds, tacitly supposing that a continuous geometry is applicable to physical space (and to time). Any full-scale examination of Zeno’s paradoxes would be obliged to discuss the geometry of space: for reasons I gave earlier, I shall not enter upon such a discussion here.

(b) Infinity again

There have been numerous and diverse attempts to deal with premiss (2); the most convenient approach begins by asking wherein the impossibility of infinite performances is judged to lie: what is it about infinite performance in general, or the infinite performance of b in particular, that involves an impossibility? I shall mention seven lines of argument.

First: ‘b cannot run through infinitely many points; for that would mean that he traversed an infinite distance’. Many philosophers have faulted Zeno in the Dichotomy, as in the logos of ‘large and small’, for bad arithmetic.⁶. Let AB measure 1 mile; then in order to reach B, b must traverse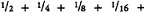 …miles. Now the sum of that series does not exceed 1 mile; but Zeno, it is alleged, supposed it to be infinitely great, and for that reason upheld (2).

If that was Zeno’s reason for asserting (2), it was a tediously bad reason. And I am not confident that Zeno can be excused: if in the logos of ‘large and small’ he supposed the sum of ½+¼+1/8 + …to be infinitely great, then he may well have made the same supposition in the Dichotomy. But whatever Zeno may have argued, others have found (2) plausible despite a degree of mathematical expertise; and we cannot dismiss the Dichotomy on the grounds that Zeno misreasoned for (2).

Aristotle’s criticism of the Dichotomy in Physics Z 2 suggests a second way of defending (2): ‘Locomotion must take a finite period of time: b gets from A to B in T; but in order to touch infinitely many ais, b requires an infinite span of time.’ Thus (2) is true because we are all hemmed in by the finitude of our lives.

Aristotle’s reply is apt: just as AB, though finite in extent, contains infinitely many points, a_i; so T, though finite in duration, contains infinitely many instants, t_i. Each a_i in AB can be uniquely paired with a t_i, in T. Similarly, every spatial sub-interval a_ia_j of AB can be uniquely paired with a temporal sub-interval t_it_j of T. If space is infinitely divisible, so too is time; and thus in his run from A to B, b will never be short of time; there are as many instants available for touchings as there are points to be touched.

Aristotle assumes that time, like space, is continuous. And Zeno might be defended by denying that assumption: space is continuous, but time is not; unlike space, time consists of a succession of discrete minima. Time is granular, space is smooth: the parallelism between the two dimensions is broken, and with it Aristotle’s objection. One of Aristotle’s successors, Strato of Lampsacus, apparently held this view; and it has its modern supporters. I content myself with asserting that it is based on a bad lot of arguments, and that its acceptance involves a host of difficulties.⁷

In any event, that strange view is not the only way of defending Zeno: the second defence of (2) fails; but (2) does not fall with it: (2) has been upheld by men who are convinced of the continuous nature of time. Aristotle himself came to see that:

But this solution [sc. that of Z 2] is adequate with regard to the questioner (for he asked whether one could traverse or count unlimited things in a limited time), but it is not adequate with regard to the facts and the truth; for if someone were to forget about the length and about asking whether one can traverse unlimited things in a limited time, and were to make this enquiry of the time itself (for the time has unlimited divisions), this solution is no longer adequate (184: Phys 263a15–22).

The observation that time as well as space is infinitely divisible only raises the further question of how we can endure through a finite stretch of time, if every such stretch contains limitless parts. Instead of one infinity to traverse, we have two: if AB is impenetrable, T is unendurable.

Aristotle is right: no Zenonian will be greatly moved by the solution of Physics Z 2. Aristotle himself suggests that we ignore AB and consider progress through T by itself; Zeno, I suspect, would have preferred to consider AB alone, without reference to T. Indeed, I am inclined to think that the reference to a finite time T did not occur in Zeno’s original paradox: Zeno considered it impossible to touch infinitely many points; the impossibility is contained in the infinity of points, and factors of time are impertinent. Time is not, and need not be, mentioned in (2).⁸

After recanting his remarks in Physics Z 2, Aristotle essays a second solution to the Dichotomy; and his second solution suggests a third reason for upholding (2). Thus: ‘If b is to touch infinitely many ais, then an infinity of points must actually exist on AB; but there cannot actually be infinitely many existent points in a finite space.’ That argument for (2) is of little intrinsic interest; but Aristotle’s second solution to the Dichotomy warrants a moment’s attention.

Here is the text:

Hence we must say when asked if it is possible to traverse unlimited things—either in time or in distance—that in a way it is, and in a way it isn’t: if they exist actually, it is not possible; if potentially, it is. For someone moving continuously traverses unlimited things incidentally, not absolutely; for it is incidental to the line to be unlimitedly many halves, but its essence and its being are different (185: Phys 263b3–9).

That is an obscure paragraph. I take Aristotle to mean that b may touch infinitely many ais provided that the ais do not all actually exist. Thus (2) would be true if touching ai involved the actual existence of ai; but in fact, the ais need only exist potentially, and that they may do.

All that, I think, has little effect on any honest Zenonian: Aristotle simply asserts that b can touch the infinitely many ais, provided that he touches them ‘incidentally’ and they exist ‘potentially’. The Aristotelian jargon only partially disguises the fact that Aristotle is offering a denial of, and not an argument against, premiss (2).

But there is something of interest here: a sufficient condition for the ‘actual’ existence of ai is b’s stopping at ai. According to Aristotle, b can touch the ais as long as he does not stop at them, and hence actualize them. The keyword here is ‘continuously (sunechôs)’: b is safe, Aristotle opines, if he runs smoothly, leaving the infinite ais in their state of innocent potentiality. Tolstoy agreed: referring to the Achilles, which raises the same puzzle as the Dichotomy, he wrote: ‘The ancients regarded, this as an unanswerable dilemma; its absurdity lies in the fact that the progress of Achilles is calculated on units with stoppage between, while it is in fact continuous’ (War and Peace, bk 12, ch. XXII).

Consider a runner c who, like b, is set to traverse AB. c is allowed 2T for his performance; and he determines to produce a staccato run. Thus in ½T he runs from A to a1; then he rests for ½T at a₁. In the next ¼T he runs to a₂, and then rests for ¼T at a₂. In general, he takes, like b, T/2ⁿ to traverse the interval a_n-₂ a_n; but, unlike b, he rests for T/2_n at each a_n.

Aristotle will allow b to reach B, but will deny c his goal; for c’s rest periods involve the impossible actualization of the infinitely numerous ais. And, of course, though we meet b every day, we do not come across staccato runners like c. Much modern discussion of the Dichotomy has in fact focussed on staccato performances; and a central problem has been to determine the truth of (2) if the performances are discrete or staccato in the way in which c’s is. We might, I think, intelligibly uphold (2) for c while rejecting it for b. Yet if that view seems reasonable, we have as yet no reason for accepting it. Aristotle’s talk about actualized points is unconvincing; and no other argument yet allows us to distinguish between b and c in respect of (2). ‘Intuition’—the kind name for untutored prejudice—favours b’s chances above c’s; but intuition is a fool’s guide in this as in every other branch of philosophy.

Aristotle’s double discussion of the Dichotomy is meritorious but not conclusive; and I turn now to the fourth of the seven reasons for maintaining premiss (2). It is comfortably simple: ‘Infinite sequences of tasks have, by definition, no last member; and it is, trivially, impossible to complete a series of operations none of which is the last operation.’

Both premisses in this argument are false. The sequence actually employed in the Dichotomy does indeed lack a last member; but Zeno could easily have provided a sequence with both a last and a first member, as the following diagram shows:

If b is to traverse AB, he must touch each of the infinitely many points a₁, a₂,…, a,…a′₁, a′₂. His first step is from A to a₁; his last is from a′₁ to B.

As for the second premiss, it owes the little plausibility it has to an equivocation: you might, I suppose, say that the ‘completion’ of a series of tasks is simply the performance of the last member of the series; I complete the crossword in entering the last light, I complete the book in writing the ultimate sentence. And in that sense of ‘complete’ (if it is really a sense at all), sequences with no last member cannot be completed. But the obvious sense of ‘complete’ does not yield that consequence: if S is the set of tasks {x₁, x₁,…x_n,…}, then b has completed S if and only if b has performed every xi. To complete a set of tasks is to perform all the tasks, not to perform a last task. From ‘b has performed every x_i’ we cannot infer ‘b performed one x_i after all the other x_is’ : even if S is finite, it need contain no last member; b may perform two, or three, or all of the x_is at the same time.

That simple reflexion may still some disquiet about the propriety of speaking of ‘completing’ an infinite sequence of operations; but it will leave some readers unsatisfied. Surely, they will feel, even if you do not need to perform a last task in S in order to complete your performance, yet you cannot complete S without coming to an end of your tasks; and your tasks, being infinite, have no end. Thus (2) is true; and its truth follows from the nature of completion: infinite tasks cannot, logically, be completed.

But that, too, is a bad argument; and it, too, trades on an equivocation. Someone who said ‘b cannot come to an end of his tasks’ might mean:

(3) (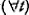) () (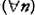if at t b has performed exactly n x_is, then there is an x_j that b has not performed by t).

He might, alternatively, mean:

(4) (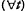) ()(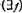has not by t performed x_j).

Now Zeno’s premiss (2) is equivalent to (4); and if S is infinite it is easy to demonstrate the truth of (3). But (3) and (4) are not equivalent; nor does (3) entail (4). By adding a further premiss:

(5) (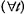) () (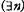by t b has performed exactly n xis) it is possible to deduce (4) from (3); but to assert (5) is precisely to deny that b can perform an infinite number of tasks—and that is the very proposition at issue. In short, to say that you can never get to the end of an infinite sequence either crudely reasserts that you cannot perform infinitely many tasks, or else observes (truly but irrelevantly) that whatever finite number of tasks you have performed, more yet remain; neither assertion has any tendency to prove the truth of (2).

The next reason for supporting (2) turns on the notion of progress: ‘If I perform a sequence of tasks, my performance is marked by a certain type of progress. I gradually tick off the tasks to be done, reducing their number until eventually all are finished and behind me. But if S is infinite, I can make no progress of that sort; for however many xis I have performed, I still have exactly as many xis left to perform: however many ais b has touched, he still has exactly as many ais left to touch. Performance depends on progress; infinitude mocks progress: (2), then, is true.’

The second premiss of this argument is true: if b has touched n ais, he still has infinitely many ais to go. In general, if S has infinitely many members, and S′ is a finite subset of S, then S-S′ has as many members as S. (The series <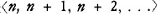,…>, where n is any natural number, can be put in one-one correspondence with the natural numbers.)

What of the first premiss? I confess I see little force in it. It decrees that progress in the performance of a sequence of tasks must consist in the performance of a successively larger fraction of those tasks. If that decree is accepted, then many performances will exhibit no progress. If I design to break every window in the quadrangle, I need not throw successive stones and do my job piecemeal; a single bomb, suitably placed, will blow in all the windows at once. And in any case, it is unnecessary to accept the decree. I may surely make progress in my plan to defenestrate the quadrangle, even if the actual blowing in of the windows occurs all at an instant: my progress might well be measured by the length of time still to elapse before my object is attained. Similarly, we may say (if we wish) that b is progressing in his task of touching all the ais, on the grounds that the time at which his task will be completed is getting nearer. In short, performance does not evidently require progress; and the notion of progress is in any case readily accommodated to apply to the performance of infinite tasks.

The sixth consideration advanced in support of (2) is more complex and more interesting. It invites us to consider the state of affairs that would hold were an infinite series of tasks to be successfully performed. Imagine a reading-lamp with a push-button switch for turning it on and off. The lamp is always either on or off; if it is on, a push of the switch turns it off; if it is off, a similar depression illuminates it. Take the lamp and depress its switch infinitely many times (first at noon, say; then at 12.30; then at 12.45…). Now consider its state after the switchings are completed, at 1.00 p.m Disregard any technological or physical obstacles which you may have met with and ask simply whether the lamp is on or off at 1.00 p.m. It cannot be on; for every time you switched it on you immediately switched it off again. It cannot be off; for every time you switched it off you immediately switched it on again. So it is neither on nor off. But by hypothesis it is always either on or off. The supposition of infinite switchings thus leads to an overt contradiction: premiss (2)—in a particular case at least—is established.⁹

That ingenious argument raises many questions; I shall not consider them in their generality, but instead construct a parallel argument for the Zenonian runner, and consider the credentials of that. ‘Zeno’s runner, b, has to complete the infinite set of tasks consisting of touching a1, touching a₂,…. Suppose that b manages to complete his tasks: where is he at the moment of completion? Not, alas, at B; for B is not a member of the set of a_is, and each task which b performs brings him to an a_i. Nor beyond B; for no 4 is situated beyond B. Nor, thirdly, is he short of B, between A and B; for suppose he is at C, between A and B; then there are a_is (infinitely many of them) between C and B, and he has not after all completed his tasks. But clearly, after the completion of the tasks b must be either at B or beyond B or short of B. Hence he cannot complete his tasks.’

The argument sounds plausible; but its conclusion is invalidly drawn. More formally stated, the argument puts up for reductio the hypothesis that b completes his infinite tasks at some time t; and it does indeed reduce that hypothesis to absurdity, by showing that there is no consistent description of b’s state at t. Hence we may conclude that there is no time at which b completes S. But from that we cannot infer that b does not complete S: he may complete S without there being any time which is the time of his completion, the last instant of his performance.

That contention may sound paradoxical; but in fact it only applies to the completion of S a general truth about the completion of any task or set of tasks. This general truth, which has nothing to do with the problems of infinity, was first grasped by Aristotle.¹⁰ Take any change; i.e., suppose that at t a changes from being 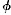to being non-, thus:

Consider the point of change, t. If t is the last point in a’s 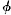ness and also the first point in a’s non- ness, then a is at t and a is non- at t. But that is impossible. Hence, in general, there can be no point that is both the first point of a’s non-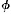ness and the last point of a’s 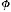ness. Suppose, then, that t is the first point of a’s non-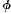ness. Suppose there is a point t’ prior to t which is the last point of a’s ness. Since time is continuous, there are points t₁, t₂,…between t′ and t′ (in fact there are infinitely many such points). At t₁ a is not 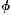, for t₁ is later than t’; and at t₁ a is not non- 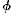, for t₁ is prior to t. But that is impossible. 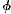Hence, in general, if there is a first point of a’s non-ness there is no last point of a’s ness.-An exactly analogous argument shows that if there is a last point of a’s ness there is no first point of a’s non-ness.

The application to Zeno is plain. There is a first point of b’s having completed the tasks in S-viz. the point at which he touches B. Hence there is no last point at which he completes the tasks in S; i.e., there is no last instant of his performance. That is no paradox: it simply brings out a general feature of all change: change can occur without there being a last moment of the unchanged state.

Thus the illustration of the lamp does show something about the logic of infinity; but it does not show that (2) is true. And I turn to the seventh and final argument for (2). The situation in which a performer of infinitely many tasks finds himself can be represented as a progress along an asymptotic curve:

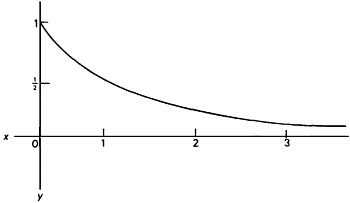
In the Zenonian case, the curve plots b’s distance from B, the x-axis representing that distance, the y-axis marking off the ais. The curve constantly approaches 0 but never reaches it. In general, progress via an infinite sequence of operations can be represented by an asymptotic line on a graph; and the discontinuity or gap between the line and the y-axis provides a puzzle; for it appears to mark a gap in the causal nexus of events. The runner’s progress through the ais is surely causally connected to his arrival at B; yet there is an unbridgeable gap between his arrival at the successive ais and his arrival at B.

Thus, first, there is always a physical gap between b’s position at the end of any run to an ai and his goal. How can causation send its spark across that spatial chasm? Second, there is no event among the touchings of the ais, which may be linked to the arrival at B; for any causal chain would bind the arrival to the last touching, and there is no last touching. How can a causal chain hold firm when there is no link locked to its last link? Third, consider the period T during which b travels from A to B. There is no last instant of b’s travelling, and hence no last instant in T. Let t be the first instant after T: given the details of b’s progress we can say for any instant within T exactly where b will be: at ti he will be at ai. Yet we cannot in the same way predict where b will be at t. (Reconsider the lamp: the plan to switch it on at 12.30, off at 12.45, and so on enables us to predict the lamp’s state at any time between 12.00 and 1.00; it does not license a prediction for 1.00.) How can a causal law cover that hole in the path of predictability?

Thus we have a seventh reason for upholding (2) : ‘If (2) were false, the great chains of causation would snap’.¹¹

The argument deserves a longer presentation than I can give it here. I content myself with three summary observations. First, the argument does not show the truth of (2); at most it shows that (2) is true in a Laplacean world, where every event is causally determined by its predecessors; and no one has yet shown that our familiar world is Laplacean. Perhaps there are causal hiatuses; many philosophers and scientists hold that there are.

Second, the argument is stated too grossly. In the case of some infinite performances there seems no difficulty in formulating causal laws that ‘bridge the gap’. The Zenonian runner provides such an example: given that he starts from A and proceeds at uniform speed through all the ais, we can predict that he will be at B at a given time after his departure from A. The fact that the ais are infinite and the distinct fact that no ai is contiguous to B have no bearing on the question: causal ‘chains’—a poor metaphor at the best of times—do not have to link events to their immediate neighbours; they can bind events together even if immediate neighbours are lacking.

Third, it is by no means clear that in any infinite performances there will or must be causal ‘gaps’. Causal laws are empirical hypotheses; as far as I can see, nothing in the description of the infinite switchings of the lamp, or in any other infinite performance, rules out any causal hypothesis. Switch the lamp off at t1, on at t2; and so on. Is the state of the lamp at t predictable? Is it causally determined by its earlier states? Those questions cannot be answered a priori. Suppose that numerous experiments of such switchings were carried out, and that in all of them the lamp was found to be on at B; then we should have reason to favour the causal hypothesis that the lamp’s state, after infinite switchings of the sort described, was on. Of course, a different result might be obtained: we might always find the lamp off; or there might be a random selection of offs and ons. Of course, we do not know, now, what the state at B would be. Of course, we shall never be able to conduct any such tests as those I have imagined. But those points are irrelevant: the seventh argument purports to show that only (2) will shield us from a world of random happenings. That is not so; and the notion of causation does not, I think, help us to ground our desire to believe (2).

I believe (2) to be false: of the many arguments designed to support (2), all are wanting in one or more particulars. But I cannot show that (2) is false; indeed, the reason why Zeno’s Dichotomy is so fascinating an argument is to be sought in (2): men want to believe (2); they cannot believe that we possess infinite powers; and they keep producing ever more ingenious arguments in favour of Zeno. For all that, until a new batch of arguments comes forward I shall continue to reject Zeno’s conclusion by rejecting (2).

(c) Achilles and the tortoise

The second paradox in Aristotle’s list is the Achilles:

Second is the one called Achilles. This says that the slow will never be caught in running by the fastest. For the pursuer must first get to where the pursued started from, so that it is necessary that the slower should always be some distance ahead (186: Phys 239b14–8 =A26=26 L).

Take a racecourse, AB, of indefinitely great length. Let Achilles be placed at A; let the tortoise—as we have come to know his opponent—be placed at any point C between A and B; and at t let Achilles and the tortoise each begin to move towards B. (The paradox says—and need say—nothing about their relative speeds, about the absolute speed of either, or about the uniformity of either’s progress.) Suppose that Achilles does catch up with the tortoise; i.e., that there is some point P on AB such that at some time t′ after t both Achilles and the tortoise are at P. Since the tortoise has been moving towards B, P is between C and B, thus:

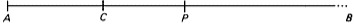
It follows that ‘the pursuer must first get to where the pursued started from’; i.e., that at some time between t and t′ Achilles is at C. Now when Achilles is at C, the tortoise is at some point, C₁, between C and B; but clearly Achilles must reach C₁ before ′; and when he is at C₁, the tortoise is already ahead, at C₂, between C₁ and B. And in general, if Achilles is at C_i, the tortoise is already at C_i+1, one step ahead of him. Thus ‘it is necessary that the slower should always be some distance ahead’, and Achilles can never catch the tortoise.

According to Aristotle, the Achilles paradox is merely a twopenny coloured version of the Dichotomy. Achilles is dramatized (tetragôdoumenos), but at bottom ‘this argument is the same as the Dichotomy (only differing in that the added magnitude is not divided in half)…so that it necessarily has the same solution’ (Phys 239b18–20; 25– 6). Most modern scholars disagree with Aristotle; at all events, the Achilles is regularly discussed at length and in its own right, whereas the Dichotomy is regularly ignored. (Most of the arguments about infinite performances which I have examined under the rubric of the Dichotomy were originally advanced in connexion with the Achilles.) And at first sight, things do seem to go against Aristotle: according to the Dichotomy, Achilles can never reach the tortoise’s starting position; according to the Achilles, even if he could do so, he could never catch the tortoise; in the Dichotomy, the race has a fixed finishing post, which can never be reached; in the Achilles, the finishing post itself is perpetually receding. Achilles, it seems, has double the toil and trouble of his undramatic counterpart in the Dichotomy. He cannot move; and if, per impossibile, he could, he would never reach his goal.

Nevertheless, a closer inspection of the Achilles vindicates Aristotle’s judgment: the paradox, if not identical with the Dichotomy, is no more than the Dichotomy with an unharmonious coda.

The last step of the argument is invalid. From:

(1) For every i, if Achilles is at C_i, then the tortoise is at C_i+1, Zeno invites us, in effect, to infer:

(2) For every point p on AB, if Achilles is at p, the tortoise is at some point p′ between p and B.

Now (1) is true; and Zeno’s argument shows it to be true. And (2) does imply that Achilles never catches the tortoise. But (2) does not follow from (1). (2) could be inferred from the conjunction of (1) and:

(3) For every point p on AB, there is an i such that C_i is between p and B.

But clearly (3) is not available to Zeno. Every C_i is, by construction, between C and the hypothetical meeting point P; for C_i is simply the point on AB where the tortoise is at the time when Achilles is at C_i-₁. Thus on the twin assumptions that the tortoise never ceases to move and that Achilles’ speed is finite, for no i does C_i=Ci-₁. But if C_i=P, then C_i=Ci-₁; hence for no i does C_i=P. Evidently, no C_i is between P and B. Hence every C_i is between C and P. It follows that Achilles and the tortoise never meet at any C_i, as (1) says. But that conclusion is now seen to be the merest triviality: the two runners will never meet at any point before their first meeting point. From this, nothing like (2) follows; from the fact that they do not meet before they meet, we can scarcely infer that they never meet.

Aristotle saw all that very clearly: ‘when [the tortoise] is ahead, he is not caught; but nevertheless he is caught if you grant that one can traverse a limited distance’ (Phys 239b27–9). According to Aristotle, (1) is true but trivial. How, then, can we get any paradox out of the Achilles? Only, Aristotle implies, by denying that Achilles can traverse the finite distance AP. And how might Zeno propel us towards such a denial? Only, Aristotle implies, by adducing the considerations that he advanced in the Dichotomy. Thus (1) brings out, in a clear enough fashion, the fact that before Achilles reaches the tortoise he must touch infinitely many points; and it is easy to see from (1) that however close to the tortoise Achilles may be—however many Cis he may have successively touched—he still has infinitely many Cis still to touch before he reaches P. And such infinite performances are, Zeno invites us to suppose, impossible.

That manoeuvre reduces the Achilles to the Dichotomy; and any objections to the argumentation in the latter paradox will apply immediately to the former. I do not deny that the Achilles is both clever and elegant; but I agree with Aristotle that it raises no philosophical difficulties which its more prosaic predecessor has not already flushed out.

(d) The arrow

The third paradox of motion does break new ground. It is the Arrow. Aristotle’s brief description and curt dismissal read thus:

Third is the one we have just mentioned—that the travelling arrow is at rest. This comes about from assuming that time is composed of’nows’ (ta nun); for if that is not granted, there will be no deduction (187: Phys 239b30–3=A 27=28 L).

Aristotle refers back to the opening of Z 9, where the transmitted text reads as follows:

Zeno misargues; for if, he says, everything always rests or moves whenever it is against what is equal (kata to ison), and what is travelling is always in the now (en tôi nun), the travelling arrow is motionless (188:239b5–7=A 27=29 L).

After that brief report there is the same dismissal as at 239b30–3.

Two further, non-Aristotelian, texts may be adduced. Epiphanius gives the following report:

He [sc. Zeno] also argues thus: what is moving moves either in the place in which it is or in the place in which it is not. And it moves neither in the place in which it is nor in that in which it is not. Therefore nothing moves (189: advenus haereticos III. 11=18 L).

The second text, from Diogenes, repeats the argument in an abbreviated form (IX.72=B 4=17 L). Some scholars think that this dilemma is an independent Zenonian argument, the fifth paradox of motion; others, judging it feeble in itself, attach it to the Arrow: ‘Either the arrow moves in the place where it is, or it moves in the place where it is not; evidently it cannot move in the place where it is not; by the Aristotelian argument it cannot move in the place where it is: hence it cannot move.’ That reconstruction may possibly be right; but it has no ancient warrant. Moreover, the sources who ascribe the dilemma to Zeno are not unimpeachable; and elsewhere the dilemma is associated with the name of Diodorus Cronos.¹² I incline to the sceptical view that a later dilemma has been anachronistically fathered on Zeno. However that may be, I do not think that the dilemma is very exciting; and I shall confine my discussion to Aristotle’s text.

That text is hard enough, in all conscience. It offers Zeno two premisses:

(1) If a is ‘against what is equal’ at t, then either a rests at t or a is moving at t.

(2) If a is moving at t, then a is ‘in the now’ at t.

From these propositions we are invited to conclude that:

(3) If a is moving at t, a is not moving at t. And hence:

And hence:

(4) a is not moving at t.

(I have replaced Aristotle’s word ‘travelling’ (pheromenon) by ‘moving’ in (1) and (3); the terms are synonymous.)

The inference from (3) to (4) is valid; and it is worth noting that Zeno uses a subtle theorem of propositional logic later known as the Lex Clavia: if if P then not-P, then not-P. (The companion law, the Consequently Mirabilis—if if not-P then P, then P— was used in a celebrated context by Aristotle.) The move from (3) to (4) is, however, the only uncontroversial element in the paradox: all scholars recognize the obscurity in (1) and (2) and the difficulty in moving from them to (3); and many philosophers deny that (4) is sufficient to establish Zeno’s desired conclusion, that nothing moves. I shall first deal with (1) and (2).

(1) and (2) will not yield (3). Instead of (1) and (2) we might well expect:

(5) If a is ‘against what is equal’ at t, then a rests at t.

(6) If a is moving at t, then a is ‘against what is equal’ at t.

If we add the further premiss:

(7) If a rests at t, then a is not moving at t, we can validly infer (3). Premiss (7), which may well seem a thoroughly trifling proposition, is easy enough to supply; but (5) and (6), neither of which follows from (1) and (2), surely need explicit statement. Scholars have accordingly emended the text of the Physics so as to produce (5) and (6).

The simplest means of producing (5) is the excision of the words ‘or moves’ (ê kineitai) from 239b6; then (1) vanishes from the argument and is replaced by an explicit statement of (5). (6) might be derived from (2) in conjunction with:

(8) If a is ‘in the now’ at t, then a is ‘against what is equal’ at t. It is possible to introduce (8) into Aristotle’s text; but it is perhaps preferable to treat (8) as a suppressed premiss. Zeno states (2) and expects us to infer (6) by way of (8).¹³

Thus I suggest that Aristotle’s text originally presented (5) and (2) explicitly, and expressly inferred (3) from those two premisses. And I suggest that Zeno’s original argument started from (5), (2) and (8); that it first inferred (6) from (2) and (8); that it then inferred (3) from (5), (6) and (7); and that it finally inferred (4) from (3), concluding that nothing moves. The textual suggestions are, I think, of no great importance: what matters is that Zeno intended us to reach (3), and hence (4), from (5) and (6).

What, then, is the precise sense of Zeno’s premisses? In particular, how are we to understand the two odd phrases ‘in the now’ and ‘against what is equal’? ‘The now (to nun)’ is Aristotle’s standard term for an instant of time; but it makes no sense to say, baldly, ‘a is at t’ where t names some instant: I may be in a place, but I cannot simply be ‘at a time’. We might construe ‘is (esti)’ strongly, as ‘exists’; or, better, we might take it as a verb-variable, so that ‘a is in the now’ means ‘a s at t’—for some suitable verb 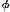and some definite instant t. (Aristotle says ‘in the now (en tôi nun)’; I say ‘at t’: some philosophers find a significant difference here; but I think that ‘at’ is simply the appropriate English translation of ‘en’.)

The commentators all gloss ‘is against what is equal’ by ‘occupies an equal space’ ; and the gloss is surely correct. Most of them add that ‘an equal space’ is elliptical for ‘a space equal to its volume’; so that ‘a is against what is equal’ becomes ‘a occupies a space equal to its own volume:

No          Creature          loves          an          empty          space;         
Their Bodies measure out their Place.

I accept that explanation: nothing else will give Zeno an argument of any plausibility.¹⁴ Thus interpreted, are Zeno’s premisses true? Premiss (2) has become:

(2*) If a is moving at t, then there is some instant t’ such that at t a is ing at t’.

And that is a tautology. The suppressed premiss (8) reads:

(8*) If there is some instant t’ such that at t a is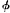 ing at t’, then at t a occupies a space equal to its own volume.

That is a peculiar observation; and I cannot divine why Zeno should have propounded it. Indeed, the very notion of being ‘in the now’ seems only to add an unnecessary complication to Zeno’s argument; for (6), which has now become:

(6*) If a is moving at t, then at t a occupies a space equal to its own volume, can be justified on far less mysterious grounds: it is a necessary truth that everything always occupies a space exactly equal to its own volume; i.e., that for any object x and time t, the volume of space occupied by x at t is equal to the volume of x at t. For what is the volume of an object if not the amount of space it occupies? But then whether or not a is moving at t, a is ‘against what is equal’ at t; hence (6) is necessarily true.

What, then, of premiss (5)? If that is true, then Zeno has reached (4) and we are potentially in trouble. (5) now reads:

(5*) If a occupies at t a space equal to its own volume, then a rests at t.

Some philosophers hold that (5*) is not even coherent, let alone true. According to Aristotle, ‘at an instant, it is not possible for anything to be either in motion or at rest’ (Phys 239bl; cf. 234a32). Rest is a matter of endurance: things rest for a period of time; they cannot intelligibly be said to rest at a point in time. Aristotle has a multitude of followers. The question is usually discussed in connexion with Zeno’s conclusion, (4); and I shall follow the custom. For at step (5) Zeno is easily and trivially defended; we need only replace (5*) by:

(5+) If a occupies at t a space equal to its own volume, then it is not the case that a is moving at t.

Indeed, (5+) not only evades the captious objection about rest; it also enables Zeno to dispense with the additional premiss (7): (5+) and

(6*) together entail (3) with no more ado.

Those many thinkers who agree with Aristotle that ‘at an instant, nothing moves’ are obliged to accept (5+). And (6*) is certainly true. Since (5+) and (6*) entail (3), it seems that Zeno is vindicated: the moving arrow does not move.

(e) Movement in a moment

Russell, for one, happily assents to (4): Zeno, he says, did prove that ‘we live in an unchanging world, and that the arrow, at every moment of its flight, is truly at rest. The only point where Zeno probably erred was in inferring (if he did infer) that, because there is no change, the world must be in the same state at one time as at another.’ In short, (4), far from being a monstrous paradox, is ‘a very plain statement of a very elementary fact’. But (4) does not entail the absence of motion. Rather, it enables us to see more clearly the real nature of motion: ‘People used to think that when a thing changes, it must be in a state of change, and that when a thing moves, it is in a state of motion. This is now known to be a mistake. When a body moves, all that can be said is that it is in one place at one time and in another at another.’¹⁵

Russell’s views are not entirely plain. I take it that he is saying three things about the inference from (4) to the denial of motion—strictly speaking, about the inference from:

(9) (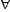 t) (if t is in T, then a is not moving at t),

to:

(10) a does not move during T. Russell says first that the inference is invalid; second, that a correct understanding of the concept of motion will reveal its invalidity; and third, that Zeno may well not have made or intended the inference. I find Russell’s view bizarre; on all three counts his reaction to the Arrow is mistaken. I take the points in reverse order.

First, then, all the ancient commentators treat the Arrow as part of Zeno’s general attack upon motion. They plainly regard (4) as the penultimate step leading to a negation of motion: I see no reason to dispute their view; and I suppose that Zeno ended his argument by explicitly saying ‘the arrow does not move’—indeed it is natural to construe Aristotle’s words at 239b7 in precisely that way.

Second, let us consider Russell’s account of motion. Russell naughtily describes it as a ‘static’ account; it can, I think, be formulated as follows:

(D1) a moves during T if and only if for every pair of distinct instants t₁ and t2 in T there is an instant t₃ between t₁ and t₂ and a pair of distinct places p1 and p₃ such as a is at p1 at t₁ and a is at p₃ at t₃.

That looks needlessly complicated. In fact its complexities are necessary, and must be multiplied (as the ancients realized) if we are to say of spinning tops that they move. Zeno in (4) talks of motion at an instant; does (D1) show such talk to be odd? does it show the inference from (9) to (10) to be invalid? Motion at an instant is easily defined:

(D2) a is moving at t if and only if for some T t is within T and a moves during T.

Given (D2), (9) immediately implies (10): if (D1) and (D2) offer a correct account of motion, they do not thereby reveal the invalidity of the Zenonian inference. Quite the contrary. (I do not mean to imply that Zeno himself had in mind a Russellian account of motion. Nor do I think that there are just two ways of envisaging motion: the one given in (D1–2), and the one rightly rejected by Russell according to which motion is an intrinsic quality of the moving object, in much the way that triangularity is an intrinsic quality of a triangular object. My point is only that Zeno has nothing to fear from (D1).)

Finally, is the inference from (9) and (10), or from (4) to Zeno’s immobile conclusion, valid? It seems to me gratuitously paradoxical to deny its validity: if the inference is invalid then we must, in Bergson’s celebrated phrase, accept ‘the absurd proposition that movement is made of immobilities’.¹⁶ Every period of motion will consist of an infinite sequence of motionless states. Ordinary usage accustoms us to talk of ‘motion at an instant’: I can say that the car was travelling at 34 m.p.h. at the moment when the bus hit it; or that at 9.10 this morning I was cycling into College. And ordinary usage sanctions inferences of the relevant sort between statements of ‘motion at an instant’ and statements of enduring motion: if I claim to have been cycling between 9–05 and 9.15 I cannot consistently deny that I was cycling at 9.10; if the car moved steadily at 34 m.p.h. until it hit the bus, then it was moving at 34 m.p.h. when it hit the bus. Indeed, it is, I think, a general truth that if a ) s during T, then a is 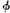ing at every instant t in T; and the acceptability of that proposition in no way depends on restricting the range of ‘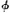’ to static verbs.

Why should any philosopher go against that natural mode of speech and argument? It cannot be said that the notion of ‘motion at an instant’ makes no sense; clearly it does make perfectly ordinary sense, and a sense that can be lucidly articulated in some such definition as (D2). Are there, then, hidden inconsistencies in the definition, or any that may replace it?

Some have argued as follows: ‘All motion has duration, and it always makes sense to ask, of a moving object, how long it has moved for; consequently, the notion of instantaneous motion is logically contradictory; and thus motion at an instant is impossible. ‘¹⁷ It is true that all motion involves duration: if a moves, then there is some period T such that a moves during T. And it does follow from this that instantaneous motion is a logical impossibility: ‘a 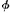s instantaneously’ means, I take it, that for some t a 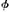s at t and for no T does a during T. In that sense some things, e.g., dying or learning—may or may not be instantaneous; and some things, of which change and all its species are the most conspicuous examples, are necessarily not instantaneous. But that does not show that the argument I have just considered is sound; for its final step involves a gross confusion: it is one thing to reject instantaneous motion, another to reject motion ‘at an instant’. To believe that motion at an instant is possible is to believe that ‘a moves at t’ is consistent; to believe that instantaneous motion is impossible is to believe that ‘a moves at t and for no T does a move during T’ is inconsistent. Plainly, those two beliefs are compatible: I uphold motion ‘at an instant’; but I also believe that if a moves then for some T a moves during T, and thus I reject instantaneous motion.

Aristotle provides a different argument against motion at an instant: ‘That nothing moves at an instant is evident thus: if it did, a thing could move both quicker and slower. Let N be an instant, and let the faster thing have moved the distance AB at N (en autôi). Now at the same instant (en tôi autôi) the slower thing will have moved a shorter distance, say AC. But since the slower has moved through AC in the whole instant, the faster will have moved [through AC] in a shorter time than this—so that the instant will have been divided. But that is impossible—hence it is not possible to move at an instant’ (Phys 234a23–31).

There are two related errors in this argument. The first is more evident in the translation than in the Greek: it consists in treating the term ‘instant (nun)’ as though it connoted a period of time, as though it were the last member of the set of terms that includes ‘year’, ‘day’, ‘hour’, ‘minute’, ‘second’. In English we do sometimes talk of things happening ‘in an instant’, and the same idiom is, I suppose, possible in Greek. But when we say ‘in an instant’ we are using the term ‘instant’ loosely, as a synonym for ‘split second’. Aristotle misses this point; and his argument depends on his construing ‘en tôi nun’ as though it were logically on a par with ‘en miai hôral’ (‘in an hour’).

The second, allied, error, is harder to exhibit clearly. It lies in Aristotle’s supposition that ‘the faster thing has moved the distance AB en autôi’. Behind that supposition lies the truism that if a has moved at all, then there is some distance through which a has moved. But from that truth Aristotle falsely infers that if a moved at t, then there is some distance through which a moved at t, say the distance AB. Now he might properly have inferred that there is some distance through which a was moving at t: at t a was moving from A to B if t falls within a period of constant motion T and if during T a moved from A to B. But from ‘a was moving from A to B at t’ we cannot infer ‘a moved from A to B at t’. Indeed, we cannot, in general, infer ‘a 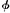ed at t’ from ‘a was 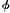ing at t’ (as, in another context, Aristotle in effect recognizes). I was eating breakfast at 8.45, but I did not eat breakfast at 8.45; I was reading a book at 10.30, but I did not read a book at

10.30. In general, if ‘a s’ entails ‘for some T, a s during T’, then ‘a is ing at t’ does not entail ‘a s at t’.

Thus Aristotle’s argument against motion ‘at an instant’ fails. And I know of no other, more compelling, argument.

I end this section by considering Aristotle’s objection to the Arrow: he says simply that ‘time is not composed of indivisible news’ (239b8). I take it that he means to ascribe the following argument to Zeno:

(11) (t) (if t is in T, a is not moving at t).

(12) T is composed of the set of instants it contains.

Hence:

(13) a does not move during T.

Here (11) represents (4), and (13) is a version of Zeno’s wholesale rejection of locomotion. And Aristotle objects that (12) is false.

I have two comments. First, we might disagree with Aristotle about (12) and yet agree with him that the argument from (11) to (13) is unsound. For the pattern of inference represented by (11)-(13) is invalid: it is a case of the ‘fallacy of composition’, the fallacy of arguing from ‘All the parts of X are F to ‘X is F’. (All the molecules that make up this glass of beer are tasteless, so the beer is tasteless.) Second, I see no reason to ascribe Aristotle’s argument to Zeno: Zeno infers (13) directly from (11). There is no need to invoke (12); and hence no occasion to charge Zeno with a fallacy of composition.

(f) The arrow blunted

If I am right, we cannot allow Zeno to reach proposition (4) without giving him his conclusion that motion is impossible. Since (6*) is true, we must reject (5+); and indeed (5+) seems to me to be clearly false: objects do, at every instant in their temporal careers, occupy a space exactly equal to their volume at that instant. And they do so even if they are in motion throughout their temporal careers. Why should anyone find that puzzling?

Some might argue as follows: ‘If we think of the arrow as occupying a given position for a time of zero duration, it will be obvious enough that it cannot be moving then: it will have no time in which to move.’¹⁸ That is a bad argument: a needs time to move from A to B; but a needs no time to be moving from A to B. The arrow is moving at t; it does not follow, as I have already said, that the arrow moves through some distance at t. If that argument lies behind (5+), then (5+) is not established.

But the argument makes no essential reference to the space which a occupies at t; and I suspect that a different consideration operated on Zeno’s mind. I suspect that he argued as follows: ‘If at t a occupies a space no greater than itself, then a has no room in which to move. Moving involves the transition from one place to another, and hence occupancy of more than one place. But at t a occupies just one place, viz. the place marked out by its own boundary. ‘That argument too is bad; and the grounds of its badness have already been presented: if a moves, then there are two points, A and B, such that a moves from A to B; and if a is moving at t, there are points A and B such that at t a is moving from A to B. But it does not follow that if a is moving at t, then there are points A and B such that at t a moves from A to B. Similarly if I smoke my pipe, there is a plug of tobacco which I consume in the process; and if I am smoking a pipe at t, then there is a plug of tobacco which I am consuming at t. But it does not follow—and it is not true—that if I am smoking a pipe at t, then there is a plug of tobacco which I consume at t.

It is perhaps worth setting out in one paragraph the various facts about motion which I have tried to express and to deploy. First, motion requires duration: ‘a moves’ entails ‘For some period T, a moves during T’. Second, motion requires extension: ‘a moves’ entails ‘For some distance AB, a moves from A to B.’ Third, motion ‘at an instant’ requires durational motion: ‘a is moving at t’ entails ‘For some period T, a moves during T’. Fourth, motion ‘at an instant’ requires motion through a space: ‘a is moving at t’ entails ‘For some distance AB, a moves from A to B’. Fifth, motion ‘at an instant’ does not require instantaneous motion: ‘a is moving at t’ does not entail ‘For no period T, a moves during T’. Sixth, motion ‘at an instant’ does not require instantaneous transition: ‘a is moving at t’ does not entail ‘For some distance AB, a moves from A to B at t’. There is evidently much more to be said about the logic of motion than that. But I believe that the six facts I have just listed are sufficient to show that the customary answers to Zeno’s Arrow are mistaken. Zeno’s argument is valid; but it relies on a false premiss.

There remains the possibility of an eleventh hour reprieve: so far I have taken Aristotle’s phrase ‘the now’ to denote an instant; and one of my complaints has been against the misconstrual of instants as small periods of time. Now some scholars suppose that Zeno’s argument should in fact be conducted entirely in terms of periods of time, and not at all in terms of instants. I do not think that Aristotle’s text encourages such a supposition; and I do not believe that we can seriously hope to recover a genuinely Zenonian argument behind a distorted Aristotelian presentation. Nonetheless, it is clearly desirable to see what difference might be made to the penetrative powers of the Arrow if it is freed from the notion of movement ‘at an instant’.

In the new version proposition (5) is replaced by:

(14) If a occupies during T a space equal to its own volume, then a is at rest during T.

As it stands, (14) seems plausible, or at least more plausible than (5). But in fact it is ambiguous. Its plausible sense is more explicitly given by:

(14a) If there is a place p equal to the volume of a such that at every instant t in T a occupies p, then a is at rest during T.

Indeed, (14a) is not only plausible: it is evidently true. Clearly, however, (14a) and (6) do not together entail (4). To secure the entailment, (6) too must be replaced by a proposition talking about periods of time. The proposition required is:

(15) If a is moving during T, then there is a place p equal to the volume of a such that at every instant t in T a occupies p. And just as (14a) is evidently true, so (15) is evidently false.

If (14) is read as (14a), the Arrow has no penetration. The alternative reading of (14) is:

(14b) If at every instant t in T there is a place p such that a occupies p at t, then a is at rest during T.

A suitable replacement can be found for (6) which, together with (14b), entails (4). And that replacement will be true. But now (14b) turns out to be false; for the antecedent of (I4b) is compatible with there being distinct places p1, p2…which a occupies at distinct instants t1, t2…in T; and occupancy of distinct places during T is incompatible with rest during T. Thus if (14) is interpreted as (14b) the Arrow gets no further. And I conclude that the proposal to read Zeno’s paradox in terms of periods of time rather than in terms of instants has no philosophical merit. Not only does it fail to give Zeno a better argument; it also fails to raise any interesting philosophical puzzles.

Let me end my discussion of the Arrow with two negatively polemical remarks. It is usually supposed.that Zeno’s paradox carries with it some philosophical theory about the nature of time; and Zeno’s commentators regularly adduce rival theories in the course of their reflexions upon it. My discussion has shown the falsity of that common supposition; for in expounding and criticizing the Arrow I have neither explicitly nor implicitly invoked any theory of time. In particular, I have not accused Zeno of treating time as being ‘composed of instants’; nor have I ascribed to him the view that time is made up of ‘atomic minimal parts’; nor have I made him assume that motion proceeds cinematographically. The paradox, as we should expect and desire, is innocent of any such theories: it presupposes only the two harmless and common notions that there are instants, as well as periods, of time; and that things move, if at all, at instants.

Many scholars find an architectonic structure uniting Zeno’s four surviving paradoxes of motion: the paradoxes form a dilemmatic attack upon movement, the Dichotomy and the Achilles supposing that time and space are infinitely divisible, the Arrow and the Stadium supposing that there are indivisible spatial and temporal quanta. My account of the Arrow seems to me to have revealed the falsity of that neat fantasy.

(g) The stadium

The fourth and final paradox is the Stadium:

[i] The fourth is the one about equal bodies which move alongside equal bodies in the stadium from opposite directions—the ones from the end of the stadium, the others from the middle—at equal speeds, in which he thinks it follows that half the time is equal to its double, [ii] The misargument consists in requiring that [a body travelling] at an equal speed travels for an equal time past a moving body and a body of the same magnitude at rest. That is false, [iii] E.g., let the stationary equal bodies be AA; let BB be those starting from the middle of the As (equal in number and in magnitude to them); and let CC be those starting from the end (equal in number and in magnitude to them, and equal in speed to the Bs). [iv] Now it follows that the first B and the first C are at the end at the same time, as they are moving past one another, [v] And it follows that the C has passed all the As, and the B half; [vi] so that the time is half, [vii] for each of the two is alongside each for an equal time, [viii] And at the same time it follows that the first B has passed all the Cs. [ix] For at the same time the first B and the first C will be at opposite ends, [x] being an equal time alongside each of the Bs as alongside each of the As, as he says, [xi] because both are an equal time alongside the As. [xii] This is the argument, and it rests on the stated falsity (190: Phys. 239b33–240a18=A 28=35 L).

The outline of that argument is clear enough. We have three equinumerous groups of bodies in a stadium, and the bodies are all equal in size. How many bodies each group possesses is not stated: the number is immaterial to the argument; and I shall take the simplest case, that in which each group contains just two bodies.¹⁹ Aristotle does not say that the members of each group are contiguous and arranged in a row (like the carriages of a railway train); but the argument plainly requires that assumption. One row of bodies, the As, is stationary. The Bs and the Cs move; and I shall refer to the leading B and the leading C as B1 and C1.

Aristotle gives, in [i] and [iii], a description of the stadium before the Bs and Cs begin their movements. I shall call this the starting position. Then [iv]–[x] list three things that ‘follow’ once the moving bodies have left the starting position. Let us call the starting time t1; then at some later point, t2, the bodies will be in what I shall call the crucial position. And if we consider what has happened during T, the interval between t1 and t2, we shall (according to Zeno), be faced with paradoxical or contradictory results. The problems of interpretation are thus three: first, to determine the starting position, at t1; second, to determine the crucial position, at t2; third, to discover what paradox is supposed to arise from our consideration of T, and how it is supposed to arise. The problems cannot be tackled separately; but it helps, I think, to begin by looking at the second of the three things that allegedly ‘follow’.

That second result is stated in [v]–[vii], which describe, or partially describe, the state of the stadium at the crucial time, t2. The description contains a vagueness; but I shall simply assume that the phrases ‘the B’ and ‘the C’ in sentence [v] denote the first B and the first C. Thus sentence [v] asserts that at t2 the first C has passed all the As and the first B has passed half the As; C1 has passed two As, B1 has passed one A. Given that the Cs and the Bs are proceeding at the same speed, we can infer that at some time prior to t2—call it, for the moment, tx—the stadium looked like this:

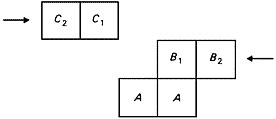
fig.1

As far as t2 goes, each of the following two diagrams seems to be consistent with the words of Aristotle’s description:

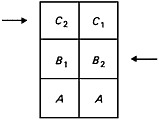
fig 2.1

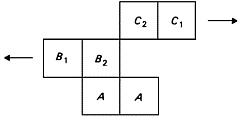
fig 2.2

Now Zeno infers in [vi] that ‘the time is half’. The obvious expansion of this reads: ‘the time taken by B₁ to get from its fig. 1 position to its new position is half that taken by C₁ to get from its fig. 1 position to its new position’. And Zeno’s argument for that, in [vii], glosses as follows: ‘In the interval between fig. 1 and the new position, B₁ has passed half as many As as C1 has; and both B₁ and C1 are travelling at the same speed.’ That reasoning allows us to fix on fig. 2.1 as the correct diagram for t₂.

Let us now glance briefly at the first result, stated in [iv]. I assume that the time of this result is the same as the time of the second result, i.e. t₂. The run of the text favours the assumption; and if we introduce a further time I see no way of reconstructing any argument. At t₂, then, B₁ and C1 are ‘at the end’. That phrase is wholly opaque. Four glosses at least are possible; and three of those glosses produce a plurality of diagrams. But given that fig. 2.1 represents the stadium at t₂, we can limit the choice to two diagrams, (a) If ‘at the end’ means ‘at the [opposite] end[s of the As]’, then the diagram must be fig. 2.1 itself, (b) If ‘at the end’ means ‘[each] at the end [of the other’s row]’, the diagram must be:

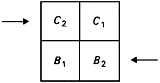
fig. 3

One manuscript has a reading which shows that fig. 3 represents an ancient interpretation; and since we do not want the second result merely to repeat the first, we should clearly plump for (b) and fig. 3.

We have thus identified the ‘crucial position’ as the position diagrammed in fig. 2.1, and it is an obvious conjecture that fig. 1 represents the starting position at t1. Can that conjecture be supported from the text?

Aristotle describes the starting position twice, in [i] and in [iii]. The latter sentence adds something to the former: it specifies that the Bs start ‘from the middle of the As’. In fig. 1 they do; and the Cs similarly start ‘from the end [of the As]’. That confirms that fig. 1 represents the starting position of the three rows at t1.

There is an objection to my reconstruction. If the bodies start in the position depicted in fig. 1 they will never reach the position of fig. 2.1; it is logically impossible, given the conditions Zeno stipulates, that both fig. 1 and fig. 2.1 should depict points in the careers of the Bs and Cs. But that objection is not fatal: Zeno, after all, is trying to find contradictions in the concept of motion; and we should not necessarily be dismayed to find that his paradoxes represent as achieved what in reality and logic is impossible. The question, then, is not: Can fig. 1 yield fig. 2.1? It is: Can Zeno have thought, or have made it seem plausible to think, that fig. 1 yields fig. 2.1? And we might attempt to answer that question by looking at the third result, sentences [viii]–[xi].

Textually, that too is uncertain. In [viii], at 240a13, where I translate ‘the first B’, most manuscripts read ‘ta B’, ‘the Bs’, Given that reading, we should have ‘at the same time’—i.e. at t₂—the following position:

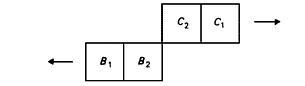
fig. 4

Now fig. 4, though a part of fig. 2.2., is not reconcilable with fig. 2.1. Nor can I find any plausible argument which makes use of fig. 4. Consequently, the majority reading must be rejected; and we must read either ‘to B (the B)’ or ‘to prôton B (the first B)’.²⁰

We now have an argument designed to show that the third result actually occurs: i.e., that:

(1) At t₂ B1 has passed both C₁ and C2. The text presents three sentences: sentence [ix] gives:

(2) At t₂ B1 is against C₂ and C₁ is against B₂. Sentence [x] gives:

(3) C₁ is alongside each B for the same length of time that it is alongside each A. Sentence [xi] gives:

(4) The Bs and the Cs spend an equal time alongside each A. Each of these three sentences allegedly supports its predecessor. Can anything be made of the argument?

Proposition (2) re-expresses the first result; and (1) follows easily enough from it and the initial description of the stadium. Proposition (4) is true, given the equal speed of the Cs and the Bs. Zeno, I suppose, argued thus: ‘If, as (4) says, B1 spends n time units against an A, and C1 spends n time units against an A, then plainly B₁ spends n time units against C1. Thus (3) is established.²¹ And since by t2 C1 has been alongside two As, it must—by (3)—have been alongside two Bs as well. Hence (2). Finally, given the starting conditions, we may deduce (1).’

Let me now try to restate Zeno’s whole argument in briefer and more perspicuous fashion. Suppose that at t1 the As, Bs and Cs are arranged as in fig. 1; and let the Bs and Cs move as specified. Let t₂ be the time at which C₁ has passed every A. Now C₁ has passed two As and hence two Bs; therefore fig, 2.1 represents the position at t₂. C₁ and B₁ each take n units of time to pass a body. Hence T, the period from t1 to t₂, is In units long. But in T B₁ has passed only one A. Hence T=_n. Hence T=½T.²²

The argument is not sound; but no version of the Stadium will yield a sound argument. It is not elegant; but Aristotle’s text does not suggest an argument with the elegance of the Achilles. I am inclined to think that this reconstruction is as close to Zeno as anything we can now produce; and I have expounded it at some length because it goes against the prevailing orthodoxy.

Different interpretations fall into two classes. First, there are those which agree that fig. 1 represents the starting position.²³ Such interpretations are only minor variants on mine; and they do not require special discussion. Second, there are those which abandon fig. 1 and adopt as a starting position:

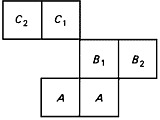
fig. 5

From fig. 5 the position of fig. 2.1 is easily reached; and in that lies the advantage of fig. 5 over fig. 1. For my part, as I have already intimated, I do not think that the advantage is very great. And on the other side, adoption of fig. 5 requires two changes in the text of 190, one of which is most implausible.²⁴ But I shall not pursue the question further: philosophically speaking, it matters little whether we choose fig. 1 or fig. 5.

(h) A most ingenious paradox?

Thus far I have concentrated on textual minutiae and little problems of interpretation; and it may well be wondered whether such attention is worth the paper it consumes. Aristotle dismisses Zeno’s argument curtly enough: Zeno, he says, wrongly assumes that the Cs will take as long to pass a moving B as they will to pass a stationary A. To most scholars the criticism seems both apt and conclusive: the paradox of the Stadium is philologically the most complicated of Zeno’s four arguments; philosophically it is the simplest and the least interesting—correct a childish mistake and all is in motion again. As Eudemus long ago saw, the puzzle is ‘very silly, because the misargument is obvious’ (fr. 106W=A 28).

Moved by those considerations, yet convinced of Zeno’s logical acumen, some scholars have inferred that Aristotle has misrepresented Zeno. Zeno’s argument, they say, in fact assumed that the As, Bs and Cs were minimal bodies, indivisible atoms of stuff. And it further assumed that the time taken for a B or a C to pass a stationary A was a minimal period of time, an indivisible temporal quantum. Given those two assumptions, the Stadium becomes a sound and a significant argument; for in effect it shows that absurd results follow from such an atomic attitude to matter and time. The Stadium, in short, is an early essay in the logic of the continuum.²⁵

I do not deny the philosophical interest of that sophisticated version of the Stadium paradox; but it was not Zeno’s. There is no evidence that anyone prior to Zeno had entertained the atomistic theory he is imagined to be attacking; and there is no reason why he should himself have invented such a theory simply to knock it down. The sophisticated Stadium has no historical support. Nor is the train of reasoning which introduced it very compelling. It is simply false that Zeno was a brilliant logician who would never have committed an elementary error—I have already discussed more than one argument indubitably Zenonian and of less subtlety than the Aristotelian Stadium. Indeed, a stronger case can be put: the Aristotelian Stadium, as it stands, is not immensely impressive; but it points to a crucial feature in the concept of locomotion. In short, the Aristotelian Stadium is philosophically important, and not ‘very silly’.

I offer the following argument as a refurbished account of the Stadium. ‘Our concept of motion is intimately connected with the two continua of space and. time. The concept is linked logically to those two notions in a variety of ways; two of the most important are mirrored in these two implications:

(1) If a moves past a sequence of n Fs and each F is k units long, then a moves nk units.

(2) If a moves for a period of T units at a constant speed of j.u.p.u., and covers m units in that time, then T=m/j units.

Now consider fig. 5 and fig. 2.1. Substitute B1 for a in (1) and (2): it is easy to show, by two applications of (1) and (2), that T, the period from t1 to t2, is equal to ½T. For the passage of B1 past the single A gives T=1k/j. And the passage of B1 past the two Cs gives T=2k/j. Thus the concept of motion implies (1) and (2); and (1) and (2) lead to contradiction. Hence the concept of motion is incoherent. Hence nothing can move.’

Such a reconstruction has two points in its favour. First, it relates the Stadium to Zeno’s general attack on motion; most accounts do not explain the connexion between the fourth paradox of motion and Zeno’s overall aim. Second, it provides an interesting argument against motion. For I am inclined to think that both (1) and (2) would have commended themselves to Zeno’s contemporaries, and do commend themselves to us in our unthinking moments. Our conception of locomotion is such that (1) and (2) seem to be implicit in it; yet (1) and (2) lead to unacceptable results. Zeno infers, I suggest, that the concept of motion is inconsistent; we may prefer to say that men who subscribe to (1) and (2) confusedly grasp the consistent concept of motion. The mode of expression is immaterial: if we are to move in the Stadium we must articulate a concept of motion which does not give rise to (1) and (2).

Aristotle’s answer to Zeno may now seem as unsatisfactory as in reality it is: according to Aristotle, Zeno ignores the fact that the As are stationary and the Bs moving. The criticism is not profound: where, we may ask, does Aristotle’s objection fit into the argument based on (1) and (2)? How would he reject those twin principles? What notion of movement would he supply which avoids (1) and (2)? I do not say that those questions are unanswerable; I do say that they are unanswered, and that that fact makes Aristotle’s reply to Zeno inadequate.

An adequate reply to Zeno, and an adequate account of motion, would focus on the truth that motion is a relational thing:’…it doth not appear to me that there can be any motion other than relative: so that to conceive motion, there must be conceived two bodies, whereof the distance or position in regard to each other is varied. Hence if there was only one body in being, it could not possibly be moved. This seems evident, in that the idea I have of motion doth necessarily include relation’ (Berkeley, Principles of Human Knowledge, § 112).

Motion, in brief, is relative not absolute. That slogan may mislead; and it is worth stating clearly two things that it does not imply. First, it does not imply the incoherence of ‘absolute’ motion in Newton’s sense: Newtonian ‘absolute’ motion is merely a privileged form of relative motion; for according to Newton a body is in ‘absolute’ motion if it is changing position relative to absolute space. (It is a further question whether anything can be made of absolute space.) Second, the rejection of ‘absolute’ motion does not require a wholesale change in our everyday language of movement. For though we do regularly speak as though motion were absolute, it is fairly simple to translate such talk into talk of motion relative to our human inertial frame, the earth: ‘he’s moving’ can regularly be taken as elliptical for ‘he’s changing position relative to (some point on) the earth’s surface’. (Regularly, but not, of course, always: in the enclosed world of an aeroplane or a ship we naturally take the enclosing vehicle as our reference frame; and Christmas cracker puzzles, such as the conundrum of the man running round the monkey, remind us that all is not plain sailing here.)

To say that motion is relative is to say no more than this: ‘a moves’ only makes sense if it is taken as elliptical for some two-place predication of the form ‘a changes position relative to b’. ‘a moves’ is comparable to ‘a leads’ or ‘a follows’; leading and following are relational notions, even though we often and intelligibly use the verbs without explicitly mentioning a relatum: and just as ‘a leads’ is elliptical for ‘a leads b’ so is ‘a moves‘ elliptical for ‘a moves vis-à-vis b’. There is, of course, nothing unusual in having such elliptical, absolute-seeming, uses for essentially relational verbs; in the case of ‘move’, however, there is a peculiar danger of taking the absolute-seeming use at face value, and inventing an absolute quality of motion to serve as denotatum for the absolute verb. (I suspect that this connects with the old Aristotelian view that motion is immediately perceptible, a ‘simple idea’: if we can simply see that a thing is in motion, surely motion is an intrinsic quality and not a relation?)

What bearing has the relativity of motion on the Stadium? It allows us to retain the essence of implications (1) and (2) while rejecting their cruel accidents. Thus, to take the case of (1), we shall have:

(1*) If a moves past a sequence of n Fs and each F is k units long, then relative to those Fs a moves nk units.

The plausibility of (1) carries over to (1*) and (1*) contains the truth which (1) strove in vain to express. Moreover (1*) has no hard consequences, once we realize that there is no contradiction between ‘a moves n units relative to b’ and ‘a moves m units relative to c’ (where b≠c and n≠m). For I may move relative to one thing while resting relative to another—there are a thousand everyday examples of that.

I do not claim that only a relative concept of motion will answer Zeno’s argument; but that such a concept is both correct in itself and sufficient to answer Zeno seems clear enough. If Zeno’s Stadium encourages us to clarify our conception of motion in that way, then that, I submit, is enough to make an honest argument of it. Zeno, of course, did not intend his Stadium to refute ‘absolute’ motion and elicit a relativized concept; and indeed he does not seem to have stirred any of his successors to develop such a sanitary notion. For all that, the Stadium does show, in a pointed and pregnant way, the need for a subtler concept of locomotion than we are apt at first sight to formulate. And that turns the paradox of the Stadium, in its plain Aristotelian form, into an argument of some significance.

(i) Two last remarks

I end my long consideration of Zeno’s paradoxes with two general comments.

First, what, we may wonder, is the connexion between the four paradoxes on motion and the Platonic schema into which I attempted to fit the paradoxes of plurality? We may always suppose that the arguments about motion, which Aristotle treats as a unitary group and which according to Elias constituted an independent Zenonian volume, were in their original form a separate publication. We might indeed conjecture that they were worked out later in Zeno’s life, the fruits of his intellectual maturity.

On the other hand, Plato names ‘at rest and moving’ as one of the set of opposites which Zeno proved to hold of ‘the many’ (Phaedrus 261D=A 13).Thus one case of the Platonic scheme will be: (Z7) (a) If P, then everything moves, and (b) if P, then nothing moves. Here (Z7a) will have required no special argument: evidently, the ‘many things’ which the pluralists admit do, all of them, move. And it is not vastly implausible to see the four paradoxes of motion as intended to support (Z7b). In that case, the paradoxes will, originally, have appeared in Zeno’s juvenile book, alongside the other arguments I have dissected; and some later editor will have assembled them in a little treatise of their own, preserving their philosophical content while divesting them of their original polemical form.

Second, what general portrait of Zeno emerges from these two chapters? My discussion has, I think, confirmed the view I sketched on an earlier page (above, p. 236). Zeno ‘put forward no view of his own but puzzled further about’ Eleatic issues (pseudo-Plutarch, A 23). Zeno was no original philosopher; he is not a member of the long line of thinkers stretching from Thales to Melissus, men of vast learning, wide pretensions, profound insights. Rather, he puzzled: negative, destructive, polemical, Zeno was the first of the ‘Sophists’. His aims were critical, not constructive; his methods subtle not solid. Yet from his Sophist’s quiver he drew a few darts of brilliance and acuity; and those darts have made him a prince of philosophers malgré lui.