XVI
Anaxagoras and the Nature of Stuffs

(a) Outlines of Anaxagoreanism

Anaxagoras’ book was available at the bouquineries in the Athenian agora (Plato, Apology 26E=59 A 35). Some infer that it was ‘read and understood without much difficulty’;¹ if that is so, times have changed: of all the Presocratics Anaxagoras is the most difficult. Thanks to Simplicius, we possess substantial portions of the first part of Anaxagoras’ work Concerning Nature;² and there is a rich doxography. But Anaxagoras’ views are of considerable complexity, his arguments subtle in conception; and his thought is often (or so I at least find) of a peculiarly elusive character.

I shall begin by offering a crude statement of what I take to be Anaxagoras’ fundamental tenets about the nature of the physical world. I shall first set them down, and then quote the several fragments in which I claim to find them expressed. The fundamental tenets are three:

(A) In the beginning, everything was mixed together.

(B) There is no smallest portion of anything.

(C) Now, everything is mixed together.

(Note that ‘mind (nous)’ is not included in ‘everything’ here: I shall leave nous out of the discussion in this chapter; it is readily separated from Anaxagoras’ physical theories, and separation makes for easier exposition.) I find these three theses in the following fragments:

All things were together [=A], unlimited both in quantity³ and in smallness; for the small too was unlimited [=B]. And since all things were together [=A], nothing was clear by reason of the smallness. For air and aether contained⁴ everything, both being unlimited. For these are the greatest items present in all things, both in quantity and in magnitude (197: B 1).

For neither of the small is there the least [=B], but there is always a less (for what is cannot not be)—but of the great too there is always a greater, and it is equal in quantity to the small. And in relation to itself each is both great and small (198: B 3).

These things being thus, it is necessary to suppose that there are many things of every sort in everything that is conjoined [=C], and seeds of all things having various aspects and colours and tastes (199: B4a).⁵

And men were compounded, and the other animals that have a soul (psuchê). And these men possess inhabited cities and cultivated fields, as we do; and they have a sun and a moon and the rest, as we have; and the earth grows for them many and various things, the most beneficial of which they gather into their dwellings and use. This, then, have I said about the separation—that it would have been separated not only by us but elsewhere too (200: B4b).

Before these things were separated off, since everything was together [=A], not even any colour was clear; for this was prevented by the commingling of all things [=A]—of the wet and the dry and the hot and the cold and the bright and the dark, there being much earth present and seeds unlimited in quantity and not like one another. For of the other things none is like any other. And these things being thus, it is necessary to suppose that all things are present in everything [=C] (201: B 4c).

And since too there are equal portions of the great and the small in quantity, for this reason too everything is in everything [=C]; nor can they exist separately, but everything shares a portion of everything [=C]. Since the least cannot be [=B], things cannot be separated nor come to be by themselves, but as in the beginning [=A], so now too everything is together [=C]. And in all things there are many even of the things that are separating off, equal in quantity in the greater and in the smaller (202: B 6).

The things in the one cosmos have not been separated from one another [=C], nor have they been cut off by an axe—neither the hot from the cold nor the cold from the hot (203: B 8).

In everything there is present a portion of everything [=C], except mind; and in some things mind too is present (204: B 11).

These are the central fragments bearing on Anaxagoras’ theory of physical nature. Thesis (B) is stated clearly enough; in the various statements of (A) and (C) I assume a synonymy among ‘everything is together’, ‘everything is (present) in everything’ and ‘everything has a portion of everything’. My first task is exegetical: what does Anaxagoras mean by ‘things’? The question is, surprisingly, difficult and controversial; and it calls for a section to itself.

(b) The nature of things

‘All things were together’: homou panta chrêmata ên. With those words Anaxagoras began his book (Simplicius, ad B 1). The Greek word ‘chrêma (thing)’ gives nothing away; and in any case Anaxagoras sometimes simply uses the pronoun ‘everything, (panta)’. The delicious suggestion that by ‘all things‘ Anaxagoras meant literally ‘all things’ is, alas, untenable: ‘all things are in all things’ will then imply that Anaxagoras is in my typewriter and Clazomenae in its keys; and those idiocies were evidently no part of Anaxagorean physics.

We might start by considering Anaxagoras’ examples of ‘things’. They are: air, fire (197); wet, dry, hot, cold, bright, dark, earth (201); hair, flesh (B 10); thin, thick (B 12); cloud, water, stone (B 16). The doxographers add such things as: gold, blood, lead (Simplicius, A 41); white, black, sweet (Aristotle, Phys 187b5= A 52). We do not, of course, know whether these latter examples actually occurred in Anaxagoras’ text.

Do the examples suggest any generic determination for the notion of a ‘thing’? Two suggestions have been widely canvassed. First, it is suggested that the Anaxagorean things are in fact the opposites: hot and cold, light and dark, wet and dry, and so on. Where we ordinarily speak of something’s being hot, philosophically-minded men may say that a thing has the property of heat or hotness, or that heat or hotness or ‘the hot’ resides or inheres in the thing. And it is those properties which Anaxagoras had in mind when he talked about ‘all things’. Such at least is the suggestion. But it is palpably false: hair and flesh, water and stone, are not properties or ‘opposites’; but they are used by Anaxagoras himself in illustration of his theory. A modified version of the suggestion has it that if X is in Y, then X, but not Y, is an ‘opposite’. That version fares no better: earth, according to 202, is ‘in’ things; and in any case, the formula ‘everything is in everything’ shows that if X is in Y then Y is in X. Specific talk of the opposites may profitably be dropped from the discussion of Anaxagoras’ theory of nature.

The second suggestion, far more complicated and influential, goes back at least to Aristotle:

But Anaxagoras says the opposite [to Empedocles]; for [he makes] the homoiomeries elements (I mean, e.g., flesh and bone and each of those things), and air and fire mixtures of these and of all the other seeds; for both of these are put together from all the invisible homoiomeries (205: Cael 302a31-b3=A 43).

The passage raises several questions: I want first to single out the ‘homoiomeries’ for attention; and I shall consider the simple suggestion, implicit in Aristotle and repeated ad nauseam by the doxographers, that Anaxagoras’ things are in fact homoiomeries.

Aristotle explains the term ‘homoiomerous’ in another passage:

For he [sc. Anaxagoras] posits the homoiomeries as elements—e.g., bone and flesh and marrow and the other things whose parts are synonymous (206: GC 314a18=A 46).

Thus an F is homoiomerous if the parts of F are themselves synonymous with the whole, i.e. if they are F: flesh is homoiomerous because parts of a lump of flesh are themselves flesh; hands are not homoiomerous, because parts of hands are not hands.⁶

It is not clear precisely what Aristotle means to ascribe to Anaxagoras. Most generously, we might imagine him to offer Anaxagoras the term ‘homoiomerous’, so that some lost part of Anaxagoras’ book will have said: ‘By “thing” I mean homoiomerous thing’. But there is no special reason to interpret Aristotle so strictly; and it seems, on linguistic grounds, improbable that Anaxagoras would have coined a word like ‘homoiomerês’.⁷ Most pinchingly, we might imagine that Anaxagoras gave no general description at all of his things: Aristotle read through his examples, saw that they were all what he would call homoiomeries, and hastily concluded that Anaxagoras meant to include all and only homoiomeries under his umbrella of things. There is a slight difficulty with this view: Anaxagoras’ examples include opposites or properties, and Aristotle more than once uses that fact in criticism of Anaxagoras’ theory (GC 327b21; Phys 188a6=A 52; Met 989b3=A 61). Now properties are not homoiomerous in Aristotle’s mind; and it is therefore a trifle hard to suppose that Aristotle eyed Anaxagoras’ examples and judged them all to be homoiomeries. The difficulty is not great; but it is enough to give some plausibility to a third way of understanding Aristotle’s ascription: Anaxagoras, we may suppose, did give some general characterization of his things, and that characterization seemed to Aristotle to fit his own notion of a homoiomery. Indeed, there is no reason why Anaxagoras should not have said something like this: ‘All things—I mean air and fire and flesh and blood and everything where the part is like the whole…’

Thus the notion of a homoiomery may point in a genuinely Anaxagorean direction; but the value of the pointer is modest. For the notion itself is neither as clear nor as precise as it appears to be. How are we to define homoiomereity? A first attempt might read:

(D1) A property P is homoiomerous if and only if if a has P then some part of a has P.

That is too weak: it will allow benches and buildings, swarms and schools, to be homoiomeries; and it is plain that they should not be included in the class. A stronger definition is:

(D2) A property P is homoiomerous if and only if if a has P then every part of a has P.

Now that, I suspect, does answer to Aristotle’s thought; but for us it is far too strong: it makes all Aristotle’s paradigmatic homoiomeries anhomoiomerous; for it is not the case that every part of a piece of flesh is itself flesh, since the atomic parts of ordinary stuffs do not share their properties.

(D2) can be emended—adding the word ‘macroscopic’ before ‘part’ might do. But it is better to abandon (D2) and to ask, more laxly, what sort of thing Aristotelian homoiomeries are supposed to be. The answer is plain: homoiomeries are stuffs; homoiomeries relate to substances as matter to formed individuals; the homoiomeries are the material of which substances are composed (e.g., Aristotle, Meteor 389b27; GA 715a11).

Thus I propose that we read Anaxagorean ‘things’ as stuffs; and I claim that the proposal is fundamentally Aristotelian.⁸ What of the obvious objection, that ‘the hot’, ‘the cold’, ‘the wet’ and so on are not stuffs?⁹ Here again I side with Aristotle: according to him, Anaxagoras mistakenly treats properties, like ‘the hot’, as substances; the criticism seems to me to be just, for the fragments reveal Anaxagoras doing exactly that. Moreover, Anaxagoras was not the only early thinker to substantialize qualities; on the contrary, such substantiation was, notoriously, a common feature of Greek thought (for a nice example see [Hippocrates], nat hom 3). In short, the occurrence of the opposites among the examples of Anaxagorean things shows not that those things are not stuffs but that Anaxagoras misidentified the opposites as stuffs.

I have not provided much argument for the suggestion that Anaxagoras, like his Ionian predecessors, has an ontology of stuffs. The proof of the suggestion must come in my exposition of his arguments.

(c) The seeds of the world

Before turning to those arguments there are some preliminary questions to be raised about Anaxagoras’ third tenet, that everything is now mixed together or that ‘everything has a portion of everything’. That tenet can now be expressed as follows:

(C*) For any pair of stuffs, S, S′: in every piece of S there is now a portion of S′.

In what sense can a portion of S′ be in a piece of S? The obvious suggestion is that the lump of S contains, scattered through its volume, particles of S′; those particles will be invisible to gross observation (for S does not wear the aspect of S′), and they will be multitudinous, or even infinite (for they permeate every part of S). Such a particulate view of matter is traditionally ascribed to Anaxagoras; and it seems to make sense. The ascription is supported by four props.

The first prop is the word ‘seed (sperma)’. Aristotle talks of the homoiomeries ‘and all the other seeds’ (Cael 302b2=A 43); and the word sperma is Anaxagorean: ‘seeds of all things’ ‘seeds unlimited in quantity’ are present in the primordial mass (199; 201).¹⁰ It is easy to imagine that ‘seeds’ of S are (minimal) particles of S: the original mass contains everything inasmuch as little seed-particles of every stuff are suspended in it like pollen in the summer air.

That is a tempting interpretation, but not an obligatory one. Sperma, in Greek, is as much a biological as a botanical term: where the word ‘seed’ suggests particles to us, the word sperma would not have done so to a Greek. The language of seeds does not imply a particulate theory of stuffs; and to say that X contains seeds of Y need mean no more than that Y may grow from X.¹¹

The second prop for particles is the word ‘unlimited’. According to Aristotle, Anaxagoras ‘says that the principles (archai) are unlimited (apeiroi)’ (Met 984a13=A 43; cf. Phys 187a25=A 52); Theophrastus repeated the assertion, with reservations (Simplicius, A 41); and it is a doxographical commonplace. Must not these ‘unlimited principles’ be an infinite set of minimal particles or atoms?

No. Aristotle, as his context shows, is thinking not of an infinity of particles, but of an infinity of kinds of stuff. Moreover, we almost certainly possess, in 197, the words that Aristotle is here interpreting: ‘All things were…unlimited both in quantity (plêthos) and in smallness’. The sentence plainly does not refer to an infinity of corpuscles, and Aristotle rightly did not so construe it; rather, he took Anaxagoras to mean that there was an unlimited quantity of kinds of thing: earth, air, stone, flesh, bone, blood, etc. Aristotle’s negative point is correct; but his positive interpretation is not. By ‘S is unlimited in smallness’ Anaxagoras means: ‘For any n and m, where m<n, if there is a portion of S of magnitude n units, then there is a portion of S of magnitude m units.’ Thus if S is ‘unlimited in smallness’ it follows that the portions of S are unlimited in number; for if two portions have a different magnitude, they cannot be identical. And that, I suggest, is precisely what Anaxagoras means by ‘S is unlimited in quantity’: for any n and m, where m>n, if there are n portions of S, then there are m portions of S (see below, pp. 33–7). That doctrine does not commit Anaxagoras to infinitely numerous discrete atoms of S; it does not commit him to an Aristotelian infinity of stuffs;¹² it does not commit him to the view that some portion of S is infinite in size—for S’s infinitely numerous portions may all be happily nested inside one another.

Third, consider Anaxagoras’ language when he talks of the composition of things and stuffs: things are ‘commingled’ (summignusthai: B 17) or ‘conjoined’ (sunkrinesthai: 199) or ‘compounded’ (sumpêgnustbai: 200; B 16). Those words surely suggest the amassing of discrete particles of stuff. Similarly, Anaxagoras uses ‘separate off (apokrinesthai: B 2; 201; etc.) and ‘separate out’ (diakrinesthai: B 5; B 12; etc.) to denominate the discrimination of sensible stuffs from the rough primordial mass; and such terms suggest an effluxion of particles.

Against that I have little to say but Boo: commingling and separating do not suggest to me the confluence or effluence of particles.¹³

The fourth prop for the view that Anaxagorean stuffs are particulate in structure is the strongest. The doxographers, who follow Aristotle in stressing the imperceptibility of Anaxagorean stuffs in the original world-mass, also follow Aristotle in explaining that imperceptibility in terms of the smallness of the stuff-particles. Stuffs, in the neat and anachronistic phrase of Aëtius, are composed of ‘intellectually contemplatable parts (moria logôi theôrêta)’ (A 46).¹⁴ We can imagine, but we cannot perceive, the fine particulate structure of chalk and cheese.

Here too we need not rely on doxographical interpretation: we have, again in 197, the original words in which Aristotle and his followers replied:

And since all things were together, nothing was clear by reason of the smallness. For air and aether contained everything, both being unlimited. For these are the greatest items present in all things, both in quantity and in magnitude.

‘Nothing was clear by reason of the smallness. ‘It is natural to explain the word ‘smallness’ by way of its first occurrence in 197: there it indicated small portions of stuff; here, accordingly, it is naturally taken in the same way, and the Aristotelian interpretation seems to be confirmed. But a portion of S is not a part of S; and portions, however small, need not be conceived of as particles. Moreover, we can find a better interpretation for the sentence ‘nothing was clear by reason of the smallness’.

Consider the word ‘greatest’ in the last sentence of the fragment. Anaxagoras’ point here is fairly straightforward: if we look about the world today we see that two stuffs, air and aether, are vastly more extensive than any others; consequently, Anaxagoras invites us to infer, air and aether must, in the original mixture, have ‘contained’ or dominated everything else. The ‘greatness’ of air and aether lies in the fact that the total amount of air and aether in the world is greater than that of any other stuff. Similarly, the ‘smallness’ of, say, gold, consists not in its being divided into minute particles but rather in the simple fact that there is very little gold in the world.

In the original mixture the proportion of gold or flesh was so small that it made no perceptible difference, as a glass of wine thrown into the sea makes no perceptible difference to the brine. (That, of course, is why the original mass has no colour (201): air and aether, themselves colourless, are large enough to absorb the colours of all the other stuffs commingled with them. A glass of Burgundy will not make the green one red.)

I conclude that we have no binding reason for ascribing to Anaxagoras a paniculate theory of matter. Moreover, there is one excellent reason for denying him such a theory.¹⁵ If every piece of S contains a particle of S′, and if every piece of a piece of S is a piece of S, then every piece of S is wholly composed of particles of S′.which is absurd. The inference is easy enough to grasp; and even if Anaxagoras had no notion of it (which I doubt), we must deny him particles if we are to give him a theory of matter consistent with his tenet (C*). Anaxagorean stuffs contain portions of all other stuffs; but those portions are not located at one or more points within the parent lump—they are mingled smoothly and regularly throughout its body. Any stuff contains every stuff; but the contained stuffs are not present by virtue of a mechanical juxtaposition of particles; they are present as the items in a chemical union.¹⁶ Every cloud contains a little silver; but the silver is not spread out as a lining: there is no part of the cloud which is pure, or even impure, silver.

A rough analogy may help. Artists may make a patch of their canvas seem green in either of two ways. First, and unusually, they may adopt a pointilliste technique, setting minute dots of blue next to minute dots of yellow: from a distance the effect is green; from close up we see adjacent spots of blue and yellow. Alternatively, they may mix masses of blue and yellow on their palette and apply the mixture to the canvas: the effect from a distance is green; and however closely we look at it, the effect is still green. No part of the canvas, however small, is painted blue; and no part yellow. For all that, the green on the canvas ‘contains’ blue and yellow; they are its constituents, and some chemical technique might, for all I know, be capable of ‘extracting’ some of the yellow from the artist’s green. Atomists are physical pointillistes: their world is made up of microscopical dots, individually indistinguishable to the eye. Anaxagoras was a painter of the traditional type: his world is made of stuffs mixed through and through, its components as invisible to the microscope as to the naked eye.

That conclusion allows us to solve a little puzzle in Anaxagorean scholarship. Anaxagoras’ theory of matter, it is said, ‘rests on two propositions which seem flatly to contradict one another. One is the principle of homoiomereity: a natural substance such as a piece of gold consists solely of parts which are like the whole and like one another—every one of them gold and nothing else. The other is: “There is a portion of everything in everything”.’¹⁷ That criticism misinterprets the principle of homoiomereity: the principle says, not that every part of a lump of gold is ‘gold and nothing else’, but that every part of a lump of gold has the same material constitution as the lump itself. If ‘everything is in everything’, then the lump of gold contains a portion of every other stuff. Hence every part of that lump contains a portion of every other stuff. Is there a contradiction, flat or curvaceous, here? Not, I think, if Anaxagorean stuffs are non-particulate. The view is certainly strange; but I see no logical inconsistency in it. In short, given a non-particulate theory of matter, Anaxagoras may safely maintain both (C*) and a principle of homoiomereity.

(d) Elements and compounds

Green is a compound colour; blue and yellow are simple or elemental. Are the stuffs in (C*) limited to elemental stuffs? Does Anaxagoras distinguish between elements and non-elemental stuffs? The doxography is clear enough: the homoiomeries are standardly called ‘elements’ (stoicheia: e.g., Cael 302a32=A 43) or ‘principles’ (archai: e.g., Met 984a13=A 43). If that does not quite suffice to distinguish elemental from non-elemental stuffs, two texts take that further step: the de Caelo asserts that ‘air and fire’ are not elements but ‘mixtures of the homoiomeries’ (302b1=A 43); and elsewhere Aristotle says that ‘they [sc. the Anaxagoreans] [say] that these [i.e. the homoiomeries] are simple and elements, and that earth and fire and water and air are compounds’ (GC 314a24=A 46). The former passage, as its context makes clear, is relying on 197. 197 does give a special status to air and aether (which Aristotle interprets as fire); but it surely does not imply that air and aether are compounds and not elemental. The second Aristotelian passage is, I suspect, no better based: Aristotle carelessly assumes that what, in his opinion, holds of two of the Empedoclean roots must hold for all four. At all events, I can find no fragment which clearly supports Aristotle’s view, or makes any distinction between elemental and non-elemental stuffs.¹⁸

‘But surely Anaxagoras must have realized that some stuffs are compounds of others: that bronze is made from copper and tin; that wine is a mixture of water, sugar, alcohol, and so on. Then why need his original mass contain bronze in addition to copper and tin, wine in addition to water, sugar and so on? At best such additions are otiose; at worst they are confused. In general, then, the original mass will contain only those stuffs which science shows not to be compounds of other stuffs.’

But what does that suggestion really amount to? If the original mass contains a portion of green then it contains, eo ipso, portions of yellow and of blue; and equally, if it contains a portion of yellow and a portion of blue, it contains a portion of green.¹⁹ It is easy to deny that; but the denial rests on an unconscious adherence to a particulate theory of stuffs: we imagine, wrongly, that the blue and the yellow must, as it were, be located in determinate parts of the mass and that they will produce green only if their locations happen to be related in one out of innumerable possible ways. But blue and yellow are not located in any such fashion; they are smoothly mixed throughout the mass of stuff. What more could possibly be required for us to say that the mass contains green? Does the mass contain green in addition to blue and yellow? It contains yellow and it contains blue and it contains green; and that is that. I conclude that Anaxagoras’ theory takes no stand on the question of elements: it has no peculiar resistance to them; and it provides no special place for them. The contrast between element and compound is of secondary interest to the theory.²⁰

But is that theory coherent? It is sometimes argued that theorem (C*) implies that there are no ‘pure’ stuffs and hence that we cannot intelligibly talk of such stuffs, let alone say that they occur in different proportions in different places. Anaxagoras’ theory is self-stultifying: it is a theory about stuffs; but its main tenet is inconsistent with the existence of stuffs.²¹

I shall approach that argument obliquely. The end of B 12 reads thus:

And there are many portions of many things; but nothing is altogether separating off or separating out, one from another, except mind. And all mind is homogeneous (homoios), both the greater and the smaller. But nothing else is homogeneous,²² but each single thing is and was most clearly those things of which most are present in it (207; cf. 301).

The last sentence is adequately glossed by Aristotle: Things seem different and are given different names from one another on the basis of what especially preponderates in quantity in the mixing of the unlimited [stuffs]. For there is no whole which is purely white or black or sweet or flesh or bone; but the nature of the thing seems to be that of which it contains the most’ (Phys 187b2–7=A 52). Simplicius puts it bluntly: ‘that is gold in which there is much gold, though many things are in it’ (A 41; cf. Lucretius, A 44); and we have already come across an Anaxagorean illustration of the point in 197: the original mixture, since it contains more air and aether than anything else, is, or wears the aspect of, air and aether. Dig up a spadeful of stuff from your back garden: you can be sure that it will not be a spade of any pure stuff; it will contain countless impurities of every sort. But you are, for all that, warranted in calling it earth; and you may properly surmise that it contains a dominant proportion of earth—which accounts for its earthy aspect.

Here the charge of incoherence shows its teeth: ‘How can you know that the dominant stuff in your spadeful is earth? How can you even speak sensibly of “earth”? It will not do to define earth by way of 207, saying that a is earth if and only if a is a lump of stuff in which earth predominates. Such a definition is vainly circular. And if we evade the circle by putting subscripts to the term “earth”—“a is earth1 if and only if a is a lump of stuff in which earth2 predominates”—then “earth2” remains unexplained. If earth2 is elemental, it cannot be explained in terms of any components; and since, by (C*), earth2 is never present in the world, we cannot learn the meaning of earth2 by “ostensive definition”. In short, “earth”, or “earth2” if you prefer, is a bogus term: it has no use in science.’

That argument constitutes a serious challenge to Anaxagoras, whether or not we ascribe to him a distinction between ‘earth1’ and ‘earth2’. Moreover, it poses, I think, a more general difficulty: every schoolboy chemist learns that all the sample elements he uses in the laboratory are impure; no process will guarantee the removal of every impurity from a bottle of stuff. Now the chemist needs and uses the notion of (pure) hydrogen. Yet he lives in an impure world, and he experiments on impure samples of hydrogen. How can Anaxagoras and the modern chemist speak intelligibly of earth or of hydrogen? How can Anaxagoras seriously say that most of the stuff on my spade is earth? How can the chemist determine that most of the stuff in the test-tube is hydrogen?

A part of the answer to those questions runs, I think, like this. We begin by observing, crudely, that different lumps of stuff have different qualities: two buckets of stuff look and smell and feel and taste different; they act and behave differently; and we give them different names—‘sand’, say, and ‘sea’. Evidently, the buckets do not contain pure samples of sand and sea; for we can see plainly that the sea is sandy, and we can feel the wetness of the sand. For all that, we can distinguish sand from sea, and begin some quasi-scientific tests. Various observations and experiments will associate one set of properties with buckets of sand and another set, largely non-overlapping, with buckets of sea. And we may now define the ‘scientific’ notion of ‘pure’ sand as ‘the stuff—whatever its structure may be—that supports those properties’; and sea as ‘the stuff—whatever its structure may be—that supports those properties’. Such definitions are dangerous and indeterminate: they are dangerous because they suppose that some single structure is common to all our buckets of sand; and closer, microscopic, observation might falsify that supposition (whales and dolphins are not, after all, fish; mercury is a metal). They are indeterminate because the batch of properties they assemble and refer to may well change in the course of time and further investigation. For all that, definitions of such a type do allow us to get a grip on the notion of a ‘pure’ substance, even though all our buckets of sand and sea are impure.

Do those definitions import new senses for our stuff names? or do they make old senses more precise? Does ‘water’ have two senses, one of which is explicable by the chemist in terms of H and O, the other of which is explained by pointing to rivers and seas? And does Anaxagoras mean to suggest that stuff names like ‘earth’ are ambiguous between ‘earth1’ and ‘earth2’? I see no hint of ambiguity in Anaxagoras;²³ I see no good reason to suppose an ambiguity in English; and I find nothing of interest in the question.

However that may be, as science advances our investigatory techniques are improved. Let us leave the seaside and enter the laboratory. We have a jar of gas which we know is predominantly oxygen. The next question is: can we discover how much oxygen the jar contains? How can we determine the degree of impurity in the gas if we can never extract all the impurities? Now our techniques will have developed a process of separating H from a predominantly O mixture, and another process of extracting O from a predominantly H mixture. Take a jar of predominantly O gas: by the first process, extract n units of predominantly H gas, leaving m units of predominantly O gas. Now apply the second process to the n units and the first to the m units; and so on. Applications of those processes will always provide results; for though we may purify our H we can never produce pure H—you cannot cut H off from O with an axe. Yet it is not hard to see that the continued applications of the two processes will enable us to give ever closer approximations to the proportion of H to O in the original jar. No doubt

of the things that are separating off one does not know the quantity either by reason or in fact (208: B 7)—but one can make an indefinitely close approximation to knowledge.²⁴

My argument here has been, I fear, somewhat jejune: to consider the issue at full length would call for a chapter on its own. Yet the issue is important enough: if the objection I have been considering is correct, then Anaxagoras’ physical theory (and with it modern chemistry) is blown up. I do not think the objection has any such explosive powers.

(e) Inherent powers

Some of the difficulties in (C*) have now been aired; and I turn to the connexion between that tenet and the other parts of Anaxagoras’ system. I begin by asking why Anaxagoras put forward his first tenet, that ‘in the beginning, everything was in everything’. That tenet can be expressed by:

(A*) For any pair of stuffs S, S′: in every piece of S there originally was a portion of S′.

Discussion may start from a passage in Aristotle:

They [the Anaxagoreans] say that everything was mixed in everything because they saw everything coming to be from everything (209: Phys 187b1=A 52).

Simplicius gives a somewhat breathless gloss:

Seeing, then, everything coming to be from everything, if not immediately at least serially (kata taxin)—for air comes from fire, and water from air, and earth from water, and stone from earth, and fire again from stone; and though the same food, e.g., bread, is applied, many different things come into being, flesh bones veins muscles hair nails—and perhaps wings and horns—even though like is increased by like: for these reasons he supposed that in the food—in water, if that is what trees feed on—there is wood and bark and fruit; and that is why he said that everything was mixed in everything, and that coming to be comes about by virtue of a separating out (210: A 45).

No extant text of Anaxagoras contains precisely that argument, and it has been supposed a Peripatetic rationalization.²⁵ But I am inclined to go along with Aristotle’s interpretation; for the alternative is baffled silence, an unendurable fate. Nor do the fragments bear no relation to the Peripatetic argument. B 16 reads as follows:

From those things as they separate off is compounded earth; for from clouds water separates off, and from water earth, and from earth stones are compounded by the cold, and these are further distant from water (211).²⁶

The fragment reveals an interest in what Simplicius calls ‘serial’ generation: A come from B serially if A comes from C₁ and C₁ comes from C₂ and…and C_n-₁ comes from C_n and C_n comes from B. An anecdote in Diogenes runs as follows: ‘they say that when someone asked him if the mountains in Lampsacus would ever be sea, he said: “If time doesn’t give out”’ (Diogenes Laertius, II.10=A 1).

But such remarks are Presocratic commonplaces. The Peripatetic argument requires us to ascribe to Anaxagoras the thesis that ‘everything comes from everything’. By ‘everything’ is meant ‘every stuff ; and I take ‘S comes from S′’ to mean ‘from any quantity of S′ a quantity of S is extractable’. Thus ‘Water comes from cloud’ means: ‘From any bit of cloud you can extract a drop or two of water’; ‘Flesh comes from bread’ means: ‘From any lump of bread you can extract a piece of flesh’; ‘Fire comes from flint’ means: ‘From any flint stone you can extract a spark of fire’. Then to say that ‘everything comes from everything’ is to assert:

(1) For any pair of stuffs S, S′: from any piece of S there is extractable a piece of S′. On the Peripatetic interpretation, proposition (1) is the logical foundation-stone of Anaxagorean physics, more fundamental even than the three tenets, (A)—(C), which I set out at the start of this chapter. (The proposition uses the word ‘extract’ in a highly general sense, to cover all cases in which one stuff is wrung from another. What particular process of extraction is appropriate in any given case is a matter for experiment: thus ice is extracted from water by refrigeration (cf. 211); flesh from bread by digestion; salt from brine by evaporation; cheese from milk by compression; fire from stone by concussion; and so on.)

Why should Anaxagoras have embraced (1)? According to Aristotle, on the basis of empirical evidence: he ‘saw’ that ‘everything comes from everything’. 211 suggests that a part of that evidence derived from the stock-in-trade of the old Ionian scientists: the familiar meteorological processes provide clear and repeated evidence for the serial generation of the main world-masses from one another. Biology provides another area of observation: Simplicius, in 210, refers to the phenomena of nutrition; and the reference is repeated (e.g., Lucretius, A 44; Aëtius, A 46). A further testimony points to the allied phenomena of reproduction, where from a seed there develops an embryo with its complement of flesh and bones and hair (B 10, see below). There are close connexions between Anaxagoras and the fifth-century doctors;²⁷ and there is biological terminology in the fragments: it is tempting to conclude that the study of biology and medicine led Anaxagoras to his philosophical position. That conclusion is conjectural, and I suspect that it is exaggerated. But it is plausible to suppose that Anaxagoras was as impressed by biological as by meteorological changes: if flesh and blood and bone may come from bread and milk and cheese, then surely anything may come from anything?

Proposition (1), then, may stand as an Anaxagorean hypothesis. Like the cosmological hypotheses of the Milesians, it is strong and simple; and it is supported by a mass of empirical evidence. It has a further dialectical advantage: it stands in the strongest possible contrast to the stability of Elea. If (1) can be defended against Eleatic attack, then any weaker hypothesis, which further experiment may put in the place of (1), need fear nothing from that quarter.²⁸

In order to proceed from proposition (1) to tenet (A*), the thesis that ‘everything was in everything’, we need a further premiss. The premiss is suggested by the following passage:

For in the same seed he says there is hair and nails and veins and arteries and muscles and bones, and they are invisible because of the smallness of their parts but as they grow they are gradually separated out. ‘For how’, he says, ‘might hair come to be from what is not hair and flesh from what is not flesh?’ (212: Scholiast on Gregory, B 10).

The passage comes from a late scholiast; but the scholiast seems to be familiar with the doxographicai tradition, and I assume that the substance of the passage is Anaxagorean, even if the final question is not (as many scholars think) an original quotation.²⁹

‘Hair cannot come from what is not hair.’ The principle suggested by that thought is: (2) For any pair of stuffs, S, S′: if S′ comes from S, then S=S′. But (2) is absurd; and Anaxagoras surely has in mind a less extravagant principle, namely:

(3) For any stuff S′ and object x: if S′ comes from x, then S′ was in x.

Hair cannot come from ‘what is not hair’, i.e. from what does not contain hair.

Is principle (3) borrowed from Elea? or is it an empirical observation? or is it, in intention at least, a truism? If I take an egg out of the egg-box, the egg was in the box; if I draw milk from a cow, the cow contained the milk; and in general, if Y comes out of X, then Y was in X. The sentiment is prehistoric: ‘deriving his fire. . . commonly from the friction of wood or bamboo, primitive man naturally concluded that fire is somehow stored up in all trees, or at all events in those trees from the wood of which he usually extracted it.’³⁰ When the iron-master extracts metal from ore, he does not need Parmenides to tell him that the metal does not spring into being; he knows that it was there all along. When the milk-maid extracts butter from her milk, she has not previously observed the butter in the unchurned milk. Principle (3), I suggest, was not forced upon Anaxagoras by Elea; nor did he propose it on the basis of empirical research: rather, it seemed to him to be a self-evident truth.

Principle (3) needs careful statement. It is easy to read it as:

(4) For any stuff S' and object x: if a piece of S′ is extracted from x, then x contained a piece of S’.

But Anaxagoras does not want to hold that x contained a piece of S′; for that wrongly suggests that extraction is a matter of isolating some part of x; and if x is a piece of S, every part of x is a piece of S and no part a piece of S′. We need to hold clearly in mind a distinction which has underlain most of this chapter: the distinction between pieces and portions.³¹ x contains a piece of S′ only if some physical part of x is a piece of S′; but x may contain a portion of S′ even if no part of x is a piece of S′. The pointilliste’s green patch contains blue pieces and yellow pieces; the orthodox or Anaxagorean green patch contains blue portions and yellow portions, but no blue or yellow pieces.

The principle Anaxagoras needs is this:

(5) For any stuff S′ and object x: if a piece of S′ is extracted from x, then x contained a portion of S′.

And (5) can be defended in the same way as (3): if I extract a pound of salt from a tub of brine, then the brine contained salt; if I get a thimble of water from a cactus plant, the cactus contained water. And if you can’t get blood from a stone, that is because (in un-Anaxagorean physics) stones do not contain blood. I propose that we grant Anaxagoras (5), and that we take it not as a piece of Eleatic metaphysics, nor as an inductive generalization, but as a safe truism.

We must make (5) a little more precise by introducing a reference to time, thus:

(5*) For any stuff S′, object x, and time t: if apiece of S′ is extracted from x at t, then prior to t x contains a portion of S′.

From (5*) it is reasonable to infer: S′, x,

(6*) For any stuff S′, object x, and time t: if it is possible to extract a piece of S′ from x at t, then x contains a portion of S′ at t.

The principle behind the inference is this: if, given that X is extracted from Y, Y contained X, then if X is extractable from Y, Y contains X; if what is extracted from Y was contained in Y, then what is extractable from Y is contained in Y.

Sentence (1), like sentence (5), requires to be made more precise, thus:

(1*) For any stuffs S and S′, object x, and time t: if x is apiece of S, then it is possible to extract a piece of S’ from x at t.

Now (1*) and (6*) entail:

(7) For any stuffs S and S′, object x, and time t: if x is a piece of S, then x contains a portion of S′ at t.

Finally, we make two trivial deductions from (7), viz:

(8) For any stuffs S and S′, and object x: if x is a piece of S, then x contained a portion of S′ at the time when the cosmogony began.

(9) For any stuffs S and S′ , and object x: if x is a piece of S, then x now contains a portion of S’.

Now (8) is, of course, nothing more than tenet (A*); and (9) is tenet (C*). Thus from the two Anaxagorean principles, (1) and (5), we have successfully inferred two of the basic tenets of Anaxagorean physics. If ‘everything comes from everything’, and if ‘what comes from a thing must have been in it’, then ‘everything was originally in everything’, and ‘everything is now in everything’.

So far so good. But the two formulations of (A) and (C), viz. (8) and (9), immediately suggest a potentially embarrassing question: (8) seems to ascribe to the original mass exactly the same constitution that (9) ascribes to the present world. Does not that lead at once to an Eleatic universe, stable and changeless? How is any sort of ‘extraction’ possible, given the fundamental similarity holding between the world past and the world present? How can Anaxagoras allow a cosmogony? How can change and variation take place in the world we know?

I shall return to these questions. First, however, I want to look at the second of Anaxagoras’ three tenets: what does (B) amount to? and how is it related to (A) and to (C)?

(f) Anaxagoras and infinity

That second tenet has it that ‘there is no smallest portion of anything’. The tenet is advanced in 198 and 202. I begin with 198:

[i] For neither of the small is there the least, but there is always a less (for [ii] what is cannot not be)—but [iii] of the great too there is always a greater, and [iv] it is equal in quantity to the small. And [v] in relation to itself each is both great and small.

Sentence [i] states tenet (B); I paraphrase this (for reasons which will become clearer later) as follows: ‘However small an object may be, there is no smallest portion of S contained in it.’ The reference to the object’s smallness is, I take it, a literary rather than a logical device; thus the tenet reads, formally: S b ,

(B*) For any stuff S and object x: if x contains a portion of S, Sb, then there is a portion S^c contained in x such that S^c<S^b.

It is easy to see that (B*) entails that if there are any portions of S in an object, there are infinitely many such portions. And there is every reason to think that Anaxagoras saw the implication: when 197 asserts that ‘all things were together, unlimited both in quantity and in smallness’, we may suppose (as I have already suggested) that the unlimited quantity of portions of stuffs as well as their unlimited smallness is inferred from thesis (B*). Anaxagoras, I think, ‘shows an understanding of the meaning of infinity which no Greek before him had attained’—not even Zeno, if Zeno indeed came before him.³²

But how did Anaxagoras acquire that understanding? And why did he adhere to thesis (B*)? A tempting suggestion has him derive (B*) directly from (C*). Take any piece of S, say a. By (C*), a contains a portion of S′. Extract that portion, or part of it, and call the resulting piece of S′ b. By (C*) b contains a portion of S: extract that, too, and call the new piece of S c. Plainly, c<a; equally plainly, successive applications of (C*) will yield an infinite sequence of pieces of S, each smaller than its predecessor. Since the extracted pieces of S all come from a, we may safely conclude that a contained no smallest portion of S.

198 does not contain that argument; instead, it offers the parenthetical reflexion, [ii]: ‘what is cannot not be’. That has foxed the commentators. Some refer, loosely and unconvincingly, to Zeno’s argument in 175=29 B 3.³³ Others offer Anaxagoras arguments of ludicrous implausibility: ‘If one presupposes that there is a smallest, one must assume that that which is less than the smallest does not exist, and consequently that there is a void.’ Others again have Anaxagoras equivocate: ‘If the division of something into smaller and smaller pieces could ever come to an end, this would mean that there was nothing further to divide; i.e., by cutting up an existing thing one would have reduced it to non-existence.’³⁴ (After such a division there is ‘nothing further to divide’, i.e. no magnitudes left which are divisible; it does not, of course, follow that the only thing left to divide is nothing—so that the dividing has somehow produced nothing or a nonentity.)

Can anything better be done for sentence [ii]? Suppose that a contains c; then, plainly, c exists. Now let a be the smallest portion of S. Then by the argument I have already rehearsed, c is smaller than a; but if a is the smallest portion of S, c cannot exist. Hence c exists and c does not exist—but ‘what is cannot not be’. On that view, sentence [ii] does not introduce the notion of division: it does not say ‘what is cannot become non-existent’. It is not making an Eleatic point at all, but stating the simple truism that what exists cannot also not exist.³⁵ The parenthesis, in short, is a reminder that a reductio argument is readily constructed for (B*).

I continue the discussion of 198. Sentence [iii] is usually taken to state either that there is an infinitely large amount of every stuff in the world (which is absurd and contradicts 197), or that the total world stuff is infinite in extent (which is implied by 197 but is wholly irrelevant to 198 and thesis (B*)). Comparison with (B*) suggests rather the following interpretation:³⁶

(1) For any stuff S and object x: if x contains a portion of S, S^b, then there is a portion S^c contained in x such that S^c>S^b,
In short: there is no largest portion of S in any given piece of stuff.

How might Anaxagoras have argued for (1)? Let Sb be the largest portion of S in a. Extract Sb from a, and call the remainder of a c. By (C*), c contains a portion of S, Sc. Now the compound portion S^c+ Sb was contained in a and is greater than S^b. Hence Sb is not the largest portion of S in a. We can, of course, say that a contains no portion of S of magnitude greater than n (if n is the magnitude of a itself); but then there is no portion of S equal to n. However much S you extract from a, there is always a little left; however large a portion of S you have discovered in a, it is possible to enlarge it.

The argument for (1) is parallel to my argument for (B*), just as (1) itself is parallel to (B*). And the language of 198 leads us to expect such a parallelism. Moreover, we can now ascribe an easy sense to sentence [iv], ‘…it is equal in quantity to the small’. Of the many interpretations of that phrase,³⁷ one has all the advantages: ‘there are as many large portions of S in a as there are small portions’. Let X count as a ‘large’ portion if; 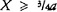; and let X count as a ‘small’ portion if 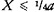. Then, as Anaxagoras has in effect already shown, a contains infinitely many large and infinitely many small portions of’ S. The large and the small portions can be matched one to one: they are, as Anaxagoras says, ‘equal in quantity’. Here again, Anaxagoras shows a sophisticated grasp of the method of ‘counting’ infinite sets.³⁸

The final sentence of 198 is no less vexing than its predecessors. A popular reading of [v] again connects 198 with Zeno. Anaxagoras is alleged to mean something like this: ‘Considered in itself, a is great—for it contains infinitely many parts or ingredients, each of them having some finite size; but, again, a is small—for each of its component parts is infinitesimally small.’ That is a very silly argument; and it hardly ‘answers Zeno’: it is silly in that neither leg contains a decent inference; and to think that ‘a is great and small’ is an answer to Zeno is grotesque—it is a mere parroting of Zeno. We do better to follow Simplicius and read ‘each (hekaston)’ not as ‘each piece of stuff but as ‘each stuff’. The sentence then merely says that there are both large and small portions of any stuff; and that unexciting fact follows from what has gone before.
202 is closely related to 198:

And [i] since too there are equal portions of the great and the small in quantity, for this reason too [ii] everything is in everything; [iii] nor can they exist separately (charts), but [iv] everything shares a portion of everything, [v] Since the least cannot be, [vi] things cannot³⁹ be separated (chôristhênai) [vii] nor come to be by themselves (eph ‘heautou); but [viii] as in the beginning, [ix] so too now everything is together, [x] And in all things there are many even⁴⁰ of the things that are separating off, equal in quantity in the greater and in the smaller.

The burden of 202 is the proof of [ix]; and [ix] states the third thesis, (C*), of Anaxagorean physics. The argument proceeds from (A*) via (B*) to (C*): the word ‘too’ in [i] marks the argument as a secondary proof; and (C*) has, of course, already been argued for. The further proof is offered, I suggest, in order to make it quite certain that you cannot have (A*) and reject (C*); you cannot suppose that an originally commingled world is now entirely separated out. Such an argument, from past commingling to present commingling, is adverted to again in 201; and it lies behind the statement in 203 that stuffs today ‘have not been separated from one another, nor have they been cut off by an axe’.

How, in detail, does the argument run? I assume that [ii], [iii], [iv] and [ix] express, in different words, the same proposition: thesis (C*); and I assume that [vi] and [vii] are equivalent to one another. Thus 202 in effect consists of three implications: the first infers [ii] from [i]; the second infers [vi] from [v]; the third infers [ii] from [viii]. (Sentence [x], as I understand it, simply presents a special case of [ii]: ‘even if S is separating off from other stuffs, still some portion of S will remain in every piece of every other stuff.) The three implications can be moulded into a single argument: ‘Given [viii], i.e. (A*), we can infer [v] and hence [i], by the argument of 198. But from [v] or [i] it follows that [vi]; and [viii] and [vi] yield [ii].’ In words: ‘Since everything was originally mixed, there are no smallest portions of any stuff. Hence, no stuff can become entirely separate from all other stuffs; hence no stuff can—now or ever—be separate from all other stuffs.’

That interpretation makes a number of disputable assumptions; and it is by no means wholly satisfactory: in particular, it leaves sentence [i] with no serious work to do; for [v] is all that Anaxagoras needs. But it does have two advantages: it gives Anaxagoras a coherent-looking argument; and it ties 202 closely to 198.

Of the three constituent implications of the argument, the first has already been discussed in connexion with 198; and the third is an evident truth: if things were once F, and if nothing can become non-F, then things still are F. What, then, of the second implication? Why, if there is no smallest portion of S, should it be thought to follow that no object can consist of nothing but S? Anaxagoras implies that ‘the very act of separation presupposes a smallest that can be separated’⁴¹; but why does he think that? Perhaps he imagines that the only way to assemble a piece of pure S would be to conglomerate a number of microscopical pieces of pure S; and those microscopical pieces could only have their purity guaranteed if they were minimal quanta of stuff, if they were simply too small to contain any impurities. That is a feeble argument; but I can find no better way of understanding Anaxagoras here.

My suggestions about how the main principles of Anaxagorean physics interlock have been a trifle complicated; and I shall end this section with a brief summary. Thus: amazed at the variety of material interchanges. Anaxagoras posits the hypothesis that any stuff can be extracted (by some method and through some intermediaries) from any other. The hypothesis leads to the conclusion that every stuff contains every other; and that, in turn, yields tenet (A), that ‘originally all things were together’, and tenet (C), that even now all things are together. Further reflexion shows, first, that matter cannot be paniculate in structure; and, second, that there can be no smallest portion of any stuff, (B). Finally, the structure of the proof is strengthened by a cross-argument deriving (C) from (A) and (B).

(g) The vortex

At the beginning of the world, everything was in everything; now, everything is still in everything. How, then, have things changed? In what does cosmogony consist? How, indeed, can cosmogony, or any other less massive process, take place at all? If a is a piece of S, then a and every part of a is predominantly composed of S; no clipping or cutting, however ingenious, can scissor off a bit of S′ from a. And if originally the world-mass, and all its parts, are pieces of air, how can it be that the world-mass now presents so various an appearance?

Anaxagorean cosmogony cannot consist of an apokrisis, or separating off, in the crude and simple sense of a cutting or chopping off of parts of the Urstoff: such operations will produce no differentiation. But Anaxagorean ‘extraction’ is not (despite the contrary hint in 203) a ‘chopping off. Miners may hack coal or gold from the rock-face; but in Anaxagorean physics extraction is a different operation: earth ‘separates off from the Ur-mass of air and aether as cheese separates off from milk, or butter from cream. The churn produces cheese or butter; but it does not do so by picking bits of cheese and butter from the milky liquid. Extraction is, to put it roughly and anachronistically, a chemical and not a mechanical operation: just as every piece of stuff is a chemical union and not a mechanical juxtaposition, so every change in stuffs is a chemical reaction and not a mechanical locomotion.

What is extraction? And how can it occur? No general account of extraction can be offered: different stuffs are extracted by different operations, and the discovery and description of such operations is an empirical, not a philosophical, chore. Thus straining will produce salt from brine; squeezing will produce water from cheese; boiling will produce jam from raspberries; and the technical sciences of biology and chemistry will gradually uncover a host of further and subtler extractive operations by which blood is produced from bread, hair from beer, nitrogen from air, copper from copper sulphate, and so on. The details are unimportant; it is the general point that matters: the general way to get a piece of S′ is to start from a piece of S and extract the portion of S′ which it contains. Philosophically, that is all that happens: we do not generate a new stuff, but only bring into perceptible form some portion of a pre-existent stuff; and how that operation is to be performed is not to be determined by a priori argument.

Yet Anaxagoras was a scientist as well as a philosopher; and he did offer some explication of extraction, though his explication remains, necessarily and properly, at a high level of generality. Part of Anaxagoras’ vocabulary for ‘extraction’ I have already mentioned: apokrinesthai, diakrinesthai, summignusthai, etc. Here I stress the locomotive element in such terms, and set them alongside three other overtly locomotive words which Anaxagoras uses in a cosmogonical context: cosmogony begins when the Ur-mass is ‘moved’ (kinein: B 13); its characteristic form of locomotion is ‘revolution’ (perichôrêsis: B 12, etc.); and as a result of the revolution or vortex certain stuffs ‘come together’ (sunchôrein: B 15).⁴² Science, Anaxagoras implies, can be saved if locomotion is possible: give the scientist a set of stuffs and the power to move their masses, and he will build on these slight foundations the mass of the physical world. It is worth underlining the economy, the power, the sophistication, and the relative coherence of Anaxagoras’ position. As an answer to Elea, it is far from despicable: how successful it is will be discussed in a later chapter; I end this chapter with two minor questions.

First, is Anaxagoras’ account of’extraction’ scientifically adequate? Can Anaxagoras really explain the phenomena of change in terms of the impoverished vocabulary and the non-particulate physics he allows himself? I suppose that the answer is: No. Certainly, Anaxagoras’ Abderite successors gave a firmly negative answer to it. But the question is surely an empirical one: the world might, logically, be as Anaxagoras describes it.

The second question is this: why does Anaxagoras suppose that the primordial Urmass was an undifferentiated mixture of stuffs, wearing the external appearance of ‘air and aether’? Nothing in the fragments suggests any answer to that question; and it cannot have been motivated by Eleatic worries. Here, I think, Anaxagoras is most clearly connected with his Milesian ancestry: those old Milesians offered as the simplest cosmogonical hypothesis a material monism and a uniform Ur-state. Anaxagoras abandons material monism; but he holds onto the second limb of the hypothesis: present differences are best explained by way of a primordial uniformity. Assume that there was a cosmogony; and that cosmogonical change had a clear point of origin. What, then, is the simplest assumption about the state of the world-stuffs at that original point? Surely, uniformity. In making these assumptions Anaxagoras proves himself a follower of the Milesians: he was attempting to salvage as many planks as possible of the old Ionian galleon from the wreck it suffered in the Eleatic tempest.⁴³