From a signal processing point of view, the novel aspect of hybrid precoding/combining in comparison with the conventional fully digital precoding/combining lies in the introduction of the precoding/combining stage in the RF domain as a result of driving a large-scale antenna array by a limited number of RF chains. By treating the cascade of the RF stage and multiple-input multiple-output (MIMO) channel as the effective channel, the system model of massive MIMO is analogous to the conventional counterpart, where various solution techniques have been proposed for the single-user and multi-user scenarios. On the other hand, problem formulation and optimization of the RF component depend on the choice of the baseband component in a joint RF-baseband design. Therefore, before we embark on the study of hybrid precoding/combining design, we give a brief review of the related background and recent developments in this chapter, which serve as the basis for our proposed research in the subsequent chapters.
2.1 Linear Precoding and Combining for Point-to-Point MIMO
2.1.1 Baseband Digital Solutions for Conventional MIMO
 data streams to a receiver with N
r receive antennas. Specifically, the receive signal
data streams to a receiver with N
r receive antennas. Specifically, the receive signal  is given as
is given as 
 is the flat-fading MIMO channel matrix with (i, j)th entry representing the channel coefficient between the ith receive antenna and the jth transmit antenna,
is the flat-fading MIMO channel matrix with (i, j)th entry representing the channel coefficient between the ith receive antenna and the jth transmit antenna,  is the linearly precoded transmit signal with
is the linearly precoded transmit signal with  as the linear precoder and
as the linear precoder and  as the Gaussian-coded data streams, and
as the Gaussian-coded data streams, and  is zero-mean, spatially white Gaussian noise with variance
is zero-mean, spatially white Gaussian noise with variance  . At the output of a linear receive combiner
. At the output of a linear receive combiner  , the signal estimate is given as
, the signal estimate is given as 
![$$\displaystyle \begin{aligned} \mathbf{E}=\mathbb{E}\big[\left(\hat{\mathbf{s}}-\mathbf{s}\right)\left(\hat{\mathbf{s}}-\mathbf{s}\right)^{\mathrm{H}}\big]={\mathbf{W}}^{\mathrm{H}}\mathbf{H}\mathbf{F}{\mathbf{F}}^{\mathrm{H}}{\mathbf{H}}^{\mathrm{H}}\mathbf{W}+\sigma_{n}^{2}{\mathbf{W}}^{\mathrm{H}}\mathbf{W}, \end{aligned}$$](../images/470489_1_En_2_Chapter/470489_1_En_2_Chapter_TeX_Equc.png)

2.1.2 Progressive Baseband Digital Solutions for Conventional MIMO ARQ
 reads as
reads as 
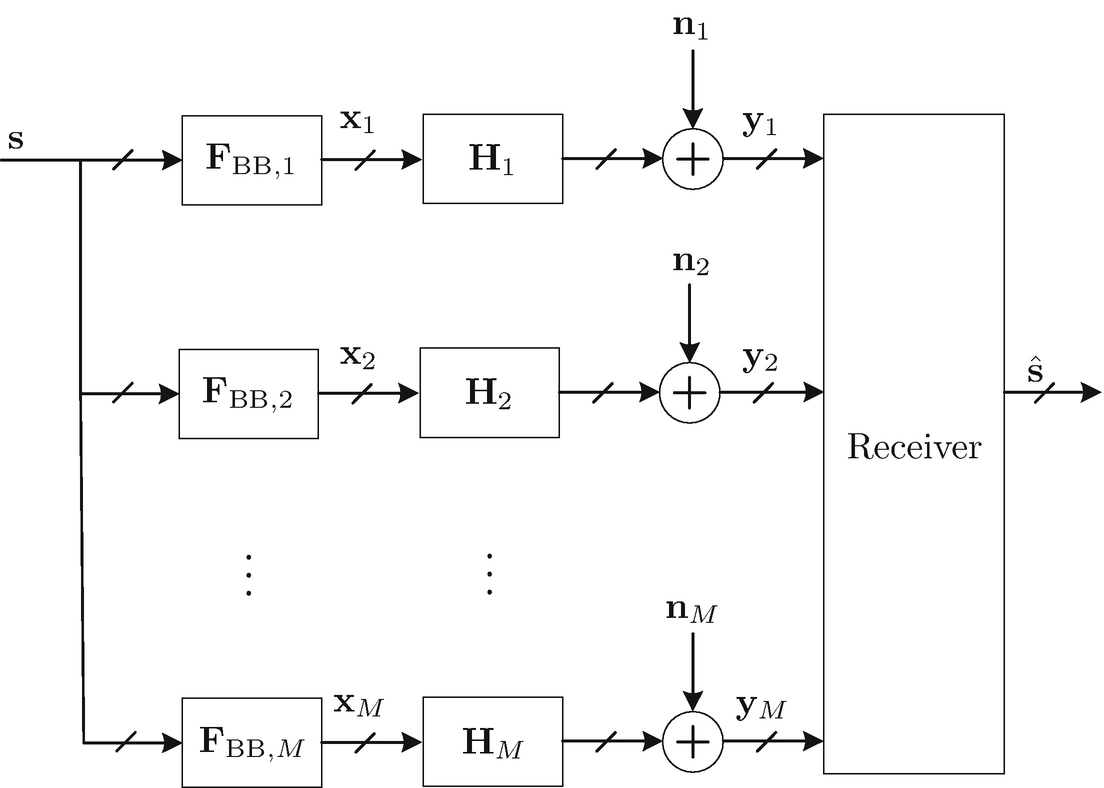
Linear precoding and combining for M retransmissions of a packet
 is the zero-mean, temporally and spatially white Gaussian noise with variance
is the zero-mean, temporally and spatially white Gaussian noise with variance  , i.e.,
, i.e., ![$$\mathbb {E}[{\mathbf {n}}_{m}{\mathbf {n}}_{l}^{\mathrm {H}}]=\delta _{ml}\sigma _{n}^{2}{\mathbf {I}}_{N_{\mathrm {r}}}$$](../images/470489_1_En_2_Chapter/470489_1_En_2_Chapter_TeX_IEq13.png) . When viewed independently, each round of ARQ retransmission is nothing but a conventional point-to-point MIMO system as presented in the previous section. Following the observation that each retransmission is likely to experience independent channel fading, the current channel realization H
m is modeled as independent of the past realizations H
1, …, H
m−1. If the linear precoder F
m is designed in accordance with the current channel realization H
m while taking into account past transmissions as represented by F
1, …, F
m−1, this will allow us to leverage the temporal diversity and therefore further performance improvement can be expected. Towards this end, the objective function can be formulated as
. When viewed independently, each round of ARQ retransmission is nothing but a conventional point-to-point MIMO system as presented in the previous section. Following the observation that each retransmission is likely to experience independent channel fading, the current channel realization H
m is modeled as independent of the past realizations H
1, …, H
m−1. If the linear precoder F
m is designed in accordance with the current channel realization H
m while taking into account past transmissions as represented by F
1, …, F
m−1, this will allow us to leverage the temporal diversity and therefore further performance improvement can be expected. Towards this end, the objective function can be formulated as 
 . Accordingly, the problem is formulated as
. Accordingly, the problem is formulated as 
 . The issue of sum MSE minimization was addressed in [8]. Instead of the highly complex ML receiver as implied by the expression of
. The issue of sum MSE minimization was addressed in [8]. Instead of the highly complex ML receiver as implied by the expression of  , a linear precoder in conjunction with nonlinear MMSE-decision feedback equalizer (DFE) was derived in [9]. By relaxing the assumption of full CSI to partial CSI, i.e., channel transmit covariance, the objective of ergodic mutual information, i.e.,
, a linear precoder in conjunction with nonlinear MMSE-decision feedback equalizer (DFE) was derived in [9]. By relaxing the assumption of full CSI to partial CSI, i.e., channel transmit covariance, the objective of ergodic mutual information, i.e., 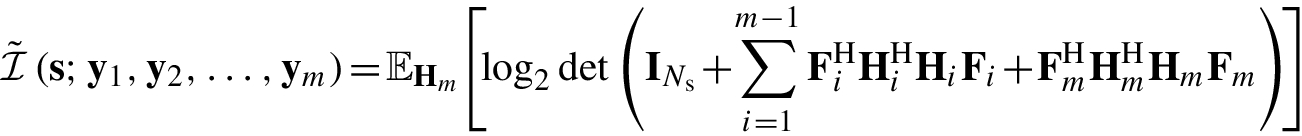
2.1.3 Hybrid RF-Baseband Solutions for Massive MIMO
 . The received signal reads as
. The received signal reads as 
 is the block fading channel matrix normalized as
is the block fading channel matrix normalized as ![$$\mathbb {E}[||\mathbf {H}||{ }_{\mathrm {F}}^{2}]=N_{\mathrm {t}}N_{\mathrm {r}}$$](../images/470489_1_En_2_Chapter/470489_1_En_2_Chapter_TeX_IEq19.png) ,
,  is the transmitted signal satisfying the normalized power constraint
is the transmitted signal satisfying the normalized power constraint ![$$\mathrm {tr}(\mathbb {E}[\mathbf {x}{\mathbf {x}}^{\mathrm {H}}])\leq P_{\mathrm {t}}$$](../images/470489_1_En_2_Chapter/470489_1_En_2_Chapter_TeX_IEq21.png) , and
, and  is the zero-mean, spatially white Gaussian noise with variance
is the zero-mean, spatially white Gaussian noise with variance  . In particular,
. In particular, 
Hybrid precoding and combining with RF phase-shifters
 and a baseband digital component
and a baseband digital component  , and
, and  is the normalized data stream. The signal estimate is given by
is the normalized data stream. The signal estimate is given by 
 and a baseband digital combiner
and a baseband digital combiner  . To reduce hardware complexity, RF elements might consist of only phase-shifters. In other words, the elements of the RF precoder F
RF and RF combiner W
RF are of constant modulus, i.e.,
. To reduce hardware complexity, RF elements might consist of only phase-shifters. In other words, the elements of the RF precoder F
RF and RF combiner W
RF are of constant modulus, i.e., ![$$\vert [{\mathbf {F}}_{\mathrm {RF}}]_{i,j}\vert =\frac {1}{\sqrt {N_{\mathrm {t}}}},\,i=1,\ldots ,N_{\mathrm {t}},j=1,\ldots ,n_{\mathrm {t}}$$](../images/470489_1_En_2_Chapter/470489_1_En_2_Chapter_TeX_IEq29.png) and
and ![$$\vert [{\mathbf {W}}_{\mathrm {RF}}]_{p,q}\vert =\frac {1}{\sqrt {N_{\mathrm {r}}}},p=1,\ldots ,N_{\mathrm {r}},q=1,\ldots ,n_{\mathrm {r}}$$](../images/470489_1_En_2_Chapter/470489_1_En_2_Chapter_TeX_IEq30.png) . On the assumption of perfect CSI, one noticeable difference in the formulation of hybrid precoding and combining from its fully digital counterpart in Sect. 2.1.1 is the introduction of the RF stages F
RF and W
RF. Although by treating
. On the assumption of perfect CSI, one noticeable difference in the formulation of hybrid precoding and combining from its fully digital counterpart in Sect. 2.1.1 is the introduction of the RF stages F
RF and W
RF. Although by treating  as the effective MIMO channel, previous baseband digital solutions for conventional MIMO are readily applicable, the RF components nonetheless need to be carefully optimized for the best performance. For example, optimal power loading schemes for fully digital solutions are unlikely to remain optimal without taking into account the presence of the RF precoder since
as the effective MIMO channel, previous baseband digital solutions for conventional MIMO are readily applicable, the RF components nonetheless need to be carefully optimized for the best performance. For example, optimal power loading schemes for fully digital solutions are unlikely to remain optimal without taking into account the presence of the RF precoder since ![$$\mathrm {tr}(\mathbb {E}[\mathbf {x}{\mathbf {x}}^{\mathrm {H}}])=\Vert {\mathbf {F}}_{\mathrm {RF}}{\mathbf {F}}_{\mathrm {BB}}\Vert _{\mathrm {F}}^{2}\leq P_{\mathrm {t}}$$](../images/470489_1_En_2_Chapter/470489_1_En_2_Chapter_TeX_IEq32.png) . In combination with the nonconvex constant-modulus constraints, such problems are in fact challenging to solve.
. In combination with the nonconvex constant-modulus constraints, such problems are in fact challenging to solve.
![$$\mathcal {D}_{\mathrm {t}}=[\frac {1}{\sqrt {N_{\mathrm {t}}}}e^{-\frac {\jmath 2\pi mn}{N_{\mathrm {t}}}}],m,n=0,\ldots ,N_{\mathrm {t}}-1$$](../images/470489_1_En_2_Chapter/470489_1_En_2_Chapter_TeX_IEq33.png) and the N
r-dimensional DFT codebook
and the N
r-dimensional DFT codebook ![$$\mathcal {D}_{\mathrm {r}}=[\frac {1}{\sqrt {N_{\mathrm {r}}}}e^{-\frac {\jmath 2\pi pq}{N_{\mathrm {r}}}}],p,q=0,\ldots ,N_{\mathrm {r}}-1$$](../images/470489_1_En_2_Chapter/470489_1_En_2_Chapter_TeX_IEq34.png) , respectively [14]. Different from the independently and identically distributed (i.i.d.) Rayleigh fading channel which corresponds to a rich scattering environment, a strongly correlated channel experiences limited scattering, and thus has a directional power spectrum in the angle domain. Intuitively, if the chosen DFT beams are well aligned with the directional scattering, it is unlikely for such an RF beamformer to cause a severe loss of channel power. Nonetheless, since the DFT beamforming directions correspond to uniformly quantized angles of arrival (AoAs)/angles of departure (AoDs), phase-shifting adaptive to instantaneous CSI as in [12] is more advantageous as the channel becomes increasingly independent. Besides, in a multi-user setting, the coarse resolution provided by DFT might not be sufficient to achieve good spatial separation between users or good coverage when the users are not located in a favorable direction.
, respectively [14]. Different from the independently and identically distributed (i.i.d.) Rayleigh fading channel which corresponds to a rich scattering environment, a strongly correlated channel experiences limited scattering, and thus has a directional power spectrum in the angle domain. Intuitively, if the chosen DFT beams are well aligned with the directional scattering, it is unlikely for such an RF beamformer to cause a severe loss of channel power. Nonetheless, since the DFT beamforming directions correspond to uniformly quantized angles of arrival (AoAs)/angles of departure (AoDs), phase-shifting adaptive to instantaneous CSI as in [12] is more advantageous as the channel becomes increasingly independent. Besides, in a multi-user setting, the coarse resolution provided by DFT might not be sufficient to achieve good spatial separation between users or good coverage when the users are not located in a favorable direction. , the hybrid precoder and combiner are obtained by optimizing the mutual information
, the hybrid precoder and combiner are obtained by optimizing the mutual information  , i.e.,
, i.e., 
 is the noise correlation after hybrid combining. In contrast with the study in [12] where the RF precoder and combiner were optimized with respect to the RF-processed channel capacity, the effect of baseband precoding and combining are explicitly incorporated in seeking a joint RF-baseband design. Due to the difficulty posed by the nonconvex constant-modulus constraint on the RF elements, joint optimization of the hybrid precoder {F
RF, F
BB} and hybrid combiner {W
RF, W
BB} is not possible. Instead, the authors focused on joint optimization of RF-baseband precoding (combining) by abstracting the effect of hybrid combining (precoding). In view of the constant-modulus property of the array steering vectors, the design of RF precoder (RF combiner) was formulated as selecting the optimal array steering vectors corresponding to all path AoAs (AoDs). In combination with the baseband digital precoder (combiner), such a hybrid design was cast as matrix reconstruction of the fully digital optimal solution for conventional MIMO as in Sect. 2.1.1, and a near-optimal precoding (combining) solution was found via an orthogonal matching pursuit algorithm. Although low-complexity, one immediate drawback of this technique is that extensive information of AoAs (AoDs) for all the propagation paths is required. In an attempt to address this practical limitation, the idea of sparse approximation was further applied to channel estimation in [16]. The sub-optimal restriction of RF elements to the space of array steering vectors incurs severe performance loss under certain channel conditions, and therefore, general formulation of constant-modulus RF design is needed. Following the idea of matrix reconstruction, improved hybrid solutions were devised in [17] using Grassmann manifold optimization and in [18] based on approximate joint diagonalization of matrices. To obviate the need for computing the optimal solution, a heuristic method was proposed in [19]. In [20], multi-layer codebook design for both RF phase-shifters and baseband precoder was considered for wideband orthogonal frequency-division multiplexing (OFDM) systems. In this case, beam-steering in the RF domain is commonly applied across all sub-carriers while baseband precoding is specific to each sub-carrier.
is the noise correlation after hybrid combining. In contrast with the study in [12] where the RF precoder and combiner were optimized with respect to the RF-processed channel capacity, the effect of baseband precoding and combining are explicitly incorporated in seeking a joint RF-baseband design. Due to the difficulty posed by the nonconvex constant-modulus constraint on the RF elements, joint optimization of the hybrid precoder {F
RF, F
BB} and hybrid combiner {W
RF, W
BB} is not possible. Instead, the authors focused on joint optimization of RF-baseband precoding (combining) by abstracting the effect of hybrid combining (precoding). In view of the constant-modulus property of the array steering vectors, the design of RF precoder (RF combiner) was formulated as selecting the optimal array steering vectors corresponding to all path AoAs (AoDs). In combination with the baseband digital precoder (combiner), such a hybrid design was cast as matrix reconstruction of the fully digital optimal solution for conventional MIMO as in Sect. 2.1.1, and a near-optimal precoding (combining) solution was found via an orthogonal matching pursuit algorithm. Although low-complexity, one immediate drawback of this technique is that extensive information of AoAs (AoDs) for all the propagation paths is required. In an attempt to address this practical limitation, the idea of sparse approximation was further applied to channel estimation in [16]. The sub-optimal restriction of RF elements to the space of array steering vectors incurs severe performance loss under certain channel conditions, and therefore, general formulation of constant-modulus RF design is needed. Following the idea of matrix reconstruction, improved hybrid solutions were devised in [17] using Grassmann manifold optimization and in [18] based on approximate joint diagonalization of matrices. To obviate the need for computing the optimal solution, a heuristic method was proposed in [19]. In [20], multi-layer codebook design for both RF phase-shifters and baseband precoder was considered for wideband orthogonal frequency-division multiplexing (OFDM) systems. In this case, beam-steering in the RF domain is commonly applied across all sub-carriers while baseband precoding is specific to each sub-carrier.2.2 Multi-User MIMO Precoding
2.2.1 Precoding for Conventional MIMO: From Linear to Nonlinear
 represent the channel between the ith user and the BS, and
represent the channel between the ith user and the BS, and ![$$\mathbf {H}\triangleq [{\mathbf {h}}_{1},\ldots ,{\mathbf {h}}_{K}]^{\mathrm {H}}\in \mathbb {C}^{K\times N_{\mathrm {t}}}$$](../images/470489_1_En_2_Chapter/470489_1_En_2_Chapter_TeX_IEq39.png) . The received signals for all K users can be collectively written as
. The received signals for all K users can be collectively written as ![$$\displaystyle \begin{aligned} \mathbf{y}=\left[{\mathbf{h}}_{1},\ldots,{\mathbf{h}}_{K}\right]^{\mathrm{H}}\mathbf{x}+\mathbf{n}=\mathbf{H}\mathbf{x}+\mathbf{n}, \end{aligned}$$](../images/470489_1_En_2_Chapter/470489_1_En_2_Chapter_TeX_Equn.png)
 is the transmit signal, and
is the transmit signal, and  is the zero-mean, spatially white Gaussian noise with variance
is the zero-mean, spatially white Gaussian noise with variance  . It is well-known that the sum capacity is achievable by encoding x by dirty paper coding (DPC) [21, 22]. However, DPC involves sophisticated random coding and binning approaches, and therefore is too computationally intensive to be useful in practice. Alternatively, a linear precoding scheme, channel inversion or zero forcing (ZF), is usually preferred because of its low complexity and being not too sensitive to channel estimation errors. At the expense of transmit power enhancement, inter-user interference is completely eliminated. In this case, the transmit signal is given as
. It is well-known that the sum capacity is achievable by encoding x by dirty paper coding (DPC) [21, 22]. However, DPC involves sophisticated random coding and binning approaches, and therefore is too computationally intensive to be useful in practice. Alternatively, a linear precoding scheme, channel inversion or zero forcing (ZF), is usually preferred because of its low complexity and being not too sensitive to channel estimation errors. At the expense of transmit power enhancement, inter-user interference is completely eliminated. In this case, the transmit signal is given as 
![$$\mathrm {tr}(\mathbb {E}[\mathbf {x}{\mathbf {x}}^{\mathrm {H}}])\leq P_{\mathrm {t}}$$](../images/470489_1_En_2_Chapter/470489_1_En_2_Chapter_TeX_IEq43.png) , and s = [s
1, s
2, …, s
K]T represents the data streams for the K users. When multi-user diversity is present in the system, i.e., there is a large number of users with heterogeneous channel realizations, it is possible to achieve the sum channel capacity by simply combining ZF precoding with greedy user selection [23, 24]. However, the effectiveness of such linear schemes might become questionable when users experience the same large-scale channel fading and require an equal-rate performance. If the system is fully loaded
, and s = [s
1, s
2, …, s
K]T represents the data streams for the K users. When multi-user diversity is present in the system, i.e., there is a large number of users with heterogeneous channel realizations, it is possible to achieve the sum channel capacity by simply combining ZF precoding with greedy user selection [23, 24]. However, the effectiveness of such linear schemes might become questionable when users experience the same large-scale channel fading and require an equal-rate performance. If the system is fully loaded  , i.e., the number of spatially multiplexed users K is equal to the maximum number of data streams N
t that can be physically supported, the sum rate unfortunately does not grow linearly with the number of users [25]. Note that the MIMO channel matrix
, i.e., the number of spatially multiplexed users K is equal to the maximum number of data streams N
t that can be physically supported, the sum rate unfortunately does not grow linearly with the number of users [25]. Note that the MIMO channel matrix  in this case is square. It was observed in [25] that all the eigenvalues except one of H have magnitudes of comparable order. On the contrary, the inverse of the peculiar, or ill-behaving, eigenvalue has an infinite mean. Intuitively, this implies that when zero-forcing (channel inversion) precoding is used to serve the K homogeneous users, transmission along the eigenvector associated with the ill-behaving eigenvalue would consume most of the power. As a result, the sum rate performance does not grow linearly with the number of users.
in this case is square. It was observed in [25] that all the eigenvalues except one of H have magnitudes of comparable order. On the contrary, the inverse of the peculiar, or ill-behaving, eigenvalue has an infinite mean. Intuitively, this implies that when zero-forcing (channel inversion) precoding is used to serve the K homogeneous users, transmission along the eigenvector associated with the ill-behaving eigenvalue would consume most of the power. As a result, the sum rate performance does not grow linearly with the number of users.
MU-MIMO downlink linear precoding for single-antenna users

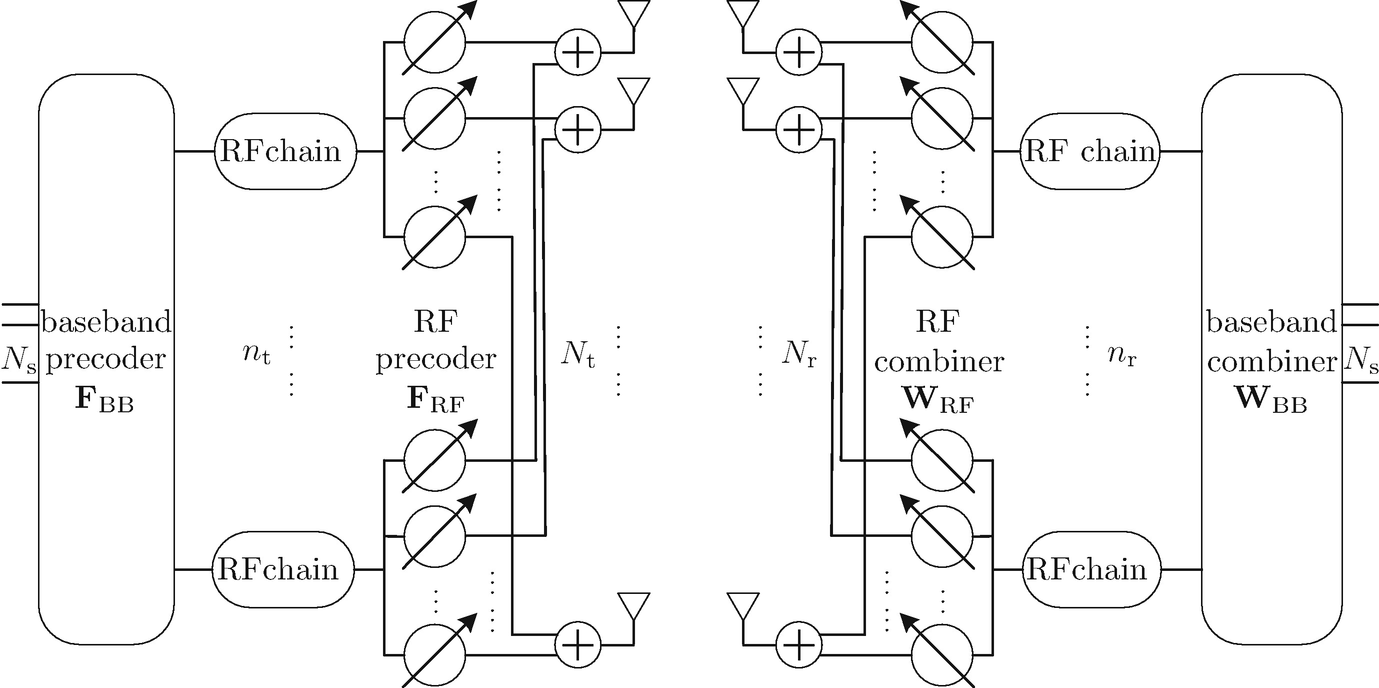
 . Such an RZF precoder can be equivalently obtained by an MMSE formulation[26]. In addition to modifying the linear precoding front-end, modification of the signal structure is another feasible avenue. Here, as illustrated in Fig. 2.4, in lieu of the original data symbol d, its perturbed version s is transmitted [27], i.e.,
. Such an RZF precoder can be equivalently obtained by an MMSE formulation[26]. In addition to modifying the linear precoding front-end, modification of the signal structure is another feasible avenue. Here, as illustrated in Fig. 2.4, in lieu of the original data symbol d, its perturbed version s is transmitted [27], i.e.,
MU-MIMO downlink nonlinear precoding for single-antenna users

 is a complex integer vector, and τ > 0 is a design parameter chosen to ensure correct recovery of s by modulo decoding. In particular, by defining the element-wise modulo-τ operation for a real vector z as
is a complex integer vector, and τ > 0 is a design parameter chosen to ensure correct recovery of s by modulo decoding. In particular, by defining the element-wise modulo-τ operation for a real vector z as 


![$$\displaystyle \begin{aligned} \mathrm{MSE}|{}_{\mathbf{d}}=\mathbb{E}\left[\left\Vert \mathbf{s}-\beta\mathbf{y}\right\Vert ^{2}\big|\mathbf{d}\right], \end{aligned}$$](../images/470489_1_En_2_Chapter/470489_1_En_2_Chapter_TeX_Equs.png)
 , and the perturbation vector
, and the perturbation vector 

Since the perturbation vector is a Gaussian integer, the search can be viewed as a problem of closest point search in a lattice. If s is picked from a high-order square constellation such as 16-, 64-, and 256-QAM as defined in Long-Term Evolution (LTE), and the optimal perturbation vector is optimally found, then by approximating the equiprobable discrete constellation points as continuous and uniformly distributed in a hyper-rectangle, the resulting errors from the search can be accordingly treated as uniformly distributed [29]. If the perturbation vector is obtained by power minimization, the error is nothing but the transmit power. In contrast to [30] where the transmit power is obtained by numerically solving a set of fixed-point equations, such lattice-theoretic approximation yields a mathematically tractable lower bound. This insight was leveraged for channel vector quantization design in [31], and for greedy user selection to alleviate the concern of power enhancement in cooperative ZF beamforming [32]. While the per-BS power constraint is more practical for multi-cell downlink beamforming, unfortunately, the MMSE-VP precoder has to be numerically optimized [33].
When users are equipped with multiple antennas, an enhanced system performance is expected from joint design of nonlinear precoding and linear combining. So far, the focus has been exclusively on non-iterative methods for the benefit of low complexity. The basic idea is to first use block diagonalization (BD) to eliminate inter-user interference and hence create parallel SU-MIMO channels, and then perform VP across the spatially multiplexed data streams in conjunction with SU-MIMO precoding and combining for each user. In [34], over each SU-MIMO channel, ZF-VP is used for spatial multiplexing while treating each receive antenna as a virtual user. In doing so, users only need to know the power scaling factor β for detection. Such a design, motivated by the need for signaling overhead reduction, was shown to approach the performance of waterfilling-based solutions [1]. The work in [35] instead combined BD with MMSE-VP, and demonstrated the benefit of geometric mean decomposition-based joint design [5] in terms of improved BER. By exploiting uniform channel decomposition [6], the linear MMSE receiver could also be incorporated [36, 37], which further decreases the BER. Assuming matched filtering at the users, a non-iterative approach for cooperative ZF-VP beamforming was proposed in [38] and compared with the linear counterpart.
2.2.2 Hybrid RF-Baseband Solutions for Massive MIMO

 , joint RF-baseband optimization can be performed sequentially in light of the following equivalence [39]:
, joint RF-baseband optimization can be performed sequentially in light of the following equivalence [39]: 
 . Here, the digital precoder F
BB at baseband generally employs traditional MU-MIMO linear schemes such as ZF and RZF, and the interest lies mainly in deriving the RF analog precoder F
RF subject to additional constraints such as constant-modulus elements, i.e., phase-shifters, and partial CSI.
. Here, the digital precoder F
BB at baseband generally employs traditional MU-MIMO linear schemes such as ZF and RZF, and the interest lies mainly in deriving the RF analog precoder F
RF subject to additional constraints such as constant-modulus elements, i.e., phase-shifters, and partial CSI.RF phase-shifting design with perfect CSI was addressed in [40, 41]. In [40], the phase-shifters in the RF domain are heuristically derived based on extracting the phases of the maximum ratio transmission (MRT) beamformer. In combination with the baseband ZF precoding, the hybrid solution was shown to perform close to the fully digital ZF counterpart in terms of sum rate. This idea was further pursued in a multi-antenna user setting in [41], where hybrid combining was also considered with the constant-modulus RF combiner reduced to DFT beam selection.
It is worth mentioning that one basic assumption in the aforementioned works [15–19, 40, 41] is that perfect knowledge of the high-dimensional MIMO channel is available at the BS. This assumption, however, could be problematic in closed-loop frequency-division duplexing (FDD) systems, in that an enormous amount of channel estimates need to be frequently fed back [42]. In an effort to remedy the issue with channel estimation overhead, one interesting idea is to adjust RF processing solely based on the statistical CSI while updating baseband processing according to the instantaneous effective CSI [43–47]. The slow-varying nature of statistical CSI renders it unnecessary for frequent update which leads to reduction in feedback overhead. In the presence of the RF stage, the dimension of the effective channel from the perspective of the baseband is significantly decreased in contrast to the original MIMO channel, and thus timely update of instantaneous CSI becomes feasible.

Massive MIMO downlink precoding for clustered users
It is worth mentioning that the effectiveness of the hybrid precoding solutions with two-timescale CSI as in [43, 50, 52] relies on the assumption that users are naturally partitioned into groups, and the same group of users experiences identical channel spatial correlation. This is however too restrictive in practice. Thus, the work in [53–55] proposed various user grouping algorithms based on the distance between the subspaces of the transmit spatial correlation, and RF beamforming was adapted to the centroid of the correlation matrices for each user group. Since the mean correlation is only a rough approximation, in this case, it is unlikely for the resulting RF beams to create near-perfect spatial separation, which casts doubt on the feasibility of group-wise spatial multiplexing at baseband.
When it comes to multi-cell systems, additional design issues, such as limited inter-BS cooperation in terms of signal and local CSI exchange, per-BS power constraint, and inter-cell interference need to be properly addressed. For example, in [45], only statistical CSI was assumed to be globally available, and the cluster-wise RF precoding was constrained to the null space of the superimposed transmit correlation matrices for interference reduction. In conjunction with local CSI-based ZF solutions, the RF solutions are derived to maximize a general utility function of spectral efficiency. In [52], RF precoding is designed with the objective of minimizing interference leakage power with linear pricing. Under the assumption that statistical CSI used for RF precoder update is outdated, a subspace tracking and compensation algorithm on Grassmann manifolds was proposed. The concept of deterministic equivalent was exploited in [47] to approximate the SINR chance constraint by deterministic functions, where accordingly, the RF precoding solutions are obtained. In [56], MMSE-VP was employed for instantaneous CSI-based two-stage precoder design in cooperative multi-cell systems.
2.3 Summary
For point-to-point massive MIMO systems, previous work has shown that even with a reduced number of RF chains, instantaneous CSI-based two-stage precoding/combining solutions are capable of delivering a performance comparable to their fully digital counterparts. This is especially the case when the MIMO channel is correlated, as commonly found in a directional propagation environment such as mmWave channels. However, because of the tremendous overhead of estimating the high-dimensional MIMO channel, one might be interested to know if such an observation is still valid when perfect CSI in the RF domain is relaxed to statistical CSI, e.g., channel covariance. Besides, it is noted that joint precoder-combiner optimization in conventional MIMO gives a substantial performance enhancement. Nonetheless, such an approach has not been attempted to derive the hybrid precoding and combining solutions yet. Finally, the design and evaluation of statistical CSI-based RF phase-shifting remain an open issue.
When packet retransmission is incorporated through hybrid ARQ mechanisms in conventional MIMO systems, previous research efforts have demonstrated that by exploiting the temporal diversity in the linear precoder optimization, the system performance can be improved. Unfortunately, such solutions cannot be directly applied to massive MIMO. To begin with, it has been assumed that the received signals from the past rounds of retransmission are fully accessible to the baseband. However, such an assumption raises concern about the storage requirement and processing complexity when the received signals are of high dimensions. A potential remedy is to introduce hybrid RF-baseband combining which reduces the dimension of the received signals to be combined through RF preprocessing. In doing this, the baseband has only access to the low-dimensional received signals at the output of the RF combiner. On the other hand, when the hybrid precoding structure with RF phase-shifting is employed, it is necessary for the optimization of baseband precoding to take into account the design of RF phase-shifting and hybrid combining at the receiver. Hence, a novel design of hybrid precoding and combining is required.
In a multi-user massive MIMO environment, the principle of hybrid RF-baseband precoding is to first create spatial separation of users in the RF beam domain and then perform spatial multiplexing at baseband. In particular, by assuming that users are geographically clustered in hotspots, it suffices to adjust the RF precoder based on the statistical CSI in consideration of the baseband precoder adaptive to the instantaneous effective CSI. As a result, only two-timescale CSI is required, which significantly reduces the channel estimation overhead. It is worth mentioning that the existing work has restricted the attention to linear precoding schemes such as ZF and RZF at baseband. Unfortunately, the linear schemes suffer severe power loss when a maximum number of equal-rate users is spatially multiplexed. On the contrary, by introducing a perturbation vector as additional DoFs for performance optimization, VP effectively addresses such an issue. A direct consequence of hybrid precoding with a reduced number of RF chains is that the number of data streams that can be physically supported is limited. Thus, it is desirable for hybrid precoding to perform well in fully loaded systems for utility maximization. In view of the drawback of linear schemes in this case, it is natural to explore how nonlinear VP techniques can be combined with the two-timescale CSI-based hybrid precoding design.
When extended to a multi-cell massive MIMO environment, the hybrid precoder needs to take into account the presence of inter-cell interference as well. The effectiveness of inter-cell interference mitigation depends on the degree of inter-cell cooperation in terms of information exchange allowed. For network MIMO processing, the technique of hybrid precoding design for single cell cannot directly carry over. In particular, because of the per-BS power constraint, closed-form expressions for the linear baseband front-end are no longer available. Given the difficulty with optimizing the statistical CSI-based RF precoder with respect to the traditional performance metrics, e.g., mutual information and MSE, the existing work has largely relied on heuristics. We remark that although the use of two-timescale CSI provides an effective alternative to addressing the issue of channel estimation overhead, it is somewhat restrictive from the perspectives of optimization and applicability. For example, in the absence of the analytical baseband solutions, iterative procedures are generally required for joint RF-baseband optimization. It is not clear how such alternating optimization can be carried out when the design variables are adaptive to different time scales. Besides, the assumption that users are geographically clustered and the user clusters are separated apart can turn out to be too ideal. Hence, novel design approaches that overcome such disadvantages while enjoying comparable channel estimation overhead with the two-timescale CSI are desired.