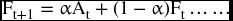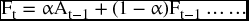CHAPTER 9
PRO FORMA STATEMENT AND FINANCIAL FORECASTING
As it was mentioned in the last chapter, a financial plan, as a major element in profit planning, would require a series of projections and preparation of the pro forma statement. The financial projections are not only required by lending institutions, potential investors, and the Small Business Administration (SBA), but they also represent the key to successful management, and they stand as a test of the project feasibility. Perhaps the most important projections of all is the sales projection which forms the basis for other projections, and their accuracy and reliability. Based on the predicted sales levels and the expected expenses, the firm's profitability would be assessed. On the same basis, other requirements can be assessed such as the size and type of financing, capital, services, obligations, personnel, and size and status of cash flow. The crucial question on how much earnings a firm would expect can be answered based on simple math using the projected values that would start with the expected sales and the expected market price of the product. Figure 9.1 confirms that a projected sale would be the start. A projected revenue would be obtained by multiplying the projected sales by the expected market price of the product. All costs of producing the goods and services would be subtracted from the projected revenue to get the gross profit or as it is sometimes called the gross earnings. The gross profit would be subject to three major deductions.
- The operating costs which often include administrative cost, marketing, advertising, and selling costs, in addition to depreciation expenses
- Interests paid on all financing loans
- Taxes due.
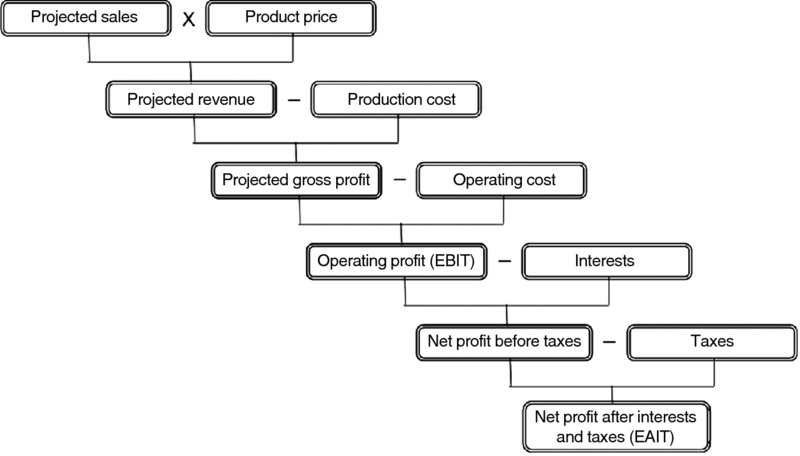
Figure 9.1 Steps to Estimate Net Profit
We should note that after the first deduction that would turn gross profit to operating profit, the latter is often called earnings before interest and taxes (EBIT). After the interests have been paid we get the net profit before taxes or earnings before taxes (EBT), and the last deduction would be the taxes. Net profit or earnings after interests and taxes (EAIT) is what we get at the end, which would be the basis for the firm real profitability.
9.1 Basic Pro Forma Statements
A pro forma statement is a financial statement, the entries of which are projected values based on a specific economic forecasting method, and a certain set of assumptions. These assumptions are usually related to the general conditions, as well as to the specific state of the project. The pro forma analysis is one of the most common and practical ways to predict the feasibility and worth of a firm in the near future. Although it is useful for both new and established firms, it is particularly valuable for a new venture, especially when it can be presented as a yardstick to show lending banks and potential investors the future performance of a project to prove how worthwhile it is for funding. An established firm would also need the pro forma analysis to catch up with changes and better prepare for them. For example, if the market conditions are good enough for a firm to expect an increase in sales by a certain percentage, it would be imperative to predict a series of consequence changes in production capacity, work shifts, inventories, transportation, storage, selling expenses, as well as the additional fund needed to undertake all of these changes.
For the startup venture, most if not all needed variables for the pro forma statements have to be estimated. Well-educated estimations can be made based on either the entrepreneur's personal knowledge and expertise or based on specific industry standards known to the public. The vast majority of entrepreneurs would not start in any venture unless they know about it, are familiar with it, or even had a past experience in it. This, by itself, would qualify them or their associates to deliver reasonable estimations to most of the needed variables. Nowadays, and with the computer revolution, there is a wide access to all kinds of information through the published reports and budgets and all kinds of documents on almost anything. It is not terribly difficult, for example, to come up with a reasonable average for the first year sales for a specific product in a certain market or time. It is also not difficult to come up with the cost of anything based on the published prices of almost any product you can think of, new or used. From these estimations that are based on the reality somewhere else, a pro forma statement can be completed. Once the firm goes through the first year of production and sales in the real market, it would accumulate all the actual data that would be used to project the next year's data. Over time and with the availability of good records, and for many years, prediction for the future becomes not only easier but also more accurate and reliable, given that an appropriate method of forecasting is used and the results are checked for reliability.
Tables 9.1 and 9.2 show general examples of an income statement and a balance sheet for 1 year. Regardless of the source and method of getting the estimated values, the pro forma statement would project the next set of values based on certain percentages concluded out of the estimation and based on certain set of assumptions.
Table 9.1 One Year Pro Forma Income Statement
| Item | Current Year | Next Year |
| Sales revenue | 450,000 | 594,000 |
| Cost of production | –202,500 | –267,300 |
| Gross profit | =247,500 | =326,700 |
| Operating expenses | –230,525 | –235,292 |
| Salaries | 135,000 | 135,000 |
| Rent | 60,750 | 60,750 |
| Utilities | 8000 | 10,000 |
| Equipment | 10,125 | 10,125 |
| Insurance | 5400 | 6480 |
| Depreciation | 11,250 | 12,937 |
| Operating profit (EBIT) | =16,975 | =91,408 |
| Interests | −5500 | –6710 |
| Net profit before taxes | =11,475 | =84,698 |
| Taxes | –4200 | –5460 |
| Net profit (EAIT) | =7275 | =79,238 |
Changes:
Sales revenue, cost of goods sold, and gross profit: 32% ↑
Operating expenses: 2%↑
Utilities: 25%↑
Insurance: 20%↑
Depreciation: 15%↑
Operating profit: 438%↑
Interests: 22%↑
Taxes: 30%↑
Net Profit: 989%↑
Table 9.2 One Year Pro Forma Balance Sheet
| Item | Current Year | Next Year |
| Current Assets: | ||
| Cash | 6600 | 13,860 |
| Account receivable | 35,343 | 47,124 |
| Inventory | 24,750 | 30,937 |
| Total current assets | 66,693 | 91,921 |
| Fixed assets: | ||
| Equipment | 49,500 | 70,950 |
| All assets | 116,193 | 162,871 |
| Current liabilities: | ||
| Account payable | 18,562 | 24,749 |
| Notes payable | 14,850 | 16,000 |
| Salaries | 4125 | 4330 |
| Total current liabilities | 37,537 | 45,079 |
| Long-term liabilities: | ||
| Loans | 49,500 | 82,500 |
| All liabilities | 87,037 | 127,579 |
| Equity | 29,156 | 35,292 |
Changes:
Cash: 110%↑
Account receivable: 33%↑
Salaries: 5%↑
Inventory: 25%↑
Total current liabilities: 20%↑
Total current assets: 38%↑
Loans: 66%↑
Equipment: 43%↑
All liabilities: 46%↑
All assets: 40%↑
Owner's equity: 21%
Account payable: 35%↑
Notes payable: 7%↑
Pro Forma Income Statement
The pro forma income statement assumes, based on the firm's records of the last 3 years, that the sale revenues for the next year will be up by 32%. This would increase the current year's revenue of $450,000 to $594,000.
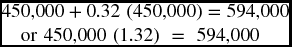
The second line is the cost of production or basically the cost of all the goods produced, which is assumed here for simplicity, to increase by the same percentage as the sales, and so would gross profit, as a result. The gross profit is obtained by subtracting the cost of production from the revenue. Operating expenses would include a variety of both fixed and variable expenses. Some do not change for next year and some do. Salaries, rent, and equipment stay the same. Utilities increase by 25% from $8000 to $10,000, insurance increases by 20% from $5400 to $6480, and depreciation increases by 15% from $11,250 to $12,937. Total operating cost would increase slightly from $230,525 to $235,292 or by only 2%. Subtracting the total operating expenses from the gross profit would yield the operating profit or, as it is also called, EBIT. This operating profit would increase dramatically in one year from $16,975 to $91,408 that is, an increase of 438%. The operating profit would be subject to the subtraction of the interest paid for the firm's loans and the taxes due. Both interest and taxes increase by 22% and 30%, respectively. Taking both interest and taxes away from the operating income would give us the net profit or what is called earnings after interest and taxes (EAIT). This net profit would have a huge increase from $7275 to $79,238, that is by 989%.
Pro Forma Balance Sheet
The example shown in Table 9.2 was constructed under the assumption that when sales are predicted to increase next year, it would mean that the current asset would need to increase as a consequence. Cash is assumed to increase by 110%, from $6600 to $13,860; account receivable would increase by 33%, from $35,343 to $47,124; and the value of inventory would increase from $24,750 to $30,937 or by 25%. As a result, the total current asset value would increase by 38%, or from $66,693 to $91,921. As for the fixed assets, the example gives only the equipment, which increased by 43%, from $49,500 to $70,950. This would complete the list of all assets making the total value $162,871, an increase from $116,193 or by 40%.
All the increase in assets and in sales would not happen without the firm's ability to pay for the cost incurred and finance the expanded operations. The firm would do that, at least partially, by buying on credit and obtaining more loans. As a result, account payable would increase from $18,562 to $24,749 or by 33%; notes payable would increase from $14,850 to $16,000 or by 7%; and loans would increase from $49,500 to $82,500 or by 66%. Also, the firm has to pay its employees with a slight increase in the total salaries from $4125 to $4330 or only by a 5% increase. All the increases in the firm's liabilities would push the total liabilities to $127,579 from $87,037. That is an increase of 46%. Finally, subtracting all the liabilities from all the firm's assets would give us the firm's net worth or its owner's equity, which also would increase from $29,156 to$35,292 or by 21%.
9.2 Pro Forma and the Sales Ratio
A pro forma balance sheet can be constructed by depending only on the ratio of sales revenue in the income statement. The ratio of the sales revenue in the projected years (St+1) to the sales revenue in the current year (St) is called the sales ratio (S%).

Multiplying the sales ratio (S%) by any entry of the current year on the balance sheet would give us the pro forma value in the next year for that specific entry.
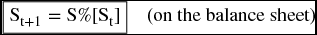
Looking at Table 9.3, we can see that all the entries on the next year column are obtained by multiplying S% by the corresponding entries on the current year column. From the income statement (Table 9.1), the sales ratio would be
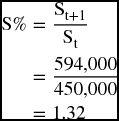
Table 9.3 Pro Forma Balance Sheet as Generated by Using % Sales
| Item | Current Year (t) | Next Year (t+1) |
| Current assets | ||
| Cash | 6600 | 8712 |
| Account receivable | 35,343 | 46,652 |
| Inventory | 24,750 | 32,670 |
| Total current assets | 66,693 | 88,034 |
| Fixed assets | ||
| Equipment | 49,500 | 65,340 |
| All assets | 116,193 | 153,374 |
| Current liabilities | ||
| Account payable | 18,562 | 24,501 |
| Notes payable | 14,850 | 19,602 |
| Salaries | 4125 | 5445 |
| Total current liabilities | 37,537 | 49,548 |
| Long-term liabilities | ||
| Loans | 49,500 | 65,340 |
| All liabilities | 87,037 | 114,888 |
| Equity | 29,156 | 38,486 |
Now we can verify all the projected entries in the next year (t+1) column on Table 9.3. For example, here are some selected entries.
-
Next year's inventory of $32,670 is obtained by

-
Next year's account payable is $24,501. It is obtained by

-
Next year's owner's equity is $38,486. It is obtained by

and so on for all entries.
9.3 Change in Sales (ΔS) and the Needed Fund
To determine whether the owner's equity on the balance sheet is enough to cover the increase in assets and whether the firm needs a new financing or not, we can use the following formula:

where
- NF: the needed fund
- ΔS: change in sales revenue between the current and next year.

- A: current year total assets obtained from the balance sheet
- L: current year total liabilities obtained from the balance sheet
- NP: net profit from the income statement
- OPO: owner's payout (the portion of profit which the owner takes as earnings. Let us assume here that the owner would take 58% of profit).
- St+1: sales in the next year
We can plug in all these values in the formula above as we obtain them from the income statement and the balance sheet.

Financial Forecasting
A forecast is an informed estimation of a future value. Financial forecasting is the process of predicting the future state and value of financial and economic variables and their changes using current knowledge and present and past data. In a simpler sense, forecasting is all about projecting the past and present into the future. Although forecasting has been described as an adventure into the practically unknown, it is ironically justified by the pressing need to reduce life uncertainties and minimize risks. We can logically say that all decisions taken today are somehow connected to past experiences, and are most likely to be connected to potential future development. This premise forms the compelling reason why most decision makers in public and private enterprises, as well as on an individual level, need to predict the future events.
Financial forecasting has proven to be critical for the efficient management of both the new venture and the established firm. Most business managers know that forecasting can be a difficult and daunting process but they also recognize the need to it as one of the most important tasks to facilitate decision-making. Managerial choice to predict sales, for example, would have a significant impact on planning for material and equipment capacities for production, employment size, inventories and storage requirements, and maintenance services. It would impact the financial manager's plans for the firm's cash flow, investment and capital budgeting, and projected profits and losses. In marketing, the sales forecast would be essential to plan for a sensible distribution program, promotional strategy, and marketing budget. Forecast of future sales would also be utilized in personnel plans for hiring, promotion, staff structure, and reward and retirement programs, and so on. The major point to emphasize here is that any business decision would not be sound if it is isolated from the future development of the contributing and related factors.
9.4 Role of Financial Forecasting
Financial forecasting acquires its importance for being instrumental in helping the firm with
- Clarifying its mission and presenting solid evidence to potential investors and lending institutions on the merits of the proposed project, its feasibility and expected profitability. This would be critical in securing the needed capital and obtain the suitable resources. It would also help in determining the proper value of the venture.
- Determining how much cash is needed for the present and future operations, and how would the cash flow changes according to the other predicted changes.
- Devising standard and aspired benchmarks for the firm's performance in order to be well prepared for the expectations, and be able to take the right and timely decisions.
- Drawing a road map for the firm's alternative business strategies as to facilitate taking the best choices and realizing the highest possible efficiency to achieve the firm's objectives.
9.5 Basic Steps of Forecasting
Although forecasting can practically be subjective and intuitive, and can rely a great deal on personal experience and philosophy, it can also be a systematic and scientific process that would apply the standard scientific research methods and procedures. This is especially true in the case of quantitative type of forecasting that would depend on data analysis and mathematical and statistical models. Generally speaking, we can summarize the basic steps of forecasting process by the following, which are also shown in Figure 9.2.
- Deciding on the major rationale and objectives of forecasting. That is to answer the questions: why are we predicting, and what do we want to achieve?
- Determining the span of time between the current time and the time in which the forecast is made. This interval is called the forecast horizon. It is known that the longer the horizon, the less the forecast accuracy. So, choosing a certain horizon is a balance act between achieving the forecast objective and keeping it as accurate and reliable as it can be. There are several factors that would play some roles into the determination of the horizon such as
- – Nature of the product and its life span
- – State of demand on the product
- – Availability of the needed data
- – Existence of the firm's strategic plan with a predetermined length
- Choosing the variables which are to be forecasted and those which are related directly to achieving the stated objectives. This step requires data collection which can be in any number of ways depending on what the forecaster sees fit.
- Selecting the appropriate forecasting model. As Figure 9.2 shows, deciding on the model would come as a result of deciding the previous three elements: the objectives, the horizon, and the variables. In the following section we will detail the many types of forecasting models. The forecaster would decide which model is more suitable based on many considerations.
- Applying the selected theoretical model and putting it into practice. In this step, calculations are made and estimates are obtained.
- Testing and evaluating the model to make sure that the forecast estimates are plausible and as close as possible to the actual data. The test also should assure if the method used is valid and appropriate. The results of one method or one model can also be evaluated in comparison to alternative methods in the light of getting the most reliable.
- Validating or modifying the model. Testing and evaluating the model should lead to
- – either validating the model if it turns out to be a reliable model which can deliver the expected accuracy, or
- – modifying the model if it fails to provide what it was set to do.
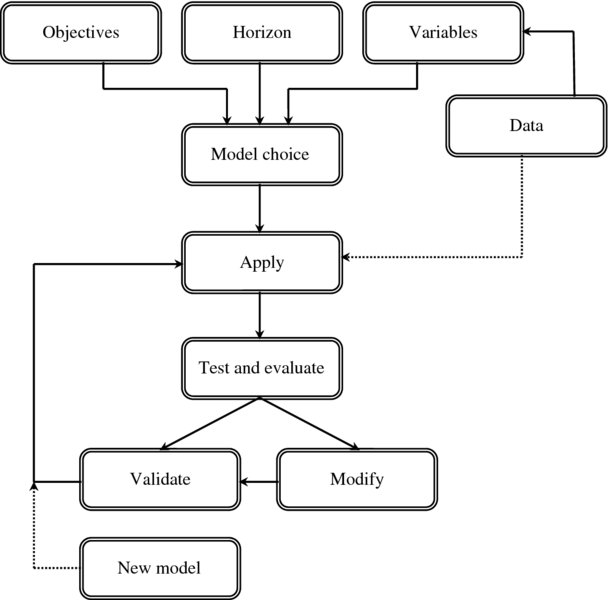
Figure 9.2 Basic Steps of Forecasting
Either way, the lessons would be directed to the subsequent application of the model. Sometimes the forecasters would like to try a new model if they cannot validate or modify the previous one. This is illustrated in Figure 9.2 by the dotted arrow which goes toward the application phase. This new model would require a new set of data and that is shown again by the dotted arrow from data to application.
9.6 Types of Forecasting Models
It has been said that forecasting is an art and science. Its major objective is to help make the best possible judgment about the future circumstances and conditions as they are predicted by a variety of methods. The most sensible approach is to combine the hard statistical facts with thoughtful, unbiased, and fair subjective judgment that utilizes solid experience and practical wisdom. There are many types of forecasting models. Each can be more appropriate than the others, depending on a host of determining factors such as
- what is being predicted and whether the purpose is to examine the trend continuation or certain turning points;
- what time considerations are being considered. Time factor may include
- – projection time whether it is for a short or long term,
- – time frame available to conduct the forecasting,
- – lead time during which the firm can make decisions using the estimations of the forecasted model;
- how much cost of the process is considered;
- what level of accuracy level is needed for a specific forecast;
- what data are available for use in the forecasting process;
- how complex is the forecasting model.
As for the scale of the process and its variables, forecasting can be macro forecasting where the subjects would be at the aggregate level such as the gross domestic product (GDP), national employment, national inflation rate, interest rate fluctuation, national money supply, and so on. On the other hand, micro forecasting involves variables at the levels of industry, firm, or specific market such as predicting the demand on a certain product or line of a product. Forecasting can also be conducted at subset micro or individual levels of consumer, market, and product.
As for the forecasting types according to the analytical methods, we can categorize them into the following:
Qualitative Models
Qualitative models use non-numerical examination and interpretation of observations for the purpose of discovering the underlying patterns of relationships and inferring their meanings and significance. They are also called judgmental models for relying on value judgment as the major tool in the analysis, as opposed to relying on the objective technical facts in the quantitative models. The best representative of the qualitative forecasting models is those which depend on expert opinion, polls and market research, and consumer surveys.
Generally speaking, judgmental models depend on people's intuitiveness and experience in determining what product sells, what consumers want or do not want, and what conditions and circumstances the market will experience. Based on that, they would decide the size of production that will be needed and the sales or profits that will be expected.
Opinions and Polls
Firms often seek the opinions and views of others who are in touch with the market and knowledgeable about the product and its customers. It can take the form of polling several groups, such as the executives, the sales staff, the customers, and the market experts. Firms can also conduct a Delphi method which uses a panel of corporate executives and experts but questioning them separately which makes it different from the jury of executives mentioned above which meet together and form a collective view. If the firm has an international connection through its product, it can also form a council of distinguished foreign dignitaries and business people to get their global perspectives on events and issues related to its market share and international consumer behavior.
Surveys and Market Research
The idea of utilizing surveys in forecasting stems from the fact that most major decisions of individuals and firms are usually preconceived and mostly predetermined. The required expenditures are planned and allocated before the actual spending. This constitutes a good rationale for surveying people on their plans and intentions which are most likely to reveal valuable information for forecasting the future. This is why it is justified for US firms to spend billions of dollars on surveys that enlist millions of people to ask them on a variety of questions which ultimately have strong economic relevance. Among the famous surveys are Surveys of Consumer's Expenditures (SCE) which are conducted by the Bureau of the Census; Surveys of Business Executives (SBE), which are conducted by a consortium of institutions such as the US Department of Commerce, the Securities and Exchange Commission, the National Industrial Conference Board, and McGraw-Hill Publishing Company. The third famous set of surveys is the Surveys of Inventory Changes and Sales Expectations (SICSE), which are conducted by the US Department of Commerce, The Institute for Supply Management, and Dun & Bradstreet Company. Yet, another important survey related to consumers in the national context is the Survey of Consumer Confidence (SCC), which produces three monthly indexes: the Consumer Confidence Index, the Present Situation Index, and the Expectations Index.
When it comes down to the short-term projections, the greatest value of surveying people would remain, as they are assumed, to provide insights into their intended actions on financial and economic matters. This technique is perhaps the only available way to predict consumer's responses on a new product. Over time, surveys have proven their large capacity to reveal the nature and direction of changes in consumer tastes and preferences.
As for market research, it is a general area that may include questionnaires, observations, “clinical tests,” field interviews, and focus groups. The primary purpose is to recognize the consumer with whom a firm is dealing. The identification and recognition of consumers could be demographically, economically, socially, and psychologically. Knowing the consumer means knowing what to produce and how to market the product. Market research is often used to introduce a new product, a new improvement on an existing product, or even to introduce a new business or new market. Data obtained through the various techniques are often extrapolated qualitatively and quantitatively to form certain predictions.
Quantitative Models
Quantitative models which involve utilizing historical data and relying on numerical representation of the observations for the purpose of describing and explaining the trends and changes that the observations reflect. There are two kinds of the quantitative models.
Structural Models
These models focus on the dependent–independent relationships between variables for the purpose of quantifying the impact of the independent variables on the variations in the dependent variable. Econometric models of forecasting are the best representative for the structural type.
Non-Structural Models
Models that focus on observing the patterns of change in the variables over time. The best representative of this type is the time series models as well as the barometric models. We shall start here with the time series model followed by a brief description of the barometric model. Time series is the most common analysis in forecasting. It constitutes more than two-thirds of the forecasting techniques used by businesses in the United States, according to a recent survey by the Institute of Business Forecasting (IBF).
9.7 The Analysis of Time Series
Time series models represent the most common analytical method in the field of forecasting. The central premise of the analysis is the use of historical data and the application of the ordinary least squares statistical techniques to obtain predictions of future values. It basically extrapolates data from the past and present into the future period for the purpose of identifying general patterns in the development of a single variable throughout time. This method allows to make forward projections out of data that have long-term trends through the utilization of a simple bivariate regression model where time trend (t) serves as the explanatory variable for the changes in the dependent variable.
Time Series and Data Variations
The long–term development of any variable can be plain and smooth if it follows a straightforward secular trend but that is not the case very often. The development of most variables historically contains several sorts of variation that would affect the real value of the variable if it is predicted out of the general unadjusted progress. This is why an essential part of this analysis is to recognize and count for these possible fluctuations within the general flow of data. Calculating the impact of these variations would allow the adjustment of the forecasts made based on the estimates that the regression equation yields. Most of the variations in the time series data are due to the following common patterns:
Secular Trends
Secular trend is a long–term consistent development in a variable value that is often characterized by a general steady increasing or decreasing pattern and most likely represented by a solid smooth line going upward or downward. Population growth and per capita income are typical examples for the increasing secular trend while goods that go out of date over time such as typewriters, cable phones, and personal train transportation are typical decreasing secular trends.
Seasonal Variations
Seasonal variations are recurring rhythmic fluctuations which are usually to reflect certain seasons, weather conditions, or specific periodic occasions such as school time or holidays like Christmas or Thanksgiving. The sales of many products can reflect typical seasonality such as air conditioners, fans, swim suits, shorts, and tourism services in summer and snow blowers, snow tires, heavy coats in winter, garden products in spring, turkey at Thanksgiving, and gifts in Christmas times.
Cyclical Fluctuations
Cyclical fluctuations are long–term patterns of expansion and contraction in the economic activity in general that reflects the recurring conditions of the economic business cycle that characterizes the free market economy. The construction and housing sector, for example, exhibits a typical long–term cycle in its activity that could last 10 years or more while other sectors may experience shorter cycles.
Random Changes
Random changes are the reflection of the irregular unpredictable fluctuations that are due to events such as war, political instability, natural disasters, strikes, and the like. This type of variation is very difficult to count for in any modeling due to the random nature of its occurring and the degree of its impact.
Mathematically, the actual value of a variable in the time series data (Yt) can be expressed as a function of all of the above variations.

where
- Sect is the secular effect for t period
- Seat is the seasonal effect for t period
- Cyct is the cyclical effect for t period
- Rant is the random effect for t period
Geometrically, Figure 9.3 shows an example of each of the patterns.
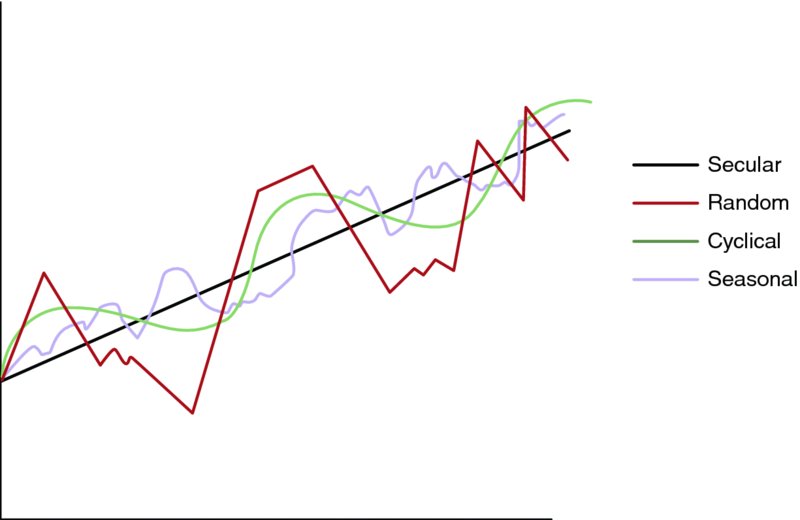
Figure 9.3 Time-Series and Data Variations
9.8 Fitting the Model
Time series data are different in terms of their appropriateness to fit into a certain function for the purpose of the regression estimation. Fortunately, most of the economic data can easily fit into the linear function.
But some may fit better into the quadratic function
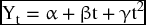
where the coefficient of t2 reflects the type of growth. Positive coefficient (γ > 0) refers to an increasing rate of growth and negative coefficient (γ < 0) refers to a decreasing rate of growth. Figure 9.4 shows both quadratic functions against the linear trend.
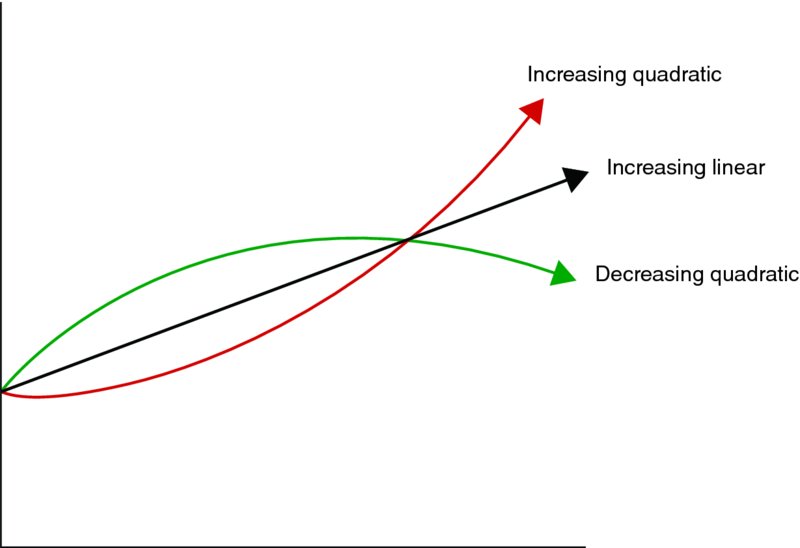
Figure 9.4 Quadratic Functions and Linear Trends
Some data may need to be fitted into an exponential function of the form
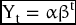
which has to be transformed to linear by the logarithmic function in order to be estimated by the ordinary least squares method:
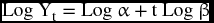
and with a slight rearrangement, we can better identify the parameters
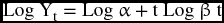
where Log α is a constant term and Log β is the time coefficient. The antilog function would return the parameters to their original state after estimation.
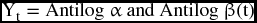
The following example shows how supportive information about a product can be used in the fitting of a certain function.
Example This example is using the linear function. It is about forecasting the size of membership in an athletic gym of a club. Suppose that the firm owning the club has conducted a survey and collected a list of related information including the following.
- – At any time period (t) number of members of the club who are resuming their membership from a previous period is a certain percentage (x) of the total number in the previous period [Mt–1]. Therefore, we can say that the number of members of the club at any time period t [Mt] would contain first those who were carried over from the previous period (xMt–1).
– Also, at any period (t), there would be a number of new members just joining the club for the first time. Suppose this number is a certain percentage (y) of the estimated total market demand on this particular service (D). Therefore, this number can be expressed as a y percentage of D after excluding those who already joined before.
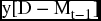
– Total number of members at period (t) can then be obtained as a summation of the two previous parts.
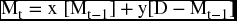
combining the similar terms, we get
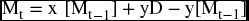
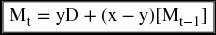
Now, let us go back to the firm's survey. Suppose that the survey revealed that the total demand on this service in the market is estimated by 1200 members and that those who carry their membership over to the next period is averaging 76% of those who already have membership last period, and that those who join the club for the first time is usually an average of 18% of the market demand. Plugging these real figures in the equation above will give us the numeric form of the function

or
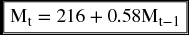
This is the linear function format that is used to forecast for the next period using the previous period. So if, for example, we look at the record of membership for the last year and find it 450 members, we can immediately extrapolate an estimation of the following year membership and probably for a few more years into the future.
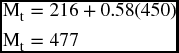
But this kind of function is usually obtained by running a simple bivariate regression analysis on two columns of data. The first is the membership size for a number of previous periods, say years, and the trend of time from 1 to n. The 216 above would be the y-intercept of the equation or the constant term, and the 0.58 would be β value or the slope of the regression line. If last year's membership was 450, we can project the membership status for the next 7 years to see that it is a secular trend that is increasing but in a decreasing rate. Table 9.4 shows the membership forecasts for the next 7 years.
Table 9.4 Membership Forecast for 7 Years
| T | Mt–1 | Mt | ΔMt |
| 0 | 450 | 477 | |
| 1 | 477 | 493 | 16 |
| 2 | 493 | 502 | 9 |
| 3 | 502 | 507 | 5 |
| 4 | 507 | 510 | 3 |
| 5 | 510 | 512 | 2 |
| 6 | 512 | 513 | 1 |
| 7 | 514 | 514 | 0 |
It is essential for the manager to know that the growth of membership is decreasing and that 7 years from now there will be no single person joining the club when the number of members in the current year would equal the number in the previous year. It is a wakeup call to change strategies and try to turn the tide around into an increasing rate growth.
The function to estimate the data at hand could also be non-linear had the conditions and information be different. Let us assume the data would fit an exponential function such as

where the coefficients that would be estimated are β and N. The value of Mt or the membership size at any period (t) would grow proportionally with time if N is larger than 1 (N > 1). However, it would decline proportionally with time if N value is less than:

For example, if running the regression yields that N is 1.23, it would mean that Mt or annual membership would increase by (N – 1) or by 23% annually. But if the estimate of N is 0.89, it would mean that membership would decline annually by 11%.
As we have seen before, an exponential function should be transformed to a linear function by applying the logarithms in order to be estimated by the ordinary least squares method.
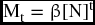
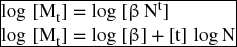
To estimate Mt, we need to take the antilog of both coefficients.
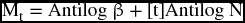
and the figures of antilog will be the values of the parameters.
9.9 Adjusting for Seasonality
Since time series data is inherently characterized by the sorts of variations mentioned above, it is essential to adjust the estimation of the regression equation for those variations so that we can get forecasts that reflect the realities of data. We will focus on the seasonal variation as it is the most common variation in the time series data, and we will calculate its impact using more than one method. It is worth noting here that isolating these variations and adjusting the value of data according to their impacts is what is called the “decomposition process.”
Let us first consider some quarterly data on a product sales for 20 quarters and let us use the following fitted regression equation to calculate quarterly forecasts out of the actual data.
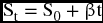
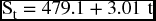
where S0 = 479.1 is the constant coefficient that stands for an average for the initial sales and β = 3.01 is the coefficient for t. Table 9.5 shows the actual and forecasted sales for the first quarter in 2001 to the fourth quarter in 2010.
Table 9.5 Sales Forecasts for 20 Quarters
| 1 | 2 | 3 | 4 |
| A | F | ||
| Year.quarter | t | Actual sale | Forecasted sale |
| 2006.1 | 1 | 529.8 | 482.11 |
| .2 | 2 | 487.6 | 485.12 |
| .3 | 3 | 505.7 | 488.13 |
| .4 | 4 | 512.2 | 491.15 |
| 2007.1 | 5 | 507.0 | 494.15 |
| .2 | 6 | 486.5 | 497.16 |
| .3 | 7 | 466.2 | 500.17 |
| .4 | 8 | 474.7 | 503.18 |
| 2008.1 | 9 | 492.7 | 506.19 |
| .2 | 10 | 496.0 | 509.20 |
| .3 | 11 | 490.6 | 512.21 |
| .4 | 12 | 483.1 | 515.22 |
| 2009.1 | 13 | 519.0 | 518.23 |
| .2 | 14 | 510.6 | 521.24 |
| .3 | 15 | 515.4 | 524.25 |
| .4 | 16 | 525.6 | 527.26 |
| 2010.1 | 17 | 526.7 | 530.27 |
| .2 | 18 | 526.2 | 533.28 |
| .3 | 19 | 560.7 | 536.29 |
| .4 | 20 | 598.6 | 539.30 |
The following are three methods to capture the impact of seasonality:
The Simple Average of Errors Method
According to this method, we calculate the simple average of error for each quarter and adjust the next prediction by its value. So, let us rearrange Table 9.5 into Table 9.6 by the following steps:
- Group the similar quarters together first.
- Create another column for the errors. The error is the difference between the forecasted and the actual values.
- Calculate the simple average for each group of similar quarters.
Table 9.6 Simple Average Errors
| 1 | 2 | 3 | 4 |
| A | F | Errors | |
| Year.quarter | Actual sales | Forecasted sales | F – A |
| 2006.1 | 529.80 | 482.11 | –47.69 |
| 2007.1 | 507.00 | 494.15 | –12.85 |
| 2008.1 | 492.70 | 506.19 | 13.49 |
| 2009.1 | 519.00 | 518.23 | –0.77 |
| 2010.1 | 526.70 | 530.27 | 3.57 |
| Average error for the first quarter | –8.85 | ||
| 2006.2 | 487.60 | 485.12 | –2.48 |
| 2007.2 | 486.50 | 497.16 | 10.66 |
| 2008.2 | 496.00 | 509.20 | 13.2 |
| 2009.2 | 510.60 | 521.24 | 10.64 |
| 2010.2 | 526.20 | 533.28 | 7.08 |
| Average error for the second quarter | 7.82 | ||
| 2006.3 | 505.70 | 488.13 | –17.57 |
| 2007.3 | 466.20 | 500.17 | 33.97 |
| 2008.3 | 490.60 | 512.21 | 21.61 |
| 2009.3 | 515.40 | 524.25 | 8.85 |
| 2010.3 | 560.70 | 536.29 | –24.41 |
| Average error for the third quarter | 4.49 | ||
| 2006.4 | 512.20 | 491.14 | –21.06 |
| 2007.4 | 474.70 | 503.18 | 28.48 |
| 2008.4 | 483.10 | 515.22 | 32.12 |
| 2009.4 | 525.60 | 527.26 | 1.66 |
| 2010.4 | 598.60 | 539.30 | –59.3 |
| Average error for the fourth quarter | –4.28 | ||
If we want to predict the four quarters of 2011, their t values would be obtained by continuing the sequence in Table 9.5. So, they would be 21, 22, 23, 24. Plugging these t values into the regression equation gives us the forecast for 2011 quarters as in Table 9.7.
Table 9.7 Regression Analysis Results
| F | |||||
| Year.Quarter | T | St = 479.1 + 3.01 t | Forecasted Sale | ||
| 2011.1 | 21 | 479.1 + 3.01(21) = | 542.31 | ||
| 2011.2 | 22 | 479.1 + 3.01(22) = | 545.32 | ||
| 2011.3 | 23 | 479.1 + 3.01(23) = | 548.33 | ||
| 2011.4 | 24 | 479.1 + 3.01(24) = | 551.34 | ||
| Multiple linear regression – estimated regression equation | |||||
| Sales [t] = 479.097368421053 + 3.01406015037595Times[t] + e[t] | |||||
| Multiple linear regression – ordinary least squares | |||||
| T-STAT | |||||
| Variable | Parameter | S.D. | HO: parameter = 0 | 2-tail P-value | 1-tail P-value |
| (Intercept) | 479.097368421053 | 11.742379 | 40.8007 | 0 | 0 |
| Time | 3.01406015037595 | 0.980235 | 3.0748 | 0.006529 | 0.003264 |
| Multiple linear regression – regression statistics | |||||
| Multiple R | 0.586832495103272 | ||||
| R-squared | 0.344372377309132 | ||||
| Adjusted R-squared | 0.307948620492972 | ||||
| F-TEST (value) | 9.45460895336176 | ||||
| F-TEST (DF numerator) | 1 | ||||
| F-TEST (DF denominator) | 18 | ||||
| p-value | 0.00652875667517216 | ||||
| Multiple linear regression = residual statistics | |||||
| Residual standard deviation | 25.2778977211252 | ||||
| Sum squared residuals | 11501.498037594 | ||||
But these forecasts are not adjusted for any seasonal variation as it is reflected by the simple average errors. This is why we should perform the adjustment. Looking at the average of errors, we can see that the forecast for the first quarter was, in general, less than the actual by an average of 8.85. So we can add back this difference to the forecast of the first quarter in 2011, as in Table 9.8.
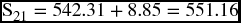
Table 9.8 Forecast Adjustment for the Four Quarters of 2011
| Year.Quarter | Fsa = F ± SAE | Fsa |
| 2011.1 | 542.31 + 8.85 | 551.16 |
| 2011.2 | 545.32 – 7.82 | 537.50 |
| 2011.3 | 548.33 – 4.49 | 543.84 |
| 2011.4 | 551.34 + 4.28 | 555.62 |
For the second quarter of 2011, the forecasted value was more than the actual by an average of 7.82. So this difference should be discounted.

For the third quarter, the average error is 4.49. So the third quarter of 2011 would be adjusted by discounting 4.49.
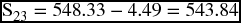
and the fourth quarter has a –4.28 average error which means it is underestimated by 4.28. So, adjusting the fourth quarter of 2011 requires adding this amount.
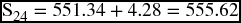
Figures 9.5, 9.6 and 9.7 show the difference between the actual and the interpolated data, as well as the path of the residual values.
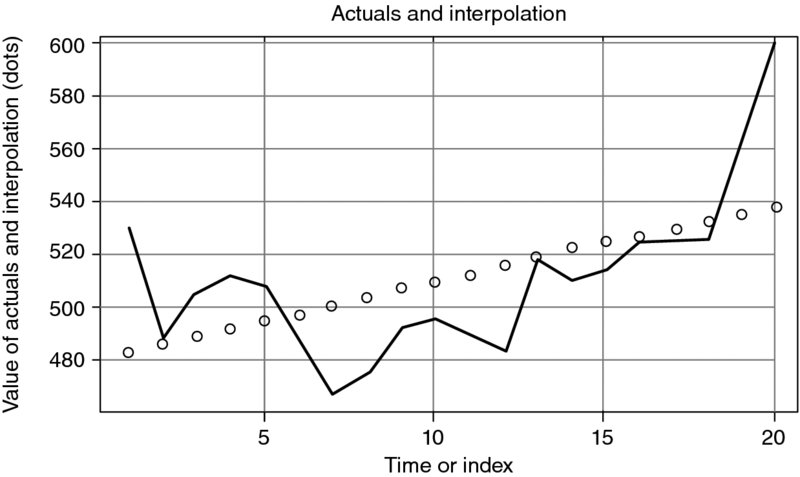
Figure 9.5 Actual Data and Interpolation I
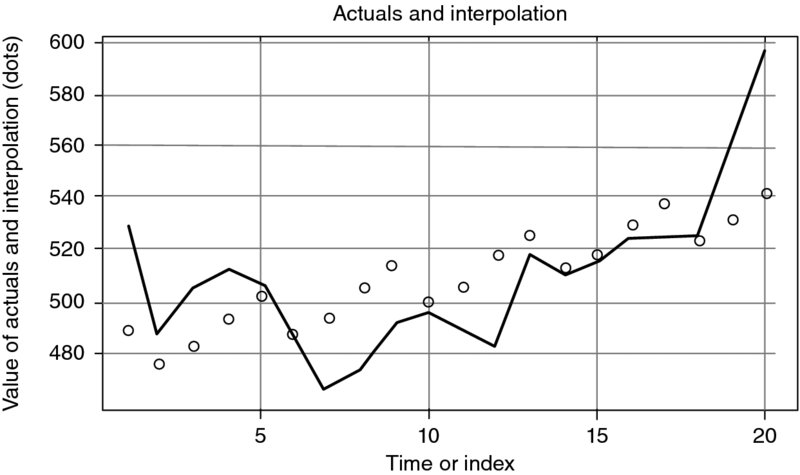
Figure 9.6 Actual Data and Interpolation II
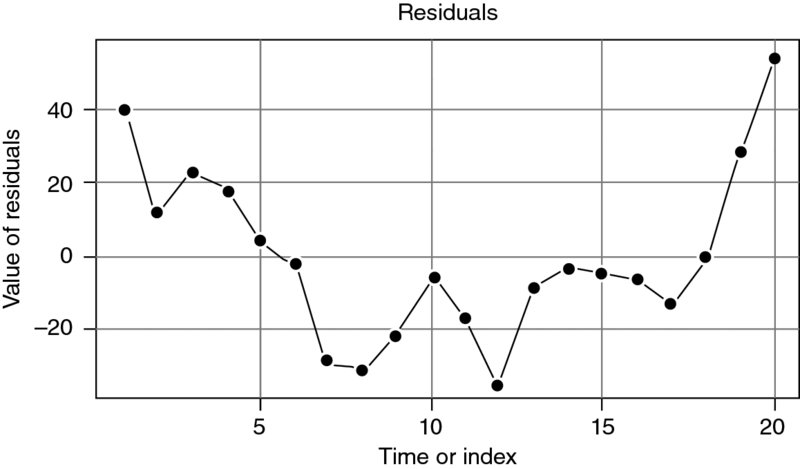
Figure 9.7 Residual Values
The Actual to Forecast (A/F) Ratio Method
We are arranging our data just like in the previous table where similar quarters of all years are grouped together. This time we calculate the A/F ratio by dividing the actual data (A) by the forecasted (F). Then we obtain a 5-year average of the ratio for the similar quarters individually. It is the A/F ratio for a specific quarter that would serve as a multiplier of the predicted values to adjust them for seasonality.

where Fsa is the seasonally adjusted forecast, F is the unadjusted forecast, and (A/F)q is the quarterly average ratio as it is calculated in Table 9.9.

Table 9.9 Five-year Average Quarterly Ratio of (A/F)
| A | F | A/F | |||
| Year | Quarter | Actual sale | Forecasted sale | Ratio | |
| 2006 | 1 | 529.80 | 482.11 | 1.10 | |
| 2007 | 1 | 507.00 | 494.15 | 1.03 | |
| 2008 | 1 | 492.70 | 506.19 | 0.97 | |
| 2009 | 1 | 519.00 | 518.23 | 1.00 | |
| 2010 | 1 | 526.70 | 530.27 | 0.99 | |
| 5–year average ratio for the first quarter | 1.02 | (A/F)q1 | |||
| 2006 | 2 | 487.60 | 485.12 | 1.01 | |
| 2007 | 2 | 486.50 | 497.16 | 0.98 | |
| 2008 | 2 | 496.00 | 509.20 | 0.97 | |
| 2009 | 2 | 510.60 | 521.24 | 0.98 | |
| 2010 | 2 | 526.20 | 533.28 | 0.97 | |
| 5–year average ratio for the second quarter | 0.99 | (A/F)q2 | |||
| 2006 | 3 | 505.70 | 488.13 | 1.04 | |
| 2007 | 3 | 466.20 | 500.17 | 0.93 | |
| 2008 | 3 | 490.60 | 512.21 | 0.96 | |
| 2009 | 3 | 515.40 | 524.25 | 0.98 | |
| 2010 | 560.70 | 536.29 | 1.04 | ||
| 5–year average ratio for the third quarter | (A/F)q3 | ||||
| 2006 | 4 | 512.20 | 491.14 | 1.04 | |
| 2007 | 4 | 474.70 | 503.18 | 0.94 | |
| 2008 | 4 | 483.10 | 515.22 | 0.94 | |
| 2009 | 4 | 525.60 | 527.26 | 0.99 | |
| 2010 | 4 | 598.60 | 539.30 | 1.11 | |
| 5–year average ratio for the fourth quarter | 1.00 | (A/F)q4 | |||
| Year.Quarter | Fsa = F(A / F)q | Fsa | |||
| 2011.1 | 542.31 (1.02) = | 553.16 | |||
| 2011.2 | 545.32 (0.98) = | 534.41 | |||
| 2011.3 | 548.33 (0.99) = | 542.85 | |||
| 2011.4 | 551.34 (1.00) = | 551.34 | |||
The Dummy Variables Method
We can adjust for seasonality by using the regression equation obtained from the run that includes dummy variables for the quarters.
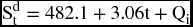
where Qi is the estimated coefficient for each quarter (Q1, Q2, Q3) while the fourth quarter is represented by the intercept only. So, the estimation of the forecasted value of sales for the first quarter of 2011 is going to use the intercept t = 21, and the Q1 coefficient (5.39). The forecasted value for the second quarter would use the intercept t = 22, and the Q2 coefficient (–11.33), and the value for the third quarter would use the intercept t = 23, and the coefficient for Q3 = –8.06. The fourth quarter would not have any Q4 coefficient since it is considered the base period.
Table 9.10 shows the calculations of the forecast sales for the four quarters of 2011 as they are adjusted for the seasonal variation according to the regression with dummies method. Table 9.11 shows the results of the Multiple Regression run.
Table 9.10 Forecasted Sales Using Regression with Dummy Variables
| Sdt = α + βt + Qi | Fdsa | ||
| Year.Quarter | t | Regression w/dummies equation | Adjusted forecast |
| 2011.1 | 21 | S21 = 482.1 + 3.06(21) + 5.39 | 551.75 |
| 2011.2 | 22 | S22 = 482.1 + 3.06(22) – 11.3 | 538.09 |
| 2011.3 | 23 | S23 = 482.1 + 3.06(23) – 8.06 | 544.42 |
| 2011.4 | 24 | S24 = 482.1 + 3.06(24) | 555.54 |
Table 9.11 Multiple Regression Results
| Multiple linear regression – estimated regression equation | |||||
| Sales [t] = + 482.09 + 3.06250000000001 Time[t] + 5.38749999999994 Q1[t] – 11.335Q2[t] – 8.05750000000001Q3[t] + e[t] | |||||
| Multiple linear regression – ordinary least squares | |||||
| T-STAT | |||||
| Variable | Parameter | S.D. | H0: parameter = 0 | 2-tail P-value | 1-tail P-value |
| (Intercept) | 482.09 | 17.359597 | 27.7708 | 0 | 0 |
| Time | 3.06250000000001 | 1.05258 | 2.9095 | 0.010784 | 0.005392 |
| Q1 | 5.38749999999994 | 17.134764 | 0.3144 | 0.757533 | 0.378767 |
| Q2 | –11.335 | 16.972345 | –0.6679 | 0.514374 | 0.257187 |
| Q3 | –8.05750000000001 | 16.874144 | –0.4775 | 0.639885 | 0.319943 |
| Multiple linear regression – regression statistics | |||||
| Multiple R | 0.627458670627651 | ||||
| R-squared | 0.393704383345819 | ||||
| Adjusted R-squared | 0.232025552238038 | ||||
| F-TEST (value) | 2.43510161873548 | ||||
| F-TEST (DF numerator) | 4 | ||||
| F-TEST (DF denominator) | 15 | ||||
| P-value | 0.0926907022517692 | ||||
| Multiple linear regression – residual statistics | |||||
| Residual standard deviation | 26.6284058854449 | ||||
| Sum squared residuals | 10636.08 | ||||
The results of the adjusted forecasts in the three methods would have been much closer if it was not for the practical rounding.
9.10 The Smoothed Forecasts
Smoothing techniques are other ways to produce forecasts values based on past observations. It is more suited for time series data that have slow and infrequent changes in the underlying pattern, and data which exhibits noticeable degree of randomness or irregularity. The objectives of the smoothed forecast techniques are to even out such irregularities as much as possible and reduce or eliminate the distortions arising from the random variations. The forecasted value of a variable according to these techniques is basically an average of the previous data. The most common of these techniques are the moving average, and the exponential smoothing.
Simple Moving Average Method
This method calculates the predicted value of a variable as a simple average of a number of observations (p) that would overlap throughout the prediction list by adding the latest observation while dropping off the earliest. For example, if we are at the end of July and we want to predict the sales for August, we can use the data we have for the previous month to get an average to represent a predicted value for August. A 3-month average would be adding the sales of July, June, and May and dividing by three. If at the end of August and after recording the actual sales of August we want to predict for September, the 3-month moving average requires that we add August being the latest and drop off May being the earliest so that the September value becomes an average of August, July, and June. The predicted sales for October would be an average of September, August, and July while June is dropped off, and so on. The average would move forward throughout the series, hence the name of the “moving” average. We can obtain the general formula for the moving average this way. Let us call the actual data of Sales At where t is the current time and can reflect the number of observations such that if we are in July, At would be A7, and the previous month is June and can be denoted by A6 which is also At–1 = A7–1 = A6. The month after July is August which can be denoted by A8 or At+1 = A7+1 = A8. So the forecast for August is an average of July, June, and May.
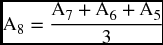
or
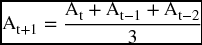
The denominator 3 is the number of periods (p) that would constitute the elements of the average according to the forecaster, and it could be any number the forecaster chooses. This would make the formula more general as
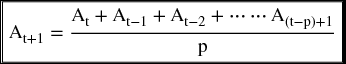
So, if we are in November (11) and want to calculate a 5-month forecast for December (12), the forecasted value for December would be
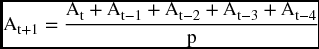
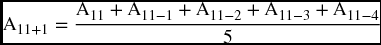
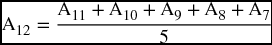
The last observation is A7 and it is equal to the last term in the general formula
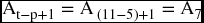
Column no. 3 of Table 9.12 shows the actual sales of customized computers as a local store during the 16 quarters of 2008–2011. The three-quarter forecasts are shown in column no. 4 starting at the fourth observation, 184.3, as the first average of observations 1, 2, and 3.
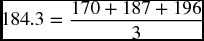
Table 9.12 Three-Quarter and Five-Quarter Forecasts of Customized Computers
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| A | F1 | F2 | ||||||
| Actual | 3–quarter | 5–quarter | ||||||
| Obs. | Year.Quarter | sale | MA | A–F1 | [A–F1]2 | MA | A–F2 | [A–F2]2 |
| 1 | 2008.1 | 170 | ||||||
| 2 | .2 | 187 | ||||||
| 3 | .3 | 196 | ||||||
| 4 | .4 | 204 | 184.5 | 19.7 | 388.09 | |||
| 5 | 2009.1 | 153 | 195.6 | –42.6 | 1814.75 | |||
| 6 | .2 | 195 | 184.3 | 10.7 | 114.49 | 182 | 13 | 169 |
| 7 | .3 | 162 | 184 | –22 | 484 | 187 | –25 | 625 |
| 8 | .4 | 144 | 170 | –26 | 676 | 182 | –38 | 1444 |
| 9 | 2010.1 | 188 | 167 | 21 | 441 | 171.6 | 16.4 | 268.96 |
| 10 | .2 | 196 | 164.6 | 31.4 | 985.96 | 168.4 | 27.6 | 761.76 |
| 11 | .3 | 150 | 176 | –26 | 676 | 177 | –27 | 729 |
| 12 | .4 | 194 | 178 | 16 | 256 | 168 | 26 | 676 |
| 13 | 2011.1 | 154 | 180 | –26 | 676 | 174.4 | –20.4 | 416.16 |
| 14 | .2 | 190 | 166 | 24 | 576 | 176.4 | 13.6 | 184.96 |
| 15 | .3 | 159 | 179.3 | –20.3 | 412.09 | 176.8 | –17.8 | 316.84 |
| 16 | .4 | 140 | 167.6 | –27.6 | 261.76 | 169.4 | –29.4 | 864.36 |
| 17 | 2012.1 | 163 | 7762.15 | 167.4 | 6456.04 |
Next on the column is 195.6 as the forecast value for sales in the first quarter of 2009. It is obtained by averaging only the previous three observations and dropping off the earliest.
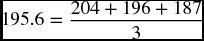
Column no. 7 of the table shows the forecasts using a five-quarter moving average. For example, the predicted value of sales for the third quarter in 2011 (176.8) is obtained by averaging out the previous five actual values.
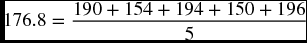
As to why and when the forecast uses a specific value of P, it depends on the forecaster's design, objectives, and justifications of the forecast. Generally speaking, the larger the P or the number of observations constituting the average, the smoother the forecasts and the more effective the impact on dealing with randomness that would be spread out over more observations, each of which would get less weight 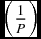 as P increases. If we graph this time series in its three columns of estimates as they are shown in Table 9.13, it would be clearer that the forecast values obtained by using five-quarter moving average produced a smoother curve (c) as compared to the other curves (Figure 9.8). The actual data (curve A), and the three-quarter moving average forecasts (curve B). It is a visual confirmation to the notion that a greater value of P would result in ironing out most of the randomness in the time series data.
as P increases. If we graph this time series in its three columns of estimates as they are shown in Table 9.13, it would be clearer that the forecast values obtained by using five-quarter moving average produced a smoother curve (c) as compared to the other curves (Figure 9.8). The actual data (curve A), and the three-quarter moving average forecasts (curve B). It is a visual confirmation to the notion that a greater value of P would result in ironing out most of the randomness in the time series data.
Table 9.13 Three-quarter and 5-quarter Forecasts of Customized Computers
| F1 | F2 | |||
| 3–quarter | 5–quarter | |||
| Obs. | Year.Quarter | A | MA | MA |
| 1 | 2008.1 | 120 | ||
| 2 | .2 | 187 | ||
| 3 | .3 | 196 | ||
| 4 | .4 | 204 | 184.3 | |
| 5 | 2009.1 | 153 | 195.6 | |
| 6 | .2 | 195 | 184.3 | 182 |
| 7 | .3 | 162 | 184 | 187 |
| 8 | .4 | 144 | 170 | 182 |
| 9 | 2010.1 | 188 | 167 | 171.6 |
| 10 | .2 | 196 | 164.6 | 168.4 |
| 11 | .3 | 150 | 176 | 177 |
| 12 | .4 | 194 | 178 | 168 |
| 13 | 2011.1 | 154 | 180 | 174.4 |
| 14 | .2 | 190 | 166 | 176.4 |
| 15 | .3 | 159 | 179.3 | 176.8 |
| 16 | .4 | 140 | 167.6 | 169.4 |
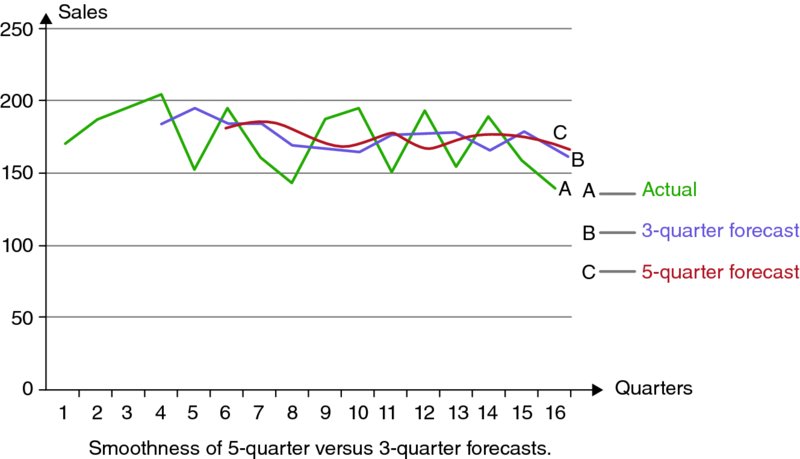
Figure 9.8 Smoothness of Five-Quarter Versus Three-Quarter Forecasts
The Weighted Moving Average
The simple moving average method assumes uniformity among the observations of time series data in terms of their impact on forming the predicted value. It is, in fact, one of the shortcomings that counteracts the simplicity of the model. As a response to such an important pitfall, forecasters came up with the idea of weighing the importance of the observations that would form the average. The weighted moving average, therefore, allows the forecasters to assign certain weights to each observation. The weights are supposed to be consistent with the external influences on the average. The forecasters may consider giving more or less importance to a specific observation or term, according to their knowledge and discretion. All assigned weights may or may not total to one (1).
The forecast value for the next period (Ft+1) will be calculated as
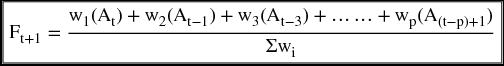
where wi = w1, w2,……, wp are the number of weights that are assigned to as many observations as available for the average. The 3-month moving average, has a P = 3 and, therefore, has three weights (w1, w2, w3) assigned to each of the three actual observations, A1, A2, A3.
Example Suppose that the forecaster assigned the following weights to the four quarters of 2011: 0.15, 0.25, 0.37, 0.23. What would be the four-quarter predicted sales for the first quarter of 2012? Use the actual sales in the previous table.

Since the summation of weights is equal to 1 (0.15 + 0.25 + 0.37 + 0.23), we can skip dividing by Σwi and just calculate the numerator part of the equation
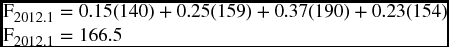
Example What if the weights are 0.18, 0.24, 0.33, 0.20?
In this case, the summation of the weights is 0.95, which would have to be the denominator.

Example Suppose that at the end of the first quarter of 2012 the sales turn out to be 164. Use the four-quarter weighted moving average to predict the sales in the second quarter of 2012 assuming the same weights of the last example.
Since we use the four-quarter moving average and we have a new actual sales of the first quarter of 2012, we should drop off the earliest quarter in the group which is the first quarter of 2011 (154). So, the four quarters forming the average now are 2012.1, 2011.4, 2011.3, and 2012.2.

Exponential Smoothing
Exponential smoothing model is another way to respond to the uniformity assumption of the moving average method, which treats all time periods in the series equally. This method assumes that the most recent past is more predictive of the future value of the forecast than the distant past. This assumption prompted the introduction of a constant (α) to signify the weight of the immediate past while the earlier data take a (1–α) weight. In this case, α is assigned by the forecaster's discretion and the extent of his belief in the increasing impact of the most recent data on the prediction. The value of α is between 0 and 1 but frequently has been given values between 0.10 and 0.35.
So, the exponential model calculates the value of the forecast for the next period (Ft+1) as a weighted average of the actual observation in the current period (At) and the forecast value for the same period (Ft), where α is assigned to the current actual and (1–α) is assigned to the smoothed forecast (Ft).
Logically, if we write this equation for the current period (t), we get
and if we substitute (2) into (1), we get

and if we substitute for Ft–1 as
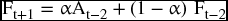
we get

and if we keep substituting for the forecast of the past periods Ft–2, Ft–3 and earlier, we will realize that we have an equation of an exponentially weighted moving average with its weights forming a geometric progression
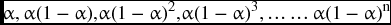
which illustrates that any value of α would produce a decreasing values of weights. For example, if α is 0.40, the rest of the weights would be calculated as in Table 9.14.
Table 9.14 Value of Weights as Geometric Progression
| Term | Weight | Value |
| 1 | α | 0.40 |
| 2 | α(1 − α)1 | 0.24 |
| 3 | α(1 − α)2 | 0.144 |
| 4 | α(1 − α)3 | 0.0864 |
| 5 | α(1 − α)4 | 0.0518 |
| 6 | α(1 − α)5 | 0.0311 |
| 7 | α(1 − α)6 | 0.0186 |
| 8 | α(1 − α)7 | 0.0111 |
| . | . | . |
| . | . | . |
| . | . | . |
This shows that the weights get smaller and smaller as we go back in the past. It dropped here to 1% at the eighth term back. It is a confirmation that assigning a higher α would place a greater importance on the most recent past as a predictor of the future forecast, and logically placing less importance on the earlier observations. However, greater value of α produces less smoothing, so for a smoother line a smaller α would help.
If we slightly rearrange the original format of the exponential smoothing model,
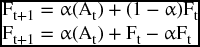
we can get the most practical format to use for calculations.
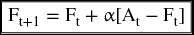
We use this equation to produce forecasts in the F1 and F2 columns of Table 9.15, using two values of α, 0.20 and 0.45. For the first forecast of the first quarter of 2008, we use the actual observation (170) for At and the general average of the actual (173.9) for Ft, but for the rest of forecasts, Ft would be the previous F. For example, to predict the sales for the second quarter of 2010, using an α of 0.20, we use 188 for At and 170.9 for Ft as they are the current data at the time to predict for the following quarter.
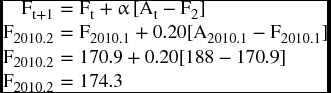
Table 9.15 Exponential Smoothing Forecasts Using Two Values of Alpha
| α = 0.20 | α = 0.45 | |||||||
| Obs. | Year.Quarter | A Actual sale | F1 | A–F1 | [A–F1]2 | F2 | A–F2 | [A–F2]2 |
| 1 | 2008.1 | 170 | 173.9 | –3.9 | 15.2 | 173.9 | –3.9 | 15.2 |
| 2 | .2 | 187 | 173.1 | 13.9 | 193.2 | 172.1 | 14.9 | 222 |
| 3 | .3 | 196 | 175.9 | 20.1 | 404 | 178.8 | 17.2 | 295.8 |
| 4 | .4 | 204 | 179.9 | 24.1 | 580.8 | 186.5 | 17.5 | 306 |
| 5 | 2009.1 | 153 | 184.7 | –31.7 | 1004.9 | 194.4 | –41.4 | 1714 |
| 6 | .2 | 195 | 178.4 | 16.6 | 275.5 | 175.8 | 19.2 | 368.6 |
| 7 | .3 | 162 | 181.7 | –19.7 | 388 | 184.4 | –22.4 | 501.8 |
| 8 | .4 | 144 | 177.7 | –33.7 | 1135.7 | 174.3 | –30.3 | 918.1 |
| 9 | 2010.1 | 188 | 170.9 | 17.1 | 292.4 | 160.7 | 27.3 | 745.3 |
| 10 | .2 | 196 | 174.3 | 21.7 | 470.9 | 173.0 | 23 | 529 |
| 11 | .3 | 150 | 178.6 | –28.6 | 817.9 | 183.3 | –33.3 | 1108.9 |
| 12 | .4 | 194 | 172.9 | 21.1 | 445.2 | 168.3 | 25.7 | 660.5 |
| 13 | 2011.1 | 154 | 177.1 | –23.1 | 533.6 | 179.8 | –25.8 | 665.6 |
| 14 | .2 | 190 | 172.5 | 17.5 | 306.2 | 168.2 | 21.8 | 475.2 |
| 15 | .3 | 159 | 176.0 | –17 | 289 | 178.0 | –19 | 361 |
| 16 | .4 | 140 | 172.6 | –32.6 | 1062.7 | 169.4 | –29.4 | 864.4 |
| Average = 173.9 | 8215 | 9737 | ||||||
9.11 Barometric Forecasting
Due to the continuous and significant overlap between micro and macro level of economic activities, firm managers have traditionally realized the need to be aware of the directions of the major macroeconomic variables when they forecast for their own variables at the micro level. For example, predicting the sales or profits for a specific product is inextricably connected to consumer demand, income, employment level, inflation, and so on of many aggregate economic variables. Generally, any business activity at the firm level can be connected to the general conditions of the economy. Economists have noticed the significant impact that some economic variables can have on the rest of the economy, and the acquired importance in the prediction of many other variables at both macro and micro levels of economics. Researchers at the National Bureau of Economic research (NBER) have considered some major economic variables as “indicators,” and have classified them into three groups.
- The leading indicators are those variables which change first, prompting other variables to follow in their changes.
- The lagging indicators are those variables whose changes tend to follow the changes of others.
- The coincidental indicators are those variables whose changes just coincide with the changes of other variable.
Based on this categorization, and on the fact that in practice certain variables tend to move ahead of others, gave the idea that the changes in the leading economic indicators (LEI) can be used to predict the changes in others which follow. Figure 9.9 shows a typical set of time series for these three groups. We can see that the turning points of peak and trough is happening first in the leading indicators followed after a period of time by the lagged indicators while the coincidental move almost in tandem with the leading group.

Figure 9.9 Major Groups of Economic Indicators
The time during which the leading change precedes the following change is called the lead time. It varies from cycle to cycle and it is different in the peak and trough cases. In Figure 9.9, we can see that it is taking the lagging indicator a shorter time to follow the peak of the leading as compared to the time it takes to follow the trough. This variability is a classic characteristic of the business cycle. Recorded data on reference dates of all peaks and troughs of the United States business cycle since 1854 shows a great deal of variability, especially in the lead time and how long each phase lasts. For example, in 1990–1991 the trough lead time was 2 months and the peak lead time was 6 months. In 2001, the trough lead time was 8 and the peak lead time was 14 months.
Once again, the main idea of the barometric forecasting is to utilize the LEI as a predictor or barometer for short-term changes in a set of time series data that exhibits a good correlation of their changes over time. A typical example to illustrate the plausibility of this idea is the causal relationship among some variables. The changes in the number of building permits issued in the entire economy can serve as a predictor of the activity of the construction sector. An increase in the new consumer orders can indicate an increase ahead in the production, employment, income, and so on. The other typical example is the fluctuation of the stock market indices such as the Dow Jones and Nasdaq and how they are used as predictors of the state of the economy.
Economic indicators data are published monthly in Business Cycle Indicators that is issued by The Conference Board. There are more than 300 major indicators but the short list of the most common include 21, 10 in the leading category, 7 in the lagging, and 4 in the coincidental, as they are shown in Table 9.16.
Table 9.16 Typical Set of the Three Major Indicators: Leading, Lagging and Coincidental
| Leading Indicators (1) |
|
| Lagging indicators (7) |
|
| Coincidental indicators (4) |
|
Barometric forecasting depends on the composite indices that are developed out of each group of these indicators. Each composite index is, in fact, a weighted average of the components of the group to signify the direction of movement in the whole group. Since some of the components move up and some move down, a so called diffusion index has been developed to represent the collective movement in the group. A diffusion index value of 100 means that all of the components in the group are increasing, a value of a means all of them are decreasing, and any other percentage would refer to the increasing aspect. A 60% means 6 out of 10 components are going up.
One of the most popular composite measures is the LEI. It has been developed by the US Bureau of Economic Analysis. Typically, the LEI can signal the march toward recession or the way to recovery. One of the known criteria is that three consecutive months of decline is a strong signal for a recession, and three consecutive quarters of decline is a confirmation to be in a recession. As for the diffusion index, history has shown that a value of about 50 reflects growth in the economic activity and under 50 reflects a downturn. Despite the fact that the leading indicators have correctly predicted all recessions which occurred since 1948, it also has predicted some recessions that did not occur. This is a matter of the extent of its accuracy that may have become part of its shortcomings in forecasting. That is its inability to measure the magnitude of the change, and being restricted to identifying only the direction of the change. Despite all the shortcomings of the economic and business indicators, they remain an important tool in the prediction of short-term changes in the general economic activity, and the turning points in business cycles. Their prediction can be highly useful, especially in conjunction with other types of forecasting techniques.
9.12 Testing Forecasting Accuracy
As it was mentioned before, the main objective of the forecasting process is to produce forecasts that are as close as possible to the actual data. By this logic, we can define any forecast error (Ef) as the difference between the actual value (A) and the forecasted value (F):

Furthermore, this logic would dictate that the accuracy of our forecast would be measured by how close the projected value is to the actual value, or how small the difference (Ef) is between them. So, the smaller the forecast error, the more accurate the forecasted value, the more reliable the forecasting model, and the more sound the forecasting process.
The difference or the error term is typically due to many reasons related to the design of model, its specifications, the type of data and the way of collecting them, and to the process of data analysis. The major reasons that produce the error are the following:
- the omitted variables
- the equation misspecification
- the random fluctuations
- the economic misinterpretations
- the explanatory variables identification and reliance
There are typical tests of the forecast goodness which targets the value of error in order to check if it is at its minimum. Among these accuracy checks are:
The RMSE Check
Considering the previous method of the moving average, we can run a simple test to check which of the two procedures the three-quarter or five-quarter forecasts is better. That is to say which procedure, would produce a forecast value closer to the actual. This test uses the squared forecast errors, and calculates and compares what is called the root-mean-square error (RMSE). The measure would be that the smaller the RMSE, the better the procedure.

where n is the total number of observations and P is the number of terms constituting the average. The end of columns 6 and 9 of Table 9.12 calculates the summation of the squared errors in both procedures. Plugging in the values 7,762.15 and 6,456.04 in the formula above reveals that:
For the three-quarter forecast, the RMSE is

and for the five-quarter forecast, the RMSE is

Since the five-quarter procedure has a relatively less RMSE (24.22 < 24.44), it would be a little better than the three-quarter procedure. So, if we want to predict for the first quarter of 2012, we will use the five-quarter procedure that produces 167.4 instead of using the three-quarter procedure that produces 163.
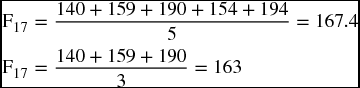
We can use the RMSE in the exponential smoothing method too. Summarizing the results of Table 9.15 in Table 9.17, we can check which α value produces a better forecast. For the forecasts produced with α = 0.20, we get
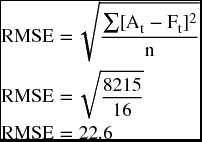
and for the forecasts produced with α = 0.45, we get
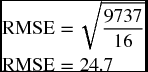
Table 9.17 Two Forecasts to Calculate the Root-Mean-Square Error (RMSE)
| F1 | F2 | |||
| Obs. | Year.Quarter | A | α = 0.20 | α = 0.45 |
| 1 | 2008.1 | 170 | 173.9 | 173.9 |
| 2 | .2 | 187 | 173.1 | 172.1 |
| 3 | .3 | 196 | 175.9 | 178.8 |
| 4 | .4 | 204 | 179.9 | 186.5 |
| 5 | 2009.1 | 153 | 184.7 | 194.4 |
| 6 | .2 | 195 | 178.4 | 175.8 |
| 7 | .3 | 162 | 181.7 | 184.4 |
| 8 | .4 | 144 | 177.7 | 174.3 |
| 9 | 2010.1 | 188 | 170.9 | 160.7 |
| 10 | .2 | 196 | 174.3 | 173.0 |
| 11 | .3 | 150 | 178.6 | 183.3 |
| 12 | .4 | 194 | 172.9 | 168.3 |
| 13 | 2011.1 | 154 | 177.1 | 179.8 |
| 14 | .2 | 190 | 172.5 | 168.2 |
| 15 | .3 | 159 | 176.0 | 178.0 |
| 16 | .4 | 140 | 172.6 | 169.4 |
Since using α of 0.20 produced a smaller RMSE (22.6 < 24.7), it means that α value of 0.22 is more appropriate than α value of 0.45 to bring the forecasts closer to their values.
This concludes that if we want to predict the sales of the first quarter of 2012, we should rely on the estimate of (166.08) instead of the estimate of (157.9) as the first one uses an α of 0.20 and the second uses an α of 0.45.
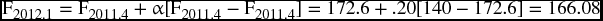
or
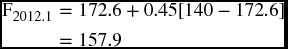
Graphing the time series in its three forms, the actual, the forecasts using an α of 0.20, and the forecasts using an α of 0.45, as they are in Figure 9.10 shows that a smaller α (0.20) produces a smoother line.
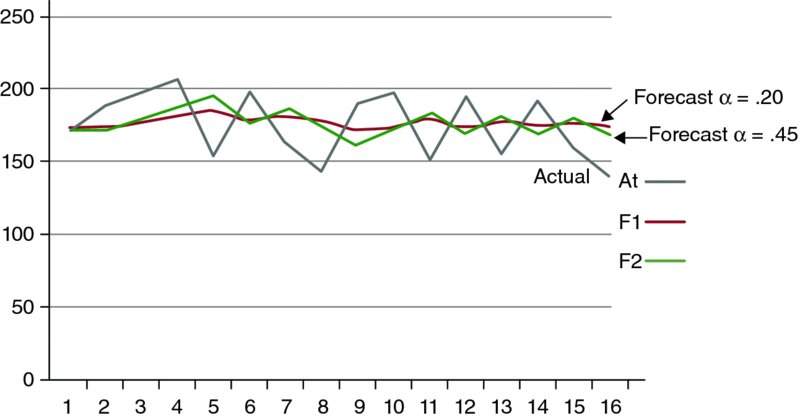
Figure 9.10 Smoothness of High vs. Low Alpha Values
The MAD Check
MAD stands for mean absolute deviation. It is another method, similar to the RMSE, to test for the appropriateness and accuracy of the forecasting techniques, especially in terms of how close the forecasted values are to the actual data. Just like the RMSE, the MAD test is particularly useful when conducting short range forecasts such as those performed by the moving average and the exponential smoothing. It is a simple measure of the overall forecast error, which depends on the absolute value of the error terms, as opposed to squaring them as it is in the RMSE calculations. The absolute value is obtained by just ignoring the signs of the deviation between the actual and predicted values. It is to say that we consider all of them positive as they are squeezed in between the two vertical lines.
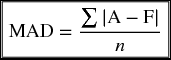
Table 9.18 shows the absolute values of the deviations between the actual sales and four different forecasts as we calculated them earlier. At the end of the table, MAD is calculated for every forecast method:
-
The three-quarter forecast:
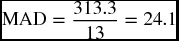
-
The four-quarter forecast:
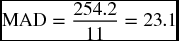
-
The exponential forecast when α = 0.20:
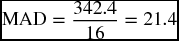
-
The exponential forecast when α = 0.45:
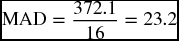
Table 9.18 Mean Absolute Deviation (MAD) for Four Forecasts
| |A − F1| | |A − F2| | ||||
| 3–quarter | 4–quarter | |A − F| | |A − F| | ||
| Obs. | Year.Quarter | MA | MA | α = 0.20 | α = 0.45 |
| 1 | 2008.1 | 3.9 | 3.9 | ||
| 2 | .2 | 13.9 | 14.9 | ||
| 3 | .3 | 20.1 | 17.2 | ||
| 4 | .4 | 19.7 | 24.1 | 17.5 | |
| 5 | 2009.1 | 42.6 | 31.7 | 41.4 | |
| 6 | .2 | 10.7 | 13 | 16.6 | 19.2 |
| 7 | .3 | 22 | 25 | 19.7 | 22.4 |
| 8 | .4 | 26 | 38 | 33.7 | 30.3 |
| 9 | 2010.1 | 21 | 16.4 | 17.1 | 27.3 |
| 10 | .2 | 31.4 | 27.6 | 21.7 | 23 |
| 11 | .3 | 26 | 27 | 28.6 | 33.3 |
| 12 | .4 | 16 | 26 | 21.1 | 25.7 |
| 13 | 2011.1 | 26 | 20.4 | 23.1 | 25.8 |
| 14 | .2 | 24 | 13.6 | 17.5 | 21.8 |
| 15 | .3 | 20.3 | 17.2 | 17 | 19 |
| 16 | .4 | 27.6 | 29.4 | 32.6 | 29.4 |
| ∑|A − F| | 313.3 | 254.2 | 342.4 | 372.1 | |
| n | 13 | 11 | 16 | 16 | |
| MAD | 24.1 | 23.1 | 21.4 | 23.2 | |
These results are very similar to what we got earlier by the RMSE tests. They confirm again that the least forecast error (21.4) was found in the exponential smoothing technique using an α value of 0.20. This would be a reason to consider this particular method as the best among the four methods used on this specific time series. The MAD results also confirmed that using the four-quarter was better than the three-quarter moving average, and using an α of 0.20 was better than an α of 0.45.
The MAPE Check
This is the third accuracy test for forecasting estimation. MAPE stands for mean absolute percent error. In this method, the forecast error is expressed as a proportion of the actual value. The summation of the absolute values of those proportions is divided by the number of observations and multiplied by 100 to get the MAPE value.
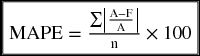
Table 9.19 shows the data related to the exponential forecasting using the two values of α, 0.20 and 0.45. We created columns 6 and 9 by taking the absolute value of the ratio of the forecast errors (in column 5 and 8) and the actual values (in column 3). The summations of columns 6 and 9 gave us the numerators in the MAPE formula above.
– For the exponential forecast when α = 0.20:
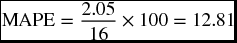
– For the exponential forecast when α = 0.45:

Table 9.19 Forecast Check by Mean Absolute Percent Error (MAPE) Method
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| α = 0.20 | α = 0.45 | |||||||
| Obs. | Year.Quarter | A Actual sale | F1 | A–F1 |  |
F2 | A–F2 | 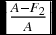 |
| 1 | 2008.1 | 170 | 173.9 | –3.9 | 0.023 | 173.9 | –3.9 | 0.023 |
| 2 | 0.2 | 187 | 173.1 | 13.9 | 0.074 | 172.1 | 14.9 | 0.079 |
| 3 | 0.3 | 196 | 175.9 | 20.1 | 0.102 | 178.8 | 17.2 | 0.088 |
| 4 | 0.4 | 204 | 179.9 | 24.1 | 0.118 | 186.5 | 17.2 | 0.086 |
| 5 | 2009.1 | 153 | 184.7 | –31.7 | 0.207 | 194.4 | –41.4 | 0.271 |
| 6 | 0.2 | 195 | 178.4 | 16.6 | 0.085 | 175.8 | 19.2 | 0.098 |
| 7 | 0.3 | 162 | 181.7 | –19.7 | 0.122 | 184.4 | –22.4 | 0.138 |
| 8 | 0.4 | 144 | 177.7 | –33.7 | 0.234 | 174.3 | –30.3 | 0.210 |
| 9 | 2010.1 | 188 | 170.9 | 17.1 | 0.091 | 160.7 | 27.3 | 0.145 |
| 10 | 0.2 | 196 | 174.3 | 21.7 | 0.111 | 173.0 | 23 | 0.117 |
| 11 | 0.3 | 150 | 178.6 | –28.6 | 0.191 | 183.3 | –33.3 | 0.222 |
| 12 | 0.4 | 194 | 172.9 | 21.1 | 0.109 | 168.3 | 25.7 | 0.132 |
| 13 | 2011.1 | 154 | 177.1 | –23.1 | 0.150 | 179.8 | –25.8 | 0.167 |
| 14 | 0.2 | 190 | 172.5 | 17.5 | 0.092 | 168.2 | 21.8 | 0.115 |
| 15 | 0.3 | 159 | 176.0 | –17 | 0.107 | 178.0 | –19 | 0.119 |
| 16 | 0.4 | 140 | 172.6 | –32.6 | 0.233 | 169.4 | –29.4 | 0.210 |
| Average = 173.9 | 2.05 | 2.22 | ||||||
This test indicates that the forecasts using an α value of 0.20 are more accurate than the forecasts using an α value of 0.45. This also confirms the results obtained by the previous checks.
Finally, it can be said that forecasting accuracy and reliability would basically refer to the predictive consistency and effectiveness of the forecasting process, and to its capacity to produce projected estimates that are significantly close to the real data that will be realized later.
Practically, forecasting accuracy proved to exhibit an inverse relationship with the time horizon of the forecast. The shorter the past period of time the forecaster uses and the shorter the future period he would predict for, the more accurate the forecast. In other words, the recent past is much more predictive for the near future. Accuracy is often related to more careful and sophisticated procedures which normally does not come cheap. It should, however, make managers aware that the more desire and enthusiasm they have to get accurate forecasts, the more understanding and willingness is required of them to bear the necessary cost.
9.13 Summary
Pro forma statement and financial forecasting is the topic of this chapter. Pro forma statement was defined and two examples were given: pro forma balance sheet and pro forma income-expense statement. Also the sales ratio method to construct a pro forma statement was explained. After that, the discussion was moved to financial forecasting. Forecasting process was defined and its role and importance, and its steps were explained. Different types of forecasting models were addressed. In the qualitative models we saw the opinions and polls, and survey and market research. In the quantitative models we discussed the structural and non-structural models, and we articulated the time series analysis as a representative of the non-structural models. To explain the variations in the economic and financial data, we defined and graphically illustrated the secular trend, seasonal variation, cyclical fluctuations, and random changes. After that, we moved to a more technical discussion to show how to fit a forecasting model, with examples and graphs. To adjust for seasonality, we discussed three methods: the simple average of errors, the actual/forecast ratio, and the dummy variables method. Other models of forecasting were addressed such as the smoothing models, where we explained with examples the simple moving average, the weighted moving average, and the exponential smoothing method. Also discussed was the barometric model of forecasting, followed by the ways to test the accuracy of the forecasting methods. In this regard, we explained the RMSE, MAD, and finally, the MAPE.
Key Concepts
- Pro forma statement
-
Pro forma analysis Sales ratio method
- Forecast
-
Financial forecasting Forecast horizon
- Qualitative models
-
Quantitative models Delphi method
- Judgmental models
-
Market research Structural models
- Non-structural models
-
Time series models Secular trend
- Seasonal variation
-
Cyclical fluctuation Random change
- Seasonability effects
-
Simple average of errors
- Actual/forecast ratio method
-
Dummy variables method
- Smoothed forecast
-
Simple moving average
- Weighted moving average
-
Experiential smoothing model
- Barometric forecasting
-
Composite index Diffusion index
- Forecasting accuracy
-
Root-mean-square error (RMSE)
- Mean absolute deviation (MAD)
-
Mean absolute percent error (MAPE)
Discussion Questions
-
What is the pro forma statement, and how important is it for a business?
-
How are the entries in the pro forma statement obtained?
-
Briefly explain the way by which a firm would know if it needs new financing.
-
What is the financial forecasting, and why do we need it?
-
What are the major models of forecasting, and how different are they from each other?
-
What is market research and how can it be used to forecast sales, for example?
-
List and briefly explain the different types of the time series data variations.
-
List and briefly explain the methods by which the data seasonality can be adjusted.
-
What does the constant x, and (1 – x) signify? Where, and how are they used?
-
What is the barometric forecasting, and how is it different from other models of forecasting?