Chapter 16 Osmosis and Regulation of Cell Volume

In whole blood, erythrocytes are biconcave disks about 7 μm in diameter and 2 μm thick. When diluted in a solution of 0.9% NaCl (w/v), erythrocytes retain this shape. When diluted with higher concentrations of salt, the erythrocytes shrink, appearing as spheres with spikes all over their surface. These cells are described as crenated. If erythrocytes are diluted with a markedly lower concentration of salt, the cells swell. They first become spherical and then, if the solution is sufficiently low in salt, the cells burst and release their contents. These simple observations give rise to the concept of tonicity. Tonicity is operationally defined as the ability of a solution to shrink or swell specified cells. Thus, an isotonic solution induces no volume change when placed in contact with the cells. The tonicity of the solution is equal to the tonicity of the cell’s contents. Hypertonic solutions shrink cells, whereas hypotonic solutions increase cell volume. A solution that is isotonic for one type of cell may or may not be isotonic for others.

All animal cells shrink or swell on exposure to anisotonic solutions. Figure 16.1 shows the volume response of single isolated heart cells on exposure to hypertonic or hypotonic solutions. In hypotonic solution, myocytes swelled to more than 1.5 times their initial volume. The swelling was complete within 2 min, the new volume was stable and volume returned to normal upon return of the isotonic solution. In hypertonic solution, cell volume decreased to about 0.65 times normal and the original volume was restored upon return of the isotonic solution.

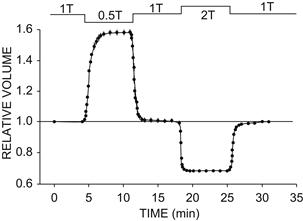
FIGURE 16.1 Response of isolated rabbit ventricular myocytes to osmotic stress. Cell volume was initially measured in isotonic solution (1T). Myocytes rapidly swelled 58% in a hypotonic solution with an osmolarity 0.5 times that of 1T and rapidly shrank 33% in a hypertonic solution with an osmolarity two times that of 1T. Cell volume was stable for the duration of perfusion with either hypotonic or hypertonic media and rapidly returned to its control value when 1T solution was readmitted. Volume was measured by digital video microscopy, and relative volume was calculated as volume_test/volume_1T. Solution osmolarity was adjusted by varying the concentration of mannitol. (From Suleymanian and Baumgarten (1996). Reproduced from The Journal of General Physiology, 1996, 107, 503–514, by copyright permission of The Rockefeller University Press.)

The data in Fig. 16.1 show that volume changes in anisotonic media are very rapid. What is moving when the cells swell or shrink? What routes do these substances take? Are there homeostatic mechanisms that limit swelling and shrinking? If so, how are the compensatory mechanisms engaged? The answers to these questions are not yet complete. The purpose of this chapter is to provide the basis for understanding regulation of cell volume through the exchange of water and solutes across the plasma membrane.

III Water Movement Across Model Membranes

IIIA. Definition of Osmosis

Osmosis refers to the movement of fluid across a membrane in response to differing concentrations of solutes on the two sides of the membrane. Osmosis has been used since antiquity to preserve foods by dehydration with salt or sugar. The removal of water from a tissue by salt was referred to as imbibition. This description comes from the notion that these solutes attracted water from material they touched. In 1748, J.A. Nollet used an animal bladder to separate chambers containing water and wine. He noted that the volume in the wine chamber increased and, if this chamber was closed, a pressure developed. He named the phenomenon osmosis from the Greek ωσμoς, meaning thrust or impulse.

Pfeffer (1877) provided early quantitative observations on osmosis. He made an artificial membrane in the walls of an unglazed porcelain vessel by reacting copper salts with potassium ferrocyanide to form a copper ferrocyanide precipitation membrane on the surface of the vessel. He used this membrane to separate a sucrose solution inside the vessel from water outside and found a volume flow from the water side to the sucrose side. Pfeffer observed that the flow was proportional to the sucrose concentration. Further, a pressure applied inside the vessel produced a filtration flow proportional to the pressure. He found that a closed vessel containing a sucrose solution would develop a pressure proportional to the concentration of sucrose. He recognized this as an equilibrium state in which the pressure balanced the osmosis caused by the sucrose solution. Pfeffer’s original data for the osmotic pressure of sucrose solutions are plotted in Fig. 16.2. He defined osmotic pressure as the hydrostatic pressure necessary to stop osmotic flow across a barrier (e.g. a membrane) that is impermeable to the solute. This concept is illustrated in Fig. 16.3. Osmotic pressure is a property intrinsic to the solution and is measured at equilibrium, when the pressure-driven flow exactly balances the osmotic-driven flow. By defining osmotic pressure in this way, we assign a positive value to an apparent reduction in pressure brought about by dissolving the solute. Thus, fluid movement occurs from the solution of low osmotic pressure (water) to the solution of high osmotic pressure, opposite in direction to the hydraulic flow of water from high to low hydrostatic pressure.

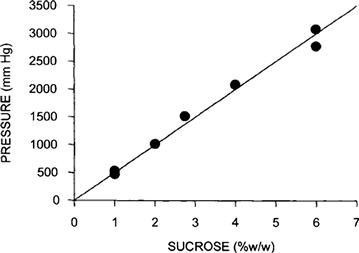
FIGURE 16.2 Plot of data from Pfeffer (1877) for the osmotic pressure of sucrose solutions. A copper ferrocyanide precipitation membrane was formed in the walls of an unglazed porcelain cup. The membrane separated a sucrose solution in the inner chamber from water in the outer chamber. The inner chamber was then attached to a manometer and sealed. The linear relation between the pressure measured with this device and the sucrose concentration were the experimental impetus for deriving van’t Hoff’s law.

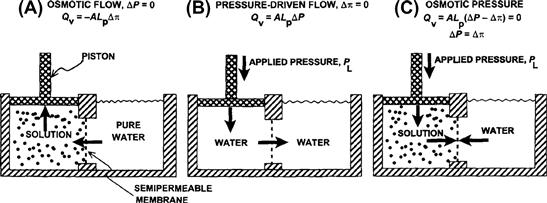
FIGURE 16.3 Equivalence of hydrostatic and osmotic pressures in driving fluid flow across a membrane. (A) An ideal, semipermeable membrane is freely permeable to water, but is impermeable to solute. When the membrane separates pure water on the right from solution on the left, water moves to the solution side. This water flow is osmosis. The flow, Q_v, in cm³·s⁻¹, is linearly related to the difference in osmotic pressure, Δπ, by the area of the membrane, A, and the hydraulic conductivity, L_p. Positive Q_v is taken as flow to the right. The flow causes expansion of the left compartment and movement of the piston (which is assumed to be weightless). (B) Application of a pressure, P_L, to the left compartment forces water out of this compartment, across the semipermeable membrane. The flow is linearly related to the pressure difference between the two compartments. (C) Application of a P_L so that ΔP = Δπ results in no net flow across the membrane. The osmotic pressure of a solution is defined as the pressure necessary to stop water movement when the ideal, semipermeable membrane separates water from the solution.

An ideal semipermeable membrane is required for determining osmotic pressure. These membranes are permeable to water but absolutely impermeable to solute. The concept of osmotic pressure differs from tonicity in that tonicity compares two solutions separated by a specific non-ideal membrane. If the membrane is highly permeable to solute as well as to water, no water flow will occur and, therefore, the externally applied pressure required to stop osmosis is zero. This observation makes it plain that the effective osmotic pressure, which is measured with a real membrane, must be due to some interaction of the membrane with the solute because pressure depends on both the specific solute and the specific membrane.

IIIB van’t Hoff’s Law

From Pfeffer’s data and thought experiments considering gases in equilibrium with water, van’t Hoff (1887) argued that the osmotic pressure should be given by:

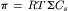(16.1)

where π is the usual symbol for osmotic pressure, R is the gas constant, T is the temperature in kelvins, and C_s is the concentration of solute particles in solution. This equation is known as van’t Hoff’s law. Table 16.1 lists common units for osmotic pressure along with the values and units of R and C_s needed to make the calculation.

TABLE 16.1. Units for Calculation of Osmotic Pressure

Osmolarity (osmol·L⁻¹) is defined as the concentration of osmotically active particles, osmolytes, in mol·L⁻¹. Therefore, the units osmoles and moles cancel in the calculation of osmotic pressure.

The concentration used in van’t Hoff’s law, ΣC_s, refers to the number of osmotically active particles that are formed upon dissolution of the solute. For example, organic compounds such as glucose ideally yield one particle, whereas strong salts such as NaCl or CaCl₂ ideally yield two (Na⁺ and Cl⁻) or three (Ca²⁺ and two Cl⁻) particles. The osmolarity of a solution equals ΣC_s and is expressed in osmol per liter to indicate that we are referring to the number of osmotically active particles, termed osmolytes, rather than the concentration of the solute. An alternative scale, osmolality, defines ΣC_s per kilogram of solvent. Although the osmolal scale better describes the osmotic pressure in van’t Hoff’s equation, the osmolar scale is more generally used in physiological studies. As we shall see, van’t Hoff’s law is a limiting law that is true only for dilute solutions. In this limit of dilute solutions, both osmolal and osmolar concentration scales converge to the same results.

To illustrate the magnitude of osmotic pressure, ideal solutions of 10 mM glucose or 5 mM NaCl, which dissociates into two particles, both have an osmolarity of 10 mosmol L⁻¹ and an osmotic pressure at 37°C of 0.082 L·atm·moL⁻¹·K⁻¹ × 310 K × 0.01 mol·L⁻¹ = 0.254 atm or 193 mmHg. Thus, the osmotic pressure of even dilute solutions are large in comparison to normal hydrostatic pressures in physiological systems.

IIIC Thermodynamic Derivation of van’t Hoff’s Law

One of the conclusions of chemistry is that all spontaneous processes are accompanied by a decrease in free energy. The total free energy of a solution can be divided among its components. This parceling out of the Gibbs free energy, G, is embodied in the concept of chemical potential:

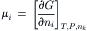(16.2)

where μ_i is the chemical potential of component i, n_i is the number of moles of component i and i≠k. The chemical potential of a component of a solution consists of three terms: a standard potential, which refers to the chemical energy involved in the formation of the material from standard states; a compositional term, which depends on the presence of other constituents; and a work term, encompassing other work required (per mole) to bring additional material into the solution. 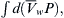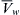The work term in the chemical potential of water is where is the volume of water per mole and P is the pressure. The electrochemical potential of ions in solution requires the inclusion of an electrical work term, 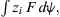where z_i is the ion’s valence, F is Faraday’s constant, and ψ is voltage.

In the case of a solution separated from pure water by an ideal semipermeable membrane, water movement will occur when there is a difference in the chemical potential of water on the two sides of the membrane, such that water movement will result in a decrease in free energy. When the pressure applied to the solution is equal to the osmotic pressure, equilibrium is established and the chemical potential of water is equal on both sides of the membrane; no net water movement occurs. This equality of chemical potential is written as:

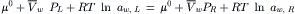(16.3)

where the subscripts L and R refer to the left and right sides of the semipermeable membrane, μ⁰ is the chemical potential of liquid water in its standard state (pure water at 1 atm pressure) and a_w is the activity of water. For an ideal solution, the activity of water can be replaced by its mole fraction, X_w

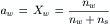(16.4)

where n_w and n_s are the moles of water and solute, respectively. The balance of the chemical potential can be written as:

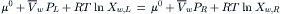(16.5)

Consider the situation in Fig. 16.3, where pure water is on the right side of the membrane and a solution is on the left. X_w,_R = 1.0 and thus, ln X_w,_R = 0. Rearranging we find:

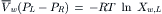(16.6)

The mole fractions of water and solute in a solution must sum to 1.0. This is expressed as:

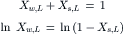(16.7)

where X_s,L is the mole fraction of solute in the solution on the left. In dilute solutions, X_s,L<<1.0, and thus, ln (1− X_S,L) ≈ −X_S,L. Substitution of this approximation in Equation 16.6 gives:

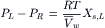(16.8)

The left-hand side of Equation 16.8 is just the osmotic pressure, π, which is equal to the extra pressure that must be applied to the solution on the left side in order to establish equality of the chemical potential of water on the two sides of the membrane. For physiological studies, it is convenient to express π in terms of concentration. From the definition of mole fraction and the assumption of dilute solutions (n_s<<n_w), we get:

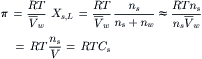(16.9)

where 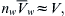is the total volume of solution and C_s is the concentration of impermeable solute on the solution side of the membrane. This last expression is the van’t Hoff equation for the osmotic pressure, Equation 16.1. The thermodynamic derivation entails two assumptions: (1) the solution is sufficiently dilute as to approach ideality; and (2) the solution is incompressible so that 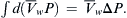It is important to recognize that Equation 16.9 is not exact for physiological solutions. Rather, it is an approximation that is strictly true only for dilute ideal solutions.

The van’t Hoff equation is based on thermodynamics and, as such, it tells us nothing about the rate of osmosis or the mechanism by which it occurs. Conceivably, the semipermeable membrane could be like a sieve that allows water to pass freely while blocking solute movement. Alternatively, solvent could dissolve in the membrane, whereas solute is insoluble. Both of these models would exhibit osmotic flow from the region of low osmotic pressure (pure water) to that of high osmotic pressure (impermeant solute solution). The mechanism by which osmosis occurs must be determined by methods of chemical kinetics, and must be determined for every membrane-solvent pair.

IIID Other Colligative Properties of Solutions

The thermodynamic derivation given previously indicates that osmotic pressure (and osmotic flow) originates in the lowering of the chemical potential of water by the amount ≈RTX_s when solute is dissolved. Several other properties of solutions also are a consequence of the lowered chemical potential of water because of dissolution of solutes. Together, these are called the colligative properties (from the Latin, ligare, meaning to bind) and include osmotic pressure, vapor pressure depression, boiling point elevation and freezing point depression. Consider two open compartments enclosed in a chamber. One compartment contains pure water and the other a solution of a non-volatile solute. The vapor pressure above a solution is defined as the partial pressure of water vapor in equilibrium with the solution. Since the vapor pressure of pure water is higher than that of the solution, water vapor above pure water will be at a higher pressure than that above the solution. As a result, water vapor will diffuse from the water side to the solution side. At the surface of the solution, water vapor will condense because the vapor pressure there will be higher than the equilibrium vapor pressure for the solution. Thus, water will move from the pure water to the solution side. In short, “osmosis” would occur through the “semipermeable membrane” represented by the surfaces of the two fluids and the intervening air. This illustrates the strong connection among the colligative properties of solutions. Laboratory osmometers typically use either vapor pressure depression or freezing point depression to determine the total solute concentration in an aqueous solution.

IIIE Osmotic Pressure of Non-ideal Solutions

As discussed above, the van’t Hoff equation is an approximation that adequately describes the osmotic pressure for dilute solutions. Its derivation requires the assumptions that the solutions are dilute and that the solutions are ideal. Here, ideal means that Raoult’s law (vapor pressure is proportional to mole fraction of solvent) is valid for the solution (Hildebrand, 1955; Kiil, 1989). Because the behavior of real solutions is not ideal, the van’t Hoff equation must be modified to include a correction term, the osmotic coefficient (ϕ_s):

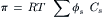(16.10)

At physiological concentrations, the osmotic coefficients for NaCl and CaCl₂ are 0.93 and 0.85, respectively. This means the osmolarity of 150 mM NaCl is 0.93 × 2 × 150 = 279 mosmol L⁻¹ and the osmolarity of 150 mM CaCl₂ is 0.85 × 3 × 150 = 382.5 mosmol L⁻¹. The osmotic coefficients for electrolytes vary with temperature, concentration and the chemical nature of the electrolyte. For most electrolytes, ϕ<1.0 for dilute solutions, due to weak attraction of the ions. At higher concentrations, ϕ increases to exceed 1.0. Values for the osmotic coefficients for electrolytes can be found in Robinson and Stokes (1959) or can be calculated from the parameters tabulated by Pitzer and Mayorga (1973). These osmotic coefficients are corrections to van’t Hoff’s law due to interactions only for the particular solute. When more than one solute is present, interactions could occur that are not accounted for by the osmotic coefficients. Therefore, calculations of the osmotic pressure of a mixture of solutes, even when osmotic coefficients are used, are only approximations.

Non-electrolytes and polyelectrolytes, especially proteins, also show marked departure from van’t Hoff’s law with increasing concentration. According to Equation 16.10, the osmotic coefficient for a single solute can be calculated as:

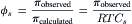(16.11)

The osmotic coefficient for sucrose is plotted against sucrose concentration in Fig. 16.4. The osmotic coefficient is nearly 1.0 in dilute solutions, but approaches 3 in saturated sucrose solutions. Thus, the van’t Hoff equation successfully describes the osmotic pressure of dilute solutions, but fails at high solute concentrations. The failure of the van’t Hoff equation for highly concentrated solutions is due to deviation of reality from the assumptions used to derive the equation, that solutions are dilute and ideal. The osmotic coefficient accounts for these deviations.

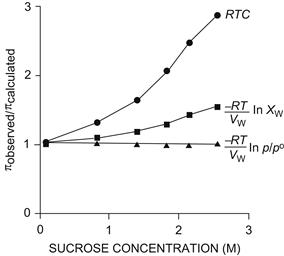
FIGURE 16.4 Osmotic coefficients as a function of sucrose concentration. Plotted are the molar osmotic coefficient, defined as ϕ_s in Equation 16.11 (•), obtained by dividing the observed osmotic pressure by RTC; the rational osmotic coefficient, g, defined in Equation 16.15 (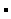 ent ), obtained by dividing the observed osmotic pressure by 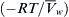ln X_w; and the observed osmotic pressure divided by that predicted by vapor pressure measurements 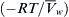ln p/p⁰ according to Equation 16.13 ( ent ). Deviation of the molar osmotic coefficient from 1.0 means that the van’t Hoff law fails to describe adequately the osmotic pressure at high concentrations, but is accurate for dilute solutions. The van’t Hoff law requires the assumption of dilute solution and ideal behavior. Deviation of the rational osmotic coefficient from 1.0 means that the solution is not ideal, as the equation requires this assumption. The nearly perfect agreement between the theoretical osmotic pressure predicted from vapor pressure measurements illustrates the connection between these two colligative properties. Data from Glasstone (1946).

For high solute concentrations, we can calculate the osmotic pressure from the mole fraction of water without assuming a dilute solution by identifying π = P_L−P_R in Equation 16.6:

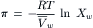(16.12)

This equation still requires the assumption of ideal solution behavior: the activity of water is equal to its mole fraction. The expression for osmotic pressure without assuming a dilute solution or ideality is given by:

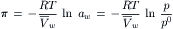(16.13)

where p and p⁰ are the vapor pressures of the solution and pure water, respectively.

The rational osmotic coefficient, g, accounts for non-ideal behavior and is defined as:

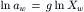(16.14)

Then, from Equations 16.12–16.14, we find that:

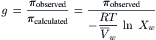(16.15)

The rational osmotic coefficient is closer to 1.0, but still deviates significantly at higher sucrose concentrations where solution behavior is further from ideal (see Fig. 16.4). In contrast, the ratio of the observed osmotic pressure to the theoretical osmotic pressure calculated from vapor pressure measurements, according to Equation 16.13, is very close to 1.0 throughout the entire concentration range. This shows the validity of Equation 16.13 and the absolute correlation between vapor pressure depression and osmotic pressure as different measures of the same phenomenon, the lowering of the activity of solvent water by the dissolution of solute. Equation 16.12 does not adequately describe the variation of π with C_s because it requires ideal adherence to Raoult’s law (vapor pressure is proportional to X_w); van’t Hoff’s limiting law further deviates from a linear relationship between π and C_s because it requires the additional approximation of dilute solutions. Despite these limitations in the high concentration domain, van’t Hoff’s law remains a good approximation for electrolyte solutions in the physiological range.

Because of their importance in physiological systems, the non-ideality of the osmotic pressure of protein solutions requires special comment. Adair (1928) found that the observed osmotic pressure increased faster than the concentration in hemoglobin solutions, as shown in Fig. 16.5. Part of the osmotic pressure was due to the unequal distribution of ions across the semipermeable membrane caused by electric charge on the immobile protein molecules. This is the Gibbs–Donnan equilibrium, discussed in more depth later. The contribution of the Gibbs–Donnan distribution to osmotic pressure is small, however, and nearly all of the non-linearity between π and C_s is due to the protein itself. From the data obtained by Adair (1928), ϕ_Hb = 4.03 at the concentration of hemoglobin within erythrocytes (34.4 g hemoglobin per 100 ml of solution).

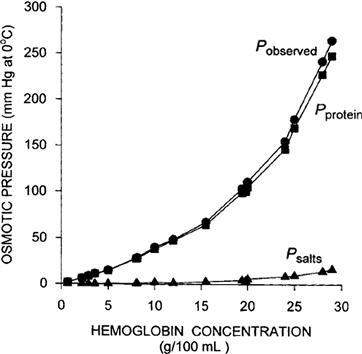
FIGURE 16.5 Dependence of the observed osmotic pressure on hemoglobin concentrations. P_observed is the observed osmotic pressure (•). P_salts is the contribution of the salts to the osmotic pressure as calculated from the Gibbs–Donnan distribution and the van’t Hoff equation (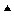 ent ). Protein is the contribution of the protein itself to the observed osmotic pressure, calculated as P_observed−P_salts ( 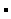ent ). Data from Adair (1928).

The observed osmotic pressure of solutions of plasma proteins also increases more rapidly than concentration, but the degree of deviation from linearity is different for different proteins. Thus, serum albumin shows marked deviation, whereas γ-globulins are more nearly linear. The empirical fits to the concentration-dependence of osmotic pressure are given by Landis and Pappenheimer (1963) as:

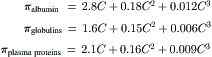(16.16)

In each of these three equations, the first term represents the limiting law of van’t Hoff.

The rather large ϕ_s for proteins and polymers is due in part to excluded volume effects. That is, proteins and polymers exclude solvent from a larger volume than inorganic ions. The lowering of the free energy of solvent water upon dissolution of solute, which gives rise to osmosis, can be calculated from the increase of entropy on mixing. This entropy of mixing depends on the volume occupied by the solute. From considerations of the excluded volume, it can be shown (Tanford, 1961) that the expected osmotic pressure is given as:

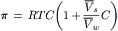(16.17)

IIIF Equivalence of Osmotic and Hydrostatic Pressure

As mentioned earlier, Pfeffer originally observed a linear relationship between the flow rate and the concentration of solute. This is expressed as:

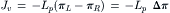(16.18)

where J_v is the volume flux in cm³·s⁻¹ per unit area of membrane, L_p is variously called the filtration coefficient, hydraulic conductivity, or hydraulic permeability and Δπ is the osmotic pressure difference. A positive J_v in Equation 16.18 represents flux from the left to the right compartment and this is the order in which the osmotic pressure difference is taken. The minus sign before L_p indicates flux is from the region of low osmotic pressure to the region of high osmotic pressure. In Fig. 16.3A, π_L>π_R, Δπ>0, and J_v is negative. This means that the flux is from the right to the left compartment. The flow across an extent of membrane is just the flux times the area exposed to the driving forces, expressed as:

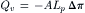(16.19)

where A is the area of the membrane and Q_v is the flow in units of cm³·s⁻¹.

In the absence of solute, the volume flow across Pfeffer’s artificial membrane was also linearly related to the hydrostatic pressure:

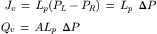(16.20)

In a study on collodion membranes, Meschia and Setnikar (1958) found that the proportionality constant for hydrostatic pressure-driven filtration was the same as the constant relating flow and osmotic pressure. That means that the L_p in Equation 16.19 is the same as the L_p in Equation 16.20. Thus, not only can the osmotic flow be nulled by opposing osmotic pressure with an equal but opposite hydrostatic pressure, but the equivalent proportionality implies that the mechanism of volume flow is also identical for osmotic and hydraulic flow. The equivalence of osmotic and hydrostatic pressures allows us to write:

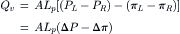(16.21)

This equation describes the net flow that would be observed in the presence of both hydrostatic and osmotic pressure differences across a semipermeable membrane.

IIIG Reflection Coefficient

Equation 16.1, van’t Hoff’s law, describes the relation between osmotic pressure and concentration when a solution is separated from water by an ideal semipermeable membrane. Recall that a semipermeable membrane is defined as absolutely impermeable to the solute. Real membranes may not fit this ideal; they may be somewhat permeable to the solute. When membranes are permeable to the solute, the measured osmotic pressure is actually less than that predicted by van’t Hoff s law. This phenomenon has led to a second membrane parameter, σ, the reflection coefficient which is defined as:

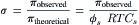(16.22)

The reflection coefficient derives its name from the idea that all of the collisions of solute with a semipermeable membrane will result in the solute being reflected back into the solution. The reflection coefficient for an ideal membrane is 1.0. For a permeable solute, some fraction of the collisions with the membrane will result in permeation of the membrane, so that σ<1.0 and the observed osmotic pressure will be less than that predicted by van’t Hoff s law. The value of σ is not simply the fraction of collisions that penetrate the membrane. It involves discrimination by the membrane between solvent and solute. Thus, σ is a parameter that is different for every membrane-solute pair. A vapor pressure osmometer or a freezing-point osmometer would still register the proper osmolarity of the solution, however (for non-volatile solutes). A molecular interpretation of the origin of the reflection coefficient is given later.

Permeation of the solute should reduce osmotic flow along with osmotic pressure. In the presence of both hydrostatic pressure differences and concentration differences across a membrane, the resulting volume flow is given by:

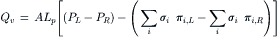(16.23)

where σ_i is the reflection coefficient of solute i, and π_i,L and π_i,R are the osmotic pressures of solute i on the left and right sides of the membrane, respectively. The π_i in this equation is that given by van’t Hoff’s law; its multiplication by the reflection coefficient, σ, gives the effective osmotic pressure. The consequence of a combination of hydrostatic and osmotic pressures on the flow across a membrane is shown in Fig. 16.6.

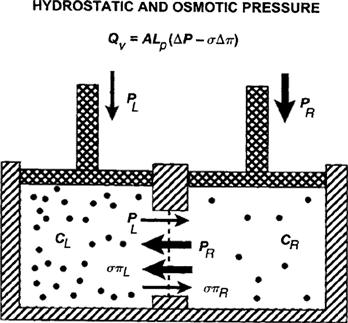
FIGURE 16.6 Net flow in the presence of osmotic and hydrostatic pressures. For a real membrane, the effective osmotic pressure on the left, σπ_L, causes flow toward the left, while the applied hydrostatic pressure, P_L, drives flow to the right. A similar situation occurs on the right. The net flow is driven by the balance of the forces, ΔP−σΔπ, and is proportional to the area, A, and the hydraulic conductivity, L_p_.

IV Mechanisms of Osmosis

The ultimate cause of osmosis is the reduction of the chemical potential of water in a solution. This thermodynamic statement and equations derived from it tell us nothing about the rate of osmosis or its mechanism. Several possible mechanisms have been investigated. As will be developed, classes of models can be distinguished by comparing the proportionality between applied force, which is either a pressure or concentration gradient, and water flow.

IVA Microporous Membranes

IVA1 Osmotic and Pressure-Driven Flow through Porous Membranes

The equivalence of L_p for osmotic and pressure-driven flow suggests a common mechanism. At least three different models have been proposed to explain flow across membranes: (1) hydrodynamic flow through a porous membrane; (2) diffusion through the membrane; and (3) non-hydrodynamic flow through narrow pores. As we shall see, it is likely that biological membranes are not modeled well by any one of these. Despite this, we shall consider these model membranes because investigators have relied heavily on them to clarify their thinking.

First, we consider a porous membrane as a model for understanding osmotic and hydrostatic pressure-driven flow and derive L_p, the proportionality constant relating pressure and flow. We assume the membrane is a flat, thin sheet of thickness δ. We imagine that the membrane is pierced by right-cylindrical pores of radius r, and the number of pores, N, per unit area is n = N/A. The membrane separates two compartments of water that are at different hydrostatic pressures. If we assume that the pores are large enough for laminar flow to occur, then the filtration flow will be given by the Poiseuille equation:

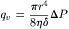(16.24)

where q_v is the flow per pore in cm³·s⁻¹, η is the viscosity of the fluid, δ is the thickness of the membrane (equal to the length of the pore), and ΔP is the pressure difference across the pore. The π in this equation is the geometric ratio, 3.14…, and should not be confused with the symbol for osmotic pressure. Since the flow through N pores is just Nq_v, the observed macroscopic flux and flow are:

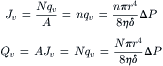(16.25)

Recall here that J_v is the flux, or flow per unit area of membrane and Q_v is the flow in units of volume per unit time.

Equation 16.25 describes the steady-state flow of water across the membrane. Because at steady-state there is no buildup or depletion of water, there is no difference in the flow of water at any two points in the pore. Consequently, pressure changes linearly with distance through the pore, and the gradient of pressure, ΔP/δ, is constant.

A comparison of Equation 16.25 with Equation 16.20 indicates that the hydraulic conductivity is:

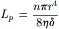(16.26)

Thus, L_p is a parameter determined by the viscosity of the fluid and by membrane characteristics including the number of pores per unit area, n, the pore radius, and the membrane thickness.

IVA2 Diffusional Permeability of Porous Membranes: P_d

In the absence of a pressure gradient, solute and water cross a porous membrane by diffusion through the pores. If we assume that the membrane is impermeable at all other points, the permeability is given by Fick’s first and second law of diffusion:

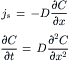(16.27)

where j_s is the flux of solute through one pore. The second expression describes the time dependence of the concentration profile over distance, x, within the pore. At steady-state, the concentration profile no longer changes. This means that 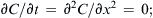the concentration gradient is linear; and δC/δx = (C_L−C_R)/(0−δ) = −ΔC/δ, where δ is the thickness of the membrane. Total solute flux across the entire membrane, J_s, is:

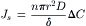(16.28)

where n is the number of pores per unit area of membrane. According to this equation, the observed macroscopic flux of solute across a porous membrane is linearly related to the concentration difference by a coefficient that includes properties of the solute (diffusion coefficient) and the membrane (thickness, pore density and pore cross-sectional area). The permeability of the membrane to solute, p_s, includes several parameters in Equation 16.28 that are difficult to obtain experimentally; p_s relates solute flux, J_s, to the difference in concentration across the membrane:

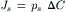(16.29)

From Equations 16.28 and 16.29, p_s is defined as:

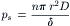(16.30)

Isotopic water on one side of a porous membrane is distinguishable from ordinary water and may be viewed as a solute. Thus, water itself will obey these equations. This allows us to define the diffusional permeability of water, P_d, for a porous membrane:

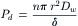(16.31)

where D_w is the diffusion coefficient of water. The units of P_d are cm·s⁻¹. Note that multiplication of a permeability by a concentration, as in Equation 16.29, gives a flux with units of mol·cm⁻² s⁻¹.

IVA3 Evidence for Pores: P_f/P_d Ratio

In the absence of a concentration gradient, pressure-driven water flow gives rise to a second permeability constant termed the filtration permeability or osmotic permeability, P_f, which has units of cm·s⁻¹. Mauro (1957) realized that the proportionality constants relating pressure and concentration-gradient-driven water flow, P_f and P_d, provide evidence for the mechanism of transport. The ratio P_f/P_d should be 1.0 if water crosses by a dissolution-diffusion process. Mauro (1957) recognized that the flux of water in response to a pressure gradient could be partitioned into two components, diffusional and non-diffusional (e.g. bulk flow) and that the diffusional component of water flux, J_w, would obey the Nernst–Planck equation:

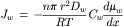(16.32)

where C_w is the concentration of water. In the case where only a hydrostatic pressure is applie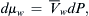d, and 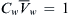. Assuming steady-state flows and a uniform membrane, dP/dx = −ΔP/δ, and Equation 16.32 becomes:

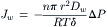(16.33)

This flow of water is in units of moles of water per second per cm² of membrane. It can be converted to units of volume per second per cm² (the units of J_v) by multiplying by the volume of water per mole, or :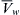

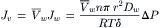(16.34)

This equation relates the volume flux to the pressure difference across the membrane.

The total volume flux was earlier given as J_v = L_pΔP (see Equation 16.20). If diffusional flux is the only component of volume flux, Equations 16.20 and 16.34 may be combined to give:

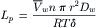(16.35)

Part of this expression for L_p incorporates P_d. Insertion of Equation 16.31 into Equation 16.35 gives:

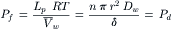(16.36)

This definition of P_f converts L_p into a parameter having the same units as P_d, thereby allowing direct comparison of filtration and diffusional permeabilities. The equality of P_f and P_d obtained in Equation 16.36 is dependent on the condition that the flow of water in response to a hydrostatic pressure difference is due only to diffusional processes. Thus, for a purely diffusional process, P_f/P_d = 1. In contrast, Mauro (1957) found that P_f/P_d was 727 in collodion membranes. That is to say, pressure-driven water movement was much greater than expected from a diffusional process. From this he concluded that pressure-driven and osmotic flow across these membranes was predominately non-diffusional.

IVA4 Physical Origin of Osmotic Pressure

If a porous membrane separates a solution containing only impermeant solutes from pure water, we observe experimentally that water flows through the membrane from the pure water to the solution side. The flow is proportional to the osmotic pressure of the solution times L_p (see Equation 16.20). The question is, what causes this water movement? Because the membrane is impermeable to solute, solute cannot enter the pores and the fluid in the pore is pure water. Consider a water molecule in the middle of the pore. How does the water “know” to move toward the solution side? It appears there are only two possible answers to this question. Either there is a concentration gradient of water within the pore, or there is a pressure gradient within the pore. These two possibilities are not mutually exclusive, but diffusion-driven water flow and pressure-driven water flow are often thought of as separate mechanisms. The dichotomy reflects the notion that water is an incompressible fluid. Water is not absolutely incompressible, however. The coefficient of compressibility is given as:

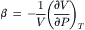(16.37)

and the value of β for water is 4.53×10⁻⁵ atm⁻¹. The equation for the volume of water is:

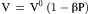(16.38)

where V⁰ is the volume at a standard temperature and pressure (1 atm), and P is the pressure in excess of 1 atm. The coefficient of compressibility is virtually constant in the range −500 to +1000 atm. Equation 16.38 indicates that application of a negative pressure of 2.5 atm would expand a pure water solution by 0.01%, which corresponds to a change in the concentration of water of about 5 mM. Looked at the other way, an expansion of water of only 0.01% would induce a negative pressure of 2.5 atm, equal to the osmotic pressure of a 0.1 molal solution at 37°C.

Dainty (1965) proposed a model in which he considered the density of water immediately within the pore opening on the solution side. As solute molecules cannot enter the pore, Dainty reasoned that the concentration of water within the pore must be higher than in the solution. Because of this difference in concentration, he argued that water would diffuse into the solution side faster than water could diffuse into the pore. The resulting net movement of water toward the solution side would lower the density of water in the pore, thereby creating a reduced pressure. Bulk movement of water down its pressure gradient would follow.

This explanation of the origin of osmotic pressure supposes that the driving force is actually water diffusing down its concentration gradient. The data in Fig. 16.7 show, however, that the concentration of water cannot be the major determinant of the colligative properties of solutions. In Fig. 16.7A, the water concentration in solutions of sucrose and glucose are plotted against the concentration of the solute. The water concentration is indeed decreased by dissolving solute, but sucrose, being almost twice as large as glucose, displaces almost twice as much solvent. As shown in Fig. 16.7B, however, the colligative properties, represented here by the freezing point depression, depend only on the concentration of solute. Solutions with equal solute concentrations but different water concentrations have the same freezing point.

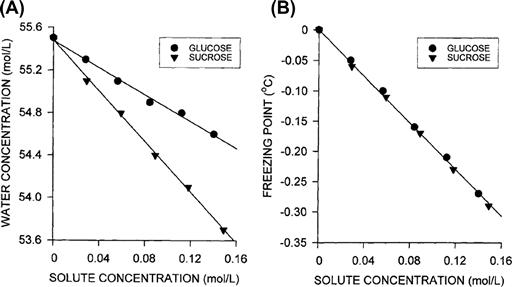
FIGURE 16.7 Effect of solute concentration on water concentration and freezing point depression in glucose and sucrose solutions. (A) Because solute displaces water, the water concentration decreases with increasing solute concentration. Sucrose is nearly twice the size of glucose. Consequently, there is less water in a sucrose solution having the same molarity as a glucose solution. (B) The freezing point depression, however, is dependent only on the solute concentration. It is the mole fraction of water that determines the colligative properties of solutions (the osmotic pressure, vapor pressure depression, boiling point elevation, and freezing point depression). (Data from The Handbook of Chemistry and Physics, Chemical Rubber Company, Cleveland, OH, 1965.)

An alternative view of the physical origin of the osmotic pressure begins with the notion of pressure as a force divided by an area. The macroscopic concept of pressure relies on the averaging over time of the myriad of collisions that produce the pressure. By Newton’s law, force is the time derivative of momentum. An elastic collision of a solvent or solute molecule with the walls of the vessel results in a momentum change of 2mv, where m is the mass of the molecule and v is its velocity, which contributes to the pressure against the vessel wall. At the entrance to the pore, however, solute molecules cannot transfer their momentum to the interior of the pore because they collide with the rim of the pore and are reflected back into the solution. Thus, the water molecules immediately inside the pore experience a momentum deficit that is equal to the component of pressure contributed by the solute molecules in the bulk phase.

Figure 16.8 shows the one-dimensional concentration profile of solute molecules near a pore opening. Because there is a steep solute gradient, there should be a diffusion of solute toward the pore opening. However, the actual steady-state flux of solute in this direction is zero because of the force exerted on the solute molecules by the membrane. The equation that describes the solute flux, J_s, in units of mol cm⁻²s⁻¹, is:

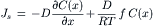(16.39)

where C(x) is the concentration of solute at position x, D is the solute diffusion coefficient in units of cm²·s⁻¹, f is the force per solute molecule and R and T have their usual meanings.

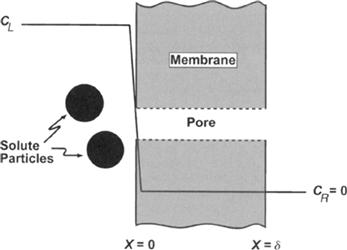
FIGURE 16.8 Concentration profile in the vicinity of a pore in a microporous membrane. The membrane is impermeable at all places except the pores, where water may penetrate but solute particles (solid circles) are too large to enter the pore. The concentration of solute in the bulk solution (C_L) must fall to zero upon entering the pore. The steep concentration gradient is accompanied by diffusion towards the pore that is balanced by reflection of solute by collision with the membrane.

Villars and Benedek (1974) derived an equation for the drop in pressure immediately inside the pore on the solution side by setting the flux in Equation 16.39 to zero and analyzing the net force on a plug of volume near the pore. Under steady-state conditions with zero J_s through the pore, Equation 16.39 gives:

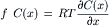(16.40)

where f C(x) is the force per molecule times the number of molecules per unit volume, or the force per unit volume. Figure 16.9 shows a volume element near the opening of the pore on the solution side. We consider the forces acting on the element of fluid with an area A from a point x well within the bulk solution to a point x + Δx just inside the pore. We assume that this element is in mechanical equilibrium; although it may be moving, it is not accelerated or decelerated. The forces acting on the volume are contact forces on the edges of the volume and additional forces acting on the solute molecules alone to counteract the diffusive flux. At mechanical equilibrium the sum of the forces must be zero. This is written as:

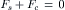(16.41)

where F_s is the total force acting on the solutes in the volume and F_c is the net contact force due to the pressure from the adjacent volume elements. The net contact forces are the result of pressure acting over an area:

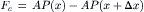(16.42)

The forces acting on the volume due to the solute particles is given by integrating Equation 16.40:

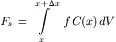(16.43)

Inserting the volume element dV = A dx and fC(x) = RT∂C(x)/∂x from Equation 16.40, we obtain:

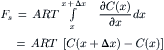(16.44)

Since C(x + Δx) = 0 because solute particles are not in the pore, this becomes:

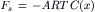(16.45)

where the negative sign indicates that F_s is directed to the left. Inserting Equations 16.42 and 16.45 into Equation 16.41, we have:

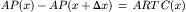(16.46)

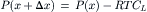(16.47)

This last equation indicates that the pressure experienced by the volume of fluid immediately inside the pore is less than the bulk pressure, P(x), by the amount RTC_L, where C_L is the concentration of impermeant solute in the solution on the left of the membrane. This analysis is consistent with the intuitive idea that water movement from the water side to the solution side of a semipermeable membrane must be due to a real force, which appears in this analysis to be due to the momentum deficit, and thus pressure deficit, within the pore on the solution side.

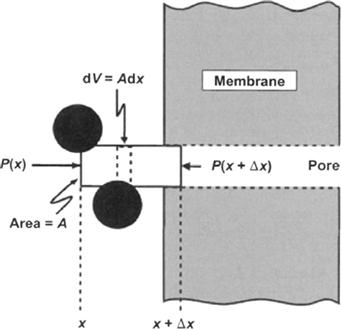
FIGURE 16.9 Forces acting on a volume element immediately adjacent to a pore opening. The ideal, porous, semipermeable membrane separates pure water on the right from solution of impermeant solute on the left. The volume element has an area, A, equal to the cross-sectional area of the pore. The pressure in the bulk phase at position x is P(x). The pressure at position x + Δx, just within the pore, is P(x + Δx). The net force on the element is the sum of the forces at both ends plus the forces acting only on the solute particles (solid circles) within the element.

IVA5 Physical Interpretation of the Reflection Coefficient, σ

The microporous semipermeable membrane presented previously distinguishes between solvent water and solute on the basis of pore and solute size. That is, the solute is too large to enter the pore and so cannot cross the membrane. If the pores were somewhat larger or the solute molecules smaller, the solute could enter the pore, but with a lower probability than water because of the tight fit. In this case, rather than the solute being absolutely impermeant, the membrane would allow its slow passage. How does this affect the situation? Let us suppose that solute molecules that hit the rim of the pore before entry are reflected back into the bulk solution. This is shown diagrammatically in Fig. 16.10, looking down the axis of the pore perpendicular to the surface of the membrane. The area of the pore that is accessible to solute is:

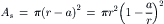(16.48)

where a is the radius of the solute molecule. Assuming that the radius of water molecules (0.75 Å) is negligible compared to the pore’s radius, the ratio of areas available to solute and solvent water is:

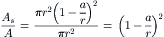(16.49)

The fraction of collisions of solute molecules with the pore opening that are reflected back, compared with those of water, is approximated by the ratio of the area of the gray annulus in Fig. 16.10 to the cross-sectional area of the pore. This is identified with the reflection coefficient:

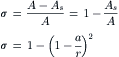(16.50)

According to this view, the concentration of solute immediately within the pore would not be zero, as in the case when the solute was impermeant, but instead would be (1−σ)C and the excluded concentration would be σC. Thus, the momentum deficit inside the pore would be due only to the excluded solute and would be equal to σRTC, which is equal to σπ.

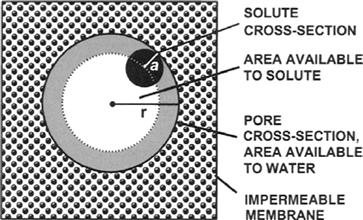
FIGURE 16.10 A physical interpretation of the reflection coefficient, σ, for a solute and a porous membrane. The view is down the pore in a direction perpendicular to the membrane. The pore is modeled as a right circular cylinder of radius r. The model assumes that any contact of the membrane with a solute particle of radius a (solid circle) will result in reflection of the particle back into the solution. The area available to solute is indicated in white. The total area of the pore, white plus gray annulus, is available for water movement.

In addition to entrance effects, the concentration profile within the pore will be influenced by the combination of diffusion through the pore, solvent drag due to movement of fluid in response to pressure gradients and interaction of the solutes with the non-linear velocity profile within the pore. Laminar flow through long pores is characterized by a parabolic velocity profile, with a motionless layer of fluid adjacent to the pore walls and most rapid flow in the center. Large solute molecules will span several layers of velocity, thereby distorting the velocity profile and changing the solute molecule’s velocity. Various equations have been derived to relax the assumption of negligible water radius and to relate the effective filtration area of the solute to the geometric radius of the pore (Renkin, 1954; Villars and Benedek, 1974; Hobbie, 1978). Although models assuming hydrodynamic flow through pores have been useful, their applicability to osmotic flow across biological membranes remains an open question.

IVB Lipid Bilayer Membranes: the Dissolution–Diffusion Model

There are two types of lipid bilayer membranes that are useful models of membranes: the lipid vesicle and the planar bilayer membrane. The lipid vesicle is a small spherical shell of lipid usually produced by sonicating a dispersion of lipid in water. Planar bilayer membranes consist of a thin film of phospholipids formed over a small hole in a partition between two aqueous compartments. The film is formed by “painting” the hole with a non-polar solvent containing the lipids, which then spontaneously form a bilayer to separate fully the two solutions. This arrangement allows measurement of electrical and permeability properties of the bilayer. In the case of the liposome, the inner compartment is exceedingly small and experimentally inaccessible. In both cases, there are no components of the membranes other than the lipid.

IVB1 Osmotic and Pressure-Driven Flow for the Dissolution-Diffusion Model: P_f

One model of water permeation through the lipid bilayer supposes that the water dissolves in the lipid phase and crosses the membrane by simple diffusion. In this model, the solution in contact with the membrane is one phase, while the hydrophobic core of the membrane is a second phase. Equilibrium of water in the solution phase with water in the membrane phase is described by equating the chemical potential of water in the two phases:

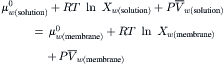(16.51)

where X_w_(solution) and X_w_(membrane) are the mole fractions of water in the solution in equilibrium with the membrane and in the membrane phase, respectively. The partition coefficient is defined as:

(16.52)

Consider the case where only osmotic pressure drives water flow and hydrostatic pressure across the membrane, ΔP, is 0. Since water generally partitions poorly into hydrocarbon solvents, we may assume that the mole fraction of water in the membrane phase is low. That is, the water concentration is dilute, and we may replace the mole fraction of water with its concentration:

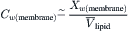(16.53)

where 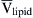is the partial molar volume of lipid in the membrane. If the concentration of water immediately inside the membrane is in equilibrium with the solution in contact with the membrane, we combine Equations 16.52 and 16.53 to get:

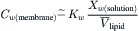(16.54)

For dilute solutions, this is approximated by:

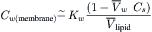(16.55)

where C_s is the solute concentration. The concentration of water immediately inside the left side of the membrane, C_w,L, is given by Equation 16.55 where C_s is the concentration of solute in the solution on the left side of the membrane. A similar expression pertains to the concentration of water immediately inside the membrane on the right side (C_w,R). From the concentrations of water at both faces of the membrane, its diffusion across the membrane is given by Fick’s law:

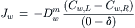(16.56)

where 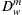is the diffusion coefficient of water in the membrane phase. Substitution from Equation 16.55 into Equation 16.56 gives:

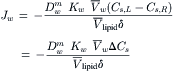(16.57)

The flux of water, J_w, is in units of moles of water per second per cm² of membrane. It is converted to units of volume flow by multiplying by V_w, as in Equation 16.34, to obtain:

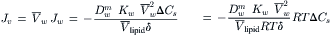(16.58)

The last term on the right is the osmotic pressure difference, Δπ. This equation relates the volume flux to the osmotic pressure difference when the mechanism of water flow is dissolution and diffusion. Comparison to the earlier description of osmotic flow by Equation 16.18 allows us to identify L_p as:

(16.59)

From the definition, P_f = L_pRT/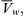 we get the expression for P_f as:

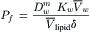(16.60)

Equation 16.58 was derived for an osmotic gradient (ΔC_s>0) in the absence of a hydrostatic gradient (ΔP = 0). The expression relating volume flux and pressure when ΔC_s = 0 can be derived by returning to Equation 16.51 and setting the mole fractions of water on the two sides of the membrane equal, while the pressures differ. The result is that exactly the same L_p is derived for pressure-driven flow as for osmotic flow when the mechanism is by rapid dissolution of water followed by slow diffusion through the lipid membrane phase (Finkelstein, 1987).

IVB2 Diffusional Water Permeability through Lipid Membranes: P_d

The permeability of lipid membranes to a diffusional water flux is expressed as:

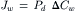(16.61)

where P_d is the diffusional permeability and ΔC_w is the difference in water concentration across the membrane. The overall permeation of the membrane by water is a consequence of three steps: dissolution into the membrane phase at the left interface; diffusion across the membrane phase; and reversal of dissolution at the right interface. If we assume, as we did in the derivation of P_f, that the rate-limiting step is diffusion through the membrane phase, then Equation 16.61 may be written as:

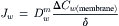(16.62)

From Equation 16.54, this is:

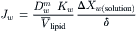(16.63)

Because 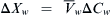, this becomes:

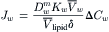(16.64)

P_d can be identified by comparing Equations 16.64 and 16.61:

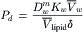(16.65)

IVB3 P_f/P_d Ratio for the Dissolution–Diffusion Model

The expressions for P_f in Equation 16.60 and P_d in Equation 16.65 derived for a lipid membrane under identical assumptions (equilibrium at the interfaces with relatively slow diffusion across the membrane), indicate that the P_f/P_d ratio for diffusive flow of water across lipid membranes should be 1.0. Cass and Finkelstein (1967) measured the osmotic and diffusive permeability of planar lipid bilayers and found that, within experimental uncertainty, the ratio was indeed 1.0. The uncertainty arose mainly in the determination of P_d because of the presence of unstirred layers adjacent to the planar lipid bilayer. These unstirred layers are an additional diffusional barrier that affects the experimental determination of P_d much more than P_f. In the flux equations, permeability appears as a conductance relating a flux (J_w or J_s) to a driving force (ΔC_w or ΔC_s). Thus, the inverse of permeability is like a resistance. For a membrane in series with unstirred layers, the total resistance is the inverse of the observed permeability, which is the sum of the resistances offered by the individual barriers, the membrane and the unstirred layers. We write this as:

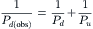(16.66)

From this equation, it is plain that if P_u, the combined permeability of the unstirred layers on both sides of the membrane, is less than infinity, the observed P_d will be less than the actual P_d of the membrane alone. Since diffusion of water through the unstirred layer is given by Fick’s law, Equation 16.66 may be rewritten as:

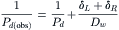(16.67)

where δ_L and δ_R are the equivalent unstirred layer thickness on the left and right sides of the membrane.

Unstirred layers also can affect measurement of the coefficients for pressure gradient-driven flow, P_f and L_p, but the error introduced is much less than for concentration gradient-driven flow, P_d (Barry and Diamond, 1984; Finkelstein, 1987), and was safely ignored in evaluating the P_f/P_d ratio (e.g. Cass and Finkelstein, 1967). The osmotic flow sweeps solute toward the membrane on the side with lower osmolarity and away from the membrane on the other side. As long as convection is faster than diffusion, this diminishes the transmembrane osmotic gradient, reducing J_v for the apparent Δπ and causing underestimation of P_f and L_p. The observed P_f, P_f_(obs), is given as:

(16.68)

where P_f_(membrane) is the true membrane parameter, δ is the unstirred layer thickness, J_v is the volume flux and D_s is the diffusion coefficient of the osmolyte. The error can be minimized by determining P_f with a small Δπ so that J_v is small. Because P_f and L_p are proportional (Equation 16.36), the errors are also proportional.

The value of P_d and P_f varies with the lipid composition of the membrane and ranges from 1×10⁻⁵ cm·s⁻¹ to 5×10⁻³ cm·s⁻¹ (Deamer and Bramhall, 1986). Cholesterol, which generally reduces the fluidity of lipid bilayers, reduces P_d and P_f progressively with increasing cholesterol content (Finkelstein and Cass, 1968). The unidirectional flux across a lipid membrane equals P_d×C_w. Using a typical P_d of 1×10⁻³ cm·s⁻¹ and a C of 55 mol·L⁻¹, the unidirectional flux across a membrane is 5.5×10⁻⁵ mol·cm⁻²·s⁻¹. By comparison, the unidirectional flux of water across a distance δ = 5 nm (approximately the thickness of the lipid bilayer) can be calculated as (D_w×C_w)/δ. Using 3×10⁻⁵ cm²·s⁻¹ for D_w, the unidirectional flux of water in water is 3.3 mol·cm⁻²·s⁻¹. Thus, water flux through the membrane is about 60 000 times slower than that through water. Nevertheless, the water flux is still enormous. Taking 0.7 nm² as the average area of a typical phospholipid in the bilayer, the unidirectional water flux corresponds to about 2.2×10⁵ water molecules passing each phospholipid molecule each second.

IVC Flow through Narrow Pores: P_f/P_d Ratio

The equations derived earlier for P_f for a porous membrane required the assumption that the pores were large enough to allow laminar flow as described by the Poiseuille equation. Suppose that the pores are so narrow that water passes through the pores in single file. It is clear that laminar flow cannot occur here and the Poiseuille equation does not apply. As shown in Fig. 16.11, the narrow pore restricts free diffusion in the pore because diffusion of one water molecule from one position in the pore to the next requires its neighbor to move away to provide a vacancy. In this way, diffusion within the restricted geometry of the pore becomes a collective property of all of the molecules in the pore. The likelihood that a tracer molecule will diffuse all the way through the pore will depend on the number of water molecules in the pore, as movement of tracer water (solid circle) through the pore requires the movement of a vacancy (×) all the way through the pore.

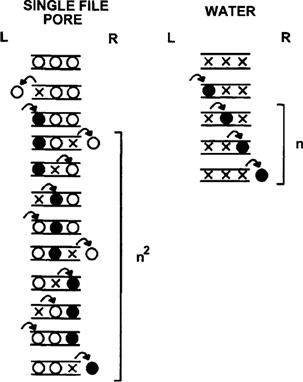
FIGURE 16.11 Jumping model of diffusion of water through a narrow pore. In the model of free water diffusion (right), tracer water (solid circles) makes successive jumps from one vacancy (×) to another. In order to move three places, it must make three jumps. In a narrow pore (left), tracer water cannot move to the next position in the pore unless a vacancy is present because unlabeled water (open circles) cannot move out of the way. Movement of tracer water from one site to the next in the pore requires a vacancy to diffuse all the way through the pore. Since the vacancy requires three steps to diffuse through the pore, tracer water diffusion through three steps in a narrow pore requires nine jumps. The result is that single-file diffusion becomes a collective property of the single file and is slower than free water diffusion.

Suppose that there are N water molecules in a pore. We may assume that the length of the pore, δ, is proportional to N, and that the water molecules reside in more or less specific positions separated by δ/N. In the free diffusion of liquid water in the bulk solution, according to Fick’s first law of diffusion, the flux of water is proportional to 1/δ or 1/N. In the case of a single-file diffusion through a narrow pore, the diffusion of a vacancy through the water within the pore looks exactly like the diffusion of water through a series of vacancies in free diffusion. Thus, the flux of the vacancy also is proportional to 1/N. The movement of tracer from one position to the next in the pore requires the diffusion of a vacancy all the way through the pore, so that the flux of tracer one step is proportional to 1/N. In order to diffuse all the way through the pore, the tracer must make N such jumps. The unidirectional flux of tracer over N steps of equal flux is given by Stein (1976):

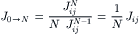(16.69)

where J_0→N is the unidirectional flux of tracer across N steps (all the way through the membrane) and J_ij is the unidirectional flux of tracer over one step. Since J_ij requires diffusion of a vacancy all the way through the pore, it is proportional to 1/N. The unidirectional diffusional flux of tracer through a single-file pore is thus proportional to 1/N², rather than 1/N. Pressure-driven flow, on the other hand, remains inversely proportional to pore length. The theoretical analysis of both pressure-driven flow and diffusive flow through a single-file pore has led to the conclusion that the proportionality constants relating P_f to 1/N and P_d to 1/N² are identical. The result, for a single-file pore, is:

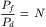(16.70)

where N is the number of water “binding sites” within the pore (Finkelstein, 1987). A more recent theoretical analysis suggests that this result is true near equilibrium, but the ratio of osmotic to diffusive permeability may exceed N for a membrane far from equilibrium (Hernandez and Fischbarg, 1992).

IVD Mechanism of Water Transport across Lipid Bilayer Membranes

The previous discussion suggests that water transport across lipid bilayer membranes occurs by rapid dissolution at the membrane interface followed by diffusion across a hydrocarbon-like interior. Three observations strongly support this mechanism: (1) the P_f/P_d ratio, after correction for unstirred layers, appears to be close to 1.0 (Cass and Finkelstein, 1967; Andreoli and Troutman, 1971); (2) insertion of pore-forming antibiotics such as nystatin, amphotericin B or gramicidin A increases the P_f/P_d ratio to small values of N (between 3 and 5) (Holz and Finkelstein, 1970; Rosenberg and Finkelstein, 1978); and (3) the activation energy for water transport, typically 10–20 kcal·moL⁻¹, is larger than the activation energy for free water diffusion, ≈4 kcal·moL⁻¹, which should apply if water moves through a pore (Solomon, 1972; Fettiplace and Haydon, 1980). However, experimental studies of water permeation across liposomes appear to give a different answer. The P_f of liposomes, measured by turbidimetric methods, is not affected by the chain length of the lipids or the degree of saturation (Carruthers and Melchior, 1983; Jansen and Blume, 1995), whereas water solubility in hydrocarbons is affected by chain length (Schatzberg, 1963). Further, the activation energy of P_f in liposomes is only 3.2 kcal·moL⁻¹ (Carruthers and Melchior, 1983), similar to the activation energy for free water diffusion. The P_f of liposomes is discontinuous near phase transitions of the lipid and P_f/P_d ratios from 7 to 23 have been reported (Jansen and Blume, 1995). From these observations, it appears that liposomes do not behave as planar lipid bilayers, perhaps because of membrane defects induced by the marked curvature of the membrane in these small structures. The activation energy has been taken as diagnostic of whether water traverses the membrane through pores or by diffusion through the lipid itself (Finkelstein, 1987; Verkman, 1993). Low activation energies of water transport are associated with a high P_f or L_p in membranes containing water channels or pores, whereas high activation energies are associated with a low P_f or L_p, indicating diffusional water transport in membranes without pores or when pores are blocked by mercurials (Table 16.2).

TABLE 16.2. Hydraulic Conductivity and its Apparent Activation Energy

Tissue	Lp 10⁻¹⁰ L·N⁻¹·s⁻¹	E_a kcal·moL⁻¹
Water channels
RBC, human	18.0	3.9
RBC, beef	18.2	4.0
RBC, dog	23.0	4.3
Prox. tubule BLM-V, rabbit	21.9	2.5
Liposomes + AQP1	30.8	3.1
Water channels + mercurials
RBC, human + PCMBS	1.3	11.6
Prox. tubule BLM-V, rabbit + Hg	4.4	8.2
Diffusional
RBC, chicken	0.6	11.4
Intestinal brush border, rat	0.9	9.8
Ventricle, rabbit	1.2	10.5
Liposomes	1.9	16.0
PC bilayer	1.6	13.0
PC/chol bilayer	0.4	12.7
Water self-diffusion	—	4.2

Hydraulic conductivity, L_p, and activation energy, E_a, are characteristic of the mechanism of water transport. High L_p and low E_a are typical of membranes containing functioning water channels, whereas low L_p and high E_a indicate diffusional water transport. Note that 10⁻¹⁰ L·N⁻¹·s⁻¹ (SI units)=10⁻¹²·cm³·dyn⁻¹·s⁻¹ (cgs units). RBC, red blood cell; BLM-V, basolateral membrane vesicles; AQP1, aquaporin-1; PCMBS, p-chloromercuribenzene sulfonate; PC, phosphatidylcholine; chol, cholesterol. For references, see Suleymanian and Baumgarten (1996).

In the dissolution–diffusion mechanism, water encounters a minimum of three sequential barriers: dissolution on one side of the membrane; transport across the hydrocarbon-like interior; and then removal from the membrane on the opposite side. Assuming rapid equilibration at the interfacial regions is equivalent to assuming that the barriers there are insignificant compared to the barrier of diffusion, but there is no a priori reason to make this assumption. The alternate view proposes that the rate-limiting step is lateral movement of the phospholipid head groups that creates a transient defect required for penetration of water into the interfacial region of the membrane (Trauble, 1971; Haines, 1994). Water transport through the hydrophobic core requires vacancies within the bilayer that form when hydrocarbon chains make gauche-trans-gauche kinks caused by the rotation of carbon–carbon bonds in the hydrocarbon tails. Kinks in the hydrocarbon tails propagate rapidly down acyl chains and provide sufficient space for water. Experimental support for this model comes from studies showing addition of cardiolipin to phosphatidylcholine liposomes decreases P_f without changing bilayer fluidity by stabilizing head group interactions (Shibata et al., 1994). These two models make very different assumptions, and the detailed mechanism of water permeation through lipid bilayers remains uncertain.

V Water Movement Across Cell Membranes

In the prior sections, we considered osmotic- or pressure-driven flow and diffusive flow of water across membranes that were characterized as: (1) porous membranes with pores large enough to allow laminar flow; (2) lipid membranes with no pores, but allowing water permeation by a dissolution–diffusion mechanism; and (3) membranes containing narrow pores. We found expressions for the osmotic permeability, P_f, and the diffusive permeability,P_d, for each and found that the membranes could be distinguished in principle by the ratio P_f /P_d: large values of P_f/P_d indicate a porous membrane, P_f/P_d = 1 signifies a diffusive mechanism and small values of P_f /P_d>1 are characteristic of narrow pores. What are the permeabilities of real biological membranes, and what do these permeabilities tell us about the routes of water transport through membranes?

VA Rate of Water Exchange: Experimental Measure of P_d

Paganelli and Solomon (1957) measured the diffusional exchange of water across erythrocyte membranes by rapidly mixing a suspension of the cells with an isotonic buffer with added tracer ³H₂O. The mixture was forced down a tube and samples of the extracellular water were obtained by filtration at various distances, corresponding to various times of exchange. Paganelli and Solomon found that the half-time for exchange of ³H₂O was 4.2 ms at room temperature. This means that 90% of all of the water within an erythrocyte is exchanged with extracellular water every 14 ms. This is an extraordinarily rapid rate of exchange. Erythrocytes are sufficiently small that the presence of an unstirred layer within the cells does not appreciably affect the determination of P_d (i.e. (δ_L + δ_R)/D_w<<1/P_d; see Equation 16.67).

Diffusional exchange of water across erythrocyte membranes also can be measured by nuclear magnetic resonance (NMR) spectroscopy. Relaxation of the nuclear spin states of hydrogen is much slower inside a cell than outside when a relatively impermeant paramagnetic ion like Mn²⁺ is added to the extracellular solution. This allows calculation of P_d because the relaxation of the spin states is then effectively limited by permeation through the membrane. The values of P_d for the erythrocyte determined by isotopic or NMR methods cluster around 4×10⁻³ cm·s⁻¹ (Solomon, 1989).

VB Rate of Osmotic Flow: Experimental Measure of P_f and L_p

According to Equation 16.23, the hydraulic conductivity, L_p, can be determined experimentally as:

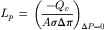(16.71)

The osmotic permeability, P_f, can then be calculated as P_f=L_pRT/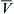_w (Equation 16.36). The experimentally determined values reflect the rate of water flow, Q_v, in the presence of a known osmotic pressure difference, Δπ, produced by a solution with a known reflection coefficient, σ≈1.0, over a known surface area, A.

The rate of water movement into or out of erythrocytes in response to mixing with hypertonic or hypotonic media has been measured by using light scattering as an index of erythrocyte volume. The experiments are similar to those used to determine P_d; a suspension of erythrocytes is mixed with media of defined osmolality and the mixture then flows down a tube passing through an observation cell. Light scattering is monitored at known distances down the tube and cell volume changes are calculated from changes in light scattering. This and other methods give values for L_p that cluster around 1.8×10⁻¹¹ cm³·dyn⁻¹·s⁻¹ (Solomon, 1989). Using R = 8.314×10⁷ dyn·cm·mol⁻¹·K⁻¹, 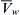= 18 cm³·mol⁻¹ and T = 298 K, this average value of L_p corresponds to a P_f of about 2.5×10⁻² cm·s⁻¹.

VC Water Channels in Biological Membranes

The ratio of P_f/P_d for the erythrocyte membrane described earlier is about 5. Although there is some uncertainty in this ratio, it is clearly in excess of the value of 1.0 predicted for a diffusive mechanism. This suggests that there are pores in the erythrocyte membrane. The actual value of P_f/P_d for the pore alone cannot be obtained from just this information, however, because the erythrocyte membrane is actually a mosaic of lipid bilayer and pores; water moves through both in parallel, so the permeabilities of the components add. Experiments that block the pore suggest that the P_f/P_d ratio for the pore alone is about 10 and that 90% of water flux is via the pore, whereas 10% crosses the lipid bilayer (Macey, 1979; Finkelstein, 1987).

Two distinct means of inhibiting water transport provide additional evidence for proteinaceous pores. Mercurial sulfhydryl reagents, such as HgCl₂, p-chloromercuribenzoate (PCMB) and p-chloromercuribenzene sulfonate (PCMBS), decrease the erythrocyte P_f by a factor of 10 and P_d by less than a factor of 2 and the osmotic and diffusional permeabilities become equal (Macey and Farmer, 1970; Macey et al., 1972). Concurrently, the activation energy for permeation is increased from about 4 kcal·mol⁻¹ expected for water-filled pores to >10 kcal·mol⁻¹, a value typical of artificial lipid bilayers (see Table 16.2). Mercurials inhibit water transport primarily by targeting protein SH groups because their effect is fully and rapidly reversed by cysteine. The second inhibitor is radiation. High doses of radiation inhibit water transport in both erythrocytes (van Hoek et al., 1992) and renal brush-border membrane vesicles (van Hoek et al., 1991). The characteristics of radiation inactivation suggest that the target is the size of a 30-kDa protein and are inconsistent with the entire membrane or transient defects serving as the major water pathway.

Although these studies and others, especially in epithelia (e.g. Verkman, 1993), made it clear that water pores or channels must exist, until recently, their identity and characteristics remained mysterious. Are what we call “water channels” simply water moving through open ion channels or through an ion exchanger or ion co-transporter? Are water channels specific, admitting water but excluding ions? These questions have been answered with the cloning and expression of a family of water channels called aquaporins (Agre et al., 1993; King and Agre, 1996; Verkman et al., 1996; Heymann et al., 1998; Nielsen et al., 1999).

VC1 Aquaporins

Water channels are related to the membrane integral protein (MIP) family (20–40% homology). The first water channel identified was cloned from a human bone marrow library by Preston and Agre (1991) based on the sequence of a purified protein of uncertain function. Initially called CHIP28 (channel-forming integral protein, 28 kDa), this protein was later redesignated aquaporin-1 (AQP1) and MIP-1 is referred to as AQP0. Ten mammalian aquaporins are known and more than 100 related proteins have been found in amphibians, Drosophila, plants, Escherichia coli and yeast, but not all of these conduct water (Heyman et al., 1998; Nielsen et al., 1999; Heymann and Engel, 1999).

The cloned AQP protein exhibits all of the characteristics of a water channel. AQP1 expressed in Xenopus oocytes induces up to 30-fold increases in P_f that is blocked by HgCl₂ (Preston et al., 1992). Reconstitution of purified AQP1 protein in liposomes verified that AQP1 itself, rather than modulation of an endogenous oocyte membrane protein, was responsible for mercurial-sensitive water permeation (Zeidel et al., 1992). Furthermore, incorporation of AQP1 into liposomes reduced the activation energy of P_f from 16.1 kcal·mol⁻¹, characteristic of permeation through the bilayer, to 3.1 kcal·mol⁻¹, characteristic of water passing through water-filled pores. Moreover, AQP1 appears to be active and highly selective for water without requiring regulatory subunits or cofactors (Preston et al., 1992; Zhang et al., 1993).

There are about 2×10⁵ AQP1 molecules per erythrocyte (Zeidel et al., 1992). Taking the erythrocyte’s membrane area as 1.35 × 10⁻⁶ cm² (Solomon, 1989), this corresponds to a density of about 1.5 × 10¹¹ AQP1 cm⁻² or 1500 AQP1 μm⁻². Despite this remarkable density of pores, the water permeability of a human erythrocyte is only ≈10 to 50 times greater than that of a phosphatidylcholine/cholesterol bilayer (Fettiplace and Haydon, 1980). Thus, 30–150 aquaporin channels are needed to equal the permeability of 1 μm² of bilayer.

AQP1 contains 269 amino acid residues and was postulated to have six membrane-spanning domains based on an analysis of hydrophilicity (Preston and Agre, 1991) and selective proteolysis of protein loops that face the intra- or extracellular side (Preston et al., 1994). The topology for the AQP1 and the other members of the AQP family is shown in Fig. 16.12. Mercurial-inhibition, N-glycosylation and PKA phosphorylation sites have been identified. There is an internal homology between the halves of AQP designated repeat-1 and -2. The greatest homology among AQPs is in the segments surrounding asparagine-proline-alanine (NPA) motifs in loops B and E. These loops are thought to be arranged antiparallel and are postulated to dip back into the membrane to form an hourglass-shaped pore represented in the cartoon in Fig. 16.12 (Jung et al., 1994). It is hypothesized that four highly conserved polar residues, E17, N76, N192, E142, comprise a critical portion of the water permeation pathway (Heymann et al., 1998).

FIGURE 16.12 AQP family portrait. Cartoon illustrating the postulated topology of AQP as a structure with six membrane spanning α-helices (top). Cysteine (C) responsible for inhibition by mercurials and consensus PKA phosphorylation (S) and glycosylation (N) sites are also shown. Loops B and E are envisioned to dip into the membrane with the two NPA motifs forming the narrow neck of an hourglass-shaped, water-filled pore (bottom). Single letter codes are standard amino acid abbreviations. The position of the Colton polymorphic blood group antigen (Co) is noted. (Reproduced from King and Agre (1996) with permission, from the Annual Review of Physiology, volume 58, © 1996, by Annual Reviews, Inc. and from Jung et al. (1994) with permission.)

The biochemical behavior of solubilized erythrocyte AQP1 suggested that it is a non-covalently-linked tetrameric structure and electron microscopy of negatively stained AQP1 confirmed this (Walz et al., 1994). Co-expression of Hg-sensitive and -insensitive recombinant proteins indicates that each AQP monomer forms an independent functioning pore, however (Preston et al., 1993). An exception to the tetrameric design of AQPs is AQP4. AQP4 forms large multimeric square arrays in the end-feet of astrocytes that surround capillaries (Rash et al., 1998). X-ray diffraction patterns at 3.5- and 6-Å resolution have been obtained from two-dimensional crystalline AQP1 arrays (Jap and Li, 1995; Walz et al., 1997). Electron density contour maps confirmed a tetrameric arrangement of monomers and each monomer appeared to have a central low density core, presumably the permeation pathway, surrounded by six tilted high density regions thought to represent membrane-spanning α-helicies.

Immunohistochemistry, Western blot (protein determination) and Northern and in situ hybridization and RNase protection assays (mRNA determinations) have identified broad but only partially overlapping distributions of AQP homologs in regions where water permeability is high (Hasegawa et al., 1993; Nielsen et al., 1993, 1999; Zhang et al., 1993; Umenishi et al., 1996; Ma and Verkman, 1999). For example, AQP1 is located in erythrocytes, renal proximal tubules and the descending thin limb of the loop of Henle (but not in the collecting duct, where water permeability is controlled by vasopressin), the choroid plexus, the iris, ciliary and lens epithelia and corneal endothelium of the eye, lung alveolar capillaries and epithelium, red splenic pulp (with erythrocyte precursors), colonic crypt epithelium and non-fenestrated capillary and lymphatic endothelium in a number of organs including cardiac, skeletal and smooth muscle. The exception with regard to broad distribution is AQP2. AQP2 underlies the vasopressin-regulated water permeation pathway of the renal collecting duct apical membrane that maintains water balance (Nielsen et al., 1995, 1999). Mutation of AQP2 is responsible for inherited nephrogenic diabetes insipidus and targeting and expression defects may cause acquired forms of this disease. On the other hand, AQP2 expression is upregulated in pregnancy and congestive heart failure, states associated with enhanced water retention (Nielsen et al., 1999).

Several cautions are warranted when drawing physiological interpretations from the localization of AQP. For example, AQP1 mRNA is higher in cardiac homogenate than in homogenate from any other organ (Umenishi et al., 1996), but functionally, the story is different. In isolated myocytes, L_p is very low and the activation energy is high, about 10 kcal·mol⁻¹ (Suleymanian and Baumgarten, 1996) (see Table 16.2). Thus, AQPs do not significantly contribute to water transport across the myocyte membrane.

Organs comprise cells with diverse functions and often different requirements for water transport. Because of its localization in vascular tissue, AQP detected in homogenates should not be attributed to the principal cells of the organ without confirmation. Even careful immunohistochemistry and in situ hybridization may lead the physiologist astray. The problem is the high density of AQP necessary to significantly affect P_f. If, for example, the density of AQP1 in the erythrocyte membrane was 10 AQP1 μm⁻² rather than 1500 AQP1 μm⁻², AQP1 would still be detected by modern techniques, but it would make a physiologically insignificant contribution to P_f.

VC2 Other Channels and Transporters

The identification of specific water channels does not exclude the possibility that water flux through ion channels or transporters significantly contributes to the water permeability of the membrane. One interesting example is the cystic fibrosis conductance regulator (CFTR). CFTR functions as a cAMP-regulated Cl⁻ channel. Hasegawa et al. (1992) recently found that CFTR expressed in oocytes also acts as a water channel with an estimated single channel P_f comparable to that of AQP1. Both P_f and Cl⁻ conductance were increased by cAMP. The effect of the CFTR channel on P_f is large but not unique. Pore-forming antibiotics such as gramicidin, nystatin and amphotericin, are reported to induce a more modest P_f. Transporters also may contribute to P_f. Fischbarg et al. (1990) found that expression of Na⁺-independent glucose transporters in oocytes increases water permeability and Solomon et al. (1983) suggested that some of the water permeability of erythrocytes was contributed by the Cl⁻-HCO⁻₃ exchanger. However, water flux mediated by these transporters does not account for the macroscopic properties of water transport.

VI Regulation of Cell Volume under Isosmotic Conditions

VIA Gibbs–Donnan Equilibrium

Because ions exert an effective osmotic pressure, the distribution of ions affects water flow across the cell membrane and thus cell volume. The starting point for understanding these effects is the theoretical ideas of Gibbs that were first demonstrated experimentally by Donnan. The phenomenon is now called Gibbs–Donnan equilibrium or simply Donnan equilibrium. Macknight and Leaf (1977) elegantly describe the history of how these ideas were applied to cell volume regulation and Overbeek (1956) provides a detailed derivation and considers non-ideal solution behavior.

In a Donnan system, the membrane permits the movement of small charged solutes (e.g. K⁺ and Cl⁻) between two compartments but restricts the movement of large charged species, such as proteins, which are usually polyvalent and negatively charged at intracellular pH. It is the inability of one (or more) charged species to distribute freely between the compartments that profoundly influences the distribution of the mobile ions and, consequently, water. For a cell, it is the cell membrane that restricts the movement of large ions. A membrane is not required to establish a Donnan equilibrium, however. All that is needed is a means of restricting one charged species to a single compartment. Donnan equilibria can arise in gels consisting of charged structural components (e.g. an ion-exchange column) because the charges on the gels are fixed in place. Donnan equilibria can also arise in cells after their membranes have been removed, leaving a cytoplasmic “gel” consisting of interconnected cellular proteins. A Donnan system represents a true equilibrium, although as we will see, an equilibrium is not attained under the usual biological conditions.

There are three important characteristics in a Donnan equilibrium system: (1) an unequal distribution of ions; (2) a potential difference between the compartments; and (3) an osmotic pressure. These characteristics can be understood from the application of a basic thermodynamic principle to the system. Species that can cross the membrane, including both mobile ions and water, will distribute themselves so that their electrochemical potential (μ_i) is the same in both compartments.

To understand how a Donnan equilibrium develops, imagine starting an experiment by “filling” the cell and the extracellular space with solutions of concentrations indicated in Fig. 16.13A. Since ions move down their electrochemical gradients, the first question is: what are the electrochemical gradients? Initially, there is no potential difference across the membrane because both internal and external solutions start with an equal number of positive and negative charges. There is no concentration gradient for K⁺ because the amount of K⁺ is the same on both sides of the membrane. Due to the presence of impermeant anions inside the cell, however, [Cl⁻]_o must be greater than [Cl⁻]_i. Consequently, Cl⁻ will enter the cell, moving down its electrochemical gradient, which is initially just the concentration gradient. Inward movement of Cl⁻ makes the inside of the cell negative with respect to the outside. The developing inside negative potential has two consequences. First, it slows the rate of further influx of Cl⁻. Second, the electrical gradient causes the accumulation of K⁺ inside the cell. As K⁺ moves down its electrochemical gradient in the direction set by the potential gradient, an opposing concentration gradient is created. Finally, an equilibrium is reached when the electrical and concentration gradients for both K⁺ and Cl⁻ are equal in magnitude and opposite in direction. This satisfies the requirement that μ_K and μ_Cl, the electrochemical potential for K⁺ and Cl⁻, respectively, are the same in both compartments.

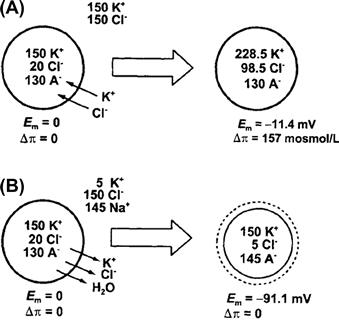
FIGURE 16.13 Development of a Donnan equilibrium. (A) Cell bathed in 150 mM KCl is “filled” with 150 mM K⁺, 20 mM Cl⁻, and 130 mM A⁻. Initially, there is no potential or osmotic gradient (left). K⁺ and Cl⁻ enter the cell until [K⁺]_o·[Cl⁻]_o=[K⁺]_i·[Cl⁻]_i and the ionic fluxes establish a potential and osmotic gradient (right). An equilibrium is achieved only if the membrane is rigid and cell volume is constant. With a biological membrane, however, water enters the cell, cell volume increases and [K⁺]_i·[Cl⁻]_i decreases. This causes further entry of solute and solvent and the cycle repeats until the cell bursts. (B) Double-Donnan system. Part of the extracellular K⁺ is replaced by Na⁺, which is assumed to be impermeant. With impermeant ions on both sides of a membrane (left), equilibrium is attained (right) without an osmotic pressure gradient. In this case, K⁺, Cl⁻, and water leave the cell, until at equilibrium [K⁺]_o·[Cl⁻]_o=[K⁺]_i·[Cl⁻]_i. The amount of A⁻ in the cell is fixed, and thus, the decrease in cell volume increases [A⁻]_i.

During the evolution of the equilibrium, the influx of K⁺ and Cl⁻ are equal on a macroscopic scale and are said to be coupled by the requirement for macroscopic electroneutrality. This is simply a shorthand for the idea that any difference in rates of anion and cation transmembrane flux (a separation of charge) gives rise to a potential that equalizes the fluxes (e.g. if the influx of K⁺ was greater than that of Cl⁻, an inside positive potential would develop, slowing K⁺ influx and accelerating Cl⁻ influx until the rates matched exactly). In the example in Fig. 16.13A, both [K⁺]_i and [Cl⁻]_i increased by ≈78.5 mM. The total entry of K⁺ and Cl⁻ cannot be precisely equal, however, because establishing a potential difference implies that a separation of charge, albeit quite small, must have taken place. If this were a spherical cell with a radius of 20 μm, an inequality of the K⁺ and Cl⁻ fluxes of less than 1 ion per 100 000 would cause a potential difference of 100 mV.1

The basis for Donnan equilibrium can be expressed in terms of the electrochemical potentials² of ions that cross the membrane, here K⁺ and Cl⁻. For ideal solutions, μ is given by:

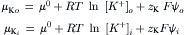(16.72a)

and

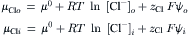(16.72b)

where the subscripts o and i represent the outside and inside of a cell, μ⁰ is the chemical potential of the standard state, ψ is the potential of the compartment, z_i is the valence of species i and R, T and F have their usual meanings. At equilibrium, each permeant species distributes so that μ is identical inside and outside the cell. Equating the expressions for μ and simplifying gives:

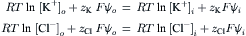(16.73)

Membrane potential, E_m, is measured as ψ_i−ψ_o. Rearranging and substituting in for E_m and z gives:

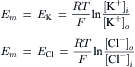(16.74)

These expressions are the Nernst equilibrium potentials for K⁺ (E_K) and Cl⁻ (E_Cl). Thus, when the mobile ions attain their equilibrium distribution in a Donnan system, the potential between the compartments, E_m, simultaneously equals both E_K and E_Cl. Equating the Nernst potentials and simplifying gives the ratio of intra and extracellular ions predicted by Donnan equilibrium:

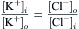(16.75)

or expressed another way:

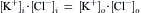(16.76)

In a Donnan equilibrium, the KCl product inside a cell equals the KCl product outside.

This simple rule implies that increasing extracellular K⁺ (e.g. by replacing Na⁺) will cause a cell obeying Donnan equilibrium to take up K⁺ and Cl⁻ and swell. Ion movements in a number of tissues appear to follow Donnan equilibrium, at least for some conditions. Boyle and Conway (1941) made careful measurements of [K⁺]_i, [Cl⁻]_i and cell water in frog sartorius muscles while varying extracellular KCl. For [K⁺]_o greater than 6 mM, the experimental ratio of the KCl products, ([K⁺]_o·[Cl⁻]_o)/([K⁺]_i·[Cl⁻]_i), was very nearly 1.0, as predicted by Equation 16.76. The deviation at low [K⁺]_o occurs because Na⁺ influx causes E_m to deviate from E_K. Accompanying changes in cell water in these experiments and in separate experiments in which K⁺ replaced Na⁺ also agreed with theory.

The expectations for a Donnan equilibrium are calculated for the system shown in Fig. 16.13A. When the intracellular and extracellular KCl products are equal, E_m = E_K = E_Cl = −11.4 mV. In addition, because the number of ions inside the cell is much greater than that outside, the Donnan system has established a significant osmotic gradient. Assuming ideal behavior, the osmolarity inside the cell, ≈457 mosmol·L⁻¹, is about 1.5 times that outside, 300 mosmol·L⁻¹. The resulting osmotic pressure can be calculated as follows:

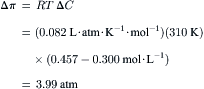(16.77)

Because most cells are readily permeable to water, the osmotic pressure generated here would cause water to enter the cell. This influx of water dilutes the intracellular ion content and the product [K⁺]_i·[Cl⁻]_i must fall below [K⁺]_o·[Cl⁻]_o. As a result, more KCl would enter the cell, followed again by more water, in an endless cycle that would lead to destruction of the cell. That is to say, the simple Donnan system described in Fig. 16.13A fails to reach equilibrium when typical cell membrane properties are assumed.

VIB Double-Donnan or Pump-Leak Hypothesis

How can we reconcile the failure of the simple Donnan equilibrium model (see Fig. 16.13A) and the experimental studies demonstrating behavior consistent with Donnan equilibrium? The Donnan system can be stabilized in two ways. A hydrostatic pressure could be applied to balance the osmotic pressure and arrest transmembrane water movement. In view of the enormous pressures required, this is not a realistic solution for animal cells. Alternatively, equilibrium can be attained by restricting an ionic species to the extracellular compartment just as one is restricted to the intracellular compartment. This arrangement is referred to as a double-Donnan (Leaf, 1959) or pump-leak system (Tosteson and Hoffman, 1960) and is illustrated diagrammatically in Fig. 16.13B. Assume that both Na⁺ and macromolecular anions, A⁻, are restricted to the extracellular and intracellular compartments, respectively. Filling the cell with the same concentrations of K⁺, Cl⁻ and A⁻ as before, we find now that [K⁺]_i·[Cl⁻]_i>[K⁺]_o·[Cl⁻]_o and thus KCl must leave the cell to establish Donnan equilibrium. In the process, water follows the KCl, adjusting cell volume until the KCl, products are equal. A consequence of water flow is that the concentration of the impermeant intracellular ion exactly equals the concentration of the impermeant extracellular ion. At equilibrium, E_m = E_K = E_Cl = −91.1 mV. In contrast to the simple Donnan system, the osmotic pressure developed by intracellular macromolecules and their counterions (sometimes referred to as colloid osmotic pressure) is exactly balanced in the double-Donnan system by the osmotic pressure developed by ions restricted to the extracellular fluid and their counterions. As a consequence, there is no net osmotic pressure across the membrane, and the system is stable.

Another approach for considering the volume change expected in the system in Fig. 16.13B is to calculate the effective osmotic pressure of each compartment. We can suppose that the reflection coefficients, σ, are 1.0 for both A⁻ and Na⁺ because they are impermeant and that the reflection coefficients are 0 for both K⁺ and Cl⁻ because they freely pass the membrane. Extracellular and intracellular osmotic pressures are given by:

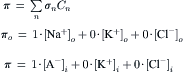(16.78)

Because only the impermeant species contribute to osmotic pressure, the only way for the cell to reach osmotic equilibrium, π_o = π_i, is to alter cell volume until [Na⁺]_o = [A⁻]_i. As a result, the ratio of volume_{t = ∞}/volume_{t = 0} must equal [A⁻]_i/[Na⁺]_o.

It is important to realize that an ion does not need to be impermeant to be effectively restricted to the extracellular space and thus counterbalance the osmotic pressure developed by intracellular macromolecules. Na⁺ is permeant, but it adequately plays this role anyway. As long as the leak of Na⁺ down its electrochemical gradient into the cell is matched by its transport back out, cell volume will remain stable. Consequently, the existence of a pump that actively extruded Na⁺ against its concentration gradient was postulated to explain cell volume (Leaf, 1956) and, subsequently, the Na⁺, K⁺-ATPase, which extrudes three Na⁺ while taking up two K⁺ at the cost of ATP hydrolysis, was identified. Because energy is consumed to extrude Na⁺, the cell is in a steady state rather than a true equilibrium.

VIC Modulation of the Na⁺-K⁺ Pump

One implication of the double-Donnan or pump-leak model is that the Na⁺-K⁺ pump is ultimately responsible for cell volume regulation. Perturbations that alter passive Na⁺ entry must lead to offsetting changes in the rate of Na⁺ extrusion by the Na⁺-K⁺ pump, or cell volume will change. Because the K_m of the Na⁺-K⁺ pump, for intracellular Na⁺ is close to the physiological [Na⁺]_i, alterations in Na⁺ influx automatically give rise to a compensatory modulation of Na⁺ efflux. Nevertheless, metabolic or pharmacologic inhibition of the Na⁺-K⁺ pump should lead to a net gain of Na⁺ and anions coupled by macroscopic electroneutrality and result in a swelling of the cell.

The effect of pump inhibition has been examined extensively (Macknight and Leaf, 1977; Macknight, 1988). The predicted cell swelling has been reported in many tissues, including brain slices, kidney slices, renal tubules, hepatocytes and sheep erythrocytes, when the Na⁺-K⁺ pump is inhibited by cardiac glycosides (e.g. ouabain) or by depleting ATP. It is equally clear, however, that swelling after pump inhibition in renal cortex, liver slices, various muscle preparations, lymphocytes and human erythrocytes is very slow or even absent, perhaps reflecting a low Na⁺ permeability.

Several processes may affect the response of cell volume to Na⁺-K⁺ pump inhibition and the outcome in some tissues depends on the experimental conditions. Rather than accumulating Cl⁻ with Na⁺, cells might instead lose K⁺ to satisfy macroscopic electroneutrality. An equivalent gain of Na⁺ and loss of K⁺ replaces one osmotically active particle with another, causing no change in cell volume. Closer consideration of this mechanism indicates that it can only be a holding action, however. The loss of intracellular K⁺ eventually must lead to a reduction of the K⁺ gradient and a less negative E_m. This will lead to accumulation of Cl⁻ with Na⁺ and cell swelling. Nevertheless, a loss of K⁺ must slow the swelling that otherwise would have occurred and this would explain the absence of swelling in cells with appropriate Na⁺ and K⁺ permeabilities over the time course of experiments.

The possibility that a mechanism other than the Na⁺-K⁺ pump can extrude Na⁺ has been considered. Although controversial, a cardiac glycoside-insensitive but metabolically dependent volume regulation mechanism in kidney that does not incorporate the Na⁺-K⁺ pump has been described (for review, see Macknight and Leaf, 1977). In addition, circulating erythrocytes from a number of carnivores, including dog, cat, bear and ferret, lack a functioning Na⁺-K⁺ pump and must regulate their volume by a different mechanism (Sarkadi and Parker, 1991). In these cells, Na⁺ efflux must depend on the gradient of other ions.

VID Isosmotic Volume Regulation

Although principles of the pump-leak or double-Donnan model are correct and still relevant to the regulation of cell volume, it has become apparent that neither the leak nor the pump is constant. Not only is the control of these fluxes more complex than originally envisioned, but a myriad of other transport processes also contribute to cell volume regulation. Stated simply, constant cell volume under isosmotic conditions implies an equality of intra- and extracellular osmolarity that is perpetuated by a continuous balance of the efflux and influx of osmolytes. The transport processes involved include, but are not limited to: (1) ion and organic osmolyte channels; (2) the Na⁺-K⁺ pump; (3) the Na⁺-K⁺-2Cl⁻, K⁺-Cl⁻ and Na⁺-Cl⁻ co-transporters, which transport the specified ions in one direction; (4) Na⁺-dependent sugar and amino acid co-transport; (5) Na⁺-Ca²⁺; exchange, which exchanges three Na⁺ for one Ca²⁺; and (6) osmotically neutral exchangers that indirectly provide a net solute flux. For example, Na⁺-H⁺ exchange allows the cell to accumulate Na⁺, but the H⁺ removed is replaced by dissociation of H⁺ from intracellular buffers. Cl⁻-HCO₃⁻ and Na⁺-H⁺ exchange can operate in parallel to mediate a net influx of Na⁺ and Cl⁻ in exchange for H⁺ and HCO₃⁻, which are converted to CO₂ and H₂O by the action of carbonic anhydrase. It should be noted that CO₂ freely crosses the cell membrane (σ = 0) and does not directly contribute to solution tonicity. Also, the direct extrusion of water by these two parallel exchangers is negligible compared to the osmotic water gain caused by the accumulation of Na⁺ and Cl⁻.

Of the number of transporters that participate in volume regulation in any given type of cell, which are most important in regulating cell volume under isosmotic conditions? No simple answer can be offered. The importance of each process to cell volume regulation depends critically upon the tissue and species under consideration as well as the conditions. Moreover, transporters and channels are modulated by multiple signaling pathways and they extensively interact by altering membrane potential or the concentration of the transported species. If the rates of ion transport are not correctly matched, cells will inappropriately shrink or swell. The precise maintenance of cell volume exemplifies the need for sensitive and complex regulatory mechanisms. Attempts to integrate mathematically the fluxes and study their interaction have been made based on the cell’s requirement for macroscopic electroneutrality and osmotic equilibrium and the equations governing ion fluxes (Jakobsson, 1980). For erythrocytes, the non-ideal behavior of hemoglobin has been added (Bookchin et al., 1989). Although these simplified models correctly predict a number of observations, they fail to explain others. In short, we remain a long way from a complete quantitative description of the processes underlying cell volume regulation. In the following sections, we will discuss three examples of isosmotic regulation of cell volume that illustrate some of the underlying principles.

VID1 Na⁺-K⁺-2Cl⁻ Co-transport in Heart

Recent findings indicate that the Na⁺-K⁺-2Cl⁻ co-transporter plays a critical role in regulating cardiac myocyte cell volume under isosmotic conditions. As in other tissues, Na⁺-K⁺-2Cl⁻ co-transport conveys osmolytes into cardiac cells under physiological conditions. Because net transmembrane fluxes control cell volume, a decreased osmolyte influx is equivalent to increased efflux. Therefore, inhibition of the Na⁺-K⁺-2Cl⁻ co-transport by bumetanide, for example, favors a reduction of cell volume. Consistent with this idea, bumetanide decreases the volume of atrial and ventricular myocytes by about 10% in less than 5 min and myocyte volume is stable at this new level (Drewnowska and Baumgarten, 1991). The Na⁺-K⁺-2Cl⁻ co-transporter cannot operate without Na⁺ and Cl⁻ in the extracellular fluid and removing either ion renders bumetanide ineffective. These data imply that ion uptake by Na⁺-K⁺-2Cl⁻ co-transport in the heart must be responsible for a significant osmolyte flux under isosmotic conditions and that other transport processes are incapable of fully compensating when this flux is removed. In contrast, myocyte volume was unchanged after inhibiting the Na⁺-K⁺ pump with 10 μM ouabain (Drewnowska and Baumgarten, 1991) or by cooling to 9°C (Drewnowska et al., 1991) for 20 min. At least in the short term, cardiac cell volume in isosmotic solution is influenced more by Na⁺-K⁺-2Cl⁻ co-transport than by the Na⁺-K⁺ pump.

Modulation of Na⁺-K⁺-2Cl⁻ co-transport by intracellular messengers, such as cGMP, may provide a physiological means of modulating cell volume in heart tissue. Figure 16.14 shows the effects of elevating intracellular cGMP in three ways: (1) by adding 8-Br-cGMP, a membrane-permeant analog of cGMP; (2) by adding atrial natriuretic factor (ANF), a natriuretic, diuretic and vasodilatory hormone released by the heart that elevates cGMP by activating guanylate cyclase; and (3) by adding sodium nitroprusside (SNP), a vasodilator, that also activates guanylate cyclase. In each case, cell volume decreased. Furthermore, blocking cGMP-specific phosphodiesterase with zaprinast (M&B22948) augmented the effect of ANF. Based on its sensitivity to bumetanide and the requirement for ions transported by Na⁺-K⁺-2Cl⁻ co-transport, cGMP-dependent volume decreases were shown to be due to an inhibition of Na⁺-K⁺-2Cl⁻ co-transport by cGMP (Clemo et al., 1992; Clemo and Baumgarten, 1995). Interestingly, lowering cGMP levels by inhibiting guanylate cyclase with LY83583 resulted in a small amount of cell swelling. Thus, changing cGMP from its physiological level in either direction altered cell volume. The mechanism and evidence for isosmotic regulation of cell volume in the heart are summarized in Fig. 16.15.

FIGURE 16.14 Changes in the volume of isolated ventricular myocytes during a 20-min exposure to: (A) 10 μM 8-Br-cGMP (8-Br-cG), a permeable cGMP analog; (B) 1 μM atrial natriuretic factor (ANF); and (C) 100 μM sodium nitroprusside (SNP). These agents reversibly decreased cell volume 11%, 8% and 11%, respectively (n=5 for each time point). The decreases in cell volume were caused by inhibition of Na⁺-K⁺-2Cl⁻ co-transport by cGMP. Relative cell volume was measured and calculated as described in the legend of Fig. 16.1. (From Clemo et al. (1992). Reproduced from The Journal of General Physiology, 1992, 100, 89–114, by copyright permission of The Rockefeller University Press.)

FIGURE 16.15 Schematic diagram of the action of atrial natriuretic factor (ANF) and cGMP on cardiac cell volume. Binding of ANF activates guanylate cyclase and increases intracellular cGMP levels. By one or more steps, cGMP inhibits Na⁺-K⁺-2Cl⁻ co-transport. Reducing ion influx by this means is equivalent to increasing net ion efflux and cell shrinkage ensues. LY83583 inhibits guanylate cyclase, thereby blocking the effect of ANF and zaprinast (M&B22948) potentiates the effect of ANF by inhibiting cGMP-specific phosphodiesterase (PDE). Sodium nitroprusside (SNP) also increases cGMP levels, and bumetanide (BUM) directly inhibits the co-transporter; both cause cell shrinkage. (From Clemo et al. (1992) Reproduced from The Journal of General Physiology, 1992, 100, 89–114, by copyright permission of The Rockefeller University Press.)

Does the same mechanism regulate cell volume under isosmotic conditions in other tissues? Perhaps it does in some cells, such as vascular endothelium, in which cGMP inhibits Na⁺-K⁺-2Cl⁻ co-transport. In other cells, Na⁺-K⁺-2Cl⁻ co-transport is stimulated by cAMP, cGMP or a PKC-dependent pathway, and perhaps by a number of other signaling pathways (Palfrey and O’Donnell, 1992; Palfrey, 1994). This diversity in the control of Na⁺-K⁺-2Cl⁻ co-transport may be related to the variety of transporter isoforms that have been identified and cloned (Haas, 1994; Kaplan et al., 1996). Although the physiological significance of this diversity in the control of ion transport is not well understood, it must lead to diversity in the regulation of cell volume.

VID2 Hormones and Substrate Transport in Liver

Another interesting example of isosmotic volume regulation is found in hepatocytes. An impressive number of hormones induce either cell swelling or cell shrinkage at physiological concentrations and these actions are related to their control of liver metabolism (Häussinger and Lang, 1991; Häussinger et al., 1994; Agius et al., 1994; Häussinger, 1998). Na⁺-H⁺ exchange, Na⁺-K⁺-2Cl⁻ co-transport and the Na⁺-K⁺ pump are stimulated in rat liver cells by insulin. The net effect is that insulin increases [K⁺]_i, [Na⁺]_i and [Cl⁻]_i and causes cells to swell by about 12%. This swelling is prevented by bumetanide, a blocker of Na⁺-K⁺-2Cl⁻ co-transport, or by amiloride, a blocker of Na⁺-H⁺ exchange. In contrast, glucagon shrinks hepatocytes by about 14%. Instead of directly opposing the action of insulin, glucagon reduces cell volume by increasing K⁺ and Cl⁻ efflux through ion channels. Other agents that swell hepatocytes include bradykinin and phenylephrine. Shrinking is initiated by adenosine, 5-HT, vasopressin and cAMP.

Hepatocytes also swell as a result of Na⁺-dependent amino acid co-transport in isosmotic media (Häussinger and Lang, 1991; Boyer et al., 1992; Häussinger et al., 1994; Häussinger, 1998). Exposure to amino acids that are accumulated with Na⁺ (e.g. alanine, glutamine, glycine, hydroxyproline, phenylalanine, proline and serine) causes cell swelling. These effects occur at amino acid levels found physiologically in the portal vein. For example, glutamine provokes up to a 10% swelling with a half-maximal effect at approximately 0.7 mM. Amino acid co-transport gives rise to an inward current and Cl⁻ enters to maintain macroscopic electroneutrality. Instead of loading the cell, Na⁺ is pumped out, mainly by the Na⁺-K⁺ pump, leaving an accumulation of K⁺ and Cl⁻. In contrast to these amino acids, substances not accumulated by the liver, such as glucose and leucine, do not affect hepatocyte volume. Cell swelling caused by Na⁺-dependent amino acid co-transport has also been observed in intestine and renal proximal tubule.

VID3 Na⁺-Ca²⁺ Exchange in Carnivore Erythrocytes

The Na⁺-K⁺ pump in erythrocytes from dogs, cats, ferrets and bears ceases to function as cells mature. As a result, [K⁺]_i and [Na⁺]_i are similar to [K⁺]_o and [Na⁺]_o. This poses a special problem for cell volume regulation. How can these cells offset the osmotic pressure generated by impermeant intracellular molecules and avoid swelling without an Na⁺-K⁺ pump to make Na⁺ effectively impermeant? Carnivore erythrocytes solve this dilemma by extruding three Na⁺ in exchange for one Ca²⁺ via the Na⁺-Ca²⁺ exchanger (Parker, 1973; Sarkadi and Parker, 1991). In most cells, the electrochemical gradients for Na⁺ and Ca²⁺ favor the efflux of Ca²⁺. In these erythrocytes, however, the gradients favor Ca²⁺ entry because the Na⁺ gradient is reduced and Na⁺-Ca²⁺ exchange operates in what is called the reverse mode. To stabilize their volume, carnivore erythrocytes also must have a means of maintaining the Ca²⁺ gradient (i.e. low [Ca²⁺]_i). This is accomplished by an ATP-dependent Ca²⁺ pump in the plasma membrane. Thus, as in other cells, maintaining cell volume in the face of impermeant intracellular colloids requires the expenditure of energy in a pump-leak mechanism. In this case, ATP is expended by a plasma membrane Ca²⁺ pump rather than by the Na⁺-K⁺ pump.

VII Regulation of Cell Volume under Anisosmotic Conditions

VIIA Osmometric Behavior of Cells

Because the permeability of most cell membranes to water is much greater than that to solutes, cells swell or shrink when placed in an environment that is hyposmotic or hyperosmotic, respectively. Water rapidly flows to equalize its chemical potential, μ_w, inside and outside the cell. The initial volume response is often close to that predicted for an ideal osmometer from van’t Hoff’s law. An example is shown in Fig. 16.16, which illustrates the response of rabbit ventricular myocytes to solutions with osmolarities ranging from 195 to 825 mosmol/L (0.60 to 2.55 times isotonic). Relative cell volume (V), calculated as V_test/V_isosmotic, is plotted against the inverse of relative osmolality, π_isosmotic/π_test, and the data are fit to

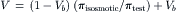(16.79)

By definition, relative volume is 1.0 at a relative osmolarity of 1.0. Two conclusions can be reached from the data in Fig. 16.16. First, as expected from van’t Hoff’s law, the relationship between relative cell volume and the inverse of relative osmolarity is linear. Second, the intercept of the relationship on the volume axis, V_b, is 0.34, which is significantly different from 0. This is interpreted as meaning that a fraction of cell volume is osmotically inactive, i.e. it apparently does not participate in the response to anisosmotic solutions.

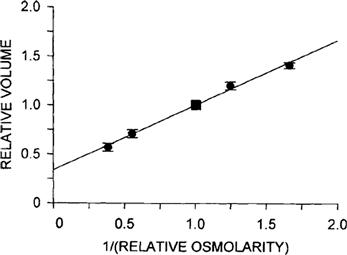
FIGURE 16.16 Relationship between relative cell volume and the inverse of relative osmolarity in cardiac ventricular myocytes. Data from 38 measurements of relative cell volume in anisosmotic solutions (0.6T, 0.8T, 1.8T and 2.6T) were fit to a least squares regression line constrained to pass through (1, 1) (square) because relative cell volume is 1 in isotonic solution by definition. The extrapolated intercept on the relative volume axis, 0.34, represents the fraction of cell volume that is osmotically inactive (see Equation 16.79). Volume measurements, calculation of relative cell volume, and means of adjusting osmolarity are as described for Fig. 16.1. (Reproduced from Drewnowska and Baumgarten, 1991.)

Several arguments can be made to justify the observation of an osmotically inactive volume. The expectation from the simplest model is that cell water should vary in proportion to osmolarity. However, not all of cell volume is water. The volume of non-aqueous components, such as small solutes and proteins, which represent 25–30% of the cell on a weight/weight basis, is unaffected by water movements. Even measurements of cell water show non-ideal behavior, however (Macknight and Leaf, 1977; Solomon, 1989), so additional explanations are necessary. One suggestion is that a fraction of cell water is intimately associated with cell proteins or membranes and thereby is bound or structured and unavailable as solvent (e.g. LeNeveu et al., 1976; Hinke, 1980). Although the state of water molecules adjacent to proteins and membranes must be different from that in the bulk phase of the cytoplasm, in light of NMR, intracellular ion activity, and other data, most investigators believe that virtually all water (≈95%) is available as solvent (Shporer and Civan, 1977; Hladky and Rink, 1978). Another possibility is that the behavior of intracellular macromolecules is concentration dependent. For example, the osmotic coefficient and charge on hemoglobin increase with its concentration as red cells shrink and anions are drawn in to maintain electroneutrality. These phenomena are important in explaining water movement in red cells (Freedman and Hoffman, 1979), but their importance in other tissues remains uncertain. A third possibility is that intracellular compartments, such as mitochondria, nuclei, endoplasmic reticulum and sarcoplasmic reticulum of muscle cells, may undergo volume changes that are not proportional to those of the whole cell. Differential responses to an osmotic challenge are expected because the plasmalemma and intracellular membranes possess distinct arrays of transporters and ion channels and each sees a unique environment. Most methods for determining cell water or cell volume fail to distinguish between cytoplasmic and total cell water or volume (for a method that does distinguish these, see Reuss, 1985).

A crucial assumption made in determining osmotically inactive volume also may affect the value obtained for V_b in Equation 16.79. The analysis assumes that only water has moved at the time volume is measured. That is to say, transmembrane ionic fluxes can be ignored. Although the permeability of the cell membrane to water is many times greater than the permeability to ions, the net fluxes of both water and ions start at the instant extracellular osmolarity is changed. If ion fluxes significantly affect intracellular osmolarity at the time of measurement, the extrapolated osmotically inactive volume will be imprecise. If, in addition, the ion fluxes depend on the direction or magnitude of the osmotic gradient, the plot of relative volume versus π_isosmotic/π_test can become non-linear (e.g. Grinstein et al., 1984).

VIIB Compensatory Regulation of Cell Volume

Although an osmotic gradient initiates cell swelling or shrinkage, the initial volume response is not maintained in a wide variety of cells. Cell swelling activates compensatory processes that lead to an efflux of osmolytes and a reduction of cell volume. This is called a regulatory volume decrease (RVD). Similarly, cell shrinking activates an influx of osmolytes in some cells, leading to a compensatory swelling referred to as a regulatory volume increase (RVI). RVD and RVI nearly restore the original cell volume in some cells, are far less complete in others and are absent in a few types of cells.

Regulatory volume effects are thought to be adaptive and were first identified in nucleated duck erythrocytes (for a review, see Kregenow, 1981). Examples of an RVD and RVI taken from work by Grinstein et al. (1983) are shown in Fig. 16.17. Exposure of human peripheral blood lymphocytes to a solution made hypotonic by 50% dilution with water leads to a rapid, 1.6-fold increase in cell volume (Fig. 16.17B). Then, over about 10 min, an RVD returned cell volume almost completely to its initial value. On switching back to isotonic solution, cell volume shrank to less than the control value and then was restored by an RVI. RVDs and RVIs may differ in magnitude, however. A much less complete RVI was observed when lymphocytes in isotonic solution were shrunk in media made hyperosmotic by adding of 300 mosmol·L⁻¹ of NaCl and the RVI was absent when the lymphocytes were challenged with 300 mosmol·L⁻¹ of sucrose instead of NaCl (Fig. 16.17A). The RVD also could be eliminated, for example, by cooling lymphocytes to 4°C (Grinstein et al., 1984). Thus, regulation of cell volume following an osmotic challenge depends on the particulars of the perturbation as well as the cell under study (compare Figs. 16.1 and 16.17).

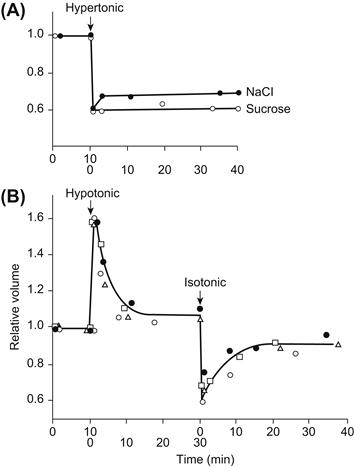
FIGURE 16.17 (A) Effect of hypertonic solution (2T) on relative cell volume of human peripheral blood mononuclear lymphocytes. Solution osmolarity was increased by adding 300 mosmol·L⁻¹ of NaCl or sucrose. Cells shrank 40% in hypertonic solution and a small regulatory volume increase (RVI) was observed in the NaCl solution. Points are representative of four experiments. (B) Response to hypotonic solution (0.5T). After swelling by nearly 60%, a regulatory volume decrease (RVD) virtually restored cell volume to its initial value in 10 min. On returning to isotonic solution, cell volume decreased below its control value, and an RVI lead to full recovery. Different symbols represent separate experiments selected from over 40. Cell volume was measured with a Coulter counter that determines volume from the change in electrical resistance of a column of solution as cells pass through an aperture. (From Grinstein et al. (1983). Reproduced from The Journal of General Physiology, 1983, 82, 619–638, by copyright permission of The Rockefeller University Press.)

VIIC Transport Processes Responsible for RVD and RVI

How do cells gain or lose osmotic equivalents in anisosmotic media? The mechanisms underlying RVDs and RVIs have been extensively characterized in a variety of cell types and exhaustively reviewed (Hoffmann and Simonsen, 1989; Chamberlin and Strange, 1989; Grinstein and Foskett, 1990; Sarkadi and Parker, 1991; Häussinger and Lang, 1991; McCarty and O’Neil, 1992; Strange, 1994; Hoffmann and Dunham, 1995; Lang et al., 1998; O’Neil, 1999). In general, cells undergo RVD or RVI by translocating Na⁺, K⁺, and Cl⁻ and a variety of channels, exchangers, co-transporters and pumps can participate. In some cases, organic osmolytes (e.g. taurine, betaine, sorbitol, and urea) are transported instead of, or in addition to, inorganic ions. Table 16.3 lists processes that are activated by altering the volume of various cells and Fig. 16.18 illustrates some of the mechanisms diagrammatically. The compensatory mechanisms invoked vary with the tissue, species and conditions under which osmotic stress is applied.

TABLE 16.3. Ionic Mechanisms of Regulatory Responses to Anisosmotic Solutions

Transport Mechanism Activated	Cell Types
Cell swelling-induced regulatory volume decrease
K⁺ and Cl⁻ conductances	Frog urinary bladder
	Chinese hamster ovary cells
	Ehrlich ascites tumor cells
	Frog skin
	HeLa carcinoma cells
	Human platelets
	Human granulocytes
	Human lymphocytes
	Intestinal 407 cells
	Madin-Darby canine kidney (MDCK) cells
	Necturus enterocytes
	Necturus gallbladder
	Rabbit renal proximal convoluted tubule
	Rat hepatocytes
K⁺-Cl⁻ co-transport	Avian, dog, fish, human, rabbit, and low-K⁺ sheep erythrocytes
	Ehrlich ascites tumor cells (Ca²⁺ depleted)
	Necturus gallbladder
Coupled K⁺-H⁺ and Cl⁻-HCO₃⁻ exchange	Amphiuma erythrocytes
Na⁺-Ca²⁺ exchange	Dog and ferret erythrocytes
Organic osmolyte efflux	Crustacean muscle and myocardium
	Ehrlich ascites tumor cells
	Elasmobranch and molluscan erythrocytes
Cell shrinkage-induced regulatory volume increase
Na⁺-K⁺-2Cl⁻ co-transport	Astrocytes
	C6 glioma cells
	Duck, fish, rat, and human erythrocytes
	Ehrlich ascites tumor cells
	Frog skin
	HeLa cells
	Rat kidney medullary thick ascending limb
	3T3 cells
Coupled Na⁺-H⁺ and Cl⁻-HCO₃⁻ exchange	Amphibian gallbladder
	Dog and amphibian erythrocytes
	Human lymphocytes
	Mouse medullary thick ascending limb
	Rabbit renal proximal straight tubule
	Ehrlich ascites tumor cells
Na⁺-Cl⁻ co-transport	Ehrlich ascites tumor cells
	Necturus gallbladder
K⁺ and Cl⁻ conductances, inhibited	Madin-Darby canine kidney (MDCK) cells
Organic osmolyte influx	Many animal and plant cells, bacteria and fungi

For references, see Yancey et al. (1982), Hoffmann and Simonsen (1989), Chamberlin and Strange (1989), Grinstein and Foskett (1990), Wolff and Balaban (1990), Sarkadi and Parker (1991), Häussinger and Lang (1991), McCarty and O’Neil (1992), Boyer et al. (1992), Strange (1994), Hoffmann and Dunham (1995), Lang et al. (1998) and O’Neil (1999).

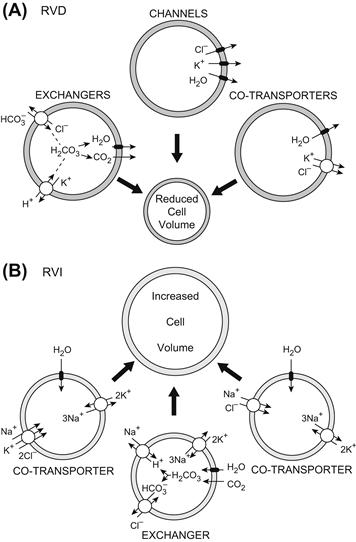
FIGURE 16.18 Schematic diagrams of the transport processes involved in (A) regulatory volume decrease (RVD) and (B) regulatory volume increase (RVI). Following cell swelling, a compensatory reduction in cell volume (RVD) may result from increased K⁺ and Cl⁻ conductance (channels), activation of functionally coupled Cl⁻-HCO₃⁻ and K⁺-H⁺ exchange (exchangers) or activation of K⁺-Cl⁻ co-transport (co-transporters). Following cell shrinking, a compensatory increase in cell volume (RVI) may result from activation of the Na⁺-K⁺-2Cl⁻ or Na⁺-Cl⁻ co-transporters (co-transporters) or activation of functionally coupled Cl⁻-HCO⁻₃) and Na⁺-H⁺ exchange (exchangers). The Na⁺-K⁺ pump extrudes the Na⁺ that enters during RVI, so that cells gain K⁺ and Cl⁻.

The primary mechanism of RVD in a number of cell types is activation of conductive pathways and this process will be discussed in more detail. Cell swelling, acting directly or via a messenger, opens ion channels that allow increased efflux of K⁺ and Cl⁻ and H₂O follows. Although the openings of cation and anion channels are independent events, K⁺ and Cl⁻ efflux are tightly coupled by the need to maintain macroscopic electroneutrality. If only the anion or cation channel were to open, the resulting change in E_m would rapidly make ion efflux self-limiting and arrest volume regulation. The effect of this coupling of K⁺ and Cl⁻ fluxes is illustrated in Fig. 16.19A, which shows RVDs in Ehrlich ascites cells (Hoffmann et al., 1986; Hoffmann and Dunham, 1995). At time zero, cells were switched from 300 to 150 mosmol·L⁻¹ media. Cells rapidly swelled to about 1.9 times their initial volume and then underwent an RVD that returned relative cell volume to about 1.3 within 5 min. When K⁺ conductance was increased by pretreating cells with 0.5 μM gramicidin, a K⁺ ionophore, the compensation by the RVD was more rapid and larger in magnitude, returning cell volume to nearly its control level in 2 min. When K⁺ channels were blocked with 1 μM quinine, however, only a feeble RVD took place. These data argue that conductive K⁺ efflux cannot keep up with Cl⁻ efflux in control cells and limits the rate of RVD (Hoffmann et al., 1986). Thus, cell swelling must increase Cl⁻ conductance more than K⁺ conductance, leading to greater efflux of Cl⁻ than of K⁺. Consistent with this idea, a depolarization is observed during the RVD. The activation of Cl⁻ conductance by swelling is only transient, however. The ability of gramicidin to induce RVD decays with time, as shown in Fig. 16.19B. In contrast to the high selectivity of Cl⁻-dependent co-transporters, RVD is also supported by Br⁻, NO₃⁻ and SCN, suggesting the Cl⁻ channel responsible for RVD poorly discriminates among these anions. Furthermore, RVD can be suppressed by Cl⁻ channel blockers such as inacrinone (MK-196) and diphenylamine-2-carboxylate (DPC), but not by the co-transport inhibitors. Taken together, the data in Ehrlich ascites cells provide strong evidence that two independent channels are responsible for RVD instead of, for example, activation of a single K⁺-Cl⁻ co-transporter. Organic osmolytes also permeate a class of swelling-activated Cl⁻ channels referred to as volume-sensitive organic osmolyte-anion channels (VSOAC) and are released by a number of cells to regulate volume (Jackson et al., 1994). VSOAC have a high permeability to taurine (P_taurine/P_Cl = 0.75) and glutamate (P_glutamate/P_Cl = 0.20) and other amino acids and small organic molecules are permeant (Bandarali and Roy, 1992).

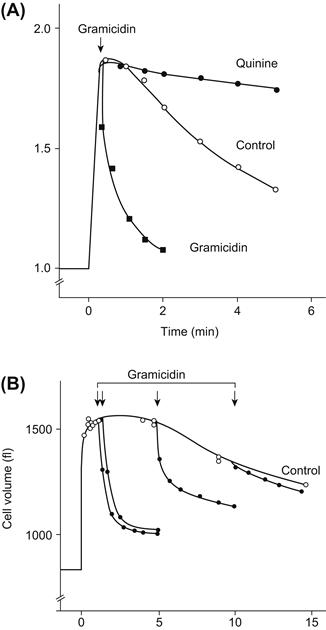
FIGURE 16.19 (A) Effects of quinidine (1 mM) and gramicidin (5 μM) on regulatory volume decrease (RVD) in Ehrlich ascites cells suspended in a Na⁺-free choline medium with 1 mM Ca²⁺. Swelling was induced by diluting the medium to 0.5T. Quinidine blocks Ca²⁺-activated K⁺ channels, and gramicidin increases cation conductance (K⁺ conductance in the absence of Na⁺). The data indicate that K⁺ permeability is rate-limiting during the RVD. (B) The swelling-induced increase in Cl⁻ conductance is transient. Same protocol as in (A), except that quinidine (1 mM) was added to the hypotonic media to reduce K⁺ conductance (control). At selected times, 0.5 μM gramicidin was added to increase cation permeability. The ability of gramicidin to induce an RVD follows the time-course of the swelling-induced Cl⁻ conductance. Relative cell volumes measured with a Coulter counter, as described for Fig. 16.17. (Reproduced with permission from Hoffmann et al., 1986.)

Whereas many types of cells exhibit extensive RVDs, fewer cells exhibit robust RVIs. RVIs are usually due to an accumulation of Na⁺, Cl⁻ and, in some cases, K⁺, which occurs over minutes. The primary mechanisms underlying RVIs are acceleration of Na⁺-K⁺-2Cl⁻ or Na⁺-Cl⁻ co-transport and coupled Na⁺-H⁺ and Cl⁻-HCO₃⁻ exchange. Volume recovery can be blocked by application of appropriate inhibitors such as bumetanide for Na⁺-K⁺-2Cl⁻ co-transport, amiloride for Na⁺-H⁺ exchange and SITS (4-acetamido-4′-isothiocyano-stilbene-2,2′-disulfonic acid) for Cl⁻-HCO₃⁻ exchange. RVI in most cells is readily observed when simple salt solutions bathe the cells, but in renal cortical collecting duct and proximal tubules, butyrate, acetate or other metabolizable fatty acids must be in the perfusate to support RVI. Substrate metabolism may provide H⁺ and HCO₃⁻ to support Na⁺-H⁺ and Cl⁻-HCO₃⁻ exchange in these cells (for a review, see McCarty and O’Neil, 1992).

VIID Organic Osmolytes

Adaptation to hyperosmolarity over a longer term also occurs in some cells and is mediated by an accumulation of organic osmolytes, including amino acids, polyols, and urea (Yancey et al., 1982; Chamberlin and Strange, 1989; Wolff and Balaban, 1990; Garcia and Berg, 1991; Yancey, 1994; Berg, 1995). Three of these organic osmolytes, taurine, betaine, and inositol, are taken up by Na⁺-dependent or Na⁺- and Cl⁻-dependent co-transporters. The taurine and betaine transporters have been cloned and belong to the same family as the Na⁺- and Cl⁻-dependent norepinephrine, γ-aminobutyric acid (GABA), dopamine, serotonin and proline transporters (Uchida, 1992). The taurine transporter is found in a variety of cell types. The distribution of mRNA levels is kidney>ileum>brain>liver>heart (Berg, 1995). This sequence for taurine transporter mRNA is surprising because heart has the highest intracellular taurine concentration among these tissues. The mRNA level for the betaine transporter is also highest in the kidney (Yamauchi et al., 1992). A different family of transporters is responsible for Na⁺-dependent inositol uptake. The inositol transporter is related to those for glucose and nucleosides and is highly expressed in renal medulla (Kwon et al., 1992). A common feature of all three osmolyte transporters is that gene transcription is upregulated by hypertonic stress. Cells cultured under hypertonic conditions slowly increase their maximum rates of transport and intracellular concentrations rise. For example, betaine transporter mRNA levels in MDCK cells peak about 16 h after the osmotic challenge, and the transport rate peaks at about 24 h (Uchida et al., 1993).

Another mechanism for accumulating organic osmolytes while adapting to hypertonicity and cell shrinkage is to modulate their synthesis. For example, renal medullary cells, which experience osmolarities of more than 1200 mosmol·L⁻¹ during antidiuresis, accumulate sorbitol and inositol to regulate their volume (Wolff and Balaban, 1990; Garcia and Berg, 1991; Sands, 1994). Sorbitol levels rise 12–24 h after osmotically challenging cultured renal medullary cells and accumulation depends on the induction of aldose reductase by enhanced transcription. Aldose reductase converts exogenous glucose to sorbitol. Sorbitol is synthesized from stored glycogen in other tissues. This requires coordinated upregulation of glycogen phosphorylase and hexosekinase to produce glucose 6-phosphate, an intermediate for sorbitol production, and the downregulation of phosphofructokinase to prevent consumption of substrates for sorbitol production.

Inhibition of degradation is another mechanism for accumulating organic osmolytes when cells are challenged by hypertonicity. This is the main mechanism by which MDCK and medullary collecting duct accumulate glycerophosphocholine (GPC) (Berg, 1995). In response to hypertonicity or elevated urea, GPC-choline phosphodiesterase is inhibited. Under some conditions, synthesis of GPC by phospholipase also may be enhanced.

The accumulation of organic osmolytes is metabolically expensive, especially considering that many cells dump organic osmolytes to respond acutely to swelling (Chamberlin and Strange, 1989; Rasmusson et al., 1993; Jackson et al., 1994, Hoffmann and Dunham, 1995). Why does the cell expend extra energy to use organic compounds rather than inorganic ions? Apparently the reason is that accumulation of inorganic ions may perturb protein structure within cells. The Hofmeister series, first described more than 100 years ago, lists inorganic ions according to their ability to alter the solubility and conformation of proteins. Non-specific effects of inorganic salts include changes in V_max, K_m, tertiary structure and subunit assembly of enzymes (Yancey et al., 1982; Somero, 1986; Yancey, 1994). Why are some organic compounds accumulated rather than others? Yancey et al. (1982) categorized osmolytes as non-perturbing (stabilizing) or perturbing (destabilizing). Elevated concentrations of non-perturbing osmolytes are compatible with normal enzyme function, whereas high concentrations of perturbing osmolytes are not. This distinction could be due either to direct interaction of osmolytes with enzymes or substrates or to effects on hydration, solubility or charge interactions of proteins. Organic solutes that are non-perturbing generally are uncharged [e.g. trimethylamine N-oxide (TMAO), glycerol] or zwitterionic (e.g. betaine, taurine), although negatively-charged octopine is used by some cells. In contrast, most perturbing organic osmolytes are positively charged (e.g. arginine, guanidinium). Neutral urea, however, perturbs proteins. Finally, non-perturbing osmolytes can counteract the destabilizing effects of perturbing osmolytes. Several organisms accumulate perturbing osmolytes, such as urea, in fixed ratios with non-perturbing osmolytes.

VIIE Signaling Pathways Underlying RVD and RVI

How do cells detect alterations in their volume and activate the transport processes underlying compensatory volume regulation? Do the transporters themselves sense cell volume and respond by changing their activity? Alternatively, does water movement simply change the concentration of a critical regulatory substance? Answers to these questions are just beginning to emerge. It appears that the signaling pathways modulated by cell volume are as diverse as the transporters that respond.

VIIE1 Anisosmotic Media

An obvious candidate for signaling a change in cell volume is the composition of the anisosmotic media itself, i.e. the ionic strength or concentrations of ions in the bathing media might initiate a regulatory volume response. Changing concentration or ionic strength must affect various ion transport processes and transmembrane ion fluxes to some degree. Nevertheless, these factors seem relatively unimportant in volume regulation because comparable responses are observed when non-electrolytes, such as mannitol or sucrose, replace a large fraction of the electrolytes in the bathing media. RVDs also are initiated in isosmotic solutions after swelling caused by sugar or amino acid uptake. Thus, it appears that regulation is initiated by the volume change itself rather than the composition of the bathing media.

VIIE2 Membrane Potential

Another possibility is that regulatory volume responses are initiated by dilution or concentration of intracellular K⁺ via an effect on E_m. A two-fold change in volume without compensatory K⁺ fluxes would alter [K⁺]_i and cause an 18 mV change in E_m in a cell that conforms to the Nernst equation. Fluxes through K⁺ and Cl⁻ channels are voltage dependent, reflecting both the electrochemical driving force and the voltage-dependent conductance. For many K⁺ channels, the current–voltage relationship is highly non-linear. Furthermore, the Na⁺-K⁺ pump and Na⁺-Ca²⁺ exchange are both voltage dependent because they mediate a net movement of charge across the membrane. Despite this, it is unlikely that changes in E_m are the primary cause of RVDs or RVIs in most cells. Regulatory responses have been observed with changes in cell volume of <5% (Hoffmann and Simonsen, 1989), which would directly alter E_m by only ≈1 mV. This is too small to have a significant effect. Nevertheless, it is clear that E_m can modulate RVDs due to activation of K⁺ and Cl⁻ channels. In most instances, the increase in Cl⁻ conductance is greater than that for K⁺ (Hoffmann and Simonsen, 1989; Grinstein and Foskett, 1990). This leads to a significant depolarization during the RVD due to a greater passive efflux of Cl⁻ than K⁺ and the depolarization equalizes the anion and cation fluxes (due to macroscopic electroneutrality). Depolarization may have additional effects that support the RVD. The sensitivity of certain K⁺ channels to intracellular Ca²⁺ (i.e. Ca²⁺-activated K⁺ channels) is increased by depolarization, and other K⁺ channels are directly opened by depolarization.

VIIE3 Cytoskeleton

The cytoskeleton consists of three main elements: actin filaments (F-actin), which are microfilaments 5–7 nm in diameter that are double-stranded α-helical polymers of globular actin (G-actin); microtubules, which are hollow tubes 25 nm in diameter that are made from tubulin monomers arranged in 13 threads; and intermediate filaments (IF), which are 10-nm diameter strands composed of tissue-specific proteins, such as keratin in epithelial cells and desmin in muscle cells (Bershadsky and Vasiliev, 1988; Luna and Hitt, 1992; Mills et al., 1994). In non-muscle cells, the majority of actin filaments are associated with the cell membrane. F-actin is tied together to integral membrane proteins by ankyrin, spectrin, MARKS (myristolated acid-rich C-kinase substrate) and other binding proteins to form a structural unit. This scaffolding undergoes constant reorganization as G-actin polymerizes and depolymerizes in response to various stimuli. The main role of microtubules in mature cells is thought to be the transport of vesicles within the cell using specific microtubule-associated proteins (MAPs) to attach to kinesin and dynein, which act as molecular motors. The functions of IF are not fully understood. Because IF binds to ankyrin and to desmosomal plaques, it is thought that these filaments have a structural role and link organelles to the membrane or cytoskeleton. Intermediate filaments are phosphorylated and dephosphorylated by protein kinases and phosphatases and it is likely that their phosphorylation state regulates function.

Alterations in cell volume lead to deformation or reorganization of the cytoskeleton, and ideas of how these effects may be linked to cell volume regulation have been proposed (Chamberlin and Strange, 1989; Sachs, 1989; Sarkadi and Parker, 1991; Mills et al., 1994; Hoffmann and Dunham, 1995; Henson, 1999). One possibility is that the cytoskeleton might mechanically resist cell swelling, but the evidence for this is inconclusive.³ Ion channels, exchangers and co-transporters are structurally anchored in the membrane by specific components of the cytoskeleton (Luna and Hitt, 1992) and their interaction may help regulate cell volume. Agents that disrupt the microfilaments, such as the cytochalasins, modify the regulatory responses to both hypotonic and hypertonic stress by inhibiting K⁺ and Cl⁻ channels that promote RVD and stimulating Na⁺-K⁺-2Cl⁻ co-transport responsible for RVI (Chamberlin and Strange, 1989; Mills et al., 1994; Hoffmann and Dunham, 1995). In a few cases, cell volume under isosmotic conditions is affected (McCarty and O’Neil, 1992). Microtubules also may be involved in some cell lines. Colchicine, which prevents microtubule polymerization, decreases macrophage volume by 20% (Mills et al., 1994). The shrinkage is inhibited by SITS, suggesting that either Cl⁻-HCO₃⁻ exchange or Cl⁻ channels are involved. Additionally, water and ion channels are inserted reversibly into the membrane in response to volume perturbations in a process that can be blocked by cytochalasin B (Lewis and de Moura, 1982). Furthermore, mechanical deformation of the membrane and supporting structures can modulate biochemical signaling systems such as the cAMP and protein kinase C cascades (Richter et al., 1987; Watson, 1991). Emerging evidence suggests that protein kinases and phosphatases may be specifically localized by cytoskeletal binding proteins to sites adjacent to their target transport proteins. Moreover, the extracellular matrix is coupled to the cytoskeleton by integrins which regulate complex signaling cascades including focal adhesion kinase (FAK) and extracellular signal regulated kinases (ERK/MAPK) (Boudreau and Jones, 1999). These developments are important because it remains obscure how the cytoskeleton exerts its regulatory effect on ion transporters and whether or not constraints imposed by three-dimensional tissues in situ affect cell volume.

Another role for the cytoskeleton involves widely distributed mechanosensitive and volume-sensitive ion channels (Sachs, 1989; Morris, 1990; Hu and Sachs, 1997; Vandenberg et al., 1996; Wright and Rees, 1998). The probability of channel opening is increased by osmotic stretch or mechanical deformation. It has been proposed that mechanical forces detected by a cytoskeletal protein, spectrin, can directly affect cation channel gating, whereas the gating of volume-sensitive anion channels is regulated by their phosphorylation state. Most stretch-activated channels poorly discriminate between permeant species (e.g. the stretch-activated cation channel admits Na⁺, K⁺, and Ca²⁺), but some are highly selective for K⁺. There are also reports of mechanosensitive channels that are inactivated by stretch (Sachs, 1989; Morris, 1990). Mechanosensitive channels are potentially important in cell volume regulation as both sensors and effectors. The evidence that they are opened by osmotic stretch is convincing and they carry substantial currents, which might directly or indirectly lead to volume regulation. For example, it has been argued that K⁺-selective stretch-activated channels in molluscan heart cells pass sufficient current to alter [K⁺]_i by 1% in 1 s when the cell is voltage-clamped away from E_K (Brezden et al., 1986) and that poorly selective cation stretch-activated channels in Necturus choroid epithelium raise Ca²⁺ sufficiently in 100 s to open Ca²⁺-activated K⁺ channels and initiate an RVD (Christensen, 1987). Such calculations must be regarded as estimates, however, because they do not reflect E_m under the relevant conditions. Nevertheless, Ca²⁺ entry via stretch-activated channels has been implicated in volume regulation in several types of cells (Foskett, 1994) and arguments favoring the idea that stretch-activated channels participate in cell volume regulation are accumulating (Sackin, 1994). It has been found that Gd³⁺, a blocker of non-selective stretch-activated cation channels, reduced swelling of both intact (i.e. unclamped) and voltage-clamped cardiac myocytes in hypoosmotic solutions and that 9-anthracene carboxylic acid (9-AC), a blocker of stretch-activated anion channels, increased swelling in the same solutions (Suleymanian et al., 1995; Clemo and Baumgarten, 1997; Clemo et al., 1998, 1999). Opposite effects of the two blockers are expected because anions and cations travel in opposite directions under these conditions. In contrast, Gd³⁺ and 9-AC have negligible effects on myocyte volume in isosmotic solution when stretch-activated channels are expected to be closed. Interestingly, the same volume-sensitive cation and anion channels became persistently activated and modulated cell volume under isosmotic conditions in a canine model of congestive heart failure (Clemo et al., 1998, 1999).

VIIE4 Calcium

A role for Ca²⁺ in cell volume regulation has been recognized for many years (Pierce and Politis, 1990; McCarty and O’Neil, 1992; Foskett, 1994; Hoffmann and Dunham, 1995). RVD is blocked by removing extracellular Ca²⁺ in Amphiuma erythrocytes, Necturus gallbladder, proximal convoluted and straight tubule, intestine 407 and osteosarcoma cells. Extracellular Ca²⁺ is not a requirement for RVD in lymphocytes and Ehrlich ascites cells, but RVD is more rapid in Ehrlich ascites cells when Ca²⁺ is present. In some tissues, it appears that the Ca²⁺ involved in RVD enters, at least in part, through dihydropyridine-sensitive, L-type Ca²⁺ channels. Significant Ca²⁺ entry can also occur via non-selective stretch-activated cation channels. Block of RVD by lanthanides and disruption of the cytoskeleton, both of which affect stretch-activated cation channels, is consistent with this possibility. Instead of the entry of extracellular Ca²⁺, release of Ca²⁺ from intracellular stores is critical for RVD in a variety of cells, including lymphocytes, Ehrlich ascites, intestine 407 and opossum kidney cells. Depletion of internal Ca²⁺ stores eliminates RVD in these cells; it is restored by extracellular Ca²⁺ and the Ca²⁺ ionophore, A23187. [Ca²⁺]_i has been shown to increase during swelling of Amphiuma erythrocytes using arsenazo III as a Ca²⁺ indicator. More recently, fluorescent Ca²⁺ indicators, quin-2 and fura-2, have been used to demonstrate increases in [Ca²⁺]_i that accompany cell swelling in urinary bladder, osteosarcoma, lymphoma and proximal and straight convoluted tubule cells. On the other hand, [Ca²⁺]_i remains unchanged during volume changes in some cells, including human lymphocytes. More evidence for elevated Ca²⁺ comes from patch-clamp studies. In a number of tissues, recordings of single channel activity established that Ca²⁺-activated K⁺ channels open more frequently during RVD than under isotonic conditions. This suggests an increase in [Ca²⁺]_i because the probability that these channels open increases as [Ca²⁺]_i increases. Although studied in less detail, a decrease in [Ca²⁺]_i has been implicated in RVI in Amphiuma erythrocytes, Ehrlich ascites cells and lymphocytes.

The mechanism by which Ca²⁺ modulates cell volume appears to vary (Table 16.4). Ca²⁺ has direct effects on ion channels, but additional signaling mechanisms may be involved. For example, calmodulin inhibitors can block the increased K⁺ conductance in lymphocytes, Ehrlich ascites cells and Necturus gallbladder; the increased Cl⁻ conductance in Ehrlich ascites cells; and increased K⁺-H⁺ exchange in Amphiuma erythrocytes. In other cells, modulation of protein kinase C and leukotriene synthesis by Ca²⁺ have been proposed as signals in volume regulation.

TABLE 16.4. Intracellular Signaling Pathways for RVD and RVI

Signal	Effector	Cell Type
Ca²⁺	K⁺ conductance	Necturus gallbladder Frog urinary bladder Ehrlich ascites cells Human lymphocytes
	Cl⁻ conductance	Ehrlich ascites cells
	Taurine efflux Na⁺-H⁺ exchange K⁺-H⁺ exchange	Elasmobranch and molluscan erythrocytes Human lymphocytes Amphiuma erythrocytes
Phosphorylation	Na⁺-H⁺ exchange Taurine efflux Na⁺-K⁺-2Cl⁻ co-transport K⁺-Cl⁻ co-transport	Human lymphocytes Elasmobranch erythrocytes Duck erythrocytes Duck, rabbit, and dog erythrocytes
Leukotrienes	K⁺ conductance Cl⁻ conductance	Ehrlich ascites cells Ehrlich ascites cells
cAMP	Na⁺-H⁺ exchange Cl⁻-HCO₃⁻ exchange Na⁺-Cl⁻ co-transport	Mouse thick ascending limb of Henle (mTALH) cells Mouse thick ascending limb of Henle (mTALH) cells Necturus gallbladder
G proteins	Na⁺-H⁺ exchange	Barnacle skeletal muscle
Voltage	K⁺ channels	Human lymphocytes

For references, see Chamberlin and Strange (1989), Sarkadi and Parker (1991), McCarty and O’Neil (1992), Strange (1994), Hoffmann and Dunham (1995), Lang et al. (1998), O’Neil (1999), Häussinger and Schliess (1999).

VIIE5 Phosphorylation

The activities of many of the transporters discussed here are modified by phosphorylation (Parker, 1992; McCarty and O’Neil, 1992; Palfrey, 1994; Hoffmann and Dunham, 1995). This raises the possibility that cell volume alterations initiate an RVD or RVI by either increasing or decreasing the fraction of transporters in the phosphorylated state. Until recently, supporting data have been lacking. Over the last few years, however, strong evidence for this idea has come from studies in several tissues. We will discuss some of these data from erythrocytes in detail.

Pewitt et al. (1990) studied RVI in duck erythrocytes and determined that activation of Na⁺-K⁺-2Cl⁻ co-transport on shrinking is caused by phosphorylation. Both cAMP-dependent and cAMP-independent protein kinase phosphorylate the Na⁺-K⁺-2Cl⁻ co-transporter (or possibly a regulatory protein), but cAMP levels in duck erythrocytes are not affected by osmotic stress. Pewitt et al. (1990) found that the protein kinase inhibitors K252a and H-9 prevent transporter activation on shrinking. Conversely, an inhibitor of serine and threonine protein-phosphatases, okadaic acid, which slows protein dephosphorylation, stimulates Na⁺-K⁺-2Cl⁻ co-transport under isotonic conditions. These changes in the activity of the transporter with phosphorylation and with shrinking apparently result largely from a modulation of the number of functioning transporters, as detected by bumetanide binding, rather than from a modulation of their turnover rate. At about the same time, Jennings and al-Rohil (1990) and Jennings and Schulz (1991) developed evidence that K⁺-Cl⁻ co-transport in rabbit erythrocytes, which is responsible for RVD, is activated by a dephosphorylation. They discovered that swelling inhibits a protein kinase distinct from protein kinases A and C. An RVD occurred only after a slow dephosphorylation, now identified as due to a type 1 protein phosphatase (PP1) that is blocked by calyculin A (Starke and Jennings, 1993). Parker et al. (1991) obtained similar results in dog erythrocytes.

Parker et al. (1991) also recognized the important reciprocal coordination of K⁺-Cl⁻ co-transport and Na⁺-H⁺ exchange by phosphorylation and dephosphorylation during both RVDs and RVIs in mammalian erythrocytes. This strategy is illustrated in Fig. 16.20 and can be summarized as follows: (1) shrinking activates and swelling inhibits a protein kinase. (2) On shrinking, activated protein kinase rapidly phosphorylates regulatory sites associated with the K⁺-Cl⁻ co-transporter and the Na⁺-H⁺ exchanger (or the Na⁺-K⁺-2Cl⁻ co-transporter in duck erythrocytes). (3) Phosphorylation inhibits the K⁺-Cl⁻ co-transporter, reducing osmolyte efflux, but stimulates the Na⁺-H⁺ exchanger or Na⁺-K⁺-2Cl⁻ co-transporter, stimulating osmolyte uptake and leading to an RVI. (4) Conversely, slow dephosphorylation on swelling stimulates K⁺-Cl⁻ co-transport and inhibits Na⁺-H⁺ exchange or Na⁺-K⁺-2Cl⁻ co-transport, leading to an RVD. Thus, the transporters underlying ion influx and efflux are regulated reciprocally by the activity of a protein kinase that reflects cell volume.

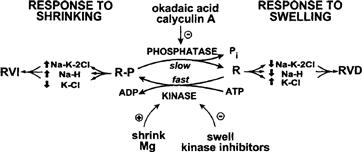
FIGURE 16.20 Schematic diagram of the mechanism of coordination of Na⁺-K⁺-2Cl⁻ co-transport and Na⁺-H⁺ and Na⁺-K⁺ exchange during cell swelling and shrinking. R-P and R represent phosphorylated and dephosphorylated regulatory sites that modulate the activity of transporters leading to a regulatory volume decrease (RVD) or regulatory volume increase (RVI). Changes in cell volume affect protein kinase activity. Several interventions that inhibit or stimulate the protein kinase and phosphatase are indicated.

How does cell volume govern the activity of a protein kinase? Several possible detectors have been considered: cell shape or cytoskeletal deformation; the concentration of an impermeant intracellular co-factor such as Mg²⁺; and a concept referred to as macromolecular crowding. The first possibility was already discussed, but experimental evidence suggests cell shape does not regulate phosphorylation of the relevant transport proteins, at least in erythrocytes. The last two possibilities will be considered next.

VIIE6 Mass Action Model

Increasing intracellular Mg²⁺ activates Na⁺-H⁺ exchange and inhibits K⁺-Cl⁻ co-transport and it has been suggested that Mg²⁺ might act by activating a kinase. Before accepting the idea that Mg²⁺ or another intracellular ion is the volume sensor, it is necessary to explain the steep dependence of ion transport on cell volume. Jennings and Schulz (1990) illustrated one possible answer for K⁺-Cl⁻ co-transport with a theoretical mass action model. They assumed: (1) the volume sensor (e.g. Mg²⁺) is an impermeant intracellular species; (2) the kinase and phosphatase are soluble enzymes; and (3) the sensor inhibits dephosphorylation. They then described the model in terms of three first-order Michaelis–Menten expressions. Taking into account that the concentrations of sensor, kinase and phosphatase vary inversely with volume, they were able to reproduce the steep volume dependence of experimental K⁺ influx data. As the authors emphasized, however, a good fit of the experimental data does not prove that the model is correct. Rather, it illustrates only that a simple dilution mechanism can give rise to a steep volume dependence of transport if dilution has different effects on the activity of enzymes that regulate the transporter (e.g. Fig. 16.20).

VIIE7 Macromolecular Crowding

The concept of macromolecular crowding comes from the idea that proteins do not behave ideally in solution at concentrations in the physiological range. We have already mentioned that the osmotic coefficient for hemoglobin and other proteins increases steeply with concentration and that Freedman and Hoffman (1979) used this fact to explain water movement in red cells. Non-ideal behavior is thought to be a more general phenomenon, however. Minton (1983, 1990, 1994) has argued that the kinetics and equilibria of enzymes (macromolecules) are markedly altered by the presence of inert macromolecules that occupy more than a few percent of the total solution volume. Just as one hemoglobin molecule affects another, macromolecules that are neither substrate nor product affect the behavior of their macromolecular neighbors in solution. This results because crowding reduces the solution volume accessible to a macromolecule by excluded-volume effects illustrated in Fig. 16.21. An excluded volume means that solution behavior is non-ideal and the chemical potential, μ_i, and activity, a_i, of a macromolecule is increased by crowding. Consequently, reaction rates are affected. On the other hand, small solutes (e.g. ions) are unaffected by the same concentration of macromolecules. Several examples are worth noting. Minton (1983) showed that the specific activity of glyceraldehyde-3-phosphate dehydrogenase decreased dramatically as the concentration of bovine serum albumin, β-lactoglobulin, polyethylene glycol (PEG) or ribonuclease in the reaction medium was increased. This was explained by suggesting that crowding favored the formation of tetramers of the enzyme that possess a lower catalytic specific activity than monomers. Similarly, the cohesion of complementary ends of λ DNA can be increased up to 2000-fold by albumin, Ficoll 70 or PEG (Zimmerman and Harrison, 1985) and the activity of T4 polynucleotide kinase is augmented by PEG (Harrison and Zimmerman, 1986). Protein concentrations within cells are sufficient to give significant excluded-volume effects (Zimmerman and Trach, 1991).

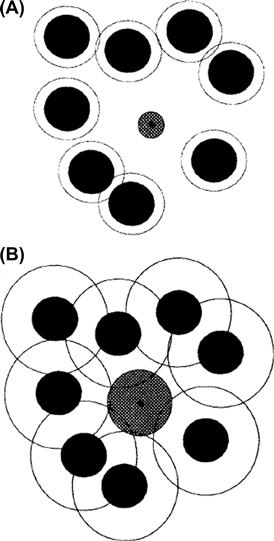
FIGURE 16.21 Diagram of macromolecular crowding. Background macromolecules (solid) in solution differentially affect the behavior of small molecules, such as ions (A) and other macromolecules (B). A test molecule (cross-hatched) cannot enter the excluded volume represented by a circle with a radius equal to the sum of the radii of the test molecule and the background macromolecule. The excluded volume is much greater for a test macromolecule (B) than for a test small molecule (A). Restricting the volume that a test molecule can enter increases its activity, a, and chemical potential, μ. Consequently, both reaction rates and equilibria are altered. (Reproduced with permission from Minton (1994). Copyright CRC Press, Boca Raton, Florida.)

How does macromolecular crowding relate to cell volume regulation? Perhaps the activity of the kinase governing the phosphorylation state of transporters decreases as macromolecular crowding is lessened during cell swelling. This would, for example, activate K⁺-Cl⁻ co-transport and inactivate Na⁺-H⁺ exchange (see Fig. 16.20) and an RVD would ensue. Colclasure and Parker (1991, 1992) provided experimental support for this hypothesis (see also Sarkadi and Parker, 1991; Parker, 1992). They osmotically ruptured dog erythrocytes and then allowed the “ghosts” to reseal in a hypotonic medium. This gave resealed ghosts with about 1/4 normal volume but with a normal protein (hemoglobin or hemoglobin plus albumin) concentration. During osmotic challenge, K⁺-Cl⁻ co-transport and Na⁺-H⁺ exchange were regulated at about the same protein concentration as in normal erythrocytes even though the volumes of the resealed ghosts were vastly different. This hypothesis is also consistent with studies on the kinetics of volume regulation by Jennings and al-Rohil (1990) who concluded that the swelling-sensitive step was a decrease in the rate of phosphorylation rather than an increase in the rate of dephosphorylation.

The new insight that macromolecular crowding may be a mechanism for volume transduction is an interesting possibility. Minton et al. (1992) have presented a model quantitatively accounting for volume-dependent stimulation of ion fluxes on this basis. It is important to recognize that operation of the scheme depends on the components having appropriate sensitivity. In erythrocytes, for example, the activities of both the kinase and the phosphatase should be reduced by swelling. Consequently, as the rate of protein phosphorylation falls, so does the rate of protein dephosphorylation. Whether this leads to an increase or decrease in the fraction of transporters in the phosphorylated state must depend both on the relative effects of macromolecular crowding and the amount of substrate available for each enzyme. With injudicious choices for the parameters (e.g. pathological interventions), this mechanism might lead to an inappropriate RVI rather than an RVD.

Acknowledgments

We thank J. Maghirang for preparing numerous figures. Supported by National Institutes of Health grants HL-24847, HL-46764, and NS-19235, and Grants-in-Aid from the American Heart Association and its Mid-Atlantic Affiliate.

BIBLIOGRAPHY

1. Adair GS. A theory of partial osmotic pressures and membrane equilibrium with special reference to the application of Dalton’s law to haemoglobin solutions in the presence of salts. Proc Roy Soc London. 1928;120A:573–603.

2. Agius L, Peak M, Beresford G, al-Habori M, Thomas T. The role of ion content and cell volume in insulin action. Biochem Soc Trans. 1994;22:518–522.

3. Agre P, Preston GM, Smith BL, et al. Aquaporin CHIP: the archetypal molecular water channel. Am J Physiol. 1993;265:F463–F476.

4. Andreoli TE, Troutman SL. An analysis of unstirred layers in series with “tight” and “porous” lipid bilayer membranes. J Gen Physiol. 1971;57:464–478.

5. Bandarali U, Roy G. Anion channels for amino acids in MDCK cells. Am J Physiol. 1992;263:C1200–C1207.

6. Barry PH, Diamond JM. Effects of unstirred layers on membrane phenomena. Physiol Rev. 1984;64:763–873.

7. Berg MB. Molecular basis of osmolyte regulation. Am J Physiol. 1995;268:F983–F996.

8. Bershadsky AD, Vasiliev JM. Cytoskeleton. New York: Plenum Press; 1988.

9. Bookchin RM, Ortiz OE, Freeman CJ, Lew VL. Predictions and tests of a new integrated reticulocyte model: implications for dehydration of sickle cells. In: The Red Cell: Seventh Annual Ann Arbor Conference. New York: Alan R. Liss Publishers; 1989;:615–625.

10. Boudreau NJ, Jones PL. Extracellular matrix and integrin signalling: the shape of things to come. Biochem J. 1999;339:481–488.

11. Boyer JL, Graf J, Meier PJ. Hepatic transport systems regulating pH_i, cell volume, and bile secretion. Annu Rev Physiol. 1992;54:415–438.

12. Boyle PJ, Conway EJ. Potassium accumulation in muscle and associated changes. J Physiol. 1941;100:1–63.

13. Brezden BL, Gardner DR, Morris CE. A potassium-selective channel in isolated Lymnaea stagnalis heart muscle cells. J Exp Biol. 1986;123:175–190.

14. Carruthers A, Melchior DL. Studies of the relationship between bilayer water permeability and bilayer physical state. Biochemistry. 1983;22:5797–5807.

15. Cass A, Finkelstein A. Water permeability of thin lipid membranes. J Gen Physiol. 1967;20:1765–1784.

16. Chamberlin ME, Strange K. Anisosmotic cell volume regulation: a comparative view. Am J Physiol. 1989;257:C159–C173.

17. Christensen O. Mediation of cell volume regulation by Ca²⁺ influx through stretch-activated channels. Nature. 1987;330:66–68.

18. Clemo HF, Baumgarten CM. cGMP and atrial natriuretic factor regulate cell volume of rabbit atrial myocytes. Circ Res. 1995;77:741–749.

19. Clemo HF, Baumgarten CM. Swelling-activated Gd³⁺-sensitive cation current and cell volume regulation in rabbit ventricular myocytes. J Gen Physiol. 1997;110:297–312.

20. Clemo HF, Feher JJ, Baumgarten CM. Modulation of rabbit ventricular cell volume and Na⁺/K⁺/2Cl⁻ cotransport by cGMP and atrial natriuretic factor. J Gen Physiol. 1992;100:89–114.

21. Clemo HF, Stambler BS, Baumgarten CM. Persistent activation of a swelling-activated cation current in ventricular myocytes from dogs with tachycardia-induced congestive heart failure. Circ Res. 1998;83:147–157.

22. Clemo HF, Stambler BS, Baumgarten CM. Swelling-activated chloride current is persistently activated in ventricular myocytes from dogs with tachycardia-induced congestive heart failure. Circ Res. 1999;84:157–165.

23. Colclasure CG, Parker JC. Cytosolic protein concentration is the primary volume signal in dog red cells. J Gen Physiol. 1991;98:881–892.

24. Colclasure CG, Parker JC. Cytosolic protein concentration is the primary volume signal for swelling-induced [KCl] cotransport in dog red cells. J Gen Physiol. 1992;100:1–10.

25. Dainty J. Osmotic flow. Symp Soc Exptl Biol. 1965;19:75–85.

26. Deamer DD, Bramhall J. Permeability of lipid bilayers to water and ionic solutes. Chem Phys Lipids. 1986;40:167–188.

27. Drewnowska K, Baumgarten CM. Regulation of cellular volume in rabbit ventricular myocytes: bumetanide, chlorothiazide, and ouabain. Am J Physiol. 1991;260:C122–C131.

28. Drewnowska K, Clemo HF, Baumgarten CM. Prevention of myocardial intracellular edema induced by St Thomas’ Hospital cardioplegic solution. J Molec Cell Cardiol. 1991;23:1215–1221.

29. Evans E, Waugh R, Melnik L. Elastic area compressibility modulus of red cell membrane. Biophys J. 1976;16:585–595.

30. Fettiplace R, Haydon DA. Water permeability of lipid membranes. Physiol Rev. 1980;60:510–550.

31. Finkelstein A. Water Movement Through Lipid Bilayers, Pores, and Plasma Membranes. Theory and Reality New York: Wiley-Interscience; 1987.

32. Finkelstein A, Cass A. Permeability and electrical properties of thin lipid membranes. J Gen Physiol. 1968;52:145s–172s.

33. Fischbarg J, Kuang K, Vera JC, et al. Glucose transporters serve as water channels. Proc Natl Acad Sci USA. 1990;87:3244–3247.

34. Foskett JK. The role of calcium in the control of volume-regulatory pathways. In: Strange K, ed. Cellular and Molecular Physiology of Cell Volume Regulation. Boca Raton: CRC Press; 1994;:259–277.

35. Freedman JC, Hoffman JF. Ionic and osmotic equilibria of human red blood cells treated with nystatin. J Gen Physiol. 1979;74:157–185.

36. Garcia A, Berg MB. Role of organic osmolytes in adaption of renal cells to high osmolarity. J Memb Biol. 1991;119:1–13.

37. Glasstone S. Textbook of Physical Chemistry. Princeton: Van Nostrand; 1946.

38. Grinstein S, Foskett JK. Ionic mechanisms of cell volume regulation in leukocytes. Annu Rev Physiol. 1990;52:399–414.

39. Grinstein S, Clarke CA, Rothstein A. Activation of Na⁺/H⁺ exchange in lymphocytes by osmotically-induced volume changes and by cytoplasmic acidification. J Gen Physiol. 1983;82:619–638.

40. Grinstein S, Rothstein A, Sarkadi B, Gelfand EW. Responses of lymphocytes to anisotonic media: volume-regulating behavior. Am J Physiol. 1984;246:C204–C215.

41. Haas M. The Na-KCl cotransporters. Am J Physiol. 1994;267:C869–C885.

42. Haines TH. Water transport across biological membranes. FEBS Lett. 1994;346:115–122.

43. Harrison B, Zimmerman SB. T4 polynucleotide kinase: macromolecular crowding increases the efficiency of reaction at DNA termini. Anal Biochem. 1986;158:307–315.

44. Hasegawa H, Skach W, Baker W, Calayag MC, Lingappa V, Verkman AS. A multifunctional aqueous channel formed by CFTR. Science. 1992;258:1477–1479.

45. Hasegawa H, Zhang R, Dohrman A, Verkman AS. Tissue-specific expression of mRNA encoding rat kidney water channel CHIP28k by in situ hybridization. Am J Physiol. 1993;264:C237–C245.

46. Häussinger D. Osmoregulation of liver cell function: signalling, osmolytes and cell heterogeneity. Contrib Nephrol. 1998;123:185–204.

47. Häussinger D, Lang F. Cell volume in the regulation of hepatic function: a mechanism for metabolic control. Biochim Biophys Acta. 1991;1071:331–350.

48. Häussinger D, Schliess F. Osmotic induction of signaling cascades: role in regulation of cell function. Biochem Biophys Res Commun. 1999;255:551–555.

49. Häussinger D, Lang F, Gerok W. Regulation of cell function by the cellular hydration state. Am J Physiol. 1994;267:E343–E355.

50. Henson JH. Relationships between the actin cytoskeleton and cell volume regulation. Microsc Res Tech. 1999;47:155–162.

51. Hernandez JA, Fischbarg J. Kinetic analysis of water transport through a single-file pore. J Gen Physiol. 1992;99:645–662.

52. Heymann JB, Engel A. Aquaporins: phylogeny, structure, and physiology of water channels. News Physiol Sci. 1999;14:187–193.

53. Heymann JB, Agre P, Engel A. Progress on the structure and function of aquaporin 1. J Struct Biol. 1998;121:191–206.

54. Hildebrand JH. Osmotic pressure. Science. 1955;121:116–119.

55. Hinke JAM. Water and electrolyte content of the myofilament phase in the chemically skinned barnacle fiber. J Gen Physiol. 1980;75:531–551.

56. Hladky SB, Rink TJ. Osmotic behaviour of human red blood cells: an interpretation in terms of negative intracellular fluid pressure. J Physiol. 1978;274:437–446.

57. Hobbie RK. Intermediate Physics for Medicine and Biology, pp 126–132. New York: John Wiley; 1978.

58. Hoffmann EK, Dunham PB. Membrane mechanisms and intracellular signalling in cell volume regulation. Int Rev Cytol. 1995;161:173–262.

59. Hoffmann EK, Simonsen LO. Membrane mechanisms in volume and pH regulation in vertebrate cells. Physiol Rev. 1989;69:315–382.

60. Hoffmann EK, Lambert IH, Simonsen LO. Separate, Ca²⁺-activated K⁺ and Cl⁻ transport pathways in Ehrlich ascites tumor cells. J Memb Biol. 1986;91:227–244.

61. Holz R, Finkelstein A. The water and nonelectrolyte permeability induced in thin lipid membranes by the polyene antibiotics nystatin and amphotericin B. J Gen Physiol. 1970;56:125–145.

62. Hu H, Sachs F. Stretch-activated ion channels in the heart. J Mol Cell Cardiol. 1997;29:1511–1523.

63. Jackson PS, Morrison R, Strange K. The volumesensitive organic osmolyte-anion channel VSOAC is regulated by nonhydrolytic ATP binding. Am J Physiol. 1994;267:C1203–C1209.

64. Jacobson BS. Interaction of the plasma membrane with the cytoskeleton: an overview. Tissue Cell. 1983;15:829–852.

65. Jakobsson E. Interactions of cell volume, membrane potential, and membrane transport parameters. Am J Physiol. 1980;238:C196–C206.

66. Jansen M, Blume A. A comparative study of diffusive and osmotic water permeation across bilayers composed of phospholipids with different head groups and fatty acyl chains. Biophys J. 1995;68:997–1008.

67. Jap BK, Li H. Structure of the osmo-regulated H₂O⁻ channel, AQP-CHIP, in projection at 3.5 Å resolution. J Mol Biol. 1995;251:413–420.

68. Jennings ML, al-Rohil N. Kinetics of activation and inactivation of swelling-stimulated K⁺/Cl⁻ transport The volume sensitive parameter is the rate constant for inactivation. J Gen Physiol. 1990;95:1021–1040.

69. Jennings ML, Schulz RK. Swelling-activated KCl cotransport in rabbit red cells: flux is determined mainly by cell volume rather than shape. Am J Physiol. 1990;259:C960–C967.

70. Jennings ML, Schulz RK. Okadaic acid inhibition of KCl cotransport Evidence that protein dephosphorylation is necessary for activation of transport by either cell swelling or N-ethylmaleimide. J Gen Physiol. 1991;97:799–817.

71. Jung JA, Preston GM, Smith BL, Guggino WB, Agre P. Molecular structure of the water channel through aquaporin CHIP: the hourglass model. J Biol Chem. 1994;269:14648–14654.

72. Kaplan MR, Mount DB, Delpire E. Molecular mechanisms of NaCl cotransport. Annu Rev Physiol. 1996;58:649–668.

73. Kiil F. Molecular mechanisms of osmosis. Am J Physiol. 1989;256:R801–R808.

74. King LS, Agre P. Pathophysiology of the aquaporin water channels. Annu Rev Physiol. 1996;58:619–648.

75. Kregenow FM. Osmoregulatory salt transporting mechanisms: control of cell volume in anisotonic media. Annu Rev Physiol. 1981;43:493–505.

76. Kwon HM, Yamauchi A, Uchida S, et al. Cloning of a Na⁺/myo-inositol cotransporter, a hypertonicity stress protein. J Biol Chem. 1992;267:6229–6301.

77. Lakshminarayanaiah N. Equations of Membrane Biophysics, pp 107–118. Orlando: Academic Press; 1984.

78. Landis EM, Pappenheimer JR. Exchange of substances through the capillary walls. Handbook of Physiology. Vol. 2 Washington, DC: American Physiological Society; 1963; Sec. 2, 961–1034.

79. Lang F, Busch GL, Volkl H. The diversity of volume regulatory mechanisms. Cell Physiol Biochem. 1998;8:1–45.

80. Leaf A. On the mechanism of fluid exchange of tissues in vitro. Biochem J. 1956;62:241–248.

81. Leaf A. Maintenance of concentration gradients and regulation of cell volume. Ann NY Acad Sci. 1959;72:396–404.

82. LeNeveu DM, Rand RP, Parsegian VA. Measurement of forces between lecithin bilayers. Nature. 1976;259:601–603.

83. Lewis SA, de Moura JL. Incorporation of cytoplasmic vesicles into apical membrane of mammalian urinary bladder epithelium. Nature. 1982;297:685–688.

84. Luna EJ, Hitt AL. Cytoskeleton-plasma membrane interactions. Science. 1992;258:955–964.

85. Ma T, Verkman AS. Aquaporin water channels in gastrointestinal physiology. Am J Physiol. 1999;517:317–326.

86. Macknight ADC. Principles of cell volume regulation. Renal Physiol Biochem. 1988;3–5:114–141.

87. Macknight ADC, Leaf A. Regulation of cellular volume. Physiol Rev. 1977;57:510–573.

88. Macey RI. Transport of water and nonelectrolytes across red cell membranes. In: Giebisch G, Tosteson DC, Ussing HH, eds. Membrane Transport in Biology, Vol II Transport Across Single Biological Membranes. Berlin: Springer Verlag; 1979;:1–57.

89. Macey RI, Farmer REL. Inhibition of water and solute permeability in human red cells. Biochim Biophys Acta. 1970;211:104–106.

90. Macey RI, Karan DM, Farmer REL. Properties of water channels in human red cells. In: Kreuzer F, Slegers JFG, eds. Biomembranes, Vol 3, Passive Permeability of Cell Membranes. New York: Plenum Press; 1972;:331–340.

91. Mauro A. Nature of solvent transfer in osmosis. Science. 1957;126:252–253.

92. McCarty NA, O’Neil RG. Calcium signaling in cell volume regulation. Physiol Rev. 1992;72:1037–1061.

93. Meschia G, Setnikar I. Experimental study of osmosis through a collodion membrane. J Gen Physiol. 1958;42:429–444.

94. Mills JW, Schweibert EM, Stanton BA. The cytoskeleton and cell volume regulation. In: Strange K, ed. Cellular and Molecular Physiology of Cell Volume Regulation. Boca Raton: CRC Press; 1994;:241–258.

95. Minton AP. The effect of volume occupancy upon the thermodynamic activity of proteins: some biochemical consequences. Molec Cell Biochem. 1983;55:119–140.

96. Minton AP. In: Holobiochemistry: the effect of local environment upon equilibria and rates of biochemical reactions. 1990;:1063–1067. Int J Biochem 22.

97. Minton AP. Influence of macromolecular crowding on intracellular association reactions: possible role in volume regulation. In: Strange K, ed. Cellular and Molecular Physiology of Cell Volume Regulation. New York: Academic Press; 1994;:181–190.

98. Minton AP, Colclasure GC, Parker JC. Model for the role of macromolecular crowding in regulation of cellular volume. Proc Natl Acad Sci USA. 1992;89:10504–10506.

99. Morris CE. Mechanosensitive ion channels. J Memb Biol. 1990;113:93–107.

100. Needham D, Nunn RS. Elastic deformation and failure of lipid bilayer membranes containing cholesterol. Biophys J. 1990;58:997–1009.

101. Nielsen S, Smith BL, Christensen EI, Knepper MA, Agre P. CHIP28 water channels are localized in constitutively wateRPermeable segments of the nephron. J Cell Biol. 1993;120:371–383.

102. Nielsen S, Chou CL, Marples D, Christensen EI, Kishore BK, Knepper MA. Vasopressin increases water permeability of kidney collecting duct by inducing translocation of aquaporin-CD water channels in rat kidney inner medulla. Proc Natl Acad Sci USA. 1995;92:1013–1017.

103. Nielsen S, Kwon TH, Christensen BM, Pomeneur D, Frokiaer J, Marples D. Physiology and pathophysiology of renal aquaporins. J Am Soc Nephrol. 1999;10:647–663.

104. O’Neil WC. Physiological significance of volume regulatory transporters. Am J Physiol. 1999;276:C995–C1011.

105. Overbeek JTG. The Donnan equilibrium. Prog Biophys Biophys Chem. 1956;3:57–84.

106. Paganelli CV, Solomon AK. The rate of exchange of tritiated water across the human red cell membrane. J Gen Physiol. 1957;41:259–277.

107. Palfrey HC. Protein phosphorylation control in the activity of volume-sensitive transport systems. In: Strange K, ed. Cellular and Molecular Physiology of Cell Volume Regulation. Boca Raton: CRC Press; 1994;:201–214.

108. Palfrey HC, O’Donnell ME. Characteristics and regulation of the Na/K/2Cl cotransporter. Cell Physiol Biochem. 1992;2:293–307.

109. Parker JC. Dog red blood cells Adjustment of density in vitro. J Gen Physiol. 1973;62:147–156.

110. Parker JC. Volume-activated cation transport in dog red cells: detection and transduction of the volume stimulus. Comp Biochem Physiol. 1992;102A:615–618.

111. Parker JC, Colclasure GC, McManus TJ. Coordinated regulation of shrinkage-induced Na/H exchange and swelling-induced [K-Cl] cotransport in dog red cells Further evidence from activation kinetics and phosphatase inhibition. J Gen Physiol. 1991;98:869–880.

112. Pewitt EB, Hegde RS, Haas M, Palfrey HC. The regulation of Na/K/2Cl cotransport and bumetanide binding in avian erythrocytes by protein phosphorylation and dephosphorylation: effects of kinase inhibitors and okadaic acid. J Biol Chem. 1990;265:20747–20756.

113. Pfeffer W. Osmotische Untersuchungen Studien zur Zellmechanik Wilhelm Engelmann, Leipzig [Translated by G.R Kepner and E.J Tadelmann (1985) Osmotic investigations Studies on cell membranes. New York: Van Nostrand Reinhold; 1877.

114. Pierce SK, Politis AD. Ca²⁺-activated cell volume recovery mechanisms. Annu Rev Physiol. 1990;52:27–42.

115. Pitzer KS, Mayorga G. Thermodynamics of electrolytes II Activity and osmotic coefficients for strong electrolytes with one or both ions univalent. J Phys Chem. 1973;77:2300–2308.

116. Preston GM, Agre P. Isolation of the cDNA for erythrocyte integral membrane protein of 28 kilodaltons member of an ancient channel family. Proc Natl Acad Sci USA. 1991;88:11110–11114.

117. Preston GM, Carroll TP, Guggino WB, Agre P. Appearance of water channels in Xenopus oocytes expressing red cell CHIP28 protein. Science. 1992;256:385–387.

118. Preston GM, Jung JS, Guggino WB, Agre P. The mercury-sensitive residue at cysteine-189 in the CHIP28 water channel. J Biol Chem. 1993;268:17–20.

119. Preston GM, Jung JS, Guggino WB, Agre P. Membrane topology of aquaporin CHIP: analysis of functional epitope scanning mutants by vectorial proteolysis. J Biol Chem. 1994;269:1668–1673.

120. Rash JE, Yasumura T, Hudson CS, Agre P, Nielsen S. Direct immunogold labeling of aquaporin-4 in square arrays of astrocyte and ependymocyte plasma membranes in rat brain and spinal chord. Proc Natl Acad Sci USA. 1998;95:11981–11986.

121. Rasmusson RL, Davis DG, Lieberman M. Amino acid loss during volume regulatory decrease in cultured chick heart cells. Am J Physiol. 1993;264:C136–C145.

122. Renkin EM. Filtration, diffusion, and molecular sieving through porous cellulose membranes. J Gen Physiol. 1954;38:225–243.

123. Reuss L. Changes in cell volume measured with an electrophysiological technique. Proc Natl Acad Sci USA. 1985;82:6014–6018.

124. Richter EA, Cleland PJF, Rattigan S, Clark MG. Contraction-associated translocation of protein kinase C. FEBS Lett. 1987;217:232–236.

125. Robinson RA, Stokes RH. Electrolyte Solutions, pp 480–490. London: Butterworth; 1959.

126. Rosenberg PA, Finkelstein A. Water permeability of gramicidin A-treated lipid bilayer membranes. J Gen Physiol. 1978;72:341–350.

127. Sachs F. Ion channels as mechanical transducers. In: Stein WD, Bronner F, eds. Cell Shape: Determinants, Regulation, and Regulatory Role. San Diego: Academic Press; 1989;:63–92.

128. Sackin H. Stretch-activated ion channels. In: Strange K, ed. Cellular and Molecular Physiology of Cell Volume Regulation. Boca Raton: CRC Press; 1994;:215–240.

129. Sands JM. Regulation of intracellular polyols and sugars in response to osmotic stress. In: Strange K, ed. Cellular and Molecular Physiology of Cell Volume Regulation. Boca Raton: CRC Press; 1994;:133–144.

130. Sarkadi B, Parker JC. Activation of ion transport pathways by changes in cell volume. Biochim Biophys Acta. 1991;1071:407–427.

131. Schatzberg P. Solubilities of water in several normal alkanes from C₇ to C₁₆. J Phys Chem. 1963;67:776–779.

132. Shibata A, Ikawa K, Shimooka T, Terada H. Significant stabilization of the phosphatidylcholine bilayer structure by incorporation of small amounts of cardiolipin. Biochim Biophys Acta. 1994;1192:71–78.

133. Shporer M, Civan MM. The state of water and alkali cations within the intracellular fluids: the contribution of NMR spectroscopy. Curr Top Membr Transport. 1977;9:1–69.

134. Solomon AK. Properties of water in red cells and synthetic membranes. In: Kreuzer F, Slegers JFG, eds. Biomembranes, Vol 3, Passive Permeability of Cell Membranes. New York: Plenum Press; 1972;:299–330.

135. Solomon AK. Water channels across the red blood cell and other biological membranes. Meth Enzymol. 1989;173:192–222.

136. Solomon AK, Chasan B, Dix JA, Lukacovic MF, Toon MR, Verkman AS. The aqueous pore in the red cell membrane: band 3 as a channel for anions, cations, nonelectrolytes, and water. Ann NY Acad Sci. 1983;414:97–124.

137. Somero GN. Protons, osmolytes, and fitness of internal milieu for protein function. Am J Physiol. 1986;251:R197–R213.

138. Starke LC, Jennings ML. K-Cl cotransport in rabbit red cells: further evidence for regulation by protein phosphatase type 1. Am J Physiol. 1993;264:C118–C124.

139. Stein WD. An algorithm for writing down flux equations for carrier kinetics, and its application to co-transport. J Theor Biol. 1976;62:467–478.

140. Strange K. Cellular and Molecular Physiology of Cell Volume Regulation. Boca Raton: CRC Press; 1994.

141. Suleymanian MA, Baumgarten CM. Osmotic gradient-induced water permeation across the sarcolemma of rabbit ventricular myocytes. J Gen Physiol. 1996;107:503–514.

142. Suleymanian MA, Clemo HF, Cohen NM, Baumgarten CM. Stretch-activated channel blockers modulate cell volume in cardiac ventricular myocytes. J Mol Cell Cardiol. 1995;27:721–728.

143. Tanford C. Physical Chemistry of Macromolecules. New York: John Wiley; 1961.

144. Tosteson DC, Hoffman JF. Regulation of cell volume by active cation transport in high and low potassium sheep red cells. J Gen Physiol. 1960;44:169–194.

145. Trauble H. The movement of molecules across lipid membranes: a molecular theory. J Memb Biol. 1971;4:193–208.

146. Uchida S, Kwon H, Yamauchi A, Preston A, Marumo F, Handler J. Molecular cloning of the cDNA for an MDCK cell Na⁺ and Cl⁻-dependent taurine transporter that is regulated by hypertonicity. Proc Natl Acad Sci USA. 1992;89:8230–8234.

147. Uchida S, Kwon H, Yamauchi A, Preston A, Kwon H, Handler J. Medium tonicity regulates expression of the Na⁺- and Cl⁻-dependent betaine transporter in Madin-Darby canine kidney cells by increasing transcription of the transporter gene. J Clin Invest. 1993;91:1604–1607.

148. Umenishi F, Verkman AS, Gropper MA. Quantitative analysis of aquaporin mRNA expression in rat tissues by RNase protection assay. DNA Cell Biol. 1996;15:475–480.

149. Vandenberg JI, Rees SA, Wright AR, Powell T. Cell swelling and ion transport pathways in cardiac myocytes. Cardiovasc Res. 1996;32:85–97.

150. van Hoek AN, Hom ML, Luthjens LH, de Jong MD, Dempster JA, van Os CH. Functional unit of 30 kDa for proximal tubule water channel as revealed by radiation inactivation. J Biol Chem. 1991;266:16633–16635.

151. van Hoek AN, Luthjens LH, Hom ML, van Os CH, Dempster JA. A 30 kDa functional size for the erythrocyte water channel determined by in situ radiation inactivation. Biochem Biophys Res Commun. 1992;184:1331–1338.

152. van’t Hoff, J.H. (1887). Die Rolle des osmotischen Druckes in der Analogie zwischen Lösungen und Gasen. Z. Physik. Chemie. 1, 481–493 [Translated by G.L. Blackshear (1979). In (G.R. Kepner, ed.) Cell Membrane Permeability and Transport. Dowden, Hutchinson and Ross, Stroudsburg, PA.].

153. Verkman AS. Water Channels. Austin: R. G. Landis Co; 1993.

154. Verkman AS, van Hoek AN, Ma T, et al. Water transport across mammalian cell membranes. Am J Physiol. 1996;270:C11–C30.

155. Villars FM, Benedek GB. Physics with Illustrative Examples from Medicine and Biology Statistical Physics. Vol. 2 Reading: Addison-Wesley; 1974.

156. Walz T, Smith BL, Agre P, Engel A. The three-dimensional structure of human erythrocyte aquaporin CHIP. EMBO J. 1994;13:2985–2993.

157. Walz T, Hirai T, Murata K, et al. The three-dimensional structure of aquaporin-1. Nature. 1997;387:624–627.

158. Watson PA. Function follows form: generation of intracellular signals by cell deformation. FASEB J. 1991;5:2013–2019.

159. Wolfe J, Dowgert MF, Steponkus PL. Mechanical study of the deformation and rupture of the plasma membranes of protoplasts during osmotic expansions. J Memb Biol. 1986;93:63–74.

160. Wolff SD, Balaban RS. Regulation of the predominant renal medullary organic solutes in vivo. Annu Rev Physiol. 1990;52:727–746.

161. Wright AR, Rees SA. Cardiac cell volume: crystal clear or murky waters? A comparison with other cell types. Pharmacol Ther. 1998;80:89–121.

162. Yamauchi A, Uchida S, Kwon H, et al. Cloning of a Na⁺ and Cl⁻ dependent betaine transporter that is regulated by hypertonicity. J Biol Chem. 1992;267:649–652.

163. Yancey PH. Compatible and counteracting solutes. In: Strange K, ed. Cellular and Molecular Physiology of Cell Volume Regulation. Boca Raton: CRC Press; 1994;:81–177.

164. Yancey PH, Clark ME, Hand SC, Bowlus RD, Somero GN. Living with water stress: evolution of osmolyte systems. Science. 1982;217:1214–1222.

165. Zeidel ML, Ambudkar SV, Smith BL, Agre P. Reconstitution of functional water channels in liposomes containing purified red cell CHIP28 protein. Biochemistry. 1992;31:7436–7440.

166. Zhang R, Skach W, Hasegawa H, van Hoek AN, Verkman AS. Cloning, functional analysis and cell localization of a kidney proximal tubule water transporter homologous to CHIP28. J Cell Biol. 1993;120:359–369.

167. Zimmermann SB, Harrison B. Macromolecular crowding accelerates the cohesion of DNA fragments with complementary termini. Nucl Acids Res. 1985;13:2241–2249.

168. Zimmerman SB, Trach S. Estimation of macromolecular concentrations and excluded volume effects for the cytoplasm of Escherichia coli. Mol Biol. 1991;222:599–620.

¹ The amount of charge, q, necessary to establish a potential difference, E_m, is related to the specific capacitance of the membrane, C_m, and its area, A, by:

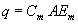
Assuming a specific membrane capacitance of 1 μF/cm², as is typical of most biological membranes, the amount of charge necessary to develop a potential of 100 mV in a spherical cell with a radius of 20 μm is:

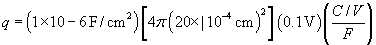
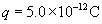
This can be converted to a change in the concentration, ΔC, of ions in the cell:

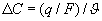
where F is Faraday’s constant, and ϑ is used for the volume of the cell here to distinguish it from voltage. For the same 20-μm-radius cell:

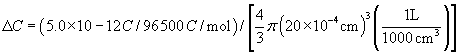
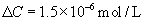
Thus, a potential gradient of 100 mV would develop if ion influx were to increase [K⁺]_i by only 1.5 μM more than it increased [Cl⁻]_i.

² Formally, as presented previously in Equation 16.3 for the chemical potential of a neutral species, μ_i should be defined in terms of the mole fraction rather than the concentration of a component and an additional term, , representing the pressure times the partial molar volume, should be added. For dilute solutions, the mole fraction of a solute closely approximates its concentration (see Equations 16.5 and 16.9). The terms are ignored in the derivation of the ion distribution for a Donnan equilibrium because to simplify we initially assume the membrane is rigid (see Fig. 16.13A) and then we consider a situation without a pressure gradient where the terms cancel (see Fig. 16.13B). Derivations of Donnan equilibrium retaining the mole fraction and the pressure-volume terms can be found in Overbeek (1956) and Lakshminarayanaiah (1984).

³ For eukaryotic cells, it is generally assumed that the osmotic gradient across a membrane is negligible. This view arises because the thin bilayer membrane is too fragile to resist the substantial forces developed by even small differences in osmotic pressure. A tension of ≈10 dyn·cm⁻² is sufficient to rupture erythrocyte (Evans et al., 1976), protoplast (Wolfe et al., 1986), or lipid bilayer (Needham and Nunn, 1990) membranes. The relationship between tension on the membrane and transmembrane pressure is given by the law of Laplace. For a thin-walled spherical cell P = 2T/r where P is pressure, T is tension and r is the cell’s radius. If we assume a radius of 10 μm, a lytic tension is developed by a pressure of 2 × 10⁴ dyn cm⁻², which equals ≈15mmHg. This is the osmotic pressure developed by only ≈0.0008 osmol L⁻¹. Hence, the membrane cannot support a sufficient hydrostatic pressure to offset an osmotic gradient.Before accepting this conclusion, it is necessary to consider the effective radius of the cell in view of the geometry of the cytoskeleton (Jacobson, 1983). For example, there are ≈10⁵ copies of ankyrin per erythrocyte. If all these attach integral membrane proteins to the cytoskeleton and are evenly distributed, the membrane is strengthened by load-bearing cytoskeletal elements at ≈40 nm intervals. Even if we assume an effective radius of 100 nm, lytic tension now requires a pressure of 2 × 10⁶ dyn cm⁻², which equals ≈1500 mmHg or nearly 2 atm. This is equivalent to the osmotic pressure generated by 0.078 osmol L⁻¹.

Chapter 16

Osmosis and Regulation of Cell Volume

Chapter Outline

I Summary

II Introduction