MARIAN and I left Berkeley in 1969 with mixed emotions, and it has remained for me a place of magic and pilgrimage: a dreamtime of lost youth, of clever and friendly colleagues, of clear, bright sunshine alternating with cooling mist over the Golden Gate, of the dawn-fresh scent of pine and eucalyptus, of flower children with decent and sincere, if naive, liberal values.
We crated and shipped our few belongings from our Berkeley apartment and drove right across the continent in our old, cream-coloured Ford Falcon station wagon, thickly encrusted with anti-war slogans and Eugene McCarthy election stickers, to New York. By prior arrangement, we sold the Ford on the quayside (amazingly, our pre-arranged customer, who had made his own laid-back Berkeley-style way to New York, showed up on time), boarded the liner France for Southampton, and prepared to resume our life at Oxford with many of our old friends still there and Colin Beer newly arrived. In the event, Colin preferred to spend his time in New College and was scarcely seen in the department, much to everyone’s disappointment. He stayed only a year. Danny Lehrman – the same Daniel S. Lehrman whose theoretical critique had so influenced my doctoral thesis – had shrewdly kept Colin’s position at Rutgers warm for him, and when it became clear that Oxford couldn’t find a position in medieval French to match the professorship his wife held in America, Colin decided to return. Once again, the lectureship in animal behaviour was advertised, once again the long-suffering New College agreed to associate a fellowship with it, and once again Niko urged me to apply. Along with a shortlist of others I was again interviewed by two committees: a university committee chaired by Laughing John Pringle, and a college committee chaired by the genuinely laughing, almost preternaturally genial Warden, Sir William Hayter, former British Ambassador in Moscow.
This time I really wanted the job, and this time I got it. The news came as Marian and I were anxiously waiting with friends in an Indian restaurant in Oxford. Suddenly, we heard the sound of Mike Cullen’s motor scooter as it pulled up outside. Mike burst into the restaurant, wordlessly pointed both index fingers at me, and vanished as quickly as he had arrived. I had got the job. With hindsight I don’t think I should have got it at the time, given that the chief competition was the wildly brilliant Juan Delius, although I like to think that I grew into it and was worthy of it in the end. Juan was a dear friend and mentor, an immensely clever, knowledgeable and funny German-Argentinian. He once defined Argentinian humour for me: ‘They enjoy slapstick, but if somebody slips on a banana skin it’s only really funny if he breaks his leg.’ The board at 13 Bevington Road was frequently adorned with wonderful notices in Juan’s unique brand of English: ‘What bastard has absconded my oles?’ (Who has taken my stencil for drawing circles of different sizes?)
The life of a tutorial fellow of an Oxford college is in many ways a charmed one. I got a room in a glowing, oolitic limestone medieval building surrounded by famously beautiful gardens; a book allowance, a housing allowance, a research allowance; and free meals (though not free wine, contrary to envious rumours) in the stimulating and entertaining company of leading scholars of every subject except my own. The stimulating scholars of my own subject were to be found in the Zoology Department – where I spent the majority of my time.
I was introduced to the strange world of high-table conversation. After dinner there would sometimes be occasion to bring out the Senior Common Room Betting Book – either to record a new wager or to browse the old ones, all written in the same affected style as high-table conversation itself. Here’s a brief sample, going back to the 1920s when the most assiduous betting man was the eccentrically brilliant G. H. Hardy, whose Lewis-Carroll-like mathematician’s sense of humour seems to have infected his colleagues:
(7th Feb 1923) The Subwarden bets Prof Hardy his fortune till death to one halfpenny that the sun will rise tomorrow.
(6.8.27) Prof Hardy bets Mr Woodward 10,000 to 1 in halfpennies that he (Prof Hardy) will not be the next President of Magdalen, and Mr Woodward bets Prof Hardy 1 to 5,000 that he (Mr Woodward) will not be the next President of Magdalen.
(Feb 1927) Professor Hardy bets Mr Creed 2/6 to 1/6 that the New Prayer Book will go phut. Mr Smith, Mr Casson and Mr Woodward to adjudicate if necessary.
I’m amused that so obvious a value judgement could be subject to a bet. No wonder an odd number of adjudicators was needed.
Another bet even leaves the size of the stake up to later judgement:
(Dec 2 1923) Professor Turner bets the Steward of SCR a large sum that it would be a good thing to have a copy of the ABC (London) Railway Guide in SCR (Won by Prof Turner, A.H.S.)
(15 Feb 1927) Mr Cox bets Professor Hardy 10/- to 1/- that Rev. Canon Cox (‘Fred’) will not be the next Bishop of Nyasaland.
I love that parenthetic ‘Fred’. Unfortunately the result of this bet was not recorded. I’d like to know whether ‘Bishop Fred’ presided over the see of my early home country. In failing to settle the question for me, Google did turn up the fact that a nineteenth-century Bishop of Nyasaland was Charles Alan Smythies – very probably related to the seven generations of my Smythies ancestors who were vicars.
(11th March 1927) Mr Yorke bets Mr Cox 2/6d that no verse occurs in the Gospel according to St Matthew the literal interpretation of which justifies or advocates self-castration. Won by Mr Cox.
(October 26th 1970) Professor Sir A Ayer bets Mr Christiansen that the Chaplain will be unable, if challenged without warning, to repeat twelve of the thirty nine articles to be found in the Book of Common Prayer. The stake to be one bottle of claret.
(24th Nov 1985) The Chaplain bets Dr Ridley a bottle of claret that Dr Bennett will be wearing a clerical collar at dinner on the occasion of the visit of the Bishop of London. (Chaplain won.)
(4th August 1993) Mr Dawkins bets Mr Raine £1 that Bertrand Russell married Lady Ottoline Morrell. Adjudicator Mlle Bruneau. (Dawkins lost and paid, 20 years late.)
Bets like the last one can’t happen any more because it is so trivially easy for everyone to check such factual questions on their smartphones without rising from their Senior Common Room armchairs. Even then, it was scarcely necessary to appoint an adjudicator for a purely factual matter.
Back to 1970, when I was twenty-nine and newly returned to Oxford. The singing Elliott had gone the way of all silicon, but Moore’s Law and the research grant that had lured me back to Oxford the previous year made it possible for me to have my ‘own’ computer, a PDP-8, which exceeded the Elliott in every respect except physical size and price. Also in accordance with Moore’s Law (which was already going strong in those days), it was functionally much smaller yet physically larger than a modern laptop, and ludicrously it had a log book in which you were supposed to record every time you switched it on (of course I didn’t). It was my pride and joy and a valued resource – together with me as sole programmer for everybody in 13 Bevington Road (which took its toll on my time). Now my addiction to computers could really take off, and I no longer had to indulge it nocturnally, as during my shameful affair with the Elliott 803.
Previously I had used only high-level compiler languages – human-friendly languages, which the computer translates into its own binary machine language. But now, in order to use the PDP-8 as a research tool, I had to master its 12-bit machine language, a task into which I threw myself with zest. My first machine-code project was the ‘Dawkins Organ’, a system for recording animal behaviour – equivalent to George Barlow’s ‘Data Acquision’ apparatus but much much cheaper. The idea was to make a keyboard which an observer could use in the field, pressing buttons to indicate actions by an animal. Key-presses would be recorded on a tape recorder, which would later automatically tell the computer exactly when each action by the animal occurred.
My keyboard literally was a makeshift electronic organ, with each key playing a different note (inaudible except to the tape recorder). This part would be easy to make. The box would contain a simple two-transistor oscillator, the pitch of whose note was tuned by a resistance. Each key on the organ would connect a different resistor and hence play a different note. The observer was to take the organ into the field and watch an animal’s behaviour like a work-study officer, pressing a specific key for each behaviour pattern. A tape recording of the sequence of notes would then constitute a timed record of the animal’s behaviour. Theoretically, a person with a good ear listening to the tape could detect which key had been pressed, but this wouldn’t be helpful. I needed to cast the computer in the role of person-with-good-ear. It could have been done electronically, with a series of tuned frequency-detectors, but that would have been an expensive hassle. Could the same feat – perfect pitch sensitivity in the computer – be achieved in software alone?
I was discussing the problem with my computer guru of the time, Roger Abbott, a clever engineer (and coincidentally organist) employed on the large research grant of Professor Pringle. Roger came up with an inspired suggestion. Every musical note has a characteristic wavelength which signifies its pitch. Computers are – and were, even in those days – so fast that the interval between wave crests within a musical note could be measured in hundreds of program cycles. Roger suggested that I should write a machine-code program to time the intervals between wave peaks: write, in other words, a little routine to act as a high-speed clock, counting how many jumping-back program loops it could walk through before being interrupted by the next wave crest (which, when averaged over lots of wave crests, tells it the pitch of the note). When a note ended (when more than a critical time elapsed since the last wave peak) the computer should make a note of the time and then wait for the next organ note. The computer’s clocking loop, in other words, would be used not only to recognize the pitch of a musical note but also, on a hugely longer timescale, to measure the passage of time between notes.
Having got this central routine working, the rest was just a matter of slogging through the writing and debugging of a user-friendly program. This took rather a long time, but it ended successfully. The Dawkins Organ was a viable product. The user of the organ began each session by playing a scale on the tape – all the notes on the organ in ascending order of pitch. The taped scale would then be used to ‘calibrate’ the software – ‘teach’ the computer the repertoire of notes it would be asked to recognize. After the calibration scale was ended (by hitting the first note for the second time), all further notes on the tape would designate behavioural events. This calibration system had the advantage that the organ did not have to be carefully tuned. Any set of notes that were sufficiently distinct from each other would do, because the computer quickly learned which notes to listen out for.
So, when the tape was brought home and played into the computer, the computer knew exactly what the animal had done, and when. The nucleus of the program was the timing loop, but it was embedded in a substantial quantity of code to punch out, on paper tape, the names of all the behaviour patterns and the exact times when they occurred.
I published a paper on the Dawkins Organ,53 and made the software available free of charge. Over the next few years Dawkins Organs were used by numerous members of the Oxford ABRG, and by some ethologists elsewhere in the world, for example in the University of British Columbia.
My addiction to machine code programming took me in a downward spiral. I even devised my own programming language, BEVPAL, with its own programming manual, a somewhat otiose exercise since the language was used by nobody except myself and, briefly, Mike Cullen. Douglas Adams amusingly satirized computer addiction of exactly the kind that hit me. The target of his satire was the programmer who had a particular problem X, which needed solving. He could have written a program in five minutes to solve X and then got on and used his solution. But instead of just doing that, he spent days and weeks writing a more general program that could be used by anybody at any time to solve all similar problems of the general class of X. The fascination lies in the generality and in the purveying of an aesthetically pleasing, user-friendly product for the benefit of a population of hypothetical and very probably non-existent users – not in actually finding the answer to the particular problem X. Another symptom of this kind of geekish addiction is that every time you solve a local problem and make the computer jump through yet another hoop, you want to rush out into the street and drag someone in to show them how elegant it is.
The productive camaraderie that a small building like 13 Bevington Road fosters came to an end around this time, and the animal behaviour group moved to the new zoology/psychology building, the huge, battleship-like horror on South Parks Road, then informally known as HMS Pringle after the ambitious Linacre Professor who persuaded the university authorities to build it – having failed to cajole them into building a pencil-thin skyscraper that would have disastrously overtopped Matthew Arnold’s dreaming spires. I have mixed feelings about my part in later getting HMS Pringle officially named the Tinbergen Building, for it is widely deplored as the ugliest building in Oxford. It won an architectural award from the Concrete Society – enough said.
Around this time I published a short paper in Nature.54 Every day hundreds of thousands of our brain cells die, and this was upsetting to me even at the age of twenty-nine. My Darwin-obsessed brain sought comfort in the idea that if the cell deaths were non-random, such apparently wholesale slaughter might be constructive, not purely destructive:
A sculptor changes a homogeneous lump of rock into a complex statue by subtraction, not addition, of material. An electronic data processing machine is most likely to be made by connecting components up in complex ways, and then enriching the connexions to make it even more complex. On the other hand, it could be constructed by starting with extremely rich, even random interconnexions, and then carving out a more meaningful organization by selectively cutting wires.
. . .
The theory proposed here may seem fanciful at first. Further reflexion shows, however, that its lack of verisimilitude is mainly a consequence of the highly improbable postulate on which it rests; namely, that brain cells are decreasing in numbers at a prodigious rate daily. Because this postulate, however far-fetched, is an established fact, the present theory is not suggesting anything very implausible in addition; rather the reverse, as it makes the process seem less wasteful. All that is at issue is whether neurones die at random, or selectively in such a way as to store information.
A curious little one-off, this paper is perhaps mildly interesting as an early example of the kind of theory that later became fashionable under the name – coined a year later, so I obviously didn’t use it – ‘apoptosis’.
Marian soon got her doctorate, and we began to collaborate on research projects growing out of the many discussions – mutual tutorials – from our Berkeley days. We planned a study that would exemplify, and clarify, one of the fundamental concepts of the ethological school of animal behaviour studies, the Fixed Action Pattern.
Lorenz and Tinbergen and their school thought that much of animal behaviour consisted of a sequence of little clockwork routines – Fixed Action Patterns (FAP). Each FAP was thought to be like a piece of anatomy, just as much a part of the animal’s bodily equipment as, say, the collar bone or the left kidney. The difference is that collar bones and kidneys are made of solid material, whereas the FAP has a time dimension: you can’t pick it up and put it in a drawer, you have to watch it play out in time. A familiar example of an FAP would be the pushing movement that a dog makes with its snout when burying a bone. These movements are identically replayed even when the bone is on a carpet and there is no soil in which to bury it. The dog really does look like a (charming) clockwork toy, although the exact direction of the movement is influenced by the position of the bone.
Every animal has a repertoire of FAPs, like one of those dolls that you wind up by pulling a string and which then utters a saying randomly plucked from a finite repertoire. Once initiated, whichever saying is chosen goes through to completion. The doll doesn’t switch messages halfway through. The decision of which of a dozen sayings to produce is unpredictable but, once taken, the consequences of the decision are followed through predictably as clockwork. That was the FAP doctrine in which Marian and I, as Tinbergenian ethologists, had been brought up; but was it a true reflection of reality? This was the question we wanted to answer – or, to be precise, the question we sought to re-express in terms that might make it answerable.
In theory, one could write down the continuous stream of animal behaviour as a sequence of muscular contractions. But if the FAP theory was right, the predictability of behaviour would render it a laborious waste of effort to write down every muscular contraction, even were it possible to do so. Instead, all we should need to do is write down the FAPs, and the sequence of FAPs would – on an extreme interpretation – be a complete description of that particular animal’s behaviour.
But this would only work if FAPs really were equivalent to organs or bones – if it were true, in other words, that each pattern occurs as a whole, not breaking off part-way through or mixing with another pattern. Marian and I wanted to find a way to assess the extent to which this proposition was true. Both our doctoral theses had been concerned – in our two ways – with decision-making, and it was natural for us to translate the FAP problem into the language of decisions. In that language, the animal takes a decision to initiate an FAP; but, once initiated, the FAP goes on to its conclusion, with no further decisions until the end. At that point the animal’s behaviour stream would enter a period of uncertainty, pending the next decision to initiate (and complete) an FAP.
We chose to study drinking in chicks as our example, and we hoped it would be representative.55 Drinking in birds (other than pigeons and doves, which suck) is an elegant glissando of a movement, and it certainly gives a subjective impression of being initiated by a discrete decision, after which it always goes through to completion. But could we back up our subjective impression with hard data?
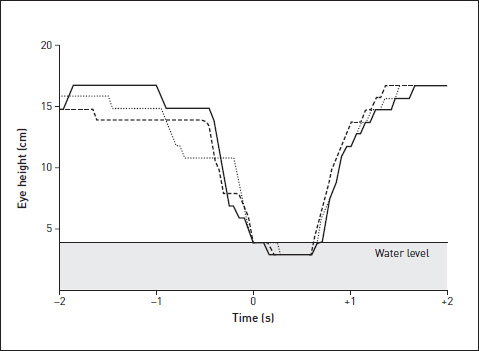
We filmed a side view of our chicks drinking, and then analysed the behaviour frame by frame to see if we could measure its ‘decision structure’. We measured the position of the bird’s head in successive frames of film, then fed the coordinates into the computer. The idea was to measure the predictability of the next frame, knowing the position of the head in previous frames.
The diagram is a graph of eye height against time, for three drinks by the same chick, lined up (zero on the time axis) on the moment when the bill hit the water. You get a sense that from that moment on, indeed from just before it, the behaviour is stereotyped and predictable, but the early part of the downstroke is more variable and subject to decisions: decisions to pause and even (as we showed separately) to abort the drink.
But how should we measure predictability? The graph below shows one way. It represents a single drink in the same way as before. But each point on the graph of eye position has arrows attached to it. The length of the arrow signifies, for each frame of film, the likelihood (as totted up over all the drinks by all the chicks) that the eye height in the next frame will be lower, higher, or the same.
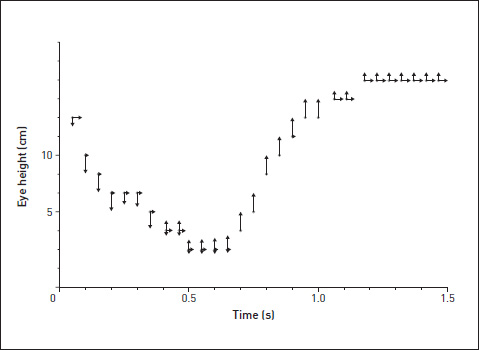
You can see that during the upstroke, when the bird is allowing the water to trickle down its throat, there is a high probability that the upstroke will continue its graceful curve in the upward direction. A decision to perform an FAP is being carried out, with no further decisions during its course. But during the downstroke there is more unpredictability. For each frame of the downstroke, the height of the eye in the next frame is undecided between lower or the same, and there is even some likelihood that it might be higher – that is, that the drink will be aborted.
Could we use these arrows to compute an index of uncertainty or ‘decisioniness’? The index we chose was based on information theory, devised in the 1940s by the inventive American engineer Claude Shannon. The information content of a message can be informally defined as its ‘surprise value’. Surprise value is a convenient opposite of predictability. Classic examples are ‘It is raining in England today’ (low information content because no surprise) versus ‘It is raining in the Sahara Desert’ (high information content because surprising). For reasons of mathematical convenience, Shannon computed his index of information content in bits (short for ‘binary digits’), by summing up the logarithm (base 2) of the prior probabilities that were open to doubt before the message was received. The information content of a penny toss is one bit, because the prior uncertainty is heads or tails – two equiprobable alternatives. The information content of a playing card’s suit is two bits (there are four equiprobable alternatives and the base two logarithm of four is two, corresponding to the minimum number of yes/no questions you’d need to ask in order to establish the suit). Most real examples are not so simple, and the possible outcomes are usually not equiprobable, but the principle is the same and a version of the same mathematical formula conveniently does the trick. It was this mathematical convenience that led us to use the Shannon Information Index as our measure of predictability or uncertainty.
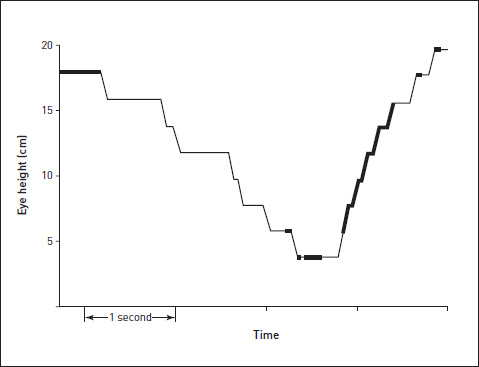
Once again we have a graph of eye height against time during a drink. The thin lines represent times of low predictability, or high probability of a decision intervening to change the future. The thick black lines represent times of high predictability (information content less than an arbitrary threshold of 0.4 bits), during which a decision is being carried out and no new decision is expected. The upstroke is predictable once it starts, but the downstroke is not. The pause between drinks is predictable for the rather boring reason that the pause is most likely to continue into the next frame – it’s hard to predict when the next drink will start.
As always, keep in mind that the particular behaviour, here drinking, is not of interest in itself. Drinking in chicks was a stand-in for behaviour generally, just as pecking was in my doctoral research. We were interested in the very idea of a decision and – in the case of drinking – whether we could identify moments of decision. We were trying to explore a way to demonstrate the very existence of a Fixed Action Pattern, rather than simply taking it for granted as ethologists were wont to do.
We adopted a different approach in our next project on decision-making, which was a study of self-grooming in flies. Ethologists often ask whether, if you know what an animal is doing now, you can predict what it will do next. Marian and I wanted to know whether, sometimes, you can predict what it will do in the more distant future better than you can predict what it will do in the more immediate future. This might be true, for instance, if behaviour is organized like human language. There are times when the beginning of a sentence predicts how the sentence will end better than it predicts the middle – which might contain any number of embedded adjectival or relative clauses, for instance. ‘The girl hit the ball’ is a sentence whose beginning demands something like the ending, whether or not there are embedded adjectives or adverbs or clauses in the middle: ‘The girl with red hair, who lives next door, vigorously hit the ball.’
We didn’t find evidence of language-like grammatical structure in the grooming behaviour of flies (although see below). But we did find an interesting zigzag pattern in the way predictability decays over time: in other words, the immediate future may be less predictable than the (slightly) more distant future. I’ll outline our research briefly here and not in detail, because it’s a bit complicated.
Flies are not normally seen as beautiful, but the way they wash their faces and their feet is rather dear. Look next time a fly lands on you: you’ll very probably see the behaviour. It may rub its front feet together, or wipe its great big eyes with them. It may rub the middle foot on one side against the hind foot on the same side, or clean its abdomen or wings with its hind feet. Somewhere inside that tiny head, decisions are spontaneously being generated, and a fair number of those decisions concern which bit of the body to clean next. The appeal of self-grooming behaviour for us was that the fly’s choice of behaviour was unlikely to be externally stimulated. We presumed that external stimulation amounted to an ever-present need to keep clean – ever-present in the sense that, though important, it was unlikely to determine exactly when a particular grooming action would be chosen. Dirty wings would impair flight. Dirt would impair the highly sensitive tasting organs in the feet, which flies use to decide whether or not to stick out the tongue and eat. So cleaning is important. But presumably the decision about which bit to clean is not determined by the sudden arrival of a new piece of dirt. Rather, we suspected that these rapid, moment-to-moment decisions were internally generated by unseen fluctuations deep inside the nervous system.
We recognized eight distinct grooming acts, which we presumed would show up as FAPs if we had the time to do a frame-by-frame analysis like the one we did with the chicks drinking: FR (rub front feet together), TG (rub tongue between front feet), HD (wipe head with front feet), FM (rub one or other middle foot between front feet), BM (rub one or other middle foot between back feet), BF (rub back feet together), AB (wipe abdomen with back feet), WG (wipe wings with back feet). Using a Dawkins Organ, we recorded the sequences of these eight grooming acts, plus MV (move away) and NO (stand still, doing nothing).
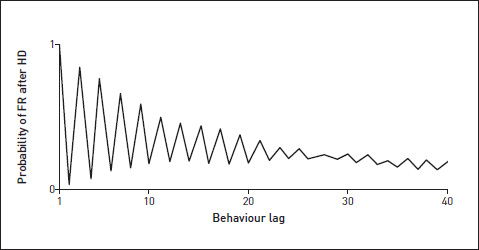
The graph shows the probability, given that the fly is now doing HD, that it will do FR next (‘lag’ = 1, probability very high), next but one (very low probability), next but two (high probability), next but three (low probability) etc. You can see that there is a pronounced tendency to alternate, and also that there is a general die-away (as you’d expect) in predictability as we look to the more distant future – longer and longer ‘lags’.
That picture was for the particular case of FR following HD. We plotted the same kind of graph for all the possible transitions, and put the graphs into a table.
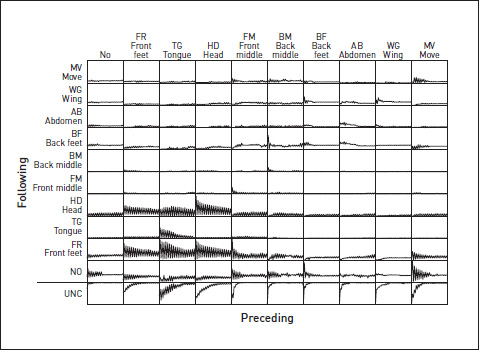
You can see that many of the transitions follow the same zig-zag pattern, although some are exactly out of phase with each other. The bottom row (UNC) shows the uncertainty attached to predictions of the future, following each behaviour, calculated using the Shannon Information Index, in the same way as for the chick drinking study.
We also tried the experiment of using the human ear to identify patterns in animal behaviour. For this, we used a Dawkins Organ rendition of fly grooming behaviour, but eliminated the true intervals between musical notes. I told the computer to reduce all the intervals to a single standard short interval and then we simply listened to the ‘music’. It sounded rather like ‘modern’ (as opposed to ‘traditional’) jazz. Also rather like the ‘singing’ Elliott computer of my juvenile insomniac dalliance – I suppose the comparison might be interesting. I thought the human ear might be a promising piece of apparatus to use in detecting patterns in animal behaviour, but didn’t follow up the method; I merely report it here as an interesting curiosity. If the World Wide Web had existed in those days, I would surely have uploaded the fly washing music and you could now dance to it. As things are, I’m afraid those Dipteran Melodies are gone for ever, like the Lost Chord.
I cannot claim that our fly study, or the other studies of decision-making that preceded it, really tell us much about how animal brains work. I see them more as explorations of methods: not just methods of doing research on animal behaviour, but methods of thinking. Marian and I did a lot more work on the flies, but it’s all published and I won’t write any more about it here. It did, however, feed into my next big writing project: a long theoretical paper on ‘Hierarchical organisation as a candidate principle for ethology’. This is the subject of a later section.
Meanwhile, in 1973, Niko Tinbergen won the Nobel Prize in Physiology or Medicine (jointly with Konrad Lorenz, his co-founder of ethology, and Karl von Frisch, the discoverer of the legendary bee dance). Just one year later, in 1974, Niko reached Oxford’s mandatory retirement age of sixty-seven, and the university agreed to appoint a successor as Reader in Animal Behaviour. ‘Reader’ was a rather prestigious rank at Oxford, now, I think, fallen into desuetude in a move to bring the title of ‘professor’ into line with American custom by sprinkling it about more liberally – the rather unkindly dubbed ‘Mickey Mouse professors’. I was very content where I was as lecturer, and had no ambition to apply for the job.
Most people thought of Mike Cullen as Niko’s natural successor. Perhaps for that very reason, in order to make a clean break, the majority of the appointment committee went for David McFarland. As Hans Kruuk wrote in his biography of Tinbergen, ‘one could hardly have found anyone more unlike Niko’. Though controversial in many quarters, David’s appointment was in some ways an inspired one, at least if you take the view that a new appointment is an opportunity for a new departure. His science was highly theoretical, indeed mathematical. He brought to it the intuitions of a mathematician, and he surrounded himself with trained mathematicians and engineers who could do the algebra. The talk in the coffee room switched from gulls and sticklebacks in the field to feedback control systems and computer simulations.
Perhaps it was a microcosm of the way biology was changing. I was young and not yet set in my ways. ‘If you can’t beat them, join them’ was my attitude. So I set to work to learn control theory from the engineers and mathematicians who now surrounded me. And what better way to learn it than hands-on? I again indulged my passion – or vice – for computer programming, and wrote a program for a digital computer (‘my’ PDP-8), enabling it to behave like an analogue computer. To this end, I invented yet another computer language, which I called SysGen.
Unlike the propositions in a conventional computer language like Fortran, which are executed sequentially, SysGen statements were executed ‘simultaneously’ – not really simultaneously, of course, because a digital computer does everything sequentially at bottom; but they could be written in any order. My task in writing the SysGen Interpreter program was to persuade the digital computer to behave as if the operations were simultaneous: a virtual analogue computer. As with an analogue computer, results were displayed as a set of graphs on an oscilloscope screen.
I’m not sure how useful SysGen was in practice, but inventing the language, and writing the Interpreter program for it, certainly helped me to understand not just control theory but also the integral calculus. It gave me a much better idea of what it means to integrate. I was mindful of my maternal grandfather’s recommendation of Calculus Made Easy, by his old mentor Silvanus Thompson (who, as quoted earlier, was fond of saying, ‘What one fool can do, another can’). Thompson introduces his explanation of integration with another phrase that has stuck in my brain: ‘So we had best lose no time in learning how to integrate.’ I had only half understood integration in Ernie Dow’s lessons, and SysGen gave me the sort of hands-on experience that assists comprehension.
Similar in intention, but much easier and less time-consuming, was my attempt to understand Chomsky-style linguistics by the hands-on method. I wrote a computer program to generate random sentences, which might not have been very meaningful but were always scrupulously grammatical. This is easy – and that very fact is instructive – given that your programming language allows procedures (subroutines) to call themselves recursively. This was true of Algol-60, the programming language that I favoured at the time under the influence of Roger Abbott, who had brilliantly succeeded in writing an Algol compiler for the PDP-8. Algol subroutines could call themselves, unlike the contemporary version of that old workhorse of scientific programmers, IBM’s Fortran language. Mention of Fortran reminds me of a nice in-joke told by Terry Winograd, pioneer of artificial intelligence. Some time in the 1970s I attended a fascinating conference in Cambridge on the state of the art of artificial intelligence programming, and Winograd was the star lecturer. At one point he gave vent to a wonderful piece of sarcasm: ‘Now, you may be one of those who says, “Fortran was good enough for my grandfather, it’s good enough for me.”‘
Given that your programming language allows procedures to call themselves recursively, writing programs to deliver correct grammar is remarkably – elegantly – easy. I wrote a program that had procedures with names like NounPhrase, AdjectivalPhrase, PrepositionalClause, RelativeClause etc., all of which could call any other procedure, including themselves, and it generated random sentences like this one:
(The adjective noun (of the adjective noun (which adverbly adverbly verbed (in noun (of the noun (which verbed))))) adverbly verbed)
Parse it carefully (as I have done here using brackets, although the computer didn’t generate them but left them implicit) and you’ll see that it is grammatically correct although not exactly dripping with information. It makes syntactic but not semantic sense. The computer could easily inject semantics (if not sense) by replacing ‘noun’, ‘adjective’ etc. with particular, randomly chosen instances of nouns and adjectives. Thus you could inject a vocabulary from a chosen domain, such as pornography or ornithology. Or you could inject the vocabulary of francophoney metatwaddle – as Andrew Bulhak was later to do when he wrote his hilarious ‘Postmodernism Generator’, which I quoted in A Devil’s Chaplain:
If one examines capitalist theory, one is faced with a choice: either reject neotextual materialism or conclude that society has objective value. If dialectic desituationism holds, we have to choose between Habermasian discourse and the subtextual paradigm of context. It could be said that the subject is contextualised into a textual nationalism that includes truth as a reality. In a sense, the premise of the subtextual paradigm of context states that reality comes from the collective unconscious.
This randomly generated garbage makes about as much sense as many a journal devoted to the metatwaddle of ‘literary theory’, and Bulhak’s program is capable of generating a literally indefinite quantity of it.
Two more programming projects date from around this time in my life, both of which also, as it turned out, served to hone my skills for the future rather than deliver results of more immediately practical usefulness. The first of these was a program to translate from one computer language to another: specifically, from BASIC to Algol-60. It worked well for those two languages, and would have worked, with minor detailed changes, to translate from any computer language of that general algorithmic type to any other. My second project of this time was STRIDUL-8: a program to make the PDP-8 computer sing like a cricket.
I had been inspired to work on crickets by my Berkeley friend, the neurobiologist David Bentley; and my entomologically inclined graduate student Ted Burk (now a professor in Nebraska) was keen to do his doctoral thesis on them. David kindly sent me some eggs of the Pacific field cricket Teleogryllus oceanicus. They hatched in Oxford and soon we had a thriving colony, which Ted looked after, feeding them on lettuce. While Ted productively pursued his own research on the crickets’ behaviour, I conceived a parallel project using computer-generated courtship song. That research project was never completed, but I did complete the writing of STRIDUL-8, and it worked pretty well.
My testing apparatus was a seesaw, made out of balsa wood so it was very light – as it had to be for crickets. It was really just a long balsa-wood passage, closed with netting at each end and over its top, and resting on a hinged fulcrum in the middle. Only one cricket was placed in the passage at a time, and it was free to walk from one end to the other as often as it liked. Whichever end it approached tipped down, as a seesaw should, and this fact was recorded by a micro-switch, which importantly also reversed the location of the sound. There were two little loudspeakers, one at each end of the seesaw. Cricket song was played through whichever of the two loudspeakers was at the opposite end of the seesaw from the cricket. So, imagine you are a female cricket, sitting somewhere towards the west end of the corridor. Song is playing from the east. You like what you hear, so you start to walk east. When you near the east end, your weight tilts the seesaw to the east, tripping the micro-switch and thereby informing the computer, which now switches the song to the west end loudspeaker. So you turn and walk west, and the whole process happens in reverse. Preferred songs therefore generate a large number of seesaw reversals and these were automatically counted by the computer. Whether the cricket thought she was pursuing an ever-receding coy male, or whether she thought the male was jumping capriciously over her head, or whether she thought at all, is impossible to say. Unpreferred songs would generate only a small number of rockings of the seesaw. Indeed, if a song was positively aversive, the cricket would stay at the opposite end of the passage and not generate any seesaw tips at all.
That, then, was my apparatus for measuring how much crickets like songs of different types. Play Song A for five minutes of the alternating seesawing regime, then do the same with Song B, and so on for many trials, properly randomized etc. Count seesaw tippings as a measure of how much the cricket liked each song. The point about computer-generated songs, as opposed to real ones, was to try to dissect out, in classic Tinbergen fashion, what it is about their own species song that crickets like. The computer would vary how it sang, in systematic ways. The initial plan was to start with a simulation of the species’ natural song and then change it – drop bits out, enhance other bits, vary the interval between chirps and so on. Later – it was a somewhat wild hope – I envisaged the computer being programmed instead to start with random song and ‘learn’ – or we could equivalently say ‘evolve’ – choosing ‘mutations’ step by step, until it progressively homed in on a synthetic preferred song. If the preferred song had turned out to be the natural song of Teleogryllus oceanicus, wouldn’t that have been sensational? And then if I had done the same thing with Teleogryllus commodus and the computer had homed in on its rather different song. What bliss that would have been for the researcher!
In programming the computer to sing, I wanted to make it as versatile as possible. Versatility is what computers are good at. As with the analogue computer simulation, as with the language translation program, I wanted to program the general case. And this is where STRIDUL-8 came in: its language allowed you to specify any combination of pulses and intervals, and therefore any cricket song in the world. STRIDUL-8 had an intuitively reasonable bracket notation, which enabled the user to insert repeats, and repeats embedded within repeats, in a manner reminiscent of the grammar of language.
STRIDUL-8 worked well. Its simulations of cricket song sounded like real crickets to human ears, and it was easy to program the computer to sing like any cricket species in the world. However, when I demonstrated the system to Dr Henry Bennet-Clark, world authority on the acoustics of insect sounds, newly arrived from Edinburgh to take up a position in Oxford, he made a face and said ‘Eeugh!’ STRIDUL-8 could only specify the pattern in time of pulses of sound, each pulse corresponding to one stroke of the wings against each other. I had made no attempt to simulate the actual wave form produced by each wing stroke, and this is what Henry objected to. He was right. STRIDUL-8, as it stood, could not have done justice to the European tree crickets of whose song Henry once wrote that if moonlight could be heard that is how it would sound. Temporarily discouraged, I put my whole cricket song project on the back burner, while I attended to other pressing tasks, notably a challenging invitation from Cambridge. And unfortunately I never returned to it: my cricketing days were over. I’ve often regretted it. I think most scientists have sad loose ends, projects started, never finished. If I ever had vague intentions to return to the crickets, they were thwarted by Moore’s Law: computers change so rapidly that if you leave a loose end of research untied for as long as I left mine, you find that the extant computers have all become newer, sexier models, and they have forgotten how to run your earlier programs. To find a computer that would run STRIDUL-8 today I’d have to go to a museum.