Data Handling using a Spreadsheet
Chapter 10 covered data analysis by manual methods to show the principles behind some common calculations. In practice, researchers do not have to carry out time-consuming manual procedures as computers can produce the answer almost instantaneously, using a spreadsheet. Spreadsheets were developed to simulate the worksheets that were used in accountancy and finance but they quickly began to be used for many other purposes. They are now generally packaged as part of the suite of tools in desktop office products, such as Excel with Microsoft Office, Calc with LibreOffice and Numbers with Apple iWork and are widely available forms of software.
A spreadsheet is a piece of software that stores information in rows and columns in a grid. The point where a row and a column intersect is known as a cell. Each cell is specified by a reference such as A2, M31, T45 or W108. The letter or letters refer to the column and move left to right across the spreadsheet in alphabetical order. The number refers to the row, counting from top to bottom. Cell references are important because they may need to be specified in a formula.
Spreadsheets are created by a user from a very basic template. This makes them a very flexible tool for a researcher. It is not necessary to be an IT expert or highly numerate to use a modern spreadsheet, as providers have now made a range of options available simply by clicking an icon on the screen.
As with all IT, the only way to gain the basic skills and confidence to use spreadsheets successfully is hands-on familiarity. Spend some time investigating what they can do. Some people approach this by entering data and mastering one function at a time, moving onto another as confidence develops. Others set themselves a definite task and work out how to perform it, whilst another group might opt to follow tutorial exercises from a book or attend lessons. Whichever method is preferred, the initial skills to develop are entering data, formatting cells, sorting entries into order based on different attributes and performing straightforward calculations. Many people who become confident with the basics find that their skills continue to grow and become more advanced than they might have envisaged.
Spreadsheets allow many tasks to be carried out by more than one method. It is only necessary to know one, so choose whatever seems the easiest, whether it is using a menu or clicking on an icon.
Learning how to use a spreadsheet needs to take place very early in the research and well before any deadline is looming. Quality insights are unlikely to follow if a user is struggling with the software, and understanding from the outset what a spreadsheet can do may assist with decisions about what to record and how. If data from the investigation is used in the learning process, make sure that there is another copy to revert to. Even experienced users can make mistakes and accidentally delete something or not be able to work out how to undo an action.
Benefits of Spreadsheets in Historical Research
• They are much quicker than manual methods for sorting, analysing and calculating.
• They are very flexible and allow a researcher to set up something bespoke for a project.
• They can store much more data than a researcher is likely to have to record.
• They store data very compactly in comparison with manual records.
• A mistake can be corrected without spoiling the appearance of the worksheet.
• They eliminate the rechecking that is necessary with manual processing.
• They can instantly perform calculations involving a large number of items.
• They allow data to be quickly sorted and analysed in a variety of ways.
• They allow variables within the data to be compared easily.
• Results can be produced as graphs which can help with interpretation and presentation.
• More fields and records can be added at any time so it is possible to extend an investigation.
• They can search on multiple fields which allows sub-sets of data to be investigated.
Drawbacks with Spreadsheets for Historical Research
Many of the drawbacks with spreadsheets would also be issues with a manual approach.
• It may not be easy to change the layout once the project is under way.
• Data can be entered inaccurately.
• If they are given an incorrect instruction they will produce the wrong result.
• It can be tempting to collect data for its own sake or perform unnecessary analyses.
• It may not be possible to see all of the information on the computer screen.
• Print outs can require several sheets, or be too small to read.
• It is possible to lose data, so good back-up routines are essential.
Developing a Spreadsheet to Analyse
Data cannot be analysed until it has been input, so the first task to work on is configuring the grid of rows and columns into something suitable. Normally a spreadsheet will be set up so that that each row represents an item in the study and each column records information about the individual attributes that are being investigated. These attributes are usually known as fields.
• Begin by deciding which attribute is being recorded in each column and on the top line of the spreadsheet give the columns an appropriate heading. Use bold type for the heading so that it stands out.
• Think about how wide each column needs to be and set them to the required size. Fields that are going to contain writing will need to be wider than those that contain figures or a code. Try to strike a balance between not having the fields cramped up together and not having too many fields flowing off the screen. The width of any column can be adjusted at any time without causing problems so it does not matter if the first attempt is not perfect.
• Text that is too long for its field can cause a problem. Decide whether this should roll onto another line (known as wrapping) or whether it should be shrunk so that it fits in the field. When text is wrapped it automatically increases the height of its row. Text that is greatly reduced in size may not be legible.
• Consider the format in each column. The spreadsheet should have an option for setting a date format, a number format and a currency format so that all items in the column are automatically displayed in this way. When using numbers, decide how many decimal places are needed and select this. When using currency select £0.00 rather that £0, as any calculations performed on this data could end in pence even if all the data is in £s.
• Consider the alignment of data in each column. It is conventional for writing to be aligned to the left and numbers to the right. Centre alignment can sometimes be useful because it helps to give visual separation between fields.
• Make sure that the font is clear and easy to read. Fonts without embellishments are often the best ones to use.
Entering Data into a Spreadsheet
This is a straightforward process. Highlight the cell where the data is to be entered, move the cursor to the input line at the top of the spreadsheet and type in the data. Then press the enter key. The data will appear in the specified cell.
A quicker method is to highlight the cell where the data is to be entered and type it in. Then press the enter key.
Spreadsheets often try to predict the next word as it is being typed. If a word has already been used, the spreadsheet may offer it based on the first couple of letters. If it is correct, press the enter key and the whole entry will appear. Prediction is a useful feature if the same word is being repeated, such as the month, as it reduces repetitive typing. If the word being offered is wrong ignore it and keep typing. It will disappear as soon as the software realises that what is being entered does not match its suggestion.
When entering data do not use any cosmetic effects to make the spreadsheet look pleasing. There are times when it is helpful to make an entry stand out for a purpose connected with the research by making it bold, underlined, italic or a different colour. It is not sensible to have information that has been highlighted for research purposes fighting with special effects.
Analysing a Spreadsheet
When all the data has been entered, ensure that there are no empty fields and that the content of each cell seems reasonable. It is easy to key in a double figure or to miss a digit out and a visual check should highlight this. When the data has been reviewed and amended, if necessary, save the spreadsheet twice, using different names. Keep one file as a back up in case a problem occurs and do not use it for any other purpose. All analysis should be carried out using the other file. It is never worth the risk of not having a back up of data that is being analysed. If more than one analysis is being performed, it may be appropriate to take a back up after each.
The data on a spreadsheet is analysed by giving instructions to perform a process using the data in one or more cells and perhaps to display the result in another cell of the user’s choice. As there are plenty of tools on a spreadsheet there is often more than one way of arriving at the same answer. Some users are very confident about constructing complex formulas or using templates, known as wizards, to get to the result in one step. Others are not. Not being ultraconfident with advanced features is no reason to avoid using a spreadsheet. The objective of a historical investigation is to answer a question about the past, not to use a sophisticated method to produce figures. Perform a calculation in several steps if necessary. It is better than making a mistake in setting up the formula and will still be much faster than using a manual method.
Arithmetic Functions
Any formula that is used in a historical investigation will probably use one or more of the four arithmetic functions. These are addition, (+) subtraction, (-) multiplication (*) and division (/).
In an arithmetic formula, one action may need to be performed before another. In this case the first action should be placed in brackets ( ).
Constructing a Formula
A user who understands the four arithmetical processes should be able to construct the formulas needed to perform calculations. It is just a matter of thinking logically and applying the process that would be used in a manual calculation. It does not matter whether letters are entered in upper or lower case.
A4 =A1+A2+A3 means add the contents of Cell A1, Cell A2 and Cell A3 and display the answer in Cell A4
A4=A1:A3 means add the contents of Cell A1, Cell A2 and Cell A3 and display the answer in Cell A4
C5=A5-B5 means subtract the contents of Cell B5 from Cell A5 and display the answer in Cell C5
D6 = D5*3 means multiply the contents of Cell D5 by 3 and display the answer in Cell D6
E8 = A4/B7 means divide the contents of Cell A4 by the contents of Cell B7 and display the answer in Cell E8
When calculations are being performed, specify the format that is needed in the answer cell. Answers may be displayed to many decimal points unless the spreadsheet has been told to round the answer to the nearest whole number, or restrict it to the first one or two decimal places.
If the symbol ###### appears as the result of a calculation it usually means that the cell is too small to display the answer. Widen the column and the answer should appear.
Sometimes, an error message appears instead of an answer. This usually means that the specified calculation is impossible to perform. When this happens the spreadsheet often highlights what has been entered which is very helpful for spotting the error and correcting the formula.
Summation
Spreadsheets sometimes try to help a user by anticipating what they are trying to calculate. The Greek letter Σ (sigma) is used in statistics to mean the sum of. If there are a number of cells to be added, placing the cursor in the box where the answer is required and then clicking the Σ icon at the top of the spreadsheet will produce the answer without the need to enter a formula. This is helpful, but not foolproof. If there is data running vertically and horizontally the spreadsheet will have to guess which total is needed and may opt for the wrong one.
When using the Σ function, check that the right range of figures has been used. The spreadsheet normally highlights the cells making it easy to see. If it has picked up the wrong range, change the formula that will be displayed in the input box.
Calculating the Mean Average
Place the cursor in an empty cell, enter the = sign followed the cell references of the items to be totalled in brackets. Count the number of items to be totalled and divide by that number.
Example
=(B2+B3+B4+B5+B6+B7+B8+B9+B10)/9
or =(B2:B10)/9
Calculations often start at Row 2 because Row 1 is used for column headings.
Finding the Median Average
Use the sort into ascending (or descending) order icon at the top of the spreadsheet to put the data being averaged into order. The sort icon is usually an arrow pointing either up or down.
When data is being sorted it is important to keep everything about an item together. The spreadsheet will normally ask whether to sort just the highlighted column or all columns before it carries out the instruction.
When the data is in order, determine the middle point and count to this. If there is an even number of values, it will be necessary to find the mean average of the two central ones unless they are the same number.
Finding the Mode Average and Frequency Information
Using the sort that has been performed for the median average, count how many times each value occurs. The value that occurs most often is the mode average. It is usually possible to spot which are the largest categories so it may not be necessary to count every one, unless frequency is also being ascertained.
There are plenty of ways to record results, either on the spreadsheet itself or somewhere separate. It is surprising how quickly detail is forgotten, so never list results without adequate explanation such as total, mean average, or percentage of successful claims. This simple task will save time later trying to remember what a figure means and how it was calculated.
Graphs
The graph or chart function on a spreadsheet is worth mastering at an early stage. From the perspective of an investigation it is a useful tool for understanding some relationships between data. It is also a simple way of presenting findings. The graphs that are produced by the spreadsheet can be printed out or exported into other documents, which can save the researcher time and effort. Always remember when creating a graph that the important aspect is the information it conveys, not fancy effects or gimmicks which can be distracting.
Column
A column chart shows information in a vertical columnar format. It can be a way of ascertaining the mode average as this can be read off the vertical axis if the chart represents a frequency.
In addition to presentation, column charts can be very useful for studying the properties of a sample because it is sometimes possible to see whether the sample, and therefore its mean and median averages, are being affected by an extreme value. If the frequency has an obvious central peak, the data being investigated is balanced. If the peak is towards one edge it is being affected at one extreme. When using advanced statistical techniques it is necessary to know whether data is balanced or skewed.
A Column Chart.
Bar
A bar chart shows the same information as a column chart but horizontally rather than vertically.
Line
Line charts represent information by a continuous line rather than in blocks. They are particularly useful when presenting data over a period of time.
A Line Chart.
A pie chart shows frequency information as percentages of a circle. It is a very simple method of showing proportions and is a method of presentation that is readily understood by most people. It can be very helpful for conveying frequency information to people who are not confident about interpreting tables, or for presenting some headline points succinctly.
A Pie Chart.
Pie charts have limitations. It is not possible to read any figures from them. Nor are they very useful with a large number of items of very low frequencies because it is hard for the eye to see what is happening. If there are a number of these items it is usually worth combining them as ‘other’ for the purposes of clear presentation.
Scatter Charts
Scatter diagrams show the relationship between two sets of data, through a number of dots. If the dots are scattered randomly there is no relationship between the two items, but if they tend to form a line then a link is likely to exist. This is known as correlation. The points do not have to be in a perfectly straight line for a relationship between them to be identified.
Extending the frequency example on page 102 about the money spent by ten customers in a hostelry, the number of people in each customer’s party was inferred from the number of items on each bill.
Amount |
Number in Party |
£1 |
1 |
£1 |
2 |
£1 |
1 |
£2 |
2 |
£2 |
3 |
£3 |
4 |
£5 |
5 |
£5 |
6 |
£7 |
6 |
£8 |
7 |
This can be represented on a scatter chart as follows
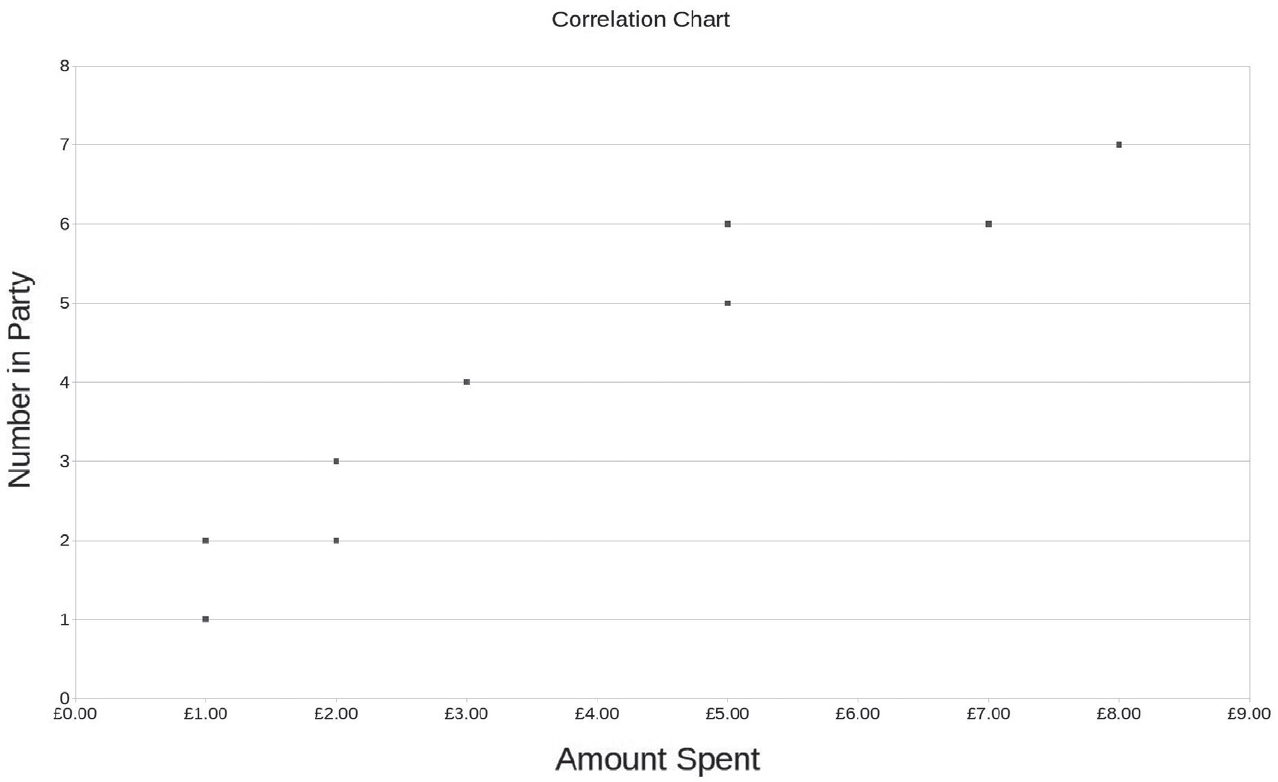
A Correlation Chart.
The points are not in a perfectly straight line, but it is clear there is a strong link between the amount spent and the number of people in each group.
As the link between number in party and size of bill is strong, there would be little to be gained from trying to answer one of the initial questions about the data sample, why no-one spent £4 or £6.
Sometimes correlation arises not from the two sets of data being tested but from some other factor that links them.
Example
A seaside music hall notices that when its matinee performance is sold out, its café sells many cups of tea but very few glasses of lemonade. Direct correlation exists between sales of tickets and hot drinks because both go up at the same time. Inverse correlation exists between between sales of tickets and cold drinks because as one rises the other falls.
Both relationships are caused by a factor that is not being studied, the weather. On a cool, wet day holidaymakers tend to visit the theatre and drink warm beverages. On a warm one they enjoy the sunshine rather than sitting indoors.
Scatter charts must always be interpreted with intelligence because there are situations when correlation exists between two variables but there is no causal link that can be found to explain it.
Example
Correlation between men with the forename Henry and a guilty verdict at the Assize Court would not indicate that men named Henry are likely to have criminal tendencies.
Correlation between men with the surname Henry and a guilty verdict at the Assize Court may indicate that there was a criminal family in the area.
Scatter diagrams are an extremely versatile tool for historical investigation as they enable a dataset with several variables to be tested pair by pair. The results should highlight relationships where further research may prove beneficial and the lines of investigation that are not worth pursuing. Once correlation between two variables has been established, this is only relevant if the researcher can explain what it means in the context of the subject being studied. Correlation is a tool, it is not an answer or a reason. Far from being the outcome of an investigation, finding a link between two variables may be just the beginning.
After an Investigation
It is perfectly acceptable to extend a study by adding more items into a spreadsheet after it has been analysed but always keep a separate copy of the data that was studied. Someone may challenge the findings or they may need to be reviewed in light of further work. If it is not possible to identify the exact information that was used, conclusions may lack credibility and the researcher may find it difficult to understand any differences between the original sample and the expanded one. Keeping a copy of important data on a memory stick prevents data loss if the computer develops a fault.
If expanding an investigation involves inserting more columns or rows into a worksheet after it has been analysed, check that a formula is properly specifying what is needed before relying on any updated answer. Often a formula adjusts automatically to take account of changes but this cannot be guaranteed.
Advanced Statistical Techniques
Modern spreadsheets have routines that guide users to calculate statistical measures. They also have an extensive help function. This guides users to a method for practically any analysis they may wish to perform, so it is not necessary to remember every formula. Carrying out any calculation is far less relevant than being able to select appropriate investigations and interpret the results. There is no merit in obtaining a wealth of statistical information if it does not give any additional insight into the topic, or if the researcher is unable to to see what that insight is.
It is not necessary to be an IT expert to use a spreadsheet in a historical investigation. Confidence with just a few simple techniques can reduce the time needed to calculate and then recheck answers. This means that there is more time to understand and interpret the results.
Spreadsheets can store large amounts of data and process it quickly, which makes it feasible for a researcher to work with a larger sample than when manual methods are being used, or to compare more variables. This can quickly highlight the areas where new insights into the subject might be discovered and help to avoid pursuing ideas that are unlikely to lead to a better understanding of the past. It might also enable a researcher to include sufficient items to make the results of a study generalisable to the total population.
