9. The Self-Confident Major and the Emotional Minor
Mood and music
There are a number of ways in which composers of symphonies, pop songs and car rental jingles can establish or change the mood of a piece of music. Some of these mood effects rely on the animal responses of human beings and some depend on a shared musical culture between the composer and the listener.
For example, when listening to music, we often find an increase in volume exciting. This excitement can prompt the usual physical reactions of increased heart rate and adrenaline production. This is because our subconscious links an increase in sound volume (people shouting, lions roaring) with possible danger.
On the other hand, we associate slow violins accompanying a piano with romance. We do this simply because we have been taught to do so from film music and TV perfume commercials. In turn, we have taught our composers that they need to include some violins and piano stuff if they want us to start getting out the handkerchiefs. In this case there is no real reason for the link other than the assortment of cultural clichés that we are all familiar with—banjos mean hillbillies and accordions mean Paris.
When all is said and done, music is a form of entertainment, so it doesn’t matter if our emotional response is “real” (adrenaline) or “learned” (clichés). We enjoy getting the Kleenex out when Pretty Woman kisses Richard Gere, and we like leaning into the curve when the Millennium Falcon turns to attack the Death Star. Music helps to complete the experience.
Even in the era of silent films there was a mood music industry. Pianists or small orchestras were hired to accompany the action with appropriate music. Sometimes the film came with specially written music, or a list of suggestions of suitable classical pieces. In many cases, however, it was left up to the pianist to improvise while watching the film. You could also buy books full of pieces specifically written to match the moods of any film. These had great names like “Dramatic Tension No. 44” or “Hurry No. 2 (duels, fights),” and my favorites: “Crafty Spy,” “Alluring Tambourine” and “Pathetic Love Theme No. 6.” I’ve been involved in a few pathetic love scenes myself—and I could have done with some background music.
Whether it accompanies film or not, the following links between mood and music are fairly reliable:
- We find increases in speed (tempo), volume and pitch exciting—and decreases in these three have a calming effect.
- Anticipation is a good mood enhancer, so if the music is quietly repetitive we expect something (frightening or marvelous) to happen soon and the anticipation helps the dramatic effect.
- Music composed in major keys sounds more self-confident and generally happier than music composed in minor keys.
This last point is very important to this chapter, and needs some clarification before we go on to discuss the method by which we build up the collections of notes which are the major and minor scales.
The major scale is made up of our old favorite, the pentatonic scale—with a couple of extra strongly related notes added to fill the gaps and take the total number up to seven. This may not seem a big jump in numbers but it makes a surprisingly large difference. When we perform music we play notes one after the other and/or in groups at the same time—and when we add a couple of extra notes into the mix we get a large increase in the number of combinations available. Think of it this way: if five of you are having lunch together and two of you have to go to the bar to get more drinks, there are ten possible combinations of two people who could go. If there were seven of you, there would be twenty-one combinations of two people. You’ve only added two people but you’ve more than doubled the possibilities. It’s the same with notes—the combinations available rise rapidly as you add more notes to the group.
The group of seven notes that make up a major scale (or key) are the most closely related group from the original choice of twelve. This makes them sound good and strong together, whether they are played one after the other as a melody, or simultaneously, to give us chords and harmony. As a result of all this solidarity, music played in a major key tends to sound complete and confident. One particular aspect of major keys is that they are very well suited to definite “periods” and “commas” at the end of phrases.
Minor keys involve substituting a couple of the major scale notes for less supportive members of the original gang of twelve—and the resulting music is generally more mysterious and vague, with less definite punctuation. Partly because the music sounds less self-satisfied, and partly because we have been trained to do so, we associate minor key music with sadness and complex emotions. One of the main reasons we link minor keys with sadness is the fact that the lyrics to songs in minor keys portray the whole gamut of human unhappiness, from “My baby done left me” to genuine tragedy, “My printer done run out of ink again.”
It’s surprising how early we begin to establish our minor key/sadness link. The other day, Herbie, the three-year-old son of a friend of mine, turned to his mother and said, “This is sad music… it’s about a cat who got left behind.” I have since inspected the sleeve notes of the CD in question and, although Rachmaninoff makes no overt references to disconsolate cats, my young friend does have a point. It will come as no surprise that the music (the first part of Rachmaninoff’s Second Symphony) is in a minor key.
This “major key happy/minor key sad” thing is not, of course, an absolute rule. Leonard Cohen, for example, is quite at home being sad and complex in either minor or major keys. And someone obviously forgot to tell Purcell that minor keys are sad before he wrote his triumphant, cheery “Round O” in D minor. It is also worth noting that in Indian traditional music, a scale very similar to our minor scale is associated with happiness and dancing. Generally, however, the existing tradition will ensure that most Western songwriters will continue to write sad songs in minor keys—and the link between sadness and minor keys will continue.
One of the best ways of recognizing the difference between major and minor keys is to listen to a piece which changes from one to the other. The first half of that famous short piece for piano by Beethoven called “Für Elise” is a good example. Like most classical pieces this can be played at a range of speeds because the composers generally give you only a rough indication of speed such as “slowly” (largo) or “walking pace” (andante). In this case we are instructed to play “with a little motion” (poco moto), which I think is almost entirely uninformative—but who am I to argue with a dead genius? If you listen to a version of this piece which lasts about four minutes, you will discover that it opens with a rather sad tune which begins with a pair of alternating notes (dee-dah, dee-dah, dee…). This part is in a minor key. This “dee-dah” tune repeats several times and, after about a minute and a half, there are four quick chords and the music changes into a much jollier mood for about fifteen seconds—this is the major key section. The music then returns to the “dee-dah” minor key theme, after which it goes off in a different direction, before finally rounding off with the dee-dah theme.
Another good example of a change from a minor key to a major one is the classical guitar piece “Adelita” by Francisco Tárrega. This piece is less than two minutes long and begins with a sad tune in a minor key, which is then repeated. After this there is a happier interlude in a major key before we finish off with a repeat of the sad, minor key tune.
Moving from one key to another during the course of a piece is called modulation, and this technique is commonly used to add interest to the music and alter its mood. Modulation from a major to a minor key (or vice versa) is a good method of mood manipulation, but music also commonly modulates between different major keys, or between different minor keys. I will discuss modulation in a bit more depth once we have established exactly what major and minor keys are.
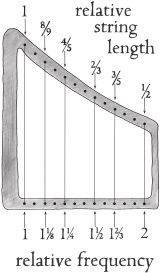
In the following discussion I’m going to be using drawings of the patented John Powell Ugly Harp to explain my points. This instrument gets its name from the fact that I invented it… and it’s ugly. “Why invent an ugly harp?” you might say…. Well, it’s not so much a musical instrument—it’s more a visual aid. I’ve assumed that all the strings are made of the same material and that they are all under the same amount of tension. This means that the length of any string is directly related to the pitch of the note it produces. For example, if one string is half as long as another it produces a note with twice the frequency. The harp also has a flat bottom—with the ends of the strings in a straight line so we can compare string lengths easily.
At the end of the previous chapter we had a scale of twelve equal steps from any note to the note an octave above it (the equally tempered, or “ET,” scale). This means that we need thirteen strings on our John Powell Ugly Harp to get a complete octave. (We have twelve different notes plus the top note, which is an octave higher version of the lowest note.) Because of the equal size of the steps between the strings we know that you can start your tune on any string and the same sequence of up and down jumps will give you exactly the same tune—the entire tune will just be higher or lower depending on what string you started on. But, as I said earlier, thirteen notes in an octave are too many for our memory to cope with, which is why we came to develop the major and minor scales.
A thirteen-string John Powell Ugly Harp which covers one octave in equal, semitone steps. The steps between the notes are chosen by the ET system.
Major scales
Choosing a family or team of notes for a major scale is similar to choosing a football team from a group of friends (in this case we are going to choose the best seven team members from our group of twelve different notes).
A simple definition of a major scale would be that you take one note* and choose the six notes which are most strongly related to it, to make a self-supporting team of seven. We know that the secret of good harmonies is to use notes with simple relationships between their frequencies so that the pressure ripples join together to make a regularly repeating, even pattern. We can achieve these simple relationships if the strings on our harp have lengths with simple fractional relationships such as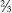 
or ¾. We have already seen that you can’t make a good scale system from these fractions but they do give us the best harmonies.
But our John Powell Ugly Harp is not tuned to simple fractional string lengths; it’s tuned using the ET system by taking a certain percentage off the length of each string. “Oh Woe!” you might say, “All is lost!” But do not despair—go and get yourself a calming cup of milky tea and I’ll tell you about a handy coincidence.
To create our thirteen-string harp to cover one octave using the ET system, we progressively reduced the length of each string by about 5.6 percent. Luckily this happens to give us a situation where a lot of the thirteen strings are almost exactly simple fractions of the length of the longest string. For example, if we call the longest string number 1, then string number 6 will be 74.9 percent as long as string number 1, which is very close to 75 percent—which is three quarters. The other strings also have lengths which are close approximations of simple fractions. These approximate fractions are so close to the real thing that the harmonies still sound good. For the rest of this chapter I will refer to the string lengths of our harp as fractions of the longest string length. Please remember that I do not mean the exact fraction—I am referring to its close approximation, which we arrived at using the ET system.
Fortunately, the ET choice of string lengths on our thirteen-string harp includes six strings which are a very good match for those used to produce a pentatonic scale—and the pentatonic scale is an obvious starting point if we are trying to create a seven-note scale of strongly related notes. So now we can draw our harp with just these notes and see what it looks like. In the illustration below I have labeled each string with its length and frequency as compared to the longest string so you can see that everything is as we want it—only simple fractions are involved.
The initial choice of notes for our major scale are the notes of the pentatonic scale. Their lengths and frequencies are shown as a fraction of the longest string.
The pentatonic harp in this illustration looks fairly useful, but both our ears and eyes tell us that there are two big gaps: one between strings 3 and 4 and another between strings 5 and 6. The obvious thing to do to increase the number of notes in our scale is to put one string in each of these gaps—but we have to choose between two possible strings in each case.
Let’s look first at the gap between strings 3 and 4. The strongest candidate with the best link with the rest of the group is the longer of the two—because it produces a note which is 1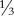
times the frequency of the longest string.
To fill the gap on the right-hand side we choose the shorter of the two possible strings. It gives a note which is 1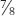
the frequency of the longest string—a good team member—and it also gives us an “almost there” feel to the final part of the rising scale, like this:
| String | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| (Home) | (Closest relative) | (Almost there) | (Home again) |
Once we add these two strings to our scale, our harp looks like this:
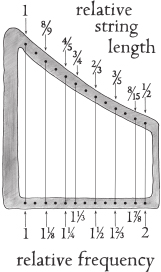
The complete major scale of notes chosen from the original thirteen strings. We have added two more team members to the original pentatonic set.
When the “almost there” note appears in the melody or the harmony it makes a fairly clear demand to get “there,” so the listener has a feeling that the next note should be the key note. In fact, this effect is so strong that the technical term for the “almost there” note is the leading note, because it leads us on to the key note. Whenever we hear the leading note we build up an expectation of returning home to the key note. This anticipation–resolution effect is used a lot in phrase endings, although sometimes the composer might deliberately frustrate our expectations to make life more interesting. The reason why the punctuation of phrases is vaguer in the case of pentatonic music is because there is no “almost there” note in a pentatonic scale.
I’m using the words “phrase” and “punctuation” here in exactly the same way we use the terms when we are discussing written language. Music has commas, periods, and paragraphs, and uses them in the same way as a storyteller does. The technical term for any phrase ending in music is a cadence.
You will notice that there are now only two sizes of gap (or interval) between adjacent notes on our eight-string harp: either the strings are next to each other and therefore a semitone apart; or they are separated by the gap and are therefore two semitones (one tone) apart. Starting from the lowest note in the octave and calling out the names of the intervals between the notes, we would say: Tone, Tone, Semitone, Tone, Tone, Tone, Semitone. Rather than continue writing out this stream of words, I will, from now on, use just the initial letters: TTSTTTS.
To create our major scale we have taken the strongest group of all, the pentatonic scale, and added two more members, one of which (the leading note) helps to strengthen the punctuation of the music. This addition of two members to our team has also given us a tremendous increase in the combinations of notes available for harmonies, without overstepping the barrier of having too many notes for our memories to cope with—a bargain all around, I think you will agree.
The only drawback to the use of major keys is that there is a continuous tendency toward definite, complete statements. Major key music sounds rather self-confident, and sometimes we want the music to be less cocky. In those situations we use minor keys as well.
Minor scales and keys
Although Western music generally restricts itself to major and minor keys nowadays, these two types were selected over time from a larger group of scale systems called modes, which used various combinations of tones and semitones to get from one end of an octave to the other. These modes date back centuries but can still be heard in folksongs such as “Scarborough Fair” and they are occasionally used to add a slightly exotic flavor to jazz, classical and pop music. I will discuss modes later in this chapter, but for the moment let’s concentrate on modern-day major and minor scales.
The TTSTTTS major scale is actually one of the original modes (it’s called the Ionian mode) and it would have been well known as being good for strong, well-organized harmonies because we are using the most closely related team. But strong, well-organized harmonies may be a bit too obvious if we are trying to write dreamy music. In this case we might change some of the team members and use TSTTTST or TSTTSTT, both of which are vaguer. If you write music using these scales the tunes don’t come to such an obvious “period” at the end of every “sentence.”
By about 1700 most Western composers and musicians had chosen their two favorite types of mode and had just about stopped using all the others which were available. As one of their favorites they naturally chose the strongest team of notes—TTSTTTS—and called it the “major” scale. The other favorite scale, which gave less definite periods, and was therefore suitable for dreamy or sad music, was called the “minor” scale.
But it’s not quite as simple as that. For any given major key we always have the same set of seven notes. The really odd thing about minor scales and keys is that we started off with one set of notes, then we altered it by one note. Then we altered it by one note again. “So what?” you might say, “There’s nothing odd about that, John—it’s called progress. Things develop and move on—get a grip.” If we had moved from the initial set of notes to the next version and then to the next, I would agree with you. But we didn’t do that. Somehow it turned out that, for the past couple of hundred years, we have been using all three types at once. And I don’t mean we use this one for this piece and that one for that piece. We use all three types of minor scale within a single piece of music. We use the original one if the tune is descending; one of the others if the tune is ascending; and the third one to make up the accompanying chords.
If music was controlled by scientists this sort of untidy non-sense would be forbidden. But music is organized by musicians, with their unkempt hair and faraway expressions. Musicians eventually settle on what sounds best—and they decided that minor keys are more emotionally effective if they change a couple of notes depending on whether the tune is rising or falling. This “deciding” process didn’t take place suddenly one night in the pub—it took centuries, as the other options were discarded one by one.
So let’s have a look at these different minor scales.
The natural minor scale
Like the major scale, the natural minor scale is one of the ancient modes. It’s called the Aeolian mode and you can read a little more about it later in this chapter. It has the pattern TSTTSTT, which means that, compared to the major scale, three of the strings on our harp have been moved down one position, to the next lowest note. As you can imagine, this substitution of three of the strongest team members weakens the team quite a bit. You can see the new arrangement in the illustration below and compare it to the major scale. Two of the original “pentatonic team” have been replaced and the “almost there” note is also no longer with us. The newcomers still make a very pretty noise, but the team lacks the oomph it had, particularly at the ends of phrases.
Still, the whole point of having these alternative sets of notes is to have a different flavor. We don’t actually want much oomph from our minor keys. When you’re singing songs about harvests failing, or your disappointing loft insulation, you don’t want every verse to end with a cheery full stop. Sometimes we need some good, solid ambiguity.
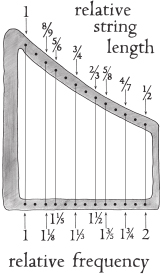
To create the minor scale, three of the notes (string numbers 3, 6 and 7 counting from the left) have been lowered by one semitone. This gives us a less cohesive group.
The natural minor scale can be used alone to improvise or compose pieces of music, but it is usually employed as one of the team of three scales used in most minor scale music.
This natural minor scale was found to be just right for the parts of melodies which were descending in pitch, so it is also called the descending melodic minor scale.
For tunes which were rising in pitch, composers found that they really missed that “almost there” feeling of the next-to-last note of the major scale—and also found that this note was very useful for harmonies. So they developed the ascending, or rising, melodic minor scale.
The ascending melodic minor scale
In the ascending melodic minor scale, two of our natural minor scale notes are reinstated back to their major scale positions. The next-to-last note is returned to its original “almost there” pitch and its neighbor follows it back up to prevent there being a big gap in the scale. You can see what has happened in the illustration below.
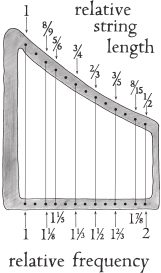
The ascending melodic minor scale. This has only one note different from the major scale (string number 3 has been lowered by one semitone).
So now we have the complete set of notes for melodies in a minor key. We use this scale for ascending parts of melodies and the natural minor scale for the descending parts.
But now, of course, we have a bit of a problem—because we need chords which will suit both the rising and falling parts of our tunes. For this reason a compromise scale was developed from which we can pick our harmony notes. Not surprisingly, it’s called the harmonic minor scale.
The harmonic minor scale
The harmonic minor scale is, as I just suggested, a compromise between the descending and ascending minor melodic scales. In this case we take the descending melodic, or natural, minor scale and return only the next-to-last note back to its major key “almost there” position (as you can see below).
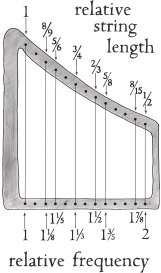
The harmonic minor scale: a compromise between the two melodic minor scales, used for chords and harmonies in minor key music.
So there we have minor keys. A weaker relationship between the various members of the team of notes results in a more complex musical experience. The music sounds less self-confident than music produced in major keys and generally we have come to associate this comparative vagueness with sadness or expressions of deep emotion.
Major and minor chords
The simplest chords consist of three notes taken from the musical scale. As I said earlier, we get harsh combinations if we choose notes which are next to each other, so most chords use alternate notes from the scale.
The most common chords include a basic note (which gives its name to the chord) and its most closely related team member—the one which has a frequency which is 1½ times that of the basic note. If we start with string 1 of a major scale then the 1½ times note is string 5. This is also true of a minor scale, because string 5 does not move when we change to a minor scale. (The fact that the 1½ times frequency note is the fifth one you come to in either scale is the reason why musicians say it is “a fifth” above the key note. The usual technical name for this second most important note in the scale is the dominant, because it dominates the tunes and harmony, along with its close relation, the key note, or tonic.)
The third note we choose for a simple chord needs to go between strings 1 and 5 but we shouldn’t choose strings 2 and 4 because they are right next to one of the others and they would clash with it. So we choose string 3. If we choose strings 1, 3 and 5 from a major scale, we get what is called a major chord and, if we choose the same strings from a minor scale, we get a minor chord.
So a major chord is a frequency we choose, plus 1¼ times that frequency plus 1½ times that frequency. In a minor chord we exchange the 1¼ for 1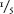
, which is less strongly linked to the other two notes.
As we know, every note involves a series of harmonics and in closely related notes some of the harmonics of one note will be the same frequency as certain harmonics of the other. For example, our old mate A2 has harmonic frequencies which are multiples of 110Hz, and its strongest team member, E3, has harmonic frequencies based on 165Hz. Two times 165 is 330, which is the same as three times 110. This means that the third harmonic of A is the same frequency as the second harmonic of E. There are many other matches of harmonic frequencies between these notes, and that’s why they sound good together. Using this type of matching we can show that the 1¼ frequency in the major chord is a more supportive match for the other two notes than 1, so the minor chord notes form a less self-confident-sounding team. Once again, as with all things to do with a minor key, we have come to associate this lack of self-confidence with sadness.
A chord is a combination of any three or more notes. The major and minor three-note chords we have just discussed are the simplest and most harmonious-sounding ones. Minor chords sound less confident than major chords, but they are stronger and more confident-sounding than a lot of the other chords we can get by putting three or more notes together. For example, by adding “clashing” notes to simple major and minor chords, we can produce chords which sound more colorful, interesting or tense. There are also lots of possible chords which don’t include the strong 1½, 1¼ or 1 team members. More complex chords like this help to add movement to the music because they do not sound relaxed or final. Our ears tell us that there must be more steps in the journey before we get to the end of the phrase. When we eventually get to the end of a phrase the music is likely to relax into a simple major or minor chord.
Naming notes and keys
At the end of chapter 1 , I mentioned the fact that notes have names which consist of one of the first seven letters of the alphabet and sometimes these letters are followed by the words “sharp” and “flat.” Back in chapter 1 I asked you simply to accept this system and not worry about it, but now it’s time to look into it properly because we can’t discuss our next subject—moving from key to key—without referring to the names of notes and keys.
The main reason we have names for notes is so that we can teach and discuss music. Although there has always been a tradition of passing on music by simply copying what someone is singing, this doesn’t work too well for complicated music if you want it to be replicated exactly.
The Western system of writing music and naming notes began with monks who wanted to record their masses and hymns. They needed to make everything easy to remember so they didn’t want to use all the letters of the alphabet as names for the notes—they chose to use only the letters A to G. Any two notes an octave apart were given the same letter because they are so closely related as far as our ears are concerned—although numbers and other techniques were used to identify which D or E you were talking about (D1, D2, D3, etc.).
So—seven letters to name all the notes in our major scale and the last note would have the same name as the first note but be written slightly differently, or numbered, like this for the scale of C:
C1, D1, E1, F1, G1, A1, B1, C2, D2, E2, F2, G2, A2, B2, C3, etc.
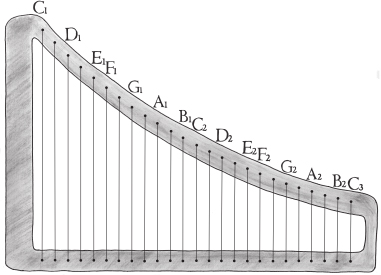
Well, this is all pretty clear so far. Let’s draw a two-octave John Powell Ugly Harp with the longest string as C, putting all of the twelve notes we discussed in chapter 8 into each octave.
A two-octave harp showing the notes of the C major scale (the longest string is a C).
This illustration introduces us to something which is rather odd and needs some explanation—we have used up all our letters but we haven’t named all the strings (this is a pretty obvious result if you remember that we only have seven letters but we have twelve different notes to the octave). For example, the string between C and D has no name in the illustration. What do we call such “in between” notes? Well, unfortunately, these notes each have two names. We can refer to them as being higher than the note below them by using the word “sharp,” or we can refer to them as being lower than the note above them by using the word “flat.” When musicians write these names they usually use the symbol “#” to indicate sharp and “
” to indicate flat. So “F sharp” is F# and “B flat” is B.
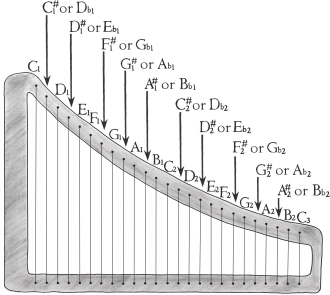
In the illustration on the next page I have labeled all the notes—giving the “in between” notes both their flat and sharp names.
A two-octave harp with all the notes named. Certain notes have both “sharp” and “flat” names.
If you have a spare minute you can pick any note and count up the strings (from long to short) with the TTSTTTS pattern to identify the notes in any major scale…. On the other hand, life is too short for this sort of shenanigan—and you didn’t buy this book as an activities kit—so I’ll do an example for all of us.
If we start the scale with A, we go up one Tone to B, up another Tone to C#, up a Semitone to D, etc., and the notes we get are the A major scale:
A—B—C#—D—E—F#—G#—A
And it’s as simple as that really: pick any of the twelve different notes as your key note or team leader—and the TTSTTTS system will identify who your team members are to give you the strongest, most closely related group—your major key.* (I have written out the notes for all the major keys in part E of the Fiddly Details section at the end of the book.)
You can, of course, do the same for a minor key using the appropriate “T, S” pattern: for example, the melodic minor rising scale is given by the pattern TSTTTTS, and if you start off on E you will get:
E—F#—G—A—B—C#—D#—E.
Of course, the sharp/flat notes are no different from the simple letter notes—they are all equally important—it’s just a naming system that has been passed down to us. One of the historic peculiarities about the system is that the only major scale which doesn’t include a sharp or flat note is C major. This makes the key of C major look important in some way—but it isn’t; it’s just the way the naming system evolved.
Changing from one key to another: modulation
It is clear from the last section that we have twelve major keys and, as I will explain later, they are all emotionally identical: one key will merely have the same pattern of notes moved up or down a bit in pitch. So let’s return to the question of why we have so many keys.
Composers and musicians are in a continual battle against boredom—not their own boredom, but the boredom of their listeners. They know very well that if they bore you their income will drop and their children will starve—or, at least, they won’t be able to go out for a burger on Wednesday. Music is a form of entertainment and so it has to stimulate the emotions—from jollity to fear (and if you think fear is a bit of an extreme claim for music, you haven’t seen the shower scene from Hitchcock’s film Psycho).
One of the ways a composer can keep up the interest level of his listeners is to change key—from one set of seven notes to another. If this happens, one or more of the notes is changed, and the listener can tell that the team leader of the group has also changed. This team analogy is particularly helpful here: imagine you are the manager of a team whose style of play becomes a bit stale during the first half of a game. At half-time you can put extra life into the team by exchanging a couple of players for substitutes and asking the team to vote in a new captain.
So now you have a slightly different team with a new team leader—which is exactly what happens if you change key in the middle of a piece of music. You might think that a non-musician would not be able to spot the change in team leader (or key note) but, in straightforward Western music such as pop, rock, folk, blues and most of the classical music written between 1700 and 1900, the key note is fairly easy to spot, even for an untrained listener. In more complicated music, such as modern classical or jazz, the team leader, and therefore the key of the music, may shift about every few seconds or may be deliberately hidden. In this case, the sense of a key becomes confused or lost.
When we are listening to a piece of straightforward music we identify the key note in two ways, although you probably won’t realize or notice that you are doing it. First, a song or any other piece of music is divided up into phrases and the key note will often be the final one of a phrase. If you play just about any pop song—even one you haven’t heard before—you will be able to hum the key note within a minute or so. Just pretend that the tune is ending and hum the note it should end on—that will almost certainly be the key note. Our old favorite “Baa Baa Black Sheep” does this: it hits the key note on the word “full” and the final word, “lane.”
The other clue which helps to identify the team leader is how often the various notes of the scale occur as the melody progresses—and here we come to an example of musicological fortitude above and beyond the call of duty. Brett Arden of Ohio State University spent many months checking thousands of melodies (more than 65,000 melody notes for the major keys and more than 25,000 for the minor keys) to find out exactly how often each of the notes in a scale occurs. For example, if we number the notes from 1 (the key note) to 7 (the “almost there” note), he found that, in major keys, note 5 occurs most frequently and will be played about four times as often as note 7, the least common member of the group. There are other relationships which hold true for most tunes. For example, in a major key, notes 1, 3 and 5 make up almost 60 percent of the head count of notes in a tune. Your brain recognizes these proportions and this helps us to tell which note the key is based upon. Obviously, you are not aware of your brain analyzing these relationships. You just pick up these clues subconsciously, as you do when you assess which of the guilty-looking eight-year-old ruffians in your garden just kicked the football through the kitchen window…
The most common type of modulation is to change from the key you are in to a key which contains only one different note.
For example, we could be playing away in the key of C major, which contains the following notes:
C, D, E, F, G, A, B.
And we could easily shift over to the key of G major:
G, A, B, C, D, E, F#,
which has the same notes, except the F has been changed for an F sharp.
If we do this, the music receives an emotional lift because one of the notes has been raised. We also get extra (subconscious) interest because the key has changed and we can sense the change of team leader—from C to G.
On the other hand, we could change from C major to F major, which contains all the same notes as C except for the fact that the B is taken down a semitone to B flat. In this case we often get the impression that the emotional intensity of the music has switched down a gear, although we still get the enhanced interest from the change in team leader.
This “up a gear” or “down a gear” effect has nothing to do with the actual properties of G major or F major—the different keys have no intrinsic emotional shading. It’s the process of change which gives us the emotional impact, and the effect fades off quite rapidly (within a few tens of seconds). Imagine yourself standing in a big hamster wheel—it has been stationary for a while and you’re bored, so you take a single step forward onto the next rung. Everything gets a lot more interesting for a little while, but soon the step you moved to becomes the one at the bottom of the wheel and it’s all boring and stationary again. Stepping backward onto the rung behind you has a slightly different effect—but it’s still transitory. The rungs are identical: it’s the changeovers which are interesting. If you want to keep life stimulating you are going to have to keep changing rungs.
Composers occasionally inject a surge of interest by shifting several rungs at once—to a key which has a lot of different notes in it—from C major to E major, for example. Ravel does this as a dramatic flourish near the end of his Boléro. But most often, keys change to a neighboring key (one with only one different note).
Modulating a repeated phrase to a key that is a semitone or a tone above the one you start in (shifting up from B major to C major, for example) never fails to brighten the music because it feels like a change in gear, which is why it has become known as the “truck driver’s gear change” or “truck driver’s modulation.” The technique also revels in the name “the cheese modulation” (“cheese” being the general name given to pop music which has passed its “best before” date).
This modulation is commonly used to give a sudden lift in energy to pop songs, particularly in cases where the chorus is repeated a lot. “I Just Called to Say I Love You” by Stevie Wonder uses this technique a couple of times, but the most notable example occurs when the title of the song is repeated, three and a half minutes into the track. Another very effective example of this type of modulation can be found in “Man in the Mirror” by Michael Jackson. In this case, the key change occurs (as Michael sings the appropriate word) two minutes and fifty seconds into the song.
If a modulation involves movement between two major keys or two minor keys, any change in mood will be short-lived, because the effect is linked to the action of changing—you are just changing rungs on the hamster wheel. If, however, you change from a major key to a minor one (or vice versa) the change in mood will remain in place. This is because, although the effect will be strongest just after the change, you have genuinely moved from one musical landscape to another—like jumping from a steel hamster wheel to one made of wood. Changing from a major key to a minor one will result in a more complex, emotional or sad mood and a move in the other direction will make the music sound more determined and self-assured.
If you change key very often (as some jazz and classical composers do), then the listener may become rather confused and the music will sound a little unstable. If, on the other hand, you don’t do this often enough (like some pop bands), the music can become very predictable and bland.
The same team of notes can sound minor or major if you change the team leader
If we consider the simplest version of a minor key, the natural minor, we can construct either a minor or a major key out of one set of seven different notes.
For example, the scale of C major is:
C—D—E—F—G—A—B—C
and the scale of A natural minor is:
A—B—C—D—E—F—G—A
This is the same group of notes except that, for the minor key, we have As at the top and bottom of the scale instead of Cs.
We can pull the same trick with pentatonic keys. The pentatonic major scale which starts on C is
C—D—E—G—A—C
This uses exactly the same group of notes as the pentatonic minor scale which starts on A:
A—C—D—E—G—A
Yes—I agree—this sounds bonkers. How can the same bunch of carefully chosen notes be either C major or A minor?
But it’s true—using the same set of notes, you can give a minor (sad, reflective, weak full stops) or a major (happy, positive, strong full stops) feel to the music simply by changing the team leader.
“Aha!” you say, “but if I’m hearing exactly the same notes, how do my ears know that the team leader has changed?” Well, as I said earlier, the team leader, the key note, is fairly easy to spot in straightforward music. It’s really all about emphasis—and we are all used to small changes in emphasis making a big difference to what we say. For example, the following two sentences have very different meanings because, although I have used all the same words in the same order, I have changed the emphasis by moving the comma, which makes one sentence insulting and the other congratulatory.
“I’m not a fool like you, I spend my money wisely.”
“I’m not a fool, like you I spend my money wisely.”
So if we take the notes of the key of C major (C, D, E, F, G, A, B) and use C, E, G as our favorites, particularly C at the end of phrases, we will hear the music as having a major key feel. If we use the same notes, but make A, C and E our favorites, particularly A at the end of phrases, then the music will have a minor feel. The “team” analogy comes in useful again here: if you took any soccer team and changed the roles of some of the players (by giving the goalkeeper the center forward’s job, etc.), then the team would perform with a different style even though the players were the same.
If you have access to a piano you can check this for yourself. Try making up simple tunes using one finger and playing only the white notes. If you end all your phrases on the note C, the music will sound fairly cheery and strong. If you stay on the white notes and end all your phrases on the note A, then the music will sound vaguer and sadder.
Choice of key
Composers need several keys, so they can, if they wish, hop from one to another during the course of a piece. But what makes them decide to start a piece in a particular major key if there is no mood difference between any of the major keys? And, similarly, why would they choose this minor key instead of that minor key?
Well, there are a number of reasons to choose a particular key to start your piece—but none of them have anything to do with emotional content. These reasons can be divided into five categories: instrument design; range; composer delusion; perfect pitch; and “first come first served.”
Instrument design
A lot of pop songs and most classical guitar pieces are written in the keys of C, G, D, A and E because these are the easiest keys to play on a guitar—the chords and tunes in these keys allow you to get the maximum reward for the minimum effort. For example, if you are a total beginner, I could teach you to play the chords to a simple pop song written in G major in about fifteen minutes, and you could accompany a singer with a fairly shabby version after about three hours’ practice. If we moved the key one semitone up—to A flat—or one semitone down—to F sharp—it would take you ten times as long to get even a shabby version together. This is because the finger positions for the chords are a lot more difficult as a result of the way guitars are tuned. Lots of other instruments are also easier to play in some keys than others, and the choice of key is driven not by musical considerations, but by ergonomics. For example, the sort of “big band” which accompanied singers like Frank Sinatra in the 1950s and 1960s involved trumpets, clarinets and trombones, which are easiest to play in the key of B flat, so a lot of those songs are in that key.
Range
Every instrument has a top note and a bottom note. You have to make sure that the piece you are writing fits on the instrument—and this could affect your choice of key. For example, the lowest note on a flute is middle C, so there won’t be much solo music written for the instrument in the key of B because it’s useful to have the key note close to the bottom of the instrument’s range.
Also, the key of a song may have to be raised or lowered to suit a particular singer’s voice.
Composer delusion
Many composers, like lots of other musicians, suffer from belief in a myth I will discuss later in this chapter, which suggests that certain keys have specific moods. So they write gloomy music in A and jolly music in A because they think that those are the most suitable keys.
Perfect pitch
If you are a composer with perfect pitch you will hear specific notes in your head every time you think up a tune. Whatever key it appears in will probably be the one you’ll use when you write it down.
First come first served
If, like most composers, you have not got perfect pitch and you quite often come across useful tunes when you are fooling around on a piano or some other instrument, you will probably stick with the notes in the key you first found them in, unless there is a good reason to change them. Some composers have favorite fooling-around keys. A famous example of this is the songwriter Irving Berlin (who wrote Bing Crosby’s hit “White Christmas” and “Let’s Face the Music and Dance”). By his own admission, Irving Berlin was a dreadful pianist, so he played and composed nearly everything in the key of F# major, a key which falls under the fingers very nicely (it uses all the black notes on a piano together with only two white notes). He couldn’t write music so he paid musicians to watch his fingers and write it all down, and later they would, if necessary, change the key to suit any instruments or singers involved.
Modes
Although our major and minor keys are a development from the ancient pentatonic scale, we have not yet discussed the story of how we got from one system to the other. It all began with the ancient Greeks, who developed a selection of different scales, all involving seven different notes in an octave, which they called modes. The history of modes is a subject of Byzantine complexity, which makes me glad I’m not a historian. Basically it goes like this:
Sometime before 300 B.C. the ancient Greeks used different scale systems of tones and semitones to divide the octave up, and named them after the peoples and territories of Greece and its neighbors. For example, the Lydian mode was named after the area called Lydia, which is now called Western Anatolia.
The Christian church developed a method of singing called Gregorian chant from about 750 onward, which used seven different scale patterns. The church gave these modes the names of the Greek modes without worrying about whether they were the same as the Greek ones. So we now have Christian modes with random Greek names.
The Holy Roman Emperor Charlemagne decided to improve the popularity of these Christian modes by threatening the clergy with death if they didn’t use them. The modes became very popular.
The modes were used successfully for several hundred years but some of them became less fashionable than others. Eventually, by about 1700, most music was using only two of the original seven—and these two became known as the major keys and the minor keys.
Today, modes are used less frequently than the major or minor keys but you will find them in folk music and some jazz, classical and pop music (when the composer wants the music to have a slightly unusual flavor). Just like the major keys, each mode consists of a set pattern of tones and semitones as you go up and down the scale.
So how do we pick our team of notes for modes? Surprisingly enough, all the modes use the same team as a major scale—but they don’t use it in the same way. This sounds a bit weird, but let’s go back to our old friend, the Ugly Harp. The next illustration is a two-octave harp showing the notes of the C major scale, and I will now demonstrate how all the modes can be played using the same notes as the C major scale.
We already know how to play the scale of C major on this harp—we just start with the longest string and pluck the C scale notes one after the other. But now we want to play a mode using the same notes. There are seven modes and they have the following names: Ionian, Dorian, Phrygian, Lydian, Mixolydian, Aeolian and Locrian. (Yes, they do all sound like heroines from Lord of the Rings—except for Mixolydian, who is obviously one of those elvish bowmen with the fancy helmets… but I digress…)
All these modes can be played on a harp tuned to a major scale like the one above. The major scale and all the modes use exactly the same team—the only difference between them is the choice of team captain.
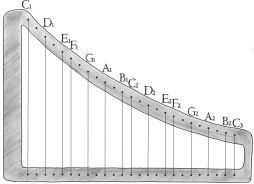
A two-octave harp showing only the notes of the C major scale (the longest string is a C).
We have seven different notes in our scale of C major (C, D, E, F, G, A, B), and seven modes. Each mode uses a different start note (team captain), so one of them must start on C—exactly as our C major scale does. The mode which does this is the Ionian, which is why we never hear of this mode; it’s the one we chose to be our modern major scale, so that’s what we call it. The other six modes use the following notes as their team captain if they are using the notes from a C major scale:
| Dorian mode | D |
| Phrygian | E |
| Lydian | F |
| Mixolydian | G |
| Aeolian | A |
| Locrian | B |
To play the Dorian mode scale on our harp, we would start and finish on the D strings so instead of the scale of C major, CDEFGABC, we would play DEFGABCD, and play tunes and harmonies which kept returning to D. To Western ears this sounds a little odd because, given that group of notes, our ears keep expecting tunes to end on C or G. However, once you get used to it, the Dorian mode makes a nice change.
The basic feel of the Dorian mode is similar to a minor key. This is not really surprising because the only difference between the Dorian mode played from D to D and our modern key of D minor (natural) is that the B is lowered to B in D minor—all the other notes are the same. The Dorian mode is used a lot in Celtic music and is also the basis for such songs as “Scarborough Fair” and The Beatles’ “Eleanor Rigby.”
As I said earlier, the major keys all have a TTSTTTS pattern of intervals as we rise through the scale. If we play a Dorian scale, we play from D to D and this gives us an interval pattern of TSTTTST. As long as you use this interval pattern you can start on any note you like (using an instrument with all the twelve different notes on it) and you will be playing a Dorian mode. You could, for example, start with an A and play the notes A, B, C, D, E, F#, G, A and that would also be a Dorian mode (just as you can start from any note to produce a major scale if you keep to the correct TTSTTTS interval pattern).
If two musicians get together to play a song written in a major key which they both know well, they won’t say “let’s play it in major” because that doesn’t tell them very much. They’ll say “let’s play it in G major” or “let’s play it in E major” and off they go. In the same way, if they wanted to play “Scarborough Fair” they can’t just say “let’s play it in Dorian”—they must identify which note the Dorian mode they are going to use begins with. They could say “Let’s play it in D Dorian” and use the notes D, E, F, G, A, B, C, D but they could just as easily say “let’s play it in G Dorian” (G, A, B, C, D, E, F, G) or “B Dorian.” Just like major keys, there are twelve different Dorian modes.
If you pick the notes from any major scale and make the second note of that scale the team leader, then you are playing in the Dorian mode. To play in a different mode, you choose a different note from your major scale as your team leader:
For the Phrygian mode the third note of the major scale is the team leader.
For the Lydian mode it’s the fourth note.
For the Mixolydian mode it’s the fifth note.
For the Aeolian mode it’s the sixth note.
For the Locrian mode it’s the seventh note.
The Lydian and Mixolydian modes are very similar to major keys—in each case one note from the major scale has been moved one semitone. Music played in these modes sounds only slightly less definite and unambiguous than major key music.
The Dorian, Phrygian and Aeolian modes are all very similar to minor keys. In fact, the Aeolian mode is the natural minor scale we met earlier in this chapter. Music performed in these keys sounds rather vague in its punctuation—and, as I said earlier, this can be a pleasant effect for sad or romantic music.
The Locrian mode is not closely related to either our major or minor keys—to our ears it sounds as if a mistake has been made somewhere along the line. For this reason it is only rarely used.
Do different ET keys have different moods?
I would now like to destroy a myth about major and minor keys which is believed by a number of musicians and music lovers. This myth has an excellent pedigree—Beethoven believed in it and lots of other composers and professional musicians have believed it—but it simply isn’t true.
The myth is that, even with equal temperament, different keys convey different emotional moods. I’m not talking about the difference between major and minor keys here—they are different from each other in the ways I described above. No, the myth says that, for example, E major has a different mood from F major, and D minor has a different mood from B minor. I tested a class of music students on this, and, before we started the tests, three quarters of them believed that different keys had different moods. I then asked them to write down which mood they associated with each key. Without discussing it between themselves, they tended to choose very similar moods for any given key. For example, there was general agreement that A major and E major are “bright and cheerful” and C major is “neutral and pure.” If you are one of the people who believes in the moods of keys I suspect that you would also have made the same basic mood choices for these keys. You would probably also agree with the students that E flat major is “romantic and serious.” Well, I hate to be a party pooper—but this is all wrong…
Do you remember that committee we discussed back in chapter 1 ? They met in London in 1939 to decide on the frequencies we were going to use for our notes from then on. They only had to decide on the frequency of one note—because you can then work out the frequencies of all the others from the one you have decided on. After consuming their own weight in chocolate chip cookies, these earnest folks decided that the fundamental frequency of the “A” just above middle C should be 440Hz (440 vibrations per second). They didn’t choose this frequency for musical or emotional reasons—they chose it because it was a nice round number which was somewhere in the middle of the range of frequencies being used for the note “A” all over Europe at that time.
Let’s go back to look at two keys and their supposed moods:
E major is supposed to be “bright, joyful and lively”;
E flat major is supposed to be “romantic and serious.”
These two key notes (E and E) are next to each other on a piano keyboard—E is only a semitone higher than E—yet the supposed moods of their keys are very different. The idea that E major is joyful and E is serious was first proposed by several authors in lists of key–mood links published in the late eighteenth century. The ideas put forward in these lists have survived to this day even though the pitches of the notes involved were not fixed until 1939 and are known to have varied by at least a couple of tones over the years.
On the day of the committee meeting there would have been pianos all over Europe with Es lower than the new standard E and other pianos with Es higher than the new standard E. In spite of the large range of frequencies involved, many of the piano owners would have insisted that the key of E on their piano was much brighter sounding than the key of E—and they would still insist that this was true after their piano tuner tuned the entire piano higher or lower, to match the new standard pitch. So if there is a key–mood link it can’t have anything to do with the frequencies of the notes involved. Also, it can’t have anything to do with slightly different tuning systems for the two keys. Piano tuners nowadays are taught to use the equal temperament system, which treats all keys in exactly the same way.
When I was investigating this phenomenon of key–mood links, the only thing left which I could think of which could give a link would be the physical layout of the piano keyboard: the black notes are farther away from your wrists when you are playing, so there might be some subtle difference in the way the black notes are played, and different keys use more or less black notes. On the other hand it could be linked to some effect I hadn’t thought of.
I was very skeptical of any key–mood link but thought that the idea deserved to be fairly tested. So, together with a professional musicologist, Dr. Nikki Dibben, I gathered together the aforementioned class of music students and asked them to listen to a specially made tape recording. On the tape were two short pieces of music—one was simple and jolly, and one was dramatic—played four times each in various keys. Between each short piece there was a recording of some Indian sitar music—which was not in any Western key—to prevent the music students from working out how the key of the piano music had changed.
We asked the students (none of whom had perfect pitch and three quarters of whom believed in key–mood association) to try to identify the mood of each piece and the key it was played in. The results showed that the simple, jolly piece stayed simple and jolly no matter what key it was played in, and the students therefore usually guessed that the music was being played in the (supposedly simple) key of G, C or F when in fact it was being played in F sharp major (which is supposed to be complex in nature). We got a similar result for the dramatic music—it stayed dramatic no matter what key it was played in—and the students guessed the keys incorrectly.
Now we have our answer—there is no link between key and mood. I think there are at least a couple of reasons why this myth has become generally accepted:
1. Composers in the past believed it and wrote their music in the “appropriate” keys. This choosing of certain keys for certain moods leads music students to believe the link is real—so they write their own compositions in the “appropriate” keys.
2. When we learn the piano, or any other instrument, we begin with pieces in the key of C because it is the easiest to read as it has no sharps or flats in its key signature (the key signature is written on the left-hand side of each line of music and tells you which notes are to be played sharp or flat throughout the piece). After a few weeks we start to come across music which begins in C but then changes key to G (which has one sharp in its signature) or F (which has one flat in its signature). Changing from C to G makes the music sound brighter, and changing from C to F makes it sound less bright. Because we see that the addition of a sharp to the key signature (as we change to G) adds brightness, and a flat (as we change to F) reduces brightness, we start associating flats with calm or sadness and sharps with brightness. In fact, it isn’t true that G is intrinsically bright—it’s just that the change up in key makes things sound brighter.
If you change from the key of C to the key of G the brightness of the music increases, but if you move from D to G the brightness decreases: in one case G is the brighter key and in the other situation it’s the less bright key.
Now a final note for hardliners—the people who still aren’t convinced that there is no link between key and mood…
Earlier in this chapter I mentioned the “truck driver’s gear change”—which involves modulating from the key you are in to one a tone or semitone above. The extra “lift” given to any song by this method is very clear—and this is where the argument of mood–key supporters collapses. If you play the relevant section of pop songs which do this on a piano, the “lift” always works, no matter which key you start off in. It works from B (which has 3 flats in it) to B (5 sharps) but it also works just as well from A (3 sharps) to B (3 flats) or from E (4 sharps) to F (1 flat). These last two examples, by the argument of those who believe in key–mood links, should not work because they involve moves from supposedly bright keys to less bright ones. There are other examples of this trick in pop music where the movement upward is more than a whole tone, but once again, it doesn’t matter which keys you move from or to—it’s the movement upward which infuses the song with new life.
So there we are—it’s the movement from key to key which provides a change in mood. The keys themselves don’t have moods of their own.
The main things to remember about keys can be summarized in just four short paragraphs.
1. Major keys are a team of seven notes which are strongly related to their team leader. The punctuation of phrases in major key music is generally clear and decisive.
2. Minor keys have a couple of different notes depending on whether or not the tune is going up or down in pitch. The team of notes is not as strongly related as a major key team and the musical experience not as decisive and clear-cut—particularly at the end of phrases. We have learned to associate sadness with this more complex interrelationship of notes.
3. Music changes from major key to major key to keep our levels of interest up, and the same is true from minor key to minor key. Certain changes increase the brightness of the music for a short while, and others can diminish the brightness. The effect does not last long because it is caused by the change itself.
4. Changes from a major key to a minor key, or vice versa, involve a strong change in mood. In this case the major (brighter) or minor (sadder) mood does not fade away—it is not merely linked to the action of changing.
But one thing we haven’t covered so far is why generations of unhappy children have been forced at knife-point to practice playing scales on their instruments when they could be having much more fun playing real pieces of music. There are two reasons for this, but I think they are rather feeble when you take into account the degree of boredom which scale practice induces, and the number of kids who have abandoned music because of it. The first reason to practice scales is that it makes you get used to using all the notes on your instrument. The second reason is that lots of tunes involve fragments of scales. In fact, if you look at them closely, most melodies are made up of a combination of arpeggios, repeated notes and parts of scales. In “Baa Baa Black Sheep,” for example, the words “sheep have you a…” are four notes of a major scale. Because scale fragments turn up so often in tunes it’s helpful to have the whole scale locked into your “muscular memory”* in the same way that it’s useful to memorize multiplication tables—it saves a lot of effort later. On the whole, though, I think far too much emphasis is placed on scale practice in the early years of musical education. If the student is going to take up music as more than a hobby, she can move on to scale practice later if she wants or needs to. While I’m feeling all hot-headed and revolutionary, why don’t all you music students abandon scale practice in favor of improvisation practice?
Although playing scales is tedious, an understanding of how scales, keys and harmonies work is an important part of musical training. An appreciation of what’s going on is very useful whether you are playing, improvising, composing or just listening. Next time you are listening to a pop song which suddenly gets a lift in energy, smile knowledgeably, point at the speakers and say “ah… a truck driver’s gear change.”
Choose your time carefully, though—you are only allowed to be this weird about once a year.