CAPÍTULO 12

El problema del movimiento

Todo se mueve

nada está quieto

salvo mi corazón.

La serpiente se arrastra

en su lecho de piedra

y la piedra se desliza

al costado del volcán

y el viento

es aire en movimiento

nada está en calma

salvo mi corazón.

Casi todo, a nuestro alrededor, se mueve. Vemos al Sol cruzar el cielo de oriente a occidente, vemos la piedra que cae, el insecto que se arrastra penosamente sobre su camino mínimo; vemos al proyectil cruzar el aire límpido de una mañana de verano, casi flotar en él, y luego de un momento de gloria, precipitarse miserablemente al suelo. Y aunque no lo vemos, ni lo sentimos, sabemos que la Tierra, que nos parece en reposo, cruza el espacio con velocidades de pesadilla. Las partículas se agitan en el fondo de los átomos. El mundo que nos rodea es cambio, no permanencia: se mueve.

Es algo con lo que convivimos día a día y a lo que, mal que mal, ya estamos acostumbrados, como lo estaban el bueno de Aristóteles o sus herederos y detractores renacentistas. Pero si es tan natural… ¿por qué, entonces, el movimiento conformó un misterio durante tantos siglos, y fue su elucidación la que dio paso a la ciencia moderna?

Porque no todas las cosas parecen moverse de la misma manera. Si se empuja una pelota, ésta rueda hasta que se detiene, como si se cansara de haberse movido. Si se suelta una piedra, cae espontáneamente, sin que nadie haga nada, y lo hace cada vez con más velocidad, como si estuviera apurada por regresar al suelo. Los objetos celestes, en cambio, parecen moverse solos y siempre de la misma forma, como si la hubieran aprendido, les gustara y no encontraran una buena razón para cambiarla. Tampoco caen al suelo, como sí lo hacen la manzana o la piedra.

Ni siquiera todos ven los mismos movimientos de la misma manera. Si se mira el libro que se lee mientras el tren nos arrastra hacia algún destino más o menos incierto, el libro parece estar quieto, en reposo, en nuestra mano. Pero el que desde afuera nos ve pasar a gran velocidad, observa que el libro se mueve, junto con el tren y con nosotros. ¿Quién tiene razón?

Milan Kundera sostiene que “la lucha del hombre contra el poder es la lucha de la memoria contra el olvido”. Forzando un poco las cosas, puede decirse que la lucha del hombre por comprender la naturaleza fue, en gran medida, la lucha por comprender el movimiento. Por qué se mueven los cuerpos es una de las preguntas más antiguas de la ciencia: desde las primitivas explicaciones hasta la teoría de la Relatividad, desde Aristóteles a Einstein, se razonó, se pensó, se especuló sobre las causas y modos del movimiento y el reposo, se trató de distinguirlos, se buscó algo cuyo movimiento —o falta de él— fuera absoluto y nadie pudiera discutirlo, y muchas veces se creyó encontrarlo. La mecánica avanzó penosamente, en ocasiones quedó estancada durante siglos y a veces produjo estallidos espectaculares, en los que las concepciones del hombre sobre el movimiento —y al mismo tiempo sus concepciones sobre el mundo— tuvieron que cambiar drásticamente.

La mano y la piedra

Se mueve el mar en el mar

Se mueve el viento en el viento

Y el viento

Es aire en movimiento

Todo se mueve

Salvo mi corazón.

La primera teoría completa la formuló, cuándo no, Aristóteles. Para él, el movimiento tenía un significado diferente al que ahora le damos nosotros, y estaba subsumido en la idea más general de cambio: los procesos de nacimiento, corrupción y muerte, el animal que salta sobre una presa o la piedra que se degrada por la acción del mar eran ejemplos de movimiento tan legítimos como el de la flecha que cruza el cielo azul o los planetas que giran en el cielo pegados a sus esferas homocéntricas. El movimiento tal como nosotros lo entendemos era sólo uno de los tantos procesos de cambio, al cual llamaba «movimiento local». Prescindiremos de esa denominación, entendiendo que cuando hablamos de «movimiento», nos referimos a lo que él, y quienes lo siguieron, denominaron «local».

Hemos hablado algo de esto, pero como la teoría del movimiento terrestre y celeste será el hilo conductor y la piedra de toque que nos guiará a lo largo de la Revolución Científica —en gran medida porque la mecánica combina perfectamente y con absoluta claridad la experimentación y la razón— debemos volver un poco a él en detalle. Lo que me gustaría poder transmitirles es la dificultad tremenda y el esfuerzo que significó establecer una teoría sobre algo que parece tan simple.

El movimiento, tal como lo entiende Aristóteles, es un proceso de restauración del orden, un impulso hacia la estabilidad y la armonía. No olvidemos que el cosmos aristotélico está jerarquizado, y ofrece de entrada una división tajante y fundamental entre la esfera supralunar, donde nada puede cambiar, y la esfera sublunar donde todo se corrompe y modifica. Son dos mundos gobernados por diferentes leyes y formados por elementos distintos: la esfera sublunar, por los cuatro elementos tradicionales de Empédocles (una esfera de tierra, rodeada por una caparazón de agua, otra de aire, y otra de fuego, que se extiende hasta la esfera de la luna); la esfera supralunar, y más allá, por un quinto elemento o quintaesencia, el éter, que es incorruptible, transparente y eterno.

Por su parte, la rotación de la esfera de la luna desordena la esfera sublunar, la vuelve confusa y promiscua, mezcla las cosas. Pero esta esfera degradada, por su propia naturaleza, trata de que el orden se restaure, y así, los objetos intentan regresar al lugar que les pertenece naturalmente: la piedra cae porque su impulso ontológico (encarnado en su peso, o su gravedad) la arrastra, precisamente, hacia su lugar natural, la lluvia cae buscando la esfera del agua, y lo mismo hacen los ríos al bajar de las montañas; las burbujas que se generan bajo el agua ascienden hasta alcanzar el aire, que les es propio, el humo sube porque su levedad (Aristóteles distinguía entre levedad y peso o gravedad) lo lleva a la esfera de fuego, la más externa.

Éstos son movimientos naturales que sólo se producen por razones constitutivas y privativas de cada cuerpo: cuando alcanzan el sitio que les corresponde, y ponen –literalmente— las cosas en su lugar, el movimiento cesa, porque no tiene razón de ser.

Aristóteles logra determinar que ciertas características del movimiento natural sublunar dependen del objeto y del medio; mientras más pesado sea el objeto, más rápido se moverá o caerá, y cuanto más denso sea el medio, más se retrasará su movimiento. Lo cual excluye, de paso, la existencia del vacío, ya que en el vacío, al ser la resistencia nula, para Aristóteles la velocidad sería infinita, lo cual no puede ser por dos razones: primero, porque si se moviera con velocidad infinita, estaría en dos lugares diferentes al mismo tiempo (lo cual es absurdo), y segundo, por otra razón más sutil: para Aristóteles no puede haber ningún fenómeno que implique el infinito de hecho, «en acto»; el infinito es solamente «potencial».

La explicación, sin embargo, deja un flanco débil: no da cuenta, por ejemplo, de por qué la piedra que cae lo hace cada vez más rápido: Aristóteles atribuye el aumento de velocidad a la proximidad cada vez mayor del lugar natural, que la apura y la impulsa a moverse más rápido. Una explicación, sí, aunque no demasiado convincente.

En el mundo supralunar las cosas son completamente distintas: el movimiento de los astros y las esferas es por naturaleza circular y eterno, aunque necesita la ayudita de un primer motor inmóvil situado más allá de la esfera de las estrellas fijas, y los motorcitos inmóviles gentilmente adosados a las esferas interiores.

Hasta ahí los movimientos naturales.

Pero hay otro tipo de movimientos, exclusivos del corrupto mundo sublunar, que de ninguna manera pueden caer dentro de esta descripción: una flecha que sube (por lo menos al principio) no se dirige a lugar natural alguno, una piedra lanzada hacia arriba tampoco, más bien se aleja de su lugar natural, violentando su naturaleza, y por lo tanto son movimientos violentos o forzados. Cualquier objeto que se mueva alejándose de su lugar natural o sin aproximarse a él, está imbuido de un movimiento violento, y como un objeto cualquiera no tiene ninguna razón para moverse abandonando o alejándose de su lugar natural, necesita algo que lo mueva, o un motor: la mano que arroja la piedra, la cuerda del arco que arroja la flecha, son los motores que permiten (causan) el movimiento. Obviamente, no puede haber movimiento violento sin motor, nada puede moverse sin que algo lo mueva.

El movimiento en Aristóteles es absoluto, por supuesto: si algo se mueve, se mueve; si está en reposo, está en reposo (lo mismo que las direcciones arriba y abajo en relación al centro del mundo). Y además, como el movimiento natural está conectado con la esencia del cuerpo y el movimiento violento es un simple accidente, son atributos contrarios, no pueden mezclarse y un móvil no puede participar de ambos a la vez.

Uno estaría tentado de preguntarse por qué nuestro filósofo elaboró una teoría tan complicada; mucho más que la de los atomistas, por ejemplo, que sostenían como axioma que los átomos se movían en el vacío al azar y espontáneamente (y con la misma velocidad).

De todos modos, la construcción de Aristóteles era mucho más completa que la de los atomistas; muy en su estilo, no sólo abarcaba todos los movimientos, sino que armonizaba más o menos bien con su esquema general del universo.

La verdad es que a primera vista no está mal: es una teoría armónica, sensata y parece acomodarse bastante bien a la experiencia cotidiana. Pero sólo a primera vista. Cuando uno la examina más de cerca, se da cuenta de que es completamente inverosímil. Y, fundamentalmente, contradice el sencillo y cotidiano hecho de que si uno arroja un proyectil, éste sigue moviéndose después de que el motor (la mano) ha cesado de actuar y el proyectil se ha separado de ella. ¿Cómo puede ser? ¿No es que no había movimiento sin motor? ¡Y resulta que cuando la mano suelta la piedra, ésta se sigue moviendo, sin motor aparente alguno!

Aristóteles toma buena nota de esta dificultad realmente fatal y elabora una respuesta que consiste en sostener que el movimiento aparentemente sin motor se debe a la reacción del medio por el que circula: la mano actúa como motor de la piedra, y, a la vez, le confiere la facultad de ser motor al aire inmediatamente vecino, que mueve a la piedra y así sucesivamente, hasta que el impulso se agota, el movimiento violento cesa, y la piedra retoma el movimiento natural y cae al suelo. La explicación es ingeniosa, pero es muy difícil de creer. A la larga, junto con el misterio de la aceleración de los cuerpos en caída libre hacia su lugar natural, terminaría por poner en entredicho toda la teoría.

La teoría presenta dos serios problemas, por lo menos: el del incremento de la velocidad en la caída libre y el del lanzamiento. Pero pese a estas dificultades, subsistió como teoría principal o estándar, durante muchos siglos, lo cual demuestra, de paso, que un par de dificultades no son un obstáculo cuando hay una teoría coherente que pretende explicar (y en cierta medida lo hace) todos los fenómenos. Lo retorcido de la elaboración aristotélica muestra, de paso, las dificultades que presenta la explicación del fenómeno.

Sería muy bueno habitar

el mundo supralunar,

¿no creen ustedes?

Aquí todo se te rompe

el teléfono no anda

el coche se descompone

la ropa se mancha

se quema la plancha

arriba no pasa nada.

Dos mundos, dos mundos

el de arriba puro

el de abajo corrupto.

Arriba éter cristalino

abajo mineral sucio.

Aire tierra, fuego y agua

arriba todo se mueve

en un perfecto círculo

abajo todo se mezcla

y la tierra está inmóvil

en el centro del mundo.

Pero….

En la esfera supralunar no hay ciencia

no hay libros

sólo un eterno movimiento circular.

Que cansaría hasta a los ángeles.

Mejor volver a la lucha, a la furia de los elementos de un mundo promiscuo y cambiante, donde por lo menos se puede hacer algo.

Por otra parte, la verdad es que no me gusta la teoría de Aristóteles. Además del pequeño detalle de ser falsa, tiene, para mí, otro gran defecto: no es elegante, está llena de parches, de divisiones arbitrarias (como la del espacio supra y sublunar), de argumentos recauchutados para arreglar las dificultades. Y tiene, además, otro defecto, que no lo era entonces, pero ahora sí: estudia el movimiento como una parte inseparable de una concepción cosmológica global, mientras que, para nosotros, es un fenómeno aislado.

Lo cual no quita que siga siendo intrigante: ¿Por qué la piedra se cae y la luna no se cae, por ejemplo? Creemos que el movimiento de la bicicleta es producido por el esfuerzo de nuestras piernas pedaleando, nada parece más evidente. Pero si colgáramos la bicicleta de un alambre no se movería por más que pedaleáramos. No son nuestras piernas, pues. ¿Qué mueve entonces a la bicicleta? ¿Y por qué si pedaleamos hacia atrás, la bicicleta se mueve hacia adelante? ¿Pueden explicarlo?

Les digo esto para mostrarles que, aún hoy, una mirada primaria al movimiento puede traer problemas y hacer evidente que una buena explicación tiene que ser forzosamente compleja. Esto justifica los intentos más o menos exitosos, más o menos fallidos, y la enorme cantidad de talento e inteligencia invertidos en resolver el misterio. Porque, obviamente, es un misterio.

La piedra y la flecha: los movimientos violentos

Aunque la de Aristóteles fue la teoría dominante, es falso pensar que perduró intacta hasta ser destruida por Galileo. Ya en el siglo VI, Juan Filopón, de Alejandría, hizo una severa crítica y demostró (parece que fue el primero) que el medio no podía ser la causa del movimiento del proyectil. Si es el aire el que transporta la piedra y la flecha, ¿por qué su batir violento no las movía directamente? ¿Por qué una piedra pesada puede ser lanzada más lejos que una liviana?

Obviamente, el aire no producía el movimiento, sino que oponía resistencia a él, y así propuso que la mano o el arco impartían «poder motor» no al aire sino al mismo proyectil: una cierta fuerza motriz incorpórea debía ser dada al proyectil a través del acto de lanzar, pero esta fuerza o energía era simplemente «prestada» —del mismo modo que el calor es «prestado» por el fuego a un objeto—, se iba disipando y decrecía.

Filopón cuestionaba también la afirmación de Aristóteles sobre la caída de los cuerpos –el movimiento «natural»— según la cual un objeto que caía lo hacía con una velocidad proporcional a su peso, argumentando, otra vez, que la experiencia mostraba que un objeto más pesado y uno menos pesado soltados desde la misma altura tocaban el suelo con una diferencia de tiempo muy pequeña.

Las observaciones de Filopón tuvieron escasa repercusión en la Edad Media, aunque tuvieron muchísimo peso en las discusiones de los autores árabes sobre el asunto (en especial Avicena y Averroes) hasta que fueron retomadas, o fueron desarrolladas independientemente, por Jean Buridan (c. 1300-c. 1360), dos veces rector de la Universidad de París y discípulo nada menos que de Guillermo de Ockham, es decir, del más alto linaje intelectual.

Buridan rechazó la teoría aristotélica, con argumentos parecidos a los de Filopón, y agregó argumentos propios: un objeto terminado en punta se movería más despacio que uno rematado en una superficie plana, ya que el aire tendría más ocasión de propulsar hacia adelante, lo cual no era el caso, según decía haber experimentado (lo cual podría ser falso). El aire no podría explicar el movimiento rotatorio de una rueda de molino, porque el movimiento continuaba aunque se colocara una cubierta sobre ella.

En lugar de la teoría aristotélica, que tantos baches empezaba a mostrar, propuso que lo que el motor confería al móvil era una cierta propiedad o virtud, el impetus, que, mientras perduraba, sostenía el movimiento; luego se iba disipando del mismo modo que se disipa el calor en un cuerpo, hasta que el móvil, finalmente, abandonaba su movimiento violento y caía a tierra siguiendo su tendencia natural.

En los proyectiles, este impetus se reducía progresivamente por la resistencia del aire y por la tendencia natural de caer; en los cuerpos que caían libremente, el impetus aumentaba gradualmente por esa tendencia natural, que actuaba como una fuerza aceleradora que añadía incrementos o impetus sucesivos a los ya adquiridos. La medida del impetus de un cuerpo era su cantidad de materia multiplicada por su velocidad.

Pero… ¿qué era este impetus? Se trataba de algo diferente del cuerpo en movimiento, algo externo, que el motor le comunicaba:

Este impetus es una cosa duradera, distinta del movimiento, por el cual el proyectil es movido… Y es probable que este impetus sea una cualidad asignada por la naturaleza para mover el cuerpo sobre el cual es impreso, de la misma manera que se dice que una cualidad impresa por un imán sobre un pedazo de hierro mueve el hierro hacia el imán. Y es probable que de la misma forma que esta cualidad es impresa por el motor en el cuerpo en movimiento juntamente con el movimiento, también sea disminuido, corrompido y obstruido, como lo es el movimiento, por la resistencia del medio o la tendencia natural contraria.

Si esto último no pasaba, el impetus permanecería, de lo cual daban buena cuenta las esferas celestes, que, al no tener resistencia, seguían moviéndose eternamente gracias al impetus conferido ab initio por Dios.

En toda esta indagación de Buridan encontramos algo muy propio del espíritu medieval: necesita preguntarse qué es el impetus; no le alcanza del todo con describirlo. Las ideas científicas necesitaban, todavía, un qué, y no se conformaban con el cómo: a este problema responderán en forma tajante, como veremos más tarde, el propio Newton y los hombres de la Revolución Científica, quienes considerarán el qué como un problema ajeno a la ciencia, de índole completamente metafísica: no objetan la metafísica pero creen que debe mantenerse apartada de la mecánica. Quiero aclararles que la actitud de preguntarse por el qué me parece científicamente legítima, aunque los mecánicos de la Revolución la van a rechazar como «puramente metafísica».

Hay otra cosa importantísima en lo hecho por Buridan, aunque ciertamente pasó desapercibida en su época: unificó los movimientos terrestres y celestes al asegurar que todos ellos tenían una misma causa, el impetus. Era una manera muy «light» de hacerlo, pero era algo: la fastidiosa división del mundo en dos empezaba a mostrar cicatrices, invisibles por ahora, pero que se irían acumulando.

La teoría del impetus fue aceptada ampliamente durante los siglos XIV y XV por todos los físicos que actuaron y abordaron el problema durante el Renacimiento, incluyendo a Leonardo da Vinci y al joven Galileo.

¿Estaba pues resuelto el problema del movimiento?

De ninguna manera.

Por empezar, no estaba claro qué era lo que gastaba o se oponía al impetus (ya que en la formulación de Buridan era una entidad permanente), ni tampoco qué ocurriría con el movimiento en el vacío (cuya existencia los físicos del impetus aceptaban): al no haber resistencia, ¿por qué habría de gastarse? ¿El móvil se seguiría moviendo siempre como las esferas celestes? ¿Y cómo lo haría? ¿En línea recta? ¿De manera circular?

Antes de seguir con los problemas y de ver cómo se fueron resolviendo, echaremos una mirada a lo que, más o menos en la misma época de Buridan, hacían los científicos de Oxford, que habían emprendido un camino diferente y complementario…

Se mueve el pez en el mar.

Se mueve el ave en el viento

y el viento

es aire en movimiento

nada está quieto

salvo mi corazón.

(Y el volcán

¡rataplán!)

Vuela el pájaro en el aire

juega la luz en la nieve

por el espacio vacío

la tierra también se mueve.

Se mueve el mar en el mar

donde relumbran los peces

y se agita entre las flores

el colibrí, que no duerme.

Y en la montaña el arroyo

y en los pastos la serpiente.

Cae el águila de pronto

sobre la presa inocente

y en el espacio vacío

también la tierra se mueve.

La Tierra se mueve, la Tierra se mueve… Tendremos que hablar del asunto.

Pero por ahora, nos mudamos a Oxford.

La escuela de Oxford y el estudio matemático del movimiento

La escuela de Oxford era heredera y el resultado de un gran linaje intelectual, que había empezado con Robert Grosseteste y Roger Bacon. Y mientras en París trataban de centrarse en los movimientos reales, lo cual era difícil dada la falta de instrumentos de medición, en Oxford todo era teórico, y se desarrolló un tipo de estudio que ya no se basaba en las propiedades del móvil, o en las causas de que se moviera, sino en la matemática de su trayectoria: es decir, una cinemática.

Parece que el primer autor en intentar ese estudio puramente cinemático del movimiento fue Gerardo de Bruselas (s. XIII), quien consideró como principal objetivo el análisis y la representación de las velocidades uniformes. Su análisis implicaba inevitablemente el concepto de velocidad y, según parece, supuso que la velocidad de un móvil puede ser expresada por un número o una cantidad.

Lo que es importante contar es que los científicos de Oxford pudieron superar una de las dificultades centrales de la teoría aristotélica: su imposibilidad de ser matematizada.

La idea de describir la posición de un punto mediante coordenadas rectangulares era conocida por geógrafos y astrónomos desde los tiempos clásicos. Los médicos estaban familiarizados con la representación del calor y el frío mediante números. Galeno mismo había sugerido un grado neutro de calor, lo que sirvió a los autores latinos y árabes, para establecer una escala que se hizo popular y que tenía cuatro grados de calor o de frío, y los filósofos de la naturaleza utilizaron una de 8 para medir las diferentes cualidades primarias (húmedo, seco….). Naturalmente, la tajante separación entre opuestos (el calor y el frío, la pesantez y la levedad) era un obstáculo imposible de sortear para poder establecer una escala unificada, como las que usamos nosotros, para la cual era necesario resolver esos pares de cualidades y subsumirlas en conceptos únicos. Fue la mecánica y la cinemática quienes lo lograron, y en ello jugaron un papel central los oxonienses.

El objetivo de los métodos desarrollados en Oxford era expresar los grados de aumento o disminución numérica de una cantidad en relación con una escala dada. Tomando como referencia una línea horizontal recta, se representaba cada grado de la intensidad por medio de una línea vertical perpendicular, de altura determinada.

La velocidad era uniforme cuando se recorrían distancias iguales en tiempos iguales, y «disforme» cuando esto no ocurría. Se decía que una velocidad disforme era uniformemente disforme cuando la aceleración o el retraso eran uniformes (lo que nosotros llamamos movimiento uniformemente acelerado).

Habitantes de un mundo visual en que todo se grafica y se representa, desde las variaciones de precios hasta las fluctuaciones de audiencia de un programa de televisión, resulta difícil medir la dificultad y la genialidad de concebir los primeros gráficos: al fin y al cabo, son construcciones numéricas y geométricas abstractas, que pretenden ser un modelo del mundo: pero no de la totalidad del mundo, sino de una cualidad que se aísla de la totalidad y se mide.

Medir: también es algo cuya dificultad nos cuesta concebir. Vivimos rodeados de relojes, de cintas métricas, de códigos de barras; aislamos intervalos muy pequeños de tiempo o espacio que eran totalmente ajenos a la percepción cotidiana de esta gente, que a duras penas podía percibir un segundo o un milímetro con sus toscos aparatos y cuya única medida regular de intervalos pequeños de tiempo, durante siglos, había sido el ritmo de la respiración.

Pero volvamos. Al postular que la velocidad podía expresarse como el cociente del espacio recorrido por un móvil por el tiempo tomado en recorrerlo, los científicos de Oxford eliminaron una dificultad central de la teoría estándar, que consideraba que este cociente era ridículo porque ponía en relación dos magnitudes por completo inconmensurables. Esto se debía, en gran parte, a lo reacios que eran los griegos a reducir segmentos a números (y si recuerdan el desastre de los pitagóricos, no les faltaba razón). Una expresión como espacio/tiempo carecía de sentido y, por eso, la física debía ser no matemática sino puramente cualitativa y descriptiva como la biología.

Pero no era una dificultad para los oxonienses, que estaban muy preocupados por determinar el «grado de intensidad» de las magnitudes (que ellos llamaban «latitud») y representaron el «grado de velocidad» en gráficos, acercándose al concepto que bastante más tarde, y tras remontar muchas colinas, sería central en el proceso de reconstruir la mecánica de arriba abajo: el de velocidad instantánea. Fíjense que el concepto de velocidad instantánea es bastante elusivo: es la velocidad que, obviamente, tiene un móvil en un instante dado… ¡pero un instante tiene una duración cero! ¡Y entonces el espacio recorrido también es cero! ¿Qué significa entonces?

El oxoniense Heyfetsbury (1313-1372) dio una definición que era algo así: la velocidad instantánea es la velocidad con que se seguiría moviendo el móvil si conservara la velocidad de ese instante, algo no muy diferente de lo que diría Newton bastante más tarde. Pero a pesar de esa definición, que parecía venida del futuro, el concepto seguía siendo prematuro.

Los oxonienses, en especial los «calculadores» del Merton College, gozaron de muchísimo prestigio y lograron establecer algunas propiedades, como, por ejemplo, el teorema del valor medio, que dice que el espacio que recorre un móvil uniformemente acelerado es igual al que recorrería con una velocidad uniforme igual a la que alcanza en la mitad de su recorrido.

Ellos no lo sabían, naturalmente, pero estaban trabajando en una dirección que tarde o temprano habría de confluir con la que se desarrollaba en París, en la línea de Buridan. Haber atacado el movimiento como un problema métrico y gráfico desbrozaba un camino que todavía estaba erizado de problemas, pero la audacia y la imaginación intelectual de estos tipos era realmente asombrosa. Nicolás de Oresme (1320-1382), precisamente discípulo de Buridan y uno de los espíritus más grandes y geniales que existieron, llevó el método gráfico a su máxima expresión (a la máxima expresión posible en ese entonces, desde ya) y con justicia se le agradece (o por lo menos se lo agradece el volátil autor de estas líneas) ser un precursor de Descartes y la geometría analítica.

Los oxonienses tampoco dejaron de prestar atención al espinoso asunto del aumento de velocidad de los cuerpos que caen, especialmente porque habían logrado demostrar que ese aumento de velocidad era uniforme, esto es uniformemente acelerado («uniformemente disforme»), y como la visión que tenían era métrica, se preguntaron cuánto se aceleraba (no por qué).

Si hacen el experimento de dejar caer una moneda al suelo, van a descubrir lo difícil que resulta darse cuenta de que la velocidad de caída aumenta de manera uniforme. Y además… ¿De manera uniforme respecto de qué? La mayoría se inclinó por pensar que la velocidad de caída era proporcional al espacio recorrido, ante la evidente constatación de que un móvil al que se dejaba caer desde una altura mayor, llegaba al suelo, como ya había observado el propio Filopón, con mayor velocidad. Casi todos coincidían en este punto: Nicolás de Oresme adheriría a esta postura, que luego adoptaría Descartes y al principio Galileo. La excepción, notable por cierto, fue Domingo de Soto (1494-1560) que intuyó que en realidad la velocidad era proporcional al tiempo de caída. Hoy en día sabemos que, en realidad, lo es al cuadrado del tiempo.

Lo cierto es que la escuela de Oxford, y sus seguidores, introdujeron una novedad que sería indispensable para el buen gusto del «cocktail» que se estaba armando, y que explotaría con Galileo y su nueva ciencia del movimiento: el aspecto métrico. El movimiento no era considerado como un juego de potestades metafísicas (parte del cambio en general, o resultado de causas borrosas como el impetus o los lugares naturales), sino como un fenómeno a medir, y sobre el cual establecer una teoría métrica.

Es interesante ver de qué manera todos estos científicos y filósofos se comunicaban y discutían entre sí. Pero qué solos, qué metafísicamente solos estaban, luchando por establecer de alguna manera, de cualquier forma, nociones elementales como las de velocidad, velocidad instantánea, aceleración, que nosotros vemos cómodamente representados en el tablero del automóvil y que para ellos eran conceptos confusos, difícilmente aprehensibles. Cuando pienso en los científicos actuales y su panoplia de aparatos (que vuelan al espacio o que permiten espiar el fondo de la materia), en los equipos gigantescos y multidisciplinarios que bombardean lo desconocido, los bordes del universo y sus primeros instantes, en la inaprehensible materia oscura y el bosón de Higgs, me invade una cálida sensación de cariño y simpatía por los científicos de Oxford o París, al lado de los cuales el mismo Galileo, con sus toscos instrumentos, pero siempre seguro de sí mismo, resulta contemporáneo.

Y ya que vimos cómo estos científicos trataban el problema de la caída de los cuerpos, veamos qué pasaba con eso en otros lados donde el asunto se mezclaba con una nueva disciplina muy propia de esos tiempos: la balística.

El cañón y la bala: la caída de los cuerpos y la acción a distancia

Ya para ese entonces se trataba de una vieja historia: ¿por qué se aceleran los cuerpos al caer? Era evidente que debía haber un aumento de la causa motriz que fuera proporcional al aumento de velocidad… ¿Pero cuál? ¿De dónde venía ese aumento?

Una de las posibilidades era «la atracción del lugar natural»: el cuerpo se aceleraba del mismo modo que una limadura de hierro se acelera al acercarse al imán, pero esta parte de la «teoría estándar» empezó a perder popularidad: Alberto de Sajonia (1316-1390) hizo una objeción seria a que el lugar natural ejerciera cualquier tipo de fuerza. Señaló que a tal fuerza, un cuerpo más pesado podía ofrecer una resistencia mayor que un cuerpo ligero y que por lo tanto, debería caer más lentamente, lo cual no era el caso.

El problema es que la atracción del lugar natural implicaba la acción a distancia, que sería objeto de largas polémicas. Los autores que consideraban la acción a distancia como algo imposible, y los que proponían la analogía del imán, tenían en mente la explicación dada por Averroes: la fuerza que movía al hierro era una cualidad inducida en él por la species magnetica que salía del imán a través del medio y lo atrapaba como una garra metafísica.

Había algunos pocos, como nuestro queridísimo Guillermo de Ockham, que no veían inconveniente alguno para la acción a distancia: si el sol, al iluminarnos, actuaba a distancia, ¿por qué no lo harían el resto de los objetos del mundo? Sea como fuere, la opinión general rechazaba tanto la acción a distancia como las fuerzas externas y adoptaba la teoría aristotélica y de Averroes de una fuerza intrínseca.

La solución de Buridan, quien pensó que en los cuerpos que caían la velocidad aumentaba debido al peso, que actuaba como una fuente aceleradora añadiendo incrementos o impetus sucesivos, fue más o menos adoptada por todos los físicos del impetus, aunque más que resolver el problema, lo aplacaba. Y ya no alcanzaba con aplacarlo: en el siglo XVI, el problema de la caída de los cuerpos se combinó con una nueva disciplina nacida al calor —literalmente— de la pólvora y la generalización de las armas de fuego durante el Renacimiento. El cañón derribó conceptos establecidos y los hizo temblar nuevamente…

Porque la nueva artillería puso sobre el tapete problemas tales como los ángulos de tiro y el alcance de las balas, evidentemente centrales para cualquier militar, ingeniero o técnico que diseñara fortalezas. La pregunta central que surgió, entonces, fue: ¿cómo es la trayectoria de una bala de cañón?

Recordemos que como tradicionalmente los movimientos natural y violento no podían mezclarse (porque representaban cualidades contradictorias que se destruirían una a la otra —para Aristóteles sería como decir que un cuerpo era caliente y frío a la vez—), se suponía que la trayectoria de una flecha o de una bala poseía un tramo de movimiento violento y, cuando éste se agotaba (fuera por razones aristotélicas, o por el agotamiento del impetus), recuperaba su movimiento natural y se precipitaba al suelo.

Alberto de Sajonia había utilizado la teoría del impetus de Buridan para explicar la trayectoria de un proyectil y había sostenido que estaba dividida en tres tramos o períodos:

• Un período inicial de movimiento puramente violento durante el cual el impetus aniquilaba la gravedad natural

• Un período intermedio de impetus compuesto durante el cual el movimiento era a la vez violento y natural.

• Un período final de movimiento puramente natural de caída vertical, después de que la gravedad natural y la resistencia habían aniquilado el impetus impreso.

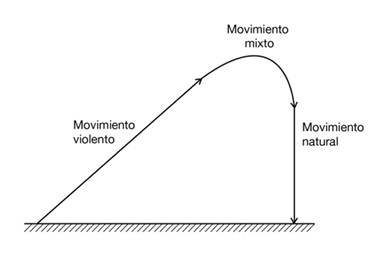
EL MOVIMIENTO SEGÚN ALBERTO DE SAJONIA

En el primer tramo, el móvil actúa por el impetus conferido; en el segundo, se combinan el movimiento violento y natural y, en el tercero, sólo actúa la gravedad.

Aquí, Alberto introducía una bienvenida cuña en el principio que emponzoñaba todo: la imposibilidad de coexistencia de movimientos naturales y violentos, que abolía con su novedoso segundo tramo.

Esta teoría fue seguida por Leonardo da Vinci, Nicolás de Cusa y muchos otros hasta que fue modificada por Tartaglia (el mismo que resolvió la ecuación de tercer grado), también fundador de un linaje: en su libro La Nova Scientia, de 1537, trataba por primera vez la balística en forma teórica, evitando toda discusión filosófica sobre los conceptos que usaba y las causas de los fenómenos: un poco porque se dirigía al ingeniero operativo renacentista, y no al filósofo, pero también porque en la lucha entre el qué y el cómo, este último empezaba a anotarse algunos tantos.

Al principio, Tartaglia aceptaba que el movimiento de un cuerpo podía ser o bien violento o bien natural, pero no «mixto». En el movimiento natural, la velocidad aumenta tanto en función del alejamiento del punto de partida, como de la proximidad del punto de llegada. El movimiento violento, en cambio, tiene la propiedad contraria: su velocidad disminuye. Tartaglia rechazó la creencia generalizada —y en cierta medida incomprensible— de que un proyectil tenía un momento de aceleración inicial al abandonar al lanzador, cosa que creían a pie juntillas todos, incluyendo a los cañoneros.

Pero el asunto aquí era la forma de la trayectoria de un proyectil. De su tesis de la imposibilidad de un movimiento mixto, tenía que resultar una trayectoria angular. Pero había un dilema, ya que esta trayectoria angular empezaba a desafiar la percepción; al fin y al cabo era más fácil creer que una flecha vuela rectilíneamente, se detiene y cae, que pensar que lo hace una pesada bala de cañón.

¿Y entonces? Y entonces nuestro amigo no aceptó esta consecuencia de su propio principio, adoptó la traza tripartita, y admitió que el movimiento de la bala, en la parte curva, aún siendo violento, lo era por efecto de su peso. Pero esto llevaba a otro absurdo porque si el peso podía curvar el movimiento violento, ¿por qué no lo hacía a lo largo de toda su trayectoria? Tartaglia se dio cuenta de la dificultad y la esquivó sosteniendo —un poco arbitrariamente en el marco de su razonamiento— que las partes rectilíneas en realidad se curvan, aunque de manera «insensible». Lo cual muestra que la ciencia se mueve de manera no exactamente racional, o mejor, rigurosa (dije «se mueve», y no «avanza», porque el desarrollo continuo, o la percepción del desarrollo continuo es un resultado de la Revolución Científica).

Iba de a poco, por lo visto, y mirando dónde pisaba, aunque no tenía mucho miedo de hacerlo en terreno barroso. Paso a paso: en su libro siguiente hizo, precisamente, una movida muy audaz: aceptó que su teoría anterior llevaba a un absurdo y rechazó la incompatibilidad de la coexistencia entre movimiento violento y natural, lo cual implicaba que no había parte alguna de la trayectoria que se produjera en línea recta porque siempre estaba actuando el peso. La creencia en la rectilinearidad del movimiento se basaba tan sólo en la imprecisión de los sentidos y la debilidad del intelecto humano. No era broma defender este resultado porque los propios cañoneros alegaban que, de acuerdo a su experiencia, la bala sí se movía en línea recta. Pero Tartaglia llegaba así a un punto en el cual trataba de asentar la balística sobre un tipo de experiencia (la verdadera, dada por la teoría) y no sobre la seudoexperiencia confusa provista por el sentido común de la vida cotidiana.

La postura era bastante radical: aunque le hubiera sido imposible expresarlo así, lo que estaba diciendo es que no es el sentido común ingenuo el que debe guiar la investigación, sino la experiencia llevada a cabo bajo la sombra de la teoría, en un espacio que imite todo lo posible el sustrato geométrico del mundo, y donde las leyes, por lo tanto, puedan manifestarse tal cual son. Estaba pidiendo, sin saberlo, el laboratorio, un lugar donde los fenómenos puedan aislarse para ser contemplados y analizados en toda su pureza.

Era prematuro. Y así, del mismo modo que la propuesta de trayectoria tripartita tuvo bastante éxito, la de una trayectoria enteramente curvilínea no tuvo ninguno, y nadie, ni siquiera mecánicos tan eminentes como Benedetti, la consideró y ni siquiera la discutió. De todos modos, aclaremos que Tartaglia no resolvió el problema, ya que no dio con la trayectoria real, que no es «curvilínea» (lo cual remite a lo circular), sino parabólica, pero es posible que en ese momento nadie fuera capaz de concebir tal cosa.

Así y todo los rasgos de la teoría de Tartaglia contenían las semillas del futuro. Era todo un manifiesto lo que declaraba en el prefacio de su libro Cuestiones e invenciones diversas, cuando dedicaba el estudio a

Quien desea ver nuevas invenciones

No tomadas de Platón ni de Plotino

Ni de ningún otro griego, ni latino

Pero sí del arte, la medida y las razones.

Porque el continuador de su linaje fue su discípulo Gianbattista Benedetti (1530-1590) que llevó el asunto de la caída de los cuerpos aún más lejos.

Benedetti llega a un paso de Galileo

En efecto, Benedetti abandonó la línea de pensamiento cualitativa aristotélica y adoptó la línea rigurosa de Arquímedes; y en vez de pensar en pesos, pensó en densidades y pesos específicos.

En un libro de 1554 explicó que la doctrina según la cual la velocidad de los cuerpos que caen es proporcional a los pesos es completamente falsa. No es el peso —aseguraba— el que determina la velocidad de caída, sino el exceso de peso sobre la resistencia del medio, y enseguida agregaba que ni siquiera es el peso en general sino el peso específico (peso sobre volumen) el que juega el papel determinante. El procedimiento mental por el que Benedetti llegó a semejante conclusión es digno de explicación.

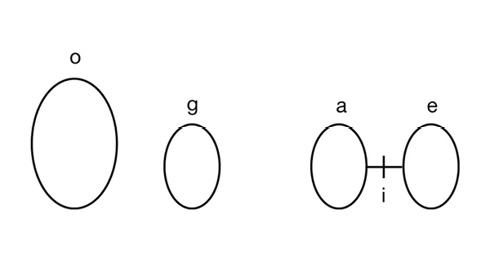
Miren la figura. Hay dos cuerpos homogéneos O y G tales que G es la mitad de O. Hay, asimismo, otros dos cuerpos compuestos de la misma materia que los primeros: A y E, cada uno de los cuales es igual a G, es decir, la mitad de O. A, E y G caen, obviamente, todos con la misma velocidad porque son idénticos. Ahora imaginemos que A y E están en las extremidades de un segmento (o, si ustedes quieren, un hilo que no pesa nada) con lo cual podemos verlos como un solo cuerpo A-E. Ese cuerpo conjunto, como es evidente, tiene su centro de gravedad en I (el punto medio del segmento) y su peso es idéntico a O, porque está compuesto por dos cuerpos que pesan exactamente la mitad de O. Por lo tanto, A-E cae con la misma velocidad que O.

Imaginémonos ahora que A-E está cayendo y, en el medio de la caída, yo le corto el hilo que los une. ¿Qué pasaría? ¿Se retrasaría la caída de A y E por haber dejado de formar parte del conjunto A-E? Es obvio que no. Por lo tanto, A y E caen con la misma velocidad que el conjunto A-E y que O. A y E, entonces, son tan rápidos como G y como el conjunto A-E. Por lo tanto, tanto G como A como E son tan rápidos como O.

Además de ponderar la importancia del peso específico para la velocidad de caída de los cuerpos, Benedetti rechazaba las ideas de peso y levedad absolutos que la mayoría de los físicos aún conservaba: los cuerpos son todos pesados en proporción a sus densidades y su peso está en relación con el medio en que están inmersos.

Aunque conservó el concepto de impetus, rechazó que fuera circular: el impetus era siempre lineal; incluso en el caso de una rueda que gira, las partículas tenderían a moverse en línea recta, pero la violencia de la cohesión material de la rueda las fuerza a seguir con el movimiento circular… La verdad es que estaba a un paso del principio de inercia.

En fin, decía Benedetti: Aristóteles no entendió nada sobre el movimiento y no lo hizo porque no comprendió un hecho fundamental: el papel de las matemáticas en la mecánica. Solamente partiendo de los resultados de las matemáticas se podía comprender el movimiento.

Pero el peor error de Aristóteles, para Benedetti, fue que negara la existencia del vacío con el argumento de que la velocidad de un cuerpo allí sería infinita en acto. Nada más falso: dado que la velocidad es proporcional al peso específico del cuerpo, retardada, pero no dividida por la resistencia, se ve que su velocidad no aumentaría indefinidamente al disminuir la resistencia del medio, y que cuando la resistencia se hiciera cero, es decir, en el vacío, alcanzaría una velocidad finita (es decir, no infinita) que dependería de su densidad. Por lo tanto, todos los cuerpos compuestos de una misma materia caerían en el vacío con la misma velocidad.

Compuestos de la misma materia… levantar esta condición conducirá a la ley de la caída de los cuerpos que enunciará Galileo.

Pero en fin, hasta aquí llegó Benedetti, y hasta aquí llegamos nosotros.

¿Qué estaba pasando?

La progresiva geometrización del espacio borraba los lugares naturales, dejando sin sustento uno de los pilares de la mecánica aristotélica: si cada lugar era exactamente igual a cualquier otro, ¿por qué la piedra debería dirigirse a él en particular? En el nuevo espacio en construcción, un punto geométrico es sólo eso, un punto geométrico, y por lo tanto inerte, sin propiedades físicas o metafísicas.

El espacio geométrico puro, al fin y al cabo, era una pura abstracción, que estaba (y sigue estando) fuera de cualquier empiria o posibilidad de experimentación, aunque el laboratorio trate de imitarlo. Sea como fuere, la experimentación no es más que un remedo parcial, y sobre todo local, del mundo.

La geometrización y matematización del espacio (y de la vida) fueron el producto de un proceso cultural profundo (que quizás no haya terminado), y quienes lo estaban haciendo no sabían, naturalmente, que lo estaban haciendo. Muy pocos, como Nicolás de Cusa o Giordano Bruno, lo proclamaron con todas las letras.

El halcón va atravesando

el aire y en él se mueve.

El barco corta las olas

de mares que nunca duermen.

Los cuerpos se precipitan

hacia la tierra inocente

donde damos nuestros pasos

y se oculta la serpiente.

Pero se está construyendo

Un nuevo mundo que tiene

en la base geometría

y en la cima nuevas leyes

matemáticas, geométricas

que lo enmarcan y defienden.

El ciervo ante el cazador

huye rápido a esconderse.

El proyectil busca el cielo

donde ya no encuentra el éter.

Todo se está transformando,

todo cambia, todo crece.

La flecha en su trayectoria

¡Y hasta la Tierra se mueve!