CAPÍTULO 17

Newton, hacedor de universos

Nature and Natures laws lay hid in night: God said, «Let Newton be!» and all was light.

(La naturaleza y sus leyes estaban ocultas en la oscuridad; Dios dijo: «Sea Newton», y todo fue claridad).

ALEXANDER POPE

Desde hace unos capítulos hemos seguido la evolución de las ideas físicas y astronómicas desde que, según la fecha que fijé (que no es tan arbitraria como dije al principio), en 1543 Copérnico abriera la Revolución Científica con su De Revolutionibus orbium caelestium. Esta línea imaginaria que hemos trazado, que pasa por Brahe, Galileo y Kepler y que funciona como la melodía fundamental que permite descubrir y reconstruir la sinfonía, culmina con otro libro, acaso el más importante de toda la historia del pensamiento científico occidental: Philosophiae naturalis Principia matematica, o Principia, como se lo nombra más frecuentemente, de Isaac Newton, de 1687. Es con los Principia que la línea se completa y la ciencia moderna sale armada prácticamente de pies a cabeza.

Pensar las cosas así, esto es, como una marcha continua, sostenida y ascendente del De Revolutionibus a los Principia, de Copérnico a Newton, puede resultar (y resultará a tantos lectores) demasiado ex post, demasiado reconstructivo a la luz de los resultados y desde el punto de vista actual.

Y sin embargo hay algo en la actitud y el pensamiento científico de estos personajes de los que hemos hablado, y de los que hablaremos ahora, que parece indicar una verdadera novedad: se trata de un esfuerzo consciente, explícito y tenaz que no se detiene ante lo ya conocido, sino que lo considera incompleto, formula sus aportes y exige a los continuadores que resuelvan los problemas que quedan abiertos. Así, por ejemplo, Brahe es perfectamente consciente de que, destruidas las esferas cristalinas, su sistema, con el Sol girando alrededor de la Tierra y el resto de los planetas girando alrededor del Sol, no está bien fundamentado y le encarga a Kepler que lo haga (cosa que Kepler no sólo no cumplió, como sabemos, sino que usó los preciosos datos de Brahe para fundamentar el sistema copernicano, lo cual seguramente hizo a Brahe revolverse en su tumba).

Galileo es consciente, también, de los problemas que quedan abiertos:

Nadie ignora que esa causa (de la caída) recibe el nombre de gravedad. Pero excepto el nombre, no comprendemos nada de esa cosa: ni de la virtud que hace bajar una piedra, ni de la que empuja una piedra proyectada hacia arriba, ni de la que mueve la Luna en su órbita.

Es, a la vez, una mirada al pasado pero un asomarse al futuro: la conciencia de la propia ignorancia no lleva a la parálisis ni a los libros de los antiguos sino a la reflexión y la investigación; la mente humana es potencialmente capaz de resolver todos los nuevos acertijos que se van planteando y el científico se convierte, en cierto modo, en un postulador de acertijos que deben funcionar como guías del pensamiento futuro y ser solucionados por los que vendrán.

Descartes escribiría:

Espero que nuestros nietos nos estarán agradecidos, no sólo por las cosas que he explicado sino también por las que voluntariamente he omitido, con el fin de dejarles el placer de inventarlas.

Los hombres de la Revolución Científica son científicos conscientes de que lo son, de que la ciencia es una tarea colectiva y pública que avanza gracias al trabajo acumulado de una comunidad dentro de la cual cada investigador ve más lejos que el anterior porque tiene la posibilidad de montarse en los hombros de sus predecesores, en «hombros de gigantes»… La frase, que define al propio Newton, no es ociosa: la ciencia está planteando un nuevo escenario y ubicándolo en el futuro.

«Si vemos más lejos es porque estamos subidos en hombros de gigantes»: es una proposición bastante elocuente. Suele atribuírsela a Newton, pensando que a lo que se refiere es a que su ley de gravitación es posible sólo gracias a que pudo subirse en los hombros de Copérnico, Galileo y Kepler. Pero no fue así. Newton la usó en una carta a Robert Hooke en la que hablaba de las críticas que éste había hecho a su teoría corpuscular de la luz, y no tiene nada que ver con los Principia ni con la ley de gravitación universal. Tampoco es original de Newton, sino, como recordarán, de Bernardo de Chartres, en el siglo XII, lo cual muestra que esta postura de los científicos de la revolución tenía algunas raíces en el pasado y que poner fechas de comienzo, o límites, o fechas de cierre, es siempre un poco arbitrario.

Sea como fuere, la línea que trazamos tiene sus justificaciones. Y si le dedicamos un capítulo a quien inaugura la Revolución Científica, tenemos que dedicarle otro a quien la culmina, produciendo esa pavorosa síntesis que marcó el rumbo que seguiría la ciencia hasta… hasta hoy.

Vida de Newton

Es muy difícil aproximarse con ecuanimidad a Newton, hacedor de universos, y considerado por muchos como el científico más grande que jamás haya existido. Inclinado al esoterismo, tuvo una personalidad extraña y enfermiza, paranoica hasta el exceso, al borde mismo de la locura, que estuvo alguna vez a punto de acabar con él. Vengativo, perseguía a sus enemigos científicos hasta el cansancio y hasta el extremo de hacer desaparecer de la Royal Society el retrato de Robert Hooke, uno de los científicos más importantes del siglo XVIII. Tenaz en sus odios, mantuvo una absurda polémica con Leibniz por la prioridad en la creación del cálculo infinitesimal que envenenó las relaciones entre la ciencia inglesa y la continental y retrasó en Inglaterra el desarrollo de las matemáticas.

Había nacido en 1642 en una granja de Woolsthorpe, una ciudad en Lincolnshire, al este de Inglaterra, que permanecería relativamente ajena al turbulento período de la historia que le tocaría vivir. Siete años después del nacimiento de Newton, la segunda guerra civil entre el rey y el Parlamento llegó a su punto de máxima tensión cuando Carlos I fue ejecutado y se instauró la república puritana de Cromwell, que duró hasta 1660, cuando la sucedió la restauración de los reyes Estuardo (que finalizaría con la «Revolución Incruenta» de 1688).

A los 12 años, es decir, en pleno proceso de protectorado de Cromwell, Newton fue enviado a estudiar a una escuela de enseñanza secundaria en Grantham, a unos 8 kilómetros de su granja natal. Tras la muerte de su padre, su madre quiso que se hiciera cargo del manejo de las propiedades familiares, para lo que Newton fue tan incapaz que finalmente lo enviaron de nuevo al colegio. En junio de 1661, a los 18 años de edad (y ya con los Estuardo en el trono de una restaurada monarquía), ingresó en el Trinity College de Cambridge, como sub-becario, lo que significaba ser criado de un estudiante más pudiente, tarea de lo más baja, que podía resultar extremadamente desagradable e incluir trabajos tales como vaciar los orinales del amo, con lo cual, supongo, no tuvo nada que ver su cariño por la mecánica de fluidos, que ocupa el segundo libro de los Principia.

El Trinity College

Platón es mi amigo, Aristóteles es mi amigo, pero mi mejor amigo es la verdad.

NEWTON

La enseñanza en Cambridge era por entonces obsoleta, o más bien apolillada; Newton, como seguramente cualquier otro estudiante interesado e informado, decidió ignorar en gran medida los programas de estudios formales y se dedicó a leer lo que le interesaba, como, por ejemplo, las obras de Galileo y de Descartes, Gassendi, Hobbes, Boyle y la geometría de Euclides. La astronomía copernicana, la mecánica de Galileo y la obra de Kepler parecen haber causado un profundo efecto en él, hasta inducirlo a cambiar el foco de sus estudios.

Sin embargo, aunque en 1660 Cambridge era aún un centro de estudios estancados, en 1663 el político y clérigo Henry Lucas aportó la dotación para que se creara allí una cátedra de matemáticas —la primera cátedra científica de la universidad y la primera cátedra de cualquier tipo que se creaba desde 1540— que fue el primer anuncio de lo que esa universidad llegaría a ser.

El primero que accedió a la cátedra lucasiana de matemáticas fue Isaac Barrow, un antiguo profesor de griego que se había volcado a las matemáticas y cuyo curso, probablemente, fue el que estimuló el interés de Newton por la ciencia. Cinco años duró Barrow en el cargo. Es poco tiempo para una tarea de semejante importancia, y esto despertó las elucubraciones y la imaginación de los hagiógrafos newtonianos. Según ellos, Barrow le dejó la cátedra a Newton porque admiraba tanto a su discípulo que simplemente consideró que merecía el cargo más que él. Lo cierto es que, aunque el propio Barrow argumentó que dimitía para ocuparse de sus asuntos religiosos, no tardó en llegar a ser capellán real y luego director del Trinity College, por lo que nos es dado pensar que su dimisión no se debió precisamente —o solamente— a una casi increíble generosidad.

Newton terminó en Cambridge sus estudios previos a la graduación, llegó a ser primero miembro del Trinity College y, en 1669, catedrático lucasiano de matemáticas, reemplazando a Barrow a los 26 años. Pero antes de llegar a ese cargo pasaron muchas cosas en su vida.

En 1665 había conseguido, sin pena ni gloria, su primer grado académico. Al poco tiempo la plaga que estalló en Inglaterra (y que mató sólo en Londres a treinta mil personas) lo obligó a refugiarse en el campo y volver a su hogar materno. Retirado en su pueblo natal, probablemente sin muchas cosas interesantes para hacer, se concentró en las propias investigaciones y entre 1665 y 1667 (¡a los 23 años!), elaboró el núcleo principal de todos sus más importantes descubrimientos matemáticos y físicos, o por lo menos así lo contó después. Las reconstrucciones de Newton hay que tomarlas con pinzas, ya que, como veremos, muchas veces eran puramente interesadas y dirigidas a disminuir a algún rival, real o fantástico. Pero fue en este lugar donde, según la leyenda, cayó la famosa manzana que disparó en su mente la idea de la gravitación universal.

Manzanas

La manzana de Newton juega en la historia de la ciencia un papel parecido al de la manzana de Adán y Eva en la cosmogonía judeocristiana: ambas están al fin relacionadas con el conocimiento, y en cierto sentido se puede decir que el mordisco dado a una (y la consecuente caída del sujeto) permitió la caída de la otra, y el ascenso del sujeto a la construcción de una explicación unificada, global y total, de la mecánica celeste y terrestre.

La historia de la manzana fue contada por Voltaire, a quien se la contó, a su vez, la sobrina de Newton, que la recibió del propio Newton. Pero la versión que se ha popularizado, según la cual lo que descubrió nuestro protagonista en ese momento es que la Tierra atraía a la manzana, alteró por completo el verdadero significado de ese momento clave, si es que alguna vez ocurrió (si no ocurrió, como veremos, Newton tuvo sus buenas razones para inventarlo).

Imaginemos la escena: Newton, forzado a la ociosidad por la epidemia que azota a Cambridge, se ha sentado bajo el manzano a reflexionar sobre los mecanismos del mundo. Ya se sabe —lo explicó Copérnico— que el Sol ocupa el centro del sistema. Ya se sabe —lo explicó Galileo— por qué no salimos disparados de la Tierra al moverse ésta, y también cuál es la ley que rige la caída vertical, por la fuerza que ejerce la Tierra y que ya se denomina gravedad. Los mecanismos del mundo sublunar, los que ocurrían en la Tierra, estaban explicados. Ya se sabe —lo expli­có Brahe— que las esferas de cristal son quimeras. Ya se sabe —lo explicó Kepler— que los planetas rodean al Sol describiendo elipses gracias a, según Kepler, una fuerza de tipo magnético que se ejerce a través de tientos magnéticos que salen del Sol.

Es un día cualquiera, en el que a la Luna le toca ser vista de día muy por encima del manzano, de una de cuyas ramas se desprende una manzana fragante que cae a los pies del joven Newton. ¿Por qué ha caído la manzana? Porque la gravedad de la Tierra tiró de ella hasta el suelo, según la ley de Galileo. ¿Pero qué habría ocurrido si la manzana hubiera estado unos metros más arriba? No cabe duda de que la gravedad la alcanzaría igualmente y la haría caer. ¿Y si hubiera estado un poco más arriba aún? Lo mismo, por supuesto. ¿Hasta dónde llega esa fuerza de gravedad entonces? ¿Por qué habría de detenerse en el árbol o en cualquier otro sitio?

Probablemente hasta el límite de la atmósfera… ¿pero esto tiene sentido? Claro que no. Si la manzana ubicada en el límite de la atmósfera cae, ¿por qué no habría de caer si está situada unos centímetros más arriba? ¿Acaso la gravedad se corta de repente?

Es decir, piensa Newton, la gravedad llega hasta muy arriba, por ejemplo hasta la Luna. Pero si la atracción terrestre alcanza a la Luna y tira de ella hacia sí, eso significa que la Luna también está cayendo, sólo que lo hace de tal manera que esa caída permanente se convierte en un permanente girar. Entonces llega a una conclusión asombrosa: la misma fuerza que tira de la manzana es la que mantiene a la Luna en su órbita y la hace girar alrededor de la Tierra, tirando de ella.

No hay una fuerza especial para los astros. La fuerza que mueve a la Luna alrededor de la Tierra es exactamente la misma que hace caer la piedra al suelo: la gravitación. De un solo golpe, Newton unifica la física del mundo, al establecer que dos fenómenos que en principio no parecen tener nada que ver responden a una sola e idéntica causa.

Es un día cualquiera, un día en el que a la Luna le toca ser vista de día muy por encima del manzano, de una de cuyas ramas se desprende una manzana fragante que cae a los pies del joven Newton y le permite unificar el insoportable universo.

Faltaba saber cómo funcionaba esa fuerza.

Óptica

Tras el fin de la plaga, Newton regresó a Cambridge. En esta época, y probablemente tras haber leído la Micrographia de Hooke, donde éste daba cuenta de sus descubrimientos microscópicos, se puso a estudiar la naturaleza de la luz, utilizando prismas y lentes.

En el trabajo más importante que hizo sobre óptica, descompuso la luz blanca (en realidad luz solar) en los colores del espectro del arco iris utilizando un prisma, para luego recombinarlos y conseguir de nuevo luz blanca, demostrando así que la luz blanca era precisamente una mezcla de todos los colores del arco iris.

A partir de este trabajo, su interés por los colores lo llevó a plantearse el problema de las franjas coloreadas que se producían en los bordes de las imágenes vistas mediante los telescopios construidos con lentes, y que se llamaba aberración cromática, llegando a diseñar y construir un telescopio de reflexión en el que no se presentaba este problema.

Cuando Newton explicó parte del trabajo realizado sobre la luz en las clases magistrales que dio como catedrático lucasiano, y a través de personas que habían visitado Cambridge y vieron el telescopio u oyeron hablar de él, empezaron a difundirse noticias relativas a todo esto. La Royal Society solicitó ver el instrumento y, a finales de 1671, Isaac Barrow llevó uno a Londres e hizo una demostración con él en el Gresham College. Inmediatamente, Newton fue elegido miembro de la Royal Society y se le preguntó si tenía algo más en reserva. Su respuesta consistió en presentar ante la Royal Society una extensa ponencia sobre la luz y los colores.

Newton estaba a favor de la teoría corpuscular de la luz, ya que la concebía como una corriente de partículas, pero los descubrimientos que presentó en aquel momento eran válidos tanto si se utilizaba este modelo como si se utilizaba el modelo ondulatorio (a favor del cual estaban, por ejemplo, el gran físico danés Christiaan Huygens y el también gran físico inglés Robert Hooke), lo cual desató una polémica con Hooke que provocó un intercambio de cartas de tono más que agresivo, hasta que la intervención de otros miembros de la Royal Society permitió un nuevo intercambio de cartas y, finalmente, una forzada reconciliación.

Hooke a Newton:

Considero que en este asunto [el estudio de la luz] ha llegado usted más lejos que yo… Creo que el tema no podría ser investigado por una persona más adecuada y capaz que usted, que está capacitado en todos los sentidos para completar, rectificar y reformar lo que fueron las ideas derivadas de mis primeros estudios, que yo me proponía haber realizado por mí mismo, si lo hubieran permitido los otros cometidos agobiantes que me fueron asignados, aunque soy bastante consciente de que lo hubiera hecho con unas capacidades muy inferiores a las de usted.

Newton a Hooke:

Es usted demasiado generoso al valorar mis capacidades. Lo que Descartes hizo fue un paso importante. Usted ha añadido mucho de distintas maneras, especialmente al tomar en consideración filosófica los colores de unas láminas muy finas. Si yo he sido capaz de ver más allá, es [y aquí viene la famosa frase] porque me encontraba sentado sobre los hombros de Gigantes.

Fue un frágil tratado de paz, que olía a hipocresía por las dos partes (aunque Hooke estaba lejos de poner en juego un carácter tan desagradable como el de Newton). En ese mismo año, Newton publicó su primer trabajo científico acerca de la luz y el color. En 1678 sufrió un ataque nervioso que lo llevó a aislarse por casi seis años y, superada su crisis, volvió a gatear lentamente hacia la teoría de la gravitación universal.

El embrollo de la fuerza centrífuga

No era el único que gateaba, por cierto. Todos lo hacían, o lo habían hecho. William Gilbert (1544-1603), que había estudiado a fondo el magnetismo, se imaginaba que la Tierra, los planetas, y el Sol eran grandes imanes que actuaban entre ellos mediante fuerzas magnéticas (recordemos que la Tierra es, en realidad, un enorme imán, aunque no hay que confundir su fuerza magnética con la gravitatoria; no tienen nada que ver); Kepler, influido por Gilbert, pensó que del Sol emanaban tientos o cadenas que arrastraban a los planetas lateralmente, con una fuerza que disminuía proporcionalmente a la distancia y evitaba que se detuvieran. Para Kepler, la tendencia natural todavía era al reposo, y las fuerzas magnéticas de Gilbert actuaban deformando las órbitas y transformando los círculos en elipses.

También en la Royal Society se discutía sobre esa fuerza, y se sospechaba que disminuía proporcionalmente al cuadrado de la distancia (es decir, seguía la ley del cuadrado inverso).

Había una razón para esta ley del cuadrado inverso, que no era al­go nuevo ni siquiera entonces. Se remontaba al menos a 1673, cuando ­Huygens (1629-1695) había calculado la fuerza centrífuga de un objeto que se desplazaba recorriendo una órbita circular y había determinado que disminuía con el cuadrado de la distancia al sol. Hooke había comenzado a especular siguiendo la misma línea de razonamiento; como veremos, en la correspondencia que sostuvo con Newton a partir de 1674 estaban de acuerdo en que las leyes del movimiento de Kepler implicaban que la fuerza centrífuga que empujaba a los planetas tendiendo a alejarlos del Sol debía ser inversamente proporcional a los cuadrados de sus distancias a este astro y que, por consiguiente, con el fin de que los planetas permanecieran en sus órbitas tenían que ser atraídos por el Sol con una fuerza equivalente que contrarrestara totalmente la fuerza centrífuga. Ésta era, también, la forma de razonar de Newton en la época del manzano: la permanencia en las órbitas era producto del equilibrio entre ambas fuerzas.

En 1674, Hooke ya había dado con el núcleo del problema del movimiento orbital. En un tratado que se publicó aquel mismo año, descartó la idea de un equilibrio entre las fuerzas que empujaban hacia dentro y las que empujaban hacia afuera para mantener a un objeto como la Luna en su órbita. Constató que el movimiento orbital resultaba de sumar, por una parte, la tendencia de la Luna a moverse en línea recta y, por otra, una fuerza «única» que la atraía hacia la Tierra. Mientras tanto, el propio Newton, Huygens y todos los demás seguían hablando de «una tendencia a alejarse del centro», y Newton había llegado al extremo de aceptar vórtices cartesianos como responsables de empujar a los objetos para que volvieran a situarse en sus órbitas, a pesar de su tendencia a desplazarse hacia el exterior.

Es decir, Hooke ya había llegado a la conclusión de que había una sola fuerza, que tiraba hacia el centro y apartaba permanentemente al planeta de su trayectoria rectilínea y uniforme.

No eran dos fuerzas que se equilibraban, sino una única fuerza que tiraba hacia el centro.

¿Y la fuerza centrífuga? Hooke se dio cuenta de que era una fuerza ficticia, que dependía del sistema de coordenadas y que sólo expresaba la tendencia del cuerpo a seguir moviéndose en una trayectoria rectilínea, como lo ordenaba el principio de inercia.

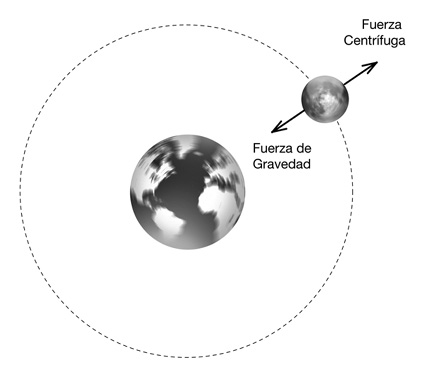
EL EMBROLLO DE LA FUERZA CENTRÍFUGA

Hooke también prescindió de los vórtices, y tuvo la audacia de introducir la idea de una «acción a distancia», ni más ni menos que la gravedad, que se transmitiría a través del espacio «vacío» para ejercer una tracción sobre la Luna o los planetas. Hooke estaba por ese entonces más adelantado que el propio Newton, enredado todavía en el rollo de la fuerza centrífuga.

En 1679, cuando ya había desaparecido la polvareda levantada por su confrontación inicial sobre la luz, Hooke escribió a Newton para pedirle su opinión sobre estas teorías (que ya se habían publicado). Le habló de la ley del cuadrado inverso, que Newton ya tenía, de la acción a distancia, y de la idea a la que había llegado: no había fuerza centrífuga ninguna, sino solamente una fuerza centrípeta que apartaba a los planetas de una trayectoria rectilínea y la curvaba mediante la gravedad.

Probablemente fue esta carta la que liberó a Newton del asunto de la fuerza centrífuga (que es una fuerza artificial, simplemente la reacción a la fuerza centrípeta —esta última sí real—) y lo estimuló para demostrar, en 1680, que una ley de la gravedad con cuadrados inversos a las distancias exige que los planetas se muevan recorriendo órbitas elípticas, e implica que los cometas deben seguir trayectorias elípticas o parabólicas alrededor del Sol. Ésta es la razón por la que ya tenía la respuesta preparada cuando, en 1684, Halley se apareció en la puerta de su casa.

Porque fue así: aprovechando un viaje, Halley, en agosto de 1684, visitó a Newton en Cambridge, donde debatieron sobre las órbitas de los planetas y la ley del cuadrado inverso. Según contó Newton después, cuando llevaban cierto tiempo reunidos, Halley le preguntó qué tipo de curva creía él que describirían los planetas, suponiendo que la fuerza de atracción hacia el Sol fuera inversa al cuadrado de las distancias respectivas de los planetas a dicho astro. Newton dijo inmediatamente «una elipse», ante lo cual Halley le preguntó cómo lo sabía. «Porque lo he calculado», respondió Newton de inmediato. Tras esto, Halley le pidió que le dejara ver los cálculos, pero Newton buscó entre sus papeles y no pudo encontrarlos. Se comprometió entonces a volver a hacerlos y a enviárselos apenas los tuviera listos.

Ese encuentro entre Halley y Newton y los cálculos que nunca encontró se convertirían en el puntapié inicial para que nuestro protagonista se pusiera a escribir los Principia.

Los Principia

Ya en 1684 Newton publicó un trabajo en el que explicaba la ley del cuadrado inverso, pero recién en 1687 vio la luz su gran obra épica, Philosophia Naturalis Principia Mathematica (Principios matemáticos de la filosofía natural).

En los trescientos y pico de años que nos separan de aquella publicación, los homenajes y las expresiones de asombro ante Newton y su obra principal se han ido acumulando desde el jocoso comentario de Hume, quien señaló que «no había cuerpos celestes cuyo movimiento Newton no hubiera explicado, con excepción del de las mujeres», el más solemne de Laplace, que calificó los Principia como «obra cumbre del pensamiento humano», hasta la encendida admiración de Einstein en el artículo conmemorativo del bicentenario de la muerte del gran físico. Prodigioso, monumental, grandioso… no hay aumentativo que se haya dejado de aplicar, y la verdad es que en ningún caso puede considerarse una exageración.

Y es que al leer los Principia uno se queda pasmado, completamente pasmado. Todos los fenómenos mecánicos del mundo quedan explicados con el más exquisito rigor: los móviles, el movimiento, las mareas, los planetas, los satélites, las estrellas, las elipses de Kepler, los cometas… Todo. Realmente es el libro de la Naturaleza reclamado por Galileo, escrito en caracteres matemáticos (básicamente geométricos), en el que todo está comprendido y explicado. Resulta increíble que semejante obra haya sido el producto de una sola persona, y no extraña que Newton haya tenido después una crisis nerviosa que lo puso al borde de la demencia.

La verdad es que uno se queda sin palabras para describirlo.

Los Principia de Newton inauguran de manera formal y orgánica la física moderna, resumen un siglo y medio de búsqueda y tanteo —en el que hay que incluir figuras del calibre de Copérnico, Galileo, Giordano Bruno, Tycho Brahe, Kepler, Descartes, Hooke—, unifican de golpe toda la mecánica del mundo, establecen leyes que describen el movimiento de todos los cuerpos, fundan una metodología, derrumban para siempre la concepción aristotélica y fabrican un nuevo universo, limpio y vacío, donde las leyes de la física se cumplen con geométrica pulcritud.

Cualquiera de sus otros descubrimientos, sea en el terreno de la óptica, sea, especialmente, la creación —en forma independiente y contemporánea con Leibniz— del cálculo infinitesimal, le hubiera valido un lugar de honor en la historia de la ciencia, pero los Principia lo situaron en la cúspide. Su larga vida, en la que alcanzó la cima del prestigio científico y la presidencia de la Royal Society, ofrece facetas múltiples, algunas bastante extravagantes, como la dedicación y el tiempo que empleó en especulaciones alquímicas y teológicas tratando de fijar la fecha exacta del Diluvio Universal o del Segundo Advenimiento.

Pero es a través de un libro, de un único libro, que lleva a cabo una hazaña muy poco usual: fabricar un mundo completo.

Los Principia exponen la física como un conjunto de proposiciones, axiomas y definiciones, con riguroso estilo matemático. Ya en el primer libro enuncian la ley de inercia, la de proporcionalidad entre la fuerza y la aceleración, y el principio de acción y reacción.

LEY I

Todo cuerpo persevera en su estado de reposo o de movimiento uniforme o rectilíneo en tanto que no sea obligado por fuerzas impresas a cambiar su estado.

(Principio de inercia)

LEY II

El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.

(F = m. a: la fuerza no produce movimiento sino cambio del estado de movimiento)

LEY III

Con toda acción ocurre siempre una reacción igual y contraria, o sea las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en direcciones opuestas.

(Principio de acción y reacción)

Si bien es cierto que la primera había sido utilizada por Galileo (aproximadamente, ya que como vimos el principio de inercia galileano era circular) y enunciada por Descartes, y la segunda había sido empleada con éxito por Huygens, es en los Principia donde se elevan a la categoría de cimientos, de leyes fundadoras de toda la mecánica y válidas para toda la materia. Con estas tres herramientas, Newton desarrolla la dinámica de la masa puntual demostrando, entre otras cosas, la ley kepleriana de las áreas como un teorema y demostrando también que un cuerpo que cumpla las leyes de Kepler se mueve según una fuerza central inversamente proporcional al cuadrado de la distancia. En este primer libro, y en el segundo, establece sobre bases firmes la cinemática y la dinámica, como preludio al tercero, con el promisorio título de «Sistema del mundo matemáticamente tratado». Título tentador, por cierto, que no defraudaría a nadie.

La ley de gravitación universal

Es allí donde aparece la ley de gravitación universal:

Siendo universalmente evidente, mediante los experimentos y las observaciones astronómicas, que de todos los cuerpos que giran alrededor de la Tierra gravitan hacia ella, que nuestro mar gravita hacia la Luna y que todos los planetas gravitan unos hacia otros y que los cometas gravitan hacia el Sol, de igual manera, entonces, debemos admitir que todos los cuerpos están dotados de gravitación recíproca.

O sea:

Dos cuerpos cualesquiera, en lugares cualesquiera, se atraen con una fuerza que es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa.

(F = G. M.m/d2 , donde G es una constante universal).

Dos cuerpos cualesquiera, en dos lugares cualesquiera…, es muy difícil transmitir la fuerza prodigiosa de esta síntesis. Dos cuerpos cualesquiera… La manzana que cae del árbol y la Luna que no cae, la gota de lluvia que se abre paso en la atmósfera y los satélites de Júpiter descubiertos por Galileo responden a la misma ley. La fuerza que nos mantiene a nosotros, los hombres, sujetos a la Tierra, mantiene los planetas en sus órbitas, es causa de las mareas y actúa, entre el Sol y las estrellas más lejanas, con matemático rigor.

Las esferas celestes tolemaicas —y aun las copernicanas—, la separación entre cielos y Tierra, entre mundo sub y supralunar, se esfuman para siempre. Después de ciento cincuenta años de especulación, de avances y retrocesos, el mundo estaba explicado.

Los Principia dieron lugar para el conventillo al que Newton era tan afecto (lo cual, como ven, caracterizaba y sigue caracterizando al mundo científico). Hooke, con quien Newton ya se había amigado «voluntariamente», se quejó porque el manuscrito, al que tuvo acceso en calidad de miembro de la Royal Society, no le daba suficiente crédito, una queja perfectamente justificada, ya que él había descubierto y comunicado ideas importantes y había sido su carta de 1679 la que había puesto a Newton en la senda correcta. La reacción de nuestro protagonista, exagerada por cierto, fue amenazar con retirar la publicación del tercer volumen y luego revisar el texto antes de enviarlo a la imprenta, suprimiendo radicalmente cualquier referencia a Hooke.

También este odio desenfrenado puede explicar la leyenda de la manzana: Newton quería aclarar que estaba en posesión de la ley mucho antes de que Hooke le enviara su famosa carta. En fin: nadie está a salvo de la banalidad.

Después de los Principia

No pasó nada nuevo, la verdad. El libro logró materializar lo que los científicos habían estado buscando a tientas, a veces sin ser conscientes de ello, desde los tiempos de Copérnico: la constatación de que el universo funciona según principios esencialmente mecánicos susceptibles de ser comprendidos por los seres humanos. Como resultado de la publicación de su libro, Newton llegó a ser un científico famoso, extendiéndose su renombre mucho más allá del círculo de la Royal Society. John Locke, amigo de Newton y el filósofo más prestigioso de la época, escribió sobre este libro lo siguiente:

El incomparable señor Newton ha demostrado lo lejos que nos pueden llevar las matemáticas en el conocimiento de algunas provincias especiales, si podemos llamarlas así, del incomprensible universo, si aplicamos esta ciencia a ciertas partes de la naturaleza, a través de principios que se justifican como una cuestión de hecho.

Sin embargo, en 1687, Newton abandonó la investigación (cumpliría 45 años al final de ese año) y no hubo nuevas publicaciones ulteriores: su obra Opticks, muy anterior, se publicaría a principios del siglo XVIII, puesto que Newton esperó para darla a la imprenta a la muerte de Hooke.

El resto de su vida tuvo poca relación directa con la ciencia: fue parlamentario, y a pesar de que se sumergió en sus trabajos de alquimia a principios de la década de 1690, parece ser que en 1693 sufrió una importante depresión nerviosa. En 1696 le ofrecieron el cargo de custodio de la Casa de la Moneda, que ejerció actuando según su carácter obsesivo, llevando a cabo una tarea importante, y con una gran efectividad a la hora de ahorcar falsificadores. En 1699, cuando el director de la Casa de la Moneda falleció, Newton ocupó su cargo. Desde 1703 hasta 1727, año en que murió, estuvo al frente de la Royal Society.

Sin lugar para los ángeles: espacio y tiempo absolutos

Pero, en realidad, el mundo no estaba solamente explicado. Lo que había sufrido era una verdadera reconstrucción: finalmente se había fabricado un escenario nuevo. Porque no alcanzaba con decir que todas estas fuerzas estaban operando; era necesario decir dónde operaban. ¿Cómo era ese lugar en el que todos los cuerpos se atraían entre sí de acuerdo con las leyes explicitadas por Sir Isaac Newton? (Habrán notado que puse Sir, porque en 1705 fue nombrado caballero.) ¿Y cómo era el tiempo en el que tales leyes cumplían su función con rigor adamantino?

El cosmos tradicional, heredado de la Antigüedad y la Edad Media, era un lugar cerrado por la esfera exterior de las estrellas fijas, que Copérnico, como vimos, no había tocado, fuera de la cual no había nada, y dentro de la cual el espacio estaba rigurosamente jerarquizado: espacio perfecto y supralunar, espacio imperfecto y mudable sublunar, donde cada cuerpo se movía según un sistema de lugares previamente asignados, o mejor, signados, y donde no existía el vacío. Cuando Copérnico alteró la visión geocéntrica, mantuvo las esferas y la finitud del universo, o por lo menos no se metió mucho con ellas. Kepler argumentó en favor de la finitud del cosmos y la existencia de la esfera de las estrellas fijas. Galileo no incursionó demasiado profundamente en el problema de la unicidad del mundo, aunque la supuso (o la sobrentendió). En el año 1600, Giordano Bruno había sido quemado —entre otras cosas— por postular un espacio infinito, con infinidad de sistemas solares, y en el que todos los lugares eran equivalentes, uniformemente llenos de materia sutil. El sistema de Descartes, que rechaza el vacío por constituir (para él) una imposibilidad lógica, es, probablemente, el primero que presupone un espacio indeterminado, aunque lleno de materia sutil, cuyos torbellinos aportaban la cantidad de movimiento constante para el funcionamiento del mundo. Indeterminado, no infinito, palabra que reserva sólo para Dios.

Pero… ¿dónde y cuándo ocurre el sistema de Newton? El marco es un espacio absoluto y vacío, sobre el que fluye el tiempo, uniforme y matemático: hay un reloj teórico que da la hora para todo el universo. Es el espacio y tiempo de Euclides, el mundo de la geometría, un receptáculo donde los cuerpos interactúan según leyes deducidas matemáticamente de algunos principios generalizados por inducción. No hay lugares ni momentos privilegiados: el espacio se extiende infinitamente hacia todos los lados, y en el tiempo, hacia atrás y hacia el futuro. El propio Newton sintetizaba así sus concepciones del espacio y del tiempo:

Nos ha parecido oportuno explicar hasta aquí los términos menos conocidos y el sentido en que se han de tomar en el futuro. En cuanto al tiempo, espacio, lugar y movimiento, son de sobra conocidos para todos. Hay que señalar, sin embargo, que el vulgo no concibe estas magnitudes si no es con respecto a lo sensible. De ello se originan prejuicios para cuya destrucción conviene que las distingamos en absolutas y relativas, verdaderas y aparentes, matemáticas y vulgares.

I. El tiempo absoluto, verdadero y matemático en sí y por su naturaleza y sin relación con algo externo, fluye uniformemente, y por otro nombre se llama duración; el relativo, aparente y vulgar, es una medida sensible y externa de cualquier duración, movimiento (sea la medida exacta o desigual) y de la que el vulgo usa en lugar del verdadero tiempo; así, la hora, el día, el mes, el año.

II. El espacio absoluto, por su naturaleza y sin relación con cualquier cosa externa, siempre permanece igual e inmóvil; el relativo es cualquier cantidad o dimensión variable de este espacio, que se define por nuestros sentidos según su situación respecto de los cuerpos, espacio que el vulgo toma por el espacio inmóvil: así, una extensión espacial subterránea, aérea o celeste definida por su situación relativa a la Tierra.

Es decir, aunque los movimientos entre los cuerpos puedan ser relativos, el espacio en sí mismo, como un todo, está inmóvil.

Esta geometrización no es una simple especulación, sino que es necesaria para que las leyes que enuncian los Principia puedan funcionar, está implícita en ellas. Si un móvil sobre el que no actúa ninguna fuerza se mueve siempre sobre una línea recta, debe encontrar siempre regiones donde moverse. Si el sistema estelar no colapsa sobre sí mismo por acción de la gravedad, siempre, y a toda distancia, se deberán encontrar estrellas, en número infinito, entre las que la fuerza de gravitación actúa en forma instantánea y a distancia, a través del espacio vacío. Y si se quiere encontrar que los fenómenos cumplan las leyes y propiedades deducidas geométricamente, el espacio-tiempo debe también ser geométrico, euclidiano, plano, infinito y único. El espacio de Newton es un espacio profano, sin lugares distintos o especiales y sin jerarquías sacralizadoras: es un espacio laico, sin lugar para los ángeles. Es el escenario ideal para que actúen los científicos del Iluminismo, es el mejor sitio imaginable para creer en la razón.

Notablemente, Newton no compartía para nada esta postura más bien volteriana (y hasta cartesiana, se podría decir, con muchos recaudos). Muy por el contrario, tanto él como los teólogos ingleses Bentley, Harris, Clarke y Derharn creyeron ver en los Principia una base perfecta para la fundación de una teología natural de cuño newtoniano y una imagen del mundo donde la Providencia estaba presente, según las exigencias del anglicanismo latitudinario, la religión que profesaba Newton. Incluso pensaban que el sistema newtoniano evitaba el mecanicismo y el ateísmo supuestamente implícito en el sistema cartesiano (del cual ya tendremos ocasión de hablar), defectos que se agregaban al no despreciable de ser falso, como el mismo Newton había demostrado. Newton mismo contribuyó activamente a sustentar esta postura y en sus últimos años llegó casi a identificar a Dios con el espacio absoluto, algo así como un éter invisible y omnipresente, cuya divina y continua intervención permitía el funcionamiento de las leyes físicas y la acción a distancia de la gravitación universal.

Buena parte de estas cuestiones ocuparon la polémica siguiente a la aparición de los Principia. La mecánica newtoniana, aunque rápidamente aceptada en Inglaterra, encontró más resistencias en Europa, donde debió luchar con paciencia contra los torbellinos y la física del plenum de Descartes. Voltaire, newtoniano acérrimo, comentaba risueñamente:

Un francés que llega a Londres encuentra las cosas muy cambiadas en filosofía, como en todo lo demás. Ha dejado el mundo lleno: se lo encuentra vacío. En París se ve el mundo compuesto de torbellinos de materia sutil; en Londres no se ve nada de eso.

El problema de la acción a distancia de la gravedad no fue el menor de los escollos: muchos científicos de la época la consideraban imposible, y criticaban la fuerza de gravitación como un elemento místico, espiritual, metafísico, que Newton había introducido de contrabando.

Newton contestó en la segunda edición de los Principia:

No he podido deducir a partir de los fenómenos las razones de estas propiedades de la gravedad y yo no imagino hipótesis. Pues lo que no se deduce de los fenómenos ha de ser llamado hipótesis; y las hipótesis, bien metafísicas, bien físicas o de cualidades ocultas o mecánicas, no tienen lugar dentro de la Filosofía experimental.

Entre otras cosas, la polémica entre Newton y Leibniz sobre la prioridad en el descubrimiento del cálculo infinitesimal erizó y emponzoñó la resistencia a la mecánica newtoniana en el continente europeo. Sin embargo, a mediados del siglo XVIII, el nuevo sistema del mundo estaba firmemente asentado, y aun los cartesianos más recalcitrantes se batían en retirada.

El regreso del cometa Halley

La primera persona que aceptó el desafío y la oportunidad que le ofrecía la obra de Newton fue Edmond Halley, que puede considerarse el primer científico posnewtoniano y que, digamos de paso, había pagado de su bolsillo la publicación de los Principia, ya que la Royal Society estaba quebrada a raíz de la publicación de otro libro científico, History of Fishes, de Ray y Willughby. Halley desarrolló su interés por los cometas intercambiando una avalancha de cartas en las que discutía el tema con Newton y demostrando que muchos de ellos recorrían órbitas elípticas alrededor del Sol. En 1682 había pasado un cometa y, estudiando los datos históricos, Halley comenzó a sospechar que ese mismo cuerpo era el que había sido visto y descripto en 1607 por Kepler y 76 años antes por Petrus Apianus. Predijo entonces que el cometa de 1682 regresaría «hacia el año 1757», cumpliendo así las leyes de Newton. No fue exacto, pero efectivamente, el día de Navidad de 1758, 16 años después de la muerte de Halley y 15 después de la de Newton, el astrónomo aficionado Johann Georg Palitzsch vio, cerca de Júpiter, un punto de luz que se agrandaba noche a noche.

¡Era el cometa Halley, que volvía!

Arrastrado por la Gran Ley de Gravitación Universal, acudía a la cita, aunque algo retrasado por culpa de la atracción de Júpiter y Saturno.

La predicción del regreso del cometa Halley aportó una prueba formidable y Newton y la física de Newton se convirtieron en el paradigma de la física y de toda ciencia. No hubo disciplina que no aspirara al rigor newtoniano.

Y, dicho sea de paso, las observaciones del cometa Halley se utilizaron para calcular la distancia de la Tierra al Sol, dando como resultado una cantidad equivalente a 153 millones de kilómetros, que se aproxima asombrosamente al resultado de la mejor medición moderna: 149,6 millones de kilómetros.

Lo interesante es que el sistema de Newton logró un triunfo casi completo y se asentó como un sistema puramente mecánico, libre de las desafortunadas especulaciones de su propio autor sobre la intervención de la Providencia para garantizar a cada instante el cumplimiento de la Ley de Gravitación Universal. El espacio absoluto, infinito, vacío, profano, geométrico y euclideano de Newton, sobre el que fluye el tiempo continuo y matemático y donde la gravedad actúa a distancia, se impuso como visión del cosmos… y así se quedaría durante más de dos siglos, hasta que las poderosas manos de Einstein lo curvaran, sometiéndolo al rigor de nuevas geometrías.

El problema —perturbador, por cierto— de la acción a distancia fue discretamente obviado y la naturaleza de la fuerza de atracción (sobre la que Newton afirmó al principio «que él no forjaba hipótesis» y que la trataba como una fuerza matemática) fue asimilada como una propiedad más en la materia sobre la que, precisamente, no se forjaban hipótesis. El problema quedó pendiente y otra vez hubo que esperar hasta 1915, cuando Einstein, al enunciar su Teoría General de la Relatividad, replanteó el asunto.