CAPÍTULO 29

El anhelo de la conservación y la ley de leyes

El siglo XIX fue el de las grandes teorías abarcadoras: ya vimos algunas de ellas, como la teoría de la evolución, la teoría cinética del calor o la teoría atómica, que habría de convertirse en el espinazo de la química. La sensación que podía tener un científico de la época es que se estaba accediendo al sustrato que anida por debajo de lo real y se estaban encontrando sus leyes fundamentales.

Pero ya no se trataba de un sustrato al estilo platónico, un mundo ideal del cual el nuestro es una suerte de imagen terrenal, por proyección, sino de un sustrato geométrico e invariante, ontológicamente previo a los fenómenos particulares: un «espacio» donde los fenómenos existen en su forma pura y del cual se puede tener un atisbo, o bien por medio del laboratorio, que es una ventana abierta hacia él, o bien por medio de ese otro laboratorio abstracto, perfecto y mental que son las matemáticas —reino de la verdad y la certeza por excelencia—, de donde resulta el mundo real por acumulación, confusión y mezcla de fenómenos.

En realidad, la búsqueda de los invariantes, de aquello que permanece frente a los cambios contingentes o a los tristes ciclos de nacimiento, crecimiento y muerte, de lo que verdaderamente existe, de los andamios oscuros y palpitantes que sostienen el edificio de la realidad, había empezado cuando empezó la ciencia. Basta, para demostrarlo, recordar el agua de Tales, el ápeiron, el aire de los milesios, el Ser de Parménides, los átomos de Demócrito y Leucipo, el propio mundo de las ideas de Platón, o la muy generalizada y pitagórica creencia de que las matemáticas subtienden la estructura de lo real.

La Edad Media no tuvo demasiado problema con este asunto, ya que el sustrato era el Dios cristiano, una postura mantenida tanto por la fe como por la coacción visible o invisible de las fuerzas que dominaban la política (la Iglesia y el Imperio, entre otras).

Pero con la ciencia moderna, todo cambió.

La búsqueda de invariantes: Descartes y Leibniz

Porque apenas la ciencia se separó de la filosofía y de la religión, sin romper lanzas del todo, la búsqueda de invariantes abandonó lo metafísico y se volcó hacia lo físico y lo geométrico. Los invariantes de los Principia de Newton fueron el espacio absoluto, siempre igual e idéntico a sí mismo, y el tiempo matemático que fluía sobre todo el universo. Una distancia espacial era siempre una distancia espacial, y un intervalo de tiempo era siempre un intervalo de tiempo, se midiera desde donde se midiera. Y, naturalmente, las leyes del movimiento y la Ley de Gravitación.

Pero antes había habido una postulación de Descartes que consideraba que Dios había puesto una cierta cantidad de movimiento al crear el mundo, y que eso era lo que permanecía siempre constante. Definía esa cantidad como el producto de la masa por la velocidad, y aunque no se refería a la conservación en relación con algún fenómeno particular, como el del choque de las bolas de billar (que estudió y describió con poco tino), proponía que Dios había creado la materia y la había organizado dotándola de un monto invariable, constante y eterno de movimiento y reposo.

Las deducciones de Descartes se derivaban generalmente más de principios metafísicos que de otra cosa, y acaso eso explique la curiosidad de que, en pleno siglo XVII, distinguiera tajantemente el movimiento y el reposo; sobre todo si tenemos en cuenta que había leído cuidadosamente a Galileo, quien como recordarán había dejado bien en claro que el movimiento y el reposo no eran dos estados sustancialmente diferentes sino relativos al observador, de modo que lo que está en reposo para un observador puede estar en movimiento para otro (y viceversa).

Más allá de sus errores mecánicos, o a pesar de ellos o —¿quién puede saberlo?— tal vez gracias a ellos, Descartes enunció el esbozo de lo que en física se llama una ley de conservación, es decir, la idea de que a través de cualquier cambio mecánico hay algo, una cantidad, que permanece invariable (en su caso, la cantidad de movimiento).

Otra de las grandes figuras de la física de aquellos tiempos, Christiaan Huygens, llegó a una conclusión diferente: aseguró que la cantidad de movimiento sólo se conservaba si se tomaban en cuenta las direcciones y sentido de las velocidades, lo cual tornaba todo demasiado complicado. Introdujo entonces otra cantidad:

La suma de los productos entre la masa y el cuadrado de la velocidad de cada cuerpo es la misma antes y después del choque.

Es decir: la masa por la velocidad al cuadrado antes del choque debía dar lo mismo que la masa por la velocidad al cuadrado después. Esa cantidad se conservaba y era un número, de modo que se podía prescindir del análisis de las direcciones y sentidos (es, ni más ni menos, el duplo de lo que hoy llamamos energía cinética, que no es exactamente m.v² sino ½ m.v²).

El siguiente actor del drama de la conservación fue el gran filósofo y científico Gottfried Leibniz (1646-1716). Leibniz, como Descartes, razonaba a partir de posturas metafísicas generales, pero estaba un poco más atento a los progresos de la física moderna: al adoptar la relatividad del movimiento enunciada por Galileo, rechazaba la posibilidad de que el sustrato de lo real fuera algo relativo al observador (y justamente el movimiento lo era) pero continuaba sosteniendo que tenía que haber algo que verdaderamente existiera de manera absoluta. Ese algo, sustrato inconfundible de lo real, era la fuerza, inherente a la materia y que subsistía por fuera de todo movimiento.

Así, pues, llamó a la cantidad en cuestión fuerza viva y consideró que se trataba de un principio general de la física: el principio de conservación de las fuerzas vivas. La fuerza viva era la causa del movimiento, la capacidad de actuar, que permitía el pasaje de la metafísica a la naturaleza. Analizando cuidadosamente el fenómeno de la caída de los cuerpos, Leibniz sostuvo que la cantidad propuesta por Huygens se conservaba en todos los casos. Lo que permanece invariante en todo cambio mecánico es el producto entre la masa del cuerpo y el cuadrado de su velocidad.

La conservación de la cantidad de movimiento (o de la vis viva), según demostró D´Alembert, podía deducirse matemáticamente a partir de la ley de Newton. Así quedó establecido un principio general en la mecánica, fundamental para los físicos de una época en que, justamente, la mecánica era el centro de la física (y de toda reflexión sobre la naturaleza).

Se había conseguido un principio de conservación, pero… ¿qué pasaba fuera de la mecánica? Porque si bien era la estrella, como ya les dije, no era la única rama de la física, sino que estaba rodeada por muchas otras, por ejemplo la que estudiaba el calor o la que estudiaba la electricidad. Empezó a dibujarse entonces la idea de que la ley de conservación de la fuerza viva había que extenderla a otros terrenos. Y así llegamos al siglo XIX, cuyo recorrido dio paso, en cincuenta o sesenta años, hacia la conquista de una formulación verdaderamente universal de conservación, la ley de leyes: el principio de conservación de la energía.

Veamos cómo se llegó hasta allí.

La causa de Mayer

Julius Robert Mayer (1814-1878) estudió medicina en Tübingen, visitó París cuando lo expulsaron, durante un año, de la universidad, y se embarcó en un navío holandés rumbo a Java, como médico de a bordo. Allí observó un fenómeno interesante y que lo sorprendió: al sangrar (el fatídico sistema «terapéutico» de las sangrías, que se aplicaba sin ton ni son y que producía los consecuentes desastres), al sangrar, decía, a los tripulantes, el rojo de la sangre era más intenso que en Europa. Lo comprobó con su propio cuerpo también y consideró que era un fenómeno que valía la pena explicar, o por lo menos tratar de hacerlo. La observación fue fortuita, desde ya, pero lo importante era tener una mente alerta para pescarla. Recordemos esta anécdota, por más que parezca que no tiene nada que ver con el asunto de la conservación, porque ya la retomaremos más adelante.

Cuando volvió a Europa, publicó un trabajo, «Sobre la determinación cuantitativa y cualitativa de las fuerzas», que fue prolijamente ignorado. Después se orientó al estudio del calor y del movimiento. Pero en 1842 escribió un segundo artículo, «Observaciones sobre las fuerzas inorgánicas de la naturaleza», donde se planteaba dos interrogantes básicos: ¿qué entendemos por fuerza? y ¿cómo se relacionan las distintas fuerzas entre sí?

Y sobre todo: ¿qué ocurre cuando el movimiento no da lugar al movimiento? ¿Qué pasa cuando un cuerpo cae desde cierta altura y se detiene al chocar con la tierra? La pregunta era, en verdad, qué era lo que ocurría cuando se salía del mundo de la mecánica.

Aclaremos una cosa: Mayer llamaba «fuerza» a un concepto que no tenía del todo claro y que no se había generalizado, pero que ya había sido propuesto y tenía su nombre, aunque él no lo sabía. La palabra había sido lanzada por Thomas Young, el mismo del experimento de las dos ranuras que explicó el fenómeno de la difracción (no lo dije en su momento, pero vale la pena aclarar que Young era un verdadero espíritu universal, de aquellos que indagan en todos los terrenos posibles del saber). El caso es que Young había propuesto una palabrita fundamental en 1807 para referirse al trabajo potencial almacenado en las cosas, que rápidamente se aplicó a cualquier fenómeno en el que se operara una conversión en trabajo.

Decía Young:

La palabra «energía» puede ser aplicada con mayor propiedad al producto entre la masa o el peso de un cuerpo y el cuadrado del número que expresa su velocidad.

Es decir, Young proponía llamar «energía» —resaltemos el término, que veremos adquirir la más alta generalidad en ciencia (aún más que la fuerza de gravitación, lo cual es decir mucho)— a la cantidad que Leibniz llamaba «vis viva», que Mayer llamaba «fuerza» y a la que nosotros, como ya les dije, llamamos energía cinética.

Mayer estaba formulando un concepto que se convertiría en la piedra basal de la física del siglo XIX. Y, como ocurre a menudo en la ciencia, lo hacía tanteando, especulando, pensando sin tener totalmente en claro las cosas. Era, en este sentido, bastante transparente en sus escritos:

Sé de qué hablo cuando digo materia pero no cuando digo fuerza. Si de un objeto afirmo que es material, quiero decir que posee unas cualidades bien definidas, como el peso o la extensión. Pero la noción de fuerza conlleva la idea de algo desconocido, hipotético. Pues bien, yo, Julius Mayer, propongo aquí una definición: las fuerzas son causas. Y antes de que objeten que en el cambio semántico no gané nada, les descubro mis intenciones: quiero aplicar a las fuerzas el principio de igualdad entre causa y efecto (causa aequat effectum).

Mayer, en realidad, razonaba así: en el mundo, las causas tienen que ser iguales a los efectos. Las causas, a su vez, se definen mediante dos propiedades esenciales:

1) En primer lugar, son indestructibles, no desaparecen (a lo sumo se vuelven efectos) y además pueden asumir diversas formas.

2) En segundo lugar, son cuantitativamente indestructibles y cualitativamente convertibles.

Mayer proponía así una especie de ley de conservación de las causas, un enunciado que a nosotros, desde nuestra terminología actual, nos puede parecer un tanto desconcertante.

Pero no para él, que además aclaraba que había solamente dos tipos de «causas» (las fuerzas y la materia) y que nunca se convertían una en otra, de acuerdo con la experiencia (lo cual era una afirmación bastante audaz). De modo que la materia, cuando funcionaba como causa, tenía a la materia por efecto y la fuerza, como causa, tenía como efecto a la fuerza.

El primer enunciado no es otro que la ley de conservación de la materia de Lavoisier: «nada se pierde, todo se transforma», esto es, la cantidad de materia involucrada en cualquier transformación química o física permanece siempre constante. El segundo es el de Leibniz.

Si era claro que la fuerza, o la fuerza viva, se conservaba, por la ya razonada indestructibilidad de las causas en el terreno de la mecánica, quedaba legitimada la pregunta de la que partía Mayer para hacer toda esta especulación, que como recordarán consistía en saber qué ocurría con las causas cuando el movimiento no tenía como consecuencia más movimiento. Por ejemplo, cuando una pelota choca contra una pared y su movimiento cesa: ¿en qué se ha convertido la causa? Si las fuerzas son causas, y las causas, como sabemos, son indestructibles, no se pueden destruir: sólo podrán cambiar de forma.

La forma de las fuerzas

Pero entonces: ¿qué otra forma, a la que nos hemos acostumbrado, como nos acostumbramos al movimiento, es capaz de asumir la fuerza? Mayer observaba que, llegados a este punto, sólo la experiencia podía conducir a una conclusión. Y su experiencia determinante había ocurrido en altamar.

En uno de los momentos angustiantes de su travesía a las entonces Indias Holandesas, actualmente Indonesia, nuestro amigo tuvo una intuición: mientras el mar se agitaba en torno y se debatían angustiosamente los tres mástiles de su nave, pensó que las aguas agitadas debían ser más cálidas que las calmas. En el momento, aquélla no era más que una impresión pasajera, y acaso equivocada, pero en cuanto las aguas se calmaron hizo lo que todo buen científico hubiese hecho en su lugar: reprodujo la situación para verificar si su intuición había sido correcta. Llenó la mitad de una botella de agua y comenzó a sacudirla violentamente. Al cabo de unos minutos, pudo comprobar que había elevado la temperatura del agua en un grado, de doce a trece grados centígrados. ¿De dónde provenía ese calor que mediante la agitación podía ser llamado a la existencia en cuanto uno quisiera? No lo dudó: de las vibraciones mismas.

Como el Beagle a Darwin, la experiencia de a bordo le sirvió a Mayer para responder a la pregunta fundamental:

La otra forma que puede asumir la fuerza es el calor, y sin el reconocimiento de una conexión causal entre movimiento y calor es tan difícil explicar la producción de calor como dar cuenta del movimiento que desaparece.

(Lo cual explicaba, de paso —y acá cumplo con mi promesa de retomar el problema de las sangrías en el barco—, el fenómeno sobre el rojo brillante de la sangre que le había llamado la atención en un principio: el calor de los trópicos hacía que el cuerpo no necesitara «quemar» tanto oxígeno para mantener la temperatura; al quedar más oxígeno en sangre, se veía con ese particular color rojo.)

Mayer fue cauteloso al respecto:

No quiero establecer definitivamente que, en muchos casos, no se pueda hallar otro efecto del movimiento más que el calor, y que no se pueda encontrar otra causa para el calor producido más que el movimiento. No hablo en esos términos. Más bien prefiero suponer que el calor procede del movimiento. De otro modo deberíamos resignarnos a la observación de una causa sin efecto, y de un efecto sin una causa.

Y trató de establecer una conexión cuantitativa:

Si existe una ecuación que relaciona las fuerzas y el movimiento, por un lado, con el calor, por el otro, su solución exige que respondamos a la siguiente pregunta: ¿cuál es la cantidad de calor que corresponde a una dada cantidad de movimiento? Podríamos, por ejemplo, preguntarnos a qué altura debe ser elevado un peso dado para que el movimiento desarrollado en la caída sea equivalente a un aumento de temperatura de un grado centígrado de una cantidad de agua que pese lo mismo que el peso.

Para determinarlo, hizo una serie de experimentos, cuya conclusión fue que

elevar la temperatura de una determinada cantidad de agua de cero a un grado centígrado corresponde a una caída de un peso igual al del agua desde una altura de trescientos sesenta y cinco metros.

La intuición de Mayer había reconocido una conexión causal entre el calor y el movimiento, una conexión que —ya vimos hace algunos capítulos— había sido registrada por el extravagante, pintoresco y poco simpático conde Rumford. Las ideas de Mayer, primero, y las de James Joule después, rescataron del olvido sus curiosas y notables experiencias con cañones y caballos.

Pero la vida de Mayer se convirtió rápidamente en un abismo. En 1848, en rápida sucesión, murieron dos de sus hijos. Al año siguiente intentó suicidarse y fracasó: saltó desde la ventana de un tercer piso y se arruinó definitivamente las piernas. Dos años después fue internado en una institución mental. Imagínense lo cruel y siniestra que era una institución mental en ese entonces: hasta hacía relativamente poco, los locos eran exhibidos los domingos en las ferias de atracciones. Mayer sobrevivió, pero nunca se recuperó completamente. Desde entonces fue hasta tal punto ignorado que cuando el editor de la revista que había publicado sus trabajos por primera vez disertó públicamente sobre las ideas de Mayer, en 1858, se refirió a él como a un hombre muerto… ¡Y viviría todavía veinte años más!

Por suerte para Mayer, a partir de 1858, Hermann von Helm­holtz (1821-1894), y Clausius (1822-1888) redescubrieron su obra y le retribuyeron la credibilidad que merecía. Mayer recobró su salud, o parte de ella, y fue premiado con la medalla Copley de la Royal Society en 1871, siete años antes de su muerte.

La fuerza de Joule

Por un camino distinto, un cierto industrial inglés llegó casi a las mismas conclusiones que Mayer: James Prescott Joule (1818-1889). A diferencia de la de su colega, su vida estuvo libre de complicaciones y desgraciados avatares: a los veintitrés años era ya un industrial establecido, que financiaba sus inquietudes científicas con las ganancias de una cervecería heredada de su padre que poseía cerca de Manchester y que se sentía fascinado por las máquinas eléctricas de su fábrica, en las que no dejaba de observar que en los hilos conductores, a medida que la corriente circulaba, se generaba calor. Resulta que el calor estaba directamente relacionado con la cantidad de combustible que la máquina consumía, lo cual lo llevó a iniciar un inmediato estudio de la cuestión.

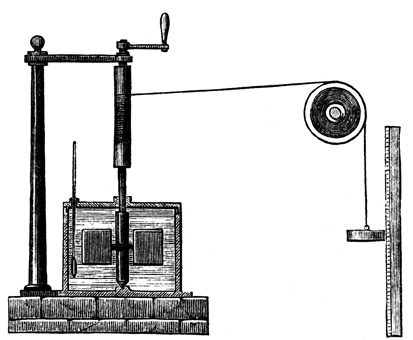
RUEDA DE PALETAS DE JOULE

Con la misma suposición de fondo que Mayer y Rumford (esto es, que de algún modo el calor y el trabajo mecánico eran dos aspectos de un mismo fenómeno, que se manifestaba, muy claramente, con el rozamiento), Joule inició sus investigaciones y llegó a la conclusión de que existía, en efecto, una relación invariable entre el trabajo y el calor. Otra vez como Mayer, supuso que si el calor podía traducirse en movimiento (y viceversa), su relación tenía que poder medirse cuantitativamente, por lo cual se concentró en establecer numéricamente esa equivalencia.

El más famoso de sus experimentos fue el de la rueda de paletas. Joule elevaba el peso mediante la manivela; el peso gradualmente descendía y hacía girar las paletas que, sumergidas en el agua, giraban. Al cabo de un cierto tiempo, el peso alcanzaba su punto más bajo y las paletas se detenían. Joule medía entonces el cambio de temperatura del agua. La explicación era sencilla: la fuerza viva del peso, como la llamaba Leibniz, o la fuerza, como la llamaba Mayer (o el propio Joule), se había convertido en calor mediante el rozamiento de las paletas contra el agua. Joule medía el cambio de temperatura y calculaba la cantidad de calor empleado, al tiempo que comprobaba que la cantidad de calor producida por el rozamiento de los cuerpos, sólidos o líquidos, era siempre proporcional a la cantidad de fuerza gastada.

La cantidad de calor necesaria para elevar la temperatura de una libra de agua en un grado Fahrenheit equivale al gasto de una fuerza mecánica que representa la caída de 50 kilos de una altura de un metro.

Establecida la relación entre calor y movimiento, en 1847 presentó sus ideas en la Asociación Británica para el Avance de las Ciencias, en Oxford. William Thomson, probablemente el más famoso científico inglés del momento (que más tarde se llamaría Lord Kelvin), asistió a aquella presentación y, tras algunas dudas, se convenció de las ideas de Joule.

Aquí hubo una pequeña disputa de prioridades. Mayer se enteró del trabajo de Joule y escribió a la Academia Francesa de Ciencias para dejar en claro que él había sido el primero que había tenido la idea de la equivalencia (en lo cual tenía perfecta razón). En cuanto su carta fue publicada, Joule reaccionó. Sabía que el prestigio científico de Thomson, que lo apoyaba a él, prevalecería ante cualquier academia.

Pero Thomson fue diplomático y obró con verdadera elegancia: le sugirió a Joule que admitiera la prioridad de Mayer sobre la idea del equivalente mecánico, pero que reclamara su propia prioridad sobre la verificación experimental.

Lo cierto es que Joule había terminado por establecer numéricamente la equivalencia entre el calor y el movimiento. Pero esa equivalencia, ¿no suponía la existencia de otras? En términos propios de Mayer: ¿no existirían nuevas formas equivalentes del calor y el movimiento a las que no nos habíamos acostumbrado todavía?

Helmholtz y, finalmente, la Gran Ley

Hermann Helmholtz nació en Potsdam, Alemania, en 1821. Hijo de un profesor mal pago de colegio secundario, que había servido en el ejército prusiano contra Napoleón, asistió a los cursos de filosofía y de literatura que impartía su padre. Le interesaba la física y quería estudiar en la universidad, pero la posición económica de la familia exigía de Hermann la obtención de una beca, y como el gobierno sólo sostenía económicamente a los estudiantes de medicina, no tuvo más remedio que iniciar el camino hacia la profesión de médico.

Así, estudió en Berlín, pero asistió paralelamente a otros cursos de la universidad, como los de química y fisiología. Incursionó en las matemáticas por cuenta propia, leyendo a Euclides obviamente y a Laplace, y llegó, de alguna manera, a las mismas conclusiones que Mayer y Joule.

En 1847 escribió un artículo («Sobre la conservación de la Fuerza») en el que estudiaba los principios matemáticos que subyacen al principio de conservación, donde mostraba que todo sistema mecánico está sometido a la ley de conservación de la fuerza.

Pero iba un paso más allá y sostenía que esa fuerza podía ser de dos tipos: o bien fuerza viva, tal como la entendía Leibniz, o bien lo que él llamaba fuerza de tensión, entre la que se incluían todas las fuerzas conocidas (la fuerza de gravedad, la de atracción eléctrica, la elástica). A partir de allí, generalizaba a una ley de conservación de la fuerza y desarrollaba las consecuencias de esa hipótesis en los distintos campos de la física (el calor, la electricidad, el magnetismo, las reacciones químicas).

La constatación del alcance general de la ley debe ser vista, al parecer, como una de las tareas principales que ocupará a los físicos en el futuro inmediato.

En 1862 avanzó un poco más: en una conferencia en Karlsruhe, la misma ciudad que dos años antes había albergado el primer congreso internacional de química, sostuvo que en las últimas décadas el desarrollo científico había conducido al reconocimiento de una nueva ley universal, rectora de todos los fenómenos naturales, incluso —afirmaba con entusiasmo— los de los tiempos más remotos y los lugares más distantes.

La ley que enunció fue la que llamamos de conservación de la energía, y establece que la cantidad de energía que puede ponerse en acción en la naturaleza es inalterable, es decir, no puede aumentarse ni disminuirse. Como muestran los experimentos, allí donde se pierde una determinada cantidad de trabajo mecánico, se obtiene una cantidad equivalente de calor, o de fuerza química, por ejemplo, e inversamente, cuando se pierde calor, se gana una cantidad equivalente de fuerza química, o mecánica, y otra vez, cuando la fuerza química desaparece, aparece una cantidad equivalente de calor o trabajo. Es decir que en todos los intercambios entre diversas fuerzas naturales inorgánicas, la capacidad para realizar trabajo, la energía, desaparece bajo una forma para reaparecer bajo otra forma, exactamente en la misma cantidad. Pero en el proceso total esa energía no aumenta ni disminuye, sino que siempre permanece constante.

Así, la cantidad de energía del universo es inalterable: podrá alterar su forma, podrá variar su ubicación, pero su cantidad no cambiará. El universo posee, de una vez y para siempre, una reserva de energía que no puede ser modificada por ningún fenómeno, que no puede aumentar ni disminuir, que permanece inconmovible mientras, a su alrededor, todo se transforma.

Era la ley de leyes

La ley de conservación de la energía era un principio feliz: todo lo que hay habrá, y nunca perderemos nada. Se sucederán las generaciones, y las máquinas, se levantará el polvo de la tierra por la acción de las ruedas que producen rozamiento y calor y volverá a posarse, pero la cantidad de energía disponible para realizar trabajo y hacer funcionar el mundo siempre será la misma y estará ahí, ya sea almacenada en la materia (energía química), en el movimiento (energía cinética), en el campo gravitatorio (energía potencial), en la incipiente electricidad o en el calor, y cualquiera de estos tipos de energía se podría reciclar indefinidamente.

¡No podía existir un principio mayor de plenitud en una ciencia que se expandía aceleradamente, y que con instrumentos cada vez más finos, con matemáticas cada vez más precisas y una confianza cada vez más robustecida, se sentía capaz de escrutar todos los rincones hasta agitarlos!

El principio de conservación de la energía (o primer principio de la termodinámica, la palabra que Lord Kelvin acuñó en 1849 para designar el estudio del calor) y el mismo concepto de energía fueron las ideas unificadoras de la física en el siglo XIX, así como la Teoría de la Evolución y la Teoría Celular lo fueron en biología.

Junto a la idea de conservación de la materia, que había enunciado Lavoisier, la conservación de la energía, que también se transforma sin perderse, pintaba un panorama del mundo: a la viejísima pregunta «¿qué es lo que hay?», que había sido respondida de maneras tan diversas a lo largo de la historia, la respuesta no era ni el agua, ni el Ser, ni los cuatro elementos, ni la fuerza vital, ni siquiera la sustancia divina (cuando Napoleón preguntó a Laplace por qué no había mencionado al Sumo Hacedor en su Mecánica Celeste, Laplace contestó: «No he tenido necesidad de esa hipótesis»): en el universo solamente hay materia y energía, y nada de ellas se pierde jamás.

Era un panorama tranquilizador: el mundo como mecanismo cedía a la imagen del mundo como un motor. La materia y todos los movimientos eran acompañados por un combustible, la energía, que no se consumía sino que se transformaba.

Entonces los científicos vieron el mundo que habían construido (o explicado) y constataron que era bueno. Aunque no por mucho tiempo.

Carnot sienta las bases

Porque pronto el segundo principio de la termodinámica iba a echar un balde de agua fría sobre el optimismo del primero.

No voy a contarles en detalle la conquista, si es que así puede llamársela, del segundo principio, porque se volvería todo demasiado técnico. Pero sí puede decirse que sus primeras formulaciones se remontan al libro Reflexions sur la puissance motive du feu (Reflexiones sobre la potencia motriz del fuego) que en 1824 publicó el joven Sadi Carnot (1796-1832), hijo del Gran Carnot, que había participado de manera decisiva en la Revolución Francesa (organizando y armando a los ejércitos de la república) y que luego se convertiría en ministro de Guerra de Napoleón Bonaparte.

En su libro, Carnot (hijo, obviamente) analizaba la eficiencia de las máquinas para convertir el calor en trabajo y demostraba que el trabajo se producía cuando el calor pasaba de una fuente con temperatura más alta a otra más baja, al tiempo que constataba que siempre el calor fluía de un objeto más caliente a otro más frío, y nunca al revés (lo cual es ya un enunciado primitivo del segundo principio).

Carnot murió de cólera a los 36 años de edad, y aunque sus cuadernos contenían más descubrimientos relacionados con esta teoría, en la época en que falleció aún no habían sido publicados y la mayoría fueron quemados, junto con sus efectos personales. Allí aparecían algunas cosas que luego proclamarían los trabajos de Mayer y Joule, lo cual muestra, de paso y una vez más, que las ideas científicas no sólo funcionan en la mente de un científico particularmente genial, sino que flotan en el «espíritu de la época».

El problema es que las Réflexions no tuvieron mucha influencia en sus tiempos: recién la tendrían sobre la generación de físicos que llevó a cabo la revolución de la termodinámica, especialmente William Thomson y Rudolf Clausius, de quienes tendremos que hablar a continuación.

William Thomson (Lord Kelvin) y las leyes de la termodinámica

William Thomson, que más tarde se llamaría lord Kelvin, pasó casi toda su vida en entornos universitarios. Su padre, James Thomson, era profesor de matemáticas en la Royal Academical Institution de Belfast hasta que se mudó a Glasgow, para ocupar un cargo allí. William asistió a clases universitarias desde los 10 años (¡desde los 10 años!) y escribió su primer trabajo a los 16. La vocación estaba clara: unos años más tarde, se trasladó a la Universidad de Cambridge y se licenció en 1845, habiendo obtenido ya varios premios por sus ensayos científicos y habiendo publicado una serie de trabajos en el Cambridge Mathematical Journal.

Tras conseguir la licenciatura, trabajó durante algún tiempo en París, donde se familiarizó con la obra de Carnot. Luego retornó a Glasgow en 1846 (cuando tenía 22 años) y ocupó la cátedra de Filosofía Natural hasta que se jubiló, a los 75 años, en 1899. Y fíjense en esta curiosidad: después de jubilarse, se matriculó como estudiante de investigación para no perder la práctica, con lo que, además de haber sido el estudiante más joven que hubo en aquella universidad, llegó a ser también el más viejo. Falleció en Largs, a unos cincuenta kilómetros de Glasgow, el 17 de diciembre de 1907.

En realidad, su fama e importancia en Inglaterra se basaban especialmente en sus contribuciones a lo que ahora llamaríamos «ciencia aplicada»: fue responsable del éxito del primer cable telegráfico que funcionó a través del océano Atlántico, que constituyó un paso fundamental en la globalización de las comunicaciones (proceso que aún estamos viviendo hoy, con Internet, y que no sabemos hasta dónde llegará) e hizo una gran fortuna con patentes de distintos inventos, lo cual le valió el título de Sir en 1866, y el de lord Kelvin en 1892, nombre que tomó del río que atraviesa la Universidad de Glasgow.

La escala de temperatura absoluta o termodinámica se llama escala Kelvin en su honor: para no entrar en demasiados detalles engorrosos, digamos que si el calor es movimiento de las partículas, el cero absoluto, la temperatura mínima posible, se alcanza (en realidad no se puede alcanzar prácticamente) cuando todas las partículas están quietas y equivale a 273,15 grados centígrados bajo cero, o 0 grado Kelvin.

Pero quizá su contribución más importante fue la de organizar la termodinámica como una disciplina científica hecha y derecha en la segunda mitad del siglo XIX.

Y aquí entra a jugar Rudolf Clausius (1822-1888), que en Alemania estaba puliendo y desarrollando las teorías de Carnot. Lord Kelvin supo de los trabajos de Clausius a principios de la década de 1850, cuando ya estaba trabajando en una línea similar. Ambos llegaron, más o menos independientemente, a la segunda ley de la termodinámica, que dice, en una de sus formulaciones más brutales, que bajo ninguna, absolutamente ninguna circunstancia, el calor puede por sí mismo pasar de un objeto más frío a otro más caliente. Pero fundamentalmente establece que si se utiliza calor para producir trabajo y luego se quiere usar ese trabajo para recuperar el calor, no se podrá recuperarlo del todo. Esto es: hay algo que se ha transformado definitivamente en calor.

La energía, en el curso de sus transformaciones, se desgasta, y en todos los procesos una parte de ella se convierte irremisible e irreversiblemente en calor. Se desgasta mediante una cantidad que Clausius llamó «entropía» y que en cada proceso físico termodinámico, o en los procesos mecánicos mediante el rozamiento, aumenta. En el universo sólo son posibles los procesos en los que la entropía aumenta. Dicho de una manera más lúgubre, toda la energía se va convirtiendo lenta, sistemática y fatalmente en calor.

Si el primer principio de la termodinámica era una ley optimista, que garantizaba la eternidad del universo, el segundo principio era decididamente pesimista, ya que aseguraba que el constante aumento de la entropía conduciría inexorablemente a la muerte térmica del cosmos: como en cada proceso físico una parte de la energía se convierte en calor, tarde o temprano la totalidad de la energía sería calor, incapaz de producir trabajo mecánico alguno, y todo movimiento cesaría, todo se hundiría en una nada sin límites, en la que flotaría la materia disgregada. Una inmensa nada inmóvil e inerte donde, aunque por supuesto la cantidad de energía total sería idéntica, la entropía alcanzaría su máximo y ningún fenómeno podría producirse, porque en ningún caso la entropía podría disminuir.

El descubrimiento de la entropía resultaba tristísimo. No era nada agradable, en medio de una época de confianza y expansión, tomar conciencia de que cada fósforo que se enciende, cada movimiento, cada pensamiento (que genera calor a partir de los circuitos eléctricos cerebrales) aceleran la muerte térmica del universo; no era el mejor momento para saber con total certeza que todos los esfuerzos terminarían siendo mera radiación térmica, vulgar temperatura, miserable vacío caliente. La entropía marcaba una flecha del tiempo que señalaba la tumba, un reloj que contaba minuciosamente los segundos hasta disolverse él mismo en un calórico final. En un mundo donde se pensaba que todos los procesos eran reversibles, el segundo principio de la termodinámica aseguraba que el mundo evolucionaba en una sola dirección: la de la muerte térmica.

No podían funcionar eternamente los ciclos geológicos que había soñado Hutton, ni resultaba cierta su idea de que la Tierra era un enorme mecanismo, sin comienzo ni atisbo de final: en cada ciclo, la entropía forzosamente tenía que aumentar. Tampoco el Sol podría brillar por siempre, porque cualesquiera que fueran las formas en que producía su calor (por entonces desconocidas), no había forma ni mecanismo natural alguno que pudiera restituir ese calor perdido para que el Sol siguiera funcionando. Y así siguiendo.

Sin embargo, había una paradoja, algo que no encajaba del todo. El segundo principio venía a declarar que los procesos termodinámicos eran irreversibles, pero resulta que el calor era un proceso mecánico, originado en el movimiento de las moléculas. Y la mecánica, a diferencia de la termodinámica, sí es reversible (salvo por el detalle del rozamiento). Dado que los flujos de calor se daban siempre de una fuente más caliente a una más fría (el único proceso permitido), era posible pensar que si se invertía el movimiento de las moléculas se podría revertir el proceso. Porque… ¿cómo podía ser que un proceso reversible como el del movimiento de las moléculas pudiera dar origen a un proceso irreversible como el flujo de calor, que no era sino el resultado de ese movimiento?

El problema dejó perplejos a los físicos que estudiaban la termodinámica, incluyendo al propio Maxwell, que sembró la sospecha de que el segundo principio era de naturaleza estadística.

Veamos cómo es eso.

Boltzmann y la interpretación estadística de la entropía

Ludwig Boltzmann nació en 1844 en Viena, en 1867 se doctoró en Física, ocupó distintas cátedras y enseguida se destacó como una autoridad en mecánica estadística, dejando su nombre vinculado a figuras de la talla de Helmholtz y el mismísimo Maxwell, dios del electromagnetismo. Su fama crecía aceleradamente y tanto prometedores talentos como figuras importantes se acercaban para trabajar o polemizar con él.

Pero además de su enorme cantidad de trabajo en la mecánica estadística, Boltzmann le encontró una vuelta al segundo principio de la termodinámica o ley del aumento de la entropía, considerada como algo inexorable por la mayoría de sus contemporáneos (aunque algunos planteaban sus dudas).

Lo que hizo fue interpretar la entropía como la medida del desorden de un sistema. Cuanto más desordenado, más entropía: por poner un solo ejemplo, el hecho de que las moléculas se distribuyan al azar ocupando todo el ámbito donde el volátil autor de estas páginas escribe hace que el sistema sea más desordenado que si todas las moléculas que hay en ese mismo ámbito se apretujaran en un rincón. Del mismo modo, el calor es el estado de máximo desorden.

Boltzmann transformó la inexorabilidad en una alta probabilidad: según su interpretación, no es que el universo deba evolucionar fatalmente del orden al desorden, sino que, puesto que el número de estados desordenados es mucho, pero muchísimo mayor que el de ordenados, naturalmente se mueve de los estados menos probables a los más probables.

No hay, así, nada devastadoramente fatal en el aumento de la entropía: después de todo, la entropía podría disminuir, del mismo modo que ninguna ley impide que en la ruleta salga el número 5 un millón de millones de veces seguidas (si ocurriera no habría que cambiar una sola palabra en los libros de probabilidad) o que las moléculas de una habitación se ordenen espontáneamente (violando la ley del aumento de la entropía) y se acumulen en una de las esquinas, asfixiando de paso a quienes estén presentes. Entonces no es que fuera imposible que el calor se transmitiera de un cuerpo más frío a uno más caliente: era, en realidad, altísimamente improbable.

En cierta medida, Boltzmann les dio al mundo y a los fenómenos una remota, remotísima esperanza. Le quitó a la segunda ley su aura funeraria, su aureola de muerte (térmica) inconmensurable; abrió, si se quiere, una rendija por la que existe una lejanísima posibilidad de atisbar. Transformó la certeza absoluta del fin en un «optimismo» atado a bajísimas probabilidades.

Pero no se hagan ilusiones: la probabilidad de que un cuerpo frío se caliente espontáneamente, o de que una mancha de tinta disuelta en un vaso se concentre en un punto, o la de que un jarrón roto vuelva a recomponerse sólo es tan remota que no alcanzaría con que el universo durara cien mil millones de millones de millones de veces lo que va a durar como para que pudiera presenciarse un fenómeno así.

El 5 de octubre de 1906, Boltzmann se suicidó, ahorcándose en una playa italiana cerca de Trieste. En su lápida figura la fórmula S= k log W base de su interpretación un poco más optimista o mejor, un poco menos pesimista de la ley que ordena a la entropía aumentar.

Síntomas

Los dos principios de la termodinámica, junto a la Teoría de la Evolución, la teoría celular y otros desarrollos que ya vimos y seguiremos viendo, parecían alcanzar la plenitud de la ciencia. No en el sentido de que ya todo estuviera dominado, sino en el no menos fuerte de que se sabía el procedimiento a seguir para aquellas regiones no conquistadas aún. No se había explorado todo el territorio, pero el mapa estaba diseñado a grandes rasgos y se avanzaba con brújulas de precisión.

Sin embargo, había algunas señales de que las cosas no eran del todo así, aunque es lógico que nadie las viera en su momento y que sólo las percibamos ahora con la ventaja que da la perspectiva.

Así como la ley de conservación de la energía, la ley de leyes, era un gran triunfo clásico, el segundo principio no respondía (en especial en la lectura de Boltzmann) exactamente al canon newtoniano y determinista. No se trataba de una ley de conservación, por empezar, e incluía el concepto no newtoniano y no determinista de probabilidad.

Y algo por el estilo estaba incrustado en la Teoría de la Evolución. La selección natural era una fuerza impredecible, que no apuntaba a ningún lugar definido, que, como el aumento de la entropía, no era reversible, y cuyo funcionamiento se podía sospechar estaba ligado de alguna manera a las probabilidades y a la forma azarosa en que los rasgos adaptativos se distribuían entre las poblaciones. Eran señales tenues, síntomas, pero no eran los únicos. Ya tendremos tiempo de analizarlos con detalle.