CAPÍTULO 30

El mapa y el territorio: las geometrías no euclidianas, el infinito y el éter

A ustedes puede sonarles conocido el título de este capítulo por dos motivos: o bien porque leyeron la preciosa novela de Michel Houllebecq, o bien porque ya lo leyeron aquí, unas páginas más atrás, cuando el volátil autor de estas páginas intentaba (acaso infructuosamente) organizar de alguna manera la enorme diversidad del pensamiento científico del siglo XIX.

Les decía allí que la ciencia de este siglo se sentía segura de sí misma y que, gracias a las grandes teorías generales y a los nuevos principios, creía contar con un mapa bien delineado y una brújula precisa con los que avanzar sobre territorios que —se sabía— restaban inexplorados.

Pero resulta que el mapa no estaba tan bien delineado y la brújula no era tan precisa como lo fueron demostrando poco a poco algunas de esas grandes teorías que, si bien fueron y siguen siendo de alguna manera el modelo y la culminación del pensamiento científico occidental, introdujeron pequeñas cuñas en el enorme edificio que había legado el siglo XVIII al introducir elementos probabilísticos que no encajaban del todo en el ideal de ciencia newtoniana y determinista.

Entre estos síntomas que ponían en duda la precisión del mapa y la afinación de la brújula apareció uno verdaderamente gravísimo. Verdaderamente gravísimo, digo, porque apuntaba ni más ni menos que al cuestionamiento de la sólida y establecida concepción del espacio, ese lugar absoluto y feliz que había sido fijado en el siglo XVII, inmóvil, eternamente igual a sí mismo, previo a todos los fenómenos que ocurrían en él y que las matemáticas y la geometría describían en forma exhaustiva. De repente, ya no era tan claro qué forma tenía.

Y todo, todo, porque había algo en los axiomas del viejo Euclides que no cerraba. ¿Recuerdan el quinto postulado? Repasemos un poco.

I. LAS GEOMETRÍAS NO EUCLIDIANAS

Recordando a Euclides

Cuando hablamos, hace ya mucho, de la Escuela de Alejandría y de Euclides, les contaba que se había hecho cargo del desastre pitagórico (el descubrimiento de la irracionalidad de la raíz cuadrada de 2) y se había puesto a edificar las matemáticas de forma exclusivamente geométrica en sus Elementos, en los que construía toda la geometría en una obra tan amplia y definitiva que puede equipararse a los Principia de Newton, o El origen de las especies de Darwin, y que fue, después de la Biblia, el libro más editado.

También les decía que Euclides tomaba uno de los grandes caminos de la filosofía griega, se apartaba de cualquier corriente empirista, se ubicaba en el «puro pensar» de los pitagóricos y, en la tradición de Parménides de Elea, enfrentaba el dilema que se había dejado sin resolver: si se construía un sistema basado en el pensar, también era necesario resolver el problema de por dónde había que empezar. Euclides lo resolvió, como recordarán, imponiendo algunos principios que daba por verdaderos sin discutirlos: los axiomas o los postulados, de los cuales debía poder deducirse todo enunciado de la geometría, aun el más intrincado. De paso sea dicho, Euclides dejaba un asuntillo sin resolver o resuelto de una manera poco convincente: el de la arbitrariedad en la elección de los postulados, que se justificaba afirmando que se trataba de verdades «autoevidentes», cosas de las que no se podía dudar, y que no necesitaban demostración. Los postulados eran claros, simples, contundentes y eso —se suponía— alcanzaba para que fueran legítimos. Repasemos brevemente algunos de ellos:

1) Que por cualquier punto se pueda trazar una recta que pase por otro punto cualquiera.

2) Que toda recta limitada pueda prolongarse indefinidamente en la misma dirección.

3) Que con un centro dado y un radio dado se pueda trazar un círculo.

4) Que todos los ángulos rectos sean iguales entre sí.

Hasta aquí, todo parece en orden. Pero presten atención al siguiente:

5) Que si una recta, al cortar a otras dos, forma los ángulos internos de un mismo lado menores que dos rectos, esas dos rectas prolongadas indefinidamente se cortan del lado en que están los ángulos menores que dos rectos.

Los primeros cuatro son sencillos y no presentan mayores dificultades. Pero el quinto postulado… daba mucha tela para cortar.

El misterio del quinto postulado

El quinto postulado era molesto. No tanto porque hubiera alguna duda sobre su verdad sino a causa de su enunciado: imagino que ustedes, amables lectores del libro, habrán tenido que examinarlo detenidamente para comprender qué es lo que está diciendo. Y seguramente recién cuando vieron el dibujo se les aclaró el panorama. Lo cual es lógico, porque tal y como fue enunciado, el postulado es demasiado complicado: parece artificioso y carece de la sencillez de los otros. El propio Euclides había tomado buena nota de este asunto y, siempre que pudo, evitó recurrir a él. De hecho, el quinto postulado y su artificiosa textura se convirtieron en un dolor de cabeza permanente… durante dos mil años, hasta tal punto que ¡en 1759! D’Alembert llamó al problema «el escándalo de los elementos de la geometría».

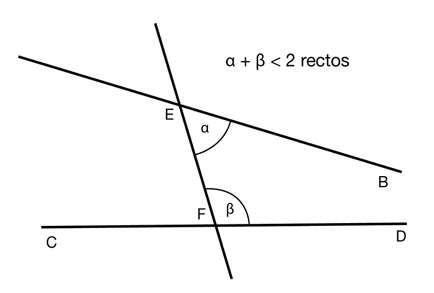
Ya desde la Antigüedad se habían hecho intentos por reemplazarlo por algún enunciado que pareciera más evidente y sencillo. Hubo muchas propuestas, pero la que se impuso y es más famosa hoy en día fue la de John Plavfair (1748-1813), quien recién en 1795 aseguró que el postulado euclidiano podía simplificarse muchísimo si se lo reemplazaba por uno que dijera que por un punto exterior a una recta pasa una sola paralela. De ahí que el quinto postulado sea conocido como «el postulado de las paralelas», como lo llamaremos en adelante.

Hubo un segundo tipo de abordaje, que consistió en intentar demostrar el quinto postulado deduciéndolo de los otros, de tal manera que dejara de ser cuestionable. Entre los que emprendieron este camino, el esfuerzo más importante, por lo menos cronológicamente, fue hecho por Gerolamo Saccheri (1667-1733), un sacerdote jesuita y profesor de la Universidad de Pavía. Lo que pretendió hacer fue negar el axioma de las paralelas y mostrar que se llegaba a una contradicción (lo que nosotros llamamos una demostración por el absurdo). Negar que por un punto exterior a una recta pasa una sola y única paralela es suponer que, o bien no pasa ninguna, o bien pasan muchas.

Saccheri empezó suponiendo que no había ninguna paralela y, trabajando con este presupuesto, llegó a la tan ansiada contradicción. Luego probó con la segunda posibilidad. Aceptó que por el dichoso punto pasa más de una paralela y logró demostrar muchos teoremas, hasta que llegó a una propiedad tan extraña que la consideró una contradicción: concluyó así que el quinto postulado estaba demostrado, y tituló su libro, por si a alguien le quedara alguna duda, Euclides ab omni naevo vindicatus (Euclides exonerado de toda culpa, 1733). El problema parecía terminado… solamente parecía.

Poco después de Saccheri, Johann Heinrich Lambert (1728-1777) abordó el asunto. En su libro (escrito en 1766 y publicado en 1786) Teoría de las rectas paralelas, Lambert, como Saccheri, consideró las dos posibles opciones. También como Saccheri, encontró que suponer que no pasa ninguna paralela conduce a una contradicción.

Sin embargo, cuando analizó la otra hipótesis (que pasan muchas) llegó a resultados muy extraños, por ejemplo, que los ángulos interiores de un triángulo suman menos que 180 grados. Resultados extrañísimos, por cierto, pero que no constituían ninguna contradicción lógica.

¿Y entonces? Y entonces ocurrió algo fundamental, porque Lambert avizoró el hecho de que cualquier colección de hipótesis que no condujera a contradicciones ofrecería una posible geometría, que sería una estructura lógica válida, aun cuando pudiera tener poco que ver con el espacio físico real y a priori verdadero. Era un paso conceptual tremendo, abismal, y Lambert dudó frente al precipicio.

Pero quien no vaciló en absoluto fue Gauss, a quien suele considerarse —si bien el asunto es discutible— el princeps mathematicorum, el más grande matemático del siglo XIX. Hasta el año 1799 Gauss trató, como tantos otros, de demostrar el dichoso postulado, hasta que se convenció de que era imposible:

He hecho ya algunos progresos en mi trabajo. Sin embargo, el camino que he elegido no conduce en absoluto a la meta que buscamos (la deducción del axioma de las paralelas). Más bien parece obligarme a dudar de la verdad de la geometría misma,

escribía a su amigo, el matemático Wolfgang Bolyai.

«Dudar de la geometría misma» era mucho decir, pero todo parecía indicar que podía existir una geometría perfectamente coherente en la que el postulado no se cumpliera. A partir de 1813 trabajó en esa dirección, aunque le parecía una idea tan audaz que, como le decía a otro amigo en una carta, probablemente jamás publicaría sus hallazgos sobre el particular, pues tenía miedo al ridículo o, como él decía, temía el clamor de los beocios (en una referencia a la tribu griega cuya torpeza los griegos ilustrados consideraban proverbial).

El miedo era razonable, porque lo cierto es que el mundo intelectual en general (y en especial la rama de los matemáticos y los físicos) estaba dominado por la convicción de que la geometría euclídea era la única posible. Y publicar semejante cosa, con un prestigio ya bien ganado y asentado, era un riesgo que Gauss no estaba dispuesto a correr.

Pero bien acorde con un siglo que empezaba a poner todo en cuestión, el asunto estaba a punto de llegar a un desenlace.

Lobachevski y Bolyai: las geometrías no euclidianas

Desenlace que se desencadenó gracias a los trabajos del matemático ruso Nicolai Ivanovich Lobachevski (1793-1856) y el húngaro Johann Bolyai (1802-1860), hijo del Wolfgang Bolyai al que le escribía Gauss. A partir de 1825, uno y otro, separadamente, desarrollaron sus propias ideas sobre la geometría y construyeron una geometría no euclidiana (lo cual hasta ese momento hubiese parecido una contradicción en los términos) partiendo de que por un punto exterior a una recta pasan infinitas paralelas.

Bolyai escribía:

He realizado descubrimientos tan maravillosos que estoy completamente asombrado.

En efecto, la nueva geometría tenía propiedades muy extrañas, pero en absoluto contradictorias. Recuerden el ejemplo que les ofrecí antes: la suma de los ángulos interiores de un triángulo, en esta geometría, es menor que 180 grados, y la diferencia depende del área (cuanto más grande el triángulo, menor la diferencia).

La nueva geometría resultaba tanto más estremecedora en tanto crecía poco a poco la sospecha de que podía aplicarse al espacio físico de manera tan precisa como la euclídea. Hasta entonces, el espacio físico en que trabajaban los científicos y vivían todos los hombres era el descripto por la geometría euclidiana: así lo había construido Newton, y así lo había sancionado el gran filósofo Kant. Se trataba de la geometría necesaria de la empiria.

Pero tanto Gauss como Lobachevski estaban convencidos de que esta nueva geometría que iban esbozando podía ser aplicable y era utilizable para describir las propiedades del espacio físico tan precisamente como la euclídea, ya que, pensaban, era poco científico garantizar la verdad física de la geometría euclídea basándose en consideraciones a priori.

Así, hacia 1830 no sólo había una geometría no euclídea (aunque aceptada por pocos), sino que su aplicabilidad al espacio físico era considerada al menos como posible. El asunto no era menor, ya que todo el edificio de la física estaba construido sobre la presunción de que la geometría euclídea era la geometría necesaria del espacio físico: si de repente, digamos, resultaba que los ángulos interiores de un triángulo medían menos que 180 grados, era necesario revisar todo lo que se apoyara en ese supuesto.

El problema de cuál era la geometría que mejor se acomodaba al espacio físico, suscitado primeramente por la obra de Gauss, estimuló la creación de una nueva geometría que dio al mundo matemático motivos frescos para creer que el espacio físico podía muy bien ser no euclidiano. Su inventor (¿o debería decir «descubridor»?) fue Georg Bernhard Riemann (1826-1866), discípulo de Gauss y posteriormente profesor de matemáticas en Gotinga. En la geometría de Riemann no sólo no pasa ninguna paralela por un punto exterior a una recta, sino que ni siquiera existen rectas paralelas. Lo cual parece rarísimo, aunque no lo es: para visualizarla, se la puede pensar como si las rectas fueran los meridianos terrestres, que al cortarse en los polos no conocen el paralelismo.

De repente toda la construcción de la mecánica newtoniana, que se había basado en la idea de un espacio euclídeo absoluto, mostraba la hilacha. En su conferencia en la Facultad de Filosofía de Gotinga de 1868, titulada «Sobre las hipótesis que se encuentran en los fundamentos de la geometría», Riemann reconsideraba el problema general de la estructura del espacio. Y lo hacía —esto es lo interesante— desde una perspectiva empírica: ya no alcanzaba con que la geometría contara con una lógica interna implacable, sino que la pregunta, ahora, era por las condiciones que se le presuponían al propio concepto de espacio antes de que se determinara mediante la experiencia cualquier propiedad que pudiera presentarse en el mundo físico. Era toda una novedad: las verdades autoevidentes de Euclides podían depender de la experiencia.

En verdad, y acá me veo obligado a hacer una digresión, es algo injusto decir que Euclides no hubiera considerado esta posibilidad. A pesar de oponerse decididamente al empirismo, el propio concepto de «autoevidencia» es una suerte de concesión. ¿Por qué sería autoevidente e indiscutible que, por ejemplo, «toda recta limitada pueda prolongarse indefinidamente en la misma dirección», salvo por el hecho de que, efectivamente, parecía que en la práctica era así? (Y digo «parecía» porque en la práctica no existen ni las rectas ni los segmentos abstractos de Euclides.) Resulta, entonces, que lo que Riemann estaba diciendo era que los axiomas de Euclides no eran las festejadas verdades autoevidentes, sino que eran simples verdades empíricas.

De este modo, la cuestión misma del espacio, de su naturaleza y su geometría, tambaleaba. El mapa que se había diseñado, que parecía tan perfecto y había conducido a creer en un progreso indefinido y sin obstáculos en la carrera del conocimiento, empezaba a generar algunas sospechas: ¿tenía que ser un mapa euclídeo? ¿O a lo mejor convenía explorar el territorio con un mapa no euclídeo, a pesar de sus extrañas y antiintuitivas propiedades? Si éste era el caso, el terreno era pantanoso. Porque si cualquier geometría lógica (es decir, que no presentara contradicciones internas) podía ser aplicada al espacio físico con éxito, resultaba que este espacio físico en realidad no era otra cosa que un espacio lógico con tantas posibilidades de ser representado como geometrías no contradictorias pudieran postularse. Definitivamente, ya no era el espacio en el que los científicos seguros del siglo XIX se manejaban.

Y el siglo XX se encargaría de demostrar que efectivamente era así, y aún más, que la geometría real del espacio no es precisamente la euclídea. Pero ya llegaremos allí.

II. EL TRIUNFO DEL INFINITO

La enorme sofisticación del postulado de las paralelas se debía en parte al recelo de Euclides (y de los matemáticos griegos en general) ante el concepto de infinito: las paralelas son rectas que no se cortan ni siquiera en el infinito, un lugar no definible, donde nadie sabía lo que pasaba realmente. Así, el postulado de las paralelas estaba relacionado con el concepto de infinito, que no había sido resuelto jamás por los matemáticos griegos: Euclides, de hecho, seguía a Aristóteles, que aceptaba el infinito como una cantidad que crecía sin límites (es decir, un infinito potencial) pero negaba la posibilidad del infinito real (o actual), es decir, del infinito existente aquí y ahora.

La respuesta aristotélica o euclidiana es la primera que se le ocurre a quien trata de responder acerca de la definición del infinito desde el sentido común, o, lo que es lo mismo, desde la intuición directa. Uno suele imaginarse una cantidad muy grande. Pero las cantidades muy grandes, como, digamos, el número de granos de arena de todas las playas de la tierra (del que, como recordarán, se ocupó Arquímedes en su momento en su Arenario) están lejísimos de ser infinitas, tan lejos como lo están las estrellas que vemos en el cielo, felizmente. Y digo felizmente porque si el número de granos de arena de una playa fuera infinito, su peso también lo sería y, en consecuencia, el de la Tierra también. La cantidad de átomos en el universo, que asciende a la friolera de 1.000.000.000.000.000.000.000.000.000.000.000.000.000. 000.000.000.000.000.000.000.000.000. 000.000.000.000.000, es tan poco infinita que da lástima. En realidad, semejante cifra no está más cerca del infinito que colegas más modestas como 2, 15 o 2089, lo cual es rarísimo, y explica por qué la dificultad para concebir el infinito, salvo como algo potencial, se arrastraba desde la Antigüedad.

El cálculo infinitesimal

Más allá de los devaneos medievales y teológicos sobre si la potencia de Dios era o no infinita, en los siglos XVI y XVII el infinito matemático, que es el que nos interesa a nosotros, había tenido un imprevisto y fructífero renacimiento. Varios matemáticos habían empezado a considerar que, por ejemplo, un cuadrado podía pensarse como un conjunto infinito de segmentos infinitamente delgados, o un volumen como una pila de infinitas rebanadas, cada una de ellas también infinitamente delgadas, y habían utilizado esa aproximación para calcular áreas y volúmenes. Newton y Leibniz, por su parte, al inventar el cálculo infinitesimal, habían utilizado cantidades «infinitamente pequeñas» y operado con ellas, sus cocientes y sus desarrollos.

Como es un poco técnico explicar qué es exactamente el cálculo infinitesimal, lo hago muy pero muy esquemáticamente. Analicemos por ejemplo el concepto de velocidad instantánea. Cuando la aguja del velocímetro marca, digamos, 60 kilómetros por hora, damos por sentado que mide la velocidad del auto en ese instante, sin pensar en la dificultad del concepto. Porque… ¿qué es un instante? Un intervalo de duración cero. ¿Y cuánto recorre el auto en un intervalo que dura cero? Obviamente 0 kilómetro. Pero si la velocidad en un instante es el cociente del espacio por el tiempo, llegaríamos al absurdo de que es 0/0, lo cual no tiene ningún sentido.

Es aquí donde irrumpe el cálculo infinitesimal para proponer otra manera: lo hace con intervalos de tiempo y de espacio infinitamente pequeños, que se dividen y se «hacen cero» (o, como ellos decían, se «desvanecen»); de esa manera evitaban el 0/0 y llegaban a un valor, la velocidad instantánea.

En términos generales, el cálculo infinitesimal, la más grande invención matemática desde la Antigüedad hasta hoy, consiste en operar con estas cantidades infinitamente pequeñas, ya sea en las magnitudes físicas o en las funciones.

El cálculo infinitesimal, si bien tuvo inmediatas aplicaciones debido a su inmensa utilidad —y se siguió utilizando pese a no estar suficientemente bien fundamentado—, recibió críticas desde el punto de vista filosófico, notablemente por parte del obispo Berkeley (1685-1753), quien preguntaba qué clase de entidades eran ésas, infinitamente pequeñas y que se «desvanecían». No le encontraba sentido alguno. Y la verdad es que no le faltaba razón, puesto que no había una buena respuesta para estas cuestiones en ese momento.

Pero finalmente, en el siglo XIX, se consiguió forjar un aparato formal que trataba estas cuestiones con rigor y más o menos explicaba qué significaban las cantidades que se «desvanecían». De modo que el problema de lo infinitamente pequeño parecía resuelto, y el análisis matemático, rigurosamente justificado. Sin embargo, el tema del infinito no hacía sino empezar. Faltaba enfrentarse con las cantidades infinitamente grandes, y ésa fue la tarea de Georg Cantor (1845-1918).

Cantor y los infinitos

Para encontrarnos con conjuntos que ningún número pueda contar debemos recurrir al mundo de los objetos matemáticos. Pero no necesitamos adentrarnos demasiado: ahí nomás, en el zaguán, tenemos a los números naturales (1, 2, 3, 4, 5, . . .), que obviamente son infinitos, terriblemente infinitos. Y cuando uno se enfrenta con conjuntos infinitos, enseguida encuentra que funcionan de manera peculiar, para decirlo suavemente. Si no, miren el famoso ejemplo del hotel de Hilbert.

Para mostrar la dificultad de concebir el infinito, el gran matemático David Hilbert ponía como ejemplo un hotel de infinitas habitaciones y un viajero que llega durante una noche de tormenta y ve en la puerta el cartel que dice COMPLETO. En un hotel finito, la temible palabra sumiría a nuestro viajero en la desesperación (el hotel de Hilbert queda a cientos de kilómetros de cualquier otro lugar civilizado, en medio de un páramo, rodeado de ciénagas espantosas repletas de cocodrilos). Pero en este caso nuestro viajero pide tranquilamente un cuarto. El conserje no se inmuta (en realidad ni siquiera se sorprende). Levanta el teléfono y da una orden general: que el ocupante de la habitación uno se mude a la habitación dos, el de la habitación dos a la habitación tres, el de la tres, a la cuatro, y así sucesivamente. Mediante esta sencilla operación, la habitación uno queda vacía, lista para el nuevo huésped, todos los ocupantes del hotel tienen, como antes, una habitación, y el hotel seguirá, también como antes, completo.

Ahora supongamos que en vez de llegar un solo viajero llegaran infinitos. El conserje, esta vez, indicaría al ocupante de la habitación uno que se mudara a la dos, al de la dos, a la cuatro, al de la tres, a la seis, y otra vez lograría acomodar a la multitud recién venida en las habitaciones impares, que quedarían todas vacías. Y si el dueño del hotel decidiera clausurar la mitad de las habitaciones, no por eso la cantidad de cuartos cambiaría. Sería la misma y tan infinita como antes. El particular comportamiento del Hotel de Hilbert es apenas una pequeña anomalía que se presenta al manejarse con el infinito. Hay más. Digamos de paso que el hotel de Hilbert es una fantasía matemática que no podría tener realidad física, ya que, si el universo es finito, no cabría en él, y si no lo es, como en el caso de los granos de arena, tendría una masa y un volumen infinitos, que producirían trastornos en cualquier tipo de universo con el que nos manejemos.

Pero volvamos a Cantor, quien empezaba a pensar las cosas desde el punto de vista de la teoría de conjuntos. Y fue justamente trabajando con conjuntos que se dio cuenta de algo muy raro. Dos conjuntos son iguales si se pueden poner en relación uno a uno sus elementos. Cuando uno se pregunta, por ejemplo, si hay más números naturales o más números pares, conjuntos infinitos ambos, la primera tentación es decir que hay más naturales que pares, ya que solamente algunos de los naturales son pares. Cantor demostró que la respuesta intuitiva, como tantas otras veces, no era correcta. Para determinarlo, no había más que poner en correspondencia los dos conjuntos:

1- 2

2- 4

3- 6

y así siguiendo.

Como es evidente, siempre habrá un número a la derecha que se puede poner en correspondencia con uno de la izquierda, y además, tanto en la columna de la derecha como en la de la izquierda están todos los elementos del conjunto. Dicho de otra manera, los números naturales y los números pares pueden ponerse en correspondencia uno a uno, lo cual significa afirmó Cantor que, aunque sean infinitos, hay exactamente la misma cantidad, a la que llamó aleph (la primera letra del alfabeto hebreo) sub cero (א0). Había inventado el primer número transfinito.

א0 mide la cantidad de números naturales, la cantidad de números pares, y la de múltiplos de cualquier número. También sirve para describir el conjunto de los números enteros negativos e incluso el de las fracciones. Esto quiere decir, nada más y nada menos, que hay tantos números naturales como números pares, como fracciones y como habitaciones en el hotel de Hilbert. La misma cantidad. Todos ellos son conjuntos numerables, como se llaman aquellos medidos por א0, el menor y más hogareño de los infinitos. Es interesante saber que ya Galileo había notado este peculiar comportamiento de los conjuntos infinitos y había notado también que, simplificando un poco, hay la misma cantidad de números naturales que de pares, con el mismo razonamiento que usaría Cantor dos siglos después.

Pero la cosa fue más allá: ese raro comportamiento fue sólo la primera sorpresa de las muchas y muy razonables que Cantor tenía para sacar de la galera. La siguiente, aún más extraña que la anterior, fue que los infinitos no son todos iguales.

En efecto, Cantor demostró que la cantidad de números irracionales, o la cantidad de puntos de una recta, es mayor que aleph cero, es decir que hay más números irracionales que números naturales, enteros o fraccionarios. El número transfinito que los mide es más grande que aleph cero: familiarmente se lo llama c, la potencia del continuo. Los puntos de una recta, las rectas de un plano, los números irracionales, tienen la potencia del continuo. En el recuadro de la página siguiente les demuestro por qué los números irracionales son más que los naturales y los pares.

De modo que si al hotel de Hilbert, que tiene aleph cero habitaciones, llegaran c viajeros, no habría manera de ubicarlos, aunque el hotel estuviera vacío: las habitaciones no alcanzarían. Esta distribución jerárquica de los infinitos, que tanto (y tan comprensiblemente) sorprendió a los colegas de Cantor, no termina con c. Existen más infinitos, cada vez más grandes, que excitan la fantasía y el misterio.

De cualquier manera, los números transfinitos de Cantor y las operaciones que éste mostró que se podían hacer con ellos no convencieron a todo el mundo.

Aunque Hilbert llegó a decir que Cantor había mostrado «un paraíso del que nadie nos expulsará», matemáticos tan importantes como Kronecker consideraron que toda la aritmética transfinita no era más que una simple locura.

Medir los infinitos

Los números irracionales son aquellos que no pueden expresarse como un cociente de dos números enteros y que tienen infinitas cifras decimales (no periódicas). Por ejemplo, la raíz de dos es 1,414213562373… y así siguiendo, o pi es 3,14159… , etcétera (ya se conocen varios millones de cifras decimales de pi, que no pongo aquí por obvias razones). Pero lo cierto es que tanto pi como la raíz de dos, dos números de la más grande importancia para la historia del pensamiento científico, tienen infinitas cifras decimales.

Ahora supongamos que efectivamente tenemos una lista que pone en correspondencia a los números naturales con los irracionales. Sería algo de este tipo (por comodidad tomamos los números irracionales comprendidos entre 0 y 1, es decir, que empiezan con 0 y tienen infinitas cifras decimales):

1 0, 34526578568987409865389….

2 0,453432349067685648738883….

3 0, 8423212154789076895674….

Y así siguiendo.

Es fácil mostrar que la lista de la derecha no es exhaustiva, es decir, si yo puedo exhibir por lo menos un número irracional que no está en la lista que estoy postulando, entonces quedaría demostrado que la lista de la derecha no es completa y, por ende, que el infinito que la representa es más grande. Y efectivamente yo puedo concebir ese número. Pensemos en un número irracional cuya primera cifra sea diferente de la primera cifra decimal del primero de la lista (o sea, diferente de 3), cuya segunda cifra sea diferente de la del segundo (5), cuya tercera cifra sea diferente de la del tercero (2) y así sucesivamente. Es evidente que ese número no está entre los números irracionales que yo emparejé con los naturales. Porque si digo que está en la posición, por ejemplo, 1.000.000, estaría mintiendo flagrantemente, porque la cifra número un millón será distinta. Y esto pasa con cualquier posición en la que pruebe.

De manera que queda demostrado que la lista de la derecha no abarca a todos los irracionales; algunos quedan afuera, y por lo tanto su cardinal, el número transfinito que lo describe, es mayor que aleph 0, lo cual significa que… ¡hay infinitos más grandes que otros!

Lo cierto es que era un verdadero sacudón: así como las geometrías no euclidianas habían puesto en cuestión el espacio cómodo y euclidiano en el que se pensaba toda la física de la época, la teoría de los conjuntos infinitos contribuiría a desatar una crisis en la teoría de conjuntos que pondría en jaque a las matemáticas de principios del siglo XX y que se conoce como «la crisis de los fundamentos». Parecía que no sólo la geometría podía estar equivocada sino, lo que era mucho más grave, todo el basamento de las matemáticas.

III. EL ÉTER

Eran épocas de conmoción. El siglo XIX parecía haber construido un edificio de conocimiento gigantesco sobre el que sólo faltaba seguir agregando pisos (acaso indefinidamente), pero cuyas bases, se creía, estaban tan sólidamente establecidas que nada podría hacerlas tambalear. Y de repente aparecían nuevas geometrías e insospechados infinitos, que, por más abstractos que fueran, hacían pensar que la estructura podía no ser tan firme. Para colmo, de un momento a otro, el longevísimo éter —esa sustancia empírica, metafísica e inasible que se arrastraba desde los tiempos de los griegos, que se aferraba con uñas y dientes a la existencia, que llenaba uniformemente el espacio y que se encargaba de sostener un edificio cuyas rajaduras ya se tornaban visibles— empezó a dar muestras de inexistencia.

Biografía del éter

Ya hemos hablado de esto antes, pero vale la pena repasarlo para entender el grado de importancia que tuvo la cuestión del éter. Cuando Aristóteles acuñó por dos milenios este feo asuntillo de los cuatro elementos (tierra, agua, aire y fuego), que había tomado de Empédocles, inventó un quinto elemento, una quintaesencia para los cielos, libres de corrupción, sujetos a regularidades eternas, y donde el cambio estaba prohibido. Como podrán adivinar, se trataba del éter, que formaba las esferas y los planetas y aseguraba la perfección del espacio supralunar.

Recordemos que para Aristóteles, discípulo de Platón a pesar de las enormes diferencias que separan sus filosofías, había dos mundos ontológicamente diferentes, gobernados por leyes diferentes y formados por sustancias diferentes: el sublunar, corrupto y cambiante, y el supralunar, de la órbita de la Luna para afuera, perfecto y eterno, donde el cambio no era posible. El hecho es que, como componente exclusivo del mundo supralunar, desde su nacimiento el éter no fue de este mundo: formaba las esferas, pero más allá de cualquier alcance. La palabra griega «aether» significaba originariamente el cielo azul, o el aire de las alturas, supuestamente más puro y distinto del aire más bajo, al nivel de tierra. Los romanos importaron la palabra, y Lucrecio (siglo I a.C.), en su De rerum natura habla del

innubilus aether divum numen sedesque quietae.

(el éter sin nubes que cubre y protege a la divinidad y sus lugares de paz)

El éter aristotélico persistió durante la Edad Media como una pieza de la cosmogonía, como aquello que ocupaba los espacios vacíos, como una sustancia metafísica y teológica no muy implicada con las cosas prácticas, modestamente fuera de alcance de los mortales —lo cual, dicho sea de paso, no era un gran inconveniente en una época poco inclinada hacia la experiencia, y más propensa al sueño y la imaginería—.

Pero cuando Descartes decidió reconstruir el conocimiento sobre bases firmes, le dio al éter un papel muy distinto. Puede parecer raro, porque uno diría que en el universo rígidamente mecanicista de Descartes, el éter (incoloro, inodoro, insípido y casi puramente metafísico), en principio no parecía un personaje adecuado. Pero como Descartes no aceptaba la existencia del vacío, ya que para él la materia era inseparable de la extensión (el espacio), su universo era un plenum, y como era un plenum algo tenía que ocupar todos los huecos en los que no hubiera nada. El candidato a ocupar ese lugar, naturalmente, fue el éter, que Descartes describió como «materia sutil», infinitamente divisible y sin límites en extensión.

El éter cartesiano era diferente del aristotélico; no se limitaba a llenar, como una mera presencia ontológica que tranquilizaba conciencias con horror al vacío. Nada de eso: el éter era activo, estaba por todas partes y transportaba las fuerzas magnética y gravitatoria (ya que, recordemos, Descartes tampoco aceptaba la acción a distancia). La fuerza no podía transmitirse sino por la presión o el impacto, esto es, sólo por contacto, de modo que el éter cartesiano era el encargado de formar los torbellinos o vórtices que funcionaban como vehículos de las acciones a distancia, fueran cuales fueren. En el sistema de Descartes, era la fuerza activa más potente del universo, aunque desde ya era imposible saber de qué estaba hecho o qué clase de cosa era.

Cuando Newton tomó las riendas del mundo, construyendo su sistema pavoroso, basado en la acción a distancia y las fuerzas que se propagan a través del vacío, el éter pudo haber sufrido un sacudón. Pero no fue así. El mismo Newton aceptaba el éter (naturalmente, un éter de naturaleza corpuscular) y le atribuía la propiedad de conducir el calor, e incluso llegó a especular con que la fuerza de gravitación se debía a presiones del éter sobre los cuerpos, o deformaciones del éter, aunque finalmente optó por atenerse a su máxima: «yo no formulo hipótesis».

En realidad, el problema, como tantas veces, era la luz. Newton concebía la luz como un flujo de corpúsculos a los cuales se les podían aplicar las leyes de la mecánica, entre ellas, la de gravitación universal. Pero tanto su rival Hooke como Huygens sostenían que los fenómenos luminosos se explicaban mucho mejor partiendo de la hipótesis de que la luz no está formada por corpúsculos, sino que consiste en ondas, pequeñas vibraciones.

¿Vibraciones de qué? Porque cuando la luz se propaga en el vacío… ¿qué es lo que vibra? El vacío no es nada, y la nada no puede vibrar. El éter se deslizó por la ranura luminosa para que la teoría ondulatoria pudiera vivir y hubiera algo que vibrara transportando la luz.

Ya no era un éter activo, como el que proponía Descartes, ni tenía las propiedades mecánicas que lo llevaban a formar torbellinos y generar los movimientos; tampoco formaba los cuerpos celestiales de Aristóteles. Ahora era puramente pasivo: no ofrecía ninguna resistencia al movimiento de los cuerpos que lo atravesaban (o que él atravesaba).

El éter ya era de por sí bastante inverosímil, pero a medida que la teoría ondulatoria de la luz se afianzaba, fue adquiriendo características estrafalarias. Los trabajos de Young y de Fresnel mostraron que las vibraciones luminosas eran perpendiculares a la dirección de propagación. Y para que esto pudiera ocurrir, el éter tenía que ofrecer algún tipo de resistencia a la deformación. Pero si esto ocurría, resultaba que el éter se comportaba como un sólido elástico, lo cual generaba un inconveniente nada pequeño: ¿cómo hacían los inmensos planetas en el cielo para atravesar enormes distancias de un sólido elástico? Este asunto de los planetas era un engorro, pero se solucionó con cierta facilidad: G. G. Stokes, en 1845 —y noten el año— sugirió que el éter se comportaba como un sólido para las vibraciones muy rápidas como las de la luz, pero como un fluido para movimientos muy lentos como los de los planetas, y describió sus propiedades mediante un conjunto de espeluznantes ecuaciones.

La hipótesis del éter se reforzó cuando el físico escocés James Clerk Maxwell, entre los años 1864 y 1873, unificó los conceptos de electricidad y magnetismo mostrando que eran aspectos de un único fenómeno, el electromagnetismo, y mediante un puñado de leyes muy simples logró explicarlo por completo y predecir la existencia de ondas electromagnéticas (entre ellas la luz). ¿Cuál era el soporte material de esas ondas? El éter, por supuesto.

Las cosas pasaban a mayores. En tiempos en que ya se manejaba la tabla de Mendeleiev y se estaba ante las puertas de la radiactividad era muy difícil aceptar una sustancia con una naturaleza química tan indeterminada. ¿De qué estaba hecho, en efecto, el éter? Parecía una sustancia puramente metafísica, por más extravagante que eso suene. Pero incluso si se hubiese aceptado que lo fuera: ¿de qué manera una sustancia puramente metafísica podía comportarse como un sólido elástico o como un fluido? El éter era químicamente molesto, completamente anacrónico.

Y además —y esto sería determinante— estaba en reposo absoluto en el propio espacio en reposo absoluto. Y si el éter estaba en reposo absoluto, el movimiento absoluto debía existir también. Porque si el éter en reposo absoluto llenaba todo el universo, la Tierra, al moverse a través de él, debía recibir una corriente de éter (de la misma manera que un avión en movimiento recibe una corriente de aire en contra de su movimiento). Y esa corriente tenía que poder ser medida.

Es lo que se propuso el físico norteamericano Abraham Michelson.

El experimento de Michelson-Morley

En el fondo, la idea de Michelson era sencilla. Puesto que el éter estacionario era una cosa material y rodeaba la tierra como un océano, ésta, al moverse en él, debía recibir una corriente de éter en contra. Así, si se enviaba un rayo de luz en la dirección contraria a la corriente de éter y un rayo de luz en dirección perpendicular a la corriente, el rayo en dirección contraria a la corriente debía mostrar un pequeño retraso respecto del otro, del mismo modo que la corriente de un río retrasa el movimiento de un bote, pero no influye en quien lo cruza a nado perpendicularmente.

En vista de ello, Michelson ideó el siguiente experimento: enviaría un rayo de luz en una distancia definida y otro en una distancia igual pero en ángulo recto a la dirección del primero. Ambos rayos se reflejarían en un espejo y volverían en seguida a su punto de partida común. El viento de éter tenía que producir un retraso en uno de los dos rayos.

El experimento tenía que estar preparado para detectar diferencias mínimas, y para no ser afectado por las condiciones externas (vibraciones del edificio, por ejemplo) pero esa exigencia no lo arredró, y diseñó un ingenioso aparato llamado interferómetro. Trazó los planos de una máquina que fue construida por un fabricante de Berlín, y con ese nuevo instrumento realizó el experimento. O los experimentos, mejor dicho.

El primero se realizó en el laboratorio de Helmholtz, en el Instituto Físico de Berlín. El instrumento fue colocado sobre un basamento de piedra, pero las vibraciones del tránsito por la noche causaban alteraciones. Michelson, en vista de ello, fue al Observatorio Astrofísico en Potsdam, en abril de 1881, para realizar otra tentativa. Allí, el instrumento extraordinariamente sensible dio resultados, aunque las pisadas en la calle a una manzana del sótano del observatorio dificultaron grandemente la medición.

La cosa es que los experimentos de Michelson no detectaron retardo alguno en la transmisión de la luz en ningún sentido: los rayos volvían en el mismo instante. Dio cuenta de sus averiguaciones en el número de agosto de 1881 del American Journal of Science bajo el título «The relative motion of the earth and the luminiferous ether» («El movimiento relativo de la Tierra y el éter lumínico»).

Desde ya, no todos se convencieron y lo que siguió fue la crítica más habitual para cualquier experimento que contradiga las creencias arraigadas: que estaba mal hecho. Así, por ejemplo, sir Oliver Lodge, una figura prominente en los círculos científicos ingleses, se negó a aceptar la conclusión experimental de Michelson, y siguió definiendo al éter como

una sustancia continua que llena todo el espacio, que puede vibrar luz, que puede ser transformado en electricidad positiva y negativa, que en torbellinos constituye materia y que transmite por continuidad y no por impacto todas las acciones y reacciones de que es capaz la materia.

Digamos, de paso, que el propio Michelson tampoco estaba demasiado convencido del asunto. De modo que decidió seguir probando. En 1866 conoció a Edward W. Morley, del Western Reserve College, y juntos proyectaron otra serie de experimentos, que fue generalmente conocida con el nombre de «experimento Michelson-Morley». En 1887, todo el voluminoso aparato (muy mejorado) fue montado en una pesada losa de piedra que flotaba en mercurio para evitar errores debidos a vibraciones, presiones y tensiones. Otra vez no apareció retraso alguno en ese ir y volver de la luz.

Los resultados eran claros: no había ningún éter estacionario. Michelson informó, sin embargo, que los resultados de su experimento podían

ser explicados por la suposición de que la Tierra arrastra al éter casi a su misma velocidad, de manera que la velocidad relativa entre el éter y la superficie de la Tierra es cero o sumamente reducida.

Pero además de esta posibilidad, existía otra. Aunque era extraña, extrañísima, tanto que era difícil creerla.

La solución de Fitzgerald-Lorentz

Aun de existir un éter, el resultado obtenido por Michelson y Morley podía explicarse. Es más, en 1895, dos matemáticos y físicos, George F. Fitzgerald, del Trinity Collage de Dublín, y Hendrik A. Lorentz, de Leyden, ofrecieron una explicación, aunque, como les dije, muy extraña. Basados en ciertas propiedades del campo eléctrico, partieron de la base de que la longitud de un objeto cambia con el movimiento. Una varilla disminuye su longitud, para un observador externo en reposo, si se mueve a través del espacio siguiendo la dirección de su longitud, y la disminución —es decir, la diferencia en la longitud de la vara cuando está inmóvil y cuando se mueve a gran velocidad— depende de esa velocidad.

Es verdad que el efecto no se siente a velocidades bajas, aunque existe, pero empieza a hacerse perceptible cuando las velocidades crecen mucho, y se aproximan a la de la luz. Los cálculos matemáticos demostraban que una velocidad de 480 kilómetros por hora causaría una reducción de sólo un billonésimo de uno por ciento, disminución que, naturalmente, nuestros instrumentos no podrían registrar. Pero cuando usaban una velocidad teórica de 145.000 kilómetros por segundo, la disminución llegaba a un trece por ciento. Al ser aumentada esta velocidad, también aumentaba ese porcentaje, hasta que finalmente, según sus cálculos, cuando la velocidad llegaba a los 300.000 kilómetros por segundo (la velocidad de la luz), el porcentaje de la reducción llegaba a un ciento por ciento. En otras palabras, a esta velocidad la vara desaparecía como consecuencia de una reducción total.

Esta nueva idea podía explicar con un grado suficiente de plausibilidad el resultado aparentemente negativo de los experimentos de Michelson-Morley, porque no habían tenido en cuenta la reducción del brazo del interferómetro durante las mediciones. El efecto de esta reducción era justo lo suficiente para contrarrestar el retardo de la luz por el éter: las conclusiones de Michelson habían ignorado totalmente el fenómeno expresado en la teoría de la contracción de Lorentz-Fitzgerald.

Era un planteo desconcertante para cualquiera acostumbrado a pensar en términos de la física tal como se conocía hasta entonces y, como era de esperar, alteró a los físicos tradicionalistas, que lo consideraron completamente fantástico. Algunos de ellos, incluso, evocaron la observación del físico norteamericano Josiah Willard Gibss, que había hecho fundamentales aportes al desarrollo de la termodinámica:

Un matemático puede decir lo que se le ocurra, pero el físico debe estar por lo menos parcialmente cuerdo.

La explicación de Lorentz-Fitzgerald, a pesar de su audacia y de su eficacia para salvar los resultados aparentemente negativos de los experimentos en la derivación del éter de Michelson, seguía basándose en las leyes de la física clásica tradicional. Y aunque hizo vacilar a los hombres de ciencia, no los derribó por completo. Al fin y al cabo, las leyes clásicas del movimiento de Newton seguían rigiendo.

Pero faltaban algunas sorpresas. De las ecuaciones de Fitzgerald-Lorentz se deducía también que el tiempo variaba con la velocidad: cuanto mayor fuera la velocidad a la que se movía un objeto, más lentamente transcurría el tiempo para un observador externo. A lo cual se agregó la masa, cuya variación con la velocidad fue confirmada por Walter Kauffman a partir de 1901. Todo se transformaba a medida que la velocidad aumentaba: parecían violarse de a poco los principios de la gran construcción de la física clásica.

Y, de hecho, se produjo un verdadero impasse en el mundo de la física, que era incapaz de explicar los insólitos resultados salvo recurriendo a hipótesis que lindaban con la fantasía. Así, el «fracaso» del experimento de Michelson-Morley abriría un nuevo capítulo, no sólo en la física, lo cual ya sería mucho decir, sino en la propia concepción que tenemos del universo.