CAPÍTULO 35

La mecánica cuántica

Muy pronto, la realidad cedió en más de un punto.

J. L. BORGES, «Tlon, Uqbar, Orbis Tertius»

Todo empezó de la manera más inocente, con la luz y la radiación. En las últimas décadas del siglo XIX, la teoría ondulatoria de la luz había triunfado contundentemente sobre la teoría corpuscular, lo cual significaba que se concebía la luz como una radiación electromagnética, tal y como había predicho Maxwell y como había demostrado experimentalmente Hertz en 1888. Una vez establecidas las dos partes que componían el mundo, la materia y la radiación, la cuestión era averiguar cómo interactuaban entre ellas.

No se notaba, a simple vista, que tal relación pudiera traer demasiadas complicaciones. Pero lo cierto es que desató una revolución tan grande en la física que todos los conceptos tuvieron que ser revisados —más aún que con la teoría de la relatividad— y se convirtieron en un cuerpo de doctrina completísimo y tremendamente eficaz: la mecánica cuántica. Es un camino ríspido y complejo, porque la mecánica cuántica lo es. Seamos pacientes, entonces, y sigamos con cuidado y atención los pasos de su construcción.

El hilo se corta por lo más grueso

Todo empezó, les decía, de la manera más inocente. A principios del siglo XX, y ya repuestos (o a medias repuestos, a decir verdad) del shock del descubrimiento de que el átomo era algo compuesto y que había partículas incluso más chicas, los físicos creían tener un mapa más o menos completo gracias al cual sabían aproximadamente bien qué debían hacer. Al menos, lo hacían bajo el amparo de una ávida y segura concepción: los objetos materiales, como los átomos, o los recién llegados y ya aceptados electrones, tenían que ser descriptos como partículas, pero la radiación electromagnética, incluida la luz, había que entenderla en forma de ondas. De lo que se trataba, ahora, era de comprender de qué manera interactuaba la radiación con la materia, una tarea, si se quiere, de rutina: parecía seguro que por ahí iban las cosas que permitirían construir una imagen armoniosa que unificara la física. Pero debemos retroceder un poco para entender la dimensión de la revolución conceptual que se desató cuando se indagó a fondo en estos temas.

Para empezar, hay que decir que todo cuerpo emite radiaciones electromagnéticas. El espectro electromagnético, que pueden ver en la imagen siguiente, clasifica las diversas radiaciones de acuerdo con su frecuencia (es decir, el número de repeticiones por unidad de tiempo) y su longitud de onda (inversamente proporcional a la frecuencia). Así, por ejemplo, un cuerpo que emite con mucha frecuencia y longitud de onda corta lo hará en ultravioleta o, aún más, emitirá rayos gamma.

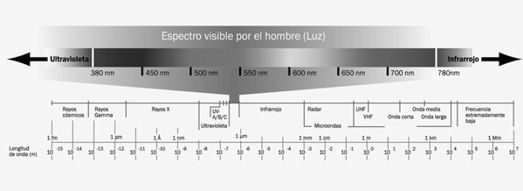
La forma de estudiar cómo interaccionan materia y radiación consiste en observar un objeto caliente, ya que éste irradia mucha energía electromagnética. Cuanto más caliente está, más energía irradia, cada vez con longitudes de onda más cortas (lo que es lo mismo que decir: con frecuencias más altas). Así, por ejemplo, un cuerpo demasiado frío para irradiar luz visible puede emitir radiación infrarroja de baja frecuencia, inaprehensible para el ojo humano, pero perfectamente detectable por los aparatos.

El recurso estándar que se utilizaba para medir la radiación en ese momento era el llamado «cuerpo negro», un objeto teórico, perfecto absorbente o emisor de radiación (es decir, que absorbe toda la radiación que le llega). Además de ser un excelente objeto teórico, es fácil construir un cuerpo negro más o menos riguroso en el laboratorio: basta tomar una esfera hueca, o un tubo con los extremos cerrados, y practicar un pequeño agujero en su superficie. Cualquier radiación, como la luz, que penetre por ese agujero, quedará atrapada en el interior, rebotando en las paredes hasta ser absorbida; es muy improbable que pueda salir a través del hueco debido a ese rebote o, si sale, lo hará en una fracción mínima. Por lo tanto, el cuerpo la absorbe y ese agujero es un cuerpo negro.

Y es entonces cuando se produjo un chispazo entre lo que se medía experimentalmente y la teoría clásica. La cuestión es así: las leyes del electromagnetismo clásico preveían que un cuerpo negro ideal, cuando estaba en equilibrio térmico, debía emitir energía en todos los rangos de frecuencia (desde las ondas más largas a las más cortas) pero siguiendo una proporcionalidad muy específica: a mayor frecuencia, mayor energía emitida. Lo cual suponía que en el rango más elevado del espectro (es decir, aquel con frecuencias más altas y longitudes de onda más cortas: el ultravioleta, dado que los rayos gamma aún no se conocían) la emisión de energía debía ser enorme, infinita, en realidad.

Y resulta que la curva de emisión del cuerpo negro no encajaba para nada con lo que se esperaba. Esa energía infinita que predecía la teoría, y que obviamente no podía ser, fue llamada «catástrofe del ultravioleta», y atrajo la atención de un buen número de físicos durante la última década del siglo XIX. Uno de ellos fue Max Planck (1858-1947), un científico a todas luces clásico que quería explicar la catástrofe del ultravioleta mediante las leyes de la termodinámica, en las cuales se había mostrado especialmente interesado.

Por entonces, se conocían dos ecuaciones que, unidas, o mejor dicho, pegadas, o enganchadas, proporcionaban una pasable descripción del comportamiento del cuerpo negro: una que daba buenos resultados para grandes longitudes de onda, y otra que se ajustaba bastante a las observaciones efectuadas a baja longitud de onda. Pero lo cierto es que era un pastiche, y nadie podía creer que no existiera una única ley que describiera el comportamiento de un cuerpo que, en el fondo, era un dispositivo sencillo y estilizado.

Planck tenía enfrente al cuerpo negro y un puñado de leyes en las que no confiaba del todo, tal fue la cuestión.

Se venía ocupando de él desde 1895 y hasta 1900 publicó varios artículos, muy interesantes, sí, pero que no resolvían el problema. Ensayaba vueltas de tuerca diferentes, pero siempre se quedaba a mitad de camino: parecía ser que, o bien había que aceptar la discrepancia entre la teoría y la empiria, o bien había que arreglárselas con la ensalada de las dos leyes.

Pero en 1900 Planck cambió de estrategia y dio un salto al vacío. Como muchas veces pasa en la historia de la ciencia, una vez agotados los recursos razonables se prueba con uno que a primera vista no lo es y esto no siempre se produce como resultado de consideraciones científicas frías, serenas y lógicas, sino como un medio extremo en el que se mezclan el azar, la intuición y la buena o mala suerte.

Así fue: ahí lo tenemos a Planck, decidido a probar con una solución inverosímil: ni más ni menos que suponer, contra toda la teoría clásica de la física y todo lo que se sabía sobre la naturaleza de la energía, que ésta no era emitida ni absorbida en forma continua, sino en pequeños «paquetes», o cuantos, tal como si se tratara de partículas. Era un disparate, cosa que él mismo pensaba a medias, pero resulta que con esa suposición en apariencia disparatada consiguió una fórmula matemática simple que proporcionaba la forma completa de la curva y que concordaba perfectamente con las observaciones de la radiación emitida por el cuerpo negro. Aunque, por supuesto, nadie —ni él— entendía cuál podía ser el soporte físico de semejante hipótesis.

Una vez que hizo conocer su fórmula en una reunión de la Sociedad de Física de Berlín en octubre de 1900, Planck intentó encontrar una interpretación física para su ley (esencialmente matemática) haciendo varias hipótesis para ver cuál encajaba mejor con las ecuaciones. Finalmente, tuvo que aceptar una que no le resultaba muy grata: imaginar a los emisores de radiación como pequeños —pequeñísimos— osciladores, que emitían energías que se expresaban por la fórmula

e = hν

donde ν es la frecuencia y h es una constante que desde entonces se conoce como la Constante de Planck. La fórmula es una de las más importantes de toda la historia de la física, comparable a la einsteiniana (y unos años posterior):

e = mc²

Lo que decía, de manera increíblemente sintética, era justamente que la radiación no puede ser emitida ni absorbida de manera continua, sino sólo en «paquetes» cuya energía depende de la frecuencia de la radiación.

Planck había logrado mostrar que si se trataba de manera discreta aquello que todo un siglo había pensado como continuo, las cosas encajaban. La energía era discreta, se comportaba como si fuera una partícula. Era increíble, tan increíble que el propio Planck, en una catarata de artículos posteriores, siguió tratando de encontrar una explicación clásica, mientras muchos de los físicos que conocieron su trabajo continuaban considerándolo simplemente un truco matemático, un artificio para salir del paso, tan provisorio, si se quiere, como el pegoteo con que se trabajaba anteriormente. En 1931, en una carta a Robert William Wood, Planck recordaba su trabajo de 1900:

Puedo caracterizar el procedimiento entero como un acto de desesperación… Tenía que encontrarse una interpretación teórica a cualquier precio, por alto que éste fuera.

Del mismo modo que los representantes de los Estados Generales franceses que se resistieron a la orden de desalojo del rey en 1789 no sabían qué era lo que estaban desatando, la fórmula de Planck, tímida por cierto, aplicable solamente a casi teóricos osciladores del cuerpo negro, era el comienzo de una profunda revolución y ponía de manifiesto una limitación a la física clásica.

No importaba el alcance exacto de tal limitación: el hecho de que existieran fenómenos que no podían ser explicados únicamente con las ideas clásicas era suficiente para anunciar la proximidad de una crisis y una nueva era en la historia de la física.

Ya no habría marcha atrás. El primer paso estaba dado; el segundo paso de la saga estaría asociado al nombre de Einstein y al fenómeno conocido como efecto fotoeléctrico.

El turno de Einstein y el efecto fotoeléctrico

Cuando hablamos de Einstein, hace un par de capítulos, nos detuvimos en el «año milagroso» de 1905 y en algunas de sus grandes contribuciones. Una era la relatividad especial; la segunda, el movimiento browniano, y la tercera, el efecto fotoeléctrico. No es disparatado considerar que esta última es tan importante como la mismísima relatividad, ya que puso en marcha la mecánica cuántica, pasando por encima de los escrúpulos de los físicos de la época. Einstein fue el primero en tomar en serio las implicaciones físicas del trabajo de Planck y en tratarlas como algo más que las consecuencias de un truco matemático al aplicarlas a otro problema, de carácter bastante misterioso, que se arrastraba desde el siglo anterior.

Resulta que dos físicos, Phillip Lenard (1862-1947) y J. J. Thomson (el descubridor del electrón) habían conseguido demostrar, en los últimos años del siglo XIX y trabajando independientemente, que si se iluminaba la superficie de un metal situado en el vacío, la luz «arrancaba» electrones. Pero había una cosa sorprendente. Era obvio que, si se aumentaba la intensidad de la luz, cada centímetro cuadrado de superficie metálica recibiría una cantidad mayor de energía, y también parecía obvio que si un electrón recibía más energía, debía ser expulsado del metal con mayor velocidad.

Pero resulta que la empiria no repara en obviedades: de nuevo, tozudamente, decía que aquello que resultaba lo más esperable no era lo que verdaderamente ocurría. Por más variaciones que se hicieran en la intensidad, la velocidad de salida de los electrones no se alteraba.

Al acercar el foco luminoso al metal, aumentaba el número de electrones liberados pero cada uno de éstos emergía con la misma velocidad con que lo hacían los expulsados por un haz de luz más débil (o más fuerte) del mismo color. Si, en cambio, se utilizaban haces de luz de frecuencia más alta (ultravioleta, por ejemplo, en lugar de luz azul o roja), los electrones avanzaban más rápidamente. El asunto era inexplicable desde la mecánica clásica. Aunque no lo era tanto si se utilizaban los resultados de Planck y se consideraban sus ecuaciones como base. Pero nadie se atrevía a dar este importante y peligroso paso…

Excepto Einstein.

Lo que hizo fue aplicar la ecuación de Planck y afirmar que, así como la radiación electromagnética se transmitía en «paquetes», la luz no es una onda continua, como los científicos habían creído durante cien años, sino que está integrada por cuantos —que después se llamarían fotones—. Con esta asunción simple se explicaba todo.

Al afirmar que la luz estaba compuesta por fotones, Einstein estaba diciendo que toda la luz de una determinada frecuencia (v), es decir, de un color particular del espectro electromagnético, consiste en fotones de la misma energía E. Cada vez que uno de estos fotones golpea a un electrón, le proporciona la misma cantidad de energía y, por tanto, la misma velocidad. Mayor intensidad de luz significa simplemente que hay más cuantos de luz (fotones) de la misma energía; sin embargo, si hay cambio del color de la luz, la frecuencia varía y, por ello, se altera la energía transportada por cada fotón. En consecuencia, ese fotón le transmite más energía al electrón, que parte con mayor velocidad.

La teoría de los fotones no fue aceptada de inmediato, y aunque los experimentos con el efecto fotoeléctrico concordaban con la propuesta de Einstein, pasaron más de diez años hasta que el físico experimental norteamericano Robert Millikan —que logró una determinación ajustadísima del valor de la constante de Planck, que midió muy precisamente la carga del electrón en un célebre experimento y que, cosa curiosa, había sido un tenaz opositor a la postulación einsteiniana— mostró experimentalmente que la teoría del efecto fotoeléctrico era correcta.

Mientras tanto, Einstein amplió sus ideas cuánticas sobre la radiación en los años que siguieron y mostró que la estructura cuántica de la luz es una consecuencia inevitable de la ecuación de Planck. Ante una comunidad científica poco receptiva, el físico más importante del siglo sostuvo que la mejor forma de entender la luz podría consistir en una fusión de las teorías ondulatoria y corpuscular que habían competido entre sí desde el siglo XVII. A pesar de que en 1917 Einstein ya estaba convencido de la realidad de lo que hoy se llaman fotones, recién en 1923 quedó completamente demostrada su existencia. El efecto fotoeléctrico, digamos de paso, se convirtió en una pieza central de la tecnología moderna: el funcionamiento de las células fotoeléctricas se basa en él, así que cada vez que veamos cómo se abren automáticamente las puertas de un ascensor, estamos recibiendo un ramalazo del trabajo de Einstein.

Pero ahora retrocedamos unos años, hasta 1912. Discúlpenme por estas idas y vueltas: la historia de la ciencia es tan desordenada como la historia humana y muchas veces la cronología es, para la narración, más un obstáculo que una herramienta. Revisitemos un tema que hemos tocado ya y que constituyó un espaldarazo más para la teoría cuántica.

El átomo de Bohr, nuevamente

Ya hablamos en su momento sobre la manera en que Bohr resolvió las dificultades del modelo de Rutherford del átomo, que lo presentaba como un sistema solar en miniatura, con un núcleo en el centro y bandas de electrones girando alrededor como los planetas alrededor del Sol. Y vimos cuál era la dificultad. Al girar, siguiendo las leyes de Maxwell, los electrones debían perder energía, con lo cual se suponía que debían caer hacia el centro, cosa que obviamente no ocurría: la materia no se suicidaba. Vimos también cómo Bohr solucionó el problema: afirmó que los electrones alrededor del núcleo de un átomo se mantenían en la misma órbita porque no podían radiar energía continuamente (como exigía la teoría clásica), sino que sólo podían emitir o absorber un cuanto completo de energía —un fotón— y eso únicamente en determinadas órbitas. Por otra parte, las mismas órbitas estaban cuantificadas, y no todas estaban permitidas. Mientras el electrón se movía en estas órbitas no irradiaba, y sólo lo hacía cuando saltaba de una órbita a otra, absorbiendo o emitiendo un fotón. El modelo de Bohr utilizaba explícitamente el modelo de los cuantos de Planck, y con eso había logrado no sólo una solución teórica al inestable átomo de Rutherford sino varias predicciones en relación con la energía radiada por un átomo de hidrógeno, que coincidían puntualmente con los resultados del laboratorio.

Era una ruptura completa con las ideas clásicas, pero resolvía las dificultades muy elegantemente. Así, Bohr introdujo la idea de cuantificación en un modelo concreto, como era el átomo de hidrógeno, aunque sus posturas, desde ya, no convencieron a todo el mundo. El propio Rutherford dudaba y recomendaba moderación.

El problema, en verdad, es que aún no había una verdadera teoría cuántica y los físicos avanzaban a tientas, mezclando conceptos nuevos y viejos para lograr que las cosas funcionaran. Durante una década, la empiria tomó la ventaja, aunque la teoría esperaba ahí, agazapada.

Pero entonces estalló la Primera Guerra Mundial, y la investigación teórica, como suele suceder en las guerras, que destruyen el libre flujo de las ideas, se detuvo.

Impasse: el azar

Mientras mantenemos en mente a las potencias europeas destrozándose en el campo de batalla, produciendo una de las masacres más espantosas de la historia, nosotros retrocederemos aún más, a los primeros años del siglo XX, cuando Rutherford y su colega Frederick Soddy estaban investigando la naturaleza de la radiactividad. Recuerden que fue allí donde apareció una nueva e intrigante propiedad del átomo, o más bien de su núcleo: la desintegración radiactiva, ya sea en partículas alfa o beta (todavía no se conocía la radiación gamma), que se producía en cada átomo individual, y no parecía verse afectada por ninguna influencia exterior. Se calentaran los átomos o se enfriaran, se les colocara en vacío o en un depósito de agua, el proceso de la desintegración radiactiva continuaba imperturbable.

Lo cual no era particularmente alarmante. Lo que sí resultaba novedoso era que no parecía existir forma alguna de predecir exactamente cuándo un átomo particular de la sustancia radiactiva se desintegraría, emitiendo una partícula alfa o una partícula beta.

Ni Rutherford ni Soddy comprendían la causa por la cual un átomo se desintegra en un momento dado y otro no, y empezaron a tratar el fenómeno estadísticamente. Y ahí, los experimentos demostraban que cuando el número de átomos radiactivos estudiado era grande, una cierta proporción se desintegraba siempre en un cierto tiempo. Recuerden que para cada elemento radiactivo existe un tiempo característico, llamado «vida media», durante el cual se desintegra exactamente la mitad de los átomos de la muestra. Ya hemos dicho esto: el radio, por ejemplo, tiene una semivida de 1.600 años; el carbono 14 tiene una semivida de un poco menos de 6.000 años (lo cual resulta útil para las dataciones arqueológicas) y el potasio radiactivo se desintegra con semivida de 1.300 millones de años.

Era una solución práctica, pero no dejaba satisfechos a los científicos que, aunque muchas veces no lo admitan, no sólo están interesados por «modelos» o explicaciones empíricas, sino por conocer la verdadera naturaleza de las cosas. En efecto, el misterio de lo que pasaba con cada átomo individual persistía tenazmente. Era, como luego lo demostraría Einstein, un problema similar al que se desprendía del modelo atómico de Bohr, que estipulaba que un electrón saltaba de una órbita prefijada a otra pero no decía nada acerca de cuándo lo hacía (y mucho menos, como se verá, qué es lo que hacía cuando estaba «en tránsito»). Rutherford, Soddy y el mismísimo Einstein pensaban que algún día alguien descubriría exactamente el mecanismo de la desintegración de un átomo individualizado y con ello se lograría explicar el asunto.

Y es aquí donde se produce una bifurcación entre las ideas clásicas y las cuánticas o, digámoslo de otra manera, entre la manera clásica de pensar el mundo y la manera cuántica de pensar el mundo.

En el mundo clásico todo tiene su causa. Y no me refiero sólo al mundo de la física clásica, sino a aquel inaugurado por la primera formulación de la ciencia hecha por nuestro viejísimo amigo Tales de Mileto: uno busca la causa, y la causa de la causa, y se remonta por la cadena causal hasta donde quiera, o hasta una causa primera, si es que la hay, o si uno cree que la hay. Pero un átomo radiactivo se desintegra en un momento dado, sin que aparentemente haya una razón para que esto ocurra. Tiene una probabilidad de hacerlo en cada momento, y en algún momento lo hace. Y punto.

Un fenómeno como éste desafía una de las más arraigadas concepciones de la ciencia: el determinismo. ¿Qué es esto? Sintéticamente, un modo de concebir la realidad de manera tal que nada está librado al azar: si hay cosas que no podemos prever o explicar no se debe a que sean naturalmente impredecibles o inexplicables sino a alguna deficiencia nuestra (falta de información, o falta de instrumentos adecuados, o falta de atención). Lo decía Pierre Simon Laplace (1749-1827):

Podemos mirar el estado presente del universo como el efecto del pasado y la causa de su futuro. Se podría concebir un intelecto que en cualquier momento dado conociera todas las fuerzas que animan la naturaleza y las posiciones de los seres que la componen; si este intelecto fuera lo suficientemente vasto como para someter los datos a análisis, podría condensar en una simple fórmula el movimiento de los grandes cuerpos del universo y del átomo más ligero; para tal intelecto nada podría ser incierto y el futuro, así como el pasado, estarían frente a sus ojos.

El azar al que nos referimos habitualmente, desde esta perspectiva, es sólo producto de nuestra falta de información: la bolilla de la ruleta gira y cae en un número «al azar», pero si un demonio, al estilo del de Descartes, o una súper súper computadora como la Multivac de Asimov, pudiera reunir todos los datos sobre la trayectoria de la bolita —sus choques con las ranuras de la ruleta, la velocidad con la que corre, la magnitud del rozamiento— podría pronosticar exactamente en qué lugar caería. Si coloco un alfiler en punta en una mesa en perfecto equilibrio y no hay una razón para que caiga para un lado o para el otro (razón que, insisto, nosotros podemos desconocer pero no pasar por alto), éste se quedará donde está por los siglos de los siglos. El universo actúa siempre y cuando haya una buena razón para que haga esto o aquello; si no, no hace nada y permanece donde está.

Pero resulta que en el mundo cuántico no es así: esta causalidad directa, determinista, que aún hoy a nosotros nos parece algo bastante intuitivo, desaparece tan pronto como nos fijemos en la desintegración radiactiva y en las transiciones de los electrones en el átomo.

En cierto modo era fatal que esto ocurriera, aunque estaba implícito en la teoría del cuerpo negro de Planck: para llegar a su fórmula, el físico alemán se había inspirado en Boltzmann (las ideas nunca surgen de la nada) y su interpretación estadística de la entropía, de la cual hablamos en el capítulo respectivo. La entropía, vimos entonces, era para él un fenómeno probabilístico. No era una «cosa» que crecía, sino que expresaba la tendencia del universo a ubicarse en los estados más probables, que son los más desordenados.

A través de ese hueco que abrían Planck, Einstein, Rutherford y Bohr, una nueva forma de azar, un azar ontológico, se deslizaba en el mundo. El asunto era saber si lo hacía para quedarse. Al principio, la mayoría de los físicos pensaban que no, pero en seguida fueron desbordados por nuevos y aún más extraños descubrimientos.

De Broglie: partículas y ondas

Ya les conté que los fotones pasaron a formar parte del lenguaje científico ordinario después de 1927, pero no hemos dicho que fue en ocasión del quinto Congreso Solvay, bajo el título «Electrones y fotones». Lo curioso era que al mismo tiempo que los fotones hacían revivir la vieja teoría corpuscular de la luz, era también evidente su naturaleza ondulatoria. Como afirmó Einstein:

resultaban entonces dos teorías de la luz, ambas indispensables… sin ninguna relación lógica.

La idea genial, que vendría a resolver las cosas —o a complicarlas, vaya uno a saber— provino de un físico francés, Louis de Broglie (1892-1987), descendiente de una familia de nobles cuyas actuaciones en la historia francesa se remontaban a dos siglos o más. A Louis de Broglie se le ocurrió un planteamiento muy simple, como muchos de los planteamientos geniales. Si la ondulatoria luz, como era evidente, se «disfrazaba» de partícula, ¿por qué un electrón no podría «disfrazarse» de onda?

De Broglie desarrolló matemáticamente esta posibilidad en su tesis doctoral, describiendo cómo se deberían comportar las ondas de materia y sugiriendo formas en las que podrían ser observadas. Al mismo tiempo, aclaraba que él no sostenía que el electrón podía estudiarse como una partícula o una onda, sino que era una partícula y una onda (significare esto lo que significare).

Sostenía que el fracaso de los experimentos para poner de manifiesto, de una vez por todas, si la luz es onda o partícula se debía a que ambos tipos de comportamiento van unidos, hasta el punto de que para medir la propiedad corpuscular que representa la velocidad hay que conocer la propiedad ondulatoria llamada frecuencia. Y lo mismo ocurría con los electrones, que por entonces eran considerados como partículas típicas —excepto por el curioso modo de ocupar los distintos niveles de energía dentro de los átomos— y que se convertían, gracias a De Broglie, en algo dual: partículas, sí, pero también ondas.

El jurado que estudió la tesis de De Broglie apreció las matemáticas que exhibía pero no creyó ni por un momento que la propuesta de una onda asociada a una partícula como el electrón tuviera algún sentido real: lo estimaron como un simple truco matemático, tal como había ocurrido en su momento con la ecuación de Planck. De Broglie no estuvo de acuerdo y cuando uno de los examinadores le preguntó si se podría diseñar algún experimento para detectar las ondas de materia, él contestó que sería posible efectuar las observaciones requeridas difractando un haz de electrones mediante un cristal, del mismo modo que se difracta una onda de luz a través de un grupo de ranuras (no sabía que ya en 1914 dos físicos norteamericanos, Clinton Davisson y su colega Charles Kunsman, habían detectado este curioso comportamiento al utilizar haces de electrones para el estudio de cristales, aunque lo interpretaron de otra manera).

De Broglie trató de persuadir a experimentalistas para llevar a cabo la prueba de la hipótesis de la onda del electrón; mientras tanto, su director de tesis envió una copia del trabajo a Einstein, quien se lo tomó muy en serio, y en vez de considerarlo un artificio matemático pensó que las ondas de materia debían ser reales:

Creo que representa más que una mera analogía,

aseguró.

Y le pasó las noticias a Max Born, de Gottingen, donde el director del Departamento de Física Experimental, James Franck, comentó que los experimentos de Davisson ya habían establecido la existencia del efecto esperado. De todos modos, los experimentalistas no se dejaron influir por esta reinterpretación de sus resultados y los devaneos de un teórico que no era más que un primerizo estudiante de veintiún años. Incluso en 1925, a pesar de haberse demostrado experimentalmente, la teoría de las ondas de materia no pasaba de ser un concepto vago.

Sólo cuando Erwin Schrödinger realizó una nueva teoría de la estructura atómica que incorporaba y ampliaba la idea de De Broglie, los experimentalistas consideraron urgente comprobar la hipótesis de la onda del electrón mediante la realización de experimentos de difracción.

Schrödinger

Cuando se tomó conciencia de que no sólo los fotones y los electrones sino todas las partículas y todas las ondas son, de hecho, una mezcla de onda y partícula, puede decirse que se consumó la ruptura con la física clásica.

En nuestro mundo ordinario, la componente corpuscular domina de manera total en el cóctel onda-partícula. Si se trata, por ejemplo, de una piedra o de un auto, el efecto ondulatorio está, pero es completamente insignificante, lo cual se debe al pequeñísimo valor de la constante de Planck, del mismo modo que los efectos relativistas están, pero son insignificantes debido al altísimo valor de la constante c, la velocidad de la luz. En el mundo de lo muy pequeño, donde los aspectos corpusculares y los ondulatorios de la realidad física son igualmente significativos, las cosas se comportan de un modo radicalmente distinto del de la experiencia cotidiana, y —lo que es peor— de la física clásica.

Sir Arthur Eddington lo resumió en 1929:

No pueden elaborarse concepciones familiares sobre el electrón

afirmó, y el átomo es

algo desconocido que hace no sabemos qué.

Era necesario desterrar la asociación instintiva de los átomos con esferas duras y de electrones con diminutas partículas.

A finales de 1925, cuando la teoría de las ondas de electrones de De Broglie ya había aparecido en escena pero no se habían realizado los experimentos definitivos que probarían la naturaleza ondulatoria del electrón, se produjo un nuevo paso adelante: el de una teoría matemática que daba cuenta de los fenómenos cuánticos basándose en la teoría ondulatoria.

Fue en uno de los trabajos de Einstein, publicado en febrero de 1925, donde Erwin Schrödinger (1887-1961) leyó los comentarios sobre la idea de De Broglie. Las opiniones de Einstein tenían un peso específico gigantesco, y fueron suficientes para que nuestro personaje se dedicara a investigar cuáles podían ser los caminos que se abrían si se tomaba a De Broglie literalmente.

Schrödinger trató de restaurar la comprensión sencilla de las ideas físicas mediante la descripción de la física cuántica en términos de ondas, entidades familiares en el mundo físico, y luchó hasta su muerte contra los nuevos conceptos de indeterminación y transición instantánea de electrones de un estado a otro.

De Broglie había indicado el camino con su idea de que las ondas de electrones en órbita alrededor de un núcleo atómico habían de ajustarse a un número entero de longitudes de onda en cada órbita, por lo que existían órbitas intermedias prohibidas. Schrödinger amplió las matemáticas sobre ondas para calcular los niveles de energía permitidos en tal situación, y consiguió un buen acuerdo con las observaciones. Las ecuaciones en la variante de Schrödinger sobre la teoría cuántica pertenecen a la misma familia que describen ondas reales en el mundo ordinario: ondas sobre la superficie del océano, o las ondas que transmiten ruidos a través de la atmósfera. El mundo de los físicos recibió esta aportación con entusiasmo, precisamente por resultar tan familiar.

Algunos habrán pensado que las cosas todavía podían encarrilarse.

Pero no. Todavía faltaba un experimento fundamental.

El experimento de la doble ranura

¿Se acuerdan del experimento de Young, de 1801, con el que se quiso verificar si la luz era una onda o una partícula? Imagínense una pantalla con dos pequeños agujeros en ella. A un lado de esta pantalla hay otra que lleva incorporada un detector. Una fuente lanza fotones, o electrones —digamos, electrones— contra la pared que tiene los dos agujeros. La pregunta es: ¿qué sucede cuando los objetos pasan a través de los agujeros y llegan hasta la pantalla? Es decir, ¿qué figura consiguen que forme el detector?

El resultado es sorprendente, por cierto. Si se tapa una de las dos rendijas, los electrones se comportan estrictamente como partículas, y caen en el sitio que corresponde en el detector, como se ve en la figura 1.

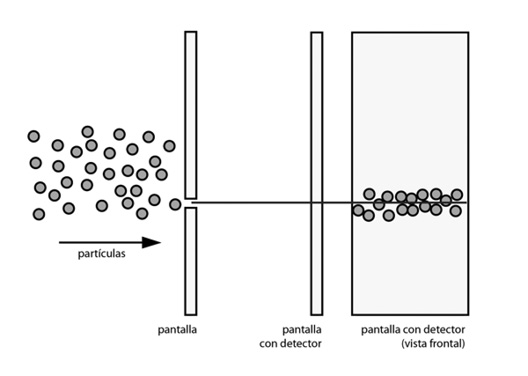
FIGURA 1

Ahora fíjense lo que pasa con una onda: la onda pasa por las dos rendijas, se bifurca y forma dos ondas diferentes, que se superponen por momentos. En donde las ondas están superpuestas, la pantalla detectora mostrará mayor intensidad: el patrón que se obtiene es como el que se ve en la figura 3.

Ahora bien, ¿qué pasa si arrojo un haz de electrones a través de las dos rendijas abiertas? Si considero que se trata de partículas, lo más lógico sería pensar que cada electrón individual pasa a través de un agujero o del otro, con lo cual se formaría un patrón similar al de la figura 1 pero con dos líneas en lugar de una sola, tal como se puede ver en la figura 2.

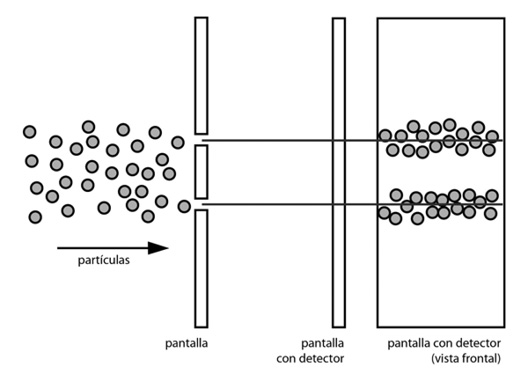
FIGURA 2

Y sin embargo, no. Cada electrón pareciera atravesar ambas rendijas como una onda, y produce sobre la pantalla figuras de interferencia, como si fuera una onda (es decir, como se ve en la figura 3). ¿Pero cómo «sabe» el electrón si está abierta una sola rendija o las dos mientras se aproxima a la pared para decidir cómo comportarse? Es un verdadero misterio.

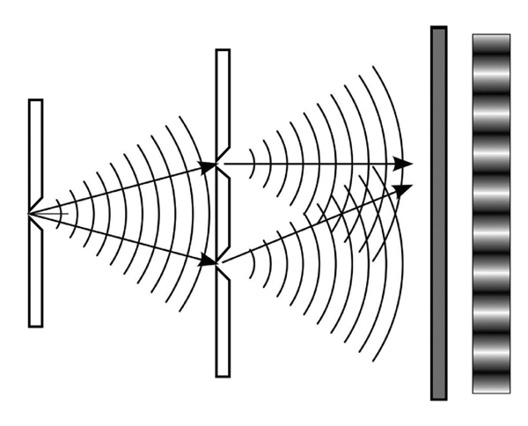
FIGURA 3

Además, supongamos que el electrón está viajando hacia las dos rendijas abiertas —se supone que como una onda— y entonces decidimos observarlo mientras las atraviesa. En ese caso, el electrón instantáneamente colapsa hacia una partícula, como si «supiera» que lo queremos observar. Y es más, colapsa si decidimos observarlo después de que haya partido, por lo cual volveríamos a obtener la figura 2.

¿Qué conclusión se puede sacar de esto? ¿Se trata de la dualidad onda-corpúsculo con la que se ha aprendido a convivir? Si es una onda, no sorprende encontrar que se difracte y produzca una figura de interferencia. Millares de electrones inciden sobre los agujeros, y se puede predecir sobre una base estadística dónde llegarán, empleando esta interpretación de la onda. Pero, ¿qué le sucede a cada electrón individual? Acá viene una de las grandes revoluciones conceptuales de la mecánica cuántica.

La interpretación de Copenhague

En todas las ficciones, cada vez que un hombre se enfrenta con diversas alternativas, opta por una y elimina las otras, en la del casi inextricable Ts’ui Pen, opta —simultáneamente— por todas. Crea, así, diversos porvenires, diversos tiempos, que también proliferan y se bifurcan.

J. L. BORGES, «El jardín de senderos que se bifurcan»

Un electrón individual, o un fotón, cuando incide sobre un agujero de la pared, obedece en cada caso a las leyes estadísticas previstas, lo cual sólo puede ocurrir si «sabe» si el otro agujero está abierto o cerrado. Se puede tratar de «despistar» al electrón disparando más o abriendo repentinamente uno de los agujeros, mientras el electrón está ya en tránsito, por el aparato. No importa; la figura en la pantalla es siempre la «correcta» atendiendo al estado de los agujeros en el instante en que el electrón llega a la primera pared.

Se puede, también, tratar de ver por cuál de los agujeros pasa el electrón. Cuando el experimento correspondiente se realiza, el resultado es todavía más extraño: los electrones se comportan como las partículas corrientes del mundo ordinario. Siempre se detecta un electrón pasando por uno u otro de los agujeros, pero nunca por los dos a la vez. Los electrones resulta que no sólo «saben» si los dos agujeros están abiertos o no, sino también si están siendo observados o no, y ajustan su comportamiento en consonancia. No existe un ejemplo más claro de interacción entre el observador y el experimento. Cuando se intenta observar la onda dispersa del electrón, ésta se colapsa en una partícula definida, pero si no se la observa mantiene su carácter ondulatorio. Salvo que alguien lo observe, la naturaleza misma «ignora» por qué agujero pasa el electrón.

Así pues, por lo que parece, el aparato, los electrones y el observador son partes integrantes del experimento. No se puede afirmar que un electrón pasa por uno de los agujeros si no se están observando los agujeros ante el paso de los electrones. Un electrón sale del disparador y llega al detector, y parece que posee información del montaje experimental completo, incluyendo al observador.

Esto es lo que se conoce como «interpretación de Copenhague», que fue encabezada por Niels Bohr. En la física clásica, cualquier sistema de partículas se comporta de manera determinista independientemente de que esté siendo observado o no; en la cuántica, el observador interactúa de tal manera con el sistema que casi no puede ser considerado un mero observador. Su actividad observante modifica el sistema que quiere estudiar: si elige medir con precisión la posición, fuerza a una partícula a presentar mayor incertidumbre en su velocidad y viceversa. Si elige algún experimento para medir propiedades ondulatorias se eliminan peculiaridades corpusculares, y no hay experiencia posible capaz de poner en juego ambas naturalezas. Las partículas cuánticas, a diferencia de las clásicas, no tienen una posición y velocidad precisas en el espacio-tiempo.

En realidad, es difícil de creer, pero la mecánica cuántica es una teoría de una firmeza que parece indestructible, es coherente con todos los experimentos, y ha permitido el desarrollo de tecnologías muy poderosas, como los láseres, los microscopios electrónicos (que utilizan ondas de electrones en lugar de ondas de luz y que son mucho más potentes que los ópticos), la generación de energía nuclear, los circuitos integrados que a su vez permiten las grandes computadoras… y la lista sigue.

Hubo de pasar mucho tiempo para que estas ideas se desarrollaran y para que su significado fuera captado. Hoy, las características de la interpretación de Copenhague se pueden explicar y entender más fácilmente en términos de lo que pasa cuando se efectúa una observación experimental. En primer lugar, se ha de aceptar que el mero hecho de observar una cosa la cambia y que el observador forma parte del experimento, es decir, no hay un mecanismo que funcione independientemente de que se lo observe o no. En segundo lugar, toda la información la constituyen los resultados de los experimentos. Se puede observar un átomo y ver un electrón en el estado de energía A, después volver a observar y ver un electrón en el estado de energía B. Se supone que el electrón saltó de A a B, quizás a causa de la observación. De hecho, no se puede asegurar siquiera que se trate del mismo electrón y no se puede hacer ninguna hipótesis sobre lo que ocurría cuando no se observaba. Lo que se puede deducir de los experimentos, o de las ecuaciones de la teoría cuántica, es la probabilidad de que si al observar el sistema se obtiene el resultado A, otra observación posterior proporciona el resultado B. Nada se puede afirmar sobre lo que pasa cuando no se observa, ni de cómo pasa el sistema de A a B, si es que pasa. Los saltos cuánticos son simplemente una interpretación subjetiva de por qué se obtienen dos resultados diferentes para el mismo experimento, y es una falsa interpretación. A veces las cosas se observan en el estado A, a veces en el B, y la cuestión de qué hay en medio o de cómo pasan de un estado a otro carece completamente de sentido.

Lo extraño de la inusual interpretación de Copenhague del mundo cuántico es que es el acto de observar al sistema físico el que lo obliga a seleccionar una de sus opciones. Nada es real salvo que sea observado, y cesa de ser real en cuanto se detiene la observación.

Vivimos en un mundo donde las partículas sólo parecen reales cuando se las observa, y donde incluso propiedades como la velocidad y la posición son únicamente artilugios de las observaciones.

En cierto modo, me hace acordar a la interpretación de Wittenberg de la astronomía copernicana, que consideraba también los resultados independientemente de la existencia de epiciclos o no, desde un punto de vista instrumentalista. Naturalmente, la astronomía de Copérnico no tenía presupuestos tan estrafalarios como que una partícula «sabe» qué pasa con las rendijas, pero quizás el movimiento de la Tierra a muchos les resultara igual de alucinante.

El principio de incertidumbre

El futuro puede predecirse a partir del pasado. Si conociéramos la velocidad y posición de todas las partículas del universo, podríamos predecir el futuro con total exactitud.

LAPLACE (otra vez)

Aunque pueda sonar un tanto omnipotente, la afirmación de Laplace, de hace menos de 200 años, reflejaba muy bien el espíritu que presidió el desarrollo y cenit de la ciencia clásica durante el siglo XIX y principios del XX: si se tuvieran a disposición todos los datos del presente, se podría predecir perfectamente el futuro. Naturalmente, nadie pensaba que se podían tener de manera efectiva esos datos, pero era tan sólo una cuestión de imposibilidad práctica. En teoría, era posible: el futuro estaba exactamente determinado por el presente, mediante la acción de las leyes físicas. El mundo, en suma, era predictible por la ciencia. Este credo determinista, del que ya hemos hablado, sufrió un duro revés con la mecánica cuántica.

Más o menos al mismo tiempo que Schrödinger desarrollaba su modelo ondulatorio, Heisenberg encontraba una formulación alternativa (que luego se mostró que era equivalente), una de cuyas consecuencias más inquietantes (y más espectaculares) es, justamente, el principio de incertidumbre, que enunció en 1927. Laplace sostenía que se podría predecir el futuro del universo si se pudieran conocer la posición y velocidad de todas las partículas del universo… El principio de incertidumbre, precisamente, afirma que esto es imposible. Pero no imposible como el sentido común sabe que es imposible (es decir, técnicamente imposible) sino ontológicamente imposible. Es más: ni siquiera se pueden conocer exactamente la posición y velocidad de una partícula aislada. Se puede medir con exactitud la posición de un electrón. También se puede medir con exactitud la velocidad de ese electrón. Lo que no se puede hacer es medir ambas, posición y velocidad, simultáneamente y con absoluta precisión. Cuanto más precisamente se mida la velocidad, más incertidumbre habrá en cuanto a la posición, y cuanto más exactamente se mida la posición, más indeterminada quedará la velocidad.

Es como si no se pudieran saber a la vez el teléfono y la dirección de una persona, como si en la agenda donde están anotados, el número de teléfono se tornara más borroso a medida que se clarifica la dirección y, a la inversa, a medida que se vuelve más fácil leer el número de teléfono, la dirección fuera borrándose. Y en el caso extremo en que el teléfono quedara absolutamente claro, el lugar correspondiente a la dirección quedaría en blanco.

El propio Heisenberg trató de explicar este curioso rasgo de la naturaleza de manera más o menos intuitiva: si uno quiere determinar la posición de un electrón, debe iluminarlo para ver dónde está, pero, para la escala del electrón, los fotones de luz son suficientemente energéticos como para alterar su velocidad. Recíprocamente, si uno quiere averiguar la velocidad, debe abstenerse de iluminarlo, y entonces no sabrá dónde se encuentra. O una magnitud, o la otra. O las dos, pero no demasiado precisamente.

El ejemplo de Heisenberg, no obstante su valor intuitivo, puede sugerir que el problema de la medición simultánea de magnitudes como la velocidad y la posición (o la energía y el tiempo) puede deberse a un problema relacionado con la medición. Nada de eso. La incertidumbre cuántica parece ser un rasgo fundamental de la naturaleza: no es que sea imposible medir simultáneamente velocidad y posición de una partícula atómica o subatómica, sino que hablar de la velocidad y la posición simultáneas de una partícula carece de sentido. Volviendo al ejemplo de la dirección y el teléfono, lo que el principio de incertidumbre afirma es que el señor X no puede tener al mismo tiempo dirección y teléfono definidos: o bien lo llamamos a un teléfono celular cuya posición es totalmente imprecisa, o bien lo llamamos a un teléfono de línea, que sabemos dónde está, pero que no nos da ninguna garantía de encontrarlo.

Naturalmente, estos fenómenos no se observan en el mundo macroscópico, debido a su incidencia infinitesimal, pero de todas maneras plantean preguntas (por ahora sin respuesta) sobre la estructura de la realidad.

Paradojas y posibilidades

No es sorprendente que muchos físicos de prestigio, incluyendo a Einstein, hayan dedicado décadas enteras a tratar de encontrar vías alternativas a esta interpretación de la mecánica cuántica. Pero sus intentos han fallado todos, y cada nuevo fracaso en la búsqueda de acabar con la interpretación de Copenhague no ha hecho sino reforzar su base.

Ya dijimos que, para los físicos de Copenhague, las imprecisiones, probabilidades e incertidumbres de la mecánica cuántica no son una limitación de la física, o la señal de que la mecánica cuántica es una teoría incompleta, sino que la naturaleza es así: un electrón es una superposición de probabilidades de estar aquí o allá, tal y como la mecánica cuántica lo describe. Pensar en un electrón en tal lugar no tiene sentido (a menos que lo observemos, en cuyo caso la función de onda «colapsa» hacia una posición fija, todos los estados se condensan y el electrón aparece tan campante ocupando una determinada posición).

La primera paradoja famosa postulada para poner en entredicho esta postura fue planteada por el mismísimo Schrödinger, quien en 1935 propuso un curioso experimento mental que quedó en el folklore como «la paradoja del gato de Schrödinger». Y es así.

Imaginemos una caja completamente cerrada que contiene un gato vivo y una pequeña cantidad de material radiactivo. Imaginemos también que dentro de la caja hay un dispositivo diabólico (pero perfectamente posible) por el cual cuando una partícula es emitida por alguno de los átomos radiactivos, se pone en funcionamiento un detector que a su vez suelta un martillo que rompe una ampolla de vidrio llena de un gas venenoso, efectivo e instantáneo. O sea, apenas un átomo se desintegra, el gato muere. Para la mecánica cuántica, no hay manera de saber en qué momento un átomo se va a desintegrar: todo se reduce a probabilidades. Solamente mirando podemos saber si el átomo se ha desintegrado o no, y mientras la caja esté cerrada, los átomos en cuestión son una mezcla de dos estados (se desintegró-no se desintegró). Entonces, razonaba Schrödinger, puesto que no tiene sentido preguntarse si el material radiactivo se desintegró o no hasta que abramos la caja y miremos, tampoco tiene sentido preguntarse si el gato está vivo o no hasta ese mismo momento. Simplemente —siguiendo la interpretación de Copenhague— el gato está en una mezcla de dos estados, «vivo» y «no vivo», y pensar que está vivo o que está muerto no tiene sentido.

Obviamente, la intención de Schrödinger fue amplificar la incertidumbre cuántica hasta llevarla a términos cotidianos (¿quién puede imaginarse a un gato como una mezcla de gato vivo y gato muerto?) de tal manera que chocara aún a los teóricos de Copenhague. Naturalmente, a éstos no les chocó, aunque hasta ahora no hay respuestas enteramente satisfactorias a la paradoja, que Einstein celebró efusivamente.

(Dicho sea de paso, no es raro que Schrödinger haya elegido a un gato, animal que tiene mucho de misterioso y extraño. El gato de Schrödinger, con su mezcla de estados, es primo directo del gato de Cheshire de Lewis Carroll en Alicia en el País de las Maravillas, capaz de esfumarse por partes y dejar su sonrisa flotando.)

La segunda paradoja corrió por cuenta de Einstein, quien durante los años treinta y cuarenta mantuvo una pertinaz y divertida discusión con Niels Bohr sobre este mismo punto. Para Einstein, el electrón tenía que tener una velocidad y una posición determinadas: si la teoría se las negaba, era una muestra de la debilidad de la teoría; para Bohr, la teoría era firme como una roca, y en todo caso la debilidad era de la naturaleza, o de nuestro concepto de la realidad. Einstein proponía experimentos (teóricos) que permitieran medir velocidad y posición de un electrón en forma simultánea (para mostrar que se violaba el Principio de Incertidumbre), experimentos que Bohr refutaba graciosamente. Uno de los más sonados quedó en la literatura como la paradoja EPR (por Einstein, Podolsky y Rosen, que lo sugirieron en 1935).

Simplificando las cosas hasta el escándalo, la idea era la siguiente: supongamos, decían Einstein, Podolsky y Rosen, que dos partículas, A y B, parten en direcciones contrarias, de tal manera que a partir de una de ellas uno pueda deducir la situación de la otra. Entonces, uno podría perfectamente medir la posición de A, y la velocidad de B. A partir de la velocidad de B, se deduce la de A, con lo cual sabríamos exactamente ambas magnitudes de A, en contra del Principio de Incertidumbre. Bohr no se inmutó y aseguró que, al medirse la posición de la partícula A, la velocidad de la partícula B se alteraría, como si «supiera» que a su compañera la estaban midiendo. En este punto, la cosa desembocó en un callejón sin salida, porque el experimento era entonces impracticable.

Pero en los años setenta el físico británico John Bell inició un camino teórico que permitió a Alain Aspect en 1982 llevar a cabo un experimento que zanjó la discusión. En vez de electrones, posiciones y velocidades, se usaron fotones y direcciones de polarización, pero el sentido del experimento fue el mismo. Y tanto los trabajos de Aspect de 1982 como las repeticiones ulteriores le dieron la razón a Niels Bohr y refutaron a Einstein.

La polémica sobre la mecánica cuántica sigue. No es para sorprenderse. En ella está comprometida nuestra concepción del mundo y de lo que entendemos por «realidad». El universo es, tal vez, un lugar aún más misterioso de lo que solemos imaginar.

INTERMEZZO MATEMÁTICO: LA CRISIS DE LOS FUNDAMENTOS

La denominada «crisis de los fundamentos», fiel al espíritu epocal, contribuyó a desarmar una imagen construida a partir de la Revolución Científica según la cual la Ciencia (así, con mayúscula) progresaba en un camino ilimitado hacia la Verdad (también así, con mayúscula), camino que no presentaba más obstáculos serios que el enorme tiempo que llevaba recorrerlo.

Paradojas

La palabra «paradoja» viene de la palabra latina «paradoxus», a su vez descendiente directa del griego «parasofos», y en los tres idiomas significa «conocimiento que choca con el sentido común». Por alguna razón las paradojas tienen algo encantador: el atractivo que despierta la posibilidad de los viajes en el tiempo, por ejemplo, aumenta con la paradoja que los impide: ¿qué ocurre si yo viajo al pasado y asesino a mis ancestros, impidiendo mi propio nacimiento? Este dilema (irresoluble), muestra que viajar al pasado es imposible, pero que es posible la trilogía Volver al Futuro, de Zemeckis y Spielberg, que es mucho mejor y es objeto de devoción por parte del volátil autor de estas páginas.

Cuando Einstein enunció la Teoría de la Relatividad Restringida, en 1905, dio pie para muchos juegos paradojales, especialmente con el tiempo, que desvelaron a los científicos. Por ejemplo, la paradoja de los gemelos: según la teoría de la relatividad (restringida), uno ve que sobre un cohete en movimiento el tiempo transcurre más lentamente. Entonces, imaginemos a dos hermanos gemelos, uno de los cuales se embarca en un cohete para emprender un largo viaje espacial. El hermano que permanece en tierra ve que el reloj del viajero va más despacio que el suyo (porque el tiempo en la nave corre más despacio), que su hermano estelar envejece más lentamente que él y, por lo tanto, lo ve más joven que él.

Pero a su vez el hermano que viaja en el cohete (siempre según la Teoría de la Relatividad Restringida) supone que en realidad él está quieto, que es la Tierra la que se mueve (con su hermano sobre ella). Y en consecuencia, el reloj de su hermano terrestre va más despacio y su hermano es más joven. O sea: cada uno ve al otro más joven. ¿Qué pasa cuando el viajero regresa y se produce el reencuentro? No puede ser que cada hermano sea más joven que el otro. La solución no es nada sencilla y requiere recursos de la Relatividad General que exceden por completo a este libro.

La mecánica cuántica, como ustedes ya saben, no dejó de agregar su cuota en este mundo contrario al sentido común (el gato de Schrödinger es el mejor ejemplo).

Éstas son paradojas planteadas por la física, pero una de las más famosas no viene de allí sino del campo de la lógica: se trata de la del «catálogo de catálogos» propuesta por el gran filósofo, matemático y lógico inglés Bertrand Russell (1872-1970).

Síganme con atención.

Como todos sabemos, hay catálogos de libros que se incluyen a sí mismos como un libro más; hay otros, en cambio, que no. Incluirse a sí mismo o no es una decisión que en cada caso toma el editor, basado en sus preferencias personales.

Pero imaginemos, propuso Bertrand Russell, que queremos hacer un Supercatálogo donde figuren todos los catálogos que no se incluyen a sí mismos y solamente ellos.

A primera vista parece fácil. Pero no es así. Porque… ¿qué hacemos con el propio Supercatálogo? ¿Lo incluimos o no lo incluimos? ¿Lo ponemos o no lo ponemos? Y, no. Porque si lo incluimos en el índice, el Supercatálogo se convierte en un catálogo de libros que se contiene a sí mismo, y por ende, no debe figurar. Entonces, no lo ponemos.

Pero si no lo ponemos, nuestro Supercatálogo es un catálogo que no se contiene a sí mismo y entonces sí debe figurar.

O sea que no hay manera de resolver el problema. Russell planteó esta paradoja en términos de la Teoría de Conjuntos y en 1902 se la envió al matemático alemán Gottlieb Frege (1848-1925).

Frege acababa de terminar el segundo volumen de un ambicioso intento de construcción de una estructura matemática coherente y completa desde el punto de vista lógico. El libro se estaba imprimiendo (salió en 1903) cuando recibió la carta de Russell. Frege comprobó que su sistema no podía resolverla, y tuvo que añadir, al final del volumen, un párrafo en el que admitía que el fundamento de su razonamiento había fallado y que, por lo tanto, el libro era inútil. Fue una verdadera catástrofe intelectual, que demostró lo que nadie podía concebir: los fundamentos de las matemáticas eran dudosos. Y si los fundamentos de la matemática están mal… ¿cómo podemos estar seguros de que la física está bien? Y si la física es dudosa…, ¿no lo será también la medicina, que le debe tanto? Los matemáticos se lanzaron entonces a tratar de encontrar un sistema de axiomas que pudiera fundamentar las matemáticas. Y, notablemente, en 1931, un lógico llamado Gödel mostró que no se puede… bueno, no exactamente, sino que el intento tiene muchos bemoles.

El teorema de Gödel

Cada hombre está eternamente obligado, en el curso de su breve vida, a elegir entre la esperanza infatigable y la prudente falta de esperanza, entre las delicias del caos y las de la estabilidad.

Memorias de Adriano, MARGUERITE YOURCENAR

Desde muy antiguo se consideró a la matemática, y con bastante justicia, como la reina de las ciencias. Este precepto, cuando Galileo en el siglo XVII proclamó que «el libro de la naturaleza está escrito con caracteres matemáticos», confirió a la corona los atributos del derecho divino. Y hasta cierto punto los de una monarquía absoluta. Si las matemáticas nunca parafrasearon a Luis XIV diciendo «la ciencia soy yo» fue tan sólo porque son incapaces de hablar, y tal vez por falsa modestia. Lo cierto es que, a partir del triunfo de la mecánica newtoniana, las matemáticas se convirtieron en la aspiración común de todas las disciplinas científicas: matematizar una ciencia garantizaba su verdad. Es preciso reconocer, de paso, y a despecho de cualquier aspiración republicana, que este sistema de gobierno dio resultados espectaculares: la reducción de las ciencias a fórmulas y su manipulación produjeron la acumulación de conocimientos más formidable que recuerde la memoria humana.

Ese papel central de la matemática deriva de su método: la obtención de resultados mediante la deducción puramente lógica a partir de un puñado de axiomas elementales que se aceptan como verdaderos. De hecho, ésta fue la metodología que utilizó Euclides en sus célebres Elementos, que conocimos en el lejano capítulo sobre la Escuela de Alejandría —aunque, como ven, todo vuelve—, que se usaron sin mayores variantes hasta hace ciento cincuenta años y que permanecen, sin demasiadas transformaciones, en los textos de geometría que se utilizan aún hoy en la escuela secundaria.

Es verdad que durante el siglo pasado la supuesta verdad absoluta de los axiomas de la geometría euclideana recibió un duro golpe: partiendo de axiomas diferentes de los de Euclides, Lobachevski y Riemann construyeron geometrías perfectamente coherentes, aunque distintas de la euclideana, y de alguna manera la búsqueda de la verdad fue sustituida por el afán de coherencia y no contradicción.

Pero hacia finales de siglo XIX, el triunfo del método axiomático era completo: las investigaciones de la lógica matemática se dirigían con especial énfasis a buscar una formalización y axiomatización de toda la matemática.

La idea se inscribía perfectamente en la muy finisecular concepción del progreso: una vez encontrados los axiomas adecuados, todas las verdades podrían ser deducidas a partir de ellos, mediante la lógica y la paciencia. Cuando en 1900 el gran matemático David Hilbert presentó un programa enunciando la lista de problemas matemáticos pendientes (apenas un puñado), hizo un alarde de confianza: resolverlos era sólo cuestión de tiempo. La potencia de las matemáticas parecía infinita, y siguió pareciendo infinita hasta 1931.

Porque en ese año, en efecto, el matemático y lógico Kurt Gödel dio a conocer un teorema que se transformó en un clásico de la lógica matemática. En él se demuestra que no todas las verdades matemáticas pueden ser alcanzadas. Más sencillamente: que en cualquier sistema que contenga la aritmética, existe por lo menos una fórmula, que, aun siendo verdadera, no podrá jamás ser demostrada. No importa cuál sea el conjunto de axiomas que se use: siempre habrá algo que, si bien es verdadero, no se puede demostrar.

Es decir: en el seno mismo de las matemáticas hay cosas no alcanzables, lugares a donde la paciente deducción no llegará jamás. Naturalmente, este curioso resultado no afecta para nada la utilización de las matemáticas por el resto de los científicos, ni al papel central que ésta juega en todo el sistema de las ciencias. Pero de alguna manera limita su omnipotencia. Desde la Revolución Francesa en adelante, y como bien lo pudo comprobar Luis XVI, ya se sabe que las monarquías absolutas no son del todo seguras, y si bien no es cierto que las matemáticas hayan perdido su cetro, puede decirse que su largo y glorioso reinado, desde el teorema de Gödel en adelante, adquirió los contornos de una monarquía constitucional.