4. Risk importance measures in NPP risk assessment

4.1 Background on importance measures in risk assessment

It can be said that the idea for risk importance measures originates from the concept of traditional sensitivity analysis, which might not necessarily be related to the risk (reliability) studies. One type of sensitivity analysis is to change one of the parameters and see how much effect it makes on the result [9]. A systematic approach would be to calculate the fractional change in result for a fractional change in a variable or parameter. As an example ([9]), suppose the risk, R, is a function of n variables:

R = R(P1,...,Pn)

The total derivative is

Partial derivative 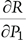appears to be a perfectly good sensitivity measure. However, it suffers a significant liability in that given absolute change in variable dP1 may be a very large or very small fractional change, depending on the range of values the variable can take. It seems, then, to be much better to assess the fractional changes, which can be done by taking the logarithmic derivative [9]:

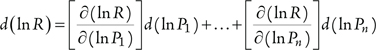
or

The term in parentheses, , represents the sensitivity of a fractional change in the result to a fractional change in the variable and is, according to [9], the commonly understood meaning of “sensitivity”. The same reference uses this term as a definition of Fussell-Vesely (F-V) importance measure, which is one of the basic risk importance measures in today’s PRAs. Indeed, if we, for simplicity, assume that R is a linear function of Pi (all other variables’ values fixed), R = kPi + l, the above term becomes

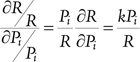
which can easily be related to the F-V, or “fractional contribution”, as it is discussed later in this monograph. (See expressions (5-10) and (5-12) and consider Pi = P(A), k = P(C) and R = P(B).)

There are a number of other importance measures which were defined and used in reliability and risk analyses. Some of them are defined in relative and some in absolute terms. Most of them are related to each other and some of them produce same risk ranking. Their theory and use is described in a number of books such as [9], [10] or [11] and studies or engineer’s handbooks and guidelines such as [12], [13] or [14]. In this monograph, however, we want to focus on those which are most widely used in current PRAs for NPPs. As an example, ASME PRA Standard of 2009 [15], explicitly defines only two importance measures: F-V and risk achievement worth. One apparent reason is that other relevant importance measures can be related to these two. But, before proceeding to these matters we will first identify a group of importance measures most commonly used in NPP PRAs.

4.2 Importance measures broadly used in PRAs for NPPs

In PRA models and applications associated with NPPs and implemented by tools such as RiskSpectrum® and others, the risk importance of a particular component or a failure mode can, most generally, be divided in two categories: importance with respect to risk increase potential and importance with respect to risk decrease potential. In this monograph we explicitly address four importance measures, related to both categories, which can be considered as most broadly used in the current PRAs and their practical applications.

We will use their definitions from NUREG/CR-3385 [12], which we consider to be one of the references to establish the use of risk importance measures in PRA applications. Let:

The first importance measure, risk achievement worth (RAW), is related to risk increase potential. It is defined as ratio:

(Beside ratio, NUREG/CR-3385 also defines the RAW on an interval scale as Ri+ − R0. These two values are related to each other. When one is known, the other can be calculated directly (considering that nominal risk R0 would normally be known).)

The second one is related to risk decrease potential. It is risk reduction worth (RRW), defined as:

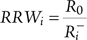
(In the similar fashion, NUREG/CR-3385 also introduces the related RRW on an interval scale, as R0 − Ri−.)

The third measure is also related to risk decrease potential. NUREG/CR-3385 refers to it as the fractional contribution (FC) of feature “i” to risk, or the Fussel-Vesely measure (F-V) of feature “i”, defined as:

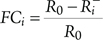
(It should be noted that, although NUREG/CR-3385 does not formally differentiate between the fractional contribution and F-V, some of the later PRA practices and tools introduced a distinction between the two measures. This distinction is discussed in Section 5.3.)

In theoretical considerations with associated demonstrating examples presented in this monograph (starting with Section 5), we will use the expression “fractional contribution” for the simple reason that it is descriptive, i.e. the meaning can directly be associated with the measure.

It can be seen from the definitions that RRW is related to FC and that the two measures will produce the same risk ranking. Both of them are included in the considerations to follow, for the sake of completeness.

Beside the above three, there is an additional measure which will be explicitly addressed. It is related to both categories, risk increase and risk decrease. It measures how the risk R changes with change in component’s failure probability pi. For this measure, the name “reliability importance” and the general definition was taken from Barlow and Proschan [11]:

As shown later (section 5.6), this measure can be related to the above measures through: Irel,i = Ri+ − Ri−. When written in this form, it is often referred to as “Birnbaum importance” (e.g. the mentioned NUREG/CR-3385 [12]).

4.3 Examples of use of risk importance measures in risk-informed applications

Many risk-informed applications have been carried out using PRAs of NPPs to improve operational safety and bring improved focus on regulatory requirements while at the same time reducing regulatory burden and operational cost. These applications are usually associated with specific uses of the risk-importance measures discussed above. In this section, we will present some examples on the use of risk-importance measures in risk-informed applications to provide a perspective on how the importance measures are the basic building blocks in these applications.

We will present a summary discussion of four different risk-informed applications that have been broadly used by nuclear operators and regulators:

  1. Risk-informed categorization of and treatment of SSCs for nuclear power reactors
  2. Risk-informed changes to NPP Technical Specifications
  3. Application of Maintenance Rule
  4. Applications associated with Reactor Oversight Process (ROP).

They are discussed in the four separate subsections below.

4.3.1 Risk-informed categorization and treatment of SSCs for nuclear power reactors

This application allows adjustment to the scope of equipment subject to special regulatory treatment (controls) to better focus regulator and plant operator’s attention on equipment with safety significance. U.S. NRC promulgated a rule, 10 CFR 50.69 [16], defining the process and our discussion uses the application of this rule to present the example.

Prior to 10 CFR 50.69, NRC’s deterministic regulations were used to categorize plant equipment as “safety-related” or “non-safety-related” (Refer, also, to Section 3.) The “safety-related” equipment is subject to NRC’s special treatment regulations whereas “non-safety-related” equipment is not. There is a set of “non-safety-related” equipment that is subject to a selected number of special treatment requirements or a subset of those requirements. This third category of equipment is referred to as “important-to-safety.”

In this application, risk-informed analyses are conducted to categorize the plant equipment in four categories:

  1. Safety-related SSCs that are identified as safety-significant (RISC-1)
  2. Some non-safety-related equipment that are identified as safety-significant (RISC-2)
  3. Some safety-related equipment that are identified as low or of no safety significance (RISC-3)
  4. Remaining non-safety-related equipment of low or no safety significance (RISC-4).

This categorization is achieved using PRA, traditional engineering analyses, and consideration of other regulatory requirements. With such a categorization, improved safety in plant operation can be achieved while reducing the regulatory burden. In such an application, it is expected that in many cases the number of SSCs or the regulatory burden associated with the “non-safety-related” equipment defined as RISC-2 will be less than the number or the regulatory burden associated with the “safety-related” equipment defined as RISC-3.

The categorization process defined in 10 CFR 50.69 requires consideration of the following:

  1. Use of results and insights from a plant-specific PRA that includes determination of SSC functional importance using an integrated, systematic process for addressing initiating events (internal and external), SSCs, and plant operating modes, including those not modeled in the plant-specific PRA
  2. Maintaining defense-in-depth
  3. Evaluations that provide reasonable confidence that for SSCs categorized a RISC-3, sufficient safety margins are maintained and that any potential increases in core damage frequency (CDF) and large early release frequency (LERF) resulting from the changes are small
  4. Performing for entire systems and structures; not for selected components within a system or structure
  5. Using an Integrated Decision-Making Panel (IDP) staffed with expert, plant-knowledgeable members whose expertise includes, at a minimum, PRA, safety analysis, plant operation, design engineering, and system engineering.

Full details of the considerations involved can be obtained from 10 CFR 50.69 and in NEI 00-04, Rev. 0 [17].

NEI 00-04 defines a process for identifying the safety significance of a component. The process includes two risk-importance measures, discussed above, as screening tools to identify candidate safety-significant SSCs:

(RRW is also considered an acceptable measure in place of F-V “because the F-V criteria can be readily converted to RRW criteria”.)

The RAW importance of a component is considered the maximum of the RAW values computed for basic events involving the failure modes of the individual component. To address the component’s contribution to common-cause failures, if applicable, a separate assessment of the common cause basic events in which the component is included is conducted. The RAW for common cause basic events reflects the relative increase in CDF/LERF if the set of components included in the common cause event is made unavailable. The risk-significance of the RAW values of common cause basic events is considered separately from the basic events that represent an individual component. Similarly, if the component is included in more than one common cause basic event, the maximum of the common cause RAW values is used to evaluate the significance.

The F-V importance of a component is considered to be the sum of the F-V importance of the failure modes of the component relevant to the measure (CDF or LERF) being addressed.

The importance measure criteria used to identify candidate safety significance are:

If any of those criteria are exceeded for a component, then the component is considered safety-significant.

If the risk importance measure criteria are not met, then it is not automatically low safety significance. Additional sensitivity evaluations are conducted for assessing it to be low safety significant for all contributors and are reviewed by the IDP. If the sensitivity studies identify that the component can be safety-significant, then the safety-significant attributes that yielded that conclusion are identified. Sensitivity studies are conducted with respect to human error rates, CCFs, and maintenance unavailabilities to ensure that the assumptions of the PRA are not masking the importance of an SSC. Details of the sensitivity studies can be obtained in NEI 00-04.

The evaluations are carried out for both CDF and LERF. NEI 00-04 discusses the considerations for truncation levels in conducting these evaluations. It is stated that when the RAW risk importance measure is calculated by a full resolution of the plant PRA model, then the truncation level does not significantly affect the RAW calculations. (Here, it is worth noting that many PRA practitioners actually use very low cut off and produce much more minimal cut sets (MCSs) for the purpose of RAW calculations than for the base case top event evaluation.) NEI 00-04 provides recommendations on how to address an impact of truncation level on calculated importance measures both for PRAs using linked fault trees (FT) and those using linked event trees (ET).

4.3.2 Risk-informed changes to NPP technical specifications

Technical Specifications (TSs) for NPPs define the limits and conditions to safe operation consistent with the analyses and evaluations in the plant’s safety analysis report. TS requirements include Limiting Conditions for Operations (LCOs) that define Conditions, Required Actions, and Completion Times (CTs); and Surveillance Requirements (SRs). A broad spectrum of assessments and experience are used to define and assess changes to these requirements that involve deterministic analyses, knowledge of lessons learned from previous changes, engineering judgments, and risk implications of the requirements.

PRAs are used to define measures that are used to quantitatively assess the risk associated with these requirements and they form a useful input in defining and evaluating changes to these requirements. These requirements which were originally based largely on engineering judgments have been improved using risk measures and risk-informed analyses.

Two of the TS requirements: CT and Surveillance Frequency (SF) are evaluated using risk-informed analyses in terms of risk measures. CT defines the time for which a component or a train in a safety system can remain inoperable before an action is required, which is typically a plant shutdown. A CT is used to repair or replace a failed or a degraded component, and sometimes, also to carry out a scheduled maintenance. SF defines the frequency of surveillance testing which is required to assure that the components of standby safety systems will be operable when they are needed in case of an accident. By testing these components, failures are detected that may have occurred since the last test or the last time the component was last known to be operational.

4.3.2.1 CT risks

Two types of CT risks are measured to evaluate the risks associated with a CT: single-event CT risk and yearly CT risk. The single-event CT risk is the risk associated with a given occurrence of the CT. The yearly CT risk contribution is the average yearly risk contribution from the CT, accounting for its yearly average frequency.

The single-event CT risk, in terms of core damage frequency, is the probability of a core damage occurring during the period the component is down. It is mathematically expressed as:

r = ΔRd

where,

r = the single-event CT risk,

ΔR = the increase in the conditional risk level, given that the component is down, and

d = the downtime associated with the CT.

The yearly CT risk is the product of the single-event CT risk and the frequency of the occurrence of the CT:

Ry = f r = f ΔRd

where,

f = the average yearly frequency of occurrences of the CT or the downtime frequency, and

Ry = the yearly CT risk contribution.

Typically, these two measures are used to define or to decide on changes to the CT in the TS.

PRA is used to calculate the increase in the risk level ΔR:

ΔR = R+ − R−

where,

R+ = the increased CDF level when the component is known to be down or unavailable, and

R– = the reduced CDF level when the component is known to be up or available.

 

So:

r = (R+ − R−)d

and

Ry = f(R+ − R−)d

As already mentioned in 4.2, the term R+ − R− represents the reliability (or the Birnbaum) importance measure. The terms R+ and R– can, also, be obtained from the RAW and RRW (or F-V) importance measures.

Thus, with the availability of Birnbaum importance or RAW and RRW (or F-V), the above discussed two measures can be calculated for evaluating the CT in TS.

4.3.2.2 SF risks

Surveillance tests detect failures that may have occurred between tests. At the same time, the test may have some adverse impacts on safety because of their undesirable effects, e.g., test errors causing plant transients, wear out of equipment caused by testing, downtime associated with the test. Thus, SF is broadly associated with two types of risks: (a) risk detected by the test and (b) risk-caused by the test. We will discuss here the risk detected by the test, sometimes called the test-limited risk, since it is associated with the risk importance measures.

The risk detected by a surveillance test (test-limited risk contribution), RD, can be written as:

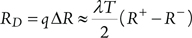
where,

q = probability of failure of a standby component on demand ,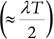

λ= the component failure rate per unit time,

T = the surveillance test interval.

Here again, the SF risk contribution is directly related to the reliability (Birnbaum) importance and also can be derived from the RAW and RRW.

These risk measures of CT and SF have been used to revise CT and SF in plant-specific TS and NRC Regulatory Guide RG 1.177 [18] provides guidance for making changes to these requirements in risk-informed analyses.

Additionally, it is worth mentioning that risk evaluations which draw more and more attention are those aiming at comparison of the risk of shutdown to the risk of continuing the operation and repairing the equipment.

4.3.3 Application in Maintenance Rule

Effective maintenance of system, structures, and equipment in an NPP has a clear link to safety and as discussed in the U.S. NRC’s Maintenance Rule 10 CFR 50.65 [19], it plays many safety enhancing roles:

The NRC’s Maintenance Rule (MR) provides regulatory framework for assessing the effectiveness of an NPP’s maintenance program. The MR is considered performance-based, risk-informed rule and allows consideration of risk in selecting and monitoring of SSCs for the rule. Paragraph (a)(1) of the MR requires licensees to monitor the performance or conditions of SSCs and to establish goals to promote improved SSC performance, when warranted. Paragraph (a)(2) of the rule states that monitoring pursuant to paragraph (a)(1) is not required for SSCs that are being effectively maintained by a preventive maintenance program. Paragraph (a)(3) of the rule requires that performance- and condition-monitoring activities and associated goals and preventive maintenance activities be evaluated at least every refueling cycle (not to exceed an interval of 24 months), taking industry-wide operating experience into account, where practical. Paragraph (a)(4) states that licensee shall assess and manage the increase in risk that may result from proposed maintenance activities.

Regulatory Guide 1.160 [20], and NUMARC 93-01 [21], provide guidance for implementing the MR. In these documents, risk importance measures are used for determining which SSCs that are under the scope of the MR will have goals and monitoring established in accordance with (a)(1).

NUMARC 93-01 calls for use of following three measures for identifying the SSCs:

SSCs selected by use of these measures are then provided to the expert panel for finalizing the SSCs to be monitored under (a)(1).

The following criteria are used in the NUMARC 93-01:

  1. RRW

    Two alternative methods are provided for applying RRW in identifying the risk significant SSCs.

    An SSC is considered risk significant if its risk reduction importance measure contributes to at least 99.0 percent of the cumulative risk reduction importance.

    Alternatively, an SSC is considered risk significant if its RRW exceeds 0.5% of the overall CDF (RRW>1.005).

  2. RAW

    An SSC is considered risk significant if its RAW shows at least a doubling, i.e. RAW > 2.0, of the overall CDF.

  3. CDF Contribution

    An SSC is considered risk significant if it is included in cut sets that, when ranked in decreasing order, cumulatively account for about 90 percent of the CDF.

The MR became effective for U.S. NPPs in 1996 and many consider that the rule have contributed to industry’s significantly improved performance by focusing attention and corrective actions on those SSCs that exhibited poor performance. In general, the rule is considered to have improved operating and maintenance practices across the industry.

4.3.4 Applications associated with ROP

The U.S. NRC’s ROP is the agency’s program to inspect, measure, and asses the safety performance of NPPs and to respond to any decline in performance, NUREG-1649 [22]. A major element of this oversight program is to focus inspections on activities where the potential risks are greater. It also calls for responding to violations of regulations in a predictable and consistent manner that reflects the potential safety impact of the violations.

The framework of the ROP defines three key areas: Reactor safety, Radiation safety, and Safeguards. It also defines seven cornerstones and three cross-cutting areas. To discuss the use of the risk importance measures, we will focus on the reactor safety area which is associated with four cornerstones: initiating events, mitigating systems, barrier integrity, and emergency preparedness. The cross-cutting areas associated with all the cornerstones are: human performance, safety conscious work environment, and problem identification and resolution.

To focus inspection on activities where the potential risks are greater, each of the cornerstones is analyzed in terms of key attributes of licensee performance contributing to the cornerstone. For example, for the initiating event cornerstone, the key attributes are: design, protection against external events, configuration control, equipment performance, procedure quality, and human performance. Each of these key attributes is then studied to define the areas and means to measure. Risk-informed inspection is defined as the means to measure in many cases. Based on these analyses, areas for inspection are defined for which inspection procedures are developed.

For the Reactor safety area and the associated cornerstones of initiating events, mitigating systems, and barrier integrity, seventeen areas for inspection are defined. Inspection Procedure 71111 under NRC Inspection Manual [23], presents these procedures. The examples of areas for inspection in these cornerstones are: adverse weather protection, equipment alignment, fire protection, maintenance effectiveness, component design bases inspection, and surveillance testing.

Inspection guidance is provided for conducting inspection in each of the areas. The inspection guidance includes risk-informed inspection planning. The risk-informed inspection planning involves selection of risk-informed inspection samples which is based on the following:

Plant-specific PRAs are used to extract risk-insights and to obtain items for inspection. The types of information that are used are the following:

Other items, as applicable, can be considered by the inspectors in finalizing the areas and items for inspection.

The consideration of the risk insights and risk-importance measures in defining the focus of inspection provides the desired emphasis on activities where the potential risks are greater and thereby making the regulatory inspection effective, contributing to safe operation of the NPP.

System performance indicators is another example of an application of risk importance measures within the ROP framework. In its ROP, the NRC used performance indicators to quantify safety system unavailability [24], which gave way to the development of a more risk-informed performance indicator known as the Mitigating Systems Performance Index (MSPI). The MSPI, in its essence, represents a change in plant risk (measured through CDF) due to a change in system’s availability or reliability. By controlling the MSPI, a decline in availability or reliability can effectively be controlled. The MSPI, as a change in plant risk due to a change in system’s availability or reliability, is assessed through the risk importance measures. As an example, the unavailability-related contribution to MSPI from a particular train can be written as ([24], [25]):

ΔCDFt,U = UAIt = Irel,t,UΔUt

where

The Birnbaum importance can further be developed into ([24], [25]):

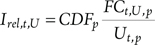
where

For the relation of the reliability importance (Birnbaum importance) to other importance measures, refer to Section 5.6.

4.4 Risk importance measures: focus of discussion in this monograph

Having in mind the considerations in the preceding sections, the discussions in the remainder of this monograph will focus on the four risk importance measures:

The risk importance measures which are directly reported by PRA tools relate, in most cases, to basic events (representing particular failure modes or human errors). On the other hand, what is in engineering practice really needed is risk importance of actual components (e.g. pumps or valves). It is, therefore, desirable to find a way to express the “component-level importance measures” for the components represented in a model.

In PRAs, components are modeled in terms of their failure modes which are represented by the basic events associated with a component in the model. When a component is involved in a common-cause failure group, i.e., a common-cause failure is associated with the component and other similar components, then the basic event for the common-cause failure of the components is also represented in the model. In many cases, more than one failure mode of a component is associated with a common-cause failure. Common-cause failure parameters of the failure modes are typically different and are represented by different basic events. Thus, multiple basic events in the model can represent a component failure, some (or all) of them being involved in common cause failure groups.

As presented above, risk importance measures obtained from a PRA model are typically obtained in terms of the basic events. However, in many PRA applications judgments are required for components and not for a specific component failure mode. Additionally, the basic event associated with a common-cause failure provides the risk significance of the common-cause failure group or the failure of the multiple components associated in a common-cause failure. The user then will have to judge the risk significance of the component by looking at the risk-significance of the multiple, different basic events associated with a component. In many cases, judgments are made without consideration of the common-cause failure basic event.

Component-level risk importance measure discussed in this monograph aims at addressing this issue in a way to provide a single measure that takes into account the different failure modes of a component along with its contribution to common-cause failures modeled for the component. This single measure would then fully represent the risk significance of the component and could be directly used in different applications. A list could be generated from the computer codes rank ordering the components in terms of the component-level measures. This would be useful for many applications and makes the process straight-forward facilitating use of PRAs.

General approach taken for establishing any of the considered component-level risk importance measures (e.g. component-level RAW) was to express it as a function of importance measures for the representative basic events which are normally reported by a PRA tool.

In order to establish analytical expression for component-level risk importance two types of issues need to be addressed:

  1. Particular component is in most cases represented by multiple basic events related to different failure modes. Sometimes, the same failure mode is represented by different basic events in different accident sequences (event sequences).
  2. Component, or some of its failure modes, may or may not be involved in CCF groups with other components.

Development of component-level risk importance measures addressing above two issues requires dealing with different scenarios that are experienced in NPP PRAs. The following cases are considered to address different failure mode combinations, including common-cause failures, of practical considerations. The cases are presented with increasing complexity considering the four risk importance measures presented at the beginning of this subsection.

  1. Component is not involved in any CCF group.
    • The simplest case is a component presented by a single basic event. This is discussed in Section 5 which introduces the definitions to be used in all sections to follow and establishes the relations between particular importance measures for a single basic event.
    • Many times, a component is in a system’s fault tree (FT) presented as a sub-tree, e.g. an “OR” gate with inputs which are basic events representing different failure modes. Similar types of components are many times presented by similar sub-trees which are often referred to as “FT modules”. Risk importance measures for such component-level “FT modules” are discussed in Section 6.
    • Sometimes, the component is presented by different FT modules in different accident (ET) sequences. (It is noted that the simplest FT module is a single basic event.) Risk importance measures for such a case are discussed in Section 7.
  2. Component is involved in a CCF group.
    • Section 8 discusses risk importance measures for the case when component is presented by a single failure mode (basic event).
    • Section 9 discusses, under some simplifications, risk importance measures for the case when component is presented by multiple failure modes (basic events) which are involved in CCF groups.

All the cases are accompanied by the demonstrations in the form of examples based on the simplified PRA model. The examples are presented in Appendix B.

The component-level risk importance measures being defined and presented in this monograph and their relevance in terms of the risk importance measures typically calculated in a (current) PRA are illustrated by a simple example as follows.

Let us consider components A, B, and C within a PRA model for an NPP. Component A is associated with three basic events: failure to start, “Comp A-FS”, failure to run, “Comp A-FR”, and test or maintenance unavailability, “Comp A-TM”. Similarly, component B is associated with three basic events: failure to start, “Comp B-FS”, failure to run, “Comp B-FR”, and test or maintenance unavailability, “Comp B-TM”. Component C is also associated with three basic events: failure to open, “Comp C-FO”, plugs during operation, “Comp C-PL”, and fails to remain open, “Comp C-FRO”. Additionally, components A and B are of the same type and there is a potential for a common-cause failure. Thus, there are two CCF basic events: components A and B fail to start due to CCF, “Comp AB-FSCC” and components A and B fail to run due to CCF, “Comp AB-FRCC”. Also, a human error of restoration is associated with component C, “Comp C-HER”. RAW is used to explain the new component-level importance measure being discussed in this monograph. Table 4-1 presents two columns explaining the RAW measures calculated currently in a PRA (column 1) and the additional RAW measures to be discussed here (column 2) to facilitate the use of risk importance measures in many applications as an additional input in the decision-making process.

Table 4-1 Risk curve or definition of risk for an engineer.

cover

As shown in the table, to decide on the risk significance of a component, a number of risk importance measures of the basic events associated with component is used to make a judgment. By creating a component-level importance, as shown in the second column, based on the basic event importances associated with the component, the use of risk importance measure becomes more direct and clearer. Considering these component-level importance measures would make the use of risk importance measures in PRA applications more straight-forward and less subject to interpretation.

The need for assessing the component-level importance measures has been recognized time ago and was present in the handbooks for PRA applications as well as in PRA-related literature for decades. Thus, for example, NEI 00-04 [17], mentioned in Section 4.3.1 above, contains a procedure for establishing component-level importance measures based on the importance measures of particular basic events mapped to the component of concern. There is, also, a number of papers published in scientific magazines or conferences’ proceedings devoted to the subject.

Thus, for example [26] pointed to and discussed some difficulties and uncertainties associated with this (importance measure for multiple basic events). Then, the paper [27], published in the same year (1998), discussed the subject of calculation of conditional core damage probability (CCDP) for nuclear power plant operation. It discussed, among others, the subject of “adjustment” of common cause failure probabilities given a failure (or unavailability) of a component involved in a CCF group. Strictly speaking, the subject matter of [27] is not calculation of importance measures but, rather, calculation of a CCDP for precursor events (initiators or conditions). However, it is relevant for the importance measures since those are related to CCDP (or conditional top event probability), as discussed in the next session. One of the more recent references is paper by Kim et al. of 2005 [28], which discussed calculation of component’s RAW involving CCFs. Then, there is one of the most recent references [29], which discusses issues with calculating the RAW (or “risk increase factor”) for a component represented by multiple basic events in a PRA model. The same reference also provides an overview of the relevant work on the risk importance measures during past decades. There are, also, other references, some of which are mentioned in the sections which follow when discussing the related matters.

The discussions and considerations of component-level risk importance in this monograph are not meant to be any further research based on mentioned (or any other) references or to evaluate the positions and/or methods described in them. They are, rather, meant to describe the principles for calculations of risk importance measures for single basic events and for components represented by multiple basic events rooted in probability theory, which is the basis for any PRA quantification. In any case, an interested reader is welcome to further explore the mentioned references for additional insights into specific aspects and difficulties associated with assessing component-level importance measures.

Additionally, there are references such as [30] which discuss practical aspects of applying risk importance measures in NPP operation. Interested readers are invited to read those for insights concerning the interpretation of RAW and FC (or F-V) in practical risk-informed applications such as use of PRA to support the demonstration of effectiveness of SSC maintenance programs, configuration risk monitoring or categorization and treatment of SSCs.