6. Risk importance of a component represented by multiple basic events, none involved in a CCF Group (FT module)

6.1 Introduction

Many times, failure of a component is in fault trees represented by some kind of a logic structure. In other words, it is provided as some kind of a logic function defined over a set of basic events representing particular failure modes:

(6.1)

In the above expression the asterisk (*) denotes that failure is represented by a logic function of basic events rather than by a single basic event. The term aA(.) represents a logic function for the failure A while the terms AX, Ay,… are basic events corresponding to particular failure modes X, Y,… etc.

If the following two conditions are fulfilled, the logic function aA(.) can be referred to as a logic module or a fault tree module: 1) logic function aA(.) is the same wherever the failure A* appears in the fault tree structure; 2) none of the basic events AX, AY, …, appears in the fault tree structure externally to the logic function aA(.). (In other words, a fault tree module is independent of the rest of the fault tree structure.) A fault tree module is, basically, a sub-tree with top event representing the failure of the considered component. It is pointed out that particular FT module (in the above sense) cannot involve a basic event which is shared by another FT module. Hence, it cannot involve a CCF basic event. Therefore, the represented component cannot be involved in a CCF group. Example of a FT module for a standby pump’s failure on demand is shown in Section 6.3.

Formulas for FC, RAW and RRW, respectively, which were derived in Section 5 for a single basic event A, can be applied for a fault tree module A*, as well. This is simply because if the logic module A* is replaced by a new single basic event (with assigned probability calculated for the whole module, P(A*)), it would not affect general logic of the fault tree as a whole, or the probability of its top event.

We will retain the definition of B as the overall top event and introduce the terms A*, C* and L* with meaning analogous to A, C and L, respectively, only that they relate to a FT module, rather than to a single basic event. Similarly, the asterisk will denote that an importance measure relates to a FT module.

6.2 FC, RAW, RRW and reliability importance for component-level FT module

Because the component failure basic events appearing in fault tree structure in a PRA are claimed to be independent, the above terms C* and A* are considered to be independent. (Note that, by the above definition of a FT module, the term C* does not include any basic event from A*). Hence, analogously to (5-11), the absolute contribution for a FT module can be written as:

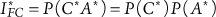
(6.2)

The FC for a FT module is then defined analogously to (5-12):

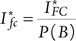
(6.3)

Once the FC for a considered FT module is known, the RAW can be calculated by a formula analogous to (5-17):

(6.4)

Likewise, the RRW can be calculated analogously to (5-18) as:

(6.5)

Finally, the corresponding reliability importance can be calculated analogously to (5-22) as:

(6.6)

We provide a simple example with calculations of all four importance measures for a FT module in the next section.

6.3 Example: importance measures for a FT module for failure of a standby pump

Many times, the FT module is simply an “OR” gate with its inputs being basic events representing different failure modes, i.e. the logic function from (6-1) is given in the form:

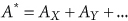
(6.7)

An example of such a FT module, representing failures or unavailability of Positive Displacement Pump (PDP), is shown in Figure 6-1. Logic function for this simple FT module can be written as:

(6.8)

where basic events AFS, AFR and ATM relate to pump’s failure to start, failure to run and unavailability (at the time of demand) due to test or maintenance (TM), respectively. (For simplicity, shorter notations are used than those for the basic events shown in the figure.)

Figure 6-1 Example FT module (CVCS PDP).

The FT module from Figure 6-1 will be used to demonstrate calculation of component-level importance measures according to Section 6.2 above. It is noted that the Positive Displacement Pump (PDP) of Chemical and Volume Control System (CVCS) from the referential PRA model was selected for this example because it is not involved in any CCF group. It is also noted that TM unavailability is grouped with component’s failure modes only for the sake of example for calculation of module-level importance measures. Such a grouping of TM unavailability with failures may or may not be appropriate, depending on the specific application.

First, the component-level failure probability P(A*) is needed for the logic function expressed by (6-8). It can be calculated as a probability of logic sum (by using the inclusion-exclusion principle). However, considering the range of the probabilities used in the PRAs for the failure modes of concern, the component level probability can be simplified to:

(6.9)

(See, also, the discussion in Section 9.1.) Any of the three probabilities on the right hand side can be directly obtained from the PRA model. Calculation of component-level importance measures starts with FC, which is then used to obtain other measures.

6.3.1 FC

With P(A*) known, the term P(C*) remains to be determined if the component-level FC is to be calculated. (See (6-2).) For the considered case this is straightforward: since the basic events appear under the “OR” gate, they will always be “challenged” by the same scenarios (representing an initiator and a combination of failures). The term “C” is same for any of them and this same term represents the component-level term C*, i.e.: CFS = CFR = CTM = C* and, accordingly:

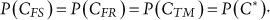
(6.10)

Any P(CX), index “X” referring to “FS”, “FR” or “TM”, can, according to (5-11), be calculated as: 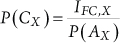. Therefore, considering (6-2) and (6-3), the component-level FC is:

(6.11)

The component-level FC can also be directly expressed by considering:

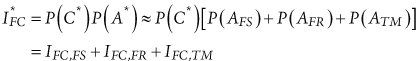
and, hence:

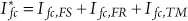
(6.12)

Therefore, the component-level FC for the considered case, in which all failure modes are logically “OR-ed” together, can be obtained as a sum of corresponding FC values. The calculation of FC for this case is demonstrated by Example B5 in Appendix B.

6.3.2 RAW, RRW and reliability importance

With Ifc* calculated above, component-level RAW, RRW and reliability importance can be calculated by formulas (6-4), (6-5) and (6-6), respectively. These calculations are also demonstrated in Example B5, Appendix B.