Nuclear Engineering and Technology for the 21st Century

8. Risk importance of component represented by a single basic event (failure mode) involved in a CCF Group

8.1 Introduction

Up to now we have considered importance measures for a component represented by a FT module (sub-tree) involving a group of basic events (Section 6) or, even, a component represented by multiple different FT modules which appear in mutually exclusive sequences of failures (Section 7). However, none of the underlying basic events was involved in any common cause failure (CCF) group of basic events. (In other words, none of those failures or failure modes was shared by another components.) We will now broaden the discussion to the component-level risk importance measures for the components which are involved in a CCF group (which is, many times, the case with most of components in a PRA model). We start, in this section, with discussing the impact of CCF on risk importance of component which is presented in the FT structure by a single basic event.

With respect to risk importance of the component (or particular failure mode) involved in a CCF group, three types of a failure or unavailability should be distinguished:

Failure or unavailability with CCF potential;
Unavailability with no impact on CCF (e.g. unavailability due to preventive maintenance);
Particular CCF event (i.e. failure due to a common cause of specified components).

For the first one it can be said that it is mostly related to design issues. For the remaining two it can be said that they are primarily related to operational issues. All three cases are further discussed in the separate subsections below.

All the calculations and use of the formulas are demonstrated in Example B7 in Appendix B.

8.2 Failure with CCF potential

Basic characteristic of this type of failure is that the considered component has failed and this can have implications on the status of the redundant components which are members of the same “CCF group”. Specifically, the status (failed or operable) of all other redundant components is defined by the conditional probabilities used to quantify the CCF model in the PRA. To take the simplest example of a beta-factor CCF model for two redundant components, with assumed beta-factor value of 0.1: assuming that first component has failed, there is 10% probability that the second component is also failed (and remaining 90% probability that failure had affected only the first component).

Risk importance of this type of failure is usually considered in evaluations of design or its modifications. For example, answering a question such as “what is the worth or significance of adding another redundant component or train?” is related to the risk importance of this type of failure.

We will start the discussion by considering a single basic event A which in the PRA model represents specific failure mode of certain component of concern. In the case that represented failure mode is not shared by any other component modelled, the basic event A would have importance measures as presented in Section 5. However, if the component is included in a CCF group, then considered failure mode of this component can be shared by a number of combinations of other components. We will simplify the notation and will not go into the details on the CCF modeling and quantification as they are described in a number of references (for example, NUREG/CR-4780 [35], or NUREG/CR-5845 [36]).

If considered component is involved in a CCF group of size m, the number of combinations of failures in which considered component can be involved is:

(8.1)

For example, let us consider a CCF group consisting of m = 4 components designated, for simplicity, as 1, 2, 3 and 4, and let us focus on the component 1. According to the above formula, this component can be involved in 23 = 8 combinations of failures, and they are: (1), (1,2), (1,3), (1,4), (1,2,3), (1,3,4), (1,2,4) and (1,2,3,4).

For simplicity, we will refer to each of these combinations simply as “combination k” and have in mind that k goes from 1 to 2m−1 = M.

The following set of m conditional mutually exclusive events can now be defined:

Uk Failure of considered component is involved in combination k, .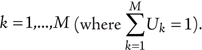

The failure of component A (which was previously presented by a single basic event A) is now partitioned into the set of mutually exclusive failure events Vk = UkA, k = 1,…,M:

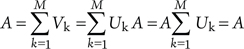
(8.2)

(Mutual exclusivity of these basic events may be subject to discussion or include certain degree of controversy. However, the fact is that at two most widely used CCF quantification methods, Multiple Greek Letters and Alpha Factors, the formulas for the set of conditional probabilities assume mutual exclusivity. Refer, e.g., to [35] or [36].)

In expression (8-2) we purposefully omitted use of the asterisk (*) with A, even if A is a kind of logic similar to “FT module” considered earlier. The reason is that in Sections 6 and 7 we have used the term “FT module” for a logic structure representing particular component, which is independent from the remaining FT structure in the PRA model. In some instances, as we have seen in Section 7, multiple “FT modules” representing the same component may be mutually dependent (involving same basic events). However, they were always independent from the rest of the FT structure. With logic expression (8-2) this is not the case, by definition. All except one of the basic events Kk, k = 1,…,M, are also involved in the logic structures representing other components in every “combination k”.

The expressions for the four component-level risk importance measures are discussed in the Sections 8.2.1 through 8.2.4. Demonstrations are provided under Example B7 in Appendix B.

Calculation of importance measures for failure modes which are involved in CCF groups are discussed in a number of references, including [27], [28] and [29]. (It is noted that subject matter of [27] is not, strictly, calculation of importance measures but, rather, calculation of a conditional risk for precursor events. However, the discussion of CCF impact is relevant and relates to the importance measures.) The focus of discussions is on RAW which is, in many practical evaluations, the most relevant of the measures (or the most difficult to asses) when CCF is involved. Interested readers are invited to check those references for further insights.

8.2.1 FC

General expression for the top event (5-3) needs now to be rewritten as:

(8.3)

Terms Ck, k = 1,…, M, represent scenarios or combinations of events such that specific CCF combination k (involving component A) is requested not to occur, in order to avoid the top event (e.g. reactor core damage). The term L’ (which is not, generally, the same as L in (5-3)) represents an occurrence of the top event such that it does not include any CCF combination k.

Note that top event minimal cutsets now show particular basic events Vk, k = 1,…,M (and not failure event A explicitly, anymore) and this is why transformation to (8-3) is important. However, considering that Vk = UkA, k = 1,…,M, the expression (8-3) can be transformed to

(8.4)

i.e. to the same general form as (5-3). Based on this, the general expression for the absolute contribution from Section 5, (5-10), can be used, i.e.:

(8.5)

This expression does not enable actual calculation of the FC since the term A is not shown in minimal cutsets. For this reason, the term IFC needs to be expressed through the basic events Vk, k = 1,…,M, i.e.:

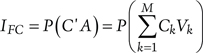
(8.6)

Considering that the terms CkVk, k = 1,…,M are mutually exclusive (because the CCF events Vk ,k = 1,…,M were defined as mutually exclusive), the above expression can, similarly as in Section 7.2, be rewritten as:

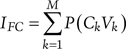
(8.7)

Thus, the absolute and fractional contribution for a single failure mode which is involved in a CCF group can be calculated as

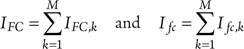
(8.8)

where the terms IFC,k and Ifc,k represent the contributions of the CCF basic events Vk k = 1,…,M. These basic events are explicitly shown in minimal cutsets and their importance measures can, therefore, be taken directly from the PRA results. Thus, component-level FC can be calculated directly.

Once the FC is known, it will be possible to calculate other importance measures for the considered component (or particular failure mode).

8.2.2 RAW

By starting with most general expression for the RAW, i.e. (5-4), and then considering the rewritten form of logic expression for top event B given by (8-3) and (8-4) it is not difficult to show that the RAW can be expressed by the formula which corresponds to (5-17):

(8.9)

Here, IFC and Ifc are total contributions calculated by (8-8), while P(A) represents the total failure probability expressed, based on (8-2), as:

(8.10)

In deriving the formula (8-9) the same kind of rationale is used as in Section 5.4, including the application of “rare event approximation”.

It is important to recognize the following: by stating A = 1 (i.e. component A has failed) we are not setting to “true” all CCF basic events which involve A, i.e. Vk, k = 1,…,M. Instead, we are modifying their probabilities to conditional values. This can be seen by considering Vk = UkA, k = 1,…,M. With setting A = 1 (“true”) Vk becomes Uk and, correspondingly, P(Vk) = P(Uk). This is important for understanding how the component-level importance measure should be calculated by modifying and rerunning the PRA model, as demonstrated in Example B7, Appendix B.

Interested readers are, also, directed to earlier mentioned references such as [27], [28] and [29] for related discussions.

8.2.3 RRW and reliability importance

Theoretical relation between RAW and RRW discussed in 5.2 is valid regardless of whether a failure mode is involved in a CCF or not. Therefore, it can be used to directly calculate RRW from RAW (formula (5-9)), with P(A) calculated by (8-10). Alternatively, it can be used to express RRW via FC in the formula corresponding to (5-18):

(8.11)

Likewise, reliability importance can theoretically be expressed through RAW and (or) RRW by (5-21) regardless of involvement in CCF. Therefore, it can be calculated directly from RAW and RRW, or it can be expressed via FC by the formula corresponding to (5-22), i.e.:

(8.12)

(where P(A) is calculated by (8-10)).

However, there are potential issues with interpretation of reliability importance in the case of involvement in a CCF group. Those are discussed under Example B7 in Appendix B.

8.3 Unavailability with no impact on CCF

In this case the fact that considered component is not able to perform its function upon demand does not provide any additional information regarding possible status of the remaining components in the CCF group. A case like this is best represented by assuming that considered component, which was otherwise normally available and operable, is taken to out-of-service status for the purpose of preventive maintenance. This action does not imply anything regarding the possible status (i.e. operable or inoperable) of other components in the CCF group. Basically, it only means that if considered component would be needed during the time of this unavailability, it would not be there to operate.

This kind of unavailability (and its associated importance) is considered in PRA applications which support plant operation, such as configuration risk monitoring.

It implies that redundancy of the system of m components has been reduced to the redundancy of m-1 components. In other words, the CCF group of size m has been reduced to the CCF group of size m-1 formed by the remaining components. However, the failure causes which the remaining components share with considered component can still affect them, regardless of the fact that considered component is now out-of-service. The simplest example to illustrate this is the one with two redundant components S1 and S2. Let us assume that they each have total failure probability P(S1) = P(S2) = Qt. Let us further assume that conditional probability of failure of any of the two being due to a cause shared with the other one is β (so-called beta-factor.) If the first component has been taken down for the preventive maintenance, failure probability for the second one would still remain (1 − β)Qt + βQt = Qt, because this failure probability is not influenced by the fact that the first component is being subjected to preventive maintenance. To use the notation from the previous section, failure probability of the second component would be Qt = P(V1) + P(V2), where P(V1) = (1 − β)Qt and P(V2) = βQt.

This discussion can be applied to the general case of component A involved in a CCF group of m components, expressed by (8-2). This expression is done in terms of M = 2m − 1 mutually exclusive basic events Vk, k = 1,…,M which represent common cause failures of all combinations of components involving the considered component. For convenience, we will specifically define V1 as basic event which represents failure of A not shared by any other component from the group. (Note that in terms of MGL quantification model, the probability of this basic event would be P(V0) = (1 − β(m))Qt, with β(m) representing corresponding beta-factor for the CCF group of m components and Qt = P(A).) Since the definition of this kind of unavailability includes that there is no impact on other CCF events, the importance measures can be taken from the basic event V1. Thus, absolute and fractional contribution of considered component A with respect to this kind of unavailability can be expressed as:

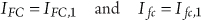
(8.13)

where the terms IFC,1 and Ifc,1 represent absolute and fractional contribution values for the basic event V1. They can be obtained directly from the PRA results. All other importance measures can then be calculated as for any other single basic event, as described in Section 5, or they can be taken directly from the reported importance measures for the basic event V1. However, it needs to be noted that actual meaning (i.e. the meaning for any practical purpose) of measures other than RAW in this case is questionable. The meaning and usability of RAW is clear: it is the measure of how much risk would increase assuming that component is taken out-of-service for preventive maintenance (without any impact on other components). However, this is not so with FC or RRW because it is not clear whether setting V1 = 0 (“false”) without any impact on other Vk basic events can reflect any real situation in the practice. The same question can be asked about changing the probability P(V1) without changing probabilities of o ther Vk basic events.

Finally, let it also be mentioned that in the base case PRA unavailability due to preventive maintenance is usually represented by a separate basic event and this event can be used to calculate the fractional contribution of this kind of activities and benefit from reducing their scope, if necessary.

For these reasons, the demonstrations under Example B7 in Appendix B focuses only on RAW importance for this case. It is taken directly from the reported importance measures for the basic event V1 and used only to put into perspective the RAW in the case of CCF potential, which was discussed in 8.2.2.

8.4 Particular CCF event

This third case simply means that considered component is failed and failure is shared by specific j other components from the CCF group, where j = 1,…,m − 1. (It is noted that j = 0 is special case which was addressed in Section 8.3.)

The risk importance of this kind of failure may, sometimes, be considered in PRA applications such as assessing risk significance of observed operational events or issues. It is included here for completeness purposes.

The most important case, by all means, is common cause failure of all m components in the group. This specific case is discussed here. Referring to earlier defined set of M = 2m − 1 mutually exclusive basic events Vk, k = 1,…,M with respect to common cause failures of component A we will, for convenience, define basic event VM as, specifically, being the failure of component A which is shared by all other components in the group. (For m = 2, P(VM) = P(V2) = β(2)Qt; for m = 3, P(VM = P(V4) = β(3)γ(3))Qt, etc.)

Without further discussion, we will here just use the importance measures of basic event VM as representatives for risk importance associated with CCF of all components in the group. Thus, absolute and fractional contribution will be expressed as:

(8.14)

where the terms IFC,M and Ifc,M represent absolute and fractional contribution values for the basic event VM. They can be obtained directly from the PRA results.

Other importance measures for the CCF of all m components can then be calculated as for any other single basic event, as described in Section 5 or they can be taken directly from the reported importance measures for the basic event VM. However, similar question can be asked as in Section 8.3 regarding the practical meaning and usability of measures other than RAW. Let it just be mentioned that statement “VM = 1” or “VM = 0” (which is made as a part of formal derivation of formulas for importance measures) may have certain implications on other basic events Vk, k = 1,…,M due to their postulated mutual exclusivity. Evaluation of possible implications would exceed the purpose of this discussion, as well as the space allowed for it. However, let it be mentioned that for the case VM = 1 (related to RAW) those implications are not relevant for practical PRA applications, since in this case all components in the group are failed by definition. For the case VM = 0, associated with FC let us just say that FC for this kind of events will generally be very low in practical PRA applications, since VM is usually a low probability event. On the other hand, RAW for VM will often be at the top of the RAW importance list, despite its low probability (or, actually, because of it).

For these reasons, the demonstrations under Example B7 in Appendix B focus only on RAW importance for this case. It is taken directly from the reported importance measures for the basic event VM and used only to put into perspective the RAW in the case of CCF potential, which was discussed in 8.2.2.

At the end, it may, also, be good to point out that importance discussed in this section is event-related importance, more than component-related importance.