IN THIS CHAPTER
 Working with graphs
Working with graphs
 Performing sorting tasks
Performing sorting tasks
 Reducing the tree size
Reducing the tree size
 Locating the shortest route between two points
Locating the shortest route between two points
This chapter is about working with graphs. You use graphs every day to perform a range of tasks. A graph is simply a set of vertexes, nodes, or points connected by edges, arcs, or lines. Putting this definition in simpler terms, every time you use a map, you use a graph. The starting point, intermediate points, and destination are all nodes. These nodes connect to each other with streets, which represent the lines. Using graphs enables you to describe relationships of various sorts. The reason that Global Positioning System (GPS) setups work is that you can use math to describe the relationships between points on the map and the streets that connect them. In fact, by the time you finish this chapter, you understand the basis used to create a GPS (but not necessarily the mechanics of making it happen). Of course, the fundamental requirement for using a graph to create a GPS is the capability to search for connections between points on the map, as discussed in the first section of the chapter.
To make sense of a graph, you need to sort the nodes, as described in the second section of the chapter, to create a specific organization. Without organization, making any sort of decision becomes impossible. An algorithm might end up going in circles or giving inconvenient output. For example, some early GPS setups didn’t correctly find the shortest distance between two points, or sometimes ended up sending someone to the wrong place. Part of the reason for these problems is the need to sort the data so that you can view it in the same manner each time the algorithm traverses the nodes (providing you with a route between your home and your business).
When you view a map, you don’t look at the information in the lower-right corner when you actually need to work with locations and roads in the upper-left corner. A computer doesn’t know that it needs to look in a specific place until you tell it to do so. To focus attention in a specific location, you need to reduce the graph size, as described in the third section of the chapter.
Now that the problem is simplified, an algorithm can find the shortest route between two points, as described in the fourth section of the chapter. After all, you don’t want to spend any more time than is necessary in traffic fighting your way from home to the office (and back again). The concept of finding the shortest route is a bit more convoluted than you might think, so the fourth section looks at some of the specific requirements for performing routing tasks in detail.
Traversing a Graph Efficiently
Traversing a graph means to search (visit) each vertex (node) in a specific order. The process of visiting a vertex can include both reading and updating it. As you traverse a graph, an unvisited vertex is undiscovered. After a visit, the vertex becomes discovered (because you just visited it) or processed (because the algorithm tried all the edges departing from it). The order of the search determines the kind of search performed, and many algorithms are available to perform this task. The following sections discuss two such algorithms.
Creating the graph
To see how traversing a graph might work, you need a graph. The examples in this section rely on a common graph so that you can see how the two techniques work. The following code shows the adjacency list found at the end of Chapter 8. (You can find this code in the A4D; 09; Graph Traversing.ipynb file on the Dummies site as part of the downloadable code; see the Introduction for details.)
graph = {'A': ['B', 'C'],
'B': ['A', 'C', 'D'],
'C': ['A', 'B', 'D', 'E'],
'D': ['B', 'C', 'E', 'F'],
'E': ['C', 'D', 'F'],
'F': ['D', 'E']}
The graph features a bidirectional path that goes from A, B, D, and F on one side (starting at the root) and A, C, E, and F along the second side (again, starting at the root). There are also connections (that act as possible shortcuts) going from B to C, from C to D, and from D to E. Using the NetworkX package presented in Chapter 8 lets you display the adjacency as a picture so that you can see how the vertexes and edges appear (see Figure 9-1) by using the following code:
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
%matplotlib inline
Graph = nx.Graph()
for node in graph:
Graph.add_nodes_from(node)
for edge in graph[node]:
Graph.add_edge(node,edge)
pos = { 'A': [0.00, 0.50], 'B': [0.25, 0.75],
'C': [0.25, 0.25], 'D': [0.75, 0.75],
'E': [0.75, 0.25], 'F': [1.00, 0.50]}
nx.draw(Graph, pos, with_labels=True)
nx.draw_networkx(Graph, pos)
plt.show()
Applying breadth-first search
A breadth-first search (BFS) begins at the graph root and explores every node that attaches to the root. It then searches the next level — exploring each level in turn until it reaches the end. Consequently, in the example graph, the search explores from A to B and C before it moves on to explore D. BFS explores the graph in a systematic way, exploring vertexes all around the starting vertex in a circular fashion. It begins by visiting all the vertexes a single step from the starting vertex; it then moves two steps out, then three steps out, and so on. The following code demonstrates how to perform a breadth-first search.
def bfs(graph, start):
queue = [start]
queued = list()
path = list()
while queue:
print ('Queue is: %s' % queue)
vertex = queue.pop(0)
print ('Processing %s' % vertex)
for candidate in graph[vertex]:
if candidate not in queued:
queued.append(candidate)
queue.append(candidate)
path.append(vertex+'>'+candidate)
print ('Adding %s to the queue'
% candidate)
return path
steps = bfs(graph, 'A')
print ('\nBFS:', steps)
Queue is: ['A']
Processing A
Adding B to the queue
Adding C to the queue
Queue is: ['B', 'C']
Processing B
Adding A to the queue
Adding D to the queue
Queue is: ['C', 'A', 'D']
Processing C
Adding E to the queue
Queue is: ['A', 'D', 'E']
Processing A
Queue is: ['D', 'E']
Processing D
Adding F to the queue
Queue is: ['E', 'F']
Processing E
Queue is: ['F']
Processing F
BFS: ['A>B', 'A>C', 'B>A', 'B>D', 'C>E', 'D>F']
 The output shows how the algorithm searches. It’s in the order that you expect — one level at a time. The biggest advantage of using BFS is that it’s guaranteed to return the shortest path between two points as the first output when used to find paths.
The output shows how the algorithm searches. It’s in the order that you expect — one level at a time. The biggest advantage of using BFS is that it’s guaranteed to return the shortest path between two points as the first output when used to find paths.
 The example code uses a simple list as a queue. As described in Chapter 4, a queue is a first in/first out (FIFO) data structure that works like a line at a bank, where the first item put into the queue is also the first item that comes out. For this purpose, Python provides an even better data structure called a deque (pronounced deck). You create it using the
The example code uses a simple list as a queue. As described in Chapter 4, a queue is a first in/first out (FIFO) data structure that works like a line at a bank, where the first item put into the queue is also the first item that comes out. For this purpose, Python provides an even better data structure called a deque (pronounced deck). You create it using the deque function from the collections package. It performs insertions and extractions in linear time, and you can use it as both a queue and a stack. You can discover more about the deque function at https://pymotw.com/2/collections/deque.html.
Applying depth-first search
In addition to BFS, you can use a depth-first search (DFS) to discover the vertexes in a graph. When performing a DFS, the algorithm begins at the graph root and then explores every node from that root down a single path to the end. It then backtracks and begins exploring the paths not taken in the current search path until it reaches the root again. At that point, if other paths to take from the root are available, the algorithm chooses one and begins the same search again. The idea is to explore each path completely before exploring any other path. To make this search technique work, the algorithm must mark each vertex it visits. In this way, it knows which vertexes require a visit and can determine which path to take next. Using BFS or DFS can make a difference according to the way in which you need to traverse a graph. From a programming point of view, the difference between the two algorithms is how each one stores the vertexes to explore the following:
- A queue for BFS, a list that works according to the FIFO principle. Newly discovered vertexes don’t wait long for processing.
- A stack for DFS, a list that works according to the last in/first out (LIFO) principle.
The following code shows how to create a DFS:
def dfs(graph, start):
stack = [start]
parents = {start: start}
path = list()
while stack:
print ('Stack is: %s' % stack)
vertex = stack.pop(-1)
print ('Processing %s' % vertex)
for candidate in graph[vertex]:
if candidate not in parents:
parents[candidate] = vertex
stack.append(candidate)
print ('Adding %s to the stack'
% candidate)
path.append(parents[vertex]+'>'+vertex)
return path[1:]
steps = dfs(graph, 'A')
print ('\nDFS:', steps)
Stack is: ['A']
Processing A
Adding B to the stack
Adding C to the stack
Stack is: ['B', 'C']
Processing C
Adding D to the stack
Adding E to the stack
Stack is: ['B', 'D', 'E']
Processing E
Adding F to the stack
Stack is: ['B', 'D', 'F']
Processing F
Stack is: ['B', 'D']
Processing D
Stack is: ['B']
Processing B
DFS: ['A>C', 'C>E', 'E>F', 'C>D', 'A>B']
The first line of output shows the actual search order. Note that the search begins at the root, as expected, but then follows down the left side of the graph around to the beginning. The final step is to search the only branch off the loop that creates the graph in this case, which is D.
Note that the output is not the same as for the BFS. In this case, the processing route begins with node A and moves to the opposite side of the graph, to node F. The code then retraces back to look for overlooked paths. As discussed, this behavior depends on the use of a stack structure in place of a queue. Reliance on a stack means that you could also implement this kind of search using recursion. The use of recursion would make the algorithm faster, so you could obtain results faster than when using a BFS. The trade-off is that you use more memory when using recursion.
 When your algorithm uses a stack, it’s using the last result available (as contrasted to a queue, where it would use the first result placed in the queue). Recursive functions produce a result and then apply themselves using that same result. A stack does exactly the same thing in an iteration: The algorithm produces a result, the result is put on a stack, and then the result is immediately taken from the stack and processed again.
When your algorithm uses a stack, it’s using the last result available (as contrasted to a queue, where it would use the first result placed in the queue). Recursive functions produce a result and then apply themselves using that same result. A stack does exactly the same thing in an iteration: The algorithm produces a result, the result is put on a stack, and then the result is immediately taken from the stack and processed again.
Determining which application to use
The choice between BFS and DFS depends on how you plan to apply the output from the search. Developers often employ BFS to locate the shortest route between two points as quickly as possible. This means that you commonly find BFS used in applications such as GPS, where finding the shortest route is paramount. For the purposes of this book, you also see BFS used for spanning tree, shortest path, and many other minimization algorithms.
A DFS focuses on finding an entire path before exploring any other path. You use it when you need to search in detail, rather than generally. For this reason, you often see DFS used in games, where finding a complete path is important. It’s also an optimal approach to perform tasks such as finding a solution to a maze.
 Sometimes you have to decide between BFS and DFS based on the limitations of each technique. BFS needs lots of memory because it systematically stores all the paths before finding a solution. On the other hand, DFS needs less memory, but you have no guarantee that it’ll find the shortest and most direct solution.
Sometimes you have to decide between BFS and DFS based on the limitations of each technique. BFS needs lots of memory because it systematically stores all the paths before finding a solution. On the other hand, DFS needs less memory, but you have no guarantee that it’ll find the shortest and most direct solution.
Sorting the Graph Elements
The ability to search graphs efficiently relies on sorting. After all, imagine going to a library and finding the books placed in any order the library felt like putting them on the shelves. Locating a single book would take hours. A library works because the individual books appear in specific locations that make them easy to find.
Libraries also exhibit another property that’s important when working with certain kinds of graphs. When performing a book search, you begin with a specific category, then a row of books, then a shelf in that row, and finally the book. You move from less specific to more specific when performing the search, which means that you don’t revisit the previous levels. Therefore, you don’t end up in odd parts of the library that have nothing to do with the topic at hand.
The following sections review Directed Acyclic Graphs (DAGs), which are finite directed graphs that don’t have any loops in them. In other words, you start from a particular location and follow a specific route to an ending location without ever going back to the starting location. When using topological sorting, a DAG always directs earlier vertexes to later vertexes. This kind of graph has all sorts of practical uses, such as schedules, with each milestone representing a particular milestone.
Working on Directed Acyclic Graphs (DAGs)
DAGs are one of the most important kinds of graphs because they see so many practical uses. The basic principles of DAGs are that they
- Follow a particular order so that you can’t get from one vertex to another and back to the beginning vertex using any route.
- Provide a specific path from one vertex to another so that you can create a predictable set of routes.
You see DAGs used for many organizational needs. For example, a family tree is an example of a DAG. Even when the activity doesn’t follow a chronological or other overriding order, the DAG enables you to create predictable routes, which makes DAGs easier to process than many other kinds of graphs you work with.
However, DAGs can use optional routes. Imagine that you’re building a burger. The menu system starts with a bun bottom. You can optionally add condiments to the bun bottom, or you can move directly to the burger on the bun. The route always ends up with a burger, but you have multiple paths for getting to the burger. After you have the burger in place, you can choose to add cheese or bacon before adding the bun top. The point is that you take a specific path, but each path can connect to the next level in several different ways.
 So far, the chapter has shown you a few different kinds of graph configurations, some of which can appear in combination, such as a directed, weighted, dense graph:
So far, the chapter has shown you a few different kinds of graph configurations, some of which can appear in combination, such as a directed, weighted, dense graph:
- Directed: Edges have a single direction and can have these additional properties:
- Cyclic: The edges form a cycle that take you back to the initial vertex after having visited the intermediary vertexes.
- A-cyclic: This graph lacks cycles.
- Undirected: Edges connect vertexes in both directions.
- Weighted: Each edge has a cost associated with it, such as time, money, or energy, which you must pay to pass through it.
- Unweighted: All the edges have no cost or the same cost.
- Dense: A graph that has a large number of edges when compared to the number of vertexes.
- Sparse: A graph that has a small number of edges when compared to the number of vertexes.
Relying on topological sorting
An important element of DAGs is that you can represent a myriad of activities using them. However, some activities require that you approach tasks in a specific order. This is where topological sorting comes into play. Topological sorting orders all the vertexes of a graph on a line with the direct edges pointing from left to right. Arranged in such a fashion, the code can easily traverse the graph and process the vertexes one after the other, in order.
When you use topological sorting, you organize the graph so that every graph vertex leads to a later vertex in the sequence. For example, when creating a schedule for building a skyscraper, you don’t start at the top and work your way down. You begin with the foundation and work your way up. Each floor can represent a milestone. When you complete the second floor, you don’t go to the third and then redo the second floor. Instead, you move on from the third floor to the fourth floor, and so on. Any sort of scheduling that requires you to move from a specific starting point to a specific ending point can rely on a DAG with topological sorting.
Topological sorting can help you determine that your graph has no cycles (because otherwise, you can’t order the edges connecting the vertexes from left to right; at least one node will refer to a previous node). In addition, topological sorting also proves helpful in algorithms that process complex graphs because it shows the best order for processing them.
You can obtain topological sorting using the DFS traversal algorithm. Simply note the processing order of the vertexes by the algorithm. In the previous example, the output appears in this order: A, C, E, F, D, and B. Follow the sequence in Figure 9-1 and you notice that the topological sorting follows the edges on the external perimeter of graph. It then makes a complete tour: After reaching the last node of the topological sort, you’re just a step away from A, the start of the sequence.
Reducing to a Minimum Spanning Tree
Many problems that algorithms solve rely on defining a minimum of resources to use, such as defining an economical way to reach all the points on a map. This problem was paramount in the late nineteenth and early twentieth centuries when railway and electricity networks started appearing in many countries, revolutionizing transportation and ways of living. Using private companies to build such networks was expensive (it took a lot of time and workers). Using less material and a smaller workforce offered savings by reducing redundant connections.
 Some redundancy is desirable in critical transportation or energy networks even when striving for economical solutions. Otherwise, if only one method connects the network, it’s easily disrupted accidentally or by a voluntary act (such as an act of war), interrupting services to many customers.
Some redundancy is desirable in critical transportation or energy networks even when striving for economical solutions. Otherwise, if only one method connects the network, it’s easily disrupted accidentally or by a voluntary act (such as an act of war), interrupting services to many customers.
In Moravia, the eastern part of Czech Republic, the Czech mathematician Otakar Borůvka found a solution in 1926 that allows constructing an electrical network using the least amount of wire possible. His solution is quite efficient because it not only allows finding a way to connect all the towns in Moravia in the most economical way possible, but it had a time complexity of O(m*log n), where m is the number of edges (the electrical cable) and n the number of vertexes (the towns). Others have improved Borůvka’s solution since then. (In fact, algorithm experts partially forgot and then rediscovered it.) Even though the algorithms you find in books are better designed and easier to grasp (those from Prim and Kruskal), they don’t achieve better results in terms of time complexity.
A minimal spanning tree defines the problem of finding the most economical way to accomplish a task. A spanning tree is the list of edges required to connect all the vertexes in an undirected graph. A single graph could contain multiple spanning trees, depending on the graph arrangement, and determining how many trees it contains is a complex issue. Each path you can take from start to completion in a graph is another spanning tree. The spanning tree visits each vertex only once; it doesn’t loop or do anything to repeat path elements.
When you work on an unweighted graph, the spanning trees are the same length. In unweighted graphs, all edges have the same length, and the order you visit them in doesn’t matter because the run path is always the same. All possible spanning trees have the same number of edges, n-1 edges (n is the number of vertexes), of the same exact length. Moreover, any graph traversal algorithm, such as BFS or DFS, suffices to find one of the possible spanning trees.
Things become tricky when working with a weighted graph with edges of different lengths. In this case, of the many possible spanning trees, a few, or just one, have the minimum length possible. A minimum spanning tree is the one spanning tree that guarantees a path with the least possible edge weight. An undirected graph generally contains just one minimum spanning tree, but, again, it depends on the configuration. Think about minimum spanning trees this way: When looking at a map, you see a number of paths to get from point A to point B. Each path has places where you must turn or change roads, and each of these junctions is a vertex. The distance between vertexes represents the edge weight. Generally, one path between point A and point B provides the shortest route.
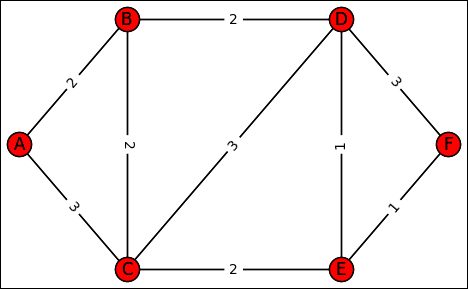
However, minimum spanning trees need not always consider the obvious. For example, when considering maps, you might not be interested in distance; you might instead want to consider time, fuel consumption, or myriad other needs. Each of these needs could have a completely different minimum spanning tree. With this in mind, the following sections help you understand minimum spanning trees better and demonstrate how to solve the problem of figuring out the smallest edge weight for any given problem. To demonstrate a minimum spanning tree solution using Python, the following code updates the previous graph by adding edge weights. (You can find this code in the A4D; 09; Minimum Spanning Tree.ipynb file on the Dummies site as part of the downloadable code; see the Introduction for details.)
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
%matplotlib inline
graph = {'A': {'B':2, 'C':3},
'B': {'A':2, 'C':2, 'D':2},
'C': {'A':3, 'B':2, 'D':3, 'E':2},
'D': {'B':2, 'C':3, 'E':1, 'F':3},
'E': {'C':2, 'D':1, 'F':1},
'F': {'D':3, 'E':1}}
Graph = nx.Graph()
for node in graph:
Graph.add_nodes_from(node)
for edge, weight in graph[node].items():
Graph.add_edge(node,edge, weight=weight)
pos = { 'A': [0.00, 0.50], 'B': [0.25, 0.75],
'C': [0.25, 0.25], 'D': [0.75, 0.75],
'E': [0.75, 0.25], 'F': [1.00, 0.50]}
labels = nx.get_edge_attributes(Graph,'weight')
nx.draw(Graph, pos, with_labels=True)
nx.draw_networkx_edge_labels(Graph, pos,
edge_labels=labels)
nx.draw_networkx(Graph,pos)
plt.show()
Figure 9-2 shows that all edges have a value now. This value can represent something like time, fuel, or money. Weighted graphs can represent many possible optimization problems that occur in geographical space (such as movement between cities) because they represent situations in which you can come and go from a vertex.
Interestingly, all edges have positive weights in this example. However, weighted graphs can have negative weights on some edges. Many situations take advantage of negative edges. For instance, they’re useful when you can both gain and lose from moving between vertexes, such as gaining or losing money when transporting or trading goods, or releasing energy in a chemical process.
 Not all algorithms are well suited for handling negative edges. It’s important to note those that can work with only positive weights.
Not all algorithms are well suited for handling negative edges. It’s important to note those that can work with only positive weights.
Discovering the correct algorithms to use
You can find many different algorithms to use to create a minimum spanning tree. The most common are greedy algorithms, which run in polynomial time. Polynomial time is a power of the number of edges, such as O(n2) or O(n3) (see Part 5 for additional information about polynomial time). The major factors that affect the running speed of such algorithms involve the decision-making process — that is, whether a particular edge belongs in the minimum spanning tree or whether the minimum total weight of the resulting tree exceeds a certain value. With this in mind, here are some of the algorithms available for solving a minimum spanning tree:
- Borůvka’s: Invented by Otakar Borůvka in 1926 to solve the problem of finding the optimal way to supply electricity in Moravia. The algorithm relies on a series of stages in which it identifies the edges with the smallest weight in each stage. The calculations begin by looking at individual vertexes, finding the smallest weight for that vertex, and then combining paths to form forests of individual trees until it creates a path that combines all the forests with the smallest weight.
- Prim’s: Originally invented by Jarnik in 1930, Prim rediscovered it in 1957. This algorithm starts with an arbitrary vertex and grows the minimum spanning tree one edge at a time by always choosing the edge with the least weight.
- Kruskal’s: Developed by Joseph Kruskal in 1956, it uses an approach that combines Borůvka’s algorithm (creating forests of individual trees) and Prim’s algorithm (looking for the minimum edge for each vertex and building the forests one edge at a time).
- Reverse-delete: This is actually a reversal of Kruskal’s algorithm. It isn’t commonly used.
 These algorithms use a greedy approach. Greedy algorithms appear in Chapter 2 among the families of algorithms, and you see them in detail in Chapter 15. In a greedy approach, the algorithm gradually arrives at a solution by taking, in an irreversible way, the best decision available at each step. For instance, if you need the shortest path between many vertexes, a greedy algorithm takes the shortest edges among those available between all vertexes.
These algorithms use a greedy approach. Greedy algorithms appear in Chapter 2 among the families of algorithms, and you see them in detail in Chapter 15. In a greedy approach, the algorithm gradually arrives at a solution by taking, in an irreversible way, the best decision available at each step. For instance, if you need the shortest path between many vertexes, a greedy algorithm takes the shortest edges among those available between all vertexes.
Introducing priority queues
Later in this chapter, you see how to implement Prim’s and Kruskal’s algorithm for a minimum spanning tree, and Dijkstra’s algorithm for the shortest path in a graph using Python. However, before you can do that, you need a method to find the edges with the minimum weight among a set of edges. Such an operation implies ordering, and ordering elements costs time. It’s a complex operation, as described in Chapter 7. Because the examples repeatedly reorder edges, a data structure called the priority queue comes in handy.
Priority queues rely on heap tree-based data structures that allow fast element ordering when you insert them inside the heap. Like the magician’s magic hat, priority heaps store edges with their weights and are immediately ready to provide you with the inserted edge whose weight is the minimum among those stores.
This example uses a class that allows it to perform priority-queue comparisons that determine whether the queue contains elements and when those elements contain a certain edge (avoiding double insertions). The priority queue has another useful characteristic (whose usefulness is explained when working on Dijkstra’s algorithm): If you insert an edge with a different weight than previously stored, the code updates the edge weight and rearranges the edge position in the heap.
from heapq import heapify, heappop, heappush
class priority_queue():
def __init__(self):
self.queue = list()
heapify(self.queue)
self.index = dict()
def push(self, priority, label):
if label in self.index:
self.queue = [(w,l)
for w,l in self.queue if l!=label]
heapify(self.queue)
heappush(self.queue, (priority, label))
self.index[label] = priority
def pop(self):
if self.queue:
return heappop(self.queue)
def __contains__(self, label):
return label in self.index
def __len__(self):
return len(self.queue)
Leveraging Prim’s algorithm
Prim’s algorithm generates the minimum spanning tree for a graph by traversing the graph vertex by vertex. Starting from any chosen vertex, the algorithm adds edges using a constraint in which, if one vertex is currently part of the spanning tree and the second vertex isn’t part of it, the edge weight between the two must be the least possible among those available. By proceeding in this fashion, creating cycles in the spanning tree is impossible (it could happen only if you add an edge whose vertexes are already both in the spanning tree) and you’re guaranteed to obtain a minimal tree because you add the edges with the least weight. In terms of steps, the algorithm includes these three phases, with the last one being iterative:
- Track both the edges of the minimum spanning tree and the used vertexes as they become part of the solution.
- Start from any vertex in the graph and place it into the solution.
- Determine whether there are still vertexes that aren’t part of the solution:
- Enumerate the edges that touch the vertexes in the solution.
- Insert the edge with the minimum weight into the spanning tree. (This is the greedy principle at work in the algorithm: Always choose the minimum at each step to obtain an overall minimum result.)
By translating these steps into Python code, you can test the algorithm on the example weighted graph using the following code:
def prim(graph, start):
treepath = {}
total = 0
queue = priority_queue()
queue.push(0 , (start, start))
while queue:
weight, (node_start, node_end) = queue.pop()
if node_end not in treepath:
treepath[node_end] = node_start
if weight:
print("Added edge from %s" \
" to %s weighting %i"
% (node_start, node_end, weight))
total += weight
for next_node, weight \
in graph[node_end].items():
queue.push(weight , (node_end, next_node))
print ("Total spanning tree length: %i" % total)
return treepath
treepath = prim(graph, 'A')
Added edge from A to B weighting 2
Added edge from B to C weighting 2
Added edge from B to D weighting 2
Added edge from D to E weighting 1
Added edge from E to F weighting 1
Total spanning tree length: 8
The algorithm prints the processing steps, showing the edge it adds at each stage and the weight the edge adds to the total. The example displays the total sum of weights and the algorithm returns a Python dictionary containing the ending vertex as key and the starting vertex as value for each edge of the resulting spanning tree. Another function, represent_tree, turns the key and value pairs of the dictionary into a tuple and then sorts each of the resulting tuples for better readability of the tree path:
def represent_tree(treepath):
progression = list()
for node in treepath:
if node != treepath[node]:
progression.append((treepath[node], node))
return sorted(progression, key=lambda x:x[0])
print (represent_tree(treepath))
[('A','B'), ('B','C'), ('B','D'), ('D','E'), ('E','F')]
 The
The represent_tree function reorders the output of Prim’s algorithm for better readability. However, the algorithm works on an undirected graph, which means that you can traverse the edges in both directions. The algorithm incorporates this assumption because there is no edge directionality check to add to the priority queue for later processing.
Testing Kruskal’s algorithm
Kruskal’s algorithm uses a greedy strategy, just as Prim’s does, but it picks the shortest edges from a global pool containing all the edges (whereas Prim’s evaluates the edges according to the vertexes in the spanning tree). To determine whether an edge is a suitable part of the solution, the algorithm relies on an aggregative process in which it gathers vertexes together. When an edge involves vertexes already in the solution, the algorithm discards it to avoid creating a cycle. The algorithm proceeds in the following fashion:
- Put all the edges into a heap and sort them so that the shortest edges are on top.
- Create a set of trees, each one containing only one vertex (so that the number of trees is the same number as the vertexes). You connect trees as an aggregate until the trees converge into a unique tree of minimal length that spans all the vertexes.
- Repeat the following operations until the solution doesn’t contain as many edges as the number of vertexes in the graph:
- Choose the shortest edge from the heap.
- Determine whether the two vertexes connected by the edge appear in different trees from among the set of connected trees.
- When the trees differ, connect the trees using the edge (defining an aggregation).
- When the vertexes appear in the same tree, discard the edge.
- Repeat steps a through d for the remaining edges on the heap.
The following example demonstrates how to turn these steps into Python code:
def kruskal(graph):
priority = priority_queue()
print ("Pushing all edges into the priority queue")
treepath = list()
connected = dict()
for node in graph:
connected[node] = [node]
for dest, weight in graph[node].items():
priority.push(weight, (node,dest))
print ("Totally %i edges" % len(priority))
print ("Connected components: %s"
% connected.values())
total = 0
while len(treepath) < (len(graph)-1):
(weight, (start, end)) = priority.pop()
if end not in connected[start]:
treepath.append((start, end))
print ("Summing %s and %s components:"
% (connected[start],connected[end]))
print ("\tadded edge from %s " \
"to %s weighting %i"
% (start, end, weight))
total += weight
connected[start] += connected[end][:]
for element in connected[end]:
connected[element]= connected[start]
print ("Total spanning tree length: %i" % total)
return sorted(treepath, key=lambda x:x[0])
print ('\nMinimum spanning tree: %s' % kruskal(graph))
Pushing all edges into the priority queue
Totally 9 edges
Connected components: dict_values([['A'], ['E'], ['F'],
['B'], ['D'], ['C']])
Summing ['E'] and ['D'] components:
added edge from E to D weighting 1
Summing ['E', 'D'] and ['F'] components:
added edge from E to F weighting 1
Summing ['A'] and ['B'] components:
added edge from A to B weighting 2
Summing ['A', 'B'] and ['C'] components:
added edge from B to C weighting 2
Summing ['A', 'B', 'C'] and ['E', 'D', 'F'] components:
added edge from B to D weighting 2
Total spanning tree length: 8
Minimum spanning tree:
[('A','B'), ('B','C'), ('B','D'), ('E','D'), ('E','F')]
 Kruskal’s algorithm offers a solution that’s similar to the one proposed by Prim’s algorithm. However, different graphs may provide different solutions for the minimum spanning tree when using Prim’s and Kruskal’s algorithms because each algorithm proceeds in different ways to reach its conclusions. Different approaches often imply different minimal spanning trees as output.
Kruskal’s algorithm offers a solution that’s similar to the one proposed by Prim’s algorithm. However, different graphs may provide different solutions for the minimum spanning tree when using Prim’s and Kruskal’s algorithms because each algorithm proceeds in different ways to reach its conclusions. Different approaches often imply different minimal spanning trees as output.
Determining which algorithm works best
Both Prim’s and Kruskal’s algorithms output a single connected component, joining all the vertexes in the graph by using the least (or one of the least) long sequences of edges (a minimum spanning tree). By summing the edge weights, you can determine the length of the resulting spanning tree. Because both algorithms always provide you with a working solution, you must rely on running time and decide whether they can take on any kind of weighted graph to determine which is best.
As for running time, both algorithms provide similar results with Big-O complexity rating of O(E*log(V)), where E is the number of edges and V the number of vertexes. However, you must account for how they solve the problem because there are differences in the average expected running time.
Prim’s algorithm incrementally builds a single solution by adding edges, whereas Kruskal’s algorithm creates an ensemble of partial solutions and aggregates them. In creating its solution, Prim’s algorithm relies on data structures that are more complex than Kruskal’s because it continuously adds potential edges as candidates and keeps picking the shortest edge to proceed toward its solution. When operating on a dense graph, Prim’s algorithm is preferred over Kruskal’s because its priority queue based on heaps does all the sorting jobs quickly and efficiently.
 The example uses a priority queue based on a binary heap for the heavy job of picking up the shortest edges, but there are even faster data structures, such as the Fibonacci heap, which can produce faster results when the heap contains many edges. Using a Fibonacci heap, the running complexity of Prim’s algorithm can mutate to O(E +V*log(V)), which is clearly advantageous if you have a lot of edges (the E component is now summed instead of multiplied) compared to the previous reported running time O(E*log(V)).
The example uses a priority queue based on a binary heap for the heavy job of picking up the shortest edges, but there are even faster data structures, such as the Fibonacci heap, which can produce faster results when the heap contains many edges. Using a Fibonacci heap, the running complexity of Prim’s algorithm can mutate to O(E +V*log(V)), which is clearly advantageous if you have a lot of edges (the E component is now summed instead of multiplied) compared to the previous reported running time O(E*log(V)).
Kruskal’s algorithm doesn’t much need a priority queue (even though one of the examples uses one) because the enumeration and sorting of edges happens just once at the beginning of the process. Being based on simpler data structures that work through the sorted edges, it’s the ideal candidate for regular, sparse graphs with fewer edges.
Finding the Shortest Route
The shortest route between two points isn’t necessarily a straight line, especially when a straight line doesn’t exist in your graph. Say that you need to run electrical lines in a community. The shortest route would involve running the lines as needed between each location without regard to where those lines go. However, real life tends not to allow a simple solution. You may need to run the cables beside roads and not across private property, which means finding routes that reduce the distances as much as possible.
Defining what it means to find the shortest path
Many applications exist for shortest-route algorithms. The idea is to find the path that offers the smallest distance between point A and point B. Finding the shortest path is useful for both transportation (how to arrive at a destination consuming the least fuel) and communication (how to route information to allow it to arrive earlier). Nevertheless, unexpected applications of the shortest-path problem may also arise in image processing (for separating contours of images), gaming (how to achieve certain game goals using the fewest moves), and many other fields in which you can reduce the problem to an undirected or directed weighted graph.
The Dijkstra algorithm can solve the shortest-path problem and has found the most uses. Edsger W. Dijkstra, a Dutch computer scientist, devised the algorithm as a demonstration of the processing power of a new computer called ARMAC (http://www-set.win.tue.nl/UnsungHeroes/machines/armac.html) in 1959. The algorithm initially solved the shortest distance between 64 cities in the Netherlands based on a simple graph map.
 Other algorithms can solve the shortest-path problem. The Bellman-Ford and Floyd-Warshall are more complex but can handle graphs with negative weights. (Negative weights can represent some problems better.) Both algorithms are beyond the scope of this book, but the site at
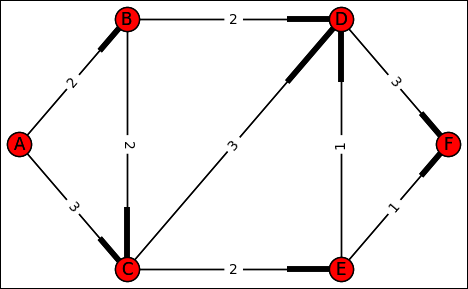
Other algorithms can solve the shortest-path problem. The Bellman-Ford and Floyd-Warshall are more complex but can handle graphs with negative weights. (Negative weights can represent some problems better.) Both algorithms are beyond the scope of this book, but the site at https://www.hackerearth.com/ja/practice/algorithms/graphs/shortest-path-algorithms/tutorial/ provides additional information about them. Because the shortest-path problem involves graphs that are both weighted and directed, the example graph requires another update before proceeding (you can see the result in Figure 9-3). (You can find this code in the A4D; 09; Shortest Path.ipynb file on the Dummies site as part of the downloadable code; see the Introduction for details.)
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
%matplotlib inline
graph = {'A': {'B':2, 'C':3},
'B': {'C':2, 'D':2},
'C': {'D':3, 'E':2},
'D': {'F':3},
'E': {'D':1,'F':1},
'F': {}}
Graph = nx.DiGraph()
for node in graph:
Graph.add_nodes_from(node)
for edge, weight in graph[node].items():
Graph.add_edge(node,edge, weight=weight)
pos = { 'A': [0.00, 0.50], 'B': [0.25, 0.75],
'C': [0.25, 0.25], 'D': [0.75, 0.75],
'E': [0.75, 0.25], 'F': [1.00, 0.50]}
labels = nx.get_edge_attributes(Graph,'weight')
nx.draw(Graph, pos, with_labels=True)
nx.draw_networkx_edge_labels(Graph, pos,
edge_labels=labels)
nx.draw_networkx(Graph,pos)
plt.show()
Explaining Dijkstra’s algorithm
Dijkstra’s algorithm requires a starting and (optionally) ending vertex as input. If you don’t provide an ending vertex, the algorithm computes the shortest distance between the starting vertex and any other vertexes in the graph. When you define an ending vertex, the algorithm stops upon reading that vertex and returns the result up to that point, no matter how much of the graph remains unexplored.
The algorithm starts by estimating the distance of the other vertexes from the starting point. This is the starting belief it records in the priority queue and is set to infinity by convention. Then the algorithm proceeds to explore the neighboring nodes, similar to a BFS. This allows the algorithm to determine which nodes are near and that their distance is the weight of the connecting edges. It stores this information in the priority queue by an appropriate weight update.
 Naturally, the algorithm explores the neighbors because a directed edge connects them with the starting vertex. Dijkstra’s algorithm accounts for the edge direction.
Naturally, the algorithm explores the neighbors because a directed edge connects them with the starting vertex. Dijkstra’s algorithm accounts for the edge direction.
At this point, the algorithm moves to the nearest vertex on the graph based on the shortest edge in the priority queue. Technically, the algorithm visits a new vertex. It starts exploring the neighboring vertexes, excluding the vertexes that it has already visited, determines how much it costs to visit each of the unvisited vertexes, and evaluates whether the distance to visit them is less than the distance it recorded in the priority queue.
When the distance in the priority queue is infinite, this means that it’s the algorithm’s first visit to that vertex, and the algorithm records the shorter distance. When the distance recorded in the priority queue isn’t infinite, but it’s more than the distance that the algorithm has just calculated, it means that the algorithm has found a shortcut, a shorter way to reach that vertex from the starting point, and it stores the information in the priority queue. Of course, if the distance recorded in the priority queue is shorter than the one just evaluated by the algorithm, the algorithm discards the information because the new route is longer. After updating all the distances to the neighboring vertexes, the algorithm determines whether it has reached the end vertex. If not, it picks the shortest edge present in the priority queue, visits it, and starts evaluating the distance to the new neighboring vertexes.
 As the narrative of the algorithm explained, Dijikstra’s algorithm keeps a precise accounting of the cost to reach every vertex that it encounters, and it updates its information only when it finds a shorter way. The running complexity of the algorithm in Big-O notation is O(E*log(V)), where E is the number of edges and V the number of vertexes in the graph. The following code shows how to implement Dijikstra’s algorithm using Python:
As the narrative of the algorithm explained, Dijikstra’s algorithm keeps a precise accounting of the cost to reach every vertex that it encounters, and it updates its information only when it finds a shorter way. The running complexity of the algorithm in Big-O notation is O(E*log(V)), where E is the number of edges and V the number of vertexes in the graph. The following code shows how to implement Dijikstra’s algorithm using Python:
def dijkstra(graph, start, end):
inf = float('inf')
known = set()
priority = priority_queue()
path = {start: start}
for vertex in graph:
if vertex == start:
priority.push(0, vertex)
else:
priority.push(inf, vertex)
last = start
while last != end:
(weight, actual_node) = priority.pop()
if actual_node not in known:
for next_node in graph[actual_node]:
upto_actual = priority.index[actual_node]
upto_next = priority.index[next_node]
to_next = upto_actual + \
graph[actual_node][next_node]
if to_next < upto_next:
priority.push(to_next, next_node)
print("Found shortcut from %s to %s"
% (actual_node, next_node))
print ("\tTotal length up so far: %i"
% to_next)
path[next_node] = actual_node
last = actual_node
known.add(actual_node)
return priority.index, path
dist, path = dijkstra(graph, 'A', 'F')
Found shortcut from A to C
Total length up so far: 3
Found shortcut from A to B
Total length up so far: 2
Found shortcut from B to D
Total length up so far: 4
Found shortcut from C to E
Total length up so far: 5
Found shortcut from D to F
Total length up so far: 7
Found shortcut from E to F
Total length up so far: 6
The algorithm returns a couple of useful pieces of information: the shortest path to destination and the minimum recorded distances for the visited vertexes. To visualize the shortest path, you need a reverse_path function that rearranges the path to make it readable:
def reverse_path(path, start, end):
progression = [end]
while progression[-1] != start:
progression.append(path[progression[-1]])
return progression[::-1]
print (reverse_path(path, 'A', 'F'))
['A', 'C', 'E', 'F']
You can also know the shortest distance to every node encountered by querying the dist dictionary:
print (dist)
{'D': 4, 'A': 0, 'B': 2, 'F': 6, 'C': 3, 'E': 5}
 Working with graphs
Working with graphs Performing sorting tasks
Performing sorting tasks Reducing the tree size
Reducing the tree size Locating the shortest route between two points
Locating the shortest route between two points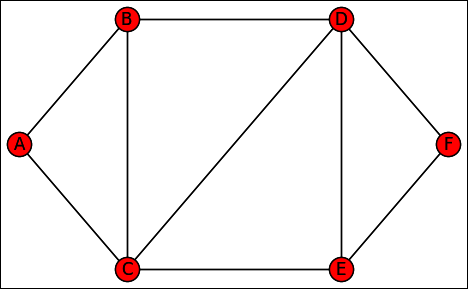
 The output shows how the algorithm searches. It’s in the order that you expect — one level at a time. The biggest advantage of using BFS is that it’s guaranteed to return the shortest path between two points as the first output when used to find paths.
The output shows how the algorithm searches. It’s in the order that you expect — one level at a time. The biggest advantage of using BFS is that it’s guaranteed to return the shortest path between two points as the first output when used to find paths. The example code uses a simple list as a queue. As described in
The example code uses a simple list as a queue. As described in