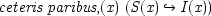world there are no causes, so every sub-population is homogeneous in all causal factors, and the maximal homogeneous population is the whole population. So if there is any C such that Prob(E/C) > Prob(E), it will be true that C causes E, and this world will not be a Hume world after all.
Apparently the laws of association underdetermine the causal laws. It is easy to construct examples in which there are two properties, P and Q, which could be used to partition a population. Under the partition into P and ┐ P, C increases the conditional probability of E in both sub-populations; but under the partition into Q and ┐ Q, Prob(E/C) = Prob(E). So relative to the assumption that P causes E, but Q does not, 'C causes E' is true. It is false relative to the assumption that Q  E, and P
E, and P  E. This suggests that, for a given set of laws of association, any set of causal laws will do. Once some causal laws have been settled, others will automatically follow, but any starting point is as good as any other. This suggestion is mistaken. Sometimes the causal laws are underdetermined by the laws of association, but not always. Some laws of association are compatible with only one set of causal laws. In general laws of association do not entail causal laws: but in particular cases they can. Here is an example.
E. This suggests that, for a given set of laws of association, any set of causal laws will do. Once some causal laws have been settled, others will automatically follow, but any starting point is as good as any other. This suggestion is mistaken. Sometimes the causal laws are underdetermined by the laws of association, but not always. Some laws of association are compatible with only one set of causal laws. In general laws of association do not entail causal laws: but in particular cases they can. Here is an example.
 E, and P
E, and P  E. This suggests that, for a given set of laws of association, any set of causal laws will do. Once some causal laws have been settled, others will automatically follow, but any starting point is as good as any other. This suggestion is mistaken. Sometimes the causal laws are underdetermined by the laws of association, but not always. Some laws of association are compatible with only one set of causal laws. In general laws of association do not entail causal laws: but in particular cases they can. Here is an example.
E. This suggests that, for a given set of laws of association, any set of causal laws will do. Once some causal laws have been settled, others will automatically follow, but any starting point is as good as any other. This suggestion is mistaken. Sometimes the causal laws are underdetermined by the laws of association, but not always. Some laws of association are compatible with only one set of causal laws. In general laws of association do not entail causal laws: but in particular cases they can. Here is an example.Consider a world whose laws of association cover three properties, A, B, and C; and assume that the following are implied by the laws of association:
In this world, B  C. The probabilities might for instance be those given in Chart 1. From just the probabilistic facts (1), (2), and (3), it is possible to infer that both A and B are causally relevant to C. Assume B
C. The probabilities might for instance be those given in Chart 1. From just the probabilistic facts (1), (2), and (3), it is possible to infer that both A and B are causally relevant to C. Assume B  ±C. Then by (1), A
±C. Then by (1), A  C, since the entire population is causally homogeneous (barring A) with respect to C and hence counts as a test population for A's effects on C. But if
C, since the entire population is causally homogeneous (barring A) with respect to C and hence counts as a test population for A's effects on C. But if
(1) |
Prob(C/A) > Prob(C)
|
(2) |
Prob(C/B & A > Prob(C/A); Prob(C/B & ┐ A) > Prob(C/┐A)
|
(3) |
Prob(C/B) = Prob(C)
|
 C. The probabilities might for instance be those given in Chart 1. From just the probabilistic facts (1), (2), and (3), it is possible to infer that both A and B are causally relevant to C. Assume B
C. The probabilities might for instance be those given in Chart 1. From just the probabilistic facts (1), (2), and (3), it is possible to infer that both A and B are causally relevant to C. Assume B  ±C. Then by (1), A
±C. Then by (1), A  C, since the entire population is causally homogeneous (barring A) with respect to C and hence counts as a test population for A's effects on C. But if
C, since the entire population is causally homogeneous (barring A) with respect to C and hence counts as a test population for A's effects on C. But if end p.41
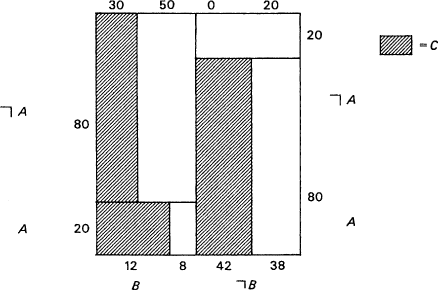
Chart 1
 C, then by (2), B
C, then by (2), B  ±C. Therefore B
±C. Therefore B  ±C. But from (3) this is not possible unless A is also relevant, either positively or negatively, to C. In the particular example pictured in the chart, A and B are both positively relevant to C.
±C. But from (3) this is not possible unless A is also relevant, either positively or negatively, to C. In the particular example pictured in the chart, A and B are both positively relevant to C.This kind of example may provide solace to the Humean. Often Humeans reject causal laws because they have no independent access to them. They suppose themselves able to determine the laws of association, but they imagine that they never have the initial causal information to begin to apply condition C. If they are lucky, this initial knowledge may not be necessary. Perhaps they live in a world that is not a Hume world; it may nevertheless be a world where causal laws can be inferred just from laws of association.
4. Conclusion
The quantity Prob(E/C.K
j ), which appears in both the causal condition of Part 1 and in the measure of effectiveness from Part 2, is called by statisticians the partial conditional probability of E on C, holding K
jfixed; and it is used in ways similar to the ways I have used it here. It forms the foundation
end p.42
for regression analyses of causation and it is applied by both Suppes and Salmon to treat the problem of joint effects. In decision theory the formula SC is structurally identical to one proposed by Brian Skyrms in his deft solution to New-comb's paradox; and elaborated further in his book Causal Necessity.25 What is especially significant about the partial conditional probabilities which appear here is the fact that these hold fixed all and only causal factors.
The choice of partition, {K
j }, is the critical feature of the measure of effectiveness proposed in SC. This is both (a) what makes the formula work in cases where the simple conditional probability fails; and (b) what makes it necessary to admit causal laws if you wish to sort good strategies from bad. The way you partition is crucial. In general you get different results from SC if you partition in different ways. Consider two different partitions for the same space, K
1 , . . . , K
nand I
1 , . . . I
s , which cross-grain each other—the K
iare mutually disjoint and exhaustive, and so are the I
j . Then it is easy to produce a measure over the field (±G, ±C, ±K
i , ±I
j ) such that
What partition is employed is thus essential to whether a strategy appears effective or not. The right partition—the one that judges strategies to be effective or ineffective in accord with what is objectively true—is determined by what the causal laws are. Partitions by other factors will give other results; and, if you do not admit causal laws, there is no general procedure for picking out the right factors. The objectivity of strategies requires the objectivity of causal laws.
25 Brian Skyrms, Causal Necessity (New Haven: Yale University Press, 1980).
end p.43
Essay 2 The Truth Doesn't Explain Much
Abstract: The standard view of explanation in science—the covering law model—assumes that knowledge of laws lies at the basis of our ability to explain phenomena. But in fact most of the high-level claims in science are ceteris paribus generalizations, which are false unless certain precise conditions obtain. Given the explanatory force of ceteris paribus generalizations but the paucity of true laws, the covering law model of explanation must be false. There is, it is argued, a trade-off between truth and explanatory power.
0. Introduction
Scientific theories must tell us both what is true in nature, and how we are to explain it. I shall argue that these are entirely different functions and should be kept distinct. Usually the two are conflated. The second is commonly seen as a by-product of the first. Scientific theories are thought to explain by dint of the descriptions they give of reality. Once the job of describing is done, science can shut down. That is all there is to do. To describe nature—to tell its laws, the values of its fundamental constants, its mass distributions—is ipso facto to lay down how we are to explain it.
This is a mistake, I shall argue; a mistake that is fostered by the covering-law model of explanation. The covering-law model supposes that all we need to know are the laws of nature—and a little logic, perhaps a little probability theory—and then we know which factors can explain which others. For example, in the simplest deductive-nomological version,1 the covering-law model says that one factor explains another just in case the occurrence of the second can be deduced from the occurrence of the first given the laws of nature.
But the D-N model is just an example. In the sense which is relevant to my claims here, most models of explanation offered recently in the philosophy of science are covering-law models. This includes not only Hempel's own inductive statistical model,2 but also Patrick Suppes's probabilistic model of causation,3 Wesley Salmon's statistical relevance model,4
1 See C. G. Hempel, 'Scientific Explanation', in C. G. Hempel (ed.), Aspects of Scientific Explanation (New York: Free Press, 1965).
2 See C. G. Hempel, 'Scientific Explanation', ibid.
3 See Patrick Suppes, A Probabilistic Theory of Causality (Amsterdam: North-Holland Publishing Co., 1970).
4 See Wesley Salmon, 'Statistical Explanation', in Wesley Salmon (ed.), Statistical Explanation and Statistical Relevance (Pittsburgh: University of Pittsburgh Press, 1971).
end p.44
and even Bengt Hanson's contextualistic model.5 All these accounts rely on the laws of nature, and just the laws of nature, to pick out which factors we can use in explanation.
A good deal of criticism has been aimed at Hempel's original covering-law models. Much of the criticism objects that these models let in too much. On Hempel's account it seems we can explain Henry's failure to get pregnant by his taking birth control pills, and we can explain the storm by the falling barometer. My objection is quite the opposite. Covering-law models let in too little. With a covering-law model we can explain hardly anything, even the things of which we are most proud—like the role of DNA in the inheritance of genetic characteristics, or the formation of rainbows when sunlight is refracted through raindrops. We cannot explain these phenomena with a covering-law model, I shall argue, because we do not have laws that cover them. Covering laws are scarce.
Many phenomena which have perfectly good scientific explanations are not covered by any laws. No true laws, that is. They are at best covered by ceteris paribus generalizations—generalizations that hold only under special conditions, usually ideal conditions. The literal translation is 'other things being equal'; but it would be more apt to read 'ceteris paribus' as 'other things being right.'
Sometimes we act as if this does not matter. We have in the back of our minds an 'understudy' picture of ceteris paribus laws: ceteris paribus laws are real laws; they can stand in when the laws we would like to see are not available and they can perform all the same functions, only not quite so well. But this will not do. Ceteris paribus generalizations, read literally without the 'ceteris paribus' modifier, are false. They are not only false, but held by us to be false; and there is no ground in the covering-law picture for false laws to explain anything. On the other hand, with the modifier the ceteris paribus generalizations may be true, but they cover only those few cases where the conditions are right. For most cases, either we have a law that purports to cover, but cannot explain
5 See Bengt Hanson, 'Explanations—Of What?' (mimeograph, Stanford University, 1974).
end p.45
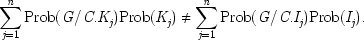


 k(n
2 /n
1 ) because sin θ = k'.
k(n
2 /n
1 ) because sin θ = k'.