Lesson 4: Geometry

The TEAS tests several fundamental concepts in geometry. You’ll need to be familiar with certain principles and formulas to answer geometry questions effectively.

Lines and Angles

To answer questions about lines and angles, you will need to know the following definitions:

A right angle is an angle equal to 90 degrees.
An acute angle is an angle less than 90 degrees.
An obtuse angle is an angle greater than 90 degrees.

Parallel lines never touch or intersect. When graphed on the coordinate plane, parallel lines have the same slope.
Perpendicular lines intersect to form a 90-degree angle (a right angle).
Vertical angles are directly across from each other when two or more lines intersect. Vertical angles are always equal to each other.
A transversal is a line that crosses two other distinct lines in a plane. When a transversal crosses two or more parallel lines, all acute angles created are equal to each other, and all obtuse angles created are equal to each other.

Two parallel lines are intersected by a third line, which is labeled "transversal"

Basic shapes

There are a few basic shapes that are commonly tested on the TEAS.

A rectangle is a four-sided shape that is made up of two pairs of parallel lines and has four right angles.
A square is a type of rectangle with four sides of equal length.
A circle is a curved, closed shape with all points equally distant from the center.
A triangle is a three-sided shape that is made up of three straight lines.

These are not the only shapes that the TEAS may test; see the table in this lesson for others.

Perimeter

Perimeter is the distance around the outside of a two-dimensional shape. Perimeter is calculated in units of length such as centimeters (cm), inches (in.), feet (ft), meters (m), and miles (mi). For example, the perimeter of a square is the length of all four sides added together. The perimeter of a circle is the distance once around the circle and is called the circumference.

Area

Area is a measure of the surface space taken up by a two-dimensional shape such as a rectangle, triangle, or circle. Area is calculated in square units such as square inches (in.²), square feet (ft²), or square centimeters (cm²).

The table contains the formulas for perimeter and area for various shapes that are tested on the TEAS.

Shape	Formula	Example
Square	Perimeter = 4 × s Area = s × s = s²	s = 5 cm Perimeter = 4 × 5 cm = 20 cm Area = 5 cm × 5 cm = 25 cm²
Rectangle	Perimeter = (2 × Width) + (2 × Length) Area = Length × Width	W = 4 ft L = 8 ft Perimeter = (2 × 4 ft) + (2 × 8 ft) = 24 ft Area = 8 ft × 4 ft = 32 ft²
Triangle	Perimeter = a + b + c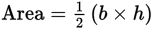	a = 5 in. b = 6 in. c = 5 in. h = 4 in. Perimeter = 5 in + 6 in + 5 in = 16 in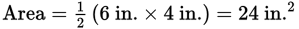
Parallelogram	Perimeter = 2a + 2b Area = b × h	a = 5 in. b = 8 in. h = 4 in. Perimeter = (2 × 5 in) + (2 × 8 in) = 26 in Area = 8 in × 4 in = 32 in²
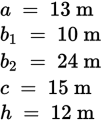
Trapezoid	Perimeter = Area =	Perimeter = 13 m + 10 m + 24 m + 15 m = 62 m
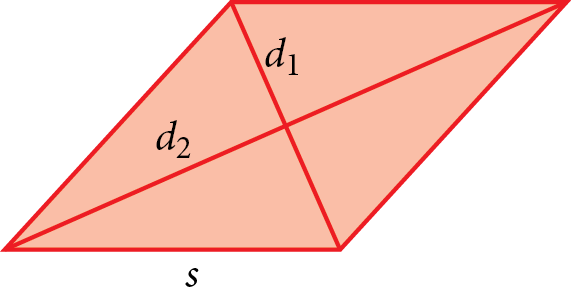
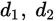
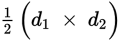
Rhombus	Perimeter = 4 × s Length of diagonals = Area =	Perimeter = 4 × 26 cm = 104 cm
Circle	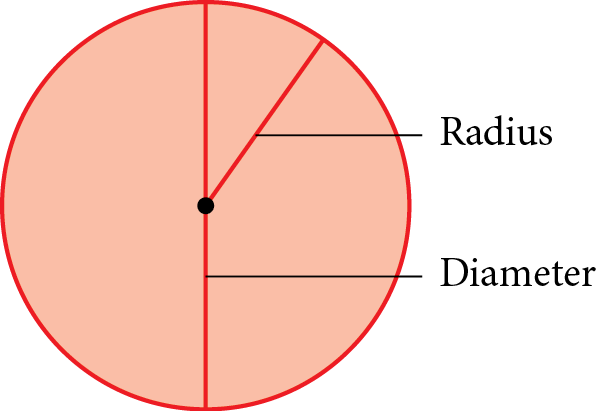Radius = r = distance from center to outer edge Diameter = d = distance across circle through the center 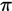= pi = approximately 3.14	r = 3

Take a look at how a test expert handles this question involving a perimeter.

A complex figure in which all angles are right, there is a rectangular indent on the upper right, the figure’s horizontal base is 15 cm, the left vertical dimension is 11 cm, the right vertical dimension is 9 cm, and the top dimension is 9 cm.

Question	Analysis
Which of the following is the perimeter of the figure above? (All angles in the figure are right angles.)	Step 1: The question provides a figure with four lengths specified and two lengths unspecified, and it asks for the perimeter of the figure.
(A) 44 cm (B) 46 cm (C) 50 cm (D) 52 cm	Step 2: Use the known dimensions to calculate the unknown dimensions. To calculate the missing top dimension, subtract the known top dimension of 9 cm from the bottom dimension of 15 cm to yield 6 cm. To calculate the missing right dimension, subtract the known right dimension of 9 cm from the left dimension of 11 cm to yield 2 cm. Next, add all lengths to find the perimeter: 11 cm + 15 cm + 6 cm + 2 cm + 9 cm + 9 cm = 52 cm.
	Step 3: The correct answer is (D).
	Step 4: Check that you’ve correctly calculated the unknown dimensions and that you added all six sides to get the perimeter.

Right triangles

A triangle that contains a right angle (90 degrees) is a right triangle. You can calculate the perimeter and area of right triangles just as you do with other triangles. The longest side of a right triangle (which is opposite the 90-degree angle) is the hypotenuse. If any two of the side lengths of a right triangle are known, the unknown length of the third side can be calculated using the Pythagorean theorem. The Pythagorean theorem states that a² + b² = c², where a and b are the lengths of the sides and c is the length of the hypotenuse, as in the figure shown.

Now try this question involving the area of an irregular shape.

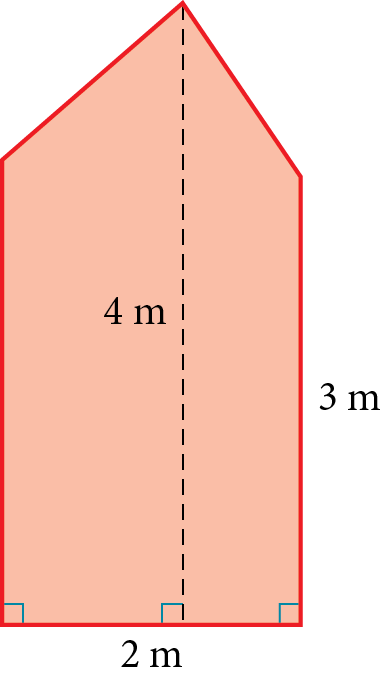
What is the area of the figure above?
1. 4 m²
2. 6 m²
3. 7 m²
4. 8 m²
Explanation

Step 1: The question provides a figure with some dimensions specified and asks you to calculate the area of the figure.

Step 2: Break the figure into familiar shapes and calculate the area of each shape; then combine them. There is a triangular portion joined to a rectangular portion. The width of the rectangle is 2 m, and the length of the rectangle is 3 m, so the area of the rectangular portion is 6 m². To determine the height of the triangular portion, subtract the height of the rectangle from the total height: h = 4 m – 3 m = 1 m. The base of the triangle is the same as the width of the rectangle, 2 m. Thus, the area of the triangle is 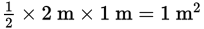. Finally, combine the areas of the two portions: 6 m² + 1 m² = 7 m².

Step 3: The correct answer is (C).

Step 4: Check that you’ve used the correct formula to calculate each area and combined them correctly.

circle proportions

The length of an arc (a portion of a circle’s circumference) can be calculated by multiplying the circumference by the fraction 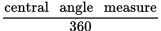. For example, the arc length of the figure shown is the circumference ×.

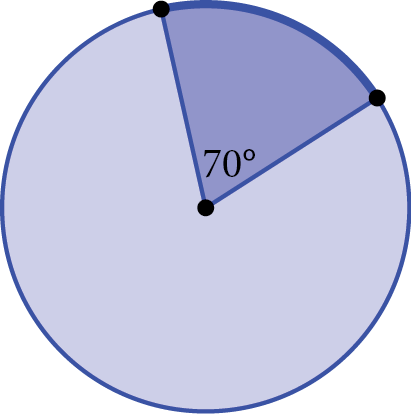
A circle with a sector designated with a central angle of 70 degrees

Try this one.

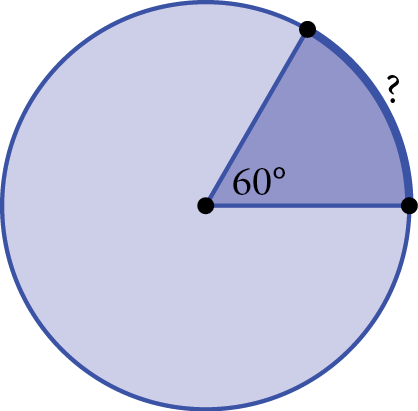
A circle with a sector of 60 degrees. A question mark indicates the arc length of the sector.

The circle above has a radius of 3 inches. What is the length, in inches, of the arc that has a central angle of 60 degrees?
1. π
2. 2π
3. 3π
4. 6π
Explanation

Step 1: The question presents a circle with a radius of 3 and a sector with a central angle of 60 degrees. Your task is to find the sector’s arc length.

Step 2: The arc length is part of the circumference, so begin by calculating circumference. Circumference = 2πr = 2 × π × 3 = 6π. To find the arc length, use the formula × circumference = × 6π = 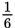× 6π = π.

Step 3: The correct answer is (A).

Step 4: Check each calculation to be sure you’ve applied the formulas correctly.