Chapter 5
Univariable Analysis of an Ordinal Dependent Variable

  1. 5.1 Chapter Summary
  2. 5.2 Glossary
  3. 5.3 Equations
  4. 5.4 Examples
  5. 5.5 Exercises

Chapter Summary

To perform statistical analysis of ordinal dependent variables, the values of those variables are converted into relative ranks. This is done regardless of whether the variables are from data that naturally occur on an ordinal scale or from continuous data that we wish to convert to an ordinal scale. Such a conversion of continuous data to ranks is done to allow statistical analysis without assuming that the distribution of estimates from all possible samples is a Gaussian distribution.

Conversion of data to ranks can be accomplished by assigning the rank of one to the smallest value, two to the next larger value, and so on. Observations that have the same value, called tied observations, are assigned the mean of the ranks they would have received if they were given separate ranks.

Estimation of parameters of a population's distribution is not relevant for ordinal dependent variables since no particular distribution is assumed. This lack of assumptions concerning distributions and parameters has led to procedures for ordinal data being referred to as distribution-free or nonparametric procedures. Even so, the median and the interquartile range can be determined from ordinal data and used as estimators of the population's values, even though they are not parameters.1

The most common method for performing statistical hypothesis testing on a single ordinal variable is the Wilcoxon signed-rank test. The test statistics for that procedure are the sum of the ranks for the negative differences and the sum of the ranks for the positive differences between paired observations. Unlike for other test statistics, we reject the null hypothesis if the calculated Wilcoxon signed-rank test statistic is equal to or smaller than the value in the table. For a two-tailed test, we calculate both the sum of the negative ranks and the sum of the positive ranks and choose the smaller of the two. A one-tailed test uses either the sum of the positive ranks or the sum of the negative ranks. Which of the two sums is used depends on the alternative hypothesis. Specifically, the appropriate test statistic is the sum that is assumed, according to the alternative hypothesis, to be the smaller of the two sums.

When continuous data are converted to an ordinal scale for statistical analysis, we are able to circumvent certain assumptions about the distribution of estimates derived from all possible samples. We cannot, however, ignore the assumption that dependent variable values are randomly selected from the population.

As a result of this conversion to an ordinal scale, we have the potential for losing statistical power. That is to say, it can become more difficult to reject a false null hypothesis. This loss of statistical power occurs when the assumptions of the statistical procedure for continuous data are not violated, but the data are analyzed as if they were ordinal. The loss of power is usually small and usually has no effect on the conclusions we draw in hypothesis testing.

Glossary

  1. Absolute Value – a value that ignores negative signs, making all values positive.
  2. Median – the physical center of a distribution above and below which are half of the data values.
  3. Nonparametric – statistical procedures for ordinal dependent variables used on continuous dependent variables converted to an ordinal scale. This has the advantage of not assuming a Gaussian sampling distribution.
  4. Relative Ranks – the magnitude of data values in comparison to other data values. The smallest data value gets a rank of one and the highest data value gets a rank equal to the number of data values. Two or more data with the same value are given the average rank.

Equations

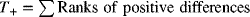T+=∑Ranks of positive differencesimg Wilcoxon signed-rank test. (see Equation {5.1})
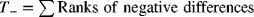T−=∑Ranks of negative differencesimg Wilcoxon signed-rank test. (see Equation {5.2})

Examples

In the examples in Chapter 4, we were interested in the change in weight of 15 persons who stayed on a particular diet for three months. The observations are in Table 5.1.

Table 5.1 Changes in weight from Table 4.1

Yimg
5
3
3
−1
0
10
3
−2
1
1
5
2
1
3
1

5.1. Determine point and (95%) interval estimates of the median.

In preparation, we sort the data according to numeric values (Table 5.2).

Table 5.2 Sorted changes in weight

Yimg Sorted
5 −2
3 −1
3 0
−1 1
0 1
10 1
3 1
−2 2
1 3
1 3
5 3
2 4
1 5
3 5
1 10

The median will be the value above and below which there are half the data values. There are 15 data values, so the median is equal to two. The limits of the interval estimate, we find in Table B.11. For 15 observations, the limits are the third and 13th largest data values. Those values are zero and five. So, we are 95% confident the median in the population is between zero and five.

5.2. Change those data to their absolute values.

To change these values to absolute values, we represent negative one and negative two with positive one and positive two (Table 5.3).

Table 5.3 Absolute values of changes in weight for a sample of 15 persons.

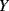Yimg |Y|
5 5
3 3
3 3
−1 1
0 0
10 10
3 3
−2 2
1 1
1 1
5 5
2 2
1 1
3 3
1 1

5.3. In preparation to use the Wilcoxon Signed-Rank test, rank the absolute values.

Since we are assigning ranks in preparation for the Wilcoxon signed-rank test, we do not rank the value of zero. Among the remaining 14 observations, one is the smallest value. There are five ones, so they are assigned the average of ranks one, two, three, four, and five. Two is the next higher number. There are two twos, so they get the average of the ranks of six and seven. There are four threes, so they are assigned the average of ranks eight, nine, 10, and 11. There are two fives, so they are assigned the average of the ranks of 12 and 13.

Table 5.4 Ranks of absolute values of changes in weight for the Wilcoxon signed-rank test.

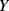Yimg |Y| Rank
5 5 12.5
3 3 9.5
3 3 9.5
−1 1 3
0 – –
10 10 14
3 3 9.5
−2 2 6.5
1 1 3
1 1 3
5 5 12.5
2 2 6.5
1 1 3
3 3 9.5
1 1 3

5.4. Test the null hypothesis that there is a balance of positive and negative differences in the population versus the alternative that there is not a balance. Allow a 5% chance of making a type I error.

To test the null hypothesis that there is a balance of positive and negative differences we chose the smaller sum of ranks for those observations that were originally positive values and for those observations that were originally negative values. The smaller sum is for the negative values. That sum is 3 + 6.5 = 9.5. To interpret this sum, we compare it to a critical value from Table B.3. For 14 (nonzero) observations, the value for an alpha of 0.05 is 21. Since the calculated value (9.5) is smaller than the critical value (21), we reject the null hypothesis and accept, through the process of elimination, the alternative hypothesis. There is a statistically significant imbalance of positive and negative changes in weight.

Exercises

5.1. Patients on a particular treatment often suffer from anemia. To counter this effect, we think that these patients might be helped if they were given folic acid. To evaluate this, we identify 8 patients on the treatment who have been diagnosed with anemia and measure their hematocrit. Then, we give these patients supplemental folic acid for a period of 14 days. Then, we measure their hematocrit again and subtract this second measurement from the initial measurement. Suppose that we observe the following differences: −0.2, 0.5, 0.8, −1.3, −1.4, −5.4, −9.7, −18.2. Create an Excel dataset from those values. Using those data, and without assuming a Gaussian sampling distribution, test the null hypothesis that there is a balance of increases and decreases in hematocrit versus the alternative hypothesis that there is not a balance. If you were to allow a 5% chance of making a type I error, which of the following is the best conclusion to draw?

  1. Accept both the null and alternative hypotheses
  2. Reject both the null and alternative hypotheses
  3. Reject the null hypothesis and accept the alternative hypothesis
  4. Accept the null hypothesis and reject the alternative hypothesis
  5. It is best not to draw a conclusion about the null and alternative hypotheses from these observations

5.2. Patients on a particular treatment often suffer from anemia. To counter this effect, we think that these patients might be helped if they were given folic acid. To evaluate this, we identify 8 patients on the treatment who have been diagnosed with anemia and measure their hematocrit. Then, we give these patients supplemental folic acid for a period of 14 days. Then, we measure their hematocrit again and subtract this second measurement from the initial measurement. Suppose that we observe the following differences: −0.2, 0.5, 0.8, −1.3, −1.4, −5.4, −9.7, −18.2. Create an Excel dataset from those values. Calculate the median of those values. Which of the following is closest to that median?

  1. −4.36
  2. −1.35
  3. 0
  4. 1.35
  5. 4.36

5.3. Suppose we are interested in a new treatment for arthritis pain. To evaluate this new treatment, we give it to 100 arthritis patients and ask them to use it for two weeks. At the end of that time, we asked them whether or not their level of pain improved, worsened, or did not change. Suppose that we make the observations in the following table.

Response Number of Patients
Very much improved 26
Somewhat improved 32
No change 25
Somewhat worse 12
Very much worse 3

Calculate the median of those values. Which of the following is closest to that median?

  1. Very much improved
  2. Somewhat improved
  3. No change
  4. Somewhat worse
  5. Very much worse

5.4. Suppose we are interested in a new treatment for arthritis pain. To evaluate this new treatment, we give it to 100 arthritis patients and ask them to use it for two weeks. At the end of that time, we asked them whether or not their level of pain improved, worsened, or did not change. Suppose that we make the observations in the following table.

Response Number of Patients
Very much improved 26
Somewhat improved 32
No change 25
Somewhat worse 12
Very much worse 3

Test the null hypothesis that there was no change in the level of pain versus the alternative hypothesis that there was a change. If you allow a 5% chance of making a type I error, which of the following is the best conclusion to draw?

  1. Accept both the null and alternative hypotheses
  2. Reject both the null and alternative hypotheses
  3. Reject the null hypothesis and accept the alternative hypothesis
  4. Accept the null hypothesis and reject the alternative hypothesis
  5. It is best not to draw a conclusion about the null and alternative hypotheses from these observations

Note