
CELESTIAL MOVEMENTS are everlasting, Copernicus declared in the title of the fourth chapter of his Derevolutionibus. And only a circle has neither beginning nor ending and can repeat what is past. Although the observed motions are complex, "it is impossible that a heavenly body should be moved irregularly by a single sphere." This could only be accomplished by an inconstancy of the moving power that drives it, and "the mind shudders" at such a prospect. Although Copernicus did not here single out Ptolemy's equant as an offense, clearly this is what he had in mind.
Ptolemy's equant produced uniform motion about an imaginary point within the circle that carried the planetary epicycle, causing the epicycle to move around that circle faster on one side than the other. Today we recognize the equant as an ingenious approximation to one of nature's most fundamental laws, the conservation of angular momentum. Without some device to account for its observed effects, the predicted positions of Mars, for example, would be wrong by many degrees.
For Aristotle, a hard-core geocentrist, with the Earth solidly fixed in the center, the motions originated at the outer edge of the system. The love of God turned the spheres, and the moving power was transmitted more and more slowly from one sphere to another, so that the inner sphere carrying the Moon took nearly twenty-five hours to turn once, whereas the stars spun about more quickly in twenty-four sidereal hours. Kepler, a confirmed helio-centrist, saw the implications more clearly than his Polish master: Mercury, the innermost planet, sped around the Sun the fastest, and therefore the driving moving power had to come from the inside out, somehow residing in the Sun itself. Because the Earth was in winter closest to the Sun, it should soak up that moving power more efficiently then and should move faster. Kepler's mind did not shudder at such inconstancy; he thought it was physically logical.
Copernicus stood at a crucial transition point as he revised the geometric blueprint but was unable to come to terms with the physical implications of the radical reahgnment. Within his own aesthetic vision he had to generate the observed unequal motion out of combinations of uniform circular motions. Because this part of his cosmology turned out to be a physical dead end, modern secondary sources tend to ignore this rather complicated part of his De revolutionibus, even though it comprised the bulk of the book. Nevertheless, it proved to be the most intriguing and most studied part of his work as far as sixteenth-century astronomers were concerned.
Somehow, somewhere, Copernicus stumbled onto the way to generate Ptolemy's equant motion by using either a concentric circle with two small epicyclets, or an eccentric circle with a single epicyclet. To introduce it this way is to conceal the iceberg below its tip. In the mid-1950s the historian of Islamic science, Edward S. Kennedy, and his students at the American University of Beirut (where I was also then teaching) showed that a series of thirteenth-and fourteenth-century Muslim astronomers in Persia and in Damascus had come up with exactly the same arrangement of epicyclets that Copernicus used, although they did not proceed to a heliocentric cosmos. In fact the two aesthetic ideas are not coupled except in some inscrutable way in the mind of Copernicus. Ever since Kennedy's work a big question has been: Did Copernicus invent the epicyclet arrangement independently, and if not, how in the world did he find out about it? (There was no available printed source, and apparently no manuscript source in Latin.) One interesting guess is that Copernicus found out through the work of a sometime ephemeris maker named Johannes Engel, who quite likely used the device, and that Copernicus himself was probably unaware of its Islamic antecedents.
The double epicyclet with the concentric circle was Copernicus' system of choice when he wrote his Commentariolus and it is the "second method" of De revolutionibus, whereas the single epicyclet was the "third method" of De revolutionibus and was the one actually employed there. It really doesn't matter, Copernicus implied, because both as well as the first arrangement gave the same result, and therefore one of them had to be real—a consummate demonstration of faulty logic! In any event, to use the twentieth-century proverb "A picture is worth a thousand words," here is a diagram to show the equivalence of Copernicus' single epicyclet and Ptolemy's equant. Note that the motion in the epicyclet is reckoned with respect to the moving line from the center of the circle, and the angle at the center matches the angle in the epicyclet. Because the radius of the epicyclet is one-third of the distance from the Sun to the center, a regular trapezoid results, and the dashed line replicates the uniform motion around the equant.
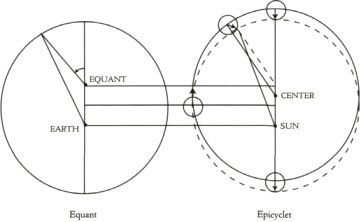
Copernicus' replacement of the equant by a pair of uniform circular motions.
The epicycle always moves to form an isosceles trapezoid.
The path that results, shown by the dashed circle, is in fact not quite a circle because it bows out slightly on the sides—the opposite way compared to Kepler's ellipse.