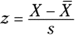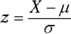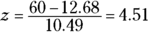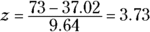Chapter 6

Meeting Standards and Standings

IN THIS CHAPTER

Standardizing scores

Making comparisons

Working with ranks in files

Rolling in the percentiles

In my left hand, I hold 100 Philippine pesos. In my right, I hold 1,000 Colombian pesos. Which is worth more? Both are called pesos, right? So shouldn’t the 1,000 be greater than the 100? Not necessarily. Peso is just a coincidence of names. Each one comes out of a different country, and each country has its own economy.

To compare the two amounts of money, you have to convert each currency into a standard unit. The most intuitive standard for U.S. citizens is our own currency. How much is each amount worth in dollars and cents? As I write this, 100 Philippine pesos are worth over $2. One thousand Colombian pesos are worth 34 cents.

So when you compare numbers, context is important. To make valid comparisons across contexts, you often have to convert numbers into standard units. In this chapter, I show you how to use statistics to do just that. Standard units show you where a score stands in relation to other scores within a group. I also show you other ways to determine a score’s standing within a group.

Catching Some Z’s

A number in isolation doesn’t provide much information. To fully understand what a number means, you have to take into account the process that produced it. To compare one number to another, they have to be on the same scale.

When you’re converting currency, it’s easy to figure out a standard. When you convert temperatures from Fahrenheit to Celsius, or lengths from feet to meters, a formula guides you.

When it’s not so clear-cut, you can use the mean and standard deviation to standardize scores that come from different processes. The idea is to take a set of scores and use its mean as a zero point, and its standard deviation as a unit of measure. Then you make comparisons: You calculate the deviation of each score from the mean, and then you compare that deviation to the standard deviation. You’re asking, “How big is a particular deviation relative to (something like) an average of all the deviations?”

To make a comparison, you divide the score’s deviation by the standard deviation. This transforms the score into another kind of score. The transformed score is called a standard score, or a z-score.

The formula for this is

if you're dealing with a sample, and

if you're dealing with a population. In either case, x represents the score you're transforming into a z-score.

Characteristics of z-scores

A z-score can be positive, negative, or zero. A negative z-score represents a score that's less than the mean, and a positive z-score represents a score that's greater than the mean. When the score is equal to the mean, its z-score is zero.

When you calculate the z-score for every score in the set, the mean of the z-scores is 0, and the standard deviation of the z-scores is 1.

After you do this for several sets of scores, you can legitimately compare a score from one set to a score from another. If the two sets have different means and different standard deviations, comparing without standardizing is like comparing apples with kumquats.

In the examples that follow, I show how to use z-scores to make comparisons.

Bonds versus the Bambino

Here's an important question that often comes up in the context of serious metaphysical discussions: Who is the greatest home run hitter of all time: Barry Bonds or Babe Ruth? Although this is a difficult question to answer, one way to get your hands around it is to look at each player's best season and compare the two. Bonds hit 73 home runs in 2001, and Ruth hit 60 in 1927. On the surface, Bonds appears to be the more productive hitter.

The year 1927 was very different from 2001, however. Baseball (and everything else) went through huge, long-overdue changes in the intervening years, and player statistics reflect those changes. A home run was harder to hit in the 1920s than in the 2000s. Still, 73 versus 60? Hmmm… .

Standard scores can help decide whose best season was better. To standardize, I took the top 50 home run hitters of 1927 and the top 50 from 2001. I calculated the mean and standard deviation of each group and then turned Ruth’s 60 and Bonds’s 73 into z-scores.

The average from 1927 is 12.68 homers with a standard deviation of 10.49. The average from 2001 is 37.02 homers with a standard deviation of 9.64. Although the means differ greatly, the standard deviations are pretty close.

And the z-scores? Ruth’s is

Bonds’s is

The clear winner in the z-score best-season home run derby is Babe Ruth. Period.

Just to show you how times have changed, Lou Gehrig hit 47 home runs in 1927 (finishing second to Ruth) for a z-score of 3.27. In 2001, 47 home runs amounted to a z-score of 1.04.

Exam scores

Getting away from sports debates, one practical application of z-scores is the assignment of grades to exam scores. Based on percentage scoring, instructors traditionally evaluate a score of 90 points or higher (out of 100) as an A, 80–89 points as a B, 70–79 points as a C, 60–69 points as a D, and less than 60 points as an F. Then they average scores from several exams together to assign a course grade.

Is that fair? Just as a peso from the Philippines is worth more than a peso from Colombia, and a home run was harder to hit in 1927 than in 2001, is a “point” on one exam worth the same as a “point” on another? Like “pesos,” isn't “points” just a coincidence?

Absolutely. A point on a difficult exam is, by definition, harder to come by than a point on an easy exam. Because points might not mean the same thing from one exam to another, the fairest thing to do is convert scores from each exam into z-scores before averaging them. That way, you're averaging numbers on a level playing field.

I do that in the courses I teach. I often find that a lower numerical score on one exam results in a higher z-score than a higher numerical score from another exam. For example, on an exam where the mean is 65 and the standard deviation is 12, a score of 71 results in a z-score of .5. On another exam, with a mean of 69 and a standard deviation of 14, a score of 75 is equivalent to a z-score of .429. (Yes, it's like Ruth’s 60 home runs versus Bonds’s 73.) Moral of the story: Numbers in isolation tell you very little. You have to understand the process that produces them.

Standard Scores in R

The R function for calculating standard scores is called scale(). Supply a vector of scores, and scale() returns a vector of z-scores along with, helpfully, the mean and the standard deviation.

To show scale() in action, I isolate a subset of the Cars93 data frame. (It’s in the MASS package. On the Packages tab, check the box next to MASS if it’s unchecked.)

Specifically, I create a vector of the horsepowers of 8-cylinder cars from the USA:

> Horsepower.USA.Eight <- with(Cars93, Horsepower[Origin ==
  "USA" & Cylinders == 8])
> Horsepower.USA.Eight
[1] 200 295 170 300 190 210

And now for the z-scores:

> scale(Horsepower.USA.Eight)
[,1]
[1,] -0.4925263
[2,] 1.2089283
[3,] -1.0298278
[4,] 1.2984785
[5,] -0.6716268
[6,] -0.3134259
attr(,"scaled:center")
[1] 227.5
attr(,"scaled:scale")
[1] 55.83458

That last value is s, not σ. If you have to base your z-scores on σ, divide each element in the vector by the square root of (N-1)/N:

> N <- length(Horsepower.USA.Eight)
> scale(Horsepower.USA.Eight)/sqrt((N-1)/N)
[,1]
[1,] -0.5395356
[2,] 1.3243146
[3,] -1.1281198
[4,] 1.4224120
[5,] -0.7357303
[6,] -0.3433408
attr(,"scaled:center")
[1] 227.5
attr(,"scaled:scale")
[1] 55.83458

Notice that scale() still returns s.

CACHING SOME Z’S

Because negative z-scores might have connotations that are, well, negative, educators sometimes change the z-score when they evaluate students. In effect, they're hiding the z-score, but the concept is the same — standardization with the standard deviation as the unit of measure.

One popular transformation is called the T-score. The T-score eliminates negative scores because a set of T-scores has a mean of 50 and a standard deviation of 10. The idea is to give an exam, grade all the tests, and calculate the mean and standard deviation. Next, turn each score into a z-score. Then follow this formula:

People who use the T-score often like to round to the nearest whole number.

Here’s how to transform the vector from the example into a set of T-scores:

T.Hp.USA.Eight <- round((10*scale(Horsepower.USA.Eight)+50), digits = 0)

The digits=0 argument in the round() function rounds off the result to the nearest whole number.

SAT scores are another transformation of the z-score. (Some refer to the SAT as a C-score.) Under the old scoring system, the SAT has a mean of 500 and a standard deviation of 100. After the exams are graded, and their mean and standard deviation calculated, each exam score becomes a z-score in the usual way. This formula converts the z-score into a SAT score:

Rounding to the nearest whole number is part of the procedure here, too.

The IQ score is still another transformed z. Its mean is 100, and its standard deviation is 15. What's the procedure for computing an IQ score? You guessed it. In a group of IQ scores, calculate the mean and standard deviation, and then calculate the z-score. Then it's

As with the other two, IQ scores are rounded to the nearest whole number.

Where Do You Stand?

Standard scores show you how a score stands in relation to other scores in the same group. To do this, they use the standard deviation as a unit of measure.

If you don't want to use the standard deviation, you can show a score's relative standing in a simpler way. You can determine the score's rank within the group: In ascending order, the lowest score has a rank of 1, the second lowest has a rank of 2, and so on. In descending order, the highest score is ranked 1, the second highest 2, and so on.

Ranking in R

Unsurprisingly, the rank() function ranks the scores in a vector. The default order is ascending:

> Horsepower.USA.Eight
[1] 200 295 170 300 190 210
> rank(Horsepower.USA.Eight)
[1] 3 5 1 6 2 4

For descending order, put a minus sign (–) in front of the vector name:

> rank(-Horsepower.USA.Eight)
[1] 4 2 6 1 5 3

Tied scores

R handles tied scores by including the optional ties.method argument in rank(). To show you how this works, I create a new vector that replaces the sixth value (210) in Horsepower.USA.Eight with 200:

> tied.Horsepower <- replace(Horsepower.USA.Eight,6,200)
> tied.Horsepower
[1] 200 295 170 300 190 200

One way of dealing with tied scores is to give each tied score the average of the ranks they would have attained. So the two scores of 200 would have been ranked 3 and 4, and their average 3.5 is what this method assigns to both of them:

> rank(tied.Horsepower, ties.method = "average")
[1] 3.5 5.0 1.0 6.0 2.0 3.5

Another method assigns the minimum of the ranks:

> rank(tied.Horsepower, ties.method = "min")
[1] 3 5 1 6 2 3

And still another assigns the maximum of the ranks:

> rank(tied.Horsepower, ties.method = "max")
[1] 4 5 1 6 2 4

A couple of other methods are available. Type ?rank into the console window for the details (which appear on the Help tab).

Nth smallest, Nth largest

You can turn the ranking process inside out by supplying a rank (like second-lowest) and asking which score has that rank. This procedure begins with the sort() function, which arranges the scores in increasing order:

> sort(Horsepower.USA.Eight)
[1] 170 190 200 210 295 300

For the second-lowest score, supply the index value 2:

> sort(Horsepower.USA.Eight)[2]
[1] 190

How about from the other end? Start by assigning the length of the vector to N:

> N <- length(Horsepower.USA.Eight)

Then, to find the second-highest score, it’s

> sort(Horsepower.USA.Eight)[N-1]
[1] 295

Percentiles

Closely related to rank is the percentile, which represents a score's standing in the group as the percent of scores below it. If you've taken standardized tests like the SAT, you've encountered percentiles. An SAT score in the 80th percentile is higher than 80 percent of the other SAT scores.

Sounds simple, doesn’t it? Not so fast. “Percentile” can have a couple of definitions, and hence, a couple (or more) ways to calculate it. Some define percentile as “greater than” (as in the preceding paragraph), some define percentile as “greater than or equal to.” “Greater than” equates to “exclusive.” “Greater than or equal to” equates to “inclusive.”

The function quantile() calculates percentiles. If left to its own devices, it calculates the 0th, 25th, 50th, 75th, and 100th percentiles. It calculates the percentiles in a manner that’s consistent with “inclusive” and (if necessary) interpolates values for the percentiles.

I begin by sorting the Horsepower.USA.Eight vector so that you can see the scores in order and compare with the percentiles:

> sort(Horsepower.USA.Eight)
[1] 170 190 200 210 295 300

And now the percentiles:

> quantile(Horsepower.USA.Eight)
0% 25% 50% 75% 100%
170.00 192.50 205.00 273.75 300.00

Notice that the 25th, 50th, and 75th percentiles are values that aren’t in the vector.

To calculate percentiles consistent with “exclusive,” add the type argument and set it equal to 6:

> quantile(Horsepower.USA.Eight, type = 6)
0% 25% 50% 75% 100%
170.00 185.00 205.00 296.25 300.00

The default type (the first type I showed you) is 7, by the way. Seven other types (ways of calculating percentiles) are available. To take a look at them, type ?quantile into the Console window (and then read the documentation on the Help tab.)

Moving forward, I use the default type for percentiles.

The 25th, 50th, 75th, and 100th percentiles are often used to summarize a group of scores. Because they divide a group of scores into fourths, they’re called quartiles.

You’re not stuck with quartiles, however. You can get quantile() to return any percentile. Suppose you want to find the 54th, 68th, and 91st percentiles. Include a vector of those numbers (expressed as proportions) and you’re in business:

> quantile(Horsepower.USA.Eight, c(.54, .68, .91))
54% 68% 91%
207.00 244.00 297.75

Percent ranks

The quantile() function gives you the scores that correspond to given percentiles. You can also work in the reverse direction — find the percent ranks that correspond to given scores in a data set. For example, in Horsepower.USA.Eight, 170 is lowest in the list of six, so its rank is 1 and its percent rank is 1/6, or 16.67 percent.

Base R doesn’t provide a function for this, but it’s easy enough to create one:

percent.ranks <-
 function(x){round((rank(x)/length(x))*100, digits = 2)}

The round() function with digits = 2 rounds the results to two decimal places.

Applying this function:

> percent.ranks(Horsepower.USA.Eight)
[1] 50.00 83.33 16.67 100.00 33.33 66.67

A NEAT TRICK

Sometimes, you might want to know only the percent rank of a single score in a set of scores — even if that score isn’t in the data set. For example, what is the percent rank of 273 in Horsepower.USA.Eight?

To answer this question, you can harness mean(). Using this function along with logical operators yields interesting results. Here’s what I mean:

xx <- c(15,20,25,30,35,40,45,50)

Here’s a result you’d expect:

> mean(xx)
[1] 32.5

But here’s one you might not:

> mean(xx > 15)
[1] 0.875

The result is the proportion of scores in xx that are greater than 15.

Here are a few more:

> mean(xx < 25)
[1] 0.25
> mean(xx <= 25)
[1] 0.375
> mean(xx <= 28)
[1] 0.375

That <= operator, of course, means “less than or equal to,” so that last one gives the proportion of scores in xx that are less than or equal to 28.

Are you catching my drift? To find the percent rank of a score (or a potential score) in a vector like Horsepower.USA.Eight, it’s

> mean(Horsepower.USA.Eight <= 273)*100
[1] 66.66667

Summarizing

In addition to the functions for calculating percentiles and ranks, R provides a couple of functions that quickly summarize data and do a lot of the work I discuss in this chapter.

One is called fivenum(). This function, unsurprisingly, yields five numbers. They’re the five numbers that box plot creator John Tukey used to summarize a data set. Then he used those numbers in his box plots. (See Chapter 3.)

> fivenum(Horsepower.USA.Eight)
[1] 170 190 205 295 300

From left to right, that’s the minimum, lower hinge, median, upper hinge, and maximum. Remember the quantile() function and the nine available ways (types) to calculate quantiles? This function’s results are what type = 2 yields in quantile().

Another function, summary(), is more widely used:

> summary(Horsepower.USA.Eight)
Min. 1st Qu. Median Mean 3rd Qu. Max.
170.0 192.5 205.0 227.5 273.8 300.0

It provides the mean along with the quantiles (as the default type in quantile() calculates them).

The summary() function is versatile. You can use it to summarize a wide variety of objects, and the results can look very different from object to object. I use it quite a bit in upcoming chapters.