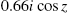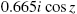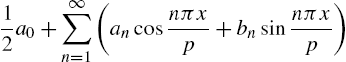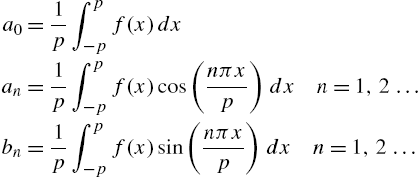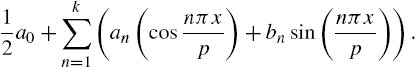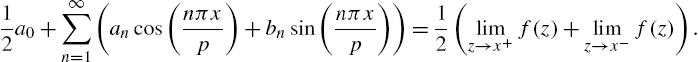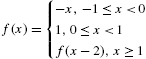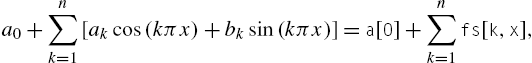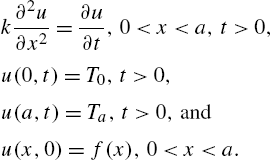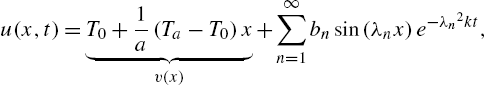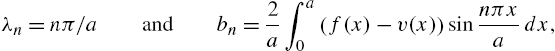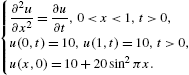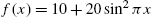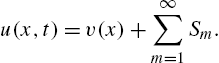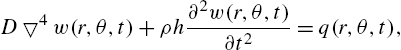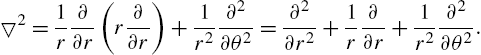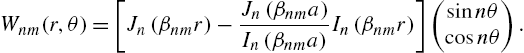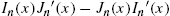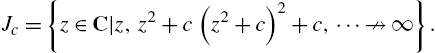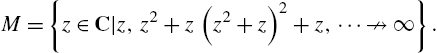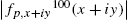Introduction to Lists and Tables
Keywords
Dynamical systems; Engineering applications; Lists; Graphing lists
4.1 Lists and List Operations
4.1.1 Defining Lists
A list of n elements is a Mathematica object of the form
list={a1,a2,a3,...,an}.
The ith element of the list is extracted from list with list[[i]] or Part[list,i].
Elements of a list are separated by commas. Lists are always enclosed in braces {...} and each element of a list may be (almost any) Mathematica object, even other lists. Because lists are Mathematica objects, they can be named. For easy reference, we will usually name lists.
Lists can be defined in a variety of ways: they may be completely typed in, imported from other programs and text files, or they may be created with either the Table or Array commands. Given a function ![]() and a number n, the command
and a number n, the command
1. Table[f[i],{i,n}] creates the list {f[1],...,f[n]};
2. Table[f[i],{i,0,n}] creates the list {f[0],...,f[n]};
3. Table[f[i],{i,n,m}] creates the list
{f[n],f[n+1],...,f[m-1],f[m]};
4. Table[f[i],{i,imin,imax,istep}] creates the list
{f[imin],f[imin+istep],f[imin+2*istep],...,f[imax]};
and
5. Array[f,n] creates the list {f[1],...,f[n]}.
In particular,
Table[f[x],{x,a,b,(b-a)/(n-1)}]
returns a list of ![]() values for n equally spaced values of x between a and b;
values for n equally spaced values of x between a and b;
Table[{x,f[x]},{x,a,b,(b-a)/(n-1)}]
returns a list of points ![]() for n equally spaced values of x between a and b.
for n equally spaced values of x between a and b.
In addition to using Table, lists of numbers can be calculated using Range.
1. Range[n] generates the list {1,2, ... , n};
2. Range[n1,n2] generates the list {n1, n1+1, ... , n2-1, n2}; and
3. Range[n1,n2,nstep] generates the list
{n1, n1+nstep,n1+2*nstep, ... , n2-nstep,n2}.
In addition, we can use Table to generate lists consisting of the same or similar objects.
Manipulate works in much the same way as Table but allows you to interactively see how adjusting parameters affects a given situation.
4.1.2 Plotting Lists of Points
Lists are plotted with ListPlot.
1. ListPlot[{{x1,y1},{x2,y2},...,{xn,yn}}] plots the list of points ![]() . The size of the points in the resulting plot is controlled with the option PlotStyle->PointSize[w], where w is the fraction of the total width of the graphic. For two-dimensional graphics, the default value is 0.008.
. The size of the points in the resulting plot is controlled with the option PlotStyle->PointSize[w], where w is the fraction of the total width of the graphic. For two-dimensional graphics, the default value is 0.008.
2. ListPlot[{y1,y2,..,yn}] plots the list of points ![]()
![]() .
.
3. ListLinePlot[{y1,y2,..,yn}] plots the list of points ![]()
![]() and connects consecutive points with line segments. Alternatively, you can use ListPlot together with the option Joined->True to connect consecutive points with line segments.
and connects consecutive points with line segments. Alternatively, you can use ListPlot together with the option Joined->True to connect consecutive points with line segments.
Working in almost the same way as Take, Span (;;) selects elements of lists: list[[n;;m]] returns the n through mth elements of list.
However, you can use Table together with Part ([[...]]) to obtain the same results as those obtained with Take or Span.
![]()
![]()
![]()
![]()
![]()
![]()
You can iterate recursively with Table. Both
![]()
![]()
![]()
![]()
5
and
![]()
![]()
compute tables of ![]() . The outermost iterator is evaluated first: in this case, i is followed by j as in t1 and the result is a list of lists. To eliminate the inner lists (that is, the braces), use Flatten. Generally, Flatten[list,n] flattens list (removes braces) to level n.
. The outermost iterator is evaluated first: in this case, i is followed by j as in t1 and the result is a list of lists. To eliminate the inner lists (that is, the braces), use Flatten. Generally, Flatten[list,n] flattens list (removes braces) to level n.
![]()
![]()
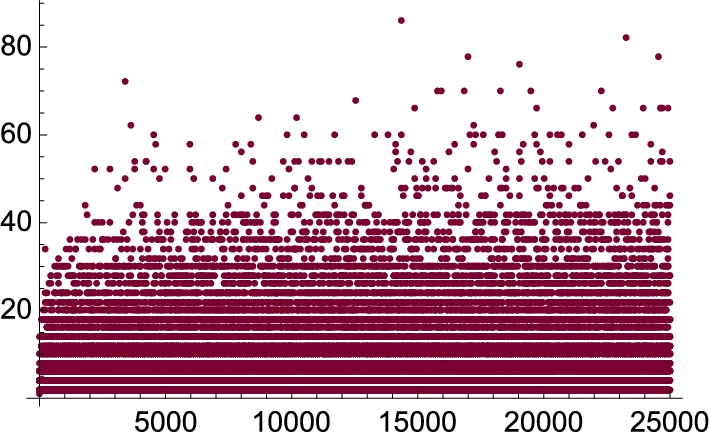
The observation is especially important when graphing lists of points obtained by iterating Table. For example,
![]()
![]()
![]()
5
is not a list of 25 points: t1 is a list of 5 lists each consisting of 5 points. t1 has two levels. For example, the 3rd element of the second level is
![]()
![]()
and the 2nd element of the third level (or the second part of the third part) is
![]()
![]()
To flatten t2 to level 1, we use Flatten.
![]()
![]()
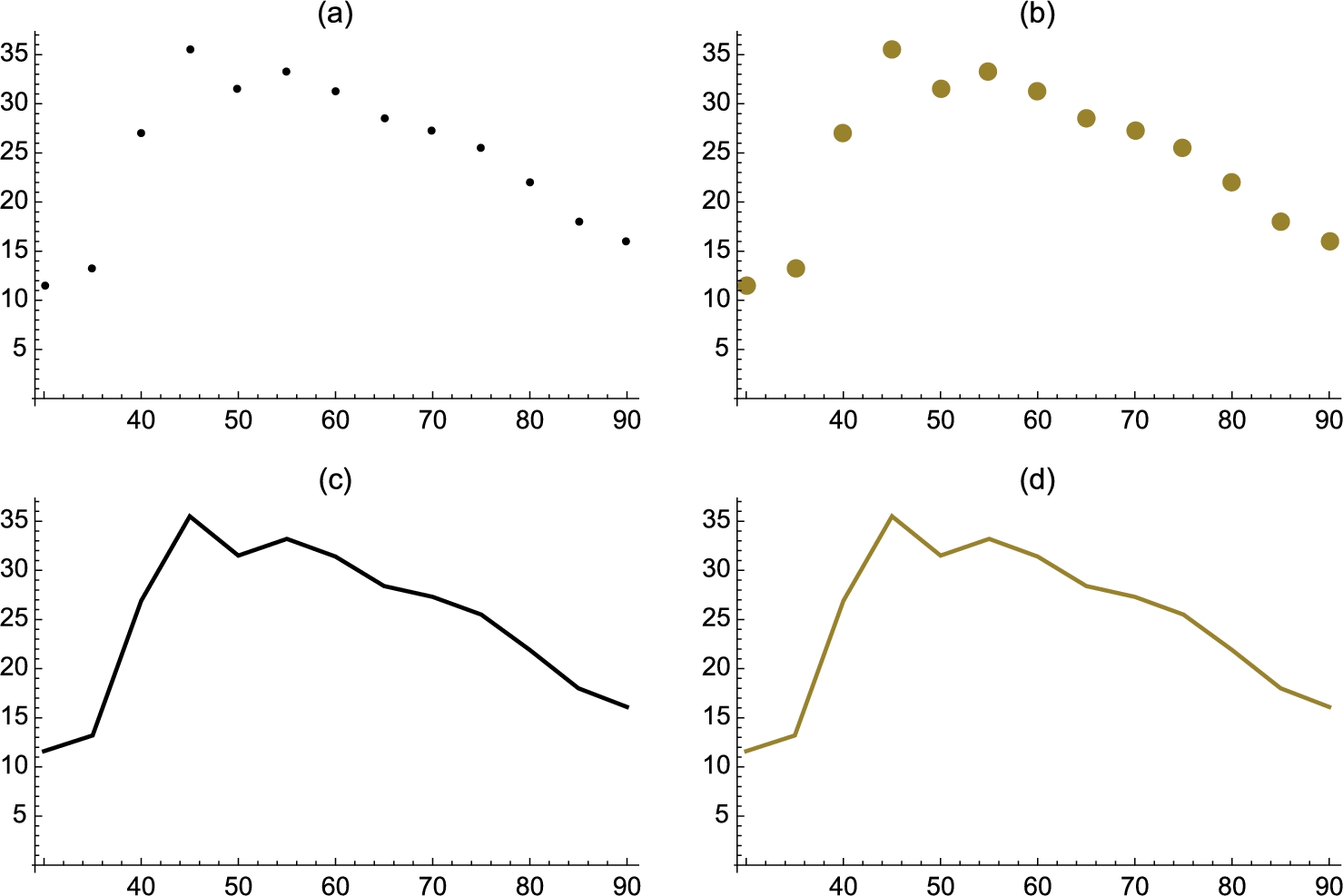
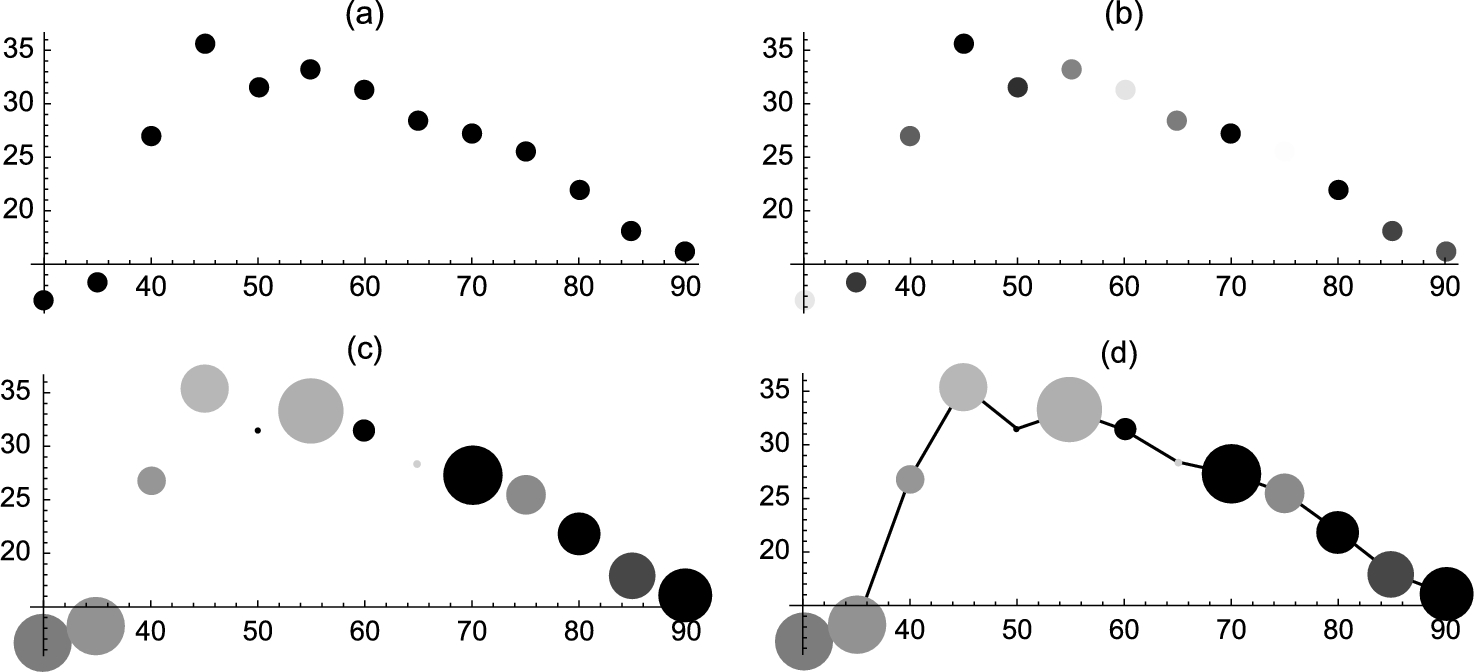
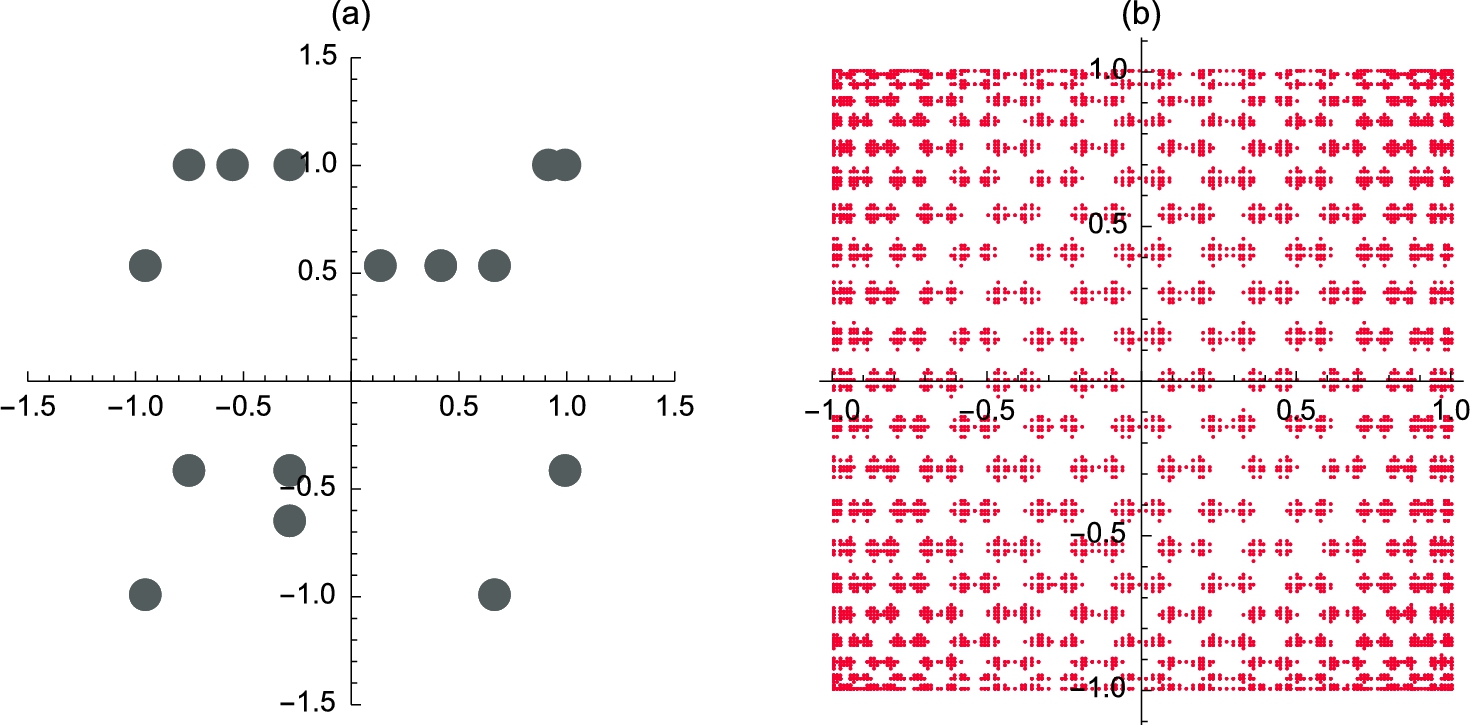
The resulting list of ordered pairs (in Mathematica, {x,y} corresponds to ![]() ). This list of points are then plotted with ListPlot in Fig. 4.6 (a). We also illustrate the use of the PlotStyle, PlotRange, and AspectRatio options in the ListPlot command.
). This list of points are then plotted with ListPlot in Fig. 4.6 (a). We also illustrate the use of the PlotStyle, PlotRange, and AspectRatio options in the ListPlot command.
![]()
![]()
![]()
Increasing the number of points further illustrates the use of Flatten. Entering
![]()
![]()
125
results in a very long nested list. t1 has 125 elements each of which has 125 elements.
An abbreviated version is viewed with Short.
![]()
![]()
After using Flatten, we see with Length and Short that t2 contains 15, 625 points,
![]()
![]()
15625
![]()
![]()
which are plotted with ListPlot in Fig. 4.6 (b).
![]()
![]()
![]()
As indicated earlier, elements of lists can be numbers, ordered pairs, functions, and even other lists. You can also use Mathematica to manipulate lists in numerous ways. Most importantly, the Map function is used to apply a function to a list: Map[f,{x1,x2,...,xn}] returns the list ![]() . We will discuss other operations that can be performed on lists in the following sections.
. We will discuss other operations that can be performed on lists in the following sections.
4.2 Manipulating Lists: More on Part and Map
Often, Mathematica's output is given to us as a list that we need to use in subsequent calculations. Elements of a list are extracted with Part ([[...]]): list[[i]] returns the ith element of list; list[[i,j]] (or list[[i]][[j]]) returns the jth element of the ith element of list, and so on.
Map is a very powerful and useful function: Map[f,list] creates a list consisting of elements obtained by evaluating f for each element of list, provided that each member of list is an element of the domain of f. Note that if f is listable, f[list] produces the same result as Map[f,list].
Lists of functions are graphed with Plot: Plot[listoffunctions,{x,a,b}] graphs the list of functions of x, listoffunctions, for ![]() . If the command is entered as Plot[Tooltip[listoffunctions],{x,a,b}], you can identify the curves in the plot by moving the cursor over the curves in the graphic.
. If the command is entered as Plot[Tooltip[listoffunctions],{x,a,b}], you can identify the curves in the plot by moving the cursor over the curves in the graphic.
4.2.1 More on Graphing Lists; Graphing Lists of Points Using Graphics Primitives
Include the Joined->True option in a ListPlot command to connect successive points with line segments or use ListLinePlot.
Using graphics primitives like Point and Line gives you even more flexibility.
Point[{x,y}] represents a point at ![]() .
.
Line[{{x1,y1},{x2,y2},...,{xn,yn}}]
represents a sequence of points ![]() ,
, ![]() , …,
, …, ![]() connected with line segments. A graphics primitive is declared to be a graphics object with Graphics: Show[Graphics[Point[{x,y}]] displays the point
connected with line segments. A graphics primitive is declared to be a graphics object with Graphics: Show[Graphics[Point[{x,y}]] displays the point ![]() . The advantage of using primitives is that each primitive is affected by the options that directly precede it.
. The advantage of using primitives is that each primitive is affected by the options that directly precede it.
With the speed of today's computers and the power of Mathematica, it is relatively easy now to carry out many calculations that required supercomputers and sophisticated programming experience just a few years ago.
4.2.2 Miscellaneous List Operations
4.2.2.1 Other List Operations
Some other Mathematica commands used with lists include:
1. Append[list,element], which appends element to list;
2. AppendTo[list,element], which appends element to list and names the result list;
3. Drop[list,n], which returns the list obtained by dropping the first n elements from list;
4. Drop[list,-n], which returns the list obtained by dropping the last n elements of list;
5. Drop[list,{n,m}], which returns the list obtained by dropping the nth through mth elements of list;
6. Drop[list,{n}], which returns the list obtained by dropping the nth element of list;
7. Prepend[list,element], which prepends element to list; and
8. PrependTo[list,element], which prepends element to list and names the result list.
4.2.2.2 Alternative Way to Evaluate Lists by Functions
Abbreviations of several of the commands discussed in this section are summarized in the following table.
| @@ Apply | // (function application) | {...} List |
| /@ Map | [[...]] Part |
4.3 Other Applications
We now present several other applications that we find interesting and require the manipulation of lists. The examples also illustrate (and combine) many of the techniques that were demonstrated in the earlier chapters.
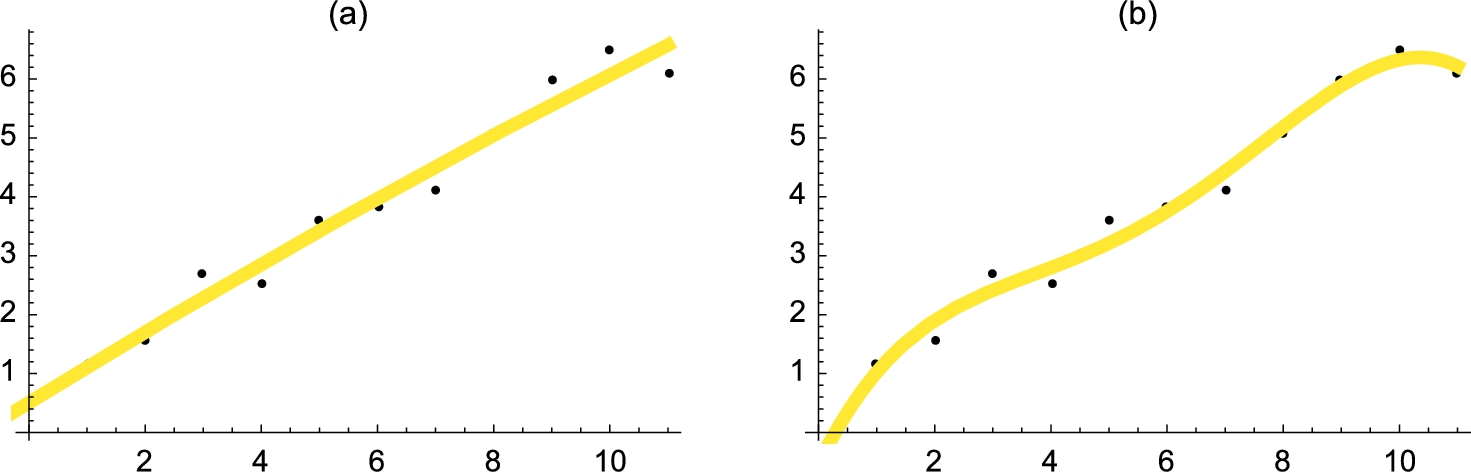
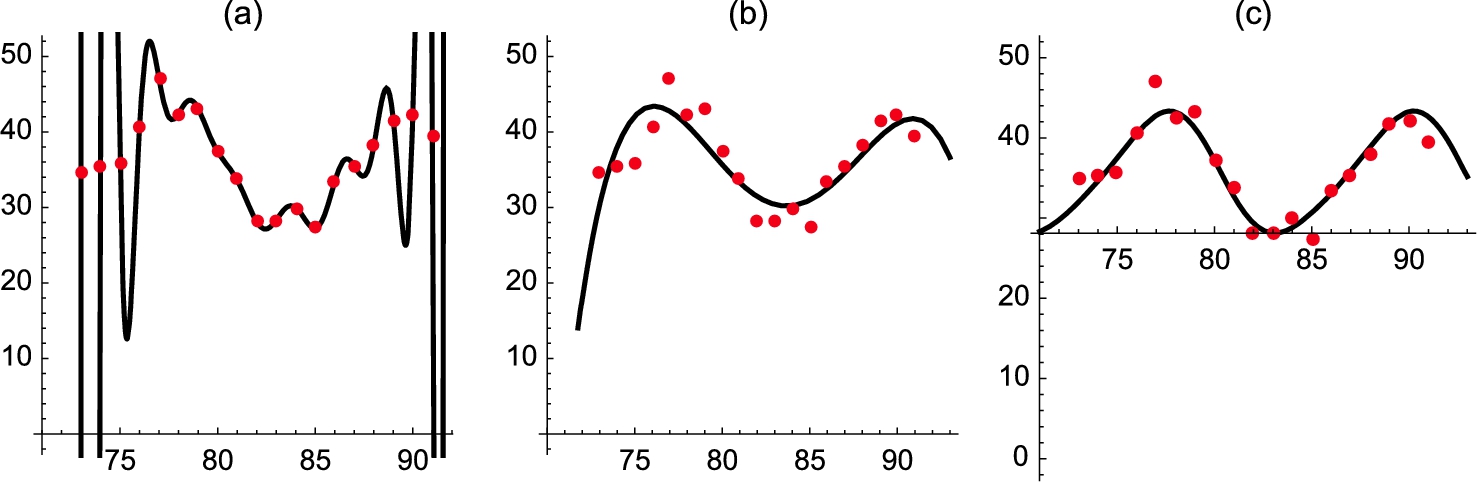
4.3.1 Approximating Lists with Functions
Another interesting application of lists is that of curve-fitting. The commands
1. Fit[data,functionset,variables] fits the list of data points data using the functions in functionset by the method of least-squares. The functions in functionset are functions of the variables listed in variables; and
2. InterpolatingPolynomial[data,x] fits the list of n data points data with an ![]() degree polynomial in the variable x.
degree polynomial in the variable x.
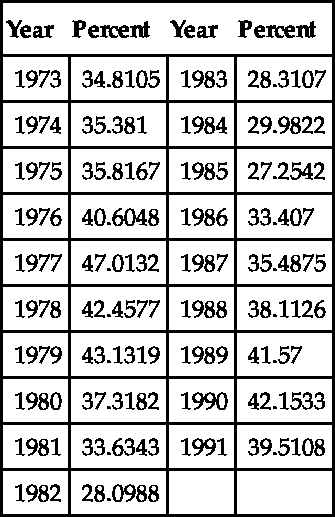
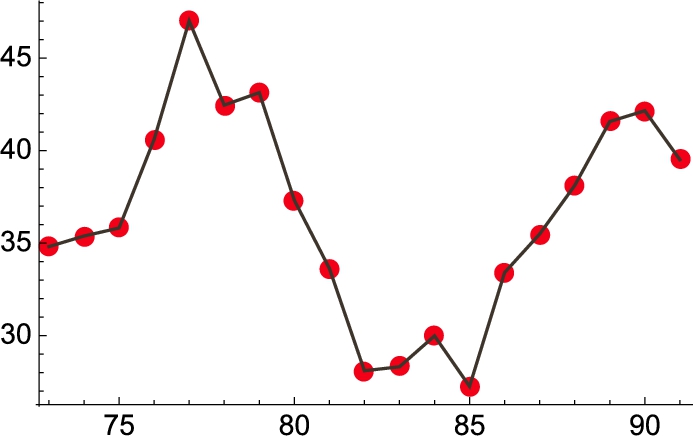
Next, consider a list of data points made up of ordered pairs.
4.3.2 Introduction to Fourier Series
Many problems in applied mathematics are solved through the use of Fourier series. Mathematica assists in the computation of these series in several ways. Suppose that ![]() is defined on
is defined on ![]() . Then the Fourier series for
. Then the Fourier series for ![]() is
is
where
The kth term of the Fourier series (4.1) is
The kth partial sum of the Fourier series (4.1) is
It is a well-known theorem that if ![]() is a periodic function with period 2p and
is a periodic function with period 2p and ![]() is continuous on
is continuous on ![]() except at finitely many points, then at each point x the Fourier series for
except at finitely many points, then at each point x the Fourier series for ![]() converges and
converges and
In fact, if the series ![]() converges, then the Fourier series converges uniformly on
converges, then the Fourier series converges uniformly on ![]() .
.
In the special case that ![]() , FourierSeries, FourierCosSeries, and FourierSinSeries can be used to carry out these calculations. If
, FourierSeries, FourierCosSeries, and FourierSinSeries can be used to carry out these calculations. If ![]() is defined on
is defined on ![]() , FourierSeries[f[x],x,n] finds the first n terms of the Fourier series for
, FourierSeries[f[x],x,n] finds the first n terms of the Fourier series for ![]() , FourierCosSeries[f[x],x,n] finds the first n terms of the Fourier cosine series for
, FourierCosSeries[f[x],x,n] finds the first n terms of the Fourier cosine series for ![]() (even extension), and FourierSinSeries[f[x],x,n] finds the first n terms of the Fourier sin series for
(even extension), and FourierSinSeries[f[x],x,n] finds the first n terms of the Fourier sin series for ![]() (odd extension).
(odd extension).
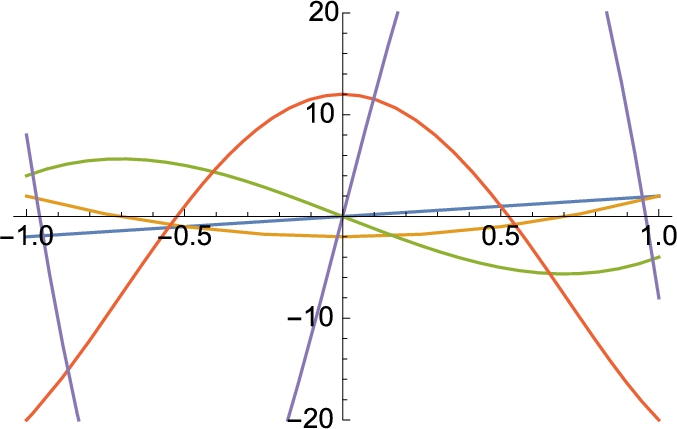
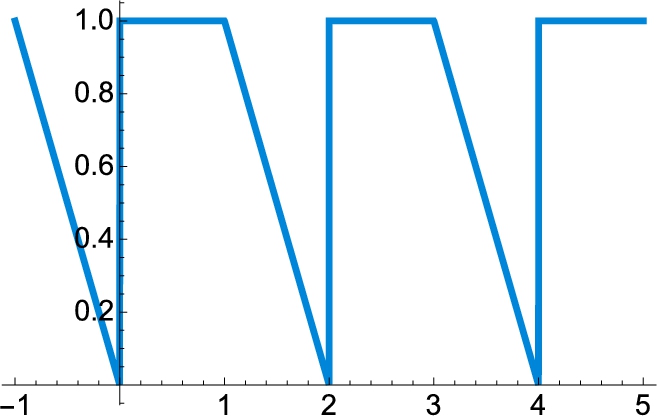
We begin by clearing all prior definitions of f. We then define the piecewise function ![]() and graph
and graph ![]() on the interval
on the interval ![]() in Fig. 4.23.
in Fig. 4.23.
![]()
![]()
![]()
![]()
![]()
![]()
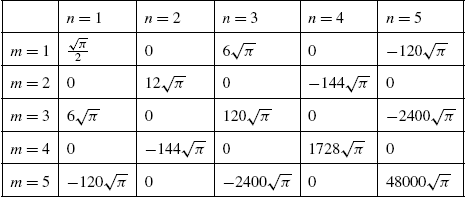
The Fourier series coefficients are computed with the integral formulas in equation (4.2). Executing the following commands defines p to be 1, a[0] to be an approximation of the integral ![]() , a[n] to be an approximation of the integral
, a[n] to be an approximation of the integral ![]() , and b[n] to be an approximation of the integral
, and b[n] to be an approximation of the integral ![]() .
.
![]()
![]()
![]()
0.75
![]()
![]()
A table of the coefficients a[i] and b[i] for ![]() , 2, 3, …, 10 is generated with Table and named coeffs. Several error messages (which are not displayed here for length considerations) are generated because of the discontinuities but the resulting approximations are satisfactory for our purposes. The elements in the first column of the table represent the
, 2, 3, …, 10 is generated with Table and named coeffs. Several error messages (which are not displayed here for length considerations) are generated because of the discontinuities but the resulting approximations are satisfactory for our purposes. The elements in the first column of the table represent the ![]() 's and the second column represents the
's and the second column represents the ![]() 's. Notice how the elements of the table are extracted using double brackets with coeffs.
's. Notice how the elements of the table are extracted using double brackets with coeffs.
![]()
![]()

The first element of the list is extracted with coeffs[[1]].
![]()
![]()
The first element of the second element of coeffs and the second element of the third element of coeffs are extracted with coeffs[[2,1]] and coeffs[[3,2]], respectively.
![]()
![]()
![]()
0.106103
After the coefficients are calculated, the nth partial sum of the Fourier series is obtained with Sum. The kth term of the Fourier series, ![]() , is defined in fs. Hence, the nth partial sum of the series is given by
, is defined in fs. Hence, the nth partial sum of the series is given by
which is defined in fourier using Sum. We illustrate the use of fourier by finding fourier[2,x] and fourier[3,x].
![]()
![]()
![]()
![]()
![]()
![]()
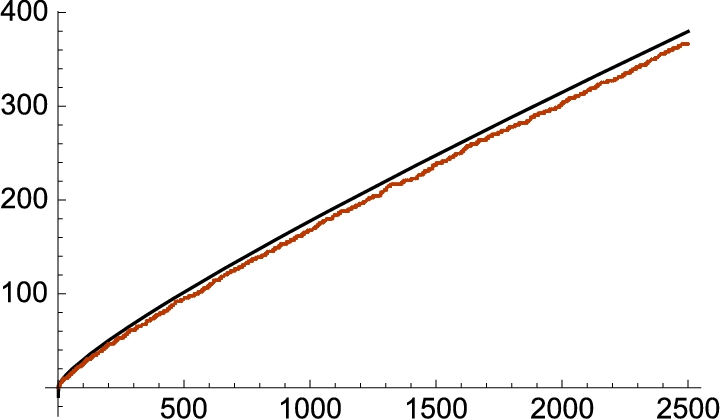
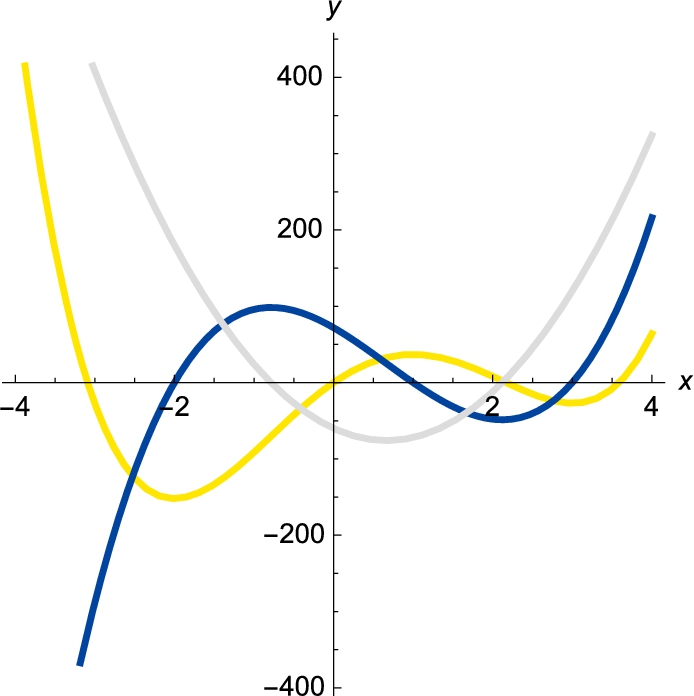
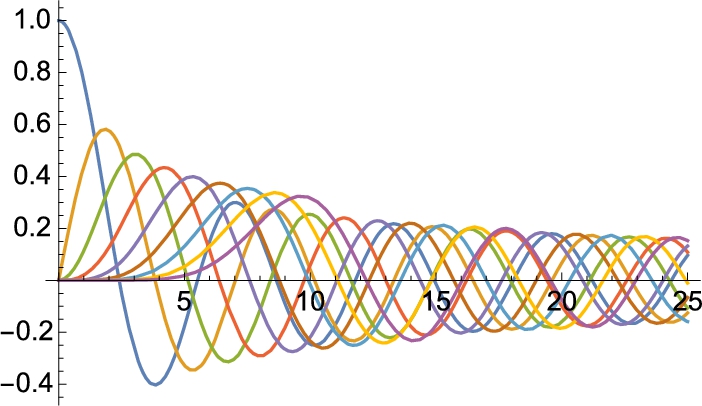
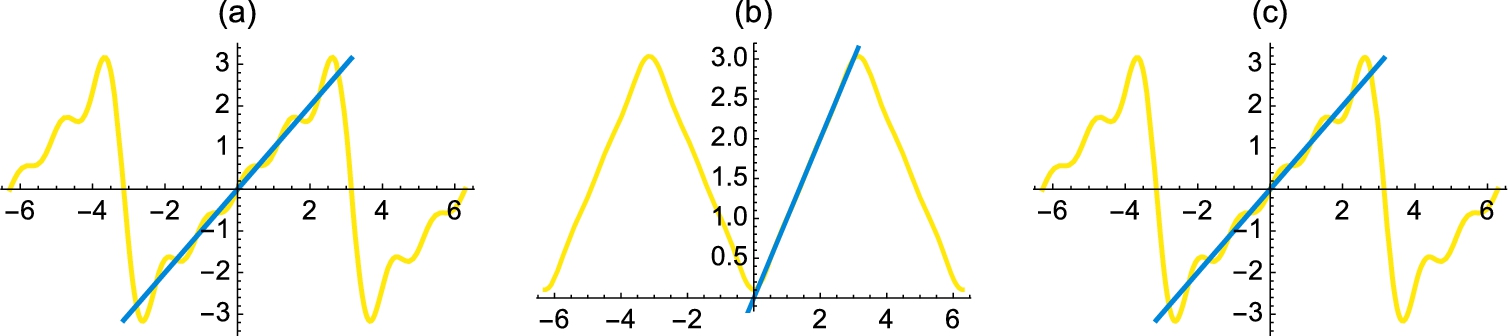
To see how the Fourier series approximates the periodic function, we plot the function simultaneously with the Fourier approximation for ![]() and
and ![]() . The results are displayed together using GraphicsArray in Fig. 4.24.
. The results are displayed together using GraphicsArray in Fig. 4.24.

![]()
![]()
![]()
![]()
![]()
![]()
![]() □
□
Application: The One-Dimensional Heat Equation
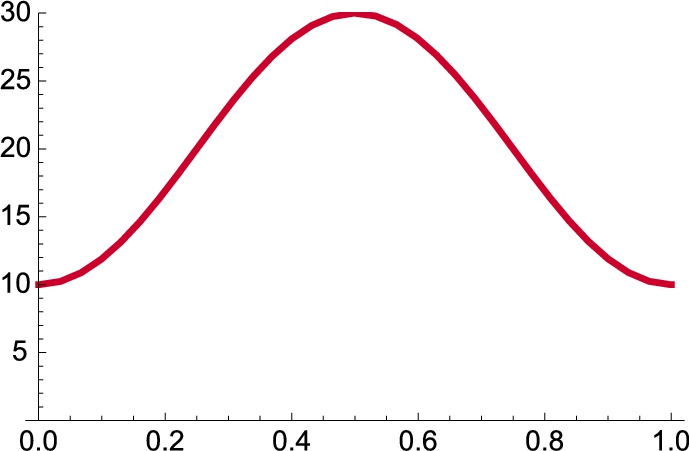
A typical problem in applied mathematics that involves the use of Fourier series is that of the one-dimensional heat equation. The boundary value problem that describes the temperature in a uniform rod with insulated surface is
In this case, the rod has “fixed end temperatures” at ![]() and
and ![]() and
and ![]() is the initial temperature distribution. The solution to the problem is
is the initial temperature distribution. The solution to the problem is
where
and is obtained through separation of variables techniques. The coefficient ![]() in the solution equation (4.6) is the Fourier series coefficient
in the solution equation (4.6) is the Fourier series coefficient ![]() of the function
of the function ![]() , where
, where ![]() is the steady-state temperature.
is the steady-state temperature.
Fourier series and generalized Fourier series arise in too many applications to list. Examples using them illustrate Mathematica's power to manipulate lists, symbolics, and graphics.
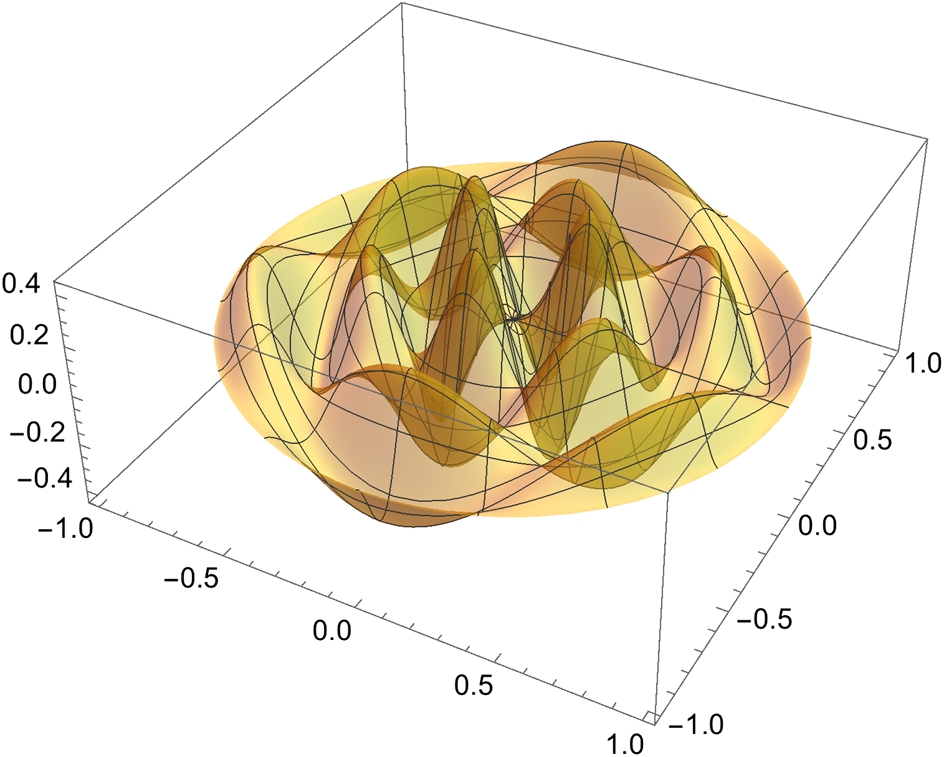
Application: The Wave Equation on a Circular Plate
The vibrations of a circular plate satisfy the equation
where ![]() and
and ![]() is the Laplacian in polar coordinates, which is defined by
is the Laplacian in polar coordinates, which is defined by
Assuming no forcing so that ![]() and
and ![]() , equation (4.7) can be written as
, equation (4.7) can be written as
For a clamped plate, the boundary conditions are ![]() and after much work (see [7]) the normal modes are found to be
and after much work (see [7]) the normal modes are found to be
In equation (4.9), ![]() where
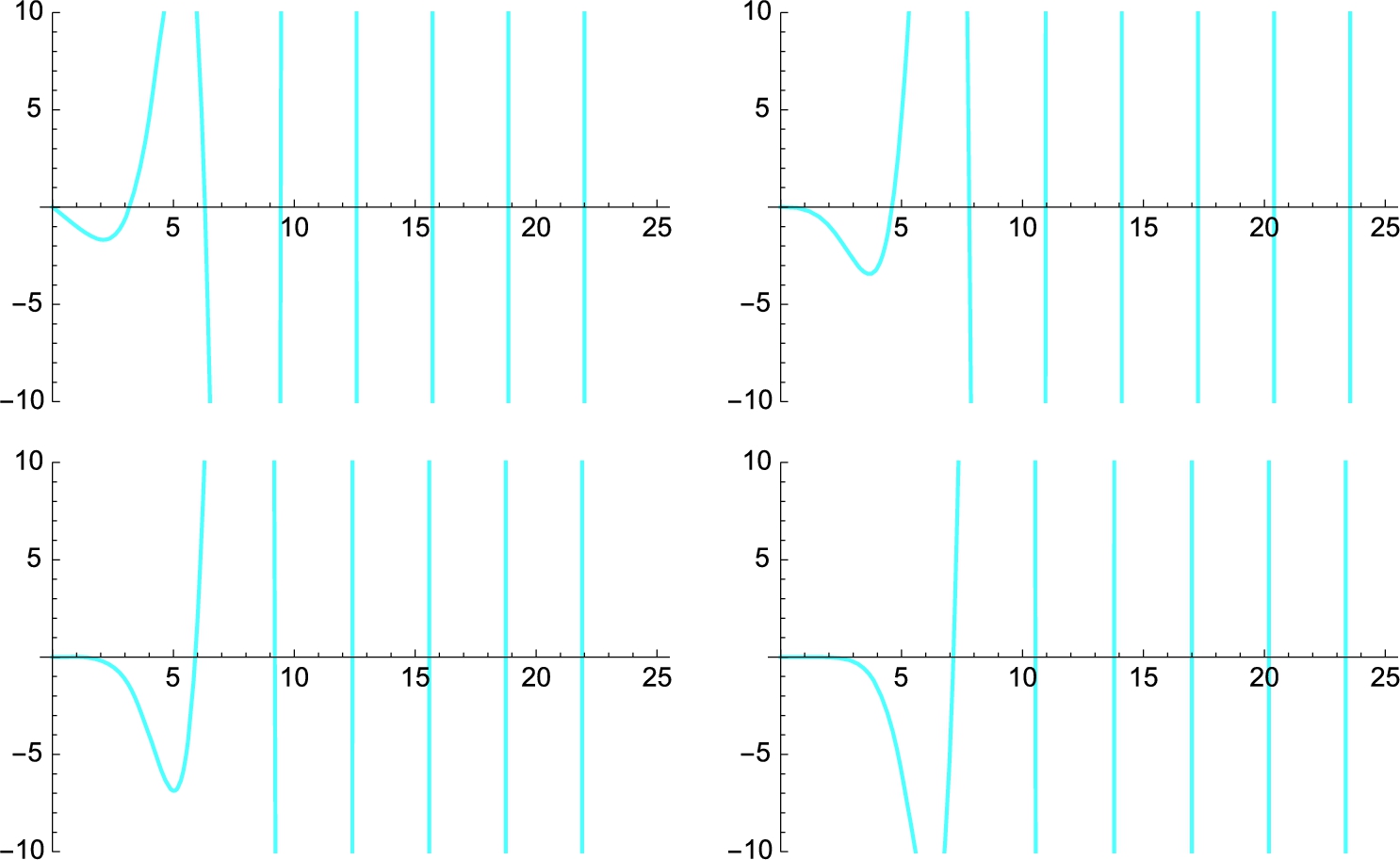
where ![]() is the mth solution of
is the mth solution of
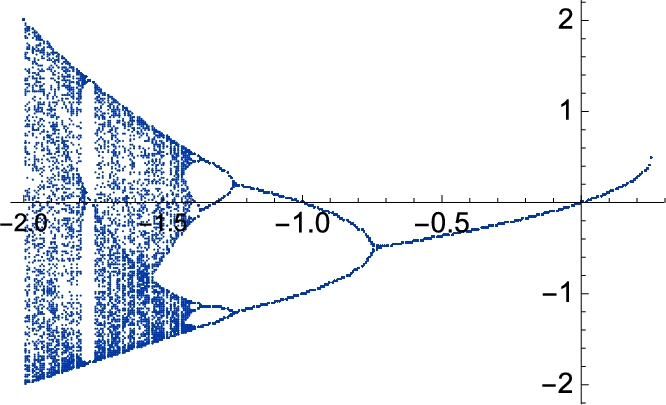
where ![]() is the Bessel function of the first kind of order n and
is the Bessel function of the first kind of order n and ![]() is the modified Bessel function of the first kind of order n, related to
is the modified Bessel function of the first kind of order n, related to ![]() by
by ![]() .
.
The Mathematica command BesselI[n,x] returns ![]() .
.
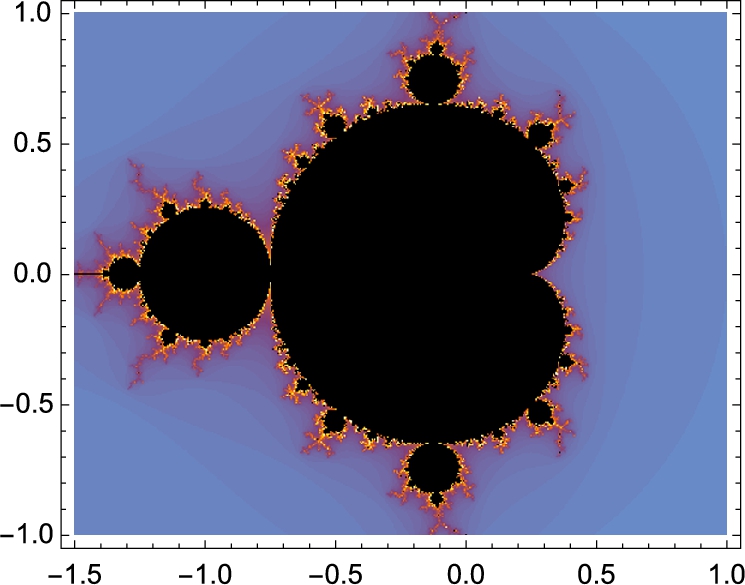
4.3.3 The Mandelbrot Set and Julia Sets
In Examples 4.9, 4.15, and 4.17 we illustrated several techniques for plotting bifurcation diagrams and Julia sets. For investigating Julia sets, try using built-in commands like JuliaSetPlot first. Similarly, for investigating the Mandelbrot set, try MandelbrotSetPlot along with its many options to see if you can obtain your desired results before spending a lot of time writing your own code.
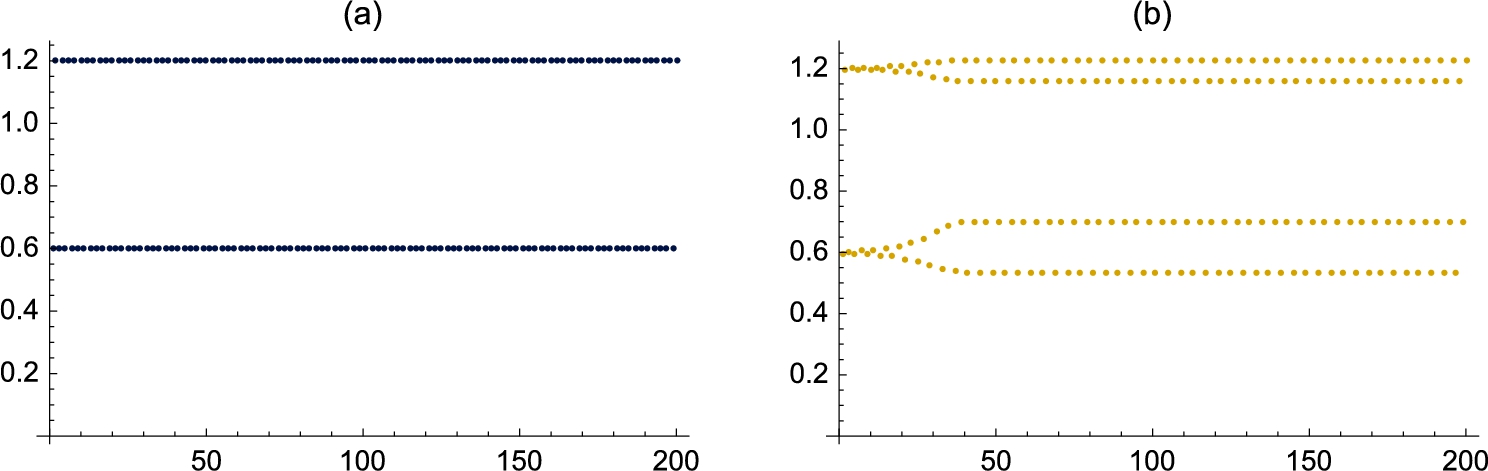
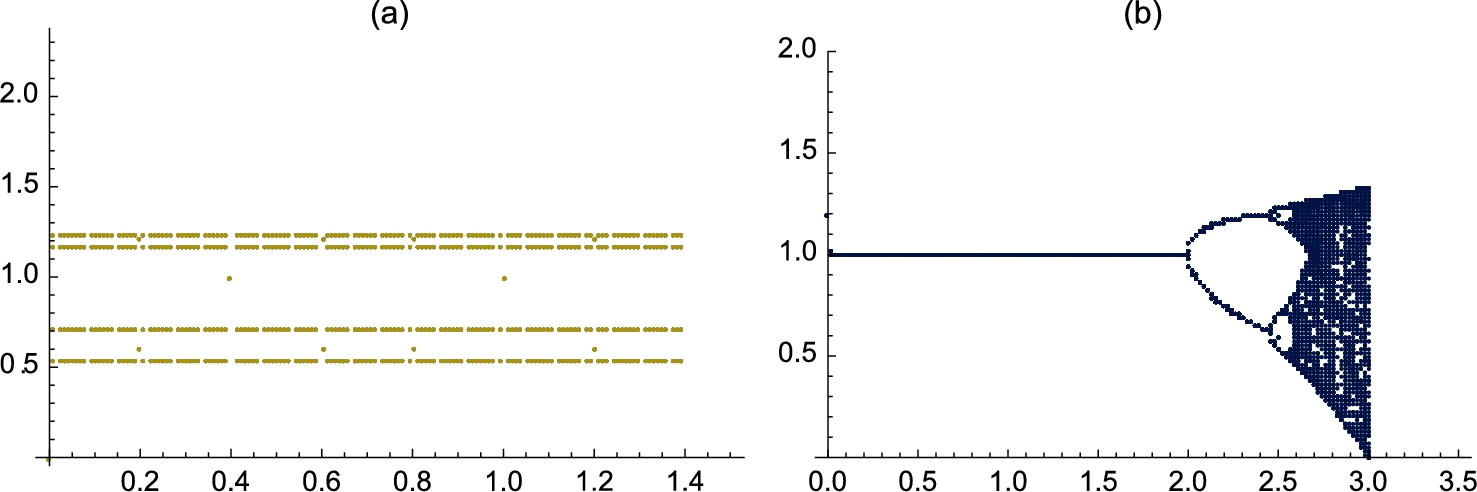
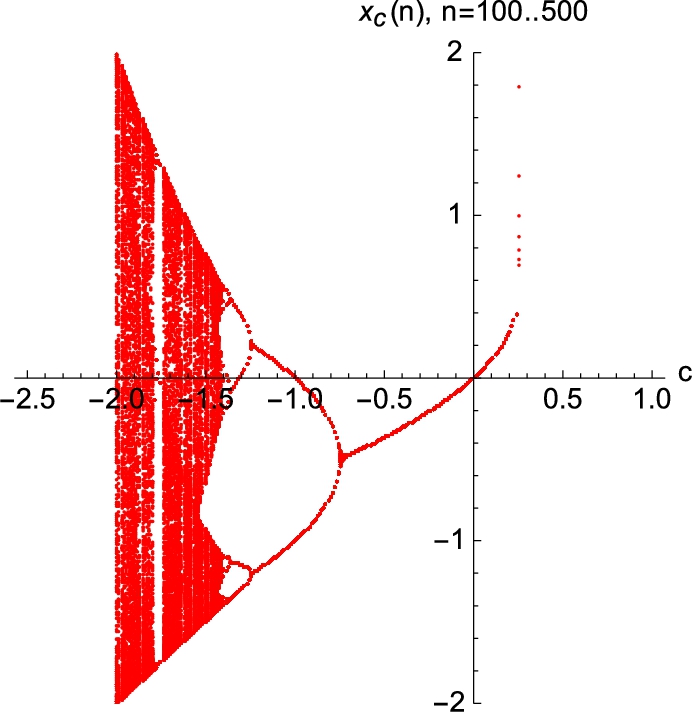
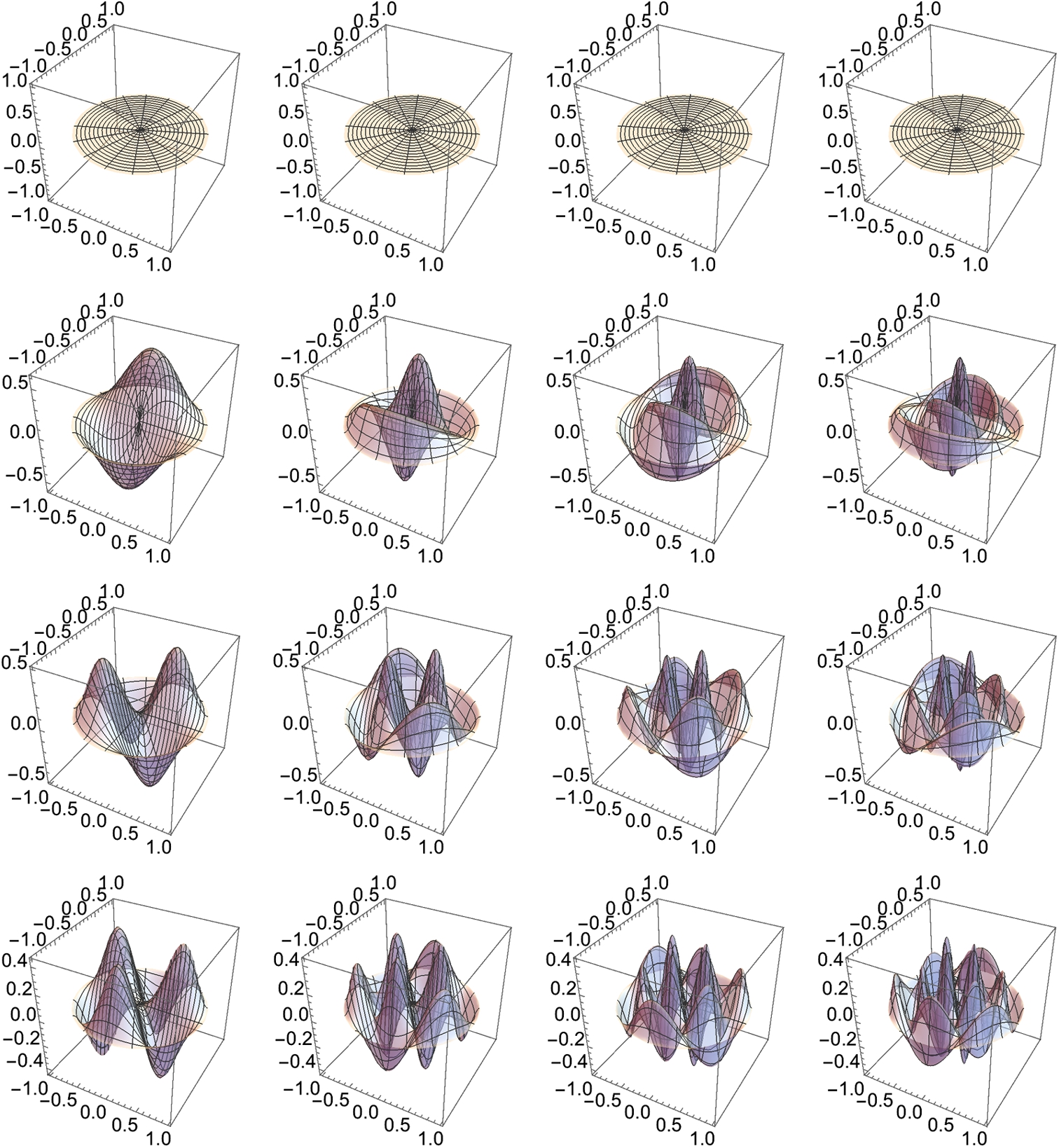
Let ![]() . In Example 4.15, we generated the c-values when plotting the bifurcation diagram of
. In Example 4.15, we generated the c-values when plotting the bifurcation diagram of ![]() . Depending upon how you think and approach various problems, some approaches may be easier to understand than others. With the exception of very serious calculations, the differences in the time needed to carry out the computations may be minimal so we encourage you to follow the approach that you understand.
. Depending upon how you think and approach various problems, some approaches may be easier to understand than others. With the exception of very serious calculations, the differences in the time needed to carry out the computations may be minimal so we encourage you to follow the approach that you understand.
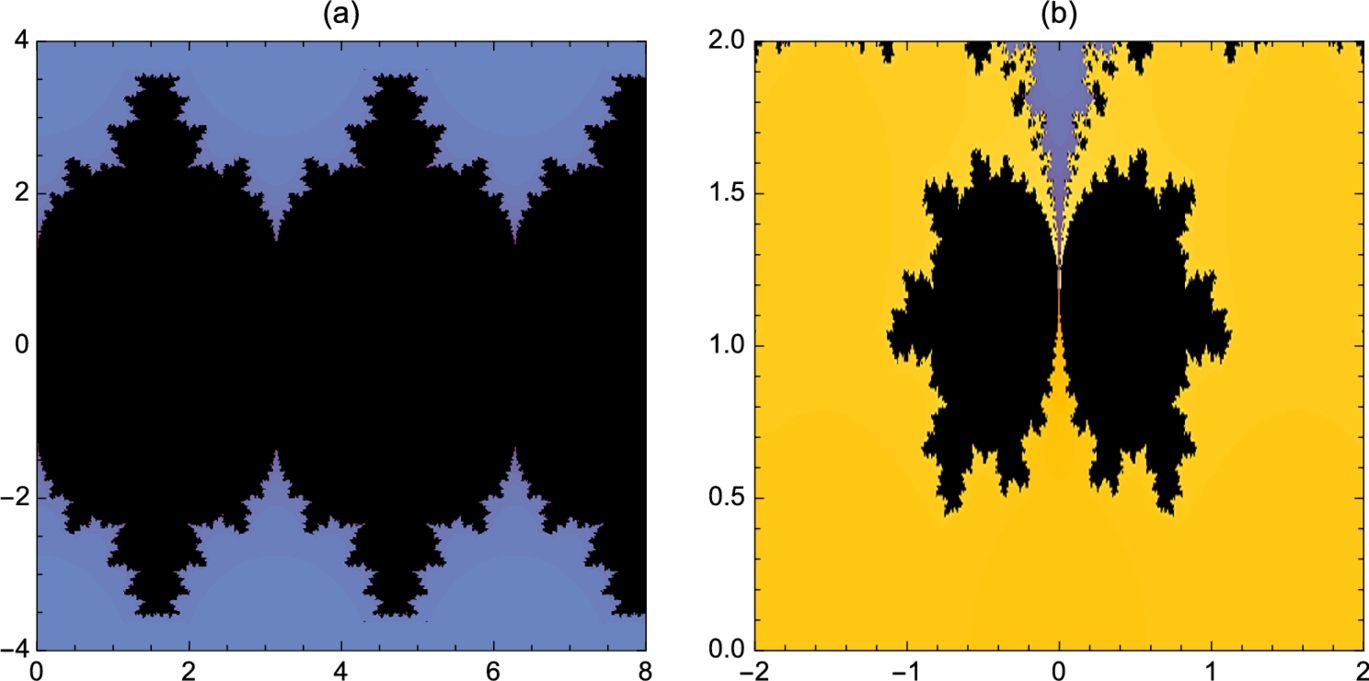
For a given complex number c the Julia set, ![]() , of
, of ![]() is the set of complex numbers,
is the set of complex numbers, ![]() ,
, ![]() real, for which the sequence z,
real, for which the sequence z, ![]() ,
, ![]() , …,
, …, ![]() , …, does not tend to ∞ as
, …, does not tend to ∞ as ![]() :
:
Using a dynamical system, setting ![]() and computing
and computing ![]() for large n can help us determine if z is an element of
for large n can help us determine if z is an element of ![]() . In terms of a composition, computing
. In terms of a composition, computing ![]() for large n can help us determine if z is an element of
for large n can help us determine if z is an element of ![]() .
.
Of course, one can consider functions other than ![]() as well as rearrange the order in which we carry out the computations.
as well as rearrange the order in which we carry out the computations.
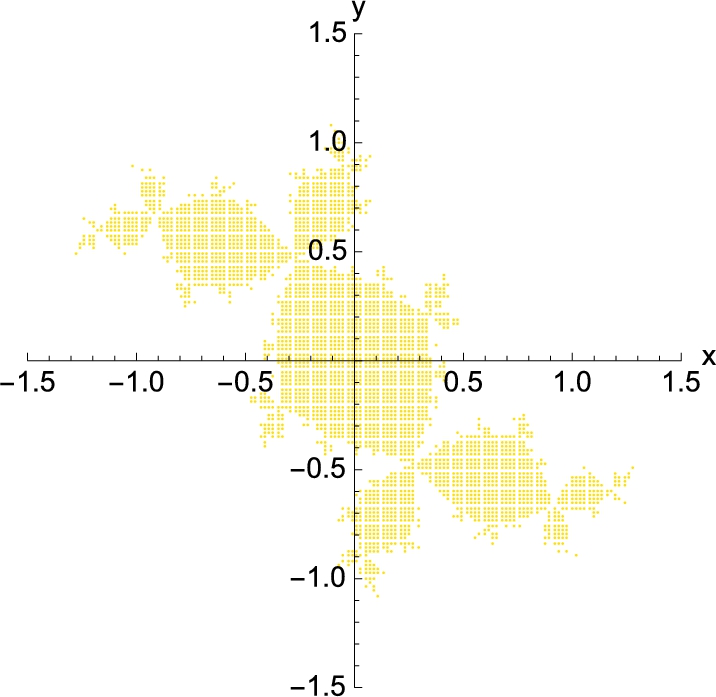
The Mandelbrot set, M, is the set of complex numbers, ![]() ,
, ![]() real, for which the sequence z,
real, for which the sequence z, ![]() ,
, ![]() , …,
, …, ![]() , …, does not tend to ∞ as
, …, does not tend to ∞ as ![]() :
:
Using a dynamical system, setting ![]() and computing
and computing ![]() for large n can help us determine if z is an element of M. In terms of a composition, computing
for large n can help us determine if z is an element of M. In terms of a composition, computing ![]() for large n can help us determine if z is an element of M.
for large n can help us determine if z is an element of M.
The command
MandelbrotSetPlot[{a+bi,c+di}]
plots the Mandelbrot set on the rectangle with lower left corner ![]() and upper right corner
and upper right corner ![]() .
.
The Mandelbrot set can be obtained (or more precisely, approximated) by repeatedly composing ![]() for a grid of z-values and then deleting those for which the values exceed machine precision or other specified “large” value. Those values greater than $MaxNumber result in an Overflow[] message; computations with Overflow[] result in an Indeterminate message.
for a grid of z-values and then deleting those for which the values exceed machine precision or other specified “large” value. Those values greater than $MaxNumber result in an Overflow[] message; computations with Overflow[] result in an Indeterminate message.
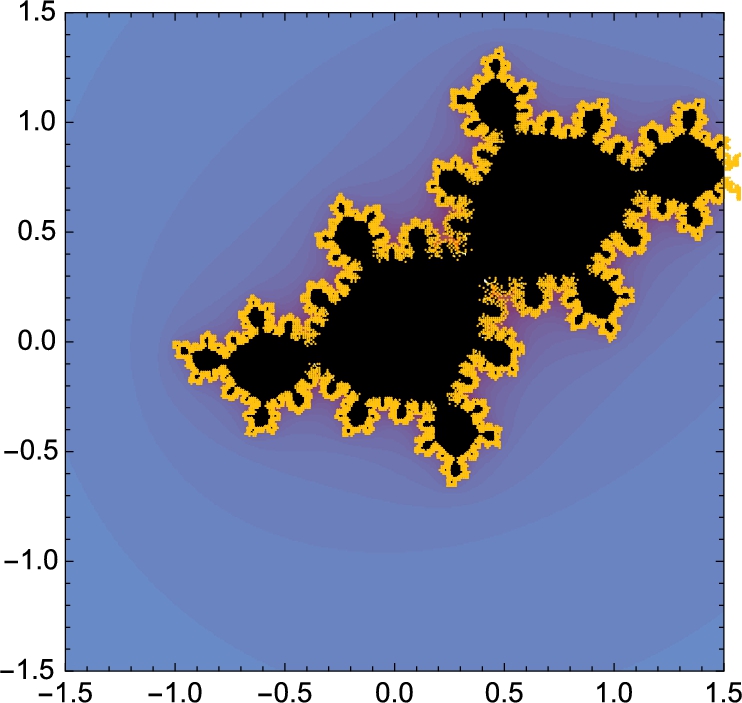
We can generalize by considering exponents other than 2 by letting ![]() . The generalized Mandelbrot set,
. The generalized Mandelbrot set, ![]() , is the set of complex numbers,
, is the set of complex numbers, ![]() ,
, ![]() real, for which the sequence z,
real, for which the sequence z, ![]() ,
, ![]() , …,
, …, ![]() , …, does not tend to ∞ as
, …, does not tend to ∞ as ![]() :
:
Using a dynamical system, setting ![]() and computing
and computing ![]() for large n can help us determine if z is an element of
for large n can help us determine if z is an element of ![]() . In terms of a composition, computing
. In terms of a composition, computing ![]() for large n can help us determine if z is an element of
for large n can help us determine if z is an element of ![]() .
.
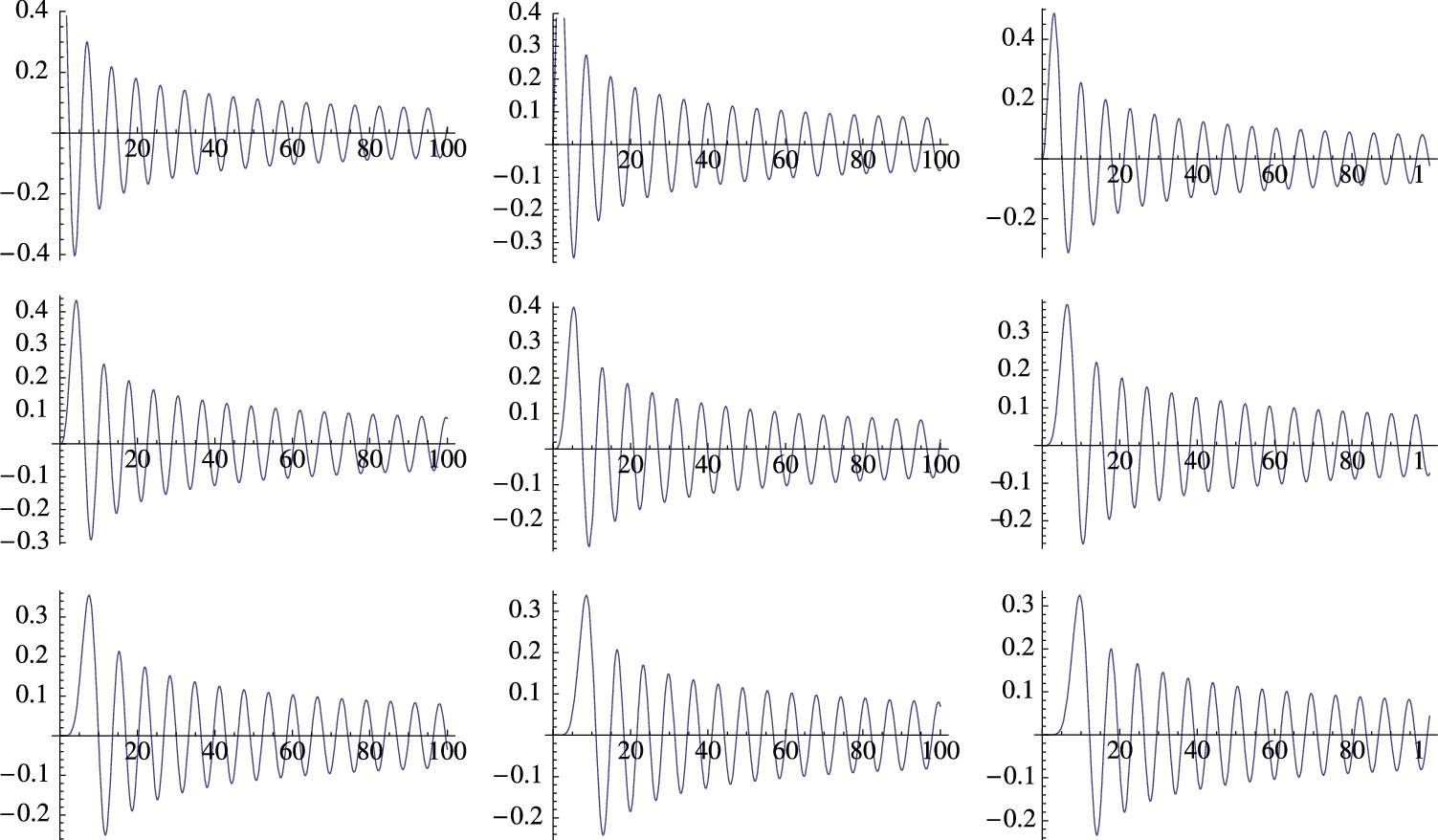
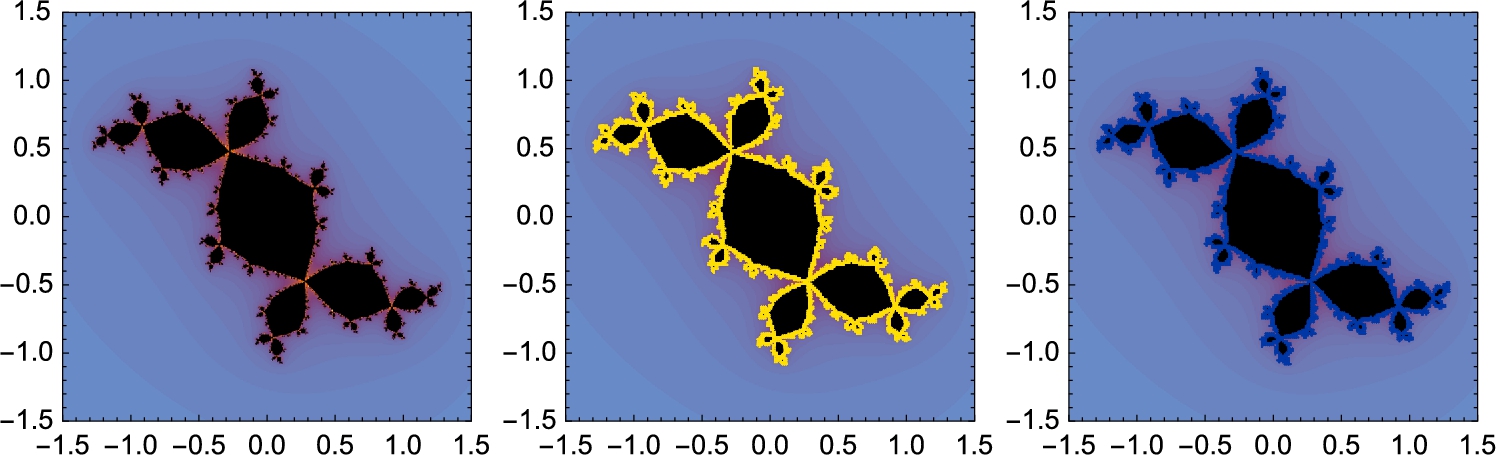
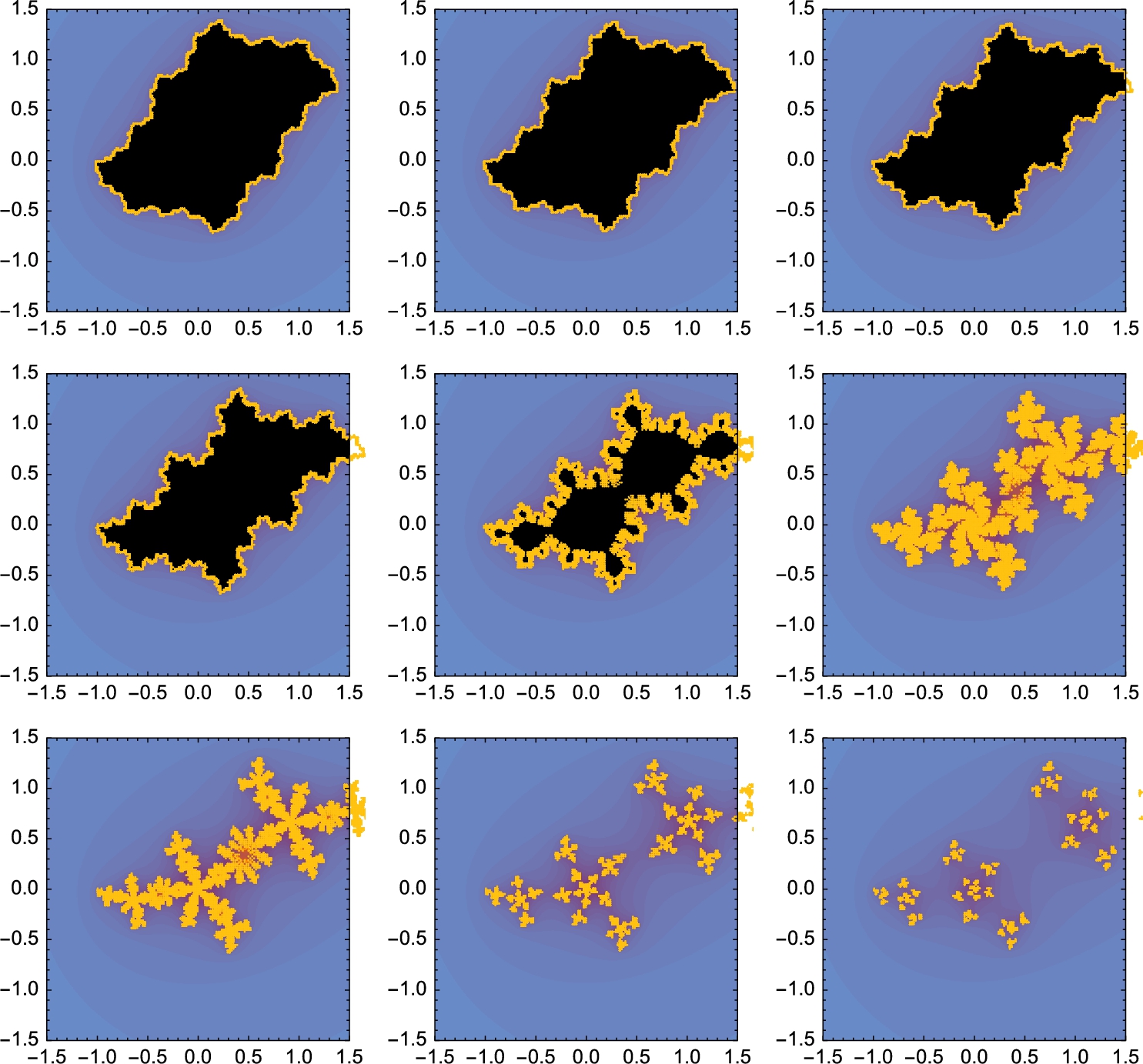
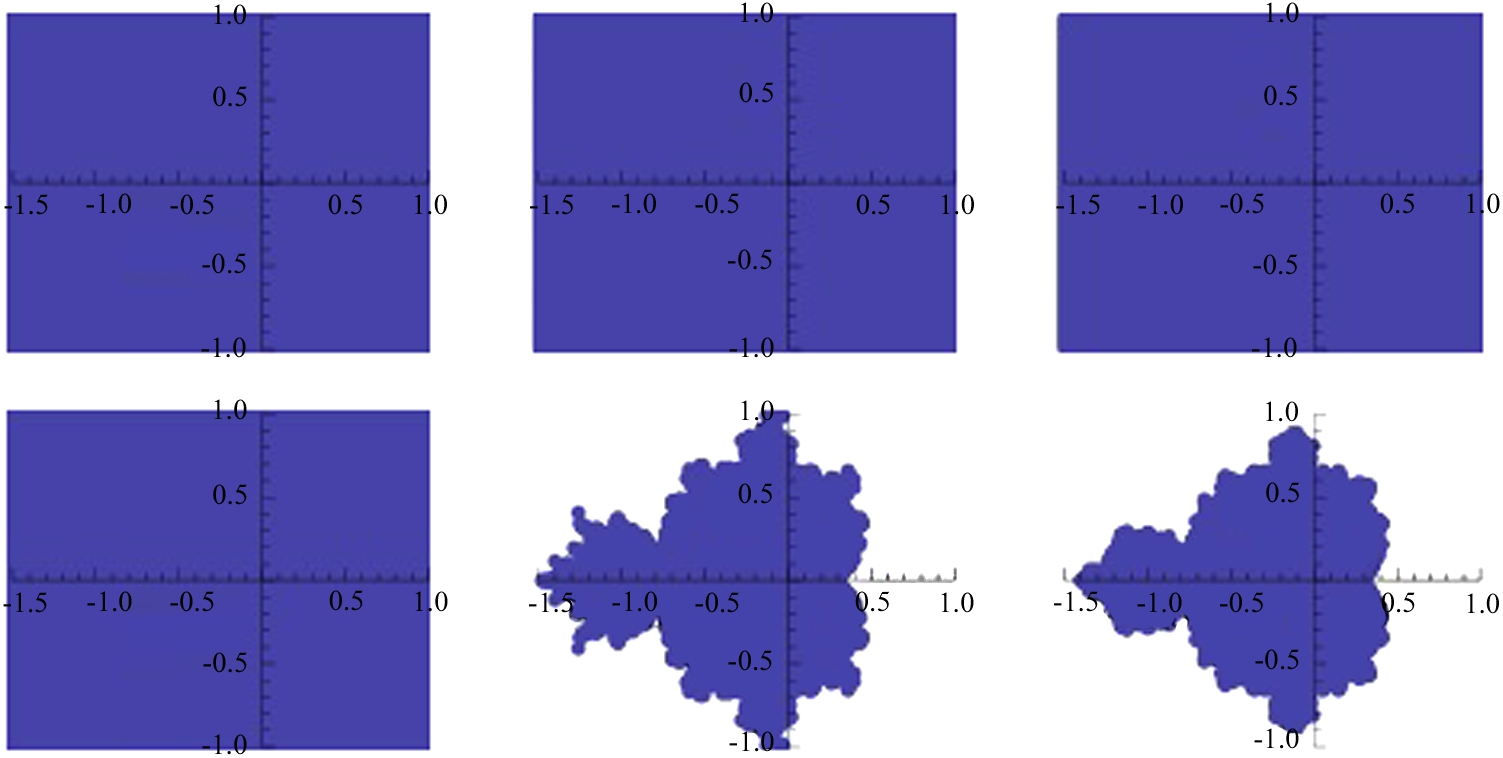
Throughout these examples, we have typically computed the iteration ![]() for “large” n like values of n between 100 and 200. To indicate why we have selected those values of n, we revisit the Mandelbrot set plotted in Example 4.28.
for “large” n like values of n between 100 and 200. To indicate why we have selected those values of n, we revisit the Mandelbrot set plotted in Example 4.28.
The examples like the ones illustrated here indicate that similar results could have been accomplished using far smaller values of n than ![]() or
or ![]() . With fast machines, the differences in the time needed to perform the calculations is minimal;
. With fast machines, the differences in the time needed to perform the calculations is minimal; ![]() and
and ![]() appear to be a “safe” large value of n for well-studied examples like these.
appear to be a “safe” large value of n for well-studied examples like these.