3 
Variations on an Arithmetic Theme

In this chapter we introduce the extremely powerful but potentially dangerous flexibility technique of predicate-dispatched generic procedures. We start out in the relatively calm waters of arithmetic, modulating the meanings of the operator symbols.

We first generalize arithmetic to deal with symbolic algebraic expressions, and then to functions. We use a combinator system where the elements being combined are packages of arithmetic operations.

But soon we want even more flexibility. So we invent dynamically extensible generic procedures, where the applicability of a handler is determined by predicates on the supplied arguments. This is very powerful and great fun. Using generic procedures to extend the arithmetic to operate on “differential objects,” we get automatic differentiation with very little work!

Predicate dispatch is pretty expensive, so we investigate ways to ameliorate that expense. In the process we invent a kind of tagged data, where a tag is just a way of memoizing the value of a predicate. To finish the chapter we demonstrate the power of generic procedures with the design of a simple, but easy to elaborate, adventure game.

3.1 Combining arithmetics

Suppose we have a program that computes some useful numerical results. It depends on the meanings of the arithmetic operators that are referenced by the program text. These operators can be extended to work on things other than the numbers that were expected by the program. With these extensions the program may do useful things that were not anticipated when the program was written. A common pattern is a program that takes numerical weights and other arguments and makes a linear combination by adding up the weighted arguments. If the addition and multiplication operators are extended to operate on tuples of numbers as well as on the original numbers, the program can make linear combinations of vectors. This kind of extension can work because the set of arithmetic operators is a well-specified and coherent entity. Extensions of numerical programs with more powerful arithmetic can work, unless the new quantities do not obey the constraints that were assumed by the author of the program. For example, multiplication of matrices does not commute, so extension of a numerical program that depends on the fact that multiplication of numbers is commutative will not work. We will ignore this problem for now.

3.1.1 A simple ODE integrator

A differential equation is a description of how the state of a system changes as an independent variable is varied; this is called the evolution of the system's state.¹ We can approximate the evolution of a system's state by sampling the independent variable at various points and approximating the state change at each sample point. This process of approximation is called numerical integration.

Let's investigate the generality of numerical operations in a numerical integrator for second-order ordinary differential equations. We will use an integrator that samples its independent variable at uniform intervals, each of which is called a step. Consider this equation:

(3.1)

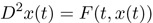
The essential idea is that a discrete approximation to the second derivative of the unknown function is a linear combination of second derivatives of some previous steps. The particular coefficients are chosen by numerical analysis and are not of interest here.

(3.2)

where h is the step size and A is the array of magic coefficients.

For example, Stormer's integrator of order 2 is

(3.3)

To use this to compute the future of x we write a program. The procedure returned by stormer-2 is an integrator for a given function and step size, that given a history of values of x, produces an estimate of the value of x at the next time, x(t + h). The procedures t and x extract previous times and values of x from the history: (x 0 history) returns x(t), (x 1 history) returns x(t − h), and (x 2 history) returns x(t − 2h). We access the time of a step from a history similarly: (t 1 history) returns t − h.

(define (stormer-2 F h)
  (lambda (history)
    (+ (* 2 (x 0 history))
       (* -1 (x 1 history))
       (* (/ (expt h 2) 12)
          (+ (* 13 (F (t 0 history) (x 0 history)))
             (* -2 (F (t 1 history) (x 1 history)))
             (F (t 2 history) (x 2 history)))))))

The procedure returned by stepper takes a history and returns a new history advanced by h for the given integrator.

(define (stepper h integrator)
  (lambda (history)
    (extend-history (+ (t 0 history) h)
                    (integrator history)
                    history)))

The procedure stepper is used in the procedure evolver to produce a procedure step that will advance a history by one step. The step procedure is used in the procedure evolve that advances the history by a given number of steps of size h. We explicitly use specialized integer arithmetic here (the procedures named n:> and n:-) for counting steps. This will allow us to use different types of arithmetic for everything else without affecting simple counting.²

(define (evolver F h make-integrator)
  (let ((integrator (make-integrator F h)))
    (let ((step (stepper h integrator)))
      (define (evolve history n-steps)
        (if (n:> n-steps 0)
            (evolve (step history) (n:- n-steps 1))
            history))
      evolve)))

A second-order differential equation like equation 3.1 generally needs two initial conditions to determine a unique trajectory: x(t₀) and x(t₀) are sufficient to get x(t) for all t. But the Stormer multistep integrator we are using requires three history values, x(t₀), x(t₀ − h), and x(t₀ − 2h), to compute the next value x(t₀ + h). So to evolve the trajectory with this integrator we must start with an initial history that has three past values of x.

Consider the very simple differential equation:

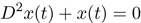
In the form shown in equation 3.1 the right-hand side is:

(define (F t x) (- x))

Because all the solutions of this equation are linear combinations of sinusoids, we can get the simple sine function by initializing the history with three values of the sine function:

(define numeric-s0
  (make-initial-history 0 .01 (sin 0) (sin -.01) (sin -.02)))

where the procedure make-initial-history takes the following arguments:

(make-initial-history t h x(t) x(t − h) x(t − 2h))

Using Scheme's built-in arithmetic, after 100 steps of size h = .01 we get a good approximation to sin(1):

(x 0 ((evolver F .01 stormer-2) numeric-s0 100))
.8414709493275624
(sin 1)
.8414709848078965

3.1.2 Modulating arithmetic operators

Let's consider the possibility of modulating what is meant by addition, multiplication, etc., for new data types unimagined by our example's programmer. Suppose we change our arithmetic operators to operate on and produce symbolic expressions rather than numerical values. This can be useful in debugging purely numerical calculations, because if we supply symbolic arguments we can examine the resulting symbolic expressions to make sure that the program is calculating what we intend it to. This can also be the basis of a partial evaluator for optimization of numerical programs.

Here is one way to accomplish this goal. We introduce the idea of an arithmetic package. An arithmetic package, or just arithmetic, is a map from operator names to their operations (implementations). We can install an arithmetic in the user's read-eval-print environment to replace the default bindings of the operators named in the arithmetic with the arithmetic's implementations.

The procedure make-arithmetic-1 generates a new arithmetic package. It takes a name for the new arithmetic, and an operation-generator procedure that given an operator name constructs an operation, here a handler procedure, for that operator. The procedure make-arithmetic-1 calls the operation-generator procedure with each arithmetic operator, accumulating the results into a new arithmetic package. For symbolic arithmetic, the operation is implemented as a procedure that creates a symbolic expression by consing the operator name onto the list of its arguments.

(define symbolic-arithmetic-1
  (make-arithmetic-1 'symbolic
    (lambda (operator)
      (lambda args (cons operator args)))))

To use this newly defined arithmetic, we install it. This redefines the arithmetic operators to use this arithmetic:³

(install-arithmetic! symbolic-arithmetic-1)

install-arithmetic! changes the values of the user's global variables that are the names of the arithmetic operators defined in the arithmetic to their values in that arithmetic. For example, after this install:

(+ ’a ’b)
(+ a b)

(+ 1 2)
(+ 1 2)

Now we can observe the result of taking one step of the Stormer evolution:^{4 5}

(pp (x 0
       ((evolver F ’h stormer-2)
        (make-initial-history 't ’h ’xt ’xt-h ’xt-2h)
        1)))
(+ (+ (* 2 xt) (* -1 xt-h))
   (* (/ (expt h 2) 12)
      (+ (+ (* 13 (negate xt)) (* -2 (negate xt-h)))
         (negate xt-2h))))

We could easily produce simplified expressions by replacing the cons in symbolic-arithmetic-1 with an algebraic simplifier, and then we would have a symbolic manipulator. (We will explore algebraic simplification in section 4.2.)

This transformation was ridiculously easy, and yet our original design didn't make any provisions for symbolic computation. We could just as easily add support for vector arithmetic, matrix arithmetic, etc.

Problems with redefining operators

The ability to redefine operators after the fact gives both extreme flexibility and ways to make whole new classes of bugs! (We anticipated such a problem in the evolver procedure and avoided it by using the special arithmetic operators n:> and n:- for counting steps.)

There are more subtle problems. A program that depends on the exactness of operations on integers may not work correctly for inexact floating-point numbers. This is exactly the risk that comes with the evolution of biological or technological systems— some mutations will be fatal! On the other hand, some mutations will be extremely valuable. But that risk must be balanced against the cost of narrow and brittle construction.

Indeed, it is probably impossible to prove very much about a program when the primitive procedures can be redefined, except that it will work when restricted to the types it was defined for. This is an easy but dangerous path for generalization.

3.1.3 Combining arithmetics

The symbolic arithmetic cannot do numerical calculation, so we have broken our integration example by replacing the operator definitions. We really want an operator's action to depend on its arguments: for example, numerical addition for (+ 1 2) but building a list for (+ ’a ’b). Thus the arithmetic packages must be able to determine which handler is appropriate for the arguments tendered.

An improved arithmetic abstraction

By annotating each operation with an applicability specification, often shortened to just an applicability, we can combine different kinds of arithmetic. For example, we can combine symbolic and numeric arithmetic so that a combined operation can determine which implementation is appropriate for its arguments.

An applicability specification is just a list of cases, each of which is a list of predicates, such as number? or symbolic?. A procedure is deemed applicable to a sequence of arguments if the arguments satisfy one of the cases—that is, if each predicate in the case is true of the corresponding argument. For example, for binary arithmetic operators, we would like the numeric operations to be applicable in just the case (number? number?) and the symbolic operations to be applicable in these cases: ((number? symbolic?) (symbolic? number?) (symbolic? symbolic?)).

We use make-operation to make an operation that includes an applicability for the handler procedure, like this:

(define (make-operation operator applicability procedure)
  (list ’operation operator applicability procedure))

It is then possible to get the applicability for an operation:

(define (operation-applicability operation)
  (caddr operation))

We introduce an abstraction for writing applicability information for an operation. The procedure all-args takes two arguments, the first being the number of arguments that the operation accepts (its arity, as on page 26), and the second being a predicate that must be true of each argument. It returns an applicability specification that can be used to determine if the operation is applicable to the arguments supplied to it. In a numeric arithmetic, each operation takes numbers for each of its arguments.

Using all-args we can implement an operation constructor for the simplest operations:

(define (simple-operation operator predicate procedure) 
  (make-operation operator
                  (all-args (operator-arity operator)
                            predicate)
                  procedure))

We will also find it useful to have a domain predicate that is true for the objects (such as functions or matrices) that a given arithmetic's operations take as arguments—for example, number? for numeric arithmetic. To support this more elaborate idea we will create a constructor make-arithmetic for arithmetic packages. The procedure make-arithmetic is like make-arithmetic-1 (see page 71) but has additional arguments.

(make-arithmetic  name
                  domain-predicate
                  base-arithmetic-packages
                  map-of-constant-name-to-constant
                  map-of-operator-name-to-operation)

An arithmetic package produced by make-arithmetic has a name that is useful for debugging. It has the domain predicate noted above. It has a list of arithmetic packages, called the bases, that the new arithmetic will be built from. In addition, the arithmetic will contain a set of named constants, and a set of operators along with their corresponding operations. The final two arguments are used to generate these sets.

An example of the use of a base arithmetic is vectors. A vector is represented as an ordered sequence of coordinates: consequently an arithmetic on vectors is defined in terms of arithmetic on its coordinates. So the base arithmetic for a vector arithmetic is the appropriate arithmetic for the vector's coordinates. A vector arithmetic with numeric coordinates will use a numeric arithmetic as its base, while a vector arithmetic with symbolic coordinates will use a symbolic arithmetic as its base. For brevity, we often use the term “over” to specify the base, as in “vectors over numbers” or “vectors over symbols.”

The base arithmetics also determine the constants and operators that the derived arithmetic will define. The defined constants will be the union of the constants defined by the bases, and the defined operators will be the union of their operators. If there are no bases, then standard sets of constant and operator names will be defined.

Using these new capabilities, we can define a numeric arithmetic with applicability information. Since numeric arithmetic is built on the Scheme substrate, the appropriate handler for the operator for Scheme number arguments is just the value of the operator symbol for the Scheme implementation. Also, certain symbols, such as the identity constants for addition and multiplication, are specially mapped.

(define numeric-arithmetic
  (make-arithmetic ’numeric number? ’()
    (lambda (name)                ;constant generator
      (case name
        ((additive-identity) 0)
        ((multiplicative-identity) 1)
        (else (default-object))))
    (lambda (operator)            ;operation generator
      (simple-operation operator number?
         (get-implementation-value
            (operator->procedure-name operator))))))

The last two lines of this code find the procedure defined by the Scheme implementation that is named by the operator.⁶

We can similarly write the symbolic-extender constructor to construct a symbolic arithmetic based on a given arithmetic.

(define (symbolic-extender base-arithmetic)
  (make-arithmetic ’symbolic symbolic? (list base-arithmetic)
    (lambda (name base-constant)        ;constant generator
      base-constant)
    (let ((base-predicate
           (arithmetic-domain-predicate base-arithmetic)))
      (lambda (operator base-operation) ;operation generator
        (make-operation operator
                        (any-arg (operator-arity operator)
                                 symbolic?
                                 base-predicate)
                        (lambda args
                          (cons operator args)))))))

One difference between this and the numeric arithmetic is that the symbolic arithmetic is applicable whenever any argument is a symbolic expression.⁷ This is indicated by the use of any-arg rather than all-args; any-arg matches if at least one of the arguments satisfies the predicate passed as the second argument, and all the other arguments satisfy the predicate passed as the third argument.⁸ Also notice that this symbolic arithmetic is based on a provided base-arithmetic, which will allow us to build a variety of such arithmetics.

Applicability specifications are not used as guards on the handlers: they do not prevent the application of a handler to the wrong arguments. The applicability specifications are used only to distinguish among the possible operations for an operator when arithmetics are combined, as explained below.

A combinator for arithmetics

The symbolic and numeric arithmetics are of the same shape, by construction. The symbolic-extender procedure produces an arithmetic with the same operators as the base arithmetic it is given. Making a combinator language for building composite arithmetics from parts might be a good approach.

The procedure add-arithmetics, below, is a combinator for arithmetics. It makes a new arithmetic whose domain predicate is the disjunction of the given arithmetics’ domain predicates, and each of whose operators is mapped to the union of the operations for the given arithmetics.⁹

(define (add-arithmetics . arithmetics)
  (add-arithmetics* arithmetics))

(define (add-arithmetics* arithmetics)
  (if (n:null? (cdr arithmetics))
      (car arithmetics)  ;only one arithmetic
      (make-arithmetic ’add
                       (disjoin*
                        (map arithmetic-domain-predicate
                             arithmetics))
                       arithmetics
                       constant-union
                       operation-union)))

The third argument to make-arithmetic is a list of the arithmetic packages being combined. The arithmetic packages must be compatible in that they specify operations for the same named operators. The fourth argument is constant-union, which combines multiple constants. Here this selects one of the argument constants for use in the combined arithmetic; later we will elaborate on this.¹⁰

(define (constant-union name . constants)
  (let ((unique
         (remove default-object?
                 (delete-duplicates constants eqv?))))
    (if (n:pair? unique)
        (car unique)
        (default-object))))

The last argument is operation-union, which constructs the operation for the named operator in the resulting arithmetic. An operation is applicable if it is applicable in any of the arithmetics that were combined.

(define (operation-union operator . operations)
  (operation-union* operator operations))

(define (operation-union* operator operations)
  (make-operation operator
                  (applicability-union*
                   (map operation-applicability operations))
                  (lambda args
                    (operation-union-dispatch operator
                                              operations
                                              args))))

The procedure operation-union-dispatch must determine the operation to use based on the arguments supplied. It chooses the operation from the given arithmetics that is appropriate to the given arguments and applies it to the arguments. If more than one of the given arithmetics has an applicable operation, the operation from the first arithmetic in the arguments to add-arithmetics is chosen.

(define (operation-union-dispatch operator operations args)
  (let ((operation
         (find (lambda (operation)
                 (is-operation-applicable? operation args))
               operations)))
    (if (not operation)
        (error "Inapplicable operation:" operator args))
    (apply-operation operation args)))

A common pattern is to combine a base arithmetic with an extender on that arithmetic. The combination of numeric arithmetic and a symbolic arithmetic built on numeric arithmetic is such a case. So we provide an abstraction for that pattern:

(define (extend-arithmetic extender base-arithmetic)
  (add-arithmetics base-arithmetic
                   (extender base-arithmetic)))

We can use extend-arithmetic to combine the numeric arithmetic and the symbolic arithmetic. Since the applicability cases are disjoint—all numbers for numeric arithmetic and at least one symbolic expression for symbolic arithmetic—the order of arguments to add-arithmetics is irrelevant here, except for possible performance issues.

(define combined-arithmetic
  (extend-arithmetic symbolic-extender numeric-arithmetic))

(install-arithmetic! combined-arithmetic)

Let's try the composite arithmetic:

(+ 1 2)
3

(+ 1 ’a)
(+ 1 a)

(+ ’a 2)
(+ a 2)

(+ ’a ’b)
(+ a b)

The integrator still works numerically (compare page 70):

(define numeric-s0
  (make-initial-history 0 .01 (sin 0) (sin -.01) (sin -.02)))

(x 0 ((evolver F .01 stormer-2) numeric-s0 100))
.8414709493275624

It works symbolically (compare page 72):

(pp (x 0
       ((evolver F ’h stormer-2)
        (make-initial-history 't ’h ’xt ’xt-h ’xt-2h)
        1)))
(+ (+ (* 2 xt) (* -1 xt-h))
   (* (/ (expt h 2) 12)
      (+ (+ (* 13 (negate xt)) (* -2 (negate xt-h)))
         (negate xt-2h))))

And it works in combination, with numeric history but symbolic step size h:

(pp (x 0 ((evolver F ’h stormer-2) numeric-s0 1)))
(+ 9.999833334166664e-3
   (* (/ (expt h 2) 12)
      -9.999750002487318e-7))

Notice the power here. We have combined code that can do symbolic arithmetic and code that can do numeric arithmetic. We have created a system that can do arithmetic that depends on both abilities. This is not just the union of the two abilities— it is the cooperation of two mechanisms to solve a problem that neither could solve by itself.

3.1.4 Arithmetic on functions

Traditional mathematics extends arithmetic on numerical quantities to many other kinds of objects. Over the centuries “arithmetic” has been extended to complex numbers, vectors, linear transformations and their representations as matrices, etc. One particularly revealing extension is to functions. We can combine functions of the same type using arithmetic operators:

(f + g)(x) = f (x) + g(x)

(f − g)(x) = f (x) − g(x)

(fg)(x) = f (x)g(x)

(f/g)(x) = f (x)/g(x)

⋮

The functions that are combined must have the same domain and codomain, and an arithmetic must be defined on the codomain.

The extension to functions is not hard. Given an arithmetic package for the codomain of the functions that we wish to combine, we can make an arithmetic package that implements the function arithmetic, assuming that functions are implemented as procedures.

(define (pure-function-extender codomain-arithmetic)
  (make-arithmetic ’pure-function function?
                   (list codomain-arithmetic)
    (lambda (name codomain-constant)    ; *** see below
      (lambda args codomain-constant))
    (lambda (operator codomain-operation)
      (simple-operation operator function?
        (lambda functions
          (lambda args
            (apply-operation codomain-operation
                             (map (lambda (function)
                                    (apply function args))
                                  functions))))))))

Notice that the constant generator (with comment ***) must produce a constant function for each codomain constant. For example, the additive identity for functions must be the function of any number of arguments that returns the codomain additive identity. Combining a functional arithmetic with the arithmetic that operates on the codomains makes a useful package:

(install-arithmetic!
  (extend-arithmetic pure-function-extender
                     numeric-arithmetic))

((+ cos sin) 3)
-.8488724885405782

(+ (cos 3) (sin 3))
-.8488724885405782

By building on combined-arithmetic we can get more interesting results:

(install-arithmetic!
  (extend-arithmetic pure-function-extender
                     combined-arithmetic))
((+ cos sin) 3)
-.8488724885405782

((+ cos sin) ’a)
(+ (cos a) (sin a))

(* ’b ((+ cos sin) (+ (+ 1 2) ’a)))
(* b (+ (cos (+ 3 a)) (sin (+ 3 a))))

The mathematical tradition also allows one to mix numerical quantities with functions by treating the numerical quantities as constant functions of the same type as the functions they will be combined with.

(3.4)

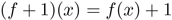
We can implement the coercion of numerical quantities to constant functions quite easily, by minor modifications to the procedure pure-function-extender:

(define (function-extender codomain-arithmetic)
  (let ((codomain-predicate
         (arithmetic-domain-predicate codomain-arithmetic)))
    (make-arithmetic ’function
                     (disjoin codomain-predicate function?)
                     (list codomain-arithmetic)
      (lambda (name codomain-constant)
        codomain-constant)
      (lambda (operator codomain-operation)
        (make-operation operator
                        (any-arg (operator-arity operator)
                                 function?
                                 codomain-predicate)
          (lambda things
            (lambda args
              (apply-operation codomain-operation
                 (map (lambda (thing)
                        ;; here is the coercion:
                        (if (function? thing)
                            (apply thing args)
                            thing))
                      things)))))))))

To allow the coercion of codomain quantities, such as numbers, to constant functions, the domain of the new function arithmetic must contain both the functions and the elements of the codomain of the functions (the possible values of the functions). The operator implementation is applicable if any of the arguments is a function; and functions are applied to the arguments that are given. Note that the constant generator for the make-arithmetic doesn't need to rewrite the codomain constants as functions, since the constants can now be used directly.

With this version we can

(install-arithmetic!
  (extend-arithmetic function-extender combined-arithmetic))

((+ 1 cos) ’a)
(+ 1 (cos a))

(* ’b ((+ 4 cos sin) (+ (+ 1 2) ’a)))
(* b (+ 4 (cos (+ 3 a)) (sin (+ 3 a))))

This raises an interesting problem: we have symbols, such as a and b, that represent literal numbers, but nothing to represent literal functions. For example, if we write

(* ’b ((+ ’c cos sin) (+ 3 ’a)))

our arithmetic will treat c as a literal number. But we might wish to have c be a literal function that combines as a function. It's difficult to do this with our current design, because c carries no type information, and the context is insufficient to distinguish usages.

But we can make a literal function that has no properties except for a name. Such a function just attaches its name to the list of its arguments.

(define (literal-function name)
  (lambda args
    (cons name args)))

With this definition we can have a literal function c correctly combine with other functions:

(* ’b ((+ (literal-function ’c) cos sin) (+ (+ 1 2) ’a)))
(* b (+ (+ (c (+ 3 a)) (cos (+ 3 a))) (sin (+ 3 a))))

This is a narrow solution that handles a useful case.

3.1.5 Problems with combinators

The arithmetic structures we have been building up to now are an example of the use of combinators to build complex structures by combining simpler ones. But there are some serious drawbacks to building this system using combinators. First, some properties of the structure are determined by the means of combination. For example, we pointed out that add-arithmetics prioritized its arguments, such that their order can matter. Second, the layering implicit in this design, such that the codomain arithmetic must be constructed prior to the function arithmetic, means that it's impossible to augment the codomain arithmetic after the function arithmetic has been constructed. Finally, we might wish to define an arithmetic for functions that return functions. This cannot be done in a general way within this framework, without introducing another mechanism for self reference, and self reference is cumbersome to arrange.

Combinators are powerful and useful, but a system built of combinators is not very flexible. One problem is that the shapes of the parts must be worked out ahead of time: the generality that will be available depends on the detailed plan for the shapes of the parts, and there must be a localized plan for how the parts are combined. This is not a problem for a well-understood domain, such as arithmetic, but it is not appropriate for open-ended construction. In section 3.2 we will see how to add new kinds of arithmetic incrementally, without having to decide where they go in a hierarchy, and without having to change the existing parts that already work.

Other problems with combinators are that the behavior of any part of a combinator system must be independent of its context. A powerful source of flexibility that is available to a designer is to build systems that do depend upon their context. By varying the context of a system we can obtain variation of the behavior. This is quite dangerous, because it may be hard to predict how a variation will behave. However, carefully controlled variations can be useful.

---

Exercise 3.1: Warmup with boolean arithmetic

In digital design the boolean operations and, or, and not are written with the operators *, +, and -, respectively.

There is a Scheme predicate boolean? that is true only of #t and #f. Use this to make a boolean arithmetic package that can be combined with the arithmetics we have. Note that all other arithmetic operators are undefined for booleans, so the appropriate result of applying something like cos to a boolean is to report an error.

The following template could help get you started:

(define boolean-arithmetic
  (make-arithmetic ’boolean boolean? ’()
    (lambda (name)
      (case name
        ((additive-identity) #f)
        ((multiplicative-identity) #t)
        (else (default-object))))
    (lambda (operator)
      (let ((procedure
             (case operator
               ((+) <...>)
               ((-) <...>)
               ((*) <...>)
               ((negate) <...>)
               (else
                (lambda args
                  (error "Operator undefined in Boolean"
                         operator))))))
        (simple-operation operator boolean? procedure)))))

In digital design the operator - is typically used only as a unary operator and is realized as negate. When an arithmetic is installed, the binary operators +, *, -, and / are generalized to be n-ary operators.

The unary application (- operand) is transformed by the installer into (negate operand). Thus to make - work, you will need to define the unary boolean operation for the operator negate.

---

---

Exercise 3.2: Vector arithmetic

We will make and install an arithmetic package on geometric vectors. This is a big assignment that will bring to the surface many of the difficulties and inadequacies of the system we have developed so far.

1. a. We will represent a vector as a Scheme vector of numerical quantities. The elements of a vector are coordinates relative to some Cartesian axes. There are a few issues here. Addition (and subtraction) is defined only for vectors of the same dimension, so your arithmetic must know about dimensions. First, make an arithmetic that defines only addition, negation, and subtraction of vectors over a base arithmetic of operations applicable to the coordinates of vectors. Applying any other operation to a vector should report an error. Hint: The following procedures will be helpful:

(define (vector-element-wise element-procedure)
  (lambda vecs    ; Note: this takes multiple vectors
    (ensure-vector-lengths-match vecs)
    (apply vector-map element-procedure vecs)))

(define (ensure-vector-lengths-match vecs)
  (let ((first-vec-length (vector-length (car vecs))))
    (if (any (lambda (v)
               (not (n:= (vector-length v)
                         first-vec-length)))
             vecs)
        (error "Vector dimension mismatch:" vecs))))

The use of apply here is subtle. One way to think about it is to imagine that the language supported an ellipsis like this:

(define (vector-element-wise element-procedure)
  (lambda (v1 v2 ...)
    (vector-map element-procedure v1 v2 ...)))

Build the required arithmetic and show that it works for numerical vectors and for vectors with mixed numerical and symbolic coordinates.

1. b. Your vector addition required addition of the coordinates. The coordinate addition procedure could be the value of the + operator that will be made available in the user environment by install-arithmetic!, or it could be the addition operation from the base arithmetic of your vector extension. Either of these would satisfy many tests, and using the installed addition may actually be more general. Which did you use? Show how to implement the other choice. How does this choice affect your ability to make future extensions to this system? Explain your reasoning.

Hint: A nice way to control the interpretation of operators in a procedure is to provide the procedure to use for each operator as arguments to a “maker procedure” that returns the procedure needed. For example, to control the arithmetic operations used in vector-magnitude one might write:

(define (vector-magnitude-maker + * sqrt)
  (let ((dot-product (dot-product-maker + *)))
    (define (vector-magnitude v)
      (sqrt (dot-product v v)))
    vector-magnitude))

1. c. What shall we do about multiplication? First, for two vectors it is reasonable to define multiplication to be their dot product. But there is a bit of a problem here. You need to be able to use both the addition and multiplication operations, perhaps from the arithmetic on the coordinates. This is not hard to solve. Modify your vector arithmetic to define multiplication of two vectors as their dot product. Show that your dot product works.
2. d. Add vector magnitude to your vector arithmetic, extending the numerical operator magnitude to give the length of a vector. The code given above is most of the work!
3. e. Multiplication of a vector by a scalar or multiplication of a scalar by a vector should produce the scalar product (the vector with each coordinate multiplied by the scalar). So multiplication can mean either dot product or scalar product, depending on the types of its arguments. Modify your vector arithmetic to make this work. Show that your vector arithmetic can handle both dot product and scalar product. Hint: The operation-union procedure on page 78 enables a very elegant way to solve this problem.

---

---

Exercise 3.3: Ordering of extensions

Consider two possible orderings for combining your vector extension (exercise 3.2) with the existing arithmetics:

(define vec-before-func
 (extend-arithmetic
  function-extender
  (extend-arithmetic vector-extender combined-arithmetic)))

(define func-before-vec
 (extend-arithmetic
  vector-extender
  (extend-arithmetic function-extender combined-arithmetic)))

How does the ordering of extensions affect the properties of the resulting arithmetic? The following procedure makes points on the unit circle:

(define (unit-circle x)
  (vector (sin x) (cos x)))

If we execute each of the following expressions in environments resulting from installing vec-before-func and func-before-vec:

((magnitude unit-circle) ’a)

((magnitude (vector sin cos)) ’a)

The result (unsimplified) should be:

(sqrt (+ (* (sin a) (sin a)) (* (cos a) (cos a))))

However, each of these expressions fails with one of the two orderings of the extensions. Is it possible to make an arithmetic for which both evaluate correctly? Explain.

---

3.2 Extensible generic procedures

Systems built by combinators, as in section 3.1, result in beautiful diamond-like systems. This is sometimes the right idea, and we will see it arise again, but it is very hard to add to a diamond. If a system is built as a ball of mud, it is easy to add more mud.¹¹

One organization for a ball of mud is a system erected on a substrate of extensible generic procedures. Modern dynamically typed programming languages, such as Lisp, Scheme, and Python, usually have built-in arithmetic that is generic over a variety of types of numerical quantities, such as integers, floats, rationals, and complex numbers [115, 64, 105]. But systems built on these languages are usually not easily extensible after the fact.

The problems we indicated in section 3.1.5 are the result of using the combinator add-arithmetics. To solve these problems we will abandon that combinator. However, the arithmetic package abstraction is still useful, as is the idea of an extender. We will build an arithmetic package in which the operations use generic procedures that can be dynamically augmented with new behavior. We can then extend the generic arithmetic and add the extensions to the generic arithmetic.¹²

We will start by implementing generic procedures, which are procedures that can be dynamically extended by adding handlers after the generic procedures are defined. A generic procedure is a dispatcher combined with a set of rules, each of which describes a handler that is appropriate for a given set of arguments. Such a rule combines a handler with its applicability.

Let's examine how this might work, by defining a generic procedure named plus that works like addition with numeric and symbolic quantities:

(define plus (simple-generic-procedure ’plus 2 #f))

(define-generic-procedure-handler plus
  (all-args 2 number?)
  (lambda (a b) (+ a b)))

(define-generic-procedure-handler plus
  (any-arg 2 symbolic? number?)
  (lambda (a b) (list ’+ a b)))

(plus 1 2)
3

(plus 1 ’a)
(+ 1 a)

(plus ’a 2)
(+ a 2)

(plus ’a ’b)
(+ a b)

The procedure simple-generic-procedure takes three arguments: The first is an arbitrary name to identify the procedure when debugging; the second is the procedure's arity. The third argument is used to provide a default handler; if none is supplied (indicated by #f), then if no specific handler is applicable an error is signaled. Here plus is bound to the new generic procedure returned by simple-generic-procedure. It is a Scheme procedure that can be called with the specified number of arguments.

The procedure define-generic-procedure-handler adds a rule to an existing generic procedure. Its first argument is the generic procedure to be extended; the second argument is an applicability specification (as on page 73) for the rule being added; and the third argument is the handler for arguments that satisfy that specification.

(define-generic-procedure-handler generic-procedure
                                  applicability
                                  handler-procedure)

It is often necessary to specify a rule in which different arguments are of different types. For example, to make a vector arithmetic package we need to specify the interpretation of the * operator. If both arguments are vectors, the appropriate handler computes the dot product. If one argument is a scalar and the other is a vector, then the appropriate handler scales the vector elements by the scalar. The applicability argument is the means by which this is accomplished.

The simple-generic-procedure constructor we used above to make the generic procedure plus is created with the procedure generic-procedure-constructor

(define simple-generic-procedure
  (generic-procedure-constructor make-simple-dispatch-store))

where make-simple-dispatch-store is a procedure that encapsulates a strategy for saving, retrieving, and choosing a handler.

The generic-procedure-constructor takes a dispatch-store constructor and produces a generic-procedure constructor that itself takes three arguments—a name that is useful in debugging, an arity, and a default handler to be used if there are no applicable handlers. If the default handler argument is #f, the default handler signals an error:

((generic-procedure-constructor dispatch-store-constructor)
 name
 arity
 default-handler)

The reason why generic procedures are made in this way is that we will need families of generic procedures that differ in the choice of dispatch store.

In section 3.2.3, we will see one way to implement this mechanism. But first let's see how to use it.

3.2.1 Generic arithmetic

We can use this new generic-procedure mechanism to build arithmetic packages in which the operators map to operations that are implemented as generic procedures. This will allow us to make self-referential structures. For example, we might want to make a generic arithmetic that includes vector arithmetic where both the vectors and the components of a vector are manipulated by the same generic procedures. We could not build such a structure using just add-arithmetics introduced earlier.

(define (make-generic-arithmetic dispatch-store-maker)
  (make-arithmetic ’generic any-object? ’()
    constant-union
    (let ((make-generic-procedure
           (generic-procedure-constructor
            dispatch-store-maker)))
      (lambda (operator)
        (simple-operation operator
                any-object?
                (make-generic-procedure
                 operator
                 (operator-arity operator)
                 #f))))))

The make-generic-arithmetic procedure creates a new arithmetic. For each arithmetic operator, it constructs an operation that is applicable to any arguments and is implemented by a generic procedure. (The predicate any-object? is true of anything.) We can install this arithmetic in the usual way.

But first, let's define some handlers for the generic procedures. It's pretty simple to do now that we have the generic arithmetic object. For example, we can grab the operations and constants from any already-constructed arithmetic.

(define (add-to-generic-arithmetic! generic-arithmetic
                                    arithmetic)
  (add-generic-arith-constants! generic-arithmetic
                                arithmetic)
  (add-generic-arith-operations! generic-arithmetic
                                 arithmetic))

This takes a generic arithmetic package and an ordinary arithmetic package with the same operators. It merges constants into the generic arithmetic using constant-union. And for each operator of the given arithmetic it adds a handler to the corresponding generic procedure.

Adding a handler for a particular operator uses the standard generic procedure mechanism, extracting the necessary applicability and procedure from the arithmetic's operation.

(define (add-generic-arith-operations! generic-arithmetic
                                       arithmetic)
  (for-each
   (lambda (operator)
     (let ((generic-procedure
            (simple-operation-procedure
             (arithmetic-operation operator
                                   generic-arithmetic)))
           (operation
            (arithmetic-operation operator arithmetic)))
       (define-generic-procedure-handler
           generic-procedure
           (operation-applicability operation)
           (operation-procedure operation))))
   (arithmetic-operators arithmetic)))

The add-generic-arith-operations! procedure finds, for each operator in the given arithmetic, the generic procedure that must be augmented. It then defines a handler for that generic procedure that is the handler for that operator in the given arithmetic, using the applicability for that handler in the given arithmetic.

The code for adding the constants from an arithmetic to the generic arithmetic is similar. For each constant name in the generic arithmetic it finds the entry in the association of names to constant values in the generic arithmetic. It then replaces the constant value with the constant-union of the existing constant and the constant it got for that same name from the given arithmetic.

(define (add-generic-arith-constants! generic-arithmetic
                                      arithmetic)
  (for-each
   (lambda (name)
     (let ((binding
            (arithmetic-constant-binding name
                                         generic-arithmetic))
           (element
            (find-arithmetic-constant name arithmetic)))
       (set-cdr! binding
                 (constant-union name
                                 (cdr binding)
                                 element))))
   (arithmetic-constant-names generic-arithmetic)))

Fun with generic arithmetics

We can add many arithmetics to a generic arithmetic to give it interesting behavior:

(let ((g
       (make-generic-arithmetic make-simple-dispatch-store)))
  (add-to-generic-arithmetic! g numeric-arithmetic)
  (add-to-generic-arithmetic! g
    (function-extender numeric-arithmetic))
  (add-to-generic-arithmetic! g
    (symbolic-extender numeric-arithmetic))
  (install-arithmetic! g))

This produces a generic arithmetic that combines numeric arithmetic with symbolic arithmetic over numeric arithmetic and function arithmetic over numeric arithmetic:

(+ 1 3 ’a ’b)
(+ (+ 4 a) b)

And we can even run some more complex problems, as on page 79:

(pp (x 0 ((evolver F ’h stormer-2) numeric-s0 1)))
(+ 9.999833334166664e-3
   (* (/ (expt h 2) 12)
      -9.999750002487318e-7))

As before, we can mix symbols and functions:

(* ’b ((+ cos sin) 3))
(* b -.8488724885405782)

but the following will signal an error, trying to add the symbolic quantities (cos a) and (sin a) as numbers:

(* ’b ((+ cos sin) ’a))

We get this error because cos and sin are numeric operators, like +. Since we have symbolic arithmetic over numeric arithmetic, these operators are extended so that for symbolic input, here a, they produce symbolic outputs, (cos a) and (sin a). We also added function arithmetic over numeric arithmetic, so if functions are numerically combined (here by +) their outputs may be combined only if the outputs are numbers. But the symbolic results cannot be added numerically. This is a consequence of the way we built the arithmetic g.

But there is magic in generic arithmetic. It can be closed: all extensions to the generic arithmetic can be made over the generic arithmetic!

(let ((g
       (make-generic-arithmetic make-simple-dispatch-store)))
  (add-to-generic-arithmetic! g numeric-arithmetic)
  (extend-generic-arithmetic! g symbolic-extender)
  (extend-generic-arithmetic! g function-extender)
  (install-arithmetic! g))

Here we use a new procedure extend-generic-arithmetic! that captures a common pattern.

(define (extend-generic-arithmetic! generic-arithmetic
                                    extender)
  (add-to-generic-arithmetic! generic-arithmetic
      (extender generic-arithmetic)))

Now we can use complex mixed expressions, because the functions are defined over the generic arithmetic:

(* ’b ((+ ’c cos sin) (+ 3 ’a)))
(* b (+ (+ c (cos (+ 3 a))) (sin (+ 3 a))))

We can even use functions that return functions:

(((+ (lambda (x) (lambda (y) (cons x y)))
      (lambda (x) (lambda (y) (cons y x))))
  3)
4)
(+ (3 . 4) (4 . 3))

So perhaps we have achieved nirvana?

3.2.2 Construction depends on order!

Unfortunately, there is a severe dependence on the order in which rules are added to the generic procedures. This is not surprising, because the construction of the generic procedure system is by assignment. We can see this by changing the order of construction:

(let ((g
       (make-generic-arithmetic make-simple-dispatch-store)))
  (add-to-generic-arithmetic! g numeric-arithmetic)
  (extend-generic-arithmetic! g function-extender) ;*
  (extend-generic-arithmetic! g symbolic-extender) ;*
  (install-arithmetic! g))

and then we will find that the example

(* ’b ((+ ’c cos sin) (+ 3 ’a)))

which worked in the previous arithmetic, fails because the symbolic arithmetic captures (+ ’c cos sin) to produce a symbolic expression, which is not a function that can be applied to (+ 3 a). The problem is that the applicability of the symbolic operation for + accepts arguments with at least one symbolic argument and other arguments from the domain predicate of the base. But the symbolic arithmetic was created over the generic arithmetic as a base, and the domain predicate of a generic arithmetic accepts anything! There is also a function operation for + that is applicable to the same arguments, but it has not been chosen because of the accidental ordering of the extensions. Unfortunately, the choice of rule is ambiguous. It would be better to not have more than one applicable operation.

One way to resolve this problem is to restrict the symbolic quantities to represent numbers. We can do this by building our generic arithmetic so that the symbolic arithmetic is over the numeric arithmetic, as we did on page 92, rather than over the entire generic arithmetic:

(let ((g
       (make-generic-arithmetic make-simple-dispatch-store)))
  (add-to-generic-arithmetic! g numeric-arithmetic)
  (extend-generic-arithmetic! g function-extender)
  (add-to-generic-arithmetic! g
      (symbolic-extender numeric-arithmetic))
  (install-arithmetic! g))

This works, independent of the ordering, because there is no ambiguity in the choice of rules. So now the ’c will be interpreted as a constant to be coerced to a constant function by the function extender.

(* ’b ((+ ’c cos sin) (+ 3 ’a)))
(* b (+ (+ c (cos (+ 3 a))) (sin (+ 3 a))))

Unfortunately, we may want to have symbolic expressions over other quantities besides numbers. We cannot yet implement a general solution to this problem. But if we really want a literal function named c, we can use literal-function as we did earlier:

(* ’b ((+ (literal-function ’c) cos sin) (+ 3 ’a)))
(* b (+ (+ (c (+ 3 a)) (cos (+ 3 a))) (sin (+ 3 a))))

This will work independent of the order of construction of the generic arithmetic.

With this mechanism we are now in a position to evaluate the Stormer integrator with a literal function:

(pp (x 0 ((evolver (literal-function ’F) ’h stormer-2)
          (make-initial-history 't ’h ’xt ’xt-h ’xt-2h)
          1))
(+ (+ (* 2 xt) (* -1 xt-h))
   (* (/ (expt h 2) 12)
      (+ (+ (* 13 (f t xt))
            (* -2 (f (- t h) xt-h)))
         (f (- t (* 2 h)) xt-2h))))

This is pretty ugly, and it would be worse if we looked at the output of two integration steps. But it is interesting to look at the result of simplifying a two-step integration. Using a magic symbolic-expression simplifier we get a pretty readable expression. This can be useful for debugging a numerical process.

(+ (* 2 (expt h 2) (f t xt))
   (* -1/4 (expt h 2) (f (+ (* -1 h) t) xt-h))
   (* 1/6 (expt h 2) (f (+ (* -2 h) t) xt-2h))
   (* 13/12
      (expt h 2)
      (f (+ h t)
         (+ (* 13/12 (expt h 2) (f t xt))
            (* -1/6 (expt h 2) (f (+ (* -1 h) t) xt-h))
            (* 1/12 (expt h 2) (f (+ (* -2 h) t) xt-2h))
            (* 2 xt)
            (* -1 xt-h))))
   (* 3 xt)
   (* -2 xt-h))

For example, notice that there are only four distinct top-level calls to the acceleration function f. The second argument to the fourth top-level call uses three calls to f that have already been computed. If we eliminate common subexpressions we get:

(let* ((G84 (expt h 2)) (G85 (f t xt)) (G87 (* -1 h))
       (G88 (+ G87 t)) (G89 (f G88 xt-h)) (G91 (* -2 h))
       (G92 (+ G91 t)) (G93 (f G92 xt-2h)))
  (+ (* 2 G84 G85)
     (* -1/4 G84 G89)
     (* 1/6 G84 G93)
     (* 13/12 G84
        (f (+ h t)
           (+ (* 13/12 G84 G85)
              (* -1/6 G84 G89)
              (* 1/12 G84 G93)
              (* 2 xt)
              (* -1 xt-h))))
     (* 3 xt)
     (* -2 xt-h)))

Here we clearly see that there are only four distinct calls to f. Though each integration step in the basic integrator makes three calls to f, the two steps overlap on two intermediate calls. While this is obvious for such a simple example, we see how symbolic evaluation might help in understanding a numerical computation.

3.2.3 Implementing generic procedures

We have used generic procedures to do amazing things. But how do we make such a thing work?

Making constructors for generic procedures

On page 89 we made a simple generic procedure constructor:

(define simple-generic-procedure
  (generic-procedure-constructor make-simple-dispatch-store))

The procedure generic-procedure-constructor is given a “dispatch strategy” procedure; it returns a generic-procedure constructor that takes a name, an arity, and a default-handler specification. When this procedure is called with these three arguments it returns a generic procedure that it associates with a newly constructed metadata store for that procedure, which holds the name, the arity, an instance of the dispatch strategy, and the default handler, if any. The dispatch-strategy instance will maintain the handlers, their applicabilities, and the mechanism for deciding which handler to choose for given arguments to the generic procedure.

The code that implements generic-procedure-constructor is:

(define (generic-procedure-constructor dispatch-store-maker)
  (lambda (name arity default-handler)
    (let ((metadata
           (make-generic-metadata
             name arity (dispatch-store-maker)
             (or default-handler
                 (error-generic-procedure-handler name)))))
      (define (the-generic-procedure . args)
        (generic-procedure-dispatch metadata args))
      (set-generic-procedure-metadata! the-generic-procedure
                                       metadata)
      the-generic-procedure)))

This implementation uses the-generic-procedure, an ordinary Scheme procedure, to represent the generic procedure, and a metadata store (for rules, etc.) that determines the procedure's behavior. This store is associated with the generic procedure using a “sticky note” (as on page 28) and can later be obtained by calling generic-procedure-metadata. This allows procedures such as define-generic-procedure-handler to modify the metadata of a given generic procedure.

The argument to generic-procedure-constructor is a procedure that creates a dispatch store for saving and retrieving handlers. The dispatch store encapsulates the strategy for choosing a handler.

Here is the simple dispatch-store constructor we have used so far. The dispatch store is implemented as a message-accepting procedure:

(define (make-simple-dispatch-store)
  (let ((rules ’()) (default-handler #f))
    (define (get-handler args)
      ;; body will be shown in text below.
      ...)
    (define (add-handler! applicability handler)
      ;; body will be shown in text below.
      ...)
    (define (get-default-handler) default-handler)
    (define (set-default-handler! handler)
      (set! default-handler handler))
    (lambda (message)      ; the simple dispatch store
      (case message
        ((get-handler) get-handler)
        ((add-handler!) add-handler!)
        ((get-default-handler) get-default-handler)
        ((set-default-handler!) set-default-handler!)
        ((get-rules) (lambda () rules))
        (else (error "Unknown message:" message))))))

The simple dispatch store just maintains a list of the rules, each of which pairs an applicability with a handler. When the get-handler internal procedure is called with arguments for the generic procedure, it scans the list sequentially for a handler whose applicability is satisfied by the arguments tendered; it returns the handler, or #f if it doesn't find one:

(define (get-handler args)
  (let ((rule
         (find (lambda (rule)
                 (predicates-match? (car rule) args))
               rules)))
    (and rule (cdr rule))))

There are many possible strategies for choosing handlers to run. The above code returns the first applicable handler in the list. Another strategy is to return all applicable handlers. If more than one handler is applicable, perhaps all should be tried (in parallel?) and the results compared! Passing a dispatch-store constructor as an argument to generic-procedure-constructor allows the strategy to be chosen when the generic-procedure constructor is created, rather than being hard-coded into the implementation.

Adding handlers to generic procedures

The handler definition procedure (see below) adds new rules by calling the internal procedure add-handler of the dispatch store. For make-simple-dispatch-store above, add-handler adds the new rule to the front of the list of rules. (But if there was already a rule for handling that applicability, it just replaces the handler.)

(define (add-handler! applicability handler)
  (for-each (lambda (predicates)
              (let ((p (assoc predicates rules)))
                (if p
                    (set-cdr! p handler)
                    (set! rules
                          (cons (cons predicates handler)
                                rules)))))
            applicability))

The define-generic-procedure-handler procedure uses the metadata table to get the metadata record for the generic procedure. It asks the dispatch store for the add-handler! procedure and uses that procedure to add a rule to the metadata that associates the applicability with the handler. The dispatch-store instance is retrieved from the metadata of the generic procedure by generic-metadata-dispatch-store.

(define (define-generic-procedure-handler generic-procedure
                                          applicability
                                          handler)
  (((generic-metadata-dispatch-store
     (generic-procedure-metadata generic-procedure))
    ’add-handler!)
   applicability
   handler))

Finally, the heart of the mechanism is the dispatch, called by a generic procedure (the-generic-procedure on page 97), which finds an appropriate handler and applies it. The default handler, as supplied during construction of the generic procedure, is called if there is no applicable handler.¹³

(define (generic-procedure-dispatch metadata args)
  (let ((handler
         (get-generic-procedure-handler metadata args)))
    (apply handler args)))

(define (get-generic-procedure-handler metadata args)
  (or ((generic-metadata-getter metadata) args)
      ((generic-metadata-default-getter metadata))))

The power of extensible generics

Construction of a system on a substrate of extensible generic procedures is a powerful idea. In our example it is possible to define what is meant by addition, multiplication, etc., for new data types unimagined by the language designer. For example, if the arithmetic operators of a system are implemented as extensible generics, a user may extend them to support arithmetic on quaternions, vectors, matrices, integers modulo a prime, functions, tensors, differential forms, This is not just making new capabilities possible; it also extends old programs, so a program that was written to manipulate simple numerical quantities may become useful for manipulating scalar-valued functions.

We have seen that there are potential problems associated with this use of extensible generic procedures. On the other hand, some “mutations” will be extremely valuable. For example, it is possible to extend arithmetic to symbolic quantities. The simplest way to do this is to make a generic extension to all of the operators to take symbolic quantities as arguments and return a data structure representing the indicated operation on the arguments. With the addition of a simplifier of algebraic expressions we suddenly have a symbolic manipulator. This is useful in debugging purely numerical calculations, because if we give them symbolic arguments we can examine the resulting symbolic expressions to make sure that the program is calculating what we intend it to. It is also the basis of a partial evaluator for optimization of numerical programs. And functional differentiation can be viewed as a generic extension of arithmetic to a compound data type (see section 3.3). The scmutils system we use to teach classical mechanics [121] implements differentiation in exactly this way.

---

Exercise 3.4: Functional values

The generic arithmetic structure allows us to close the system so that functions that return functions can work, as in the example

(((* 3
    (lambda (x) (lambda (y) (+ x y)))
    (lambda (x) (lambda (y) (vector y x))))
 ’a)
4)
(* (* 3 (+ a 4)) #(4 a))

1. a. How hard is it to arrange for this to work in the purely combinator-based arithmetic introduced in section 3.1? Why?
2. b. Exercise 3.3 on page 86 asked about the implications of ordering of vector and functional extensions. Is the generic system able to support both expressions discussed there (and copied below)? Explain.

((magnitude unit-circle) ’a)
((magnitude (vector sin cos)) ’a)

1. c. Is there any good way to make the following work at all?

((vector cos sin) 3)
#(-.9899924966004454 .1411200080598672)

Show code that makes this work or explain the difficulties.

---

---

Exercise 3.5: A weird bug

Consider the +-like (“plus-like”) procedure in arith.scm, shown below, which implements n-ary procedures + and * as part of installing an arithmetic. It returns a pair of a name and a procedure; the installer will bind the name to the procedure.

It seems that it is written to execute the get-identity procedure that computes the identity every time the operation is called with no arguments.

(define (+-like operator identity-name)
  (lambda (arithmetic)
    (let ((binary-operation
           (find-arithmetic-operation operator arithmetic)))
      (and binary-operation
           (let ((binary
                  (operation-procedure binary-operation))
                 (get-identity
                  (identity-name->getter identity-name
                                         arithmetic)))
             (cons operator
                   (lambda args
                     (case (length args)
                       ((0) (get-identity))
                       ((1) (car args))
                       (else (pairwise binary args))))))))))

Perhaps the identity for an operator should be computed only once, not every time the handler is called. As a consequence, it is proposed that the code should be modified as follows:

(define (+-like operator identity-name)
  (lambda (arithmetic)
    (let ((binary-operation
           (find-arithmetic-operation operator arithmetic)))
      (and binary-operation
           (let ((binary
                  (operation-procedure binary-operation))
                 (identity
                  ((identity-name->getter identity-name
                                          arithmetic))))
             (cons operator
                   (lambda args
                     (case (length args)
                       ((0) identity)
                       ((1) (car args))
                       (else (pairwise binary args))))))))))

However, this has a subtle bug! Can you elicit the bug? Can you explain it?

---

---

Exercise 3.6: Matrices

Matrices are ubiquitous in scientific and technical computing.

1. a. Make and install an arithmetic package for matrices of numbers, with operations +, -, negate, and *. This arithmetic needs to be able to know the number of rows and the number of columns in a matrix, since matrix multiplication is defined only if the number of columns in the first matrix is equal to the number of rows in the second one.

Make sure that your multiplier can multiply a matrix with a scalar or with a vector. For matrices to play well with vectors you probably need to distinguish row vectors and column vectors. How does this affect the design of the vector package? (See exercise 3.2 on page 85.)

You may assume that the vectors and matrices are of small dimension, so you do not need to deal with sparse representations. A reasonable representation of a matrix is a Scheme vector in which each element is a Scheme vector representing a row.

1. b. Vectors and matrices may contain symbolic numerical quantities. Make this work.
2. c. Matrix inversion is appropriate for your arithmetic. If a symbolic matrix is dense, the inverse may take space that is factorial in the dimension. Why?

Note: We are not asking you to implement matrix inversion.

---

---

Exercise 3.7: Literal vectors and matrices

It is also possible to have arithmetic on literal matrices and literal vectors with an algebra of symbolic expressions of vectors and matrices. Can you make symbolic algebra of these compound structures play well with vectors and matrices that have symbolic numerical expressions as elements? Caution: This is quite hard. Perhaps it is appropriate as part of a long-term project.

---

3.3 Example: Automatic differentiation

One remarkable application of extensible generic procedures is automatic differentiation.¹⁴ This is a beautiful way to obtain a program that computes the derivative of the function computed by a given program.¹⁵ Automatic differentiation is now an important component in machine learning applications.

We will see that a simple way to implement automatic differentiation is to extend the generic arithmetic primitives to work with differential objects, a new compound data type. This will enable the automatic differentiation of symbolic as well as numerical functions. It will also enable us to make automatic differentiation work with higher-order procedures—procedures that return other procedures as values.

Here is a simple example of automatic differentiation to illustrate what we are talking about:

((derivative (lambda (x) (expt x 3))) 2)
12

Note that the derivative of the function that computes the cube of its argument is a new function, which when given 2 as its argument returns 12 as its value.

If we extend the arithmetic to handle symbolic expressions, and we do some algebraic simplification on the result, we get:

((derivative (lambda (x) (expt x 3))) ’a)
(* 3 (expt a 2))

And the full power of the programming language is available, including higher-order procedures. This kind of system is useful in working with the very large expressions that occur in interesting physics problems.¹⁶

Let's look at a simple application: the computation of the roots of an equation by Newton's method. The idea is that we want to find values of x for which f (x) = 0. If f is sufficiently smooth, and we have a sufficiently close guess x₀, we can improve the guess by computing a new guess x₁ by the formula:

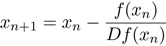
This can be repeated, as necessary, to get a sufficiently accurate result. An elementary program to accomplish this is:

(define (root-newton f initial-guess tolerance)
  (let ((Df (derivative f)))
    (define (improve-guess xn)
      (- xn (/ (f xn) (Df xn))))
    (let loop ((xn initial-guess))
      (let ((xn+1 (improve-guess xn)))
        (if (close-enuf? xn xn+1 tolerance)
            xn+1
            (loop xn+1))))))

Notice that the local procedure named Df in root-newton is a procedure that computes the derivative of the function computed by the procedure passed in as f.

For example, suppose we want to know the angle θ in the first quadrant for which cos(θ) = sin(θ). (The answer is π/4 ≈ .7853981633974484) We can write:

(define (cs theta)
  (- (cos theta) (sin theta)))

(root-newton cs 0.5 1e-8)
.7853981633974484

This result is correct to full machine accuracy.

3.3.1 How automatic differentiation works

The program for automatic differentiation is directly derived from the definition of the derivative. Suppose that given a function f and a point x in its domain, we want to know the value of the function at a nearby point f (x + Δx), where Δx is a small increment. The derivative of a function f is defined to be the function Df whose value for particular arguments x is something that can be “multiplied” by an increment Δx of the argument to get the best possible linear approximation to the increment in the value of f:

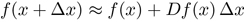
We implement this definition using a data type that we call a differential object. A differential object [x, δx] can be thought of as a number with a small increment, x + δx. But we treat it as a new numerical quantity similar to a complex number: it has two components, a finite part and an infinitesimal part.¹⁷ We extend each primitive arithmetic function to work with differential objects: each primitive arithmetic function f must know its derivative function Df , so that:

(3.5)

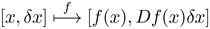
Note that the derivative of f at the point x, Df (x), is the coefficient of δx in the infinitesimal part of the resulting differential object.

Now here is the powerful idea: If we then pass the result of f ([x, δx]) (equation 3.5) through another function g, we obtain the chain-rule answer we would hope for:

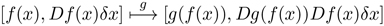
Thus, if we can compute the results of all primitive functions on differential objects, we can compute the results of all compositions of functions on differential objects. Given such a result, we can extract the derivative of the composition: the derivative is the coefficient of the infinitesimal increment in the resulting differential object.

To extend a generic arithmetic operator to compute with differential objects, we need only supply a procedure that computes the derivative of the primitive arithmetic function that the operator names. Then we can use ordinary Scheme compositions to get the derivative of any composition of primitive functions.¹⁸

Given a procedure implementing a unary function f, the procedure derivative produces a new procedure the-derivative that computes the derivative of the function computed by f.¹⁹ When applied to some argument, x, the derivative creates a new infinitesimal increment dx and adds it to the argument to get the new differential object [x, δx] that represents x + δx. The procedure f is then applied to this differential object and the derivative of f is obtained by extracting the coefficient of the infinitesimal increment dx from the value:

(define (derivative f)
  (define (the-derivative x)
    (let* ((dx (make-new-dx))
           (value (f (d:+ x (make-infinitesimal dx)))))
      (extract-dx-part value dx)))
  the-derivative)

The procedure make-infinitesimal makes a differential object whose finite part is zero and whose infinitesimal part is dx. The procedure d:+ adds differential objects. The details will be explained in section 3.3.3.

Extending the primitives

We need to make handler procedures that extend the primitive arithmetic generic procedures to operate on differential objects. For each unary procedure we have to make the finite part of the result and the infinitesimal part of the result, and we have to put the results together, as expressed in equation 3.5. So the handler for a unary primitive arithmetic procedure that computes function f is constructed by diff:unary-proc from the procedure f for f and the procedure df for its derivative Df. These are glued together using special addition and multiplication procedures d:+ and d:* for differential objects, to be explained in section 3.3.3.

(define (diff:unary-proc f df)
  (define (uop x)       ; x is a differential object
      (let ((xf (finite-part x))
            (dx (infinitesimal-part x)))
        (d:+ (f xf) (d:* (df xf) dx))))
  uop)

For example, the sqrt procedure handler for differential objects is just:

(define diff:sqrt
  (diff:unary-proc sqrt (lambda (x) (/ 1 (* 2 (sqrt x))))))

The first argument of diff:unary-proc is the sqrt procedure and the second argument is a procedure that computes the derivative of sqrt.

We add the new handler to the generic sqrt procedure using

(assign-handler! sqrt diff:sqrt differential?)

where differential? is a predicate that is true only of differential objects. The procedure assign-handler! is just shorthand for a useful pattern:

(define (assign-handler! procedure handler . preds)
  (define-generic-procedure-handler procedure
    (apply match-args preds)
    handler))

And the procedure match-args makes an applicability specification from a sequence of predicates.

Handlers for other unary primitives are straightforward:²⁰

(define diff:exp (diff:unary-proc exp exp))

(define diff:log (diff:unary-proc log (lambda (x) (/ 1 x))))

(define diff:sin (diff:unary-proc sin cos))

(define diff:cos
        (diff:unary-proc cos (lambda (x) (* -1 (sin x)))))
⋮

Binary arithmetic operations are a bit more complicated.

(3.6)

where ∂₀f and ∂₁f are the partial derivative functions of f with respect to the two arguments. Let f be a function of two arguments; then ∂₀f is a new function of two arguments that computes the partial derivative of f with respect to its first argument:

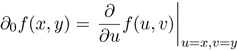
So the rule for binary operations is

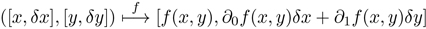
To implement binary operations we might think that we could simply follow the plan for unary operations, where d0f and d1f are the two partial derivative functions:

(define (diff:binary-proc f d0f d1f)
  (define (bop x y)
    (let ((dx (infinitesimal-part x))
          (dy (infinitesimal-part y))
          (xf (finite-part x))
          (yf (finite-part y)))
      (d:+ (f xf yf)
           (d:+ (d:* dx (d0f xf yf))
                (d:* (d1f xf yf) dy)))))
  bop)

This is a good plan, but it isn't quite right: it doesn't ensure that the finite and infinitesimal parts are consistently chosen for the two arguments. We need to be more careful about how we choose the parts. We will explain this technical detail and fix it in section 3.3.3, but let's go with this approximately correct code for now.

Addition and multiplication are straightforward, because the partial derivatives are simple, but division and exponentiation are more interesting. We show the assignment of handlers only for diff:+ because all the others are similar.

(define diff:+
  (diff:binary-proc +
                    (lambda (x y) 1)
                    (lambda (x y) 1)))

(assign-handler! + diff:+ differential? any-object?)
(assign-handler! + diff:+ any-object? differential?)

(define diff:*
  (diff:binary-proc *
                    (lambda (x y) y)
                    (lambda (x y) x)))

(define diff:/
  (diff:binary-proc /
                    (lambda (x y)
                      (/ 1 y))
                    (lambda (x y)
                      (* -1 (/ x (square y))))))

The handler for exponentiation f (x, y) = x is a bit more complicated. The partial with respect to the first argument is simple: ∂₀f (x, y) = yx⁻¹. But the partial with respect to the second argument is usually ∂₁f (x, y) = x log x, except for some special cases:

(define diff:expt
  (diff:binary-proc expt
    (lambda (x y)
      (* y (expt x (- y 1))))
    (lambda (x y)
      (if (and (number? x) (zero? x))
          (if (number? y)
              (if (positive? y)
                  0
                  (error "Derivative undefined: EXPT"
                         x y))
              0)
          (* (log x) (expt x y))))))

Extracting the derivative's value

To compute the value of the derivative of a function, we apply the function to a differential object and obtain a result. We have to extract the derivative's value from that result. There are several possibilities that must be handled. If the result is a differential object, we have to pull the derivative's value out of the object. If the result is not a differential object, the derivative's value is zero. There are other cases that we have not mentioned. This calls for a generic procedure with a default that produces a zero.

(define (extract-dx-default value dx) 0)

(define extract-dx-part
  (simple-generic-procedure ’extract-dx-part 2
                            extract-dx-default))

In the case where a differential object is returned, the coefficient of dx is the required derivative. This will turn out to be a bit complicated, but the basic idea can be expressed as follows:

(define (extract-dx-differential value dx)
  (extract-dx-coefficient-from (infinitesimal-part value) dx))

(define-generic-procedure-handler extract-dx-part
  (match-args differential? diff-factor?)
  extract-dx-differential)

The reason this is not quite right is that for technical reasons the structure of a differential object is more complex than we have already shown. It will be fully explained in section 3.3.3.

Note: We made the extractor generic to enable future extensions to functions that return functions or compound objects, such as vectors, matrices, and tensors. (See exercise 3.12 on page 124.)

Except for the fact that there may be more primitive operators and data structures to be included, this is all that is really needed to implement automatic differentiation! All of the procedures referred to in the handlers are the usual generic procedures on arithmetic; they may include symbolic arithmetic and functional arithmetic.

3.3.2 Derivatives of n-ary functions

For a function with multiple arguments we need to be able to compute the partial derivatives with respect to each argument. One way to do this is:²¹

(define ((partial i) f)
  (define (the-derivative . args)
    (if (not (< i (length args)))
        (error "Not enough arguments for PARTIAL" i f args))
    (let* ((dx (make-new-dx))
           (value
            (apply f (map (lambda (arg j)
                            (if (= i j)
                                (d:+ arg
                                     (make-infinitesimal dx))
                                arg))
                          args (iota (length args))))))
      (extract-dx-part value dx)))
  the-derivative)

Here we are extracting the coefficient of the infinitesimal dx in the result of applying f to the arguments supplied with the ith argument incremented by dx.²²

Now consider a function g of two arguments. Expanding on equation 3.6 we find that the derivative Dg is multiplied by a vector of increments to the arguments:

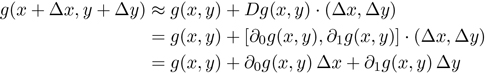
The derivative Dg of g at the point x, y is the pair of partial derivatives in square brackets. The inner product of that covector of partials with the vector of increments is the increment to the function g. The general-derivative procedure computes this result:

(define (general-derivative g)
  (define ((the-derivative . args) . increments)
    (let ((n (length args)))
      (assert (= n (length increments)))
      (if (= n 1)
          (* ((derivative g) (car args))
             (car increments))
          (reduce (lambda (x y) (+ y x))
                  0
                  (map (lambda (i inc)
                         (* (apply ((partial i) g) args)
                             inc))
                       (iota n)
                       increments)))))
  the-derivative)

Unfortunately general-derivative does not return the structure of partial derivatives. It is useful in many contexts to have a derivative procedure gradient that actually gives the covector of partial derivatives. (See exercise 3.10.)

---

Exercise 3.8: Partial derivatives

Another way to think about partial derivatives is in terms of λ-calculus currying. Draw a diagram of how the data must flow. Use currying to fix the arguments that are held constant, producing a one-argument procedure that the ordinary derivative will be applied to. Write that version of the partial derivative procedure.

---

---

Exercise 3.9: Adding handlers

There are primitive arithmetic functions for which we did not add handlers for differential objects, for example tan.

1. a. Add handlers for tan and atan1 (atan1 is a function of one argument).
2. b. It would be really nice to have atan optionally take two arguments, as in the Scheme Report [109], because we usually want to preserve the quadrant we are working in. Fix the generic procedure atan to do this correctly—using atan1 for one argument and atan2 if given two arguments. Also, install an atan2 handler for differentials. Remember, it must coexist with the atan1 handler.

---

---

Exercise 3.10: Vectors and covectors

As described above, the idea of derivative can be generalized to functions with multiple arguments. The gradient of a function of multiple arguments is the covector of partial derivatives with respect to each of the arguments.

1. a. Develop data types for vectors and covectors such that the value of Dg(x, y) is the covector of partials. Write a gradient procedure that delivers that value. Remember, the product of a vector and a covector should be their inner product—the sum of the componentwise products of their elements.
2. b. Notice that if the input to a function is a vector, that is similar to multiple inputs, so the output of the gradient should be a covector. Note also that if the input to a function is a covector, then the output of the gradient should be a vector. Make this work.

---

3.3.3 Some technical details

Although the idea behind automatic differentiation is not complicated, there are a number of subtle technical details that must be addressed for it to work correctly.

Differential algebra

If we want to compute a second derivative we must take a derivative of a derivative function. The evaluation of such a function will have two infinitesimals in play. To enable the computation of multiple derivatives and derivatives of functions of several variables we define an algebra of differential objects in “infinitesimal space.” The objects are multivariate power series in which no infinitesimal increment has exponent greater than one.²³

A differential object is represented by a tagged list of the terms of a power series. Each term has a coefficient and a list of infinitesimal incremental factors. The terms are kept sorted, in descending order. (Order is the number of incrementals. So δxδy is higher order than δx or δy.) Here is a quick and dirty implementation:²⁴

(define differential-tag 'differential)

(define (differential? x)
  (and (pair? x) (eq? (car x) differential-tag)))

(define (diff-terms h)
  (if (differential? h)
      (cdr h)
      (list (make-diff-term h ’()))))

The term list is just the cdr of the differential object. However, if we are given an object that is not explicitly a differential object, for example a number, we coerce it to a differential object with a single term and with no incremental factors. When we make a differential object from a (presorted) list of terms, we always try to return a simplified version, which may be just a number, which is not explicitly a differential object:

(define (make-differential terms)
  (let ((terms                       ; Nonzero terms
         (filter
          (lambda (term)
            (let ((coeff (diff-coefficient term)))
              (not (and (number? coeff) (= coeff 0)))))
          terms)))
    (cond ((null? terms) 0)
          ((and (null? (cdr terms))
                ;; Finite part only:
                (null? (diff-factors (car terms))))
           (diff-coefficient (car terms)))
          ((every diff-term? terms)
           (cons differential-tag terms))
          (else (error "Bad terms")))))

In this implementation the terms are also represented as tagged lists, each containing a coefficient and an ordered list of factors.

(define diff-term-tag 'diff-term)

(define (make-diff-term coefficient factors)
  (list diff-term-tag coefficient factors))

(define (diff-term? x)
  (and (pair? x) (eq? (car x) diff-term-tag)))

(define (diff-coefficient x)
  (cadr x))

(define (diff-factors x)
  (caddr x))

To compute derivatives we need to be able to add and multiply differential objects:

(define (d:+ x y)
  (make-differential
   (+diff-termlists (diff-terms x) (diff-terms y))))

(define (d:* x y)
  (make-differential
   (*diff-termlists (diff-terms x) (diff-terms y))))

and we also need this:

(define (make-infinitesimal dx)
  (make-differential (list (make-diff-term 1 (list dx)))))

Addition of term lists is where we enforce and use the sorting of terms, with higher-order terms coming earlier in the lists. We can add two terms only if they have the same factors. And if the sum of the coefficients is zero we do not include the resulting term.

(define (+diff-termlists l1 l2)
  (cond ((null? l1) l2)
        ((null? l2) l1)
        (else
         (let ((t1 (car l1)) (t2 (car l2)))
           (cond ((equal? (diff-factors t1) (diff-factors t2))
                  (let ((newcoeff (+ (diff-coefficient t1)
                                     (diff-coefficient t2))))
                    (if (and (number? newcoeff)
                             (= newcoeff 0))
                        (+diff-termlists (cdr l1) (cdr l2))
                        (cons
                         (make-diff-term newcoeff
                                         (diff-factors t1))
                         (+diff-termlists (cdr l1)
                                          (cdr l2))))))
                 ((diff-term>? t1 t2)
                  (cons t1 (+diff-termlists (cdr l1) l2)))
                 (else
                  (cons t2
                        (+diff-termlists l1 (cdr l2)))))))))

Multiplication of term lists is straightforward, if we can multiply individual terms. The product of two term lists l1 and l2 is the term list resulting from adding up the term lists resulting from multiplying every term in l1 by every term in l2.

(define (*diff-termlists l1 l2)
  (reduce (lambda (x y)
            (+diff-termlists y x))
          ’()
          (map (lambda (t1)
                 (append-map (lambda (t2)
                               (*diff-terms t1 t2))
                             l2))
               l1)))

A term has a coefficient and a list of factors (the infinitesimals). In a differential object no term may have an infinitesimal with an exponent greater than one, because δx² = 0. Thus, when we multiply two terms we must check that the lists of factors we are merging have no factors in common. This is the reason that *diff-terms returns a list of the product term or an empty list, to be appended in *diff-termlists. We keep the factors sorted when we merge the two lists of factors; this makes it easier to sort the terms.

(define (*diff-terms x y)
  (let ((fx (diff-factors x)) (fy (diff-factors y)))
    (if (null? (ordered-intersect diff-factor>? fx fy))
        (list (make-diff-term
               (* (diff-coefficient x) (diff-coefficient y))
               (ordered-union diff-factor>? fx fy)))
        ’())))

Finite and infinitesimal parts

A differential object has a finite part and an infinitesimal part. Our diff:binary-proc procedure on page 109 is not correct for differential objects with more than one infinitesimal. To ensure that the parts of the arguments x and y are selected consistently we actually use:

(define (diff:binary-proc f d0f d1f)
  (define (bop x y)
    (let ((factor (maximal-factor x y)))
      (let ((dx (infinitesimal-part x factor))
            (dy (infinitesimal-part y factor))
            (xe (finite-part x factor))
            (ye (finite-part y factor)))
        (d:+ (f xe ye)
             (d:+ (d:* dx (d0f xe ye))
                  (d:* (d1f xe ye) dy))))))
  bop)

where factor is chosen by maximal-factor so that both x and y contain it in a term with the largest number of factors.

The finite part of a differential object is all terms except for terms containing the maximal factor in a term of highest order, and the infinitesimal part is the remaining terms, all of which contain that factor.

Consider the following computation:

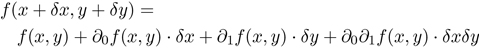
The highest-order term is ∂₀∂₁f (x, y) · δxδy. It is symmetrical with respect to x and y. The crucial point is that we may break the differential object into parts in any way consistent with any one of the maximal factors (here δx or δy) being primary. It doesn't matter which is chosen, because mixed partials of R → R commute.²⁵

(define (finite-part x #!optional factor)
  (if (differential? x)
      (let ((factor (default-maximal-factor x factor)))
        (make-differential
         (remove (lambda (term)
                   (memv factor (diff-factors term)))
                 (diff-terms x))))
      x))

(define (infinitesimal-part x #!optional factor)
  (if (differential? x)
      (let ((factor (default-maximal-factor x factor)))
        (make-differential
         (filter (lambda (term)
                   (memv factor (diff-factors term)))
                 (diff-terms x))))
      0))

(define (default-maximal-factor x factor)
  (if (default-object? factor)
      (maximal-factor x)
      factor))

How extracting really works

As explained on page 114, to make it possible to take multiple derivatives or to handle functions with more than one argument, a differential object is represented as a multivariate power series in which no infinitesimal increment has exponent greater than one. Each term in this series has a coefficient and a list of infinitesimal incremental factors. This complicates the extraction of the derivative with respect to any one incremental factor. Here is the real story:

In the case where a differential object is returned we must find those terms of the result that contain the infinitesimal factor dx for the derivative we are evaluating. We collect those terms, removing dx from each. If there are no terms left after taking out the ones with dx, the value of the derivative is zero. If there is exactly one term left, which has no differential factors, then the coefficient of that term is the value of the derivative. But if there are remaining terms with differential factors, we must return the differential object with those residual terms as the value of the derivative.

(define (extract-dx-differential value dx)
  (let ((dx-diff-terms
         (filter-map
          (lambda (term)
            (let ((factors (diff-factors term)))
              (and (memv dx factors)
                   (make-diff-term (diff-coefficient term)
                                   (delv dx factors)))))
          (diff-terms value))))
    (cond ((null? dx-diff-terms) 0)
          ((and (null? (cdr dx-diff-terms))
                (null? (diff-factors (car dx-diff-terms))))
           (diff-coefficient (car dx-diff-terms)))
          (else (make-differential dx-diff-terms)))))

(define-generic-procedure-handler extract-dx-part
  (match-args differential? diff-factor?)
  extract-dx-differential)

Higher-order functions

For many applications we want our automatic differentiator to work correctly for functions that return functions as values:

(((derivative
   (lambda (x)
     (lambda (y z)
       (* x y z))))
  2)
 3
 4)
;Value: 12

Including literal functions and partial derivatives makes this even more interesting.

((derivative
  (lambda (x)
    (((partial 1) (literal-function ’f))
     x ’v)))
 ’u)
(((partial 0) ((partial 1) f)) u v)

And things can get even more complicated:

(((derivative
   (lambda (x)
     (derivative
      (lambda (y)
        ((literal-function ’f)
         x y)))))
  ’u)
 ’v)
(((partial 0) ((partial 1) f)) u v)

Making this work introduces serious complexity in the procedure extract-dx-part.

If the result of applying a function to a differential object is a function—a derivative of a derivative, for example—we need to defer the extraction until that function is called with arguments:

In a case where a function is returned, as in

(((derivative
   (lambda (x)
     (derivative
      (lambda (y)
        (* x y)))))
  ’u)
 ’v)
1

we cannot extract the derivative until the function is applied to arguments. So we defer the extraction until we get the value resulting from that application. We extend our generic extractor:

(define (extract-dx-function fn dx)
  (lambda args
    (extract-dx-part (apply fn args) dx)))

(define-generic-procedure-handler extract-dx-part
  (match-args function? diff-factor?)
  extract-dx-function)

Unfortunately, this version of extract-dx-function has a subtle bug.²⁶ Our patch is to wrap the body of the new deferred procedure with code that remaps the factor dx to avoid the unpleasant conflict. So, we change the handler for functions to:

(define (extract-dx-function fn dx)
  (lambda args
    (let ((eps (make-new-dx)))
       (replace-dx dx eps
        (extract-dx-part
         (apply fn
           (map (lambda (arg)
                  (replace-dx eps dx arg))
                args))
         dx)))))

This creates a brand-new factor eps and uses it to stand for dx in the arguments, thus preventing collision with any other instances of dx.

Replacement of the factors is itself a bit more complicated, because the code has to grovel around in the data structures. We will make the replacement a generic procedure, so we can extend it to new kinds of data. The default is that the replacement is just the identity on the object:

(define (replace-dx-default new-dx old-dx object) object)

(define replace-dx
  (simple-generic-procedure ’replace-dx 3
                            replace-dx-default))

For a differential object we have to actually go in and substitute the new factor for the old one, and we have to keep the factor lists sorted:

(define (replace-dx-differential new-dx old-dx object)
  (make-differential
   (sort (map (lambda (term)
                (make-diff-term
                 (diff-coefficient term)
                 (sort (substitute new-dx old-dx
                                   (diff-factors term))
                       diff-factor>?)))
              (diff-terms object))
         diff-term>?)))

(define-generic-procedure-handler replace-dx
  (match-args diff-factor? diff-factor? differential?)
  replace-dx-differential)

Finally, if the object is itself a function we have to defer it until arguments are available to compute a value:

(define (replace-dx-function new-dx old-dx fn)
  (lambda args
    (let ((eps (make-new-dx)))
      (replace-dx old-dx eps
        (replace-dx new-dx old-dx
          (apply fn
            (map (lambda (arg)
                   (replace-dx eps old-dx arg))
                 args)))))))

(define-generic-procedure-handler replace-dx
  (match-args diff-factor? diff-factor? function?)
  replace-dx-function)

This is quite a bit more complicated than we might expect. It actually does three replacements of the differential factors. This is to prevent collisions with factors that may be free in the body of fn that are inherited from the lexical environment of definition of the function fn.²⁷

---

Exercise 3.11: The bug!

Before we became aware of the bug pointed out in footnote 26 on page 121, the procedure extract-dx-function was written:

(define (extract-dx-function fn dx)
  (lambda args
    (extract-dx-part (apply fn args) dx)))

Demonstrate the reason for the use of the replace-dx wrapper by constructing a function whose derivative is wrong with this earlier version of extract-dx-part but is correct in the fixed version. This is not easy! You may want to read the references pointed at in footnote 26.

---

3.3.4 Literal functions of differential arguments

For simple arguments, applying a literal function is just a matter of constructing the expression that is the application of the function expression to the arguments. But literal functions must also be able to accept differential objects as arguments. When that happens, the literal function must construct (partial) derivative expressions for the arguments that are differentials. For the ith argument of an n-argument function the appropriate derivative expression is:

(define (deriv-expr i n fexp)
  (if (= n 1)
      ‘(derivative ,fexp)
      ‘((partial ,i) ,fexp)))

Some arguments may be differential objects, so a literal function must choose, for each argument, a finite part and an infinitesimal part. Just as for binary arithmetic handlers, the maximal factor must be consistently chosen. Our literal functions are able to take many arguments, so this may seem complicated, but we wrote the maximal-factor procedure to handle many arguments. This is explained in section 3.3.3.

If there are no differential objects among the arguments we just cons up the required expression. If there are differential objects we need to make a derivative of the literal function. To do this we find a maximal factor from all of the arguments and separate out the finite parts of the arguments—the terms that do not have that factor. (The infinitesimal parts are the terms that have that factor.) The partial derivatives are themselves literal functions with expressions that are constructed to include the argument index. The resulting differential object is the inner product of the partial derivatives at the finite parts of the arguments with the infinitesimal parts of the arguments.

This is all brought together in the following procedure:

(define (literal-function fexp)
  (define (the-function . args)
    (if (any differential? args)
        (let ((n (length args))
              (factor (apply maximal-factor args)))
          (let ((realargs
                 (map (lambda (arg)
                        (finite-part arg factor))
                      args))
                (deltargs
                 (map (lambda (arg)
                        (infinitesimal-part arg factor))
                      args)))
            (let ((fxs (apply the-function realargs))
                  (partials
                   (map (lambda (i)
                          (apply (literal-function
                                  (deriv-expr i n fexp))
                                 realargs))
                        (iota n))))
              (fold d:+ fxs
                (map d:* partials deltargs)))))
        ‘(,fexp ,@args)))
  the-function)

---

Exercise 3.12: Functions with structured values

We made the extract-dx-part procedure generic (page 110) so we could extend it for values other than differential objects and functions. Extend extract-dx-part to work with derivatives of functions that return vectors. Note: You also have to extend the replace-dx generic procedure (page 122) in the extractor.

---

3.4 Efficient generic procedures

In section 3.2.3 we dispatched to a handler by finding an applicable rule using the dispatch store provided in the metadata:

(define (generic-procedure-dispatch metadata args)
  (let ((handler
         (get-generic-procedure-handler metadata args)))
    (apply handler args)))

The implementation of the dispatch store (on page 98) we used (on page 89) to make the simple-generic-procedure constructor was rather crude. The simple dispatch store maintains the rule set as a list of rules. Each rule is represented as a pair of an applicability and a handler. The applicability is a list of lists of predicates to apply to tendered arguments. The way a generic procedure constructed by simple-generic-procedure finds an appropriate handler is to sequentially scan the list of rules looking for an applicability that is satisfied by the arguments.

This is seriously inefficient, because the applicability of many rules may have the same predicate in a given operand position: For example, for multiplication in a system of numerical and symbolic arithmetic there may be many rules whose first predicate is number?. So the number? predicate may be applied many times before finding an applicable rule. It would be good to organize the rules so that finding an applicable one does not perform redundant tests. This is usually accomplished by the use of an index.

3.4.1 Tries

One simple index mechanism is based on the trie.²⁸

A trie is traditionally a tree structure, but more generally it may be a directed graph. Each node in the trie has edges connecting to successor nodes. Each edge has an associated predicate. The data being tested is a linear sequence of features, in this case the arguments to a generic procedure.

Starting at the root of the trie, the first feature is taken from the sequence and is tested by each predicate on an edge emanating from the root node. The successful predicate's edge is followed to the next node, and the process repeats with the remainder of the sequence of features. When we run out of features, the current node will contain the associated value, in this case an applicable handler for the arguments.

It is possible that at any node, more than one predicate may succeed. If this happens, then all of the successful branches must be followed. Thus there may be multiple applicable handlers, and there must be a separate means of deciding what to do.

Here is how we can use a trie. Evaluating the following sequence of commands will incrementally construct the trie shown in figure 3.1.

Figure 3.1 A trie can be used to classify sequences of features. A trie is a directed graph in which each edge has a predicate. Starting at the root, the first feature is tested by each predicate on an edge proceeding from the root. If a predicate is satisfied, the process moves to the node at the end of that edge and the next feature is tested. This is repeated with successive features. The classification of the sequence is the set of terminal nodes arrived at.

(define a-trie (make-trie))

We can add an edge to this trie

(define s (add-edge-to-trie a-trie symbol?))

where add-edge-to-trie returns the new node that is at the target end of the new edge. This node is reached by being matched against a symbol.

We can make chains of edges, which are referenced by lists of the corresponding edge predicates

(define sn (add-edge-to-trie s number?))

The node sn is reached from the root via the path (list symbol? number?). Using a path, there is a simpler way to make a chain of edges than repeatedly calling add-edge-to-trie:

(define ss (intern-path-trie a-trie (list symbol? symbol?)))

We can add a value to any node (here we show symbolic values, but we will later store values that are procedural handlers):

(trie-has-value? sn)
#f

(set-trie-value! sn ’(symbol number))

(trie-has-value? sn)
#t

(trie-value sn)
(symbol number)

We can also use a path-based interface to set values

(set-path-value! a-trie (list symbol? symbol?)
                ’(symbol symbol))

(trie-value ss)
(symbol symbol)

Note that both intern-path-trie and set-path-value! reuse existing nodes and edges when possible, adding edges and nodes where necessary.

Now we can match a feature sequence against the trie we have constructed so far:

(equal? (list ss) (get-matching-tries a-trie ’(a b)))
#t

(equal? (list s) (get-matching-tries a-trie ’(c)))
#t

We can also combine matching with value fetching. The procedure get-a-value finds all matching nodes, picks one that has a value, and returns that value.

(get-a-value a-trie ’(a b))
(symbol symbol)

But not all feature sequences have an associated value:

(get-a-value a-trie ’(-4))
;Unable to match features: (-4)

We can incrementally add values to nodes in the trie:

(set-path-value! a-trie (list negative-number?)
                 ’(negative-number))
(set-path-value! a-trie (list even-number?)
                 ’(even-number))

(get-all-values a-trie ’(-4))
((even-number) (negative-number))

where get-all-values finds all the nodes matching a given feature sequence and returns their values.

Given this trie implementation, we can make a dispatch store that uses a trie as its index:

(define (make-trie-dispatch-store)
  (let ((delegate (make-simple-dispatch-store))
        (trie (make-trie)))
    (define (get-handler args)
      (get-a-value trie args))
    (define (add-handler! applicability handler)
      ((delegate ’add-handler!) applicability handler)
      (for-each (lambda (path)
                  (set-path-value! trie path handler))
                applicability))
    (lambda (message)
      (case message
        ((get-handler) get-handler)
        ((add-handler!) add-handler!)
        (else (delegate message))))))

We make this dispatch store simple by delegating most of the operations to a simple dispatch store. The operations that are not delegated are add-handler!, which simultaneously stores the handler in the simple dispatch store and also in the trie, and get-handler, which exclusively uses the trie for access. The simple dispatch store manages the default handler and also the set of rules, which is useful for debugging. This is a simple example of the use of delegation to extend an interface, as opposed to the better-known inheritance idea.

---

Exercise 3.13: Trie rules

To make it easy to experiment with different dispatch stores, we gave generic-procedure-constructor and make-generic-arithmetic the dispatch store maker. For example, we can build a full generic arithmetic as on page 95 but using make-trie-dispatch-store as follows:

(define trie-full-generic-arithmetic
  (let ((g (make-generic-arithmetic make-trie-dispatch-store)))
    (add-to-generic-arithmetic! g numeric-arithmetic)
    (extend-generic-arithmetic! g function-extender)
    (add-to-generic-arithmetic! g
       (symbolic-extender numeric-arithmetic))
    g))

(install-arithmetic! trie-full-generic-arithmetic)

1. a. Does this make any change to the dependence on order that we wrestled with in section 3.2.2?
2. b. In general, what characteristics of the predicates could produce situations where there is more than one appropriate handler for a sequence of arguments?
3. c. Are there any such situations in our generic arithmetic code?

---

We have provided a crude tool to measure the effectiveness of our dispatch strategy. By wrapping any computation with with-predicate-counts we can find out how many times each dispatch predicate is called in an execution. For example, evaluating (fib 20) in a generic arithmetic with a trie-based dispatch store may yield something like this:²⁹

(define (fib n)
  (if (< n 2)
      n
      (+ (fib (- n 1)) (fib (- n 2)))))

(with-predicate-counts (lambda () (fib 20)))
(109453 number)
(109453 function)
(54727 any-object)
(109453 symbolic)
6765

---

Exercise 3.14: Dispatch efficiency: gotcha!

Given this performance tool it is instructive to look at executions of

(define (test-stormer-counts)
  (define (F t x) (- x))
  (define numeric-s0
    (make-initial-history 0 .01 (sin 0) (sin -.01) (sin -.02)))
  (with-predicate-counts
   (lambda ()
     (x 0 ((evolver F ’h stormer-2) numeric-s0 1)))))

for the rule-list–based dispatch in make-simple-dispatch-store, in the arithmetic you get by:

(define full-generic-arithmetic
  (let ((g (make-generic-arithmetic make-simple-dispatch-store)))
    (add-to-generic-arithmetic! g numeric-arithmetic)
    (extend-generic-arithmetic! g function-extender)
    (add-to-generic-arithmetic! g
            (symbolic-extender numeric-arithmetic))
    g))

(install-arithmetic! full-generic-arithmetic)

and the trie-based version (exercise 3.13), in the arithmetic you get by:

(install-arithmetic! trie-full-generic-arithmetic)

For some problems the trie should have much better performance than the simple rule list. We expect that the performance will be better with the trie if we have a large number of rules with the same initial segment.

Understanding this is important, because the fact that sometimes the trie does not help with the performance appears counterintuitive. We explicitly introduced the trie to avoid redundant calls. Explain this phenomenon in a concise paragraph.

For an additional insight, look at the performance of (fib 20) in the two implementations.

---

When more than one handler is applicable for a given sequence of arguments, it is not clear how to use those handlers; addressing this situation is the job of a resolution policy. There are many considerations when designing a resolution policy. For example, a policy that chooses the most specific handler is often a good policy; however, we need more information to implement such a policy. Sometimes it is appropriate to run all of the applicable handlers and compare their results. This can be used to catch errors and provide a kind of redundancy. Or if we have partial information provided by each handler, such as a numerical interval, the results of different handlers can be combined to provide better information.

3.4.2 Caching

With the use of tries we have eliminated redundant evaluation of argument predicates. We can do better by using abstraction to eliminate the evaluation of predicates altogether. A predicate identifies a set of objects that are distinguished from all other objects; in other words, the predicate and the set it distinguishes are effectively the same. In our trie implementation, we use the equality of the predicate procedures to avoid redundancy; otherwise we would have redundant edges in the trie and it would be no help at all. This is also why the use of combinations of predicates doesn't mix well with the trie implementation.

The problem here is that we want to build an index that discriminates objects according to predicates, but the opacity of procedures makes them unreliable when used as keys to the index. What we'd really like is to assign a name to the set distinguished by a given predicate. If we had a way to get that name from a given object by superficial examination, we could avoid computing the predicate at all. This name is a “type”; but in order to avoid confusion we will refer to this name as a tag.

Given a way to get a tag from an object, we can make a cache that saves the handler resulting from a previous dispatch and reuses it for other dispatches whose arguments have the same tag pattern. But in the absence of explicitly attached tags, there are limitations to this approach, because we can only discriminate objects that share an implementation-specified representation. For example, it's easy to distinguish between a number and a symbol, but it's not easy to distinguish a prime number, because it's unusual for an implementation to represent them specially.

We will return to the problem of explicit tagging in section 3.5, but in the meantime it is still possible to make a useful cache using the representation tags from the Scheme implementation. Given an implementation-specific procedure implementation-type-name to obtain the representation tag of an object, we can make a cached dispatch store:

(define a-cached-dispatch-store
  (cache-wrapped-dispatch-store (make-trie-dispatch-store)
                                implementation-type-name))

This dispatch store wraps a cache around a trie dispatch store, but it could just as well wrap a simple dispatch store.

The heart of the cached dispatch store is a memoizer built on a hash table. The key for the hash table is the list of representation tags extracted by the implementation-type-name procedure from the arguments. By passing implementation-type-name into this dispatch-store wrapper (as get-key) we can use it to make cached dispatch stores for more powerful tag mechanisms that we will develop soon.

(define (cache-wrapped-dispatch-store dispatch-store get-key)
  (let ((get-handler
         (simple-list-memoizer
           eqv?
           (lambda (args) (map get-key args))
           (dispatch-store ’get-handler))))
    (lambda (message)
      (case message
        ((get-handler) get-handler)
        (else (dispatch-store message))))))

The call to simple-list-memoizer wraps a cache around its last argument, producing a memoized version of it. The second argument specifies how to get the cache key from the procedure's arguments. The eqv? argument specifies how the tags will be identified in the cache.

---

Exercise 3.15: Cache performance

Using the same performance tool we introduced for exercise 3.14 on page 130, make measurements for execution of (test-stormer-counts) and (fib 20) in the cached version of dispatch with the same generic arithmetics explored in exercise 3.14. Record your results. How do they compare?

---

3.5 Efficient user-defined types

In section 3.4.2 we introduced tags as part of a caching mechanism for dispatch. Each argument is mapped to a tag, and the list of tags is then used as a key in a cache to obtain the handler. If the cache has a handler associated with this list of tags, it is used. If not, the trie of predicates is used to find the appropriate handler and it is entered into the cache associated with the list of tags.

This mechanism is pretty crude: the predicates that can be used for the applicability specifications are restricted to those that always give the same boolean value for any two objects with the same tag. So the discrimination of types cannot be any finer than the available tags. The tags were implementation-specific symbols, such as pair, vector, or procedure. So this severely limits the possible predicates. We could not have rules that distinguish between integers that satisfy even-integer? and integers that satisfy odd-integer?, for example.

What is needed is a system of tagging that makes it computationally easy to obtain the tag associated with a data item, but where the tags are not restricted to a small set of implementation-specific values. This can be accomplished by attaching a tag to each data item, either with an explicit data structure or via a table of associations.

We have several problems interwoven here: we want to use predicates in applicability specifications; we want an efficient mechanism for dispatch; and we want to be able to specify relationships between predicates that can be used in the dispatch. For example, we want to be able to say that the predicate integer? is the disjunction of the predicates even-integer? and odd-integer?, and also that integer? is the disjunction of positive-integer?, negative-integer?, and zero?.

To capture such relationships we need to put metadata on the predicates; but adding an associative lookup to get the metadata of a predicate, as we did with the arity of a function (on page 28), adds too much overhead, because the metadata will contain references to other tags, and chasing these references must be efficient.

One way out is to register the needed predicates. Registration creates a new kind of tag, a data structure that is associated with the predicate. The tag will be easy to attach to objects that are accepted by the predicate. The tag will provide a convenient place to store metadata.

We will construct a system in which each distinct object can have only one tag and where relationships between predicates can be declared. This may appear to be overly simple, but it is adequate for our purposes.

3.5.1 Predicates as types

Let's start with some simple predicates. For example, the primitive procedure exact-integer? is preregistered in our system as a simple predicate:

(predicate? exact-integer?)
#t

Now let's define a new predicate that's not a primitive. We will build it on this particularly slow test for prime numbers.

(define (slow-prime? n)
  (and (n:exact-positive-integer? n)
       (n:>= n 2)
       (let loop ((k 2))
         (or (n:> (n:square k) n)
             (and (not (n:= (n:remainder n k) 0))
                  (loop (n:+ k 1)))))))

Note that all of the arithmetic operators are prefixed with n: to ensure that we get the underlying Scheme operations.

We construct the prime-number? abstract predicate, with a name for use in error messages and a criterion, slow-prime?, for an object to be considered a prime number:

(define prime-number?
  (simple-abstract-predicate ’prime-number slow-prime?))

The procedure simple-abstract-predicate creates an abstract predicate, which is a clever trick for memoizing the result of an expensive predicate (in this case slow-prime?). An abstract predicate has an associated constructor that is used to make a tagged object, consisting of the abstract predicate's tag and an object. The constructor requires that the object to be tagged satisfies the expensive predicate. The resulting tagged object satisfies the abstract predicate, as well as carrying its tag. Consequently the tagged object can be tested for the property defined by the expensive predicate by using the fast abstract predicate (or, equivalently, by dispatching on its tag).

For example, the abstract predicate prime-number? is used to tag objects that are verified prime numbers, for the efficient implementation of generic dispatch. This is important because we do not want to execute slow-prime? during the dispatch to determine whether a number is prime. So we build a new tagged object, which contains both a tag (the tag for prime-number?) and a datum (the raw prime number). When a generic procedure is handed a tagged object, it can efficiently retrieve its tag and use that as a cache key.

In order to make tagged objects, we use predicate-constructor to get the constructor associated with the abstract predicate:

(define make-prime-number
  (predicate-constructor prime-number?))

(define short-list-of-primes
  (list (make-prime-number 2)
        (make-prime-number 7)
        (make-prime-number 31)))

The constructor make-prime-number requires that its argument be prime, as determined by slow-prime?: the only objects that can be tagged by this constructor are prime numbers.

(make-prime-number 4)
;Ill-formed data for prime-number: 4

3.5.2 Relationships between predicates

The sets that we can define with abstract predicates can be related to one another. For example, the primes are a subset of the positive integers. The positive integers, the even integers, and the odd integers are subsets of the integers. This is important because any operation that is applicable to an integer is applicable to any element of any subset, but there are operations that can be applied to an element of a subset that cannot be applied to all elements of an enclosing superset. For example, the even integers can be halved without leaving a remainder, but that is not true of the full integers.

When we defined prime-number?, we effectively defined a set of objects. But that set has no relation to the set defined by exact-integer?:

(exact-integer? (make-prime-number 2))
#f

We would like these sets to be properly related, which is done by adding some metadata to the predicates themselves:

(set-predicate<=! prime-number? exact-integer?)

This procedure set-predicate<=! modifies the metadata of its argument predicates to indicate that the set defined by the first argument is a (non-strict) subset of the set defined by the second argument. In our case, the set defined by prime-number? is declared to be a subset of the set defined by exact-integer?. Once this is done, exact-integer? will recognize our objects:

(exact-integer? (make-prime-number 2))
#t

3.5.3 Predicates are dispatch keys

The abstract predicates we have defined are suitable for use in generic dispatch. Even better, they can be used as cache keys to make dispatch efficient. As we described above, when a predicate is registered, a new tag is created and associated with the predicate. All we need is a way to get the tag for a given object: the procedure get-tag does this.

If we pass get-tag to cache-wrapped-dispatch-store as its get-key argument, we have a working implementation. However, since the set defined by a predicate can have subsets, we need to consider a situation where there are multiple potential handlers for some given arguments. There are a number of possible ways to resolve this situation, but the most common is to identify the “most specific” handler by some means, and invoke that one. Since the subset relation is a partial order, it may not be clear which handler is most specific, so the implementation must resolve the ambiguity by independent means.

Here is one such implementation. It uses a procedure rule< to sort the matching rules into an appropriate order, then chooses a handler from the result.³⁰

(define (make-subsetting-dispatch-store-maker choose-handler)
  (lambda ()
    (let ((delegate (make-simple-dispatch-store)))
      (define (get-handler args)
        (let ((matching
               (filter (lambda (rule)
                        (is-generic-handler-applicable?
                         rule args))
                      ((delegate ’get-rules)))))
         (and (n:pair? matching)
              (choose-handler    ; from sorted handlers
               (map cdr (sort matching rule<))
               ((delegate ’get-default-handler))))))
     (lambda (message)
       (case message
         ((get-handler) get-handler)
         (else (delegate message)))))))

The procedure make-most-specific-dispatch-store chooses the first of the sorted handlers to be the effective handler:

(define make-most-specific-dispatch-store
  (make-subsetting-dispatch-store-maker
   (lambda (handlers default-handler)
     (car handlers))))

Another possible choice is to make a “chaining” dispatch store, in which each handler gets an argument that can be used to invoke the next handler in the sorted sequence. This is useful for cases where a subset handler wants to extend the behavior of a superset handler rather than overriding it. We will see an example of this in the clock handler of the adventure game in section 3.5.4.

(define make-chaining-dispatch-store
  (make-subsetting-dispatch-store-maker
   (lambda (handlers default-handler)
     (let loop ((handlers handlers))
       (if (pair? handlers)
           (let ((handler (car handlers))
                 (next-handler (loop (cdr handlers))))
             (lambda args
               (apply handler (cons next-handler args))))
           default-handler)))))

Either one of these dispatch stores can be made into a cached dispatch store by adding a caching wrapper:

(define (make-cached-most-specific-dispatch-store)
  (cache-wrapped-dispatch-store
     (make-most-specific-dispatch-store)
     get-tag))

(define (make-cached-chaining-dispatch-store)
  (cache-wrapped-dispatch-store
     (make-chaining-dispatch-store)
     get-tag))

Then we create the corresponding generic-procedure constructors:

(define most-specific-generic-procedure
  (generic-procedure-constructor
   make-cached-most-specific-dispatch-store))

(define chaining-generic-procedure
  (generic-procedure-constructor
   make-cached-chaining-dispatch-store))

3.5.4 Example: An adventure game

One traditional way to model a world is “object-oriented programming.” The idea is that the world being modeled is made up of objects, each of which has independent local state, and the coupling between the objects is loose. Each object is assumed to have particular behaviors. An object may receive messages from other objects, change its state, and send messages to other objects. This is very natural for situations where the behavior we wish to model does not depend on the collaboration of multiple sources of information: each message comes from one other object. This is a tight constraint on the organization of a program.

There are other ways to break a problem into pieces. We have looked at “arithmetic” enough to see that the meaning of an operator, such as *, can depend on the properties of multiple arguments. For example, the product of a number and a vector is a different operation from the product of two vectors or of two numbers. This kind of problem is naturally formulated in terms of generic procedures.³¹

Consider the problem of modeling a world made of “places,” “things,” and “people” with generic procedures. How should the state variables that are presumed to be local to the entities be represented and packaged? What operations are appropriately generic over what kinds of entities? Since it is natural to group entities into types (or sets) and to express some of the operations as appropriate for all members of an inclusive set, how is subtyping to be arranged? Any object-oriented view will prescribe specific answers to these design questions; here we have more freedom, and must design the conventions that will be used.

To illustrate this process we will build a world for a simple adventure game. There is a network of rooms connected by passages and inhabited by a variety of creatures, some of which are autonomous in that they can wander around. There is an avatar that is controlled by the player. There are things, some of which can be picked up and carried by the creatures. There are ways that the creatures can interact: a troll can bite another creature and damage it; any creature can take a thing carried by another creature.

Every entity in our world has a set of named properties. Some of these are fixed and others are changeable. For example, a room has exits to other rooms. These represent the topology of the network and cannot be changed. A room also has contents, such as the creatures who are currently in the room and things that may be acquired. The contents of a room change as creatures move around and as they carry things to and from other rooms. We will computationally model this set of named properties as a table from names to property values.

There is a set of generic procedures that are appropriate for this world. For example, some things, such as books, creatures, and the avatar, are movable. In every case, moving a thing requires deleting it from the contents of the source, adding it to the contents of the destination, and changing its location property. This operation is the same for books, people, and trolls, all of which are members of the “movable things” set.

A book can be read; a person can say something; a troll can bite a creature. To implement these behaviors there are specific properties of books that are different from the properties of people or those of trolls. But these different kinds of movable things have some properties in common, such as location. So when such a thing is instantiated, it must make a table for all of its properties, including those inherited from more inclusive sets. The rules for implementing the behavior of operators such as move must be able to find appropriate handlers for manipulating the properties in each case.

The game

Our game is played on a rough topological map of MIT. There are various autonomous agents (non-player characters), such as students and officials. The registrar, for example, is a troll. There are movable and immovable things, and movable things can be taken by an autonomous agent or the player's avatar. Although this game has little detail, it can be expanded to be very interesting.

We create a session with an avatar named gjs who appears in a random place. The game tells the player about the environment of the avatar.

(start-adventure ’gjs)
You are in dorm-row
You see here: registrar
You can exit: east

Since the registrar is here it is prudent to leave! (He may bite, and after enough bites the avatar will die.)

(go ’east)
gjs leaves via the east exit
gjs enters lobby-7
You are in lobby-7
You can see: lobby-10 infinite-corridor
You can exit: up west east
alyssa-hacker enters lobby-7
alyssa-hacker says: Hi gjs
ben-bitdiddle enters lobby-7
ben-bitdiddle says: Hi alyssa-hacker gjs
registrar enters lobby-7
registrar says: Hi ben-bitdiddle alyssa-hacker gjs

Notice that several autonomous agents arrive after the avatar, and that they do so one at a time. So we see that the report is for an interval of simulated time rather than a summary of the state at an instant. This is an artifact of our implementation rather than a deliberate design choice.

Unfortunately the registrar has followed, so it's time to leave again.

(say "I am out of here!")
gjs says: I am out of here!

(go ’east)
gjs leaves via the east exit
gjs enters lobby-10
You are in lobby-10
You can see: lobby-7 infinite-corridor great-court
You can exit: east south west up

(go ’up)
gjs leaves via the up exit
gjs enters 10-250
You are in 10-250
You see here: blackboard
You can exit: up down

Room 10-250 is a lecture hall, with a large blackboard. Perhaps we can take it?

(take-thing ’blackboard)
blackboard is not movable

So sad—gjs loves blackboards. Let's keep looking around.

(go ’up)
gjs leaves via the up exit
gjs enters barker-library
You are in barker-library
You see here: engineering-book
You can exit: up down
An earth-shattering, soul-piercing scream is heard...

Apparently, a troll (maybe the registrar) has eaten someone. However, here is a book that should be takable, so we take it and return to the lecture hall.

(take-thing ’engineering-book)
gjs picks up engineering-book

(go 'down)
gjs leaves via the down exit
gjs enters 10-250
You are in 10-250
Your bag contains: engineering-book
You see here: blackboard
You can exit: up down

From the lecture hall we return to lobby-10, where we encounter lambda-man, who promptly steals our book.

(go ’down)
gjs leaves via the down exit
gjs enters lobby-10
gjs says: Hi lambda-man
You are in lobby-10
Your bag contains: engineering-book
You see here: lambda-man
You can see: lobby-7 infinite-corridor great-court
You can exit: east south west up
alyssa-hacker enters lobby-10
alyssa-hacker says: Hi gjs lambda-man
lambda-man takes engineering-book from gjs
gjs says: Yaaaah! I am upset!

The object types

To create an object in our game, we define some properties with make-property, define a type predicate with make-type, get the predicate's associated instantiator with type-instantiator, and call that instantiator with appropriate arguments.

How do we make a troll? The make-troll constructor for a troll takes arguments that specify the values for properties that are specific to the particular troll being constructed. The troll will be created in a given place with a restlessness (proclivity to move around), an acquisitiveness (proclivity to take things), and a hunger (proclivity to bite other people).

(define (create-troll name place restlessness hunger)
  (make-troll ’name name
              ’location place
              ’restlessness restlessness
              ’acquisitiveness 1/10
              ’hunger hunger))

We create two trolls: grendel and registrar. They are initially placed in random places, with some random proclivities.

(define (create-trolls places)
  (map (lambda (name)
         (create-troll name
                       (random-choice places)
                       (random-bias 3)
                       (random-bias 3)))
       ’(grendel registrar)))

The procedure random-choice randomly selects one item from the list it is given. The procedure random-bias chooses a number (in this case 1, 2, or 3) and returns its reciprocal.

The troll type is defined as a predicate that is true only of trolls. The make-type procedure is given a name for the type and a descriptor of the properties that are specific to trolls. (Only trolls have a hunger property.)

(define troll:hunger
  (make-property ’hunger ’predicate bias?))

(define troll?
  (make-type 'troll (list troll:hunger)))

The troll is a specific type of autonomous agent. Thus the set of trolls is a subset of (<=) the set of autonomous agents.

(set-predicate<=! troll? autonomous-agent?)

The constructor for trolls is directly derived from the predicate that defines the type, as is the accessor for the hunger property.

(define make-troll
  (type-instantiator troll?))

(define get-hunger
  (property-getter troll:hunger troll?))

Autonomous agents are occasionally stimulated by the “clock” to take some action. The distinctive action of the troll is to bite other people.

(define-clock-handler troll? eat-people!)

A biased coin is flipped to determine whether the troll is hungry at the moment. If it is hungry it looks for other people (trolls are people too!), and if there are some it chooses one to bite, causing the victim to suffer some damage. The narrator describes what happens.

(define (eat-people! troll)
  (if (flip-coin (get-hunger troll))
      (let ((people (people-here troll)))
        (if (n:null? people)
            (narrate! (list (possessive troll) "belly rumbles")
                      troll)
            (let ((victim (random-choice people)))
              (narrate! (list troll "takes a bite out of"
                              victim)
                        troll)
              (suffer! (random-number 3) victim))))))

The procedure flip-coin generates a random fraction between 0 and 1. If that fraction is greater than the argument, it returns true. The procedure random-number returns a positive number less than or equal to its argument.

The procedure narrate! is used to add narration to the story. The second argument to narrate! (troll in the above code) may be anything that has a location. The narrator announces its first argument in the location thus determined. One can only hear that announcement if one is in that location.

We said that a troll is a kind of autonomous agent. The autonomous agent type is defined by its predicate, which specifies the properties that are needed for such an agent. We also specify that the set of autonomous agents is a subset of the set of all persons.

(define autonomous-agent:restlessness
  (make-property 'restlessness ’predicate bias?))

(define autonomous-agent:acquisitiveness
  (make-property ’acquisitiveness ’predicate bias?))

(define autonomous-agent?
  (make-type ’autonomous-agent
             (list autonomous-agent:restlessness
                   autonomous-agent:acquisitiveness)))

(set-predicate<=! autonomous-agent? person?)

The constructor for trolls specified values for the properties restlessness and acquisitiveness, which are needed to make an autonomous agent, in addition to the hunger property specific to trolls. Since trolls are autonomous agents, and autonomous agents are persons, there must also be values for the properties of a person and all its supersets. In this system almost all properties have default values that are automatically filled if not specified. For example, all objects need names; the name was specified in the constructor for trolls. But a person also has a health property, necessary to accumulate damage, and this property value was not explicitly specified in the constructor for trolls.

The generic procedures

Now that we have seen how objects are built, we will look at how to implement their behavior. Specifically, we will see how generic procedures are an effective tool for describing complex behavior.

We defined get-hunger, which is used in eat-people!, in terms of property-getter. A getter for a property of objects of a given type is implemented as a generic procedure that takes an object as an argument and returns the value of the property.

(define (property-getter property type)
  (let ((procedure    ; the getter
         (most-specific-generic-procedure
          (symbol ’get- (property-name property))
          1           ; arity
          #f)))       ; default handler
    (define-generic-procedure-handler procedure
      (match-args type)
      (lambda (object)
        (get-property-value property object)))
    procedure))

This shows the construction of a generic procedure with a generated name (for example get-hunger) that takes one argument, and the addition of a handler that does the actual access. The last argument to most-specific-generic-procedure is the default handler for the procedure; specifying #f means that the default is to signal an error.

We also used define-clock-handler to describe an action to take when the clock ticks. That procedure just adds a handler to a generic procedure clock-tick!, which is already constructed.

(define (define-clock-handler type action)
  (define-generic-procedure-handler clock-tick!
    (match-args type)
    (lambda (super object)
      (super object)
      (action object))))

This generic procedure supports “chaining,” in which each handler gets an extra argument (in this case super) that when called causes any handlers defined on the supersets of the given object to be called. The arguments passed to super have the same meaning as the arguments received here; in this case there's just one argument and it is passed along. This is essentially the same mechanism used in languages such as Java, though in that case it's done with a magic keyword rather than an argument.

The clock-tick! procedure is called to trigger an action, not to compute a value. Notice that the action we specify will be taken after any actions specified by the supersets. We could have chosen to do the given action first and the others later, just by changing the order of the calls.

The real power of the generic procedure organization is illustrated by the mechanisms for moving things around. For example, when we pick up the engineering book, we move it from the room to our bag. This is implemented with the move! procedure:

(define (move! thing destination actor)
  (generic-move! thing
                 (get-location thing)
                 destination
                 actor))

The move! procedure is implemented in terms of a more general procedure generic-move! that takes four arguments: the thing to be moved, the thing's current location, its destination location, and the actor of the move procedure. This procedure is generic because the movement behavior potentially depends on the types of all of the arguments.

When we create generic-move! we also specify a very general handler to catch cases that are not covered by more specific handlers (for specific argument types).

(define generic-move!
  (most-specific-generic-procedure ’generic-move! 4 #f))

(define-generic-procedure-handler generic-move!
  (match-args thing? container? container? person?)
  (lambda (thing from to actor)
    (tell! (list thing "is not movable")
           actor)))

The procedure tell! sends the message (its first argument) to the actor that is trying to move the thing. If the actor is the avatar, the message is displayed.

In the demo we picked up the book. We did that by calling the procedure take-thing with the name engineering-book. This procedure resolves the name to the thing and then calls take-thing!, which invokes move!:

(define (take-thing name)
  (let ((thing (find-thing name (here))))
    (if thing
        (take-thing! thing my-avatar)))
  'done)

(define (take-thing! thing person)
  (move! thing (get-bag person) person))

There are two procedures here. The first is a user-interface procedure to give the player a convenient way of describing the thing to be taken by giving its name. It calls the second, an internal procedure that is also used in other places.

To make this work we supply a handler for generic-move! that is specialized to moving mobile things from places to bags:

(define-generic-procedure-handler generic-move!
  (match-args mobile-thing? place? bag? person?)
  (lambda (mobile-thing from to actor)
    (let ((new-holder (get-holder to)))
      (cond ((eqv? actor new-holder)
             (narrate! (list actor
                             "picks up" mobile-thing)
                       actor))
            (else
             (narrate! (list actor
                             "picks up" mobile-thing
                             "and gives it to" new-holder)
                       actor)))
      (if (not (eqv? actor new-holder))
          (say! new-holder (list "Whoa! Thanks, dude!")))
      (move-internal! mobile-thing from to))))

If the actor is taking the thing, the actor is the new-holder. But it is possible that the actor is picking up the thing in the place and putting it into someone else's bag!

The say! procedure is used to indicate that a person has said something. Its first argument is the person speaking, and the second argument is the text being spoken. The move-internal! procedure actually moves the object from one place to another.

To drop a thing we use the procedure drop-thing to move it from our bag to our current location:

(define (drop-thing name)
  (let ((thing (find-thing name my-avatar)))
    (if thing
        (drop-thing! thing my-avatar)))
  'done)

(define (drop-thing! thing person)
  (move! thing (get-location person) person))

The following handler for generic-move! enables dropping a thing. The actor may be dropping a thing from its own bag or it might pick up something from another person's bag and drop it.

(define-generic-procedure-handler generic-move!
  (match-args mobile-thing? bag? place? person?)
  (lambda (mobile-thing from to actor)
    (let ((former-holder (get-holder from)))
      (cond ((eqv? actor former-holder)
             (narrate! (list actor
                             "drops" mobile-thing)
                       actor))
            (else
             (narrate! (list actor
                             "takes" mobile-thing
                             "from" former-holder
                             "and drops it")
                       actor)))
      (if (not (eqv? actor former-holder))
          (say! former-holder
                (list "What did you do that for?")))
      (move-internal! mobile-thing from to))))

Yet another generic-move! handler provides for gifting or stealing something, by moving a thing from one bag to another bag. Here the behavior depends on the relationships among the actor, the original holder of the thing, and the final holder of the thing.

(define-generic-procedure-handler generic-move!
  (match-args mobile-thing? bag? bag? person?)
  (lambda (mobile-thing from to actor)
    (let ((former-holder (get-holder from))
          (new-holder (get-holder to)))
      (cond ((eqv? from to)
             (tell! (list new-holder "is already carrying"
                          mobile-thing)
                    actor))
            ((eqv? actor former-holder)
             (narrate! (list actor
                             "gives" mobile-thing
                             "to" new-holder)
                       actor))
            ((eqv? actor new-holder)
             (narrate! (list actor
                             "takes" mobile-thing
                             "from" former-holder)
                       actor))
            (else
             (narrate! (list actor
                             "takes" mobile-thing
                             "from" former-holder
                             "and gives it to" new-holder)
                       actor)))
      (if (not (eqv? actor former-holder))
          (say! former-holder (list "Yaaaah! I am upset!")))
      (if (not (eqv? actor new-holder))
          (say! new-holder
                (list "Whoa! Where'd you get this?")))
      (if (not (eqv? from to))
          (move-internal! mobile-thing from to)))))

Another interesting case is the motion of a person from one place to another. This is implemented by the following handler:

(define-generic-procedure-handler generic-move!
  (match-args person? place? place? person?)
  (lambda (person from to actor)
    (let ((exit (find-exit from to)))
      (cond ((or (eqv? from (get-heaven))
                 (eqv? to (get-heaven)))
             (move-internal! person from to))
            ((not exit)
             (tell! (list "There is no exit from" from
                          "to" to)
                    actor))
            ((eqv? person actor)
             (narrate! (list person "leaves via the"
                             (get-direction exit) "exit")
                       from)
             (move-internal! person from to))
            (else
             (tell! (list "You can't force"
                          person
                          "to move!")
                    actor))))))

There can be many other handlers, but the important thing to see is that the behavior of the move procedure can depend on the types of all of the arguments. This provides a clean decomposition of the behavior into separately understandable chunks. It is rather difficult to achieve such an elegant decomposition in a traditional object-oriented design, because in such a design one must choose one of the arguments to be the principal dispatch center. Should it be the thing being moved? the source location? the target location? the actor? Any one choice will make the situation more complex than necessary.

As Alan Perlis wrote: “It is better to have 100 functions operate on one data structure than 10 functions on 10 data structures.”

Implementing properties

We saw that the objects in our game are created by defining some properties with make-property, defining a type predicate with make-type, getting the predicate's associated instantiator with type-instantiator, and calling that instantiator with appropriate arguments. This simple description hides a complex implementation that is worth exploring.

The interesting aspect of this code is that it provides a simple and flexible mechanism for managing the properties that are associated with a type instance, which is robust when subtyping is used. Properties are represented by abstract objects rather than names, in order to avoid namespace conflicts when subtyping. For example, a type mammal might have a property named forelimb that refers to a typical front leg. A subtype bat of mammal might have a property with the same name that refers to a different object, a wing! If the properties were specified by their names, then one of these types would need to change its name. In this implementation, the property objects are specified by themselves, and two properties with the same name are distinct.

The procedure make-property creates a data type containing a name, a predicate, and a default-value supplier. Its first argument is the property's name, and the rest of the arguments are a property list with additional metadata about the property. For example, see the definition of troll:hunger on page 143. We will ignore how the property list is parsed since it's not interesting.³²

(define (make-property name . plist)
  (guarantee n:symbol? name)
  (guarantee property-list? plist)
  (%make-property name
                  (get-predicate-property plist)
                  (get-default-supplier-property plist)))

A property is implemented as a Scheme record [65], which is a data structure that consists of a set of named fields. It is defined by elaborate syntax that specifies a constructor, a type predicate, and an accessor for each field:

(define-record-type <property>
    (%make-property name predicate default-supplier) 
    property?
  (name property-name)
  (predicate property-predicate)
  (default-supplier property-default-supplier))

We chose to give the primitive record constructor %make-property a name with an initial percent sign (%). We often use the initial percent sign to indicate a low-level procedure that will not be used except to support a higher-level abstraction. The %make-property procedure is used only in make-property, which in turn is used by other parts of the system.

Given a set of properties, we can construct a type predicate:

(define (make-type name properties)
  (guarantee-list-of property? properties)
  (let ((type
         (simple-abstract-predicate name instance-data?)))
    (%set-type-properties! type properties)
    type))

A type predicate is an ordinary abstract predicate (see page 134) along with the specified properties, which are stored in an association using %set-type-properties!. Those specified properties aren't used by themselves; instead they are aggregated with the properties of the supersets of this type. The object being tagged satisfies instance-data?. It is an association from the properties of this type to their values.

(define (type-properties type)
  (append-map %type-properties
              (cons type (all-supertypes type))))

And type-instantiator builds the instantiator, which accepts a property list using property names as keys, parses that list, and uses the resulting values to create the instance data, which associates each property of this instance with its value. It also calls the set-up! procedure, which gives us the ability to do type-specific initialization.

(define (type-instantiator type)
  (let ((constructor (predicate-constructor type))
        (properties (type-properties type)))
    (lambda plist
      (let ((object
             (constructor (parse-plist plist properties))))
        (set-up! object)
        object))))

---

Exercise 3.16: Adventure warmup

Load the adventure game and start the simulation by executing the command (start-adventure your-name). Walk your avatar around. Find some takable object and take it. Drop the thing you took in some other place.

---

---

Exercise 3.17: Health

Change the representation of the health of a person to have more possible values than are given in the initial game. Scale your representation so that the probability of death from a troll bite is the same as it was before you changed the representation. Also make it possible to recover from a nonfatal troll bite, or other loss of health, by some cycles of rest.

---

---

Exercise 3.18: Medical help

Make a new place, the medical center. Make it easily accessible from the Green building and the Gates tower. If a person who suffers a nonfatal injury (perhaps from a troll bite) makes it to the medical center, their health may be restored.

---

---

Exercise 3.19: A palantir

Make a new kind of thing called a palantir (a “seeing stone,” as in Tolkien's Lord of the Rings). Each instance of a palantir can communicate with any other instance; so if there is a palantir in lobby-10 and another in dorm-row, you can observe the goings-on in dorm-row by looking into a palantir in lobby-10. (Basically, a palantir is a magical surveillance camera and display.)

Plant a few immovable palantiri in various parts of the campus, and enable your avatar to use one. Can you keep watch on the positions of your friends? Of the trolls?

Can you make an autonomous person other than your avatar use a palantir for some interesting purpose? The university's president might be a suitable choice.

---

---

Exercise 3.20: Invisibility

Make an “Invisibility Cloak” that any person (including an avatar) can acquire to become invisible, thus invulnerable to attacks by trolls. However, the cloak must be discarded (dropped) after a short time, because possession of the cloak slowly degrades the person's health.

---

---

Exercise 3.21: Your turn

Now that you have had an opportunity to play with our “world” of characters, places, and things, extend this world in some substantial way, limited only by your creativity. One idea is to have mobile places, such as elevators, which have entrances and exits that change with time, and are perhaps controllable by persons. But that is just one suggestion—invent something you like!

---

---

Exercise 3.22: Multiple players

This is a pretty big project rather than a simple exercise.

1. a. Extend the adventure game so that there can be multiple players, each controlling a personal avatar.
2. b. Make it possible for players to be on different terminals.

---

3.6 Summary

The use of generic procedures introduced in this chapter is both powerful and dangerous—it is not for the faint of heart. Allowing the programmer to dynamically change the meanings of the primitive operators of the language can result in unmanageable code. But if we are careful to extend operators to only new types of arguments, without changing their behavior on the original types, we can get powerful extensions without breaking any old software. Most programming languages do not allow the freedom to modify the existing behavior of primitive operators, for good reason. However, many of the ideas here are portable and can be safely used. For example, in many languages, as diverse as C++ and Haskell, one can overload operators to have new meanings on user-defined types.

Extensions of arithmetic are pretty tame, but we must be aware of the problems that can come up, and the subtle bugs that can be evoked: addition of integers is associative, but addition of floating-point numbers is not associative; multiplication of numbers is commutative, but multiplication of matrices is not. And if we extend addition to be concatenation of strings, that extension is not commutative. On the good side, it is straightforward to extend arithmetic to symbolic expressions containing literal numbers as well as purely numerical quantities. It is not difficult, but lots of work, to continue to expand to functions, vectors, matrices, and tensors. However, we eventually run into real problems with the ordering of extensions—symbolic vectors are not the same as vectors with symbolic coordinates! We also can get into complications with the typing of symbolic functions.

One beautiful example of the power of extensible generics is the almost trivial implementation of forward-mode automatic differentiation by extending each primitive arithmetic procedure to handle differential objects. However, making this work correctly with higher-order functions that return functions as values was difficult. (Of course, most programmers writing applications that need automatic differentiation do not need to worry about this complication.)

In our system the “type” is represented by a predicate that is true of elements of that type. In order to make this efficient we introduced a predicate registration and tagging system that allowed us to add declarations of relationships among the types. For example, we could have prime numbers be a subset of the integers, so numbers that satisfy the user-defined prime? predicate automatically satisfy the integer? predicate.

Once we have user-defined types with declared subset relationships, we enter a new realm of possibilities. We demonstrated this with a simple but elegantly extensible adventure game. Because our generic procedures dispatch on the types of all of their arguments, the descriptions of the behaviors of the entities in our adventure game are much simpler and more modular than they would be if we dispatched on the first argument to produce a procedure that dispatched on the second argument, and so on. So modeling these behaviors in a typical single-dispatch objectoriented system would be more complicated.

We used tagged data to efficiently implement extensible generic procedures. The data was tagged with the information required to decide which procedures to use to implement the indicated operations. But once we have the ability to tag data, there are other uses tags can be put to. For example, we may tag data with its provenance, or how it was derived, or the assumptions it was based on. Such audit trails may be useful for access control, for tracing the use of sensitive data, or for debugging complex systems [128]. So there is power in the ability to attach arbitrary tags to any data item, in addition to the use of tags to determine the handlers for generic procedures.

 

1 ODE means “ordinary differential equation,” meaning a differential equation with a single independent variable.

2 Because we anticipated varying the meanings of many operators in the MIT/GNU Scheme system, we made a special set of operators that name primitive procedures we might need later. We named the copies with the prefix n:. In MIT/GNU Scheme the original primitive procedures are always available, with their original names, in the system-global-environment, so we could have chosen to get them from there.

3 A recent Scheme standard [109] introduced “libraries,” which provide a way to specify bindings of the free references in a program. We could use libraries to connect an arithmetic with the code that uses it. But here we demonstrate the ideas by modifying the read-eval-print environment.

4 The procedure pp prints a list “prettily” by using line breaks and indentation to reveal the list's structure.

5 You may have noticed that in these symbolic expressions the additions and multiplications are expressed as binary operations, even though in Scheme they are allowed to take many arguments; the installer implements the n-ary versions as nested binary operations. Similarly, the unary - is converted to negate. Subtractions and divisions with multiple arguments are also realized as nested binary operations.

6 The procedure default-object produces an object that is different from any possible constant. The procedure default-object? identifies that value.

7 Another difference you may have noticed is that the constant-generator and operation-generator procedures for the numeric arithmetic have only one formal parameter, while the generator procedures for the symbolic extender have two. The symbolic arithmetic is built on a base arithmetic, so the constant or operation for the base arithmetic is given to the generator.

8 The call (any-arg 3 p1? p2?) will produce an applicability specification with seven cases, because there are seven ways that this applicability can be satisfied: ((p2? p2? p1?) (p2? p1? p2?) (p2? p1? p1?) (p1? p2? p2?) (p1? p2? p1?) (p1? p1? p2?) (p1? p1? p1?))

9 disjoin* is a predicate combinator. It accepts a list of predicates and produces the predicate that is their disjunction.

10 Making this arbitrary choice is not really reasonable. For example, a vector's zero is not only distinct from the numerical zero, but also is not the same for vectors of different dimension. We have chosen to ignore this problem here.

11 At the APL-79 conference Joel Moses is reported to have said: “APL is like a beautiful diamond—flawless, beautifully symmetrical. But you can't add anything to it. If you try to glue on another diamond, you don't get a bigger diamond. Lisp is like a ball of mud. Add more and it's still a ball of mud—it still looks like Lisp.” But Joel denies that he said this.

12 A mechanism of this sort is implicit in most “object-oriented languages,” but it is usually tightly bound to ontological mechanisms such as inheritance. The essential idea of extensible generics appears in SICP [1] and is usefully provided in tinyCLOS [66] and SOS [52].A system of extensible generics, based on predicate dispatching, is used to implement the mathematical representation system in SICM [121]. A nice exposition of predicate dispatching is given by Ernst [33].The idea that generic procedures are a powerful tool has been percolating in the Lisp community for decades. The fullest development of these ideas is in the Common Lisp Object System (CLOS) [42]. The underlying structure is beautifully expressed in the Metaobject Protocol [68]. It is further elaborated in the “Aspect-oriented programming” movement [67].

13 generic-metadata-getter and generic-metadata-default-getter retrieve the get-handler procedure and the get-default-handler procedure from the dispatch-store instance stored in the metadata of the generic procedure.

14 The term automatic differentiation was introduced by Wengert [129] in 1964.

15 The derivative here is the derivative of a function, not the derivative of an expression. If f is a function, the derivative Df of f is a new function, which when applied to x gives a value Df (x). Its relation to an expression derivative is:

16 The automatic differentiation code we present here is derived from the code that we wrote to support the advanced classical mechanics class that Sussman teaches at MIT with Jack Wisdom [121, 122].

17 Differential objects like these are sometimes referred to as dual numbers. Dual numbers, introduced by Clifford in 1873 [20], extend the real numbers by adjoining one new element E with the property є² = 0. However, in order to conveniently compute multiple derivatives (and derivatives of functions with multiple arguments) it helps to introduce a new infinitesimal part for each independent variable. So our differential algebra space is much more complicated than the single-E dual number space. Our differential objects are also something like the hyperreal numbers, invented by Edwin Hewitt in 1948 [59].

18 This idea was “discovered” by Dan Zuras (then of Hewlett Packard Corporation) and Gerald Jay Sussman in an all-night programming binge in 1992. We assumed at the time that this had also been discovered by many others, and indeed it had [129, 12], but we were overjoyed when we first understood the idea ourselves! See [94] for a formal exposition of automatic differentiation.

19 We will get to binary functions soon. This is just to make the idea clear before things get complicated. We will extend to n-ary functions in section 3.3.2

20 We are showing the definitions of handlers but we are not showing the assignment of the handlers here.

21 For an alternative strategy, see exercise 3.8 on page 113.

22 The procedure iota returns a list of consecutive integers from 0 through (length args).

23 The formal algebraic details were clarified by Hal Abelson around 1994, as part of an effort to fix a bug. The code was painfully reworked in 1997 by Sussman with the help of Hardy Mayer and Jack Wisdom.

24 A nicer version would use record structures, but that would be harder to debug without having a way to print them nicely.

25 The fact that any factor of any highest-order term in the series can be used was a central insight of Hal Abelson in the 1994 revision of this idea.

26 A bug of this class was pointed out to us by Alexey Radul in 2011. The general problem was first identified by Siskind and Perlmutter in 2005 [111]: the differential tags created to distinguish the infinitesimals incrementing an argument for a derivative calculation can be confused in the evaluation of a derivative of a function whose value is a function. The deferred derivative procedure may be called more than once, using the tag that was created for the outer derivative calculation. More recently, Jeff Siskind showed us another bug that plagued our patch for the first one: there was a potential collision between a tag occurring in an argument and a tag inherited from the lexical scope of a derivative function. These very subtle bugs are explained, along with a careful analysis of ways to fix them, in a beautiful paper by Manzyuk et al. [87].

27 This is carefully explained in Manzyuk et al. [87].

28 The trie data structure was invented by Edward Fredkin in the early 1960s.

29 The names printed for predicates by with-predicate-counts do not end in a question mark; for example the name printed for the predicate number? is simply number. The reason for this is obscure, and the curious are welcome to track it down in the code.

30 The procedure is-generic-handler-applicable? abstracts the handler checking that we previously did using predicates-match? in get-handler on page 98. This gives us a hook for later elaboration.

31 In languages such as Haskell and Smalltalk, multiple arguments are handled by dispatching on the first argument, producing an object that then dispatches on the second argument, etc.

32 The make-property procedure uses a helper called guarantee to do argument checking. The first argument to guarantee is a predicate (preferably a registered predicate) and the second argument is an object to be tested. There may be a third argument, to identify the caller. If the object doesn't satisfy the predicate, guarantee signals an error. The procedure guarantee-list-of works similarly except that it requires the object to be a list of elements satisfying the predicate.

We have used assert earlier in this text. assert is more convenient for posing assertions that must be true where they are made. guarantee is preferable for the more restricted case of argument type checking.