CHAPTER

1

Why Should K–5 Educators Teach Coding?

It’s time we realize and put to action Steve Jobs’ words: “Everyone in this country should learn how to program a computer … because it teaches you how to think.”

This quote appears at the beginning of a video entitled “What Most Schools Don’t Teach” (youtu.be/nKIu9yen5nc) that was published in 2013 by Code.org (a non-profit organization dedicated to giving every student in every school the opportunity to learn computer programming). Starring many famous people, including Bill Gates of Microsoft, Mark Zuckerberg of Facebook, and will.i.am of the Black Eyed Peas, the video’s message is a simple one: anyone and everyone should learn to code.

Within our schools we must build upon the belief that coding is for everyone. There are many reasons for teaching coding, including:

Coding Is for Everyone, and Parents Agree!

According to an infographic published on the Code.org website, 90 percent of parents want their child to study computer science. One major reason for this thinking might be due to the data recently updated on the Code.org blog “Anybody Can Learn,” which reports that computing occupations are now the number one source of new wages in the U.S. (Code.org, 2016).

The blog ends by asking an important question: why isn’t the option to learn computer science offered in more U.S. schools? While computer science electives in high schools are increasing, CSforALL initiatives have been focused on providing opportunities for all students, at all grade levels, to have experiences with computer science, coding, and computational thinking. For elementary teachers, that means exploring ways in which teachers can embed this type of learning into content areas they are already responsible for teaching.

Figure 1.1. Number of university computer science programs compared to other programs. Source: Code.org (2017).

Teacher preparation for embedding computer science and computational thinking into instruction will need to occur at a variety of levels. According to a Code.org data analysis, it is clear that universities are not preparing enough computer science teachers (2017). The numbers in figure 1.1 show the disparity between CS and other programs of study.

While this may address middle and high school teachers, it is still unclear how many universities are preparing elementary teachers to integrate computer science and computational thinking into their already overloaded academic-focused days. Therefore, it is essential that school districts provide professional development for educators to engage in learning new knowledge, provide time for discussion and reflection, and allow for experimentation in creating best practices for integrating these essential skills into the context of their local learning environments.

Five Reasons Why Coding Is Critical for K–5 Students

1. Making Their Thinking Visible

We know that young students are concrete thinkers and are beginning to follow step-by-step directions. These beginning stages of following first one step, then two steps, then multiple steps, are the start of algorithmic thinking in action. While the youngest learners may not understand this abstract concept, we can use computer science to make their thinking visible.

One of the behaviors of strong readers is to visualize the story in their mind as they are reading. By learning how to code, students have an opportunity to give shapes, thoughts, and actions to their thinking.

2. Sustaining Creativity

In Sir Ken Robinson’s TED Talk, “Do Schools Kill Creativity?” the renowned educator and speaker tells the audience that creativity is as important in education as literacy. He points out that young learners will take a chance and are not afraid to be wrong. Coding allows students to be creative without being wrong. If something doesn’t work, the student must analyze what isn’t working, ask why it isn’t working, and determine how to correct it so that it works. In essence, coding is the process of continually making mistakes, learning from them, and correcting them.

3. Encouraging Computational Thinking

As a teacher, how many times have you heard the following feedback? “Johnny is great at solving computational math problems, but he continues to struggle with word problems.”

Teaching how to read and write code supports a student’s ability to think computationally in the context of a complex and open-ended problem. When students decompose problems, they can begin to see patterns within the word problems they solve. They can then create a step-by-step procedure (algorithm) that will help them in solving all similar problems.

Our world continually presents us with roadblocks that, given the correct framework of thinking, have solutions that can harness the power of technology to make a difference in the world. Jeanette Wing defines computational thinking as “the thought processes involved in formulating problems and their solutions so that the solutions are represented in a form that can be efficiently carried out by an information-processing agent” (Wing, 2006). For the classroom teacher, this means they can also consider their students’ unique approach to solving a problem as a simplistic form of an “information-processing agent.”

4. Fostering Future-Ready Skills

The Partnership for 21st Century Learning (P21) developed a framework describing the “skills, knowledge and expertise students should master to succeed in work and life in the 21st century” (Partnership for 21st Century Learning, 2007). The framework identified three learning and innovation skills essential in preparing our children for increasingly complex life and work environments that don’t yet exist.

These skills, often referred to as the 4 Cs, are critical thinking, communication, collaboration, and creativity. When we put all of these together into a complex and open-ended problem, we are essentially asking students to engage in the practices needed for computational thinking.

5. Empowering Students to Take Action

Coding is about applying skills and creativity to solve problems. For example, in the winter of 2011, a group of young coders were stuck in Boston during a snow storm. Their task was to create a new website for Boston’s Public Schools; however, within days of their arrival the city had shut down. What resulted was the coders creating a website called Adopt a Hydrant (adoptahydrant.org) that allowed area residents to adopt a fire hydrant and keep it clear of snow for emergency personnel during the winter months.

Coding can be used to create real-world contexts for students. When we blur the lines between school and the real world, we allow children to examine problems, engage them in exploring the problems, and empower them to take action in finding a solution.

Why Should K–5 Educators Teach Coding?

Collaboration and communication are rapidly changing with the use of technology. As the COVID-19 pandemic pushed many educators out of traditional classrooms, many have been collaborating by communicating across the state, country, and world in real time. Due to advances in computer programming that run digital tools such as Neapod, Kahoot, and Khan Academy, working on an assignment and receiving instant feedback has pushed us into needing a workforce that can think computationally and understand code.

Creativity and critical thinking can be used with coders of all ages. Coding allows the user to become the creator of content, rather than just the consumer of content. When we consume content, we are learning about the “what” and the “how,” but when we create content, we have engaged the “why” of learning.

Fostering Student Inquiry and Action

Many people think action is something you do and is therefore easy to define; however, if we go back to the Golden Circle, we recognize that action stems from the reason why we do something. If we want children to make a difference in the world, we need to help them understand that action is not a mandate from parents or teachers, but a lifelong mindset that teachers and parents can help develop. It must be developed with scaffolded lessons that include explicitly taught skills, modeled behaviors, and a gradual release of responsibility.

The following teacher reflection questions can help you begin to think about the process:

Why Not Teach Coding?

While there are many reasons for adding coding to your instruction, there are an equal or greater number of arguments against. The first step to incorporating coding into existing curriculum is to identify the roadblocks.

Roadblock 1: Getting Comfortable with “Living in Beta”

In many schools across the country, there are after-school clubs dedicated to computer science and coding. While this is a great start for exposure, it does not allow all students to access the computational thinking skills that are developed by coding. Teachers who have a passion for computer science are usually the ones running these clubs, but how do we get all K–5 teachers comfortable with coding?

This brings us to the ability to “live in beta.” This concept is explored by Molly Schroeder in her 2013 TED Talk “Living in Beta” (youtu.be/0nnYI3ePrY8). Schroeder defines beta as “the space between A and B” and adds that this is where the learning happens. She points out that with the ever-changing nature of technology, we would best serve our students by jumping in with them as they approach solving a problem. New discoveries in neuroscience and revelations on how the brain works are changing the way teachers interact with student learning opportunities. Coding is a new literacy that is upon us, and as Schroeder states in her TED Talk, “If we sit around waiting until it all shakes out, we’re going to miss the boat. Not only will we be too late and learn nothing along the way, but we’ll also lose out on the opportunity to help influence how things evolve and take shape” (Schroeder, 2013).

Roadblock 2: Fear of Failure

Often I have heard K–5 teachers say, “But I can’t do that without a lot of professional development.” Teachers may fear the unknown and feel they don’t understand, or have time to learn, how to code. More importantly, the field of education has an overall fear of failing, spreading to the paralyzing fear of risk-taking. This is our biggest hurdle! Allowing teachers to take risks, fail, and learn to improve the process from their failure is what coding is all about.

The essential question becomes, how do we get off this escalator we are stuck on? Take a moment to watch the YouTube video “Stuck on an Escalator—Take Action” (youtu.be/VrSUe_m19FY). It shows two people who are literally stuck on an escalator when it stops moving. When showing this to a group of educators, they all laughed as the lady asks the gentleman stuck on the escalator with her for a cell phone. The gentleman then proceeds to shout, “Hello … there are two people stuck on an escalator, and we need help … now! Would somebody please do something?” The two proceed to sit down on their respective steps until a repair technician comes to fix the escalator, only to get stuck about half way up the escalator. The video concludes by stating that most problems are easy to solve—you just need to get off the escalator. In order to get off our escalator and face our fear of coding, we need to understand the Law of Diffusion of Innovation and how it relates to coding in K–5.

Everett Rogers, a professor of communication studies, popularized this theory in his 1962 book Diffusion of Innovations. The book has since been revised, and the fifth edition was published in 2003. The basis of the theory is that diffusion is the process by which an innovation is communicated over time among an organization. According to Rogers’s theory, there are five categories of those who adopt an innovation.

The innovators of K–5 coding include Seymore Papert, Mitchel Resnick, Fred Martin, and others who developed and adopted early programming languages, beginning in the 1970s with Logo, which was used to draw shapes, designs, and patterns by typing in simple commands on the screen, and leading to the development of Scratch, a visual-block programming language made specifically for young coders, in 2004.

The early adopters began catching on to these coding platforms, and coding grew in popularity throughout the first decade of the digital age. In 2004, the Computer Science Teachers Association (CSTA) was founded, and it created recommended computer science standards. Coding gained more popularity though collaborative social platforms like the one created for Scratch (scratch.mit.edu) in 2012. Hadi Partovi followed suit and launched Code.org in 2013. Each year, Code.org organizes the Hour of Code, which, according to their 2019 Annual Report, has engaged more than 900 million students, with more than 30% of activity coming from 180 countries outside of the U.S. (Code.org, 2019). Figure 1.2 shows the tipping point that Code.org and others hope to achieve through the resources they provide for students and educators.

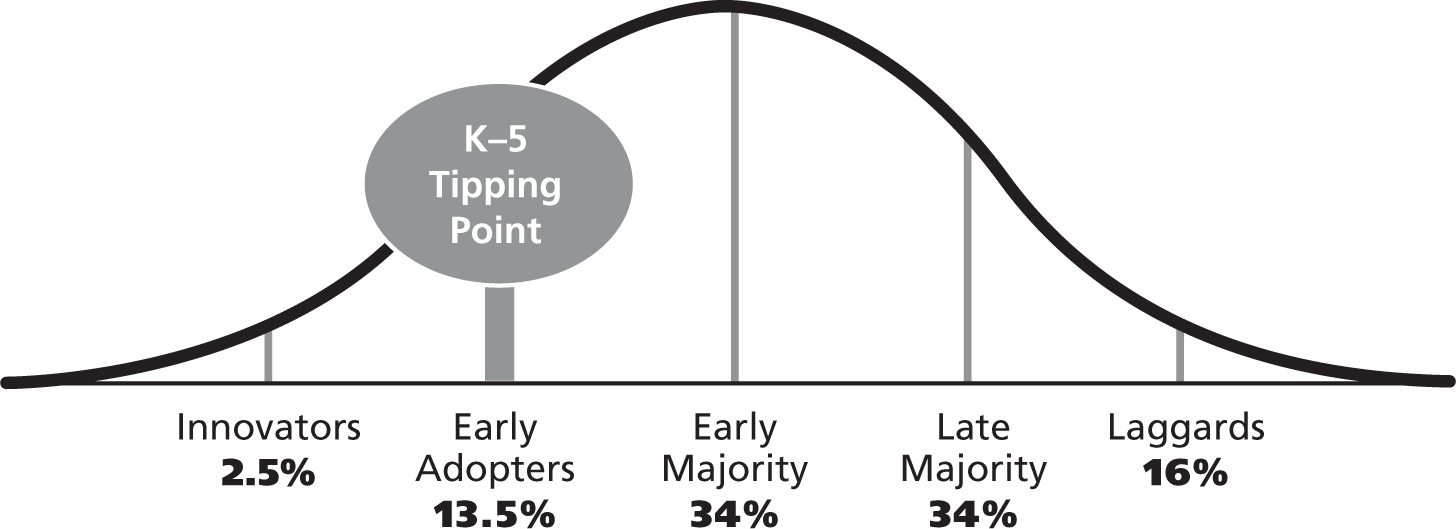
Figure 1.2. Innovation diffusion curve showing rate of adoption of coding by K–5 students.

By picking up this book and trying out at least one activity, you will be an early adopter by bringing coding into the curriculum and fostering development of this important digital age literacy in your school!

Roadblock 3: Time

For K–5 teachers to incorporate coding and computational thinking, we simply cannot add another subject to their already full schedules. Teachers are already tasked with creating learning experiences in reading, writing, science, social studies, health, and habits of mind. How can they be expected to add another thing to their busy schedules?

What teachers may not realize is that they are already teaching many of the foundational components of computational thinking. When they ask students to read a story and then sequence the events into the correct order, they are using the same process a computer programmer uses in decomposition, data analysis, and data representation. For example, when computer programmers are presented with a complex problem to solve, they first need to break the problem down into simple parts. Then the programmer will analyze the parts and put them in the correct order. Finally, the computer will represent the data in a simple way that the user can understand. Our youngest readers use this same process when the teacher reads them a story and they must take the picture representation of the story and put it into the correct sequence of events to make meaning. It is not more time we need, but the ability to help our students make the connections.

The required skills within the Common Core State Standards and particularly the Standards for Mathematical Practice can be taught using coding as a tool. I often hear of teachers struggling to find concrete ways to teach and observe these eight mathematics standards. Appendix A shares connections between computational thinking and the Standards for Mathematical Practice, and strategies for implementing coding within the math classroom. Again, it is not a matter of adding more time to another new subject, but instead using a digital age tool in a way that will help the concrete understanding of what are often abstract mathematical concepts.