1

Primordial Seeds

LA FIN DE SIÈCLE, LA BELLE EPOQUE. Paris was abuzz with progress. In the west, Gustave Eiffel’s new tower — still considered a controversial eyesore by Parisians living in its shadow — shot up over the site of the 1889 World’s Fair. In the north, at the foot of Montmartre, a new cabaret called the Moulin Rouge had just opened to such fanfare that the Prince of Wales came over from Britain to see the show. Closer to the center of town, word had begun to spread of certain unexplained accidents at the magnificent and still-new home of the city’s opera, the Palais Garnier — accidents that would lead to at least one death when part of a chandelier fell. Rumor had it that a phantom haunted the building.

Just a few blocks east from the Palais Garnier lay the beating heart of the French empire: the Paris Bourse, the capital’s principal financial exchange. It was housed in a palace built by Napoleon as a temple to money, the Palais Brongniart. Its outside steps were flanked by statues of its idols: Justice, Commerce, Agriculture, Industry. Majestic neoclassical columns guarded its doors. Inside, its cavernous main hall was large enough to fit hundreds of brokers and staff members. For an hour each day they met beneath ornately carved reliefs and a massive skylight to trade the permanent government bonds, called rentes, that had funded France’s global ambitions for a century. Imperial and imposing, it was the center of the city at the center of the world.

Or so it would have seemed to Louis Bachelier as he approached it for the first time, in 1892. He was in his early twenties, an orphan from the provinces. He had just arrived in Paris, fresh from his mandatory military service, to resume his education at the University of Paris. He was determined to be a mathematician or a physicist, whatever the odds — and yet, he had a sister and a baby brother to support back home. He had recently sold the family business, which had provided sufficient money for the moment, but it wouldn’t last forever. And so, while his classmates threw themselves into their studies, Bachelier would have to work. Fortunately, with a head for numbers and some hard-won business experience, he had been able to secure a position at the Bourse. He assured himself it was only temporary. Finance would have his days, but his nights were saved for physics. Nervously, Bachelier forced himself to walk up the stairs toward the columns of the Bourse.

Inside, it was total bedlam. The Bourse was based on an open outcry system for executing trades: traders and brokers would meet in the main hall of the Palais Brongniart and communicate information about orders to buy or sell by yelling or, when that failed, by using hand signals. The halls were filled with men running back and forth executing trades, transferring contracts and bills, bidding on and selling stocks and rentes. Bachelier knew the rudiments of the French financial system, but little more. The Bourse did not seem like the right place for a quiet boy, a mathematician with a scholar’s temperament. But there was no turning back. It’s just a game, he told himself. Bachelier had always been fascinated by probability theory, the mathematics of chance (and, by extension, gambling). If he could just imagine the French financial markets as a glorified casino, a game whose rules he was about to learn, it might not seem so scary.

He repeated the mantra — just an elaborate game of chance — as he pushed forward into the throng.

“Who is this guy?” Paul Samuelson asked himself, for the second time in as many minutes. He was sitting in his office, in the economics department at MIT. The year was 1955, or thereabouts. Laid out in front of him was a half-century-old PhD dissertation, written by a Frenchman whom Samuelson was quite sure he had never heard of. Bachelor, Bacheler. Something like that. He looked at the front of the document again. Louis Bachelier. It didn’t ring any bells.

Its author’s anonymity notwithstanding, the document open on Samuelson’s desk was astounding. Here, fifty-five years previously, Bachelier had laid out the mathematics of financial markets. Samuelson’s first thought was that his own work on the subject over the past several years — the work that was supposed to form one of his students’ dissertation — had lost its claim to originality. But it was more striking even than that. By 1900, this Bachelier character had apparently worked out much of the mathematics that Samuelson and his students were only now adapting for use in economics — mathematics that Samuelson thought had been developed far more recently, by mathematicians whose names Samuelson knew by heart because they were tied to the concepts they had supposedly invented. Weiner processes. Kolmogorov’s equations. Doob’s martingales. Samuelson thought this was cutting-edge stuff, twenty years old at the most. But there it all was, in Bachelier’s thesis. How come Samuelson had never heard of him?

Samuelson’s interest in Bachelier had begun a few days before, when he received a postcard from his friend Leonard “Jimmie” Savage, then a professor of statistics at the University of Chicago. Savage had just finished writing a textbook on probability and statistics and had developed an interest in the history of probability theory along the way. He had been poking around the university library for early-twentieth-century work on probability when he came across a textbook from 1914 that he had never seen before. When he flipped through it, Savage realized that, in addition to some pioneering work on probability, the book had a few chapters dedicated to what the author called “speculation” — literally, probability theory as applied to market speculation. Savage guessed (correctly) that if he had never come across this work before, his friends in economics departments likely hadn’t either, and so he sent out a series of postcards asking if anyone knew of Bachelier.

Samuelson had never heard the name. But he was interested in mathematical finance — a field he believed he was in the process of inventing — and so he was curious to see what this Frenchman had done. MIT’s mathematics library, despite its enormous holdings, did not have a copy of the obscure 1914 textbook. But Samuelson did find something else by Bachelier that piqued his interest: Bachelier’s dissertation, published under the title A Theory of Speculation. He checked it out of the library and brought it back to his office.

Bachelier was not, of course, the first person to take a mathematical interest in games of chance. That distinction goes to the Italian Renaissance man Gerolamo Cardano. Born in Milan around the turn of the sixteenth century, Cardano was the most accomplished physician of his day, with popes and kings clamoring for his medical advice. He authored hundreds of essays on topics ranging from medicine to mathematics to mysticism. But his real passion was gambling. He gambled constantly, on dice, cards, and chess — indeed, in his autobiography he admitted to passing years in which he gambled every day. Gambling during the Middle Ages and the Renaissance was built around a rough notion of odds and payoffs, similar to how modern horseraces are constructed. If you were a bookie offering someone a bet, you might advertise odds in the form of a pair of numbers, such as “10 to 1” or “3 to 2,” which would reflect how unlikely the thing you were betting on was. (Odds of 10 to 1 would mean that if you bet 1 dollar, or pound, or guilder, and you won, you would receive 10 dollars, pounds, or guilders in winnings, plus your original bet; if you lost, you would lose the dollar, etc.) But these numbers were based largely on a bookie’s gut feeling about how the bet would turn out. Cardano believed there was a more rigorous way to understand betting, at least for some simple games. In the spirit of his times, he wanted to bring modern mathematics to bear on his favorite subject.

In 1526, while still in his twenties, Cardano wrote a book that outlined the first attempts at a systematic theory of probability. He focused on games involving dice. His basic insight was that, if one assumed a die was just as likely to land with one face showing as another, one could work out the precise likelihoods of all sorts of combinations occurring, essentially by counting. So, for instance, there are six possible outcomes of rolling a standard die; there is precisely one way in which to yield the number 5. So the mathematical odds of yielding a 5 are 1 in 6 (corresponding to betting odds of 5 to 1). But what about yielding a sum of 10 if you roll two dice? There are 6 × 6 = 36 possible outcomes, of which 3 correspond to a sum of 10. So the odds of yielding a sum of 10 are 3 in 36 (corresponding to betting odds of 33 to 3). The calculations seem elementary now, and even in the sixteenth century the results would have been unsurprising — anyone who spent enough time gambling developed an intuitive sense for the odds in dice games — but Cardano was the first person to give a mathematical account of why the odds were what everyone already knew them to be.

Cardano never published his book — after all, why give your best gambling tips away? — but the manuscript was found among his papers when he died and ultimately was published over a century after it was written, in 1663. By that time, others had made independent advances toward a full-fledged theory of probability. The most notable of these came at the behest of another gambler, a French writer who went by the name of Chevalier de Méré (an affectation, as he was not a nobleman). De Méré was interested in a number of questions, the most pressing of which concerned his strategy in a dice game he liked to play. The game involved throwing dice several times in a row. The player would bet on how the rolls would come out. For instance, you might bet that if you rolled a single die four times, you would get a 6 at least one of those times. The received wisdom had it that this was an even bet, that the game came down to pure luck. But de Méré had an instinct that if you bet that a 6 would get rolled, and you made this bet every time you played the game, over time you would tend to win slightly more often than you lost. This was the basis for de Méré’s gambling strategy, and it had made him a considerable amount of money. However, de Méré also had a second strategy that he thought should be just as good, but for some reason had only given him grief. This second strategy was to always bet that a double 6 would get rolled at least once, if you rolled two dice twenty-four times. But this strategy didn’t seem to work, and de Méré wanted to know why.

As a writer, de Méré was a regular at the Paris salons, fashionable meetings of the French intelligentsia that fell somewhere between cocktail parties and academic conferences. The salons drew educated Parisians of all stripes, including mathematicians. And so, de Méré began to ask the mathematicians he met socially about his problem. No one had an answer, or much interest in looking for one, until de Méré tried his problem out on Blaise Pascal. Pascal had been a child prodigy, working out most of classical geometry on his own by drawing pictures as a child. By his late teens he was a regular at the most important salon, run by a Jesuit priest named Marin Mersenne, and it was here that de Méré and Pascal met. Pascal didn’t know the answer, but he was intrigued. In particular, he agreed with de Méré’s appraisal that the problem should have a mathematical solution.

Pascal began to work on de Méré’s problem. He enlisted the help of another mathematician, Pierre de Fermat. Fermat was a lawyer and polymath, fluent in a half-dozen languages and one of the most capable mathematicians of his day. Fermat lived about four hundred miles south of Paris, in Toulouse, and so Pascal didn’t know him directly, but he had heard of him through his connections at Mersenne’s salon. Over the course of the year 1654, in a long series of letters, Pascal and Fermat worked out a solution to de Méré’s problem. Along the way, they established the foundations of the modern theory of probability.

One of the things that Pascal and Fermat’s correspondence produced was a way of precisely calculating the odds of winning dice bets of the sort that gave de Méré trouble. (Cardano’s system also accounted for this kind of dice game, but no one knew about it when de Méré became interested in these questions.) They were able to show that de Méré’s first strategy was good because the chance that you would roll a 6 if you rolled a die four times was slightly better than 50% — more like 51.7747%. De Méré’s second strategy, though, wasn’t so great because the chance that you would roll a pair of 6s if you rolled two dice twenty-four times was only about 49.14%, less than 50%. This meant that the second strategy was slightly less likely to win than to lose, whereas de Méré’s first strategy was slightly more likely to win. De Méré was thrilled to incorporate the insights of the two great mathematicians, and from then on he stuck with his first strategy.

The interpretation of Pascal and Fermat’s argument was obvious, at least from de Méré’s perspective. But what do these numbers really mean? Most people have a good intuitive idea of what it means for an event to have a given probability, but there’s actually a deep philosophical question at stake. Suppose I say that the odds of getting heads when I flip a coin are 50%. Roughly, this means that if I flip a coin over and over again, I will get heads about half the time. But it doesn’t mean I am guaranteed to get heads exactly half the time. If I flip a coin 100 times, I might get heads 51 times, or 75 times, or all 100 times. Any number of heads is possible. So why should de Méré have paid any attention to Pascal and Fermat’s calculations? They didn’t guarantee that even his first strategy would be successful; de Méré could go the rest of his life betting that a 6 would show up every time someone rolled a die four times in a row and never win again, despite the probability calculation. This might sound outlandish, but nothing in the theory of probability (or physics) rules it out.

So what do probabilities tell us, if they don’t guarantee anything about how often something is going to happen? If de Méré had thought to ask this question, he would have had to wait a long time for an answer. Half a century, in fact. The first person who figured out how to think about the relationship between probabilities and the frequency of events was a Swiss mathematician named Jacob Bernoulli, shortly before his death in 1705. What Bernoulli showed was that if the probability of getting heads is 50%, then the probability that the percentage of heads you actually got would differ from 50% by any given amount got smaller and smaller the more times you flipped the coin. You were more likely to get 50% heads if you flipped the coin 100 times than if you flipped it just twice. There’s something fishy about this answer, though, since it uses ideas from probability to say what probabilities mean. If this seems confusing, it turns out you can do a little better. Bernoulli didn’t realize this (in fact, it wasn’t fully worked out until the twentieth century), but it is possible to prove that if the chance of getting heads when you flip a coin is 50%, and you flip a coin an infinite number of times, then it is (essentially) certain that half of the times will be heads. Or, for de Méré’s strategy, if he played his dice game an infinite number of times, betting on 6 in every game, he would be essentially guaranteed to win 51.7477% of the games. This result is known as the law of large numbers. It underwrites one of the most important interpretations of probability.

Pascal was never much of a gambler himself, and so it is ironic that one of his principal mathematical contributions was in this arena. More ironic still is that one of the things he’s most famous for is a bet that bears his name. At the end of 1654, Pascal had a mystical experience that changed his life. He stopped working on mathematics and devoted himself entirely to Jansenism, a controversial Christian movement prominent in France in the seventeenth century. He began to write extensively on theological matters. Pascal’s Wager, as it is now called, first appeared in a note among his religious writings. He argued that you could think of the choice of whether to believe in God as a kind of gamble: either the Christian God exists or he doesn’t, and a person’s beliefs amount to a bet one way or the other. But before taking any bet, you want to know what the odds are and what happens if you win versus what happens if you lose. As Pascal reasoned, if you bet that God exists and you live your life accordingly, and you’re right, you spend eternity in paradise. If you’re wrong, you just die and nothing happens. So, too, if you bet against God and you win. But if you bet against God and you lose, you are damned to perdition. When he thought about it this way, Pascal decided the decision was an easy one. The downside of atheism was just too scary.

Despite his fascination with chance, Louis Bachelier never had much luck in life. His work included seminal contributions to physics, finance, and mathematics, and yet he never made it past the fringes of academic respectability. Every time a bit of good fortune came his way it would slip from his fingers at the last moment. Born in 1870 in Le Havre, a bustling port town in the northwest of France, young Louis was a promising student. He excelled at mathematics in lycée (basically, high school) and then earned his baccalauréat ès sciences — the equivalent of A-levels in Britain or a modern-day AP curriculum in the United States — in October 1888. He had a strong enough record that he could likely have attended one of France’s selective grandes écoles, the French Ivy League, elite universities that served as prerequisites for life as a civil servant or intellectual. He came from a middle-class merchant family, populated by amateur scholars and artists. Attending a grande école would have opened intellectual and professional doors for Bachelier that had not been available to his parents or grandparents.

But before Bachelier could even apply, both of his parents died. He was left with an unmarried older sister and a three-year-old brother to care for. For two years, Bachelier ran the family wine business, until he was drafted into military service in 1891. It was not until he was released from the military, a year later, that Bachelier was able to return to his studies. By the time he returned to academia, now in his early twenties and with no family back home to support him, his options were limited. Too old to attend a grande école, he enrolled at the University of Paris, a far less prestigious choice.

Still, some of the most brilliant minds in Paris served as faculty at the university — it was one of the few universities in France where faculty could devote themselves to research, rather than teaching — and it was certainly possible to earn a first-rate education in the halls of the Sorbonne. Bachelier quickly distinguished himself among his peers. His marks were not the best at the university, but the small handful of students who bested him, classmates like Paul Langevin and Alfred-Marie Liénard, are now at least as famous as Bachelier himself, among mathematicians anyway. It was good company to be in. After finishing his undergraduate degree, Bachelier stayed at the University of Paris for his doctorate. His work attracted the attention of the best minds of the day, and he began to work on a dissertation — the one Samuelson later discovered, on speculation in financial markets — with Henri Poincaré, perhaps the most famous mathematician and physicist in France at the time.

Poincaré was an ideal person to mentor Bachelier. He had made substantial contributions to every field he had come in contact with, including pure mathematics, astronomy, physics, and engineering. Although he did attend a grande école as an undergraduate, like Bachelier he had done his graduate work at the University of Paris. He also had experience working outside of academia, as a mine inspector. Indeed, for most of his life he continued to work as a professional mining engineer, ultimately becoming the chief engineer of the French Corps de Mines, and so he was able to fully appreciate the importance of working on applied mathematics, even in areas so unusual (for the time) as finance. It would have been virtually impossible for Bachelier to produce his dissertation without a supervisor who was as wide-ranging and ecumenical as Poincaré. And more, Poincaré’s enormous success had made him a cultural and political figure in France, someone who could serve as a highly influential advocate for a student whose research was difficult to situate in the then-current academic world.

And so it was that Bachelier wrote his thesis, finishing in 1900. The basic idea was that probability theory, the area of mathematics invented by Cardano, Pascal, and Fermat in the sixteenth and seventeenth centuries, could be used to understand financial markets. In other words, one could imagine a market as an enormous game of chance. Of course, it is now commonplace to compare stock markets to casinos, but this is only testament to the power of Bachelier’s idea.

By any intellectual standard, Bachelier’s thesis was an enormous success — and it seems that, despite what happened next, Bachelier knew as much. Professionally, however, it was a disaster. The problem was the audience. Bachelier was at the leading edge of a coming revolution — after all, he had just invented mathematical finance — with the sad consequence that none of his contemporaries were in a position to properly appreciate what he had done. Instead of a community of like-minded scholars, Bachelier was evaluated by mathematicians and mathematically oriented physicists. In later times, even these groups might have been sympathetic to Bachelier’s project. But in 1900, Continental mathematics was deeply inward-looking. The general perception among mathematicians was that mathematics was just emerging from a crisis that had begun to take shape around 1860. During this period many well-known theorems were shown to contain errors, which led mathematicians to fret that the foundation of their discipline was crumbling. At issue, in particular, was the question of whether suitably rigorous methods could be identified, so as to be sure that the new results flooding academic journals were not themselves as flawed as the old. This rampant search for rigor and formality had poisoned the mathematical well so that applied mathematics, even mathematical physics, was looked at askance by mainstream mathematicians. The idea of bringing mathematics into a new field, and worse, of using intuitions from finance to drive the development of new mathematics, was abhorrent and terrifying.

Poincaré’s influence was enough to shepherd Bachelier through his thesis defense, but even he was forced to conclude that Bachelier’s essay fell too far from the mainstream of French mathematics to be awarded the highest distinction. Bachelier’s dissertation received a grade of honorable, and not the better très honorable. The committee’s report, written by Poincaré, reflected Poincaré’s deep appreciation of Bachelier’s work, both for the new mathematics and for its deep insights into the workings of financial markets. But it was impossible to grant the highest grade to a mathematics dissertation that, by the standards of the day, was not on a topic in mathematics. And without a grade of très honorable on his dissertation, Bachelier’s prospects as a professional mathematician vanished. With Poincaré’s continued support, Bachelier remained in Paris. He received a handful of small grants from the University of Paris and from independent foundations to pay for his modest lifestyle. Beginning in 1909, he was permitted to lecture at the University of Paris, but without drawing a salary.

The cruelest reversal of all came in 1914. Early that year, the Council of the University of Paris authorized the dean of the Faculty of Science to create a permanent position for Bachelier. At long last, the career he had always dreamed of was within reach. But before the position could be finalized, fate threw Bachelier back down. In August of that year, Germany marched through Belgium and invaded France. In response, France mobilized for war. On the ninth of September, the forty-four-year-old mathematician who had revolutionized finance without anyone noticing was drafted into the French army.

Imagine the sun shining through a window in a dusty attic. If you focus your eyes in the right way, you can see minute dust particles dancing in the column of light. They seem suspended in the air. If you watch carefully, you can see them occasionally twitching and changing directions, drifting upward as often as down. If you were able to look closely enough, with a microscope, say, you would be able to see that the particles were constantly jittering. This seemingly random motion, according to the Roman poet Titus Lucretius (writing in about 60 B.C.), shows that there must be tiny, invisible particles — he called them “primordial bits” — buffeting the specks of dust from all directions and pushing them first in one direction and then another.

Two thousand years later, Albert Einstein made a similar argument in favor of the existence of atoms. Only he did Lucretius one better: he developed a mathematical framework that allowed him to precisely describe the trajectories a particle would take if its twitches and jitters were really caused by collisions with still-smaller particles. Over the course of the next six years, French physicist Jean-Baptiste Perrin developed an experimental method to track particles suspended in a fluid with enough precision to show that they indeed followed paths of the sort Einstein predicted. These experiments were enough to persuade the remaining skeptics that atoms did indeed exist. Lucretius’s contribution, meanwhile, went largely unappreciated.

The kind of paths that Einstein was interested in are examples of Brownian motion, named after Scottish botanist Robert Brown, who noted the random movement of pollen grains suspended in water in 1826. The mathematical treatment of Brownian motion is often called a random walk — or sometimes, more evocatively, a drunkard’s walk. Imagine a man coming out of a bar in Cancun, an open bottle of sunscreen dribbling from his back pocket. He walks forward for a few steps, and then there’s a good chance that he will stumble in one direction or another. He steadies himself, takes another step, and then stumbles once again. The direction in which the man stumbles is basically random, at least insofar as it has nothing to do with his purported destination. If the man stumbles often enough, the path traced by the sunscreen dripping on the ground as he weaves his way back to his hotel (or just as likely in another direction entirely) will look like the path of a dust particle floating in the sunlight.

In the physics and chemistry communities, Einstein gets all the credit for explaining Brownian motion mathematically, because it was his 1905 paper that caught Perrin’s eye. But in fact, Einstein was five years too late. Bachelier had already described the mathematics of random walks in 1900, in his dissertation. Unlike Einstein, Bachelier had little interest in the random motion of dust particles as they bumped into atoms. Bachelier was interested in the random movements of stock prices.

Imagine that the drunkard from Cancun is now back at his hotel. He gets out of the elevator and is faced with a long hallway, stretching off to both his left and his right. At one end of the hallway is room 700; at the other end is room 799. He is somewhere in the middle, but he has no idea which way to go to get to his room. He stumbles to and fro, half the time moving one way down the hall, and half the time moving in the opposite direction. Here’s the question that the mathematical theory of random walks allows you to answer: Suppose that with each step the drunkard takes, there is a 50% chance that that step will take him a little farther toward room 700, at one end of the long hallway, and a 50% chance that it will take him a little farther toward room 799, at the other end. What is the probability that, after one hundred steps, say, or a thousand steps, he is standing in front of a given room?

To see how this kind of mathematics can be helpful in understanding financial markets, you just have to see that a stock price is a lot like our man in Cancun. At any instant, there is a chance that the price will go up, and a chance that the price will go down. These two possibilities are directly analogous to the drunkard stumbling toward room 700, or toward room 799, working his way up or down the hallway. And so, the question that mathematics can answer in this case is the following: If the stock begins at a certain price, and it undergoes a random walk, what is the probability that the price will be a particular value after some fixed period of time? In other words, which door will the price have stumbled to after one hundred, or one thousand, ticks?

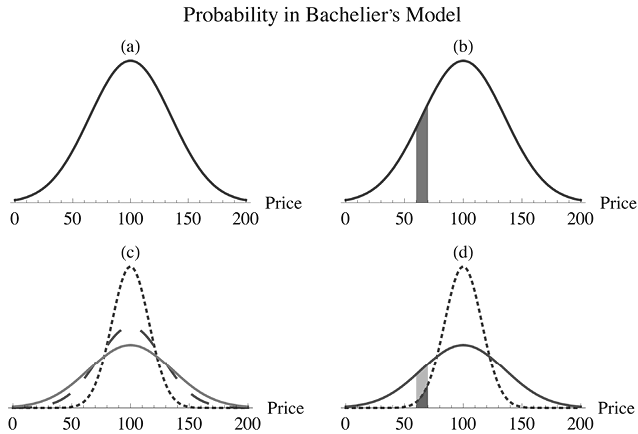
This is the question Bachelier answered in his thesis. He showed that if a stock price undergoes a random walk, the probability of its taking any given value after a certain period of time is given by a curve known as a normal distribution, or a bell curve. As its name suggests, this curve looks like a bell, rounded at the top and widening at the bottom. The tallest part of this curve is centered at the starting price, which means that the most likely scenario is that the price will be somewhere near where it began. Farther out from this center peak, the curve drops off quickly, indicating that large changes in price are less likely. As the stock price takes more steps on the random walk, however, the curve progressively widens and becomes less tall overall, indicating that over time, the chances that the stock will vary from its initial value increase. A picture is priceless here, so look at Figure 1 to see how this works.

Figure 1: Bachelier discovered that if the price of a stock undergoes a random walk, the probability that the price will take a particular value in the future can be calculated from a curve known as a normal distribution. These plots show how that works for a stock whose price is $100 now. Plot (a) is an example of a normal distribution, calculated for a particular time in the future, say, five years from now. The probability that, in five years, the price of the stock will be somewhere in a given range is given by the area underneath the curve — so, for instance, the area of the shaded region in plot (b) corresponds to the probability that the stock will be worth somewhere between $60 and $70 in five years. The shape of the plot depends on how long into the future you are thinking about projecting. In plot (c), the dotted line would be the plot for a year from now, the dashed line for three years, and the solid line for five years from now. You’ll notice that the plots get shorter and fatter over time. This means that the probability that the stock will have a price very far from its initial price of $100 gets larger, as can be seen in plot (d). Notice that the area of the shaded region under the solid line, corresponding to the probability that the price of the stock will be between $60 and $70 five years from now, is much larger than the area of the shaded region below the dotted line, which corresponds to just one year from now.

Thinking of stock movements in terms of random walks is astoundingly modern, and it seems Bachelier was essentially unprecedented in conceiving of the market in this way. And yet on some level, the idea seems crazy (perhaps explaining why no one else entertained it). Sure, you might say, I believe the mathematics. If stock prices move randomly, then the theory of random walks is well and good. But why would you ever assume that markets move randomly? Prices go up on good news; they go down on bad news. There’s nothing random about it. Bachelier’s basic assumption, that the likelihood of the price ticking up at a given instant is always equal to the likelihood of its ticking down, is pure bunk.

This thought was not lost on Bachelier. As someone intimately familiar with the workings of the Paris exchange, Bachelier knew just how strong an effect information could have on the prices of securities. And looking backward from any instant in time, it is easy to point to good news or bad news and use it to explain how the market moves. But Bachelier was interested in understanding the probabilities of future prices, where you don’t know what the news is going to be. Some future news might be predictable based on things that are already known. After all, gamblers are very good at setting odds on things like sports events and political elections — these can be thought of as predictions of the likelihoods of various outcomes to these chancy events. But how does this predictability factor into market behavior? Bachelier reasoned that any predictable events would already be reflected in the current price of a stock or bond. In other words, if you had reason to think that something would happen in the future that would ultimately make a share of Microsoft worth more — say, that Microsoft would invent a new kind of computer, or would win a major lawsuit — you should be willing to pay more for that Microsoft stock now than someone who didn’t think good things would happen to Microsoft, since you have reason to expect the stock to go up. Information that makes positive future events seem likely pushes prices up now; information that makes negative future events seem likely pushes prices down now.

But if this reasoning is right, Bachelier argued, then stock prices must be random. Think of what happens when a trade is executed at a given price. This is where the rubber hits the road for a market. A trade means that two people — a buyer and a seller — were able to agree on a price. Both buyer and seller have looked at the available information and have decided how much they think the stock is worth to them, but with an important caveat: the buyer, at least according to Bachelier’s logic, is buying the stock at that price because he or she thinks that in the future the price is likely to go up. The seller, meanwhile, is selling at that price because he or she thinks the price is more likely to go down. Taking this argument one step further, if you have a market consisting of many informed investors who are constantly agreeing on the prices at which trades should occur, the current price of a stock can be interpreted as the price that takes into account all possible information. It is the price at which there are just as many informed people willing to bet that the price will go up as are willing to bet that the price will go down. In other words, at any moment, the current price is the price at which all available information suggests that the probability of the stock ticking up and the probability of the stock ticking down are both 50%. If markets work the way Bachelier argued they must, then the random walk hypothesis isn’t crazy at all. It’s a necessary part of what makes markets run.

This way of looking at markets is now known as the efficient market hypothesis. The basic idea is that market prices always reflect the true value of the thing being traded, because they incorporate all available information. Bachelier was the first to suggest it, but, as was true of many of his deepest insights into financial markets, few of his readers noted its importance. The efficient market hypothesis was later rediscovered, to great fanfare, by University of Chicago economist Eugene Fama, in 1965. Nowadays, of course, the hypothesis is highly controversial. Some economists, particularly members of the so-called Chicago School, cling to it as an essential and irrefutable truth. But you don’t have to think too hard to realize it’s a little fishy. For instance, one consequence of the hypothesis is that there can’t be any speculative bubbles, because a bubble can occur only if the market price for something becomes unmoored from the thing’s actual value. Anyone who remembers the dot-com boom and bust in the late nineties/early 2000s, or anyone who has tried to sell a house since about 2006, knows that prices don’t behave as rationally as the Chicago School would have us believe. Indeed, most of the day-to-day traders I’ve spoken with find the idea laughable.

But even if markets aren’t always efficient, as they surely aren’t, and even if sometimes prices get quite far out of whack with the values of the goods being traded, as they surely do, the efficient market hypothesis offers a foothold for anyone trying to figure out how markets work. It’s an assumption, an idealization. A good analogy is high school physics, which often takes place in a world with no friction and no gravity. Of course, there’s no such world. But a few simplifying assumptions can go a long way toward making an otherwise intractable problem solvable — and once you solve the simplified problem, you can begin to ask how much damage your simplifying assumptions do. If you want to understand what happens when two hockey pucks bump into each other on an ice rink, assuming there’s no friction won’t get you into too much trouble. On the other hand, assuming there’s no friction when you fall off a bicycle could lead to some nasty scrapes. The situation is the same when you try to model financial markets: Bachelier begins by assuming something like the efficient market hypothesis, and he makes amazing headway. The next step, which Bachelier left to later generations of people trying to understand finance, is to figure out when the assumption of market efficiency fails, and to come up with new ways to understand the market when it does.

It seems that Samuelson was the only recipient of Savage’s postcards who ever bothered to look Bachelier up. But Samuelson was impressed enough, and influential enough, to spread what he found. Bachelier’s writings on speculation became required reading among Samuelson’s students at MIT, who, in turn, took Bachelier to the far corners of the world. Bachelier was officially canonized in 1964, when Paul Cootner, a colleague of Samuelson’s at MIT, included an English translation of Bachelier’s thesis as the first essay in an edited volume called The Random Character of Stock Market Prices. By the time Cootner’s collection was published, the random walk hypothesis had been ventured independently and improved upon by a number of people, but Cootner was unambiguous in assigning full credit for the idea to Bachelier. In Cootner’s words, “So outstanding is [Bachelier’s] work that we can say that the study of speculative prices has its moment of glory at its moment of conception.”

In many ways, Samuelson was the ideal person to discover Bachelier and to effectively spread his ideas. Samuelson proved to be one of the most influential economists of the twentieth century. He won the second Nobel Prize in economics, in 1970, for “raising the level of analysis in economic science,” the prize committee’s code for “turning economics into a mathematical discipline.” Indeed, although he studied economics both as an undergraduate at the University of Chicago and as a graduate student at Harvard, he was deeply influenced by a mathematical physicist and statistician named E. B. Wilson. Samuelson met Wilson while still a graduate student. At the time, Wilson was a professor of “vital statistics” at the Harvard School of Public Health, but he had spent the first twenty years of his career as a physicist and engineer at MIT. Wilson had been the last student of J. W. Gibbs, the first great American mathematical physicist — indeed, the first recipient of an American PhD in engineering, in 1863 from Yale. Gibbs is most famous for having helped lay the foundations of thermodynamics and statistical mechanics, which attempt to explain the behavior of ordinary objects like tubs of water and car engines in terms of their microscopic parts.

Through Wilson, Samuelson became a disciple of the Gibbsian tradition. His dissertation, which he wrote in 1940, was an attempt to rewrite economics in the language of mathematics, borrowing extensively from Gibbs’s ideas about statistical thermodynamics. One of the central aims of thermodynamics is to offer a description of how the behavior of particles, the small constituents of ordinary matter, can be aggregated to describe larger-scale objects. A major part of this analysis is identifying variables like temperature or pressure that don’t make sense with regard to individual particles but can nonetheless be used to characterize their collective behavior. Samuelson pointed out that economics can be thought of in essentially the same way: an economy is built out of people going around making ordinary economic decisions. The trick to understanding large-scale economics — macroeconomics — is to try to identify variables that characterize the economy as a whole — the inflation rate, for instance — and then work out the relationship of these variables to the individuals who make up the economy. In 1947, Samuelson published a book based on his dissertation at Harvard, called Foundations of Economic Analysis.

Samuelson’s book was groundbreaking in a way that Bachelier’s thesis never could have been. When Bachelier was studying, economics was only barely a professional discipline. In the nineteenth century, it was basically a subfield of political philosophy. Numbers played little role until the 1880s, and even then they entered only because some philosophers became interested in measuring the world’s economies to better compare them. When Bachelier wrote his thesis, there was essentially no field of economics to revolutionize — and of the few economists there were, virtually none would have been able to understand and appreciate the mathematics Bachelier used.

Over the next forty years, economics matured as a science. Early attempts to measure economic quantities gave way to more sophisticated tools for relating different economic quantities to one another — in part because of the work of Irving Fisher, the first American economist and another student of Gibbs’s at Yale. For the first decades of the twentieth century, research in economics was sporadic, with some mild support from European governments during World War I, as the needs of war pushed governments to try to enact policies that would increase production. But the discipline fully came into its own only during the early 1930s, with the onset of the Depression. Political leaders across Europe and the United States came to believe that something had gone terribly wrong with the world’s economy and sought expert advice on how to fix it. Suddenly, funding for research spiked, leading to a large number of university and government positions. Samuelson arrived at Harvard on the crest of this new wave of interest, and when his book was published, there was a large community of researchers who were at least partially equipped to understand its significance. Samuelson’s book and a subsequent textbook, which has since gone on to become the best-selling economics book of all time, helped others to appreciate what Bachelier had accomplished nearly half a century earlier.

In modern parlance, what Bachelier provided in his thesis was a model for how market prices change with time, what we would now call the random walk model. The term model made its way into economics during the 1930s, with the work of another physicist turned economist, Jan Tinbergen. (Samuelson was the second Nobelist in economics; Tinbergen was the first.) The term was already being used in physics, to refer to something just shy of a full physical theory. A theory, at least as it is usually thought of in physics, is an attempt to completely and accurately describe some feature of the world. A model, meanwhile, is a kind of simplified picture of how a physical process or system works. This was more or less how Tinbergen used the term in economics, too, although his models were designed specifically to devise ways of predicting relationships between economic variables, such as the relationship between interest rates and inflation or between different wages at a single firm and the overall productivity of that firm. (Tinbergen famously argued that a company would become less productive if the income of the highest-paid employee was more than five times the income of the lowest-paid employee — a rule of thumb largely forgotten today.) Unlike in physics, where one often works with full-blown theories, mathematical economics deals almost exclusively with models.

By the time the Cootner book was published in 1964, the idea that market prices follow a random walk was well entrenched, and many economists recognized that Bachelier was responsible for it. But the random walk model wasn’t the punch line of Bachelier’s thesis. He thought of it as preliminary work in the service of his real goal, which was developing a model for pricing options. An option is a kind of derivative that gives the person who owns the option the right to buy (or sometimes sell) a specific security, such as a stock or bond, at a predetermined price (called the strike price), at some future time (the expiration date). When you buy an option, you don’t buy the underlying stock directly. You buy the right to trade that stock at some point in the future, but at a price that you agree to in the present. So the price of an option should correspond to the value of the right to buy something at some time in the future.

Even in 1900, it was obvious to anyone interested in trading that the value of an option had to have something to do with the value of the underlying security, and it also had to have something to do with the strike price. If a share of Google is trading at $100, and I have a contract that entitles me to buy a share of Google for $50, that option is worth at least $50 to me, since I can buy the share of Google at the discounted rate and then immediately sell it at a profit. Conversely, if the option gives me the right to buy a share at $150, the option isn’t going to do me much good — unless, of course, Google’s stock price shoots up to above $150. But figuring out the precise relationship was a mystery. What should the right to do something in the future be worth now?

Bachelier’s answer was built on the idea of a fair bet. A bet is considered fair, in probability theory, if the average outcome for both people involved in the bet is zero. This means that, on average, over many repeated bets, both players should break even. An unfair bet, meanwhile, is when one player is expected to lose money in the long run. Bachelier argued that an option is itself a kind of bet. The person selling the option is betting that between the time the option is sold and the time it expires, the price of the underlying security will fall beneath the strike price. If that happens, the seller wins the bet — that is, makes a profit on the option. The option buyer, meanwhile, is betting that at some point the price of the underlying security will exceed the strike price, in which case the buyer makes a profit, by exercising the option and immediately selling the underlying security. So how much should an option cost? Bachelier reasoned that a fair price for an option would be the price that would make it a fair bet.

In general, to figure out whether a bet is fair, you need to know the probability of every given outcome, and you need to know how much you would gain (or lose) if that outcome occurred. How much you gain or lose is easy to work out, since it’s just the difference between the strike price on the option and the market price for the underlying security. But with the random walk model in hand, Bachelier also knew how to calculate the probabilities that a given stock would exceed (or fail to exceed) the strike price in a given time window. Putting these two elements together, Bachelier showed just how to calculate the fair price of an option. Problem solved.

There’s an important point to emphasize here. One often hears that markets are unpredictable because they are random. There is a sense in which this is right, and Bachelier knew it. Bachelier’s random walk model indicates that you can’t predict whether a given stock is going to go up or down, or whether your portfolio will profit. But there’s another sense in which some features of markets are predictable precisely because they are random. It’s because markets are random that you can use Bachelier’s model to make probabilistic predictions, which, because of the law of large numbers — the mathematical result that Bernoulli discovered, linking probabilities with frequency — give you information about how markets will behave in the long run. This kind of prediction is useless for someone speculating on markets directly, because it doesn’t let the speculator pick which stocks will be the winners and which the losers. But that doesn’t mean that statistical predictions can’t help investors — just consider Bachelier’s options pricing model, where the assumption that markets for the underlying assets are random is the key to its effectiveness.

That said, even a formula for pricing options isn’t a guaranteed trip to the bank. You still need a way to use the information that the formula provides to guide investment decisions and gain an edge on the market. Bachelier offered no clear insight into how to incorporate his options pricing model in a trading strategy. This was one reason why Bachelier’s options pricing model got less attention than his random walk model, even after his thesis was rediscovered by economists. A second reason was that options remained relatively exotic for a long time after he wrote his dissertation, so that even when economists in the fifties and sixties became interested in the random walk model, the options pricing model seemed quaint and irrelevant. In the United States, for instance, most options trading was illegal for much of the twentieth century. This would change in the late 1960s and again in the early 1970s. In the hands of others, Bachelier-style options pricing schemes would lay the foundations of fortunes.

Bachelier survived World War I. He was released from the military on the last day of 1918. On his return to Paris, he discovered that his position at the University of Paris had been eliminated. But overall, things were better for Bachelier after the war. Many promising young mathematicians had perished in battle, opening up university positions. Bachelier spent the first years after the war, from 1919 until 1927, as a visiting professor, first in Besançon, then in Dijon, and finally in Rennes. None of these were particularly prestigious universities, but they offered him paid teaching positions, which were extremely rare in France. Finally, in 1927, Bachelier was appointed to a full professorship at Besançon, where he taught until he retired in 1937. He lived for nine years more, revising and republishing work that he had written earlier in his career. But he stopped doing original work. Between the time he became a professor and when he died, Bachelier published only one new paper.

An event that occurred toward the end of Bachelier’s career, in 1926 (the year before he finally earned his permanent position), cast a pall over his final years as a teacher and may explain why he stopped publishing. That year, Bachelier applied for a permanent position at Dijon, where he had been teaching for several years. One of his colleagues, in reviewing his work, became confused by Bachelier’s notation. Believing he had found an error, he sent the document to Paul Lévy, a younger but more famous French probability theorist. Lévy, examining only the page on which the error purportedly appeared, confirmed the Dijon mathematician’s suspicions. Bachelier was blacklisted from Dijon. Later, he learned of Lévy’s part in the fiasco and became enraged. He circulated a letter claiming that Lévy had intentionally blocked his career without understanding his work. Bachelier earned his position at Besançon a year later, but the damage had been done and questions concerning the legitimacy of much of Bachelier’s work remained. Ironically, in 1941, Lévy read Bachelier’s final paper. The topic was Brownian motion, which Lévy was also working on. Lévy found the paper excellent. He corresponded with Bachelier, returned to Bachelier’s earlier work, and discovered that he, not Bachelier, had been wrong about the original point — Bachelier’s notation and informal style had made the paper difficult to follow, but it was essentially correct. Lévy wrote to Bachelier and they reconciled, probably sometime in 1942.

Bachelier’s work is referenced by a number of important mathematicians working in probability theory during the early twentieth century. But as the exchange with Lévy shows, many of the most influential people working in France during Bachelier’s lifetime, including people who worked on topics quite close to Bachelier’s specialties, were either unaware of him or dismissed his work as unimportant or flawed. Given the importance that ideas like his have today, one is left to conclude that Bachelier was simply too far ahead of his time. Soon after his death, though, his ideas reappeared in the work of Samuelson and his students, but also in the work of others who, like Bachelier, had come to economics from other fields, such as the mathematician Benoît Mandelbrot and the astrophysicist M.F.M. Osborne. Change was afoot in both the academic and financial worlds that would bring these later prophets the kind of recognition that Bachelier never enjoyed while he was alive.