3

From Coastlines to Cotton Prices

SZOLEM MANDELBROJT WAS THE very model of a modern mathematician. An expert in analysis (the area of abstract mathematics that includes, among other things, standard college calculus), he had studied in Paris with the best of the best, including Emile Picard and Henri Lebesgue. He was a founding member of a group of French mathematicians who, under the pseudonym Nicolas Bourbaki, endeavored to bring the highest possible level of rigor and abstraction to the field; the group’s collected works set the tone for two generations of mathematicians. When his mentor, Jacques Hadamard, one of the most famous mathematicians of the late nineteenth century, retired from his position at the prestigious Collège de France, the Collège invited Mandelbrojt to replace him. He was a serious man, doing serious work.

Or at least he would have been doing serious work if his nephew hadn’t been constantly hounding him. In 1950, Benoît Mandelbrot was a doctoral student at the University of Paris, Szolem’s alma mater, seeking (Szolem imagined) to follow in his eminent uncle’s footsteps. When Szolem first learned that Benoît wanted to pursue mathematics, he was thrilled. But gradually, Szolem began to question Benoît’s seriousness. Despite his uncle’s advice, Benoît showed no interest in the pressing mathematical matters of the day. His work lacked the rigor that had brought Szolem such success. Worst of all, Benoît seemed intent on geometrical methods, which every self-respecting mathematician knew had been abandoned a century before because they had led so many people astray. Real mathematics couldn’t be done by drawing pictures.

Benoît’s father, Szolem’s oldest brother, had helped raise Szolem. He had supported Szolem through graduate school, creating opportunities Szolem would never have had otherwise. To Szolem, then, Benoît was more like a brother than a nephew, and Szolem felt that he owed Benoît his continued patience and support. But Szolem was at the end of his rope. Benoît just wasn’t getting it. He had as much mathematical aptitude as anyone, but when it came to picking projects, he was hopeless.

One day, while Benoît was in his office talking about his crazy dissertation ideas, Szolem snapped. He reached into his trash can and pulled out a discarded paper. If Benoît wanted to work on trash, Szolem had plenty of it to give him — a whole bin filled with papers of no interest or importance. “This is for you,” he said dismissively. “That’s the kind of silly stuff you like.”

Szolem must have hoped his dramatic gesture would knock some sense into his young nephew. But the plan backfired magnificently. Benoît took the paper — a review of a recent book by a Harvard linguist named George Kingsley Zipf — and studied it carefully on his way home. Zipf was a famously eccentric character and few took him seriously. He had spent his career arguing for a universal law of physical, social, and linguistic phenomena. Zipf’s law said that if you constructed a list of all the things in some natural category, say, all of the cities in France, or all of the libraries in the world, and ranked them according to their size — you might rank cities by population; libraries, by collection size — you would always find that the size of each thing on the list was related to its rank on the list. In particular, the second thing on each list would always be about half the size of the first thing, the third thing on the list would be about a third the size of the first thing, and so on. The review that Benoît read focused on a particular example of the law in action: Zipf had gone through and counted how often various words appeared in various texts. He then showed that if you ordered the words by how often they appeared in a piece of writing, you usually found that the most common word appeared about twice as often as the second most common word, three times as often as the third most common word, and so on for all of the words in the document.

Szolem was right that Zipf’s work was just the kind of thing his nephew would be interested in. But he was wrong that it was trash — or at least that it was all trash. Zipf’s law is a peculiar combination of estimation and numerology and Zipf was a crank. But there was a gem hidden in his book: Zipf had worked out a formula that could be used to calculate how often a particular word would appear in a book, given its rank on the list and the total number of different words appearing in the text. Mandelbrot quickly realized that the formula could be improved upon, and moreover that it had some unexpected and interesting mathematical properties. Despite the resistance of the brightest lights in the mathematical establishment, his uncle included, Mandelbrot wrote a dissertation on Zipf’s law and its applications. He did so without an advisor and received his degree only by pushing his thesis through the university’s bureaucratic channels himself. It was highly irregular.

Indeed, Mandelbrot made a career out of the highly irregular, both in his impetuous rejection of the mathematical community and in his topics of study. Whereas the vast majority of mathematicians focus on shapes that are “smooth,” the kinds of shapes you can make out of Play-Doh, Mandelbrot’s most famous discovery, which he named “fractal geometry,” arose out of the study of jagged and fractured shapes, like the surface of a mountain or a shard of broken glass. This work on fractal shapes made Mandelbrot realize that there are varieties of randomness in nature that are far more extreme than the kind of randomness you get by flipping a coin over and over again — with consequences for virtually all mathematical science, including finance.

Mandelbrot was a revolutionary. Even today, decades after his most important papers, his ideas remain radical, with mainstream scientists in many fields still debating them. The situation is particularly striking in economics, where Mandelbrot’s central ideas have gone down like a bitter pill. If they are correct, almost everything traditional economists believe about markets is fundamentally flawed. It didn’t help that Mandelbrot was uncompromising, both as a person and as a scientist, never bending to academic pressures. He often found himself at the fringes of respectability: esteemed, though never as highly as he deserved; criticized and dismissed as much for his style as for the unconventionality of his work. Yet over the past four decades, as Wall Street and the scientific community have encountered new, seemingly insurmountable challenges, Mandelbrot’s insights into randomness have seemed ever more prescient — and more essential to understand.

Benoît Mandelbrot was born in 1924, to Lithuanian parents living in Warsaw, Poland. Although his father was a businessman, two of his uncles (including Szolem) were scholars. Many of his father’s other relatives were, in Mandelbrot’s words, “wise men” with no particular employment, but with a group of followers in the community who would trade money or goods in exchange for advice or learning. His mother, meanwhile, was also well educated, trained as a physician. As a boy, Mandelbrot often felt that he was expected to pursue an academic life of one sort or another, though his father urged him to choose a practical form of scholarship, such as engineering or applied science.

Despite the family’s focus on learning, however, the young Mandelbrot had a very unusual education. His parents’ first child, a daughter, died very young when an epidemic ripped through Warsaw. Benoît’s mother developed a deep fear of childhood illnesses and sought to protect her two young sons from her daughter’s fate. So rather than send Benoît to school, she hired one of his uncles to tutor him. This uncle, though related by marriage, was cast firmly in the mold of Mandelbrot’s father’s family: well educated and unemployed, with esoteric interests. He despised rote learning, so didn’t bother to teach Benoît such mundane topics as arithmetic or the alphabet (indeed, in a speech he gave after receiving the Wolf Prize for physics, Mandelbrot admitted that he still had trouble multiplying, as he had never learned his multiplication tables). Instead, the uncle encouraged creative thought and voracious reading. Mandelbrot spent most of his time playing chess and studying maps.

Warsaw was hit hard by the Depression — worse than western Europe or the United States — and Mandelbrot’s father’s clothing business was essentially destroyed in 1931. His father then moved to France, hoping that the slightly better economic situation there would enable him to support his wife and sons from afar. With their large extended family in Warsaw, however, the Mandelbrots were strongly tied to the city. The hope was that Benoît’s father would eventually be able to move back to Poland and reestablish his business there. But as the 1930s droned on and the Depression worsened, Poland became increasingly unsettled. Ethnic and political violence grew. As Jews, the Mandelbrots realized that Warsaw had become dangerous for them. Benoît’s mother packed what belongings she could and followed her husband to Paris. Though a difficult decision at the time, the move to Paris almost certainly bought the Mandelbrots their lives: of the more than 3 million Jews who lived in Poland before World War II, only a few hundred thousand survived the Holocaust.

Szolem was already in Paris when Benoît’s father arrived. He had moved to France in 1919, a refugee of an entirely different sort. In the immediate aftermath of World War I, mathematics in Poland was dominated by a brilliant young mathematician named Wacław Sierpiński. Sierpiński worked on a topic known as set theory. He was militant about his preferred style of mathematics and powerful enough to dictate the terms of success for any graduate student in Warsaw. Later in life, Szolem may have seemed unbearably rigid to the geometrically minded Mandelbrot, but Sierpiński was too formal even for Szolem. Refusing to work on the topics Sierpiński required, Szolem fled to Paris, where the prevailing mathematical ideology was more in line with his own. Ironically, Sierpiński was also the discoverer of an unusual geometrical object known as the Sierpiński triangle — an early example of a fractal.

It wasn’t until Mandelbrot arrived in Paris that he had the opportunity to interact with his famous mathematician uncle. Mandelbrot was eleven years old. Though the two would later have their differences, their early relationship was deeply formative. Since Mandelbrot spoke little French, he was placed two grades behind his age level. To keep him interested in his education and to encourage his talents, Szolem fed him bits of mathematics. It was largely Szolem’s influence during this period that pushed Mandelbrot toward mathematics. Despite the difficult economic and political situation, under Szolem’s tutelage Benoît found a way to thrive in his new home.

Unfortunately, it would not last. In 1940, Germany invaded France. And once again, the Mandelbrots were forced to flee.

How long is Britain’s coastline? This might seem like a simple question — one that could be easily settled, say, by a team of competent surveyors. As it turns out, however, the question is more complicated than it appears. There’s a deep puzzle built into it, sometimes known as the coastline paradox. To figure out the length of a coastline, you need to take some measurements, presumably with some sort of ruler. The puzzle concerns how long your ruler needs to be. Suppose you started with a single enormous ruler that stretched from Cape Wrath, at the northernmost tip of Scotland, all the way down to Penzance, at the southwestern tip of Cornwall. This would give you an estimate of the length of the coastline.

But not a very good one. A coastline is hardly a straight line. The coast of Britain dips in at the Bristol Channel and the Irish Sea, jutting out again near Wales, so taking one very long ruler isn’t going to give an accurate measurement. To get a better measurement, you would want to use a somewhat smaller ruler — one that could easily accommodate the additional length that the various peninsulas and bays add to the coast. You might try adding up the distances from, say, Penzance to Bristol, and then from Bristol to St. David’s in Wales, and then from St. David’s to Carmel Head at the northwestern tip of Wales, and so on all the way up the coast. This total distance would be a lot longer than the first distance you calculated, but it would be more accurate.

Now, though, a pattern begins to emerge. This smaller ruler, it turns out, underestimates the length in the same way the original long ruler did. Using the smaller ruler, you miss Cardigan Bay altogether, not to mention the dozens of smaller harbors and inlets along the Cornish and Welsh coasts. To account for these features, which turn out to add rather a lot of distance, you need a smaller ruler still. But again, the same problem arises. In fact, no matter what size ruler you pick, the answer you get by measuring the coastline with that ruler is always too small. In other words, you can always get a larger answer to the question by picking a smaller ruler.

This is where the paradox arises. It is often the case that choosing more precise instruments gives you a better measurement of something. You can get a sense of how hot a pot of water is by sticking your finger in it. An alcohol thermometer would do the job even better, and a high-tech digital thermometer would bring the accuracy to within a fraction of a degree. There is a sense in which the imprecise tools are adding measurement error, and as you devise better and better instruments, you home in on the real temperature. But with a coastline, no matter how precise your measuring device — that is, no matter how small your ruler — your measurement is always much too small. In some sense, a coastline doesn’t have a length, or at least not in the way that simple shapes like a line or a circle do.

Mandelbrot addressed the coastline paradox in a groundbreaking paper in 1967. It was one of his first attempts to describe a fractal shape — as, indeed, a coastline turns out to be, though Mandelbrot didn’t coin the term until 1975. Coastlines (and other fractals) are remarkable from a mathematical point of view because they have a property called self-similarity. To say that something is self-similar is to say that it is composed of pieces that look just like the whole; these pieces in turn are composed of still smaller pieces that also look like the whole, and so on ad infinitum. If you begin with the whole west coast of Britain and carve it up into several pieces, you will notice that each of these also looks like a coastline; just like the full coastline, the smaller stretches of coast have their own little inlets and peninsulas. And if you break up one of these smaller bits of coast further, the still-smaller pieces exhibit all the same features of the larger structures.

Once you start looking for self-similarity, you quickly realize it’s a ubiquitous feature of nature. A mountaintop looks much like a whole mountain in miniature; a tree branch looks like a little tree, with smaller branches of its own; river systems are built out of smaller rivers and estuaries. The principle even seems to extend to the social world. As Mandelbrot later pointed out, a battle is made up of smaller skirmishes, and a war is composed of battles, each a microcosm of the war as a whole.

When World War II broke out, the Mandelbrots fled Paris, where they expected the fighting to be quite intense, and settled in a town called Tulle, in the region of France known as Corrèze. Once again, the Mandelbrots showed great foresight, not to mention luck: they left Paris in late 1939, mere months before the Nazi invasion of France. Tulle turned out to be an extremely fortuitous choice. It was far enough south that it would soon become part of unoccupied (Vichy) France.

The Vichy government cooperated with the Germans, but anti-Semitism in the south was less virulent than in the German-occupied territories. For a few years, at least, Mandelbrot was able to attend high school in Tulle. He was now fluent in French and he quickly moved through school, catching up to his peers by the time the Germans took control in 1942. Still, the Mandelbrots lived in constant fear of deportation. In 1940, the Vichy government had begun to review the status of all immigrants naturalized after 1927. They stripped about fifteen thousand (mostly Jews) of their citizenship, as a precursor to sending them to German concentration camps. Though the Mandelbrots managed to escape notice in little Tulle, the threat was ever present.

Matters became worse in 1942. On November 8, the British and American armies invaded French North Africa. In response, the Germans occupied southern France, anticipating an assault on continental Europe. With the German army came the Gestapo, and as southern France became a staging ground for defensive Panzer divisions, even Tulle became a minor battleground. Though it was home to only a few thousand people, Tulle was the traditional capital of the region. As the German presence in southern France increased, Tulle became a place of strategic interest to both the vestiges of the Vichy government and the leaders of the resistance. The Mandelbrots could no longer rely on the obscurity of their little town for safety.

In his autobiographical writings and interviews, Mandelbrot often spoke of the war’s impact on his education. After finishing secondary school in 1942, he found himself unable to proceed to a grande école because his movements were so constrained. (Here his education is reminiscent of Bachelier’s, who was also unable to attend a grande école.) But Mandelbrot never went into detail about his experiences during this period, except to say that the year and a half after finishing school was “very, very rough” and he had “several very close calls with disaster.”

Since further schooling was out of the question, and because he needed to maintain a low profile, he avoided cities and moved often. He lived with members of the resistance, who took him in and attempted to hide him. He worked a series of odd jobs, attempting to disguise himself as a provincial Frenchman. For some months he worked as a horse groom, and then as an apprentice toolmaker for the French railroad. But he was never a very convincing tradesman. Missing the scholarly life, Mandelbrot clung to the few books he managed to find during this period, carrying them with him and reading whenever he had an opportunity — not the smartest move for someone trying to pass as a horse groom.

At one point, at least, Mandelbrot very narrowly escaped deportation — and likely execution. But mostly he managed to keep clear of German forces. His father had a closer call. As Mandelbrot would later tell it, his father was arrested during this period and sent to a nearby prison camp. Not long after, the prison was attacked by members of the resistance. The guards were neutralized and the prisoners were set free. But the resistance fighters were ill prepared to defend the camp, so they urged the prisoners to flee quickly to escape capture by German reinforcements.

Lacking a plan or a clear route to safety, the prisoners set out in a group on the road to Limoges, the nearest major town. Shortly after leaving the camp, however, the elder Mandelbrot realized that this was a disastrous idea: they were traveling in a large pack, moving in the open on a major road. Tracking them would be easy. The others couldn’t be persuaded, so Mandelbrot’s father left the group and struck out on his own. He headed toward a nearby forest, planning to slowly make his way back to where his family had been hiding before his arrest. As he moved through the wilderness, he heard a gut-wrenching noise: behind him, back at the main road, a German dive bomber had found the other prisoners.

Life during wartime is an unpredictable thing. In Thomas Pynchon’s novel Gravity’s Rainbow, one of the characters, Roger Mexico, is a statistician charged with keeping track of where the V-2 rockets land in London during the final days of the Third Reich. He finds that the rockets are falling according to a particular statistical distribution — the one you would expect if they were equally likely to fall anywhere in the city. Mexico is surrounded by people desperate to control their lives, to save themselves from the rockets’ whimsical paths. To these onlookers, Mexico’s charts and graphs hint at some underlying pattern, something they might use to predict where the next rocket will fall.

Some areas of the city seem to be hit quite often. Others, rarely. But to assume that these patterns say anything about where the next rocket will fall is to commit the same fallacy as the roulette player who is convinced that a particular number is “due.” Mexico knows this. And yet he, too, finds the data seductive, as though the very randomness of the pattern holds the key to its power. And it does, at least if you happen to be standing on the street where the next rocket falls.

Yet mathematically, this sort of randomness is mild. The V-2 rockets were fired systematically, several a day, aimed roughly at London. Working out the odds of how many rockets would land on St. Paul’s Cathedral or in Hammersmith was a lot like working out how many times a roulette ball would fall into red 25. Indeed, many of the situations we think of as random are like this. So many, in fact, that it’s easy to fall prey to the idea that all random events are like coin tosses or simple casino games.

This assumption underlies much of modern financial theory. Think back to when Bachelier was imagining how stock prices would change over time if they underwent a random walk. Every few moments, the price would tick up or down by some small amount as though God were flipping a coin. Bachelier discovered that if this was a good approximation of what was happening, the distribution of prices would look like a bell curve, a normal distribution. Osborne of course pointed out that this wasn’t quite right; really, you expect the prices to change by some fixed percentage each time God flips his coin, rather than some fixed amount. This modification led to the observations that rates of return should be normally distributed and prices should be log-normally distributed.

The normal distribution shows up in all sorts of places in nature. If you took the heights of all of the men in a given part of the world and plotted how many of them were 5 feet 6 inches, how many 5 feet 7 inches, and so on, you would get a normal distribution. If you used a thousand thermometers and tried to take your temperature with each of them, the results would look like a normal distribution. If you played a coin-flipping game in which you got a dollar every time the coin landed heads, and you lost a dollar every time it landed tails, the probabilities governing your profits after many plays would look like a normal distribution. This is convenient: normal distributions are easy to understand and to work with. For instance, if something is normally distributed and your sample is large enough, the sample’s average value tends to converge to a particular number; white men, on average, are about 5 feet 9 inches, and unless you are ill, the thousand thermometers’ readings will average 98.6 degrees Fahrenheit. Your average profits in the coin-tossing game will converge to zero.

This rule can be thought of as the law of large numbers for probability distributions — a generalization of the principle discovered by Bernoulli, linking probabilities to the long-run frequencies with which events occur. It says that if something is governed by certain probability distributions, as men’s heights are governed by a normal distribution, then once you have a large enough sample, new instances aren’t going to affect the average value very much. Once you have measured many men’s heights in a given region of the world, measuring one more man won’t change the average height by much.

Not all probability distributions satisfy the law of large numbers, however. The location of the drunken vacationer in Cancun does — he is taking a random walk, so on average, he will stay right where he started, just as the average profits from a coin-tossing game converge to zero. But what if instead of a drunk trying to walk to his hotel, you had a drunken firing squad? Each member stands, rifle in hand, facing a wall. (For argument’s sake, assume the wall is infinitely long.) Just like the drunk walking, the drunks on the firing squad are equally liable to stumble one way as another. When each one steadies himself to shoot the rifle, he could be pointing in any direction at all. The bullet might hit the wall directly in front of him, or it might hit the wall 100 feet to his right (or it might go off in the entirely opposite direction, missing the wall completely).

Suppose the group engages in target practice, firing a few thousand shots. If you make a note of where each bullet hits the wall (counting only the ones that hit), you can use this information to come up with a distribution that corresponds to the probability that any given bullet will hit any given part of the wall. When you compare this distribution to the plain old normal distribution, you’ll notice that it’s quite different. The drunken firing squad’s bullets hit the middle part of the wall most of the time — more often, in fact, than the normal distribution would have predicted. But the bullets also hit very distant parts of the wall surprisingly often — much, much more often than the normal distribution would have predicted.

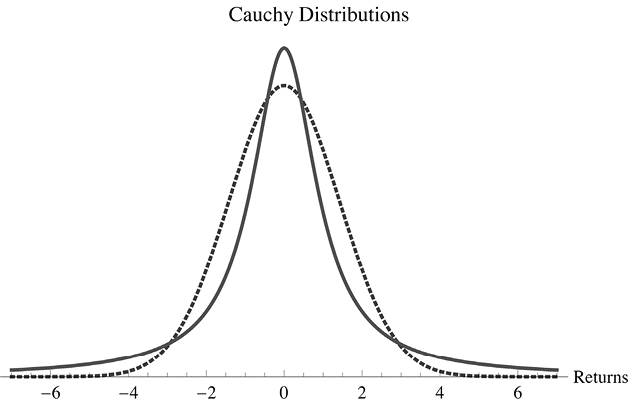
This probability distribution is called a Cauchy distribution. Because the left and right sides of the distribution don’t go to zero as quickly as in a normal distribution (because bullets hit distant parts of the wall quite often), a Cauchy distribution is said to have “fat tails.” (You can see what the Cauchy distribution looks like in Figure 3.)

One of the most striking features of the Cauchy distribution is that it doesn’t obey the law of large numbers: the average location of the firing squad’s bullets never converges to any fixed number. If your firing squad has fired a thousand times, you can take all of the places their bullets hit and come up with an average value — just as you can average your winnings if you’re playing the coin-flip game. But this average value is highly unstable. It’s possible for one of the squad members to get so turned around that when he fires next, the bullet goes almost parallel with the wall. It could travel a hundred miles (these are very powerful guns) — far enough, in fact, that when you add this newest result to the others, the average is totally different from what it was before. Because of the distribution’s fat tails, even the long-term average location of a drunken firing squad’s bullets is unpredictable.

Figure 3: The location of a drunken vacationer trying to find his hotel room on a long corridor is governed by a normal distribution. But not all random processes are governed by normal distributions. Where the bullets fired by a drunken firing squad will land is determined by a different sort of distribution, called a Cauchy distribution. (Note that the angle at which the members of the drunken firing squad fire will be governed by a normal distribution; it’s the location on the wall that they are trying to hit that is governed by the Cauchy distribution!) Cauchy distributions (the solid line in this figure) are thinner and taller than normal distributions (the dashed line) around their central values, but their tails drop off more slowly — which means that events far from the center of the distribution are more likely than a normal distribution would predict. For this reason, Cauchy distributions are called “fat-tailed” distributions. Mandelbrot called phenomena governed by fat-tailed distributions “wildly random” because they experience many more extreme events.

As Mandelbrot described it, the war, especially during the first two years under Vichy rule, left huge swaths of France unaffected for long periods. But then “a storm” would come through and wreak havoc, followed by another period of calm. So perhaps it is no surprise that Mandelbrot was fascinated by these bursts, by random processes that couldn’t be tamed like a casino game. He called events that obeyed a Cauchy distribution wildly random, to distinguish them from the plain, mild randomness of the random walk, and he devoted much of his career to studying them. When Mandelbrot began his career, most statisticians assumed that the world is filled with normally distributed events; though Cauchy and other fat-tailed distributions might show up sometimes, they were believed to be the exception. More than anyone else, Mandelbrot showed just how many of these so-called exceptions there are.

Think back to the coastline of Britain. Suppose you want to figure out the average size of a promontory, or any outcropping of land. You might start by looking at boulders and jetties, things of a manageable size. You take the average size of all of these. But you aren’t done, because you realize that these jetties and outcroppings are themselves parts of small peninsulas. So you take out your surveying equipment, sensing that you’re about to fall down a rabbit hole, and start measuring the sizes of these peninsulas. There aren’t many of these, but they are much bigger than the jetties and boulders you’ve looked at already, and now your new average is totally different from what it was after the first round of measurement. And what’s more, you haven’t even taken into account the still-larger structures, like Cornwall. Or the whole west coast of Britain itself, since from a geological perspective it’s just an outcropping from mainland Eurasia. And while you’re at it, you probably need to consider smaller structures, too. Why count boulders that are several feet across, but not rocks that are just a few inches across?

Each time you cast your net wider, the average changes dramatically. You can’t seem to narrow in on a single figure. Dismaying as it is for our Sisyphean surveyor, there’s no expected value for the average size of a feature on a coastline. This is a general property of fractals, following from their self-similarity. From one point of view, they are beautifully ordered and regular; from another, wildly random. And if fractals are everywhere, as Mandelbrot believed, the world is a place dominated by extremes, where our intuitive ideas about averages and normalcy can only lead us astray.

Though he never provided details, Mandelbrot often alluded to a particularly harrowing experience toward the end of 1943, while he was hiding with members of the French resistance. Afterward, his protectors realized that Mandelbrot couldn’t remain in Tulle, and they secured a place for him as a postgraduate student at a preparatory school in Lyon.

Moving Mandelbrot was a risky proposition. Lyon was one of the most dangerous cities in southern France for both Jews and resistance sympathizers; Mandelbrot was both. Nikolaus Barbie, an SS officer, led the local Gestapo outpost from a hotel near the center of town. Known as the Butcher of Lyon, he was later convicted of war crimes for the deportation of nearly one thousand of the region’s Jews. But Mandelbrot was not proving to be a very persuasive rural journeyman, and the resistance fighters who were caring for him needed a place where he wouldn’t be so conspicuous. A school was a natural choice: Mandelbrot was the right age and he carried himself like a scholar. He would attend under an assumed identity and live in the dormitories. Yet even with a good cover, Mandelbrot couldn’t risk venturing beyond school grounds. He was a prisoner as much as a student.

To complete the deception, Mandelbrot sat in on classes. But no one expected him to learn much. The school was designed to prepare the very brightest students for the difficult exams required for entrance to the grandes écoles. The atmosphere was often competitive and fast paced. Since Mandelbrot had not engaged in any academic work from the spring of 1942 to early 1944, when he enrolled at the school, he had once again fallen far behind his peers. It would be virtually impossible for him to catch up, given the caliber of his classmates and their ample head start.

At first, things went as expected. Mandelbrot sat quietly in the classes, pretending to be a student. He understood nothing. A week went by and then another. Mandelbrot listened as the instructor quizzed students on problems in abstract algebra, pushing them to compete to find the solutions as quickly as possible in preparation for the timed exams. Still, Mandelbrot understood nothing. He could guess at what the problems meant, but he had no clue how to solve them, and the discussions of various methods were lost on him. And then something remarkable happened. One day, after the teacher gave the class a problem to solve, an image appeared in Mandelbrot’s mind. Without thinking, he raised his hand. Surprised, the teacher called on him. “Isn’t this equivalent to asking whether these two surfaces intersect one another?” Mandelbrot asked, describing the two shapes he was picturing. The teacher agreed that the problems were equivalent but pointed out that the goal was to solve the problems quickly, not interpret them geometrically.

Mandelbrot sat back in his chair, silenced by the rebuke. But when the teacher read the next problem, he again tried to think of it in spatial terms. He very quickly saw what the shapes in question were. Soon he realized he could do this reliably. He had, it turned out, a “freakish” (his word) gift for visualizing abstract algebraic problems. But as his teacher reminded him, just coming up with a geometrical interpretation of a problem wouldn’t help him on the test, and so Mandelbrot began thinking about how to put his talent to use. He didn’t see a way to solve the problems using just his geometrical intuition, at least not in the way the teacher wanted. But he could very quickly guess what the answer had to be. And he was usually right. Soon, despite his poor preparation and unusual status, Mandelbrot was embraced by the school.

Liberation came in the summer of 1944. By the end of August, the Mandelbrots had moved back to Paris. Though he had been in Lyon for only six months, a single academic term, Mandelbrot’s experience there changed the course of his life. He learned an enormous amount and discovered an unusual gift for geometry, but more importantly, he had reclaimed his education. He decided to continue his preparations for the grande école examinations, and in 1944, he was admitted to one of the most prestigious preparatory schools in Paris. After performing well on the exams, he gained entrance to several grandes écoles, including the most selective of all, the École Normale Supérieure.

He attended the École Normale Supérieure for two days before deciding that he couldn’t bear life in an ivory tower. His time away from the academy had made him all too conscious of real-world problems. Mandelbrot immediately transferred to the more practical and scientifically oriented École Polytechnique. The choice augured Mandelbrot’s path through academia: in each instance, faced with a choice between the pure and the applied, Mandelbrot chose the applied. In doing so, he brought his “freakish” geometrical gifts to bear on applied problems that had previously been overlooked, or that had seemed too difficult to crack. Like Bachelier before him, Mandelbrot asked questions that had never before occurred to anyone with his mathematical abilities — and he found answers that changed how scientists see the world.

Much later, Mandelbrot would attribute his remarkable career to two things. First was his unusual and oft-disrupted education. Mandelbrot ultimately made his way to a grande école, and on to a PhD. But the journey wasn’t easy, and it forced him to be resourceful and independent in ways that he wouldn’t have been had he followed a more traditional path. The second was a series of serendipitous discoveries that introduced him to various pieces of an intellectual puzzle. Zipf’s formula, which he learned about when his uncle tossed a review in his face, was one such discovery. Another occurred several years later, soon after Mandelbrot finished graduate school.

At the time, he was working at IBM, another beneficiary of the industrialization of physics. Though he often expressed pride at having completed graduate school without an advisor, this didn’t help when it came to seeking employment. He enjoyed a stint as a postdoctoral researcher at Princeton’s Institute for Advanced Study and then spent some time back in Europe, working on thermodynamics for the French government’s research center, CNRS. But a full-time faculty position proved elusive, and Mandelbrot’s nascent disillusionment with the mathematical firmament deepened. When he at last received an offer from IBM in 1958 to work as a staff scientist for its research division, he jumped at the chance, even though, in his words, “there was no great distinction [in] getting an offer from IBM then.”

One of the goals of IBM’s research division was to find applications for its newest computers. Mandelbrot was assigned to work on economic data. His bosses hoped that if Mandelbrot could show how useful computers were for economics, banks and investment houses might be convinced to buy an IBM mainframe. In particular, he was looking at data describing income distributions throughout society. (Banks weren’t necessarily interested in this specific question; rather, the idea was to use Mandelbrot’s research as proof of concept, to demonstrate how efficient a computer could be at number-crunching financial data.)

Income distribution had been studied before, most famously by a nineteenth-century Italian engineer, industrialist, and economist named Vilfredo Pareto. A strong believer in laissez-faire economics, Pareto was obsessed with the workings of the free market and the accumulation of capital. He wanted to understand how people got rich, who controlled wealth, and how resources were doled out by market forces. To this end, he gathered an immense amount of data on wealth and income, drawing on such diverse sources as real estate transactions, personal income data from across Europe, and historical tax records. To analyze these data, Pareto would make elaborate graphs, with income levels and wealth on one axis, and the number of people who had access to that wealth on the other.

For all the diversity of his data sources, Pareto found a single pattern over and over again. As he described it, 80% of the wealth in any country, in any era, is controlled by 20% of the population. The pattern is now known as Pareto’s principle, or sometimes the 80–20 rule. At the time, Pareto interpreted these results much as Zipf would have, as evidence for a “social law” revealing that wealth is not distributed randomly but rather by some mysterious force that shapes markets and societies. Once Pareto began looking, the law seemed to apply to everything. Eighty percent of a company’s sales are usually due to just 20% of its customers. Eighty percent of crimes can be traced to just 20% of criminals. And so on. (Nowadays, Pareto’s principle is seen to hold approximately in many places, such as in the ratio of health-care costs to patients in the United States.)

The most interesting thing about Pareto’s work, at least from Mandelbrot’s point of view, wasn’t the idea that Pareto’s data revealed some mathematical law of society. Instead, it was the particular relationship between the income distribution for a whole country and for a small portion of that country. Pareto showed that the 80–20 rule held, at least approximately, for a country as a whole. But what if you asked a slightly different question: How is income distributed among that 20% of the population that controls the overwhelming majority of wealth? Remarkably, the same pattern emerges. If you look at just the wealthiest people in a country, 80% of their wealth is controlled by just 20% of them. The superrich tend to have the same disproportionate amount of wealth as the plain old rich. And indeed, the pattern continues. Eighty percent of the resources controlled by the superrich are consolidated in the hands of the ultra-superrich. And so on.

This kind of pattern should be familiar by now. Wealth distribution across a population displays a kind of self-similarity, or a fractal pattern. In fact, the distributions that Pareto discovered, called Paretian distributions, are a type of fat-tailed distribution — revealing a kind of wild randomness in income distribution, though not quite as wild as the drunken firing squad’s shots. When Mandelbrot was looking at the data for IBM, he had not yet invented fractals. His seminal work on the coastline paradox was almost a decade away. But similarly to Pareto half a century before him, something about the pattern struck Mandelbrot. It reminded him of his doctoral work on Zipf, who also had discovered an odd self-similarity in how word frequencies were distributed.

Although Mandelbrot had largely left academia, his work for IBM on wealth distribution was of some interest to mainstream economists, and so he was occasionally invited to give scholarly talks. It was in 1961, immediately before one of these lectures, that he made his second serendipitous discovery.

The talk was to be delivered to Harvard’s economics department. Shortly before it was scheduled to begin, Mandelbrot met with one of the faculty members, an economist named Hendrik Houthakker. As soon as he walked into Houthakker’s office, Mandelbrot noticed a drawing on Houthakker’s chalkboard. It was nearly identical to the graph that Mandelbrot was planning to use in his talk, as part of his discussion of income distribution and Pareto’s principle. Mandelbrot guessed that Houthakker must have been working on a similar problem and made some comment about their shared interests. Houthakker responded with a blank stare.

After another awkward attempt or two, Mandelbrot realized that something was wrong. He backed up and pointed to the graph on the board. “Isn’t that a wealth distribution plot?” Puzzled, Houthakker explained that the drawing on his board had been from a meeting with a graduate student earlier in the day, during which Houthakker and the student were discussing historical data on cotton prices. The picture was a graph of daily returns from cotton markets.

Houthakker went on to explain that he had been working on cotton markets for a while now, but the data weren’t cooperating with theory. By this time, Bachelier’s work had been rediscovered and economists had begun to accept that markets undergo a random walk, as Bachelier and Osborne had argued. Houthakker was interested in verifying this hypothesis by looking at historical data. If the random walk thesis was correct, you should see many small price changes over the course of a day or a week or a month, but very few large ones. What Houthakker’s data showed, however, was not what the theory predicted: he was seeing too many very small changes, but also far too many very large ones. Worse, he was struggling to come up with a value for the average price change, as Bachelier’s theory predicted must exist. Every time Houthakker looked at a new set of data, the average would change, often dramatically. In other words, cotton prices seemed to behave more like a drunken firing squad than a drunken vacationer.

Mandelbrot was intrigued. He asked Houthakker if he could look more closely at the data, and Houthakker agreed; in fact, Houthakker told Mandelbrot that he could have it all, since he was ready to abandon the project.

Back at IBM, Mandelbrot had a small team of programmers tear through boxes of Houthakker’s cotton data, analyzing everything in detail. He quickly confirmed Houthakker’s most troubling findings: it appeared that there was no “average” rate of return. The prices looked random, but they weren’t explained by the standard statistical tools or Bachelier’s and Osborne’s theories. Something weird was going on.

Mandelbrot had seen unusual distributions before. In addition to studying Zipf’s and Pareto’s work, he was familiar with a third kind of distribution, discovered by one of his professors in Paris, Paul Lévy. It was Lévy who, upon reading a small section of one of Bachelier’s papers, concluded that Bachelier’s work was plagued with errors. Much later, Lévy would recognize his own mistake and apologize to Bachelier. Part of what made Lévy return to Bachelier’s work was a renewed interest in random walk processes and probability distributions. Ironically, this later work of Lévy’s received far less attention than his earlier work, leaving Lévy alienated and obscure at the twilight of his career.

Lévy’s work on random processes had led him to study a class of probability distribution now called Lévy-stable distributions. The normal and Cauchy distributions are both examples of Lévy-stable distributions, but Lévy showed that there is a spectrum of randomness, ranging between the two. (In fact, there are even wilder varieties of randomness than the Cauchy distribution.) Wildness can be captured by a number, usually called alpha, that characterizes the tails of a Lévy-stable distribution (see Figure 4). Normal distributions have an alpha of 2; Cauchy distributions have an alpha of 1. The lower the number, the more wildly random the process (and the fatter the tails). Distributions that have alpha of 1 or less don’t satisfy the law of large numbers — in fact, it isn’t possible to even define the average value for a quantity that wild. Distributions with alpha between 1 and 2, meanwhile, have average values, but they don’t have a well-defined average variability — what statisticians call volatility or variance — which means it can be very hard to calculate an average value from empirical data, even when the average exists.

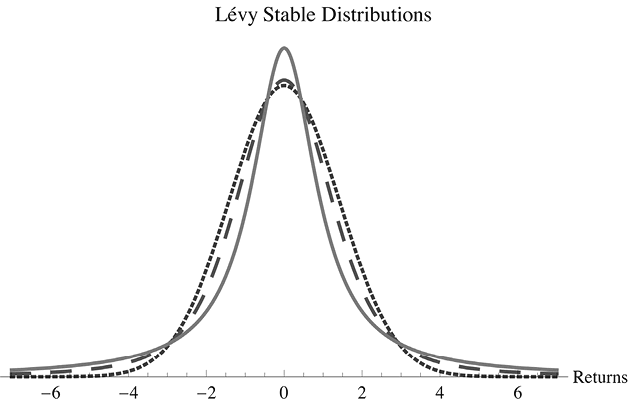
Figure 4: Normal distributions and Cauchy distributions are two extreme cases of a class of distributions called Lévy-stable distributions. Lévy-stable distributions are characterized by a parameter called alpha. If alpha = 2, the distribution is a normal distribution; if alpha = 1, it is a Cauchy distribution. Mandelbrot argued that real market returns are governed by Lévy-stable distributions with alpha between 1 and 2, which means that returns are more wildly random than Osborne had thought, though not as wild as a drunken firing squad. This figure shows three Lévy-stable distributions. As in Figure 3, the solid line corresponds to a Cauchy distribution and the dotted line is a normal distribution. But the third curve is a Lévy-stable distribution with alpha = 3/2. It’s a little taller and a little narrower than a normal distribution, and its tails are a little fatter, but it’s not so extreme as a Cauchy distribution.

Houthakker, trained as an economist, likely knew very little about Lévy’s late work. But Mandelbrot had been a disciple of Lévy’s. And so when he saw the detailed data from Houthakker, something clicked. Houthakker was right that cotton prices didn’t follow a normal distribution — but they also didn’t follow a Cauchy distribution. They were somewhere in between, with an alpha of 1.7. Cotton prices were random, all right — far more wildly random than Bachelier or Osborne could have imagined.

Cotton markets were the first place that Mandelbrot found evidence of Lévy-stable distributions. But if cotton prices varied wildly, he wondered, why should other markets be different? Mandelbrot quickly began collecting data on markets of all sorts: other commodities (like gold or oil), stocks, bonds. In every case he found the same thing: the alphas associated with these markets were less than 2, often substantially so. This meant that Bachelier’s and Osborne’s theories of random walks and normal distributions faced a big problem.

Mandelbrot made the connection between Pareto distributions and Lévy-stable distributions in 1960, the year after Osborne’s first paper; he published the extension of this work to cotton prices in 1963, early enough that Paul Cootner, the MIT economist who edited the collection of essays that included Bachelier’s and Osborne’s work, was able to include a paper by Mandelbrot outlining his alternative theory. This meant that the volume that brought Bachelier’s and Osborne’s work to the wider community of economists and financial theorists already included hints that simple random walk models were not the whole story. Around 1965, financial theorists had a choice, though it surely didn’t feel that way to them at the time: they could follow Osborne and others who showed how traditional statistical methods, developed largely in the context of physics, could be used to analyze and model stock market returns; or they could follow Mandelbrot, who showed that despite this remarkable power, there was reason to think the traditional methods had shortcomings. Weighing in on the traditionalists’ side was the fact that the older methods were better understood and simpler. Mandelbrot, meanwhile, had some highly suggestive data on his side.

The field chose Osborne. Cootner made the argument this way at a 1962 meeting of the Econometric Society [econometrics is the statistical study of economic data, including but not limited to finance], in response to Mandelbrot’s work on cotton prices:

Mandelbrot, like Prime Minister Churchill before him, promises us not utopia but blood, sweat, toil, and tears. If he is right, almost all of our statistical tools are obsolete. . . . Almost without exception, past econometric work is meaningless. Surely, before consigning centuries of work to the ash pile, we should like to have some assurance that all our work is truly useless.

Much of the field took a similar view. At this point, the (mild) random walk hypothesis was still young, but a growing number of researchers, Cootner included, had already staked their careers on it. It is easy to see Cootner’s remarks as a reactionary attempt to fend off a young researcher who had caught out the errors of the (recent) past. Surely Mandelbrot saw it this way, and perhaps we all should now that many practitioners and theorists alike have recognized the importance of fat-tailed distributions. For instance, some people — most notably, Nassim Taleb, a hedge fund manager and professor at Polytechnic Institute of New York University who wrote an influential book called The Black Swan, as well as Mandelbrot himself — have recently argued that finance took a wrong turn in 1965 by continuing to assume mild randomness when really financial markets are wild.

But that argument misses an important point about the way the science of finance has developed. In the 1960s, traditional statistics was a mature field with an enormous toolbox. Mandelbrot was coming forward with little more than a suggestion and a few pictures. It would have been essentially impossible to do the kind of work that Osborne, Samuelson, and many others working in finance and econometrics did during this period without the tools of traditional statistics. Mandelbrot’s project simply wasn’t well enough understood. It would be like telling a carpenter that screws are much stronger than nails, when the carpenter has a hammer and no one has yet invented the screwdriver. Even if the house would be stronger if built with screws, you’d still get much farther working with a hammer and nails, at least for a while.

For this reason, pushing forward with the simpler available tools while Mandelbrot and his early converts worked out the consequences of his work on fractals and self-similarity was the only sensible choice. What the field implicitly understood is that you need to start with the simplest theory that works, get as far as you can, and then ask where the theory you’ve built has gone wrong. In this case, once you have established that stock market prices are random (at least in some sense), the next step is to assume that they are random in the simplest possible way: that they just follow a random walk. This is what Bachelier did. Osborne then pointed out that this couldn’t be right, since it would mean that stock prices could become negative, and so he complicated the model ever so slightly by suggesting that market rates of return follow a random walk. He then showed that this suggestion explained the data much better than Bachelier’s model.

Then came Mandelbrot, who said that Osborne’s suggestion wasn’t quite right either, because if you looked at price data in detail, you would see a different pattern from the one Osborne thought he had found. Not dramatically different, though; the pattern Mandelbrot identified doesn’t say that prices aren’t random, but that prices are random in a slightly different way from what Osborne had believed. The differences between Osborne’s model and Mandelbrot’s can hardly be dismissed, but they become important only in the context of extreme events. On a typical day, there aren’t going to be any extreme events (according to either theory), and so you usually won’t notice much of a difference between the two models.

For this reason — as we will see in the next several chapters — when it came time for economists interested in financial markets to try to extend the ideas presented in Cootner’s book, to put the randomness of stock market prices to work by using statistics to predict derivatives prices or to calculate the amount of risk in a portfolio, they had to pick between the simple theory that gave good results the vast majority of the time and the more cumbersome one that better accounted for certain extreme events. It made perfect sense to start with the simpler one and see what happened. If you make good assumptions, if you idealize effectively, you can often solve a problem that otherwise couldn’t be solved — and get a solution that is quite close to correct, even if some of the details are wrong. Of course, all along, you know you’ve made assumptions that aren’t quite right (markets are not perfectly efficient; returns and not prices follow a simple random walk). But they’re a start.

It is also too simple to say that Mandelbrot was ignored in the decades immediately following his early papers on cotton. Most economists followed Osborne’s lead when building on the randomness of markets to study related topics. But a dedicated core of mathematicians, statisticians, and economists put Mandelbrot’s proposals to the test with ever more detailed data, and ever more sophisticated mathematical methods — most of which were developed specifically for the purpose of better understanding what it would mean if the world were really as wildly random as Mandelbrot said. This work confirmed Mandelbrot’s basic thesis, that normal and log-normal distributions are insufficient to capture the statistical properties of markets. Rates of return have fat tails.

That said, there’s a wrinkle in the story. Mandelbrot made a very specific claim in his 1963 papers: he said that markets were Lévy-stable distributed. And except for the normal distribution, the volatility of Lévy-stable distributions is infinite, which means that most standard statistical tools don’t apply for analyzing such distributions. (This is what Cootner was alluding to when he said that if Mandelbrot was correct, the standard statistical tools were obsolete.) Today, the best evidence indicates that this specific claim, regarding infinite variability and the inapplicability of standard statistical tools, is false. After almost fifty years of research, the consensus is that rates of return are fat-tailed, but they aren’t Lévy-stable. If this is correct, as most economists and physicists working on these topics believe it is, then the standard statistical tools do apply, even though the simplest assumptions of normal and log-normal distributions do not. But evaluating Mandelbrot’s claims is an extremely tricky business — mostly because the important differences between his proposal and its nearest alternatives apply only in extreme cases, data for which are very hard to come by. And even today, there is disagreement about how to interpret the data we do have.

The fact that Mandelbrot’s claims were likely too aggressive makes his legacy a little more difficult to evaluate. Some writers today insist that Mandelbrot was never given his due, and that a proper appreciation of his ideas would solve all the world’s problems. While this is not entirely true, a few things are certain. Extreme events occur far more often than Bachelier and Osborne believed they would, and markets are wilder places than normal distributions can describe. To fully understand markets, and to model them as safely as possible, these facts must be accounted for. And Mandelbrot is singularly responsible for discovering the shortcomings of the Bachelier-Osborne approach, and for developing the mathematics necessary to study them. Getting the details right may be an ongoing project — indeed, we should never expect to finish the iterative process of improving our mathematical models — but there is no doubt that Mandelbrot took a crucially important step forward.

After a decade of interest in the statistics of markets, Mandelbrot gave up on his crusade to replace normal distributions with other Lévy-stable distributions. By this time, his ideas on randomness and disorder had begun to find applications in a wide variety of other fields, from cosmology to meteorology. These fields were closer to his starting point in applied mathematics and mathematical physics. He remained affiliated with IBM for his entire career; in 1974, he was named an IBM Fellow, which gave him considerable freedom to identify and develop his own projects, much like an academic researcher.

Gradually, as his ideas percolated through the many different scientific disciplines, Mandelbrot began to receive some recognition for his work. The book that introduced the term fractals to the wider world went through several revisions beginning in 1975 and culminated in The Fractal Geometry of Nature in 1982. It was a cult sensation, and it turned Mandelbrot into a semi-public figure. By the early 1990s, he had collected a long list of significant honors and awards, including election to the French Legion of Honor in 1990 and the Wolf Prize for physics in 1993. In 1987, he began teaching mathematics part-time at Yale — ultimately receiving his first tenured faculty position in 1999, at the age of seventy-five. He continued to lecture and work on original research, right up to his death, on October 14, 2010.

In the early 1990s, Mandelbrot sensed that the moment had arrived to move back into finance, and this time he had more success. Over the previous three decades, his ideas had developed and matured — benefiting greatly from their application to other fields — and so when he returned to thinking about economics, he had a much larger set of mathematical tools on which to draw. Meanwhile, markets had changed, so that far more practitioners on Wall Street and elsewhere were equipped to understand and incorporate Mandelbrot’s ideas. It was at this point that the recognition of fat-tailed distributions reached the financial mainstream. But I am getting ahead of the story. It would take a blackjack sharp and a dilettantish ex-physicist to move finance to a place where it could take advantage of the insights of Bachelier, Osborne, and, ultimately, Mandelbrot.