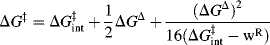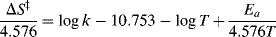Chapter 6

Mechanisms and Methods of Determining Them

A mechanism is the actual process by which a reaction takes place: which bonds are broken, in what order, how many steps are involved, the relative rate of each step, and so on. In order to state a mechanism completely, the positions of all atoms should be specified, including those in solvent molecules, and the energy of the system, at every point in the process. A proposed mechanism must fit all the facts available. It is always subject to change as new facts are discovered. The usual course is that the gross features of a mechanism are the first to be known and then increasing attention is paid to finer details. The tendency is always to probe more deeply, to get more detailed descriptions.

Although for most reactions gross mechanisms can be written today with a good degree of assurance, no mechanism is known completely.¹ There is much about the fine details that is still puzzling, and for some reactions even the gross mechanism is not yet clear. The problems involved are difficult because there are so many variables. Many examples are known where reactions proceed by different mechanisms under different conditions. In some cases, there are several proposed mechanisms, each of which completely explains all the data.

6.A. Types of Mechanism

In most reactions of organic compounds, one or more covalent bonds are broken. Organic mechanisms may be divided into three basic types, depending on how the bonds break.

1. If a bond breaks in such a way that both electrons remain with one fragment, the mechanism is called heterolytic. Such reactions do not necessarily involve ionic intermediates, although they often do. The important thing is that the electrons are never unpaired. For most reactions, it is convenient to call one reactant the attacking reagent and the other the substrate. In this book, the substrate is always designated as that molecule that supplies carbon to the new bond. When carbon–carbon bonds are formed via heterolytic reactions, the reagent generally brings a pair of electrons to the substrate or takes a pair of electrons from it. A reagent that brings an electron pair is called a nucleophile and the reaction is nucleophilic. A reagent that takes an electron pair is called an electrophile and the reaction is electrophilic. For a reaction in which the substrate molecule becomes cleaved, part of it (the part not containing the carbon) is usually called the leaving group. A leaving group that carries away an electron pair is called a nucleofuge. If it comes away without the electron pair, it is called an electrofuge.

2. If a bond breaks in such a way that each fragment gets one electron, free radicals are formed and such reactions are said to take place by homolytic or free radical mechanisms.

3. It would seem that all bonds must break in one of the two ways previously noted. But there is a third type of mechanism in which electrons (usually six, but sometimes some other number) move in a closed ring. There are no intermediates, ions or free radicals, and it is impossible to say whether the electrons are paired or unpaired. Reactions with this type of mechanism are called pericyclic2 (see Reactions 15-58–15-61 and 18-29–18-33.

Examples of all three types of mechanisms are given in Section 6.B.

6.B. Types of Reaction

The number and range of organic reactions is so great as to seem bewildering, but actually almost all of them can be fitted into just six categories. In the description of the six types that follows, the immediate products are shown, although in many cases they then react with something else. All the species are shown without charges, since differently charged reactants can undergo analogous changes. The descriptions given here are purely for the purpose of classification and comparison. All are discussed in detail in Part II.

1. Substitutions. If heterolytic, these reactions can be classified as nucleophilic or electrophilic depending on which reactant is designated as the substrate and which as the attacking reagent (very often Y must first be formed by a previous bond cleavage).

a. Nucleophilic substitution (Chaps 10 and 13).

b. Electrophilic substitution (Chaps 11 and 12).

c. Free radical substitution (Chap 14).

In free radical substitution, Y√ is usually produced by a previous free radical cleavage, and X√ goes on to react further.

2. Additions to Double or Triple Bonds (Chaps 15 and 16). These reactions can take place by all three of the mechanistic possibilities.

a. Electrophilic addition (heterolytic).

b. Nucleophilic addition (heterolytic).

c. Free-radical addition (homolytic).

d. Simultaneous addition (pericyclic).

The examples show Y and W coming from the same molecule, but very often (except in simultaneous addition) they come from different molecules, as illustrated by (b). Cleavage of the Y–W bond may occur at the same time that Y is bonding to B, but the cleavage may also occur earlier.

3. β Elimination (Chap 17).

These reactions can take place by either heterolytic or pericyclic mechanisms. Examples of the latter are shown in Section 17.C.i. Free radical β eliminations are extremely rare. In heterolytic eliminations, W and X may or may not leave simultaneously and may or may not combine afterwards.

4. Rearrangement (Chap 18). Many rearrangements involve migration of an atom or group from one atom to another. There are three types, depending on how many electrons the migrating atom or group carries with it.

a. Migration with electron pair (nucleophilic; common).

b. Migration with one electron (free radical; rare).

c. Migration without electrons (electrophilic; rare).

The generic examples show 1,2 rearrangements, in which the migrating group moves to the adjacent atom. These are the most common, although longer rearrangements are also possible. There are also some rearrangements that do not involve simple migration at all, but rather migration across a π-framework (see Chap 18). Some of the latter involve pericyclic mechanisms.

5. Oxidation and Reduction (Chap 19). Many oxidation and reduction reactions fall naturally into one of the four types mentioned above, but many others do not. For a description of oxidation–reduction mechanistic types, see Section 19.A.

6. Combinations of the Above. Note that arrows are used to show movement of electrons. An arrow always follows the motion of electrons and never of a nucleus or anything else (it is understood that the rest of the molecule follows the electrons). Ordinary arrows (double-headed) follow electron pairs, while single-headed arrows follow unpaired electrons. Double-headed arrows are also used in pericyclic reactions for convenience, but in these reactions how or in which direction the electrons are moving is usually unknown.

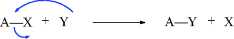
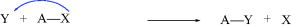
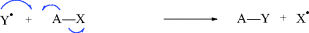
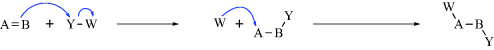
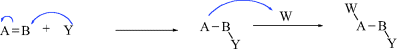
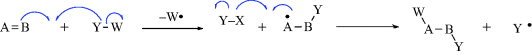
While not mentioned here as a distinct category, it must be said that many reactions, including some examples of 1–6 are actually acid–base reactions. In other cases, an acid–base reaction initiates the process or sometimes ends the process. In 2a, for example, Y = H and this is an acid–base reaction in which the π bond is the base and the proton is the acid. If W = H in 3a, then the elimination process begins with an acid–base reaction in which a base donates two electrons to H (= W). In 2b, if A donates electrons to W and W = H, this is another example of an acid–base reaction. Always be mindful of the acid–base properties of reactions.

Many, if not most of the reactions, noted above are subject to modification of the reactivity by the introduction of π bonds. Most reactions involve the transfer of two electrons to make or break a bond. The presence of two electrons in a π bond allows this two- electron-transfer process to proceed through the intervening atoms. In effect, the reactivity of a given center is extended by the presence of π bonds. This is the concept of vinylogy: the extension of points of reactivity by intervening π bonds. In other words, if a system X—C-1—C-2 undergoes a reaction at C-2 with loss of X from C-1, X—C-1—C-2=C-3—C-4 may undergo reaction at C-4. Reaction at C-4 initiates electron transfer via the π bond that is extended to C-1 for loss of X. Several examples of this type of reaction will be presented in later chapters.

6.C. Thermodynamic Requirements For Reaction

In order for a reaction to take place spontaneously, the free energy of the products must be lower than the free energy of the reactants (i.e., ΔG must be negative). Reactions can go the other way, of course, but only if free energy is added. Like water on the surface of the earth, which naturally flows only downhill and never uphill, molecules seek the lowest possible potential energy. Free energy is made up of two components, enthalpy (H) and entropy (S). These quantities are related by the equation

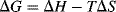
The enthalpy change in a reaction is essentially the difference in bond energies (including resonance, strain,3 and solvation energies) between the reactants and the products. The enthalpy change can be calculated by totaling the bond energies of all the bonds broken, subtracting from this the total of the bond energies of all the bonds formed, and adding any changes in resonance, strain, or solvation energies. Entropy changes are quite different, and refer to the disorder or randomness of the system. The lower the order in a system, the greater the entropy. The preferred conditions in Nature are low enthalpy and high entropy, and in reacting systems, enthalpy spontaneously decreases while entropy spontaneously increases.

For many reactions, entropy effects are small and it is the enthalpy that mainly determines whether the reaction can take place spontaneously. However, in certain processes entropy is important and can sometimes dominate enthalpy. Several examples will be discussed.

1. In general, liquids have lower entropies than gases, since the molecules of gas have much more freedom and randomness. Solids, of course, have still lower entropies. Any reaction in which the reactants are all liquids and one or more of the products is a gas is therefore thermodynamically favored by the increased entropy; the equilibrium constant for that reaction will be higher than it would otherwise be. Similarly, the entropy of a gaseous substance is higher than that of the same substance dissolved in a solvent.

2. In a reaction in which the number of product molecules is equal to the number of reactant molecules (e.g., A + B → C + D), entropy effects are usually small, but if the number of molecules is increased, (e.g., A → B + C), there is a gain in entropy because more arrangements in space are possible when more molecules are present. Reactions in which a molecule is cleaved into two or more parts are likely to be thermodynamically favored by the entropy factor. Conversely, reactions in which the number of product molecules is less than the number of reactant molecules show entropy decreases, and in such cases there must be a sizable decrease in enthalpy to overcome the unfavorable entropy change.

3. Although reactions in which molecules are cleaved into two or more pieces have favorable entropy effects, many potential cleavages do not take place because of large increases in enthalpy.⁴ An example is cleavage of ethane into two methyl radicals. In this case, a bond of ~79 kcal mol⁻¹ (330 kJ mol⁻¹) is broken, and no new bond is formed to compensate for this enthalpy increase. However, ethane can be cleaved at very high temperatures, which illustrates the principle that entropy becomes more important as the temperature increases, as is obvious from the equation ΔG = ΔH − TΔS. The enthalpy term is independent of temperature, while the entropy term is directly proportional to the absolute temperature.

4. An acyclic molecule has more entropy than a similar cyclic molecule because there are more conformations (cf. hexane and cyclohexane). Ring opening therefore correlates with a gain in entropy and ring closing a loss.

6.D. Kinetic Requirements For Reaction

Just because a reaction has a negative ΔG does not necessarily mean that it will take place in a reasonable period of time. A negative ΔG is a necessary, but not a sufficient, condition for a reaction to occur spontaneously. For example, the reaction between H₂ and O₂ to give H₂O has a large negative ΔG, but mixtures of H₂ and O₂ can be kept at room temperature for many centuries without reacting to any significant extent. In order for a reaction to take place, free energy of activation (ΔG^‡) must be added.5 This situation is illustrated in Fig. 6.1,⁶ which is an energy profile for a one-step reaction without an intermediate. In this type of diagram, the horizontal axis (called the reaction coordinate)⁷ signifies the progression of the reaction. The parameter 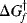is the free energy of activation for the forward reaction. If the reaction shown in Fig. 6.1 is reversible, 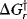must be > 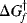, since it is the sum of ΔG and .

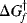Fig. 6.1 Free energy profile of a reaction without an intermediate where the products have a lower free energy than the reactants.

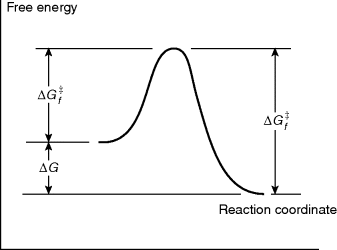
When a reaction between two or more molecules has progressed to the point corresponding to the top of the curve, the term transition state is applied to the positions of the nuclei and electrons. The transition state possesses a definite geometry and charge distribution, but has no finite existence; the system passes through it. The system at this point is called an activated complex.⁸

In transition-state theory,⁹ the starting materials and the activated complex are taken to be in equilibrium, the equilibrium constant being designated K^‡. According to the theory, all activated complexes go on to product at the same rate (which, although at first sight is surprising, is not unreasonable since they are all “falling downhill”) so that the rate constant (see Sec. 6.J.vi) of the reaction depends only on the position of the equilibrium between the starting materials and the activated complex, (i.e., on the value of K^‡). The parameter ΔG^‡ is related to K^‡ by

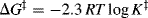
so that a higher value of ΔG^‡ is associated with a smaller rate constant. The rates of nearly all reactions increase with increasing temperature because the additional energy thus supplied helps the molecules to overcome the activation energy barrier.¹⁰ Some reactions have no free energy of activation at all, meaning that K^‡ is essentially infinite and that virtually all collisions lead to reaction. Such processes are said to be diffusion controlled.¹¹

Like ΔG, ΔG^‡ is made up of enthalpy and entropy components

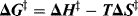
ΔH^‡, the enthalpy of activation, is the difference in bond energies, including strain, resonance, and solvation energies, between the starting compounds and the transition state. In many reactions, bonds have been broken or partially broken by the time the transition state is reached; the energy necessary for this is ΔH^‡. It is true that additional energy will be supplied by the formation of new bonds, but if this occurs after the transition state, it can affect only ΔH and not ΔH^‡.

Entropy of activation, (ΔS^‡), which is the difference in entropy between the starting compounds and the transition state, becomes important when two reacting molecules must approach each other in a specific orientation in order for the reaction to take place. For example, the reaction between a simple non-cyclic alkyl chloride and hydroxide ion to give an alkene (Reaction 17-13) takes place only if, in the transition state, the reactants are oriented as shown. This is an acid–base reaction because the proton on the carbon β to the chlorine is polarized δ⁺, and is a weak acid. Removal of that proton initiates loss of the chlorine atom and formation of the alkene. The electrons in the C–H bond (the acidic proton) must align anti to the leaving groups (Cl) for the reaction to proceed.¹²

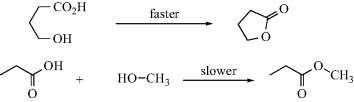
When the two reacting molecules collide, if the 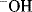should approach the molecule, the chlorine atom, or near R¹ or R², no reaction can take place. In order for a reaction to occur, the molecules must surrender the freedom they normally have to assume many possible arrangements in space because only one leads to reaction. Thus, a considerable loss in entropy is involved, (i.e., ΔS^‡ is negative).

Entropy of activation is also responsible for the difficulty in closing rings¹³ larger then six membered. Consider a ring-closing reaction in which the two groups that must interact are situated on the ends of a 10-carbon chain. In order for reaction to take place, the groups must encounter each other. But a 10-carbon chain has many conformations, and in only a few of these are the ends of the chain near each other. Thus, forming the transition state requires a great loss of entropy.¹⁴ This factor is also present, although less so, in closing rings of six members or less (except three-membered rings), but with rings of this size the entropy loss is less than that of bringing two individual molecules together. For example, a reaction between an OH group and a COOH group in the same molecule to form a lactone with a five- or six-membered ring takes place much faster than the same reaction between a molecule containing an OH group and another containing a COOH group. Although ΔH^‡ is about the same, ΔS^‡ is much less for the cyclic case. However, if the ring to be closed has three or four members, small-angle strain is introduced and the favorable ΔS^‡ may not be sufficient to overcome the unfavorable ΔH^‡ change. Table 6.1¹⁵ shows the relative rate constants for the closing of rings of 3–23 members all by the same reaction.¹⁵ Reactions in which the transition state has more disorder than the starting compounds, for example, the pyrolytic conversion of cyclopropane to propene, have positive ΔS^‡ values and are thus favored by the entropy effect.

Table 6.1¹⁵Relative Rate Constants at 50 °C^a

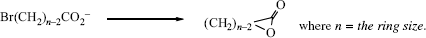Ring Size	Relative Rate
3	21.7
4	5.4 × 103
5	1.5 × 106
6	1.7 × 104
7	97.3
8	1.00
9	1.12
10	3.35
11	8.51
12	10.6
13	32.2
14	41.9
15	45.1
16	52.0
18	51.2
23	60.4
a. The rate for an eight-membered ring = 1 for the reaction.
Reprinted with permission from Mandolini, L. J. Am. Chem. Soc. 1978, 100, 550. Copyright © 1978 American Chemical Society. Reprinted with permission from Galli, C.; Illuminati, G.; Mandolini, L., Tamborra, P. J. Am. Chem. Soc. 1977, 99, 2591. Copyright © 1977 American Chemical Society.

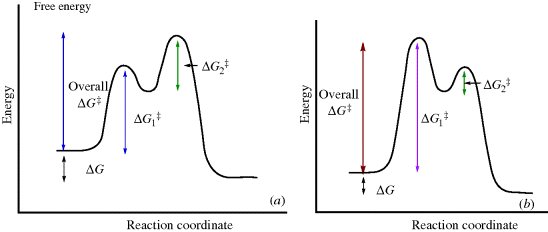
Reactions with intermediates are two-step (or more) processes. In these reactions, there is an energy “well”. There are two transition states, each with an energy higher than the intermediate (Fig. 6.2). The deeper the well, the more stable the intermediate. In Fig. 6.2a, the second peak is higher than the first. The opposite situation is shown in Fig. 6.2b. Note that in reactions in which the second peak is higher than the first, the overall ΔG^‡ is less than the sum of the ΔG^‡ values for the two steps. Minima in free energy profile diagrams (intermediates) correspond to real species that have a finite though usually short existence. These may be the carbocations, carbanions, free radicals, and so on., discussed in Chapter 5 or molecules in which all the atoms have their normal valences. In either case, under the reaction conditions they do not live long (because 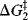is small), but rapidly go on to products. Maxima in these curves, however, do not correspond to actual species, but only to transition states in which bond breaking and/or bond making have partially taken place. Transition states have only a transient existence with an essentially zero lifetime.¹⁶

Fig. 6.2 (a) Free energy profile for a reaction with an intermediate 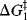and 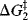are the free energy of activation for the first and second stages, respectively. (b) Free energy profile for a reaction with an intermediate in which the first peak is higher than the second

6.E. The Baldwin Rules For Ring Closure17

In previous sections, the kinetic and thermodynamic aspects of ring-closure reactions were discussed in a general way. J.E. Baldwin¹⁸ supplied a more specific set of rules for certain closings of three seven-membered rings. These rules distinguish two types of ring closure, called exo and endo, and three kinds of atoms at the starred positions: Tet for sp³, Trig for sp², and Dig for sp. The following are Baldwin's rules for closing rings of 3–7 members.

Rule 1. Tetrahedral systems

a. 3-7-Exo–Tet are all favored processes

b. 5-6-Endo–Tet are disfavored

Rule 2. Trigonal systems

a. 3-7-Exo–Trig are favored

b. 3-5-Endo–Trig are disfavored¹⁹

c. 6-7-Endo–Trig are favored

Rule 3. Digonal systems

a. 3-4-Exo–Dig are disfavored

b. 5-7-Exo–Dig are favored

c. 3-7-Endo–Dig are favored

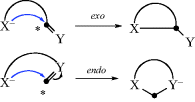
“Disfavored” does not mean it cannot be done, only that it is more difficult than the favored cases. These rules are empirical and have a stereochemical basis. The favored pathways are those in which the length and nature of the linking chain will enable the terminal atoms to achieve the proper geometries for reaction. The disfavored cases require severe distortion of bond angles and distances. Many cases in the literature are in substantial accord with these rules, and they are important in the formation of five- and six-membered rings.²⁰

Although Baldwin's rules can be applied to ketone enolates,²¹ additional rules were added to make the terminology more specific.²² The orientation of the orbital as it approaches the reactive center must be considered for determining the correct angle of approach. Diagrams that illustrate the enolate rules are shown.

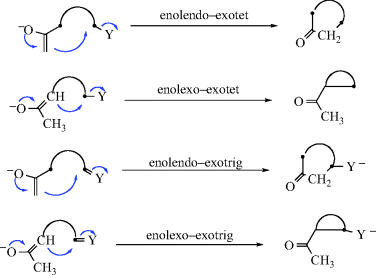
The rules are

a. 6–7 enolendo–exo–tet reactions are favored

b. 3–5 enolendo–exo–tet reactions are disfavored

c. 3–7 enolexo–exo–tet reactions are favored

d. 3–7 enolexo–exo–trig reactions are favored

e. 6–7 enolendo–exo–trig reactions are favored

f. 3–5 enolendo–exo–trig reactions are disfavored

6.F. Kinetic and Thermodynamic Control

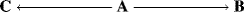
There are many cases in which a compound under a given set of reaction conditions can undergo competing reactions to give different products. Starting material A may give either B or C, for example. Figure 6.3 shows a free energy profile for a reaction in which B is thermodynamically more stable than C (ΔG_B is > ΔG_C), but C is formed faster (lower ΔG^‡). If neither reaction is reversible, C will be formed in a larger amount because it is formed faster. The product is said to be kinetically controlled. However, if the reactions are reversible, this will not necessarily be the case. If such a process is stopped well before the equilibrium has been established, the reaction will be kinetically controlled since more of the faster-formed product will be present. However, if the reaction is permitted to approach equilibrium, the predominant or even exclusive product will be B. Under these conditions the C that is first formed reverts to A, while the more stable B does so much less. We say the product is thermodynamically controlled.²³ Of course, Fig. 6.3 does not describe all reactions in which a compound A can give two different products. In many cases the more stable product is also the one that is formed faster. In such cases, the product of kinetic control is also the product of thermodynamic control.

Fig. 6.3 Free energy profile illustrating kinetic versus thermodynamic control of products. The starting compounds (A) can react to give either B or C.

6.G. The Hammond Postulate

Transition states are not detectable and have zero lifetimes, so it is impossible to observe them directly. Information about their geometries must be obtained from inference and modeling. In some cases, the inferences can be very strong. For example, in the S_N2 reaction (Sec. 10.A.i) between CH₃I and I⁻ (a reaction in which the product is identical to the starting compound), the transition state should be perfectly symmetrical. In most cases, however, it is not possible to reach such easy conclusions, and conclusions are greatly aided by the Hammond postulate,24 which states that for any single reaction step, the geometry of the transition state for that step resembles the side to which it is closer in free energy. Thus, for an exothermic reaction like that shown in Fig. 6.1, the transition state resembles the reactants more than the products, although not much more because there is a substantial ΔG^‡ on both sides.

The postulate is most useful in dealing with reactions with intermediates. In the reaction illustrated in Fig. 6.2a, the first transition state lies much closer in energy to the intermediate than to the reactants, and it is possible to predict that the geometry of the transition state resembles that of the intermediate more than it does that of the reactants. Likewise, the second transition state also has a free energy much closer to that of the intermediate than to the products, so that both transition states resemble the intermediate more than they do the products or reactants. This is generally the case in reactions that involve very reactive intermediates. More is usually known about the structure of intermediates than of transition states, so a knowledge of intermediates is used to draw conclusions about the transition states (e.g., see Sec. 10.G.i and 15.B.i).

6.H. Microscopic Reversibility

In the course of a reaction, the nuclei and electrons assume positions that at each point correspond to the lowest free energies possible. If the reaction is reversible, these positions must be the same in the reverse process, too. This means that the forward and reverse reactions (run under the same conditions) must proceed by the same mechanism. This is called the principle of microscopic reversibility. For example, if in a reaction A → B there is an intermediate C, then C must also be an intermediate in the reaction B → A. This is a useful principle since it enables one to know the mechanism of reactions in which the equilibrium lies far over to one side. Reversible photochemical reactions are an exception, since a molecule that has been excited photochemically does not have to lose its energy in the same way (Chap 7).

6.I. Marcus Theory

It is often useful to compare the reactivity of one compound with that of similar compounds. The real goal is to find out how a reaction coordinate (and in particular the transition state) changes when one reactant molecule is replaced by a similar molecule. Marcus theory is a method for doing this.25

In this theory, the activation energy (ΔG^‡) is thought of as consisting of two parts.

1. An intrinsic free energy of activation, which would exist if the reactants and products had the same ΔG°.²⁶

This is a kinetic part, called the intrinsic barrier

2. A thermodynamic part, which arises from the ΔG° for the reaction.

The Marcus equation says that the overall ΔG^‡ for a one-step reaction is²⁷

where the term ΔG^Δ stands for

w^R, a work term, is the free energy required to bring the reactants together and w^P is the work required to form the successor configuration from the products.

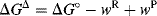
For a reaction of the type AX + B → BX, the intrinsic barrier²⁸ is taken to be the average ΔG^‡ for the two symmetrical reactions

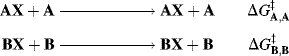
so that

One type of process that can successfully be treated by the Marcus equation is the S_N2 mechanism (Sec. 10.A.i).

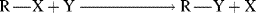
When R is CH₃ the process is called methyl transfer.²⁹ For such reactions, the work terms w^R and w^P are assumed to be very small compared to ΔG°, and can be neglected, so that the Marcus equation simplifies to

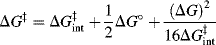
The Marcus equation allows ΔG^‡ for RX + Y → RY + X to be calculated from the barriers of the two symmetrical reactions RX + X → RX + X and RY + Y → RY + Y. The results of such calculations are generally in agreement with the Hammond postulate.

Marcus theory can be applied to any single-step process where something is transferred from one particle to another. It was originally derived for electron transfers,³⁰ and then extended to transfers of H⁺ (see Sec. 8.D), H⁻,³¹ and H√³², as well as methyl transfers.

6.J. Methods of Determining Mechanisms33

There are a number of commonly used methods for determining mechanisms.³⁴ In most cases, one method is not sufficient, and the problem is generally approached from several directions.

6.J.i. Identification of Products

Obviously any mechanism proposed for a reaction must account for all the products obtained and for their relative proportions, including products formed by side reactions. Incorrect mechanisms for the von Richter reaction (Reaction 13-30) were accepted for many years because it was not realized that nitrogen was a major product. A proposed mechanism cannot be correct if it fails to predict the products in approximately the observed proportions. For example, any mechanism for the reaction

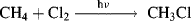
that fails to account for the formation of a small amount of ethane cannot be correct (see Reaction 14-1), and any mechanism proposed for the Hofmann rearrangement (Reaction 18-13):

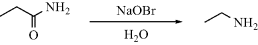
must account for the fact that the carbonyl carbon is lost as CO₂.

6.J.ii. Determination of the Presence of an Intermediate

Intermediates are postulated in many mechanisms, and the presence or absence of an intermediate is essential information. There are several methods, none of them foolproof,³⁵ for attempting to learn whether or not an intermediate is present and, if so, its structure. All methods are experimental, and an intermediate must be detected in one way or another, often by isolation or trapping.

1. Isolation of an Intermediate. It is sometimes possible to isolate an intermediate from a reaction mixture by stopping the reaction after a short time or by the use of very mild conditions. For example, in the Neber rearrangement (Reaction 18-12) the intermediate 1 (an azirene)³⁶ has been isolated. If it can be shown that the isolated compound gives the same product when subjected to the reaction conditions, and at a rate no slower than the starting compound, this constitutes strong evidence that the reaction involves that intermediate, although it is not conclusive, since the compound may arise by an alternate path and by coincidence give the same product.

2. Detection of an Intermediate. In many cases an intermediate cannot be isolated, but can be detected by normal IR, ReactIR,³⁷ NMR, or other spectra.³⁸ The detection by Raman spectra of NO₂⁺ was regarded as strong evidence that this is an intermediate in the nitration of benzene (see Reaction 11-2). Free radical and triplet intermediates can often be detected by ESR and by CIDNP (see Chap 5). Free radicals (as well as radical ions and EDA complexes) can also be detected by a method that does not rely on spectra. In this method, a double-bond compound is added to the reaction mixture, and its fate traced.³⁹ One possible result is cis–trans conversion. For example, cis-stilbene is isomerized to the trans isomer in the presence of RS√ radicals, by this mechanism:

Since the trans isomer is more stable than the cis, the reaction does not go the other way, and the detection of the isomerized product is evidence for the presence of the RS√ radicals.

3. Trapping of an Intermediate. In some cases, the suspected intermediate is known to be one that reacts in a given way with a certain compound. The intermediate can then be trapped by running the reaction in the presence of that compound. For example, benzynes (Sec. 13.A.iii) react with dienes in the Diels–Alder reaction (15-60). In any reaction where a benzyne is a suspected intermediate, the addition of a diene and the detection of the Diels–Alder adduct indicate that the benzyne was probably present.

4. Addition of a Suspected Intermediate. If a certain intermediate is suspected, and if it can be obtained by other means, then under the same reaction conditions it should give the same products. This kind of experiment can provide conclusive negative evidence: if the correct products are not obtained, the suspected compound is not an intermediate. However, if the correct products are obtained, this is not conclusive since they may arise by coincidence. The von Richter reaction (Reaction 13-30) provides a good example here too. For many years, it had been assumed that an aryl cyanide was an intermediate, since cyanides are easily hydrolyzed to carboxylic acids (Reaction 16-4). Indeed, p-chlorobenzonitrile was shown to give p-chlorobenzoic acid under normal von Richter conditions.⁴⁰ However, when the experiment was repeated with 1-cyanonaphthalene, no 1-naphthoic acid was obtained, although 2-nitronaphthalene gave 13% 1-naphthoic acid under the same conditions.⁴¹ This proved that 2-nitronaphthalene must have been converted to 1-naphthoic acid by a route that does not involve 1-cyanonaphthalene. It also showed that even the conclusion that p-chlorobenzonitrile was an intermediate in the conversion of m-nitrochlorobenzene to p-chlorobenzoic acid must now be suspect, since it is not likely that the mechanism would substantially change in going from the naphthalene to the benzene system.

6.J.iii. The Study of Catalysis⁴²

Many organic reactions are slow in the absence of a catalyst. Acid-catalyzed reactions are prevalent for example. Once it is known that a reaction is subject to catalysis, much information about the mechanism of a reaction can be obtained from a knowledge of which substances catalyze the reaction, which inhibit it, and which do neither. Of course, just as a mechanism must be compatible with the products, so must it be compatible with its catalysts. In general, catalysts perform their actions by providing an alternate pathway for the reaction in which ΔG^‡ is less than it would be without the catalyst. Catalysts do not change ΔG.

6.J.iv. Isotopic Labeling⁴³

Molecules that have been isotopically labeled can be used to trace the path of the reaction, which may provide much useful mechanistic information. For example, in the reaction

does the CN group in the product come from the CN in the BrCN? The use of supplied the answer, since 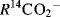gave radioactive RCN.⁴⁴ This surprising result saved a lot of labor, since it ruled out a mechanism involving the replacement of CO₂ by CN (see Reaction 16-94). Other radioactive isotopes are also frequently used as tracers, but even stable isotopes can be used. An example is the hydrolysis of esters

Which bond of the ester is broken, the acyl–O or the alkyl–O bond? The answer is found by the use of 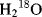. If the acyl–O bond breaks, the labeled oxygen will appear in the acid; otherwise it will be in the alcohol (see Reaction 16-59). Although neither compound is radioactive, the one that contains 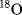can be determined by submitting both to mass spectrometry. In a similar way, deuterium can be used as a label for hydrogen. In this case, mass spectrometry is not the only option since IR 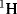and and NMR⁴⁵ spectra can be used to determine when deuterium has been substituted for hydrogen.

In the labeling technique, it is not generally necessary to use completely labeled compounds. Partially labeled material is usually sufficient.

6.J.v. Stereochemical Evidence⁴⁶

If the products of a reaction are capable of existing in more than one stereoisomeric form, the form that is obtained may give information about the mechanism.⁴⁷ For example, Walden⁴⁸ discovered that (+)-malic acid gives (−)-chlorosuccinic acid when treated with PCl₅ and the (+) enantiomer when treated with SOCl₂, showing that the mechanisms of these apparently similar conversions could not be the same (see Sec. 10.A.i and 10.D). Much useful information has been obtained about nucleophilic substitution, elimination, rearrangement, and addition reactions from this type of experiment. The isomers involved need not be enantiomers. Thus, the fact that cis-2-butene treated with KMnO₄ gives meso-2,3-butanediol and not the racemic mixture is evidence that the two OH groups attack the double bond from the same side (see Reaction 15-48).

6.J.vi. Kinetic Evidence⁴⁹

The rate of a homogeneous reaction⁵⁰ is the rate of disappearance of a reactant or appearance of a product. The rate nearly always changes with time, since it is usually proportional to concentration and the concentration of reactants decreases with time. However, the rate is not always proportional to the concentration of all reactants. In some cases, a change in the concentration of a reactant produces no change at all in the rate, while in other cases the rate may be proportional to the concentration of a substance (a catalyst) that does not even appear in the stoichiometric equation. A study of which reactants affect the rate often tells a good deal about the mechanism.

If the rate is proportional to the change in concentration of only one reactant (A), the rate law (the rate of change of concentration of A with time t) is

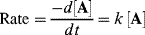
where k is the rate constant for the reaction.⁵¹ There is a minus sign because the concentration of A decreases with time. A reaction that follows such a rate law is called a first-order reaction. The units of k for a first-order reaction are reciprocal second (s⁻¹). The rate of a second-order reaction is proportional to the concentration of two reactants, or to the square of the concentration of one:

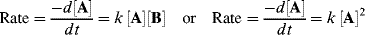
For a second-order reaction, the units are L mol⁻¹ s⁻¹ or some other units expressing the reciprocal of concentration or pressure per unit time interval.

Similar expressions can be written for third-order reactions. A reaction whose rate is proportional to [A] and to [B] is said to be first order in A and in B, second order overall. A reaction rate can be measured in terms of any reactant or product, but the rates so determined are not necessarily the same. For example, if the stoichiometry of a reaction is 2A + B → C + D then, on a molar basis, A must disappear twice as fast as B, so that −d[A]/dt and −d[B]/dt are not equal but the former is twice as large as the latter.

The rate law of a reaction is an experimentally determined fact. The rate law leads to an understanding of the molecularity, which may be defined as the number of molecules that come together to form the activated complex. It is obvious that if it is known how many (and which) molecules take part in the activated complex, a good deal is known about the mechanism. The experimentally determined rate order is not necessarily the same as the molecularity. Any reaction, no matter how many steps are involved, has only one rate law, but each step of the mechanism has its own molecularity. For reactions that take place in one step (reactions without an intermediate), the order is the same as the molecularity. A first-order, one-step reaction is always unimolecular; a one-step reaction that is second order in A always involves two molecules of A; if it is first order in A and in B, then a molecule of A reacts with one of B, and so on. For reactions that take place in more than one step, the order for each step is the same as the molecularity for that step. This fact enables us to predict the rate law for any proposed mechanism, although the calculations may get lengthy at times.⁵² If any one step of a mechanism is considerably slower than all the others (this is usually the case), the rate of the overall reaction is essentially the same as that of the slow step, which is consequently called the rate-determining step.⁵³

For reactions that take place in two or more steps, two broad cases can be distinguished:

1. The first step is slower than any subsequent step and is consequently rate determining. In such cases, the rate law simply includes the reactants that participate in the slow step. For example, if the reaction A + 2B → C has the mechanism

where I is an intermediate, the reaction is second order, with the rate law

2. When the first step is not rate determining, determination of the rate law is usually much more complicated. For example, consider the mechanism

where the first step is a rapid attainment of equilibrium, followed by a slow reaction to give C. The rate of disappearance of A is

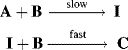
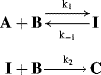
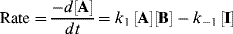
Both terms must be included because A is being formed by the reverse reaction, as well as being used up by the forward reaction. This equation is of very little help as it stands since the concentration of the intermediate cannot be measured. However, the combined rate law for the formation and disappearance of I is

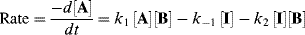
This equation is of little help unless the assumption is made that the concentration of I does not change with time, since it is an intermediate that is used up (going either to A + B or to C) as fast as it is formed. This assumption, called the assumption of the steady state,⁵⁴ enables d[I]/dt to be set equal to zero, and hence to solve for [I] in terms of the measurable quantities [A] and [B]:

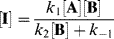
Inserting this value for [I] into the original rate expression gives

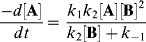
Note that this rate law is valid whatever the values of k₁, k₋₁, and k₂. However, our original hypothesis was that the first step was faster than the second, or that

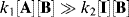
Since the first step is an equilibrium

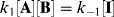
this gives

Canceling [I] gives

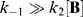
Neglecting k₂[B] in comparison with k₋₁ gives

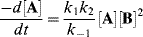
The overall rate is thus third order: first order in A and second order in B. Incidentally, if the first step is rate determining (as was the case in the preceding paragraph), then

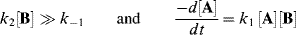
which is the same rate law deduced from the rule that where the first step is rate determining, the rate law includes the reactants that participate in that step.

It is possible for a reaction to involve A and B in the rate-determining step, although only [A] appears in the rate law. This occurs when a large excess of B is present, say 100 times the molar quantity of A. In this case, the complete reaction of A uses up only 1 equiv of B, leaving 99 equiv. It is not easy to measure the change in concentration of B with time in such a case, and it is seldom attempted, especially when B is also the solvent. Since [B], for practical purposes, does not change with time, the reaction appears to be first order in A although actually both A and B are involved in the rate-determining step. This is often referred to as a pseudo-first-order reaction. Pseudo-order reactions can also come about when one reactant is a catalyst whose concentration does not change with time because it is replenished as fast as it is used up and when a reaction is conducted in a medium that keeps the concentration of a reactant constant, for example, in a buffer solution where H⁺ or 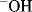is a reactant. Pseudo-first-order conditions are frequently used in kinetic investigations for convenience in experimentation and calculations.

What is actually being measured is the change in concentration of a product or a reactant with time. Many methods have been used to make such measurements.⁵⁵ The choice of a method depends on its convenience and its applicability to the reaction being studied. Among the most common methods are the following:

1. Periodic or Continuous Spectral Readings. In many cases, the reaction can be carried out in the cell while it is in the instrument. Then all that is necessary is that the instrument be read, periodically or continuously. Among the methods used are IR and UV spectroscopy, polarimetry, NMR, and ESR.⁵⁶

2. Quenching and Analyzing. A series of reactions can be set up and each stopped in some way (perhaps by suddenly lowering the temperature or adding an inhibitor) after a different amount of time has elapsed. The materials are then analyzed by spectral readings, titrations, chromatography, polarimetry, or any other method.

3. Removal of Aliquots at Intervals. Each aliquot is then analyzed as in method 2.

4. Measurement of Changes in Total Pressure, for Gas-Phase Reactions.⁵⁷

5. Calorimetric Methods. The output or absorption of heat can be measured at time intervals.

Special methods exist for kinetic measurements of very fast reactions.⁵⁸

A graph is usually obtained that shows the change in concentration with time. Interpretation⁵⁹ is required to obtain a rate law and a value of k. If a reaction obeys simple first- or second-order kinetics, the interpretation is generally not difficult. For example, for a concentration at the start = A₀, the first-order rate law

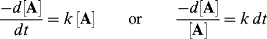
can be integrated between the limits t = 0 and t = t to give

Therefore, if a plot of ln [A] against t is linear, the reaction is first order and k can be obtained from the slope. For first-order reactions, it is customary to express the rate not only by the rate constant k, but also by the half-life, which is the time required for one-half of any given quantity of a reactant to be used up. Since the half-life is the time required for [A] to reach A_o/2,:

so that

For the general case of a reaction first order in A and first order in B, second order overall, integration is complicated, but it can be simplified if equimolar amounts of A and B are used, so that A_o = B_o. In this case,

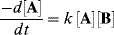
is equivalent to

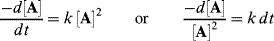
Integrating as before gives

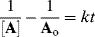
Thus, under equimolar conditions, if a plot of 1/[A] against t is linear, the reaction is second order with a slope of k. It is obvious that the same will hold true for a reaction second order in A.⁶⁰

Although many reaction-rate studies do give linear plots, which are easily interpreted, the results in many other studies are not so simple. In some cases, a reaction may be first order at low concentrations but second order at higher concentrations. In other cases, fractional orders are obtained, and even negative orders. The interpretation of complex kinetics often requires much skill and effort. Even where the kinetic data are relatively simple, there is often a problem in interpreting the data because of the difficulty of obtaining sufficiently precise measurements.⁶¹

Nuclear magnetic resonance spectra can be used to obtain kinetic information in a completely different manner from that mentioned above. This method, which involves the study of NMR line shapes,⁶² depends on the fact that NMR spectra have an inherent time factor: If a proton changes its environment less rapidly than ~ 10³ times s⁻¹, an NMR spectrum shows a separate peak for each position the proton assumes. For example, if the rate of rotation around the C–N bond of N,N-dimethylacetamide is slower than 10³ rotations per second, the two N-methyl groups appear as a separate signal with different chemical shifts indicating that they are not equivalent, one being cis to the oxygen and the other trans to the acyl methyl group. However, if the environmental change takes place more rapidly than ~ 10³ times per second, only one signal is found, at a chemical shift that is the weighted average of the two individual positions. In many cases, two or more signals are found at low temperatures, but as the temperature is increased, the lines coalesce because the interconversion rate increases with temperature and passes the 10³ per second mark. From studies of the way line shapes change with temperature it is often possible to calculate rates of reactions and of conformational changes. This method is not limited to changes in proton line shapes, but can also be used for other atoms that give NMR and ESR spectra (Sec. 5.C.i).

Several types of mechanistic information can be obtained from kinetic studies.

1. Information can be obtained from the order of a reaction. Which molecules and how many take part in the rate-determining step may be determined. Such knowledge is very useful and often essential in elucidating a mechanism. For any mechanism that can be proposed for a given reaction, a corresponding rate law can be calculated by the methods discussed in the beginning of this section. If the experimentally obtained rate law fails to agree with this, the proposed mechanism is wrong. However, it is often difficult to relate the order of a reaction to the mechanism, especially when the order is fractional or negative. It is frequently the case that two or more proposed mechanisms for a reaction are kinetically indistinguishable, that is, they predict the same rate law.

2. Probably the most useful data obtained kinetically are the rate constants themselves. They are important since they can relate the effect on the rate of a reaction of changes in the structure of the reactants (see Chapter 9), the solvent,⁶³ the ionic strength, the addition of catalysts, and so on.

3. If the rate is measured at several temperatures, in most cases a plot of ln k against l/T (T stands for absolute temperature) is nearly linear⁶⁴ with a negative slope, and fits the equation

where R is the gas constant and A is a constant called the frequency factor. This permits the calculation of E_a, which is the Arrhenius activation energy of the reaction. Now ΔH^‡ can then be obtained by

It is also possible to use these data to calculate ΔS^‡ by the formula⁶⁵

for energies in calorie units. For joule units, the formula is

One then obtains ΔG^‡ from ΔG^‡ = ΔH^‡ − TΔS^‡.

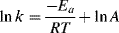
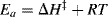
6.J.vii. Isotope Effects

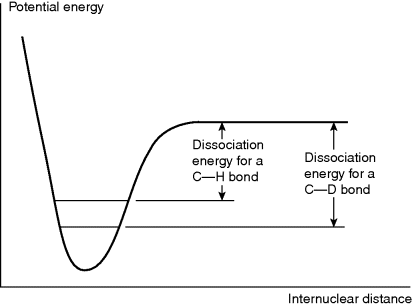
When a hydrogen atom in a reactant molecule is replaced by deuterium, there is often a change in the rate. Such changes are known as deuterium isotope effects⁶⁶ and are expressed by the ratio k_H/k_D. The ground-state vibrational energy (called the zero-point vibrational energy) of a bond depends on the mass of the atoms and is lower when the reduced mass is higher.⁶⁷ Therefore, D–C, D–O, D–N bonds, and so on, have lower energies in the ground state than the corresponding H–C, H–O, H–N bonds, and so on. Complete dissociation of a deuterium bond consequently requires more energy than that for a corresponding hydrogen bond in the same environment (Fig. 6.4). If a H–C, H–O, or H–N bond is not broken at all in a reaction or is broken in a non-rate-determining step, substitution of deuterium for hydrogen causes no change in the rate (see below for an exception to this statement), but if the bond is broken in the rate-determining step, the rate must be lowered by the substitution.

Fig. 6.4 A C–D bond has a lower zero point than a corresponding C–H bond; thus the dissociation energy is higher.

This provides a valuable diagnostic tool for determination of mechanism. For example, in the bromination of acetone (Reaction 12-4) the fact that the rate is independent of the bromine concentration led to the postulate that the rate-determining step was prior to tautomerization of the acetone:

In turn, the rate-determining step of the tautomerization involves cleavage of a C–H bond (see Reaction 12-3). Thus there should be a substantial isotope effect if deuterated acetone is brominated. In fact, k_H/k_D was found to be ~ 7.⁶⁸ Deuterium isotope effects usually range from 1 (no isotope effect at all) to ~ 7 or 8, although in a few cases, larger⁶⁹ or smaller values have been reported.⁷⁰ Values of k_H/k_D < 1 are called inverse isotope effects. Isotope effects are greatest when, in the transition state, the hydrogen is symmetrically bonded to the atoms between which it is being transferred.⁷¹ Also, calculations show that isotope effects are at a maximum when the hydrogen atom in the transition state is on the straight line connecting the two atoms between which it is being transferred, and that for sufficiently nonlinear configurations, they decrease to k_H/k_D = 1–2.⁷² Of course, in open systems there is no reason for the transition state to be nonlinear, but this is not the case in many intramolecular mechanisms, (e.g., in a 1,2-migration of a hydrogen)

To measure isotope effects, it is not always necessary to prepare deuterium-enriched starting compounds. It can also be done by measuring the change in deuterium concentration at specific sites between a compound containing deuterium in natural abundance and the reaction product, using a high field NMR instrument.⁷³

The substitution of tritium for hydrogen gives isotope effects that are numerically larger. Isotope effects have also been observed with other elements, but they are much smaller, ~ 1.02–1.10. For example, 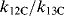for the reaction of methoxide with benzyl bromide is 1.053.⁷⁴ Although they are small, heavy-atom isotope effects can be measured quite accurately and are often very useful.⁷⁵

Deuterium isotope effects have been found even where it is certain that the C–H bond does not break at all in the reaction. Such effects are called secondary isotope effects,⁷⁶ the term primary isotope effect being reserved for the type discussed previously. Secondary isotope effects can be divided into α and β effects. In a β secondary isotope effect, substitution of deuterium for hydrogen β to the position of bond breaking slows the reaction. An example is solvolysis of 2-bromopropane to 2-propanol,where k_H/k_D was found to be 1.34.⁷⁷ The cause of β isotope effects has been a matter of much controversy, but they are most likely due to hyperconjugation effects in the transition state. The effects are greatest when the transition state has considerable carbocation character.⁷⁸ Although the C–H bond in question is not broken in the transition state, the carbocation is stabilized by hyperconjugation (Sec. 2.M) involving this bond. Because of hyperconjugation, the difference in vibrational energy between the C–H bond and the C–D bond in the transition state is less than it is in the ground state, so the reaction is slowed by substitution of deuterium for hydrogen.

Support for hyperconjugation as the major cause of β isotope effects is the fact that the effect is greatest when D is anti to the leaving group⁷⁹ (because of the requirement that all atoms in a resonance system be coplanar, planarity of the D–C–C–X system would most greatly increase the hyperconjugation), and the fact that secondary isotope effects can be transmitted through unsaturated systems.⁸⁰ There is evidence that at least some β isotope effects are steric in origin⁸¹ (e.g., a CD₃ group has a smaller steric requirement than a CH₃ group) and a field-effect explanation has also been suggested (CD₃ is apparently a better electron donor than CH₃⁸²), but hyperconjugation is the most probable cause in most instances.⁸³ Part of the difficulty in attempting to explain these effects is their small size, ranging only as high as ~ 1.5.⁸⁴ Another complicating factor is that they can change with temperature. In one case,⁸⁵k_H/k_D was 1.00 ± 0.01 at 0 °C, 0.90 ± 0.01 at 25 °C, and 1.15 ± 0.09 at 65 °C. Whatever the cause, there seems to be a good correlation between β secondary isotope effects and carbocation character in the transition state. They are thus a useful tool for probing mechanisms.

The other type of secondary isotope effect results from a replacement of hydrogen by deuterium at the carbon containing the leaving group. These so-called secondary isotope effects are varied, with values so far reported⁸⁶ ranging from 0.87 to 1.26.⁸⁷ These effects are also correlated with carbocation character. Nucleophilic substitutions that do not proceed through carbocation intermediates (S_N2 reactions) have an isotope effect near unity.⁸⁸ Those that do involve carbocations (S_N1 reactions) have higher isotope effects, which depend on the nature of the leaving group.⁸⁹ The accepted explanation for a isotope effects is that one of the bending C–H vibrations is affected by the substitution of D for H more or less strongly in the transition state than in the ground state.⁹⁰ Depending on the nature of the transition state, this may increase or decrease the rate of the reaction. The α isotope effects on S_N2 reactions can vary with concentration,⁹¹ an effect attributed to a change from a free nucleophile to one that is part of an ion pair⁹² (see Sec. 10.G.ii). This illustrates the use of secondary isotope effects as a means of studying transition state structure. The γ secondary isotope effects have also been reported.⁹³

Another kind of isotope effect is the solvent isotope effect.⁹⁴ Reaction rates often change when the solvent is changed from H₂O to D₂O or from ROH to ROD. These changes may be due to any of three factors or a combination of all of them.

1. The solvent may be a reactant. If an O–H bond of the solvent is broken in the rate-determining step, there will be a primary isotope effect. If the molecules involved are D₂O or D₃O⁺ there may also be a secondary effect caused by the O–D bonds that are not breaking.

2. The substrate molecules may become labeled with deuterium by rapid hydrogen exchange, and then the newly labeled molecule may become cleaved in the rate-determining step.

3. The extent or nature of solvent–solute interactions may be different in the deuterated and non-deuterated solvents; this may change the energies of the transition state, and hence the activation energy of the reaction. These are secondary isotope effects. Two physical models for this third factor have been constructed.⁹⁵

It is obvious that in many cases the first and third factors at least, and often the second, are working simultaneously. Attempts have been made to separate them.⁹⁶

The methods described in this chapter are not the only means of determining mechanisms. A detailed examination of the literature, coupled with well-planned experiments is the best way to devise an approach to the mechanism of a given reaction.

Notes

1. Perspectives on Structure and Mechanism in Organic Chemistry, Carroll, F.A., Wiley, 2010; Arrow-Pushing in Organic Chemistry: An Easy Approach to Understanding Reaction Mechanisms, Levy, D.E., Wiley–Interscience, 2008; Guidebook to Mechanism in Organic Chemistry, 6th Edition, Sykes, P., Prentice Hall, 1996.

2. For a classification of pericyclic reactions, see Hendrickson, J.B. Angew. Chem. Int. Ed. 1974, 13, 47. Also see, Fleming, I. Pericyclic Reactions, Oxford University Press, Oxford, 1999.

3. For a discussion of the activation strain model of chemical reactivity, see van Zeist, W.-J.; Bickelhaupt, F.M. Org. Biomol. Chem., 2010, 8, 3118.

4. For calculations of long-chain alkane energies see Song, J.-W.; Tsuneda, T.; Sato, T.; Hirao, K. Org. Lett. 2010, 12, 1440.

5. To initiate a reaction of a mixture of H₂ and O₂, energy must be added such as by striking a match.

6. Strictly speaking, this is an energy profile for a reaction of the type XY + Z → X + YZ. However, it may be applied, in an approximate way, to other reactions.

7. For a review of reaction coordinates and structure–energy relationships, see Grunwald, E. Prog. Phys. Org. Chem. 1990, 17, 55.

8. For a discussion of transition states, see Laidler, K.J. J. Chem. Educ. 1988, 65, 540.

9. See Kreevoy, M.M.; Truhlar, D.G. in Bernasconi, C.F. Investigation of Rates and Mechanisms of Reactions, 4th ed. (Vol. 6 of Weissberger, A. Techniques of Chemistry), pt. 1, Wiley, NY, 1986, pp. 13–95; Moore, J.W.; Pearson, R.G. Kinetics and Mechanism, 3rd ed., Wiley, NY, 1981, pp. 137–181; Klumpp, G.W. Reactivity in Organic Chemistry, Wiley, NY, 1982; pp. 227–378. See Zevatskii, Y.E.; Samoilov, D.V. Russ. J. Org. Chem. 2007, 43, 483.

10. See Donahue, N.M. Chem. Rev. 2003, 103, 4593.

11. For a monograph on diffusion-controlled reactions, see Rice, S.A. Comprehensive Chemical Kinetics, Vol. 25 (edited by Bamford, C.H.; Tipper, C.F.H.; Compton, R.G.); Elsevier: NY, 1985.

12. As will be seen in Chapter 17, elimination is also possible with some molecules if the hydrogen is oriented syn, instead of anti, to the chlorine atom. Of course, this orientation also requires a considerable loss of entropy.

13. See De Tar, D.F.; Luthra, N.P.J. Am. Chem. Soc. 1980, 102, 4505; Mandolini, L. Bull. Soc. Chim. Fr. 1988, 173. For a related discussion, see Menger, F.M. Acc. Chem. Res. 1985, 18, 128.

14. See Nakagaki. R.; Sakuragi, H.; Mutai, K. J. Phys. Org. Chem. 1989, 2, 187; Mandolini, L. Adv. Phys. Org. Chem. 1986, 22, 1; Winnik, M.A. Chem. Rev. 1981, 81, 491; Valters, R. Russ. Chem. Rev. 1982, 51, 788.

15. The values for ring sizes 4, 5, and 6 are from Mandolini, L. J. Am. Chem. Soc. 1978, 100, 550; the others are from Galli, C.; Illuminati, G.; Mandolini, L.; Tamborra, P. J. Am. Chem. Soc. 1977, 99, 2591. See also, Illuminati, G.; Mandolini, L. Acc. Chem. Res. 1981, 14, 95. See, however, Benedetti, F.; Stirling, C.J.M. J. Chem. Soc. Perkin Trans. 2 1986, 605.

16. See laser femtochemistry: Zewall, A.H.; Bernstein, R.B. Chem. Eng. News 1988, 66, No. 45 (Nov. 7), 24–43. For another method, see Collings, B.A.; Polanyi, J.C.; Smith, M.A.; Stolow, A.; Tarr, A.W. Phys. Rev. Lett. 1987, 59, 2551.

17. See Smith, M.B. Organic Synthesis, 3rd ed., Wavefunction Inc./Elsevier, Irvine, CA/London, England, 2010, pp. 564–572.

18. Baldwin, J.E. J. Chem. Soc. Chem. Commun. 1976, 734; Baldwin, J.E. in Further Perspectives in Organic Chemistry (Ciba Foundation Symposium 53), Elsevier, Amsterdam, The Netherlands, 1979, pp. 85–99. See also, Baldwin, J.E.; Thomas, R.C.; Kruse, L.I.; Silberman, L. J. Org. Chem. 1977, 42, 3846; Baldwin, J.E.; Lusch, M.J. Tetrahedron 1982, 38, 2939; Fountain, K.R.; Gerhardt, G. Tetrahedron Lett. 1978, 3985.

19. For some exceptions to the rule in this case, see Trost, B.M.; Bonk, P.J. J. Am. Chem. Soc. 1985, 107, 1778; Torres, L.E.; Larson, G.L. Tetrahedron Lett. 1986, 27, 2223.

20. Johnson, C.D. Accts. Chem. Res. 1997, 26, 476.

21. Baldwin, J.E.; Kruse, L.I. J. Chem. Soc. Chem. Commun. 1977, 233.

22. Baldwin, J.E.; Lusch, M.J. Tetrahedron 1982, 38, 2939.

23. See Klumpp, G.W. Reactivity in Organic Chemistry, Wiley, NY, 1982, pp. 36–89.

24. Hammond, G.S. J. Am. Chem. Soc. 1955, 77, 334. For a discussion, see Farcasiu, D. J. Chem. Educ. 1975, 52, 76.

25. See Albery, W.J. Annu. Rev. Phys. Chem. 1980, 31, 227; Kreevoy, M.M.; Truhlar, D.G. in Bernasconi, C.F. Investigation of Rates and Mechanisms of Reactions, 4th ed. (Vol. 6 of Weissberger, A. Techniques of Chemistry), pt. 1, Wiley, NY, 1986, pp. 13–95.

26. The parameter ΔG° is the standard free energy; that is, ΔG at atmospheric pressure.

27. Albery, W.J.; Kreevoy, M.M. Adv. Phys. Org. Chem. 1978, 16, 87, pp. 98–99.

28. See Lee, I. J. Chem. Soc. Perkin Trans. 2 1989, 943, Chem. Soc. Rev. 1990, 19, 133.

29. See Albery, W.J.; Kreevoy, M.M. Adv. Phys. Org. Chem. 1978, 16, 87. See also, Lee, I. J. Chem. Soc., Perkin Trans. 2 1989, 943; Lewis, E.S.; McLaughlin, M.L.; Douglas, T.A. J. Am. Chem. Soc. 1985, 107, 6668; Lewis, E.S. Bull. Soc. Chim. Fr. 1988, 259.

30. Marcus, R.A. J. Phys. Chem. 1963, 67, 853, Annu. Rev. Phys. Chem. 1964, 15, 155; Eberson, L. Electron Transfer Reactions in Organic Chemistry; Springer: NY, 1987.

31. Kim, D.; Lee, I.H.; Kreevoy, M.M. J. Am. Chem. Soc. 1990, 112, 1889 and references cited therein.

32. See, for example, Dneprovskii, A.S.; Eliseenkov, E.V. J. Org. Chem. USSR 1988, 24, 243.

33. The Investigation of Organic Reactions and their Mechanisms Maskill, H. (Ed.), Blackwell, Oxford, 2006.

34. See Bernasconi, C.F. Investigation of Rates and Mechanisms of Reactions, 4th ed. (Vol. 6 of Weissberger, A. Techniques of Chemistry), 2 pts., Wiley: NY, 1986; Carpenter, B.K. Determination of Organic Reaction Mechanisms, Wiley: NY, 1984.

35. For a discussion, see Martin, R.B. J. Chem. Educ. 1985, 62, 789.

36. See Gentilucci, L.; Grijzen, Y.; Thijs, L.; Zwanenburg, B. Tetrahedron Lett. 1995, 36, 4665.

37. ReactIR uses mid-range IR spectroscopy for the identification and monitoring of critical reaction species and follows the changes in the reaction on a second-by-second basis. For applications, see Stead, D.; Carbone, G.; O'Brien, P.; Campos, K.R.; Coldham, I; Sanderson, A. J. Am. Chem. Soc. 2010, 132, 7260; Pippel, D.J.; Weisenburger, G.A.; Faibish, N.C.; Beak, P. J. Am. Chem. Soc. 2001, 123, 4919.; Rutherford, J.L.; Hoffmann, D.; Collum, D.B. J. Am. Chem. Soc. 2002, 124, 264.

38. See Parker, V.D. Adv. Phys. Org. Chem. 1983, 19, 131; Sheridan, R.S. Org. Photochem. 1987, 8, 159.

39. For a review, see Todres, Z.V. Tetrahedron 1987, 43, 3839.

40. Bunnett, J.F.; Rauhut, M.M.; Knutson, D.; Bussell, G.E. J. Am. Chem. Soc. 1954, 76, 5755.

41. Bunnett, J.F.; Rauhut, M.M. J. Org. Chem. 1956, 21, 944.

42. See Jencks, W.P. Catalysis in Chemistry and Enzymology, McGraw-Hill, NY, 1969; Bender, M.L. Mechanisms of Homogeneous Catalysis from Protons to Proteins, Wiley, NY, 1971; Coenen, J.W.E. Recl. Trav. Chim. Pays-Bas, 1983, 102, 57; and in Bernasconi, C.F. Investigation of Rates and Mechanisms of Reactions, 4th ed. (Vol.6 of Weissberger, A. Techniques of Chemistry), pt. 1, Wiley, NY, 1986, the articles by Keeffe, J.R.; Kresge, A.J. pp. 747–790; Haller, G.L.; Delgass, W.N. pp. 951–979.

43. See Wentrup, C. in Bernasconi, C.F. Investigation of Rates and Mechanisms of Reactions, 4th ed. (Vol. 6 of Weissberger. A. Techniques of Chemistry), pt. 1, Wiley, NY, 1986, pp. 613–661; Collins, C.J. Adv. Phys. Org. Chem. 1964, 2, 3. See also, the series Isotopes in Organic Chemistry.

44. Douglas, D.E.; Burditt, A.M. Can. J. Chem. 1958, 36, 1256.

45. For a review, see Hinton, J.; Oka, M.; Fry, A. Isot. Org. Chem. 1977, 3, 41.

46. See Billups, W.E.; Houk, K.N.; Stevens, R.V. in Bernasconi, C.F. Investigation of Rates and Mechanisms of Reactions, 4th ed. (Vol. 6 of Weissberger, A. Techniques of Chemistry), pt. 1, Wiley, NY, 1986, pp. 663–746; Eliel, E.L. Stereochemistry of Carbon Compounds, McGraw-Hill, NY, 1962; Newman, M.S. Steric Effects in Organic Chemistry, Wiley, NY, 1956.

47. Bonnet, L.; Larrégaray, P.; Duguay, B.; Rayez, J.-C.; Che, D.C.; Kasai, T. Bull. Chem. Soc. Jpn. 2007, 80, 707.

48. Walden, P. Ber. 1896, 29, 136; 1897, 30, 3149; 1899, 32, 1833.

49. See Connors, K.A. Chemical Kinetics, VCH, NY, 1990; Zuman, P.; Patel, R.C. Techniques in Organic Reaction Kinetics, Wiley, NY, 1984; Drenth, W.; Kwart, H. Kinetics Applied to Organic Reactions, Marcel Dekker, NY, 1980; Hammett, L.P. Physical Organic Chemistry, 2nd ed., McGraw-Hill, NY, 1970, pp. 53–100; Gardiner Jr., W.C. Rates and Mechanisms of Chemical Reactions, W.A. Benjamin: NY, 1969; Leffler, J.E.; Grunwald, E. Rates and Equilibria of Organic Reactions, Wiley, NY, 1963; Jencks, W.P. Catalysis in Chemistry and Enzymology, McGraw-Hill, NY, 1969, pp. 555–614.

50. A homogeneous reaction occurs in one phase. Heterogeneous kinetics have been studied much less.

51. Colins, C.C.; Cronin, M.F.; Moynihan, H.A.; McCarthy, D.G. J. Chem. Soc. Perkin Trans. 1 1997, 1267.

52. For a discussion of how order is related to molecularity in many complex situations, see Szabó, Z.G. in Bamford, C.H.; Tipper, C.F.H. Comprehensive Chemical Kinetics, Vol.2, Elsevier, NY, 1969, pp. 1–80.

53. Many chemists prefer to use the term rate-limiting step or rate-controlling step for the slow step, rather than rate-determining step. See the definitions in Gold, V.; Loening, K.L.; McNaught, A.D.; Sehmi, P. IUPAC Compendium of Chemical Terminology, Blackwell Scientific Publications, Oxford, 1987, p. 337. For a discussion of rate-determining steps, see Laidler, K.J. J. Chem. Educ. 1988, 65, 250.

54. For a discussion, see Raines, R.T.; Hansen, D.E. J. Chem. Educ. 1988, 65, 757.

55. See Zuman, P.; Patel, R.C. Techniques in Organic Reaction Kinetics, Wiley, NY, 1984. See Batt, L. in Bamford, C.H.; Tipper, C.F.H. Comprehensive Chemical Kinetics, Vol. 1, Elsevier, NY, 1969, pp. 1–111.

56. For a review of ESR to measure kinetics, see Norman, R.O.C. Chem. Soc. Rev. 1979, 8, 1.

57. See le Noble, W.J. Prog. Phys. Org. Chem. 1967, 5, 207; Matsumoto, K.; Sera, A.; Uchida, T. Synthesis 1985, 1; Matsumoto, K.; Sera, A. Synthesis 1985, 999.

58. See Connors, K.A. Chemical Kinetics, VCH, NY, 1990, pp. 133–186; Zuman, P.; Patel, R.C. Techniques in Organic Reaction Kinetics, Wiley, NY, 1984, pp. 247–327; Krüger, H. Chem. Soc. Rev. 1982, 11, 227; Bernasconi, C.F. Investigation of Rates and Mechanisms of Reactions, 4th ed. (Vol. 6 of Weissberger, A. Techniques of Chemistry), pt. 2, Wiley, NY, 1986. See also, Bamford, C.H.; Tipper, C.F.H. Comprehensive Chemical Kinetics, Vol.24, Elsevier, NY, 1983.

59. See Connors, K.A. Chemical Kinetics, VCH, NY, 1990, pp. 17–131; Ritchie, C.D. Physical Organic Chemistry, 2nd ed., Marcel Dekker, NY, 1990, pp. 1–35; Zuman, P.; Patel, R.C. Techniques in Organic Reaction Kinetics, Wiley, NY, 1984; Margerison, D. in Bamford, C.H.; Tipper, C.F.H. Comprehensive Chemical Kinetics, Vol. 1, Elsevier, NY, 1969, pp. 343–421; Moore, J.W.; Pearson, R.G. Kinetics and Mechanism, 3rd ed., Wiley, NY, 1981, pp. 12–82; in Bernasconi, C.F. Investigation of Rates and Mechanisms of Reactions, 4th ed. (Vol. 6 of Weissberger, A. Techniques of Chemistry), pt. 1, Wiley, NY, 1986, the articles by Bunnett, J.F. pp. 251–372, Noyes Pub., pp. 373–423, Bernasconi, C.F. pp. 425–485, Wiberg, K.B. pp. 981–1019.

60. See Margerison, D. in Bamford, C.H.; Tipper, C.F.H. Comprehensive Chemical Kinetics, Vol. 1, Elsevier, NY, 1969, p. 361.

61. See Hammett, L.P. Physical Organic Chemistry, 2nd ed., McGraw-Hill, NY, 1970, pp. 62–70.

62. See Öki, M. Applications of Dynamic NMR Spectroscopy to Organic Chemistry, VCH, NY, 1985; Fraenkel, G. in Bernasconi, C.F. Investigation of Rates and Mechanisms of Reactions, 4th ed. (Vol. 6 of Weissberger, A. Techniques of Chemistry), pt. 2, Wiley, NY, 1986, pp. 547–604; Roberts, J.D. Pure Appl. Chem.1979, 51, 1037; Binsch, G. Top. Stereochem.1968, 3, 97.

63. For a discussion of organic reaction rate acceleration by immediate solvent evaporation, see Orita, A.; Uehara, G.; Miwa, K.; Otera, J. Chem. Commun. 2006, 4729.

64. See Blandamer, M.J.; Burgess, J.; Robertson, R.E.; Scott, J.M.W. Chem. Rev. 1982, 82, 259.

65. See Bunnett, J.F. in Bernasconi, C.F. Investigation of Rates and Mechanisms of Reactions, 4th ed. (Vol. 6 of Weissberger, A. Techniques of Chemistry), pt. 1, Wiley, NY, 1986, p. 287.

66. See Melander, L.; Saunders, Jr., W.H. Reaction Rates of Isotopic Molecules, Wiley, NY, 1980. For reviews, see Isaacs, N.S. Physical Organic Chemistry, Longman Scientific and Technical, Essex, 1987, pp. 255–281; Lewis, E.S. Top. Curr. Chem. 1978, 74, 31; Saunders, Jr., W.H. in Bernasconi, C.F. Investigation of Rates and Mechanisms of Reactions, 4th ed. (Vol. 6 of Weissberger, A. Techniques of Chemistry), pt. 1, Wiley, NY, 1986, pp. 565–611; Bell, R.P. Chem. Soc. Rev. 1974, 3, 513; Bigeleisen, J.; Lee, M.W.; Mandel, F. Annu. Rev. Phys. Chem. 1973, 24, 407; Wolfsberg, M. Annu. Rev. Phys. Chem. 1969, 20, 449. Also see Kwart, H. Acc. Chem. Res. 1982, 15, 401; Isaacs, E.S. Isot. Org. Chem. 1984, 6, 67; Thibblin, A.; Ahlberg, P. Chem. Soc. Rev. 1989, 18, 209. See also, the series Isotopes in Organic Chemistry.

67. The reduced mass μ of two atoms connected by a covalent bond is μ = m₁m₂/(m₁ + m₂).

68. Reitz, O.; Kopp, J. Z. Phys. Chem. Abt. A 1939, 184, 429.

69. For an example of a reaction with a deuterium isotope effect of 24.2, see Lewis, E.S.; Funderburk, L.H. J. Am. Chem. Soc. 1967, 89, 2322. The high isotope effect in this case has been ascribed to tunneling of the proton: See Lewis, E.S.; Robinson, J.K. J. Am. Chem. Soc. 1968, 90, 4337; Kresge, A.J.; Powell, M.F. J. Am. Chem. Soc. 1981, 103, 201; Caldin, E.F.; Mateo, S.; Warrick, P. J. Am. Chem. Soc. 1981, 103, 202. For arguments that high isotope effects can be caused by factors other than tunneling, see Thibblin, A. J. Phys. Org. Chem. 1988, 1, 161; Kresge, A.J.; Powell, M.F. J. Phys. Org. Chem. 1990, 3, 55.

70. See Sims, L.B.; Lewis, D.E. Isot. Org. Chem. 1984, 6, 161.

71. Bethell, D.; Hare, G.J.; Kearney, P.A. J. Chem. Soc. Perkin Trans. 2 1981, 684, and references cited therein. See, however, Motell, E.L.; Boone, A.W.; Fink, W.H. Tetrahedron 1978, 34, 1619.

72. More O'Ferrall, R.A. J. Chem. Soc. B 1970, 785, and references cited therein.

73. Pascal, R.A.; Baum, M.W.; Wagner, C.K.; Rodgers, L.R.; Huang, D. J. Am. Chem. Soc. 1986, 108, 6477.

74. Stothers, J.B.; Bourns, A.N. Can. J. Chem. 1962, 40, 2007. See also, Ando, T.; Yamataka, H.; Tamura, S.; Hanafusa, T. J. Am. Chem. Soc. 1982, 104, 5493.

75. For a review of carbon isotope effects, see Willi, A.V. Isot. Org. Chem. 1977, 3, 237.

76. See Westaway, K.C. Isot. Org. Chem. 1987, 7, 275; Sunko, D.E.; Hehre, W.J. Prog. Phys. Org. Chem. 1983, 14, 205; Halevi, E.A. Prog. Phys. Org. Chem. 1963, 1, 109. See McLennan, D.J. Isot. Org. Chem. 1987, 7, 393. See also, Sims, L.B.; Lewis, D.E. Isot. Org. Chem. 1984, 6, 161.

77. Leffek, K.T.; Llewellyn, J.A.; Robertson, R.E. Can. J. Chem. 1960, 38, 2171.

78. Bender, M.L.; Feng, M.S. J. Am. Chem. Soc. 1960, 82, 6318; Jones, J.M.; Bender, M.L. J. Am. Chem. Soc. 1960, 82, 6322.

79. DeFrees, D.J.; Hehre, W.J.; Sunko, D.E. J. Am. Chem. Soc. 1979, 101, 2323. See also, Siehl, H.; Walter, H. J. Chem. Soc. Chem. Commun. 1985, 76.

80. Shiner, Jr., V.J.; Kriz, Jr., G.S. J. Am. Chem. Soc. 1964, 86, 2643.

81. Carter, R.E.; Dahlgren, L. Acta Chem. Scand. 1970, 24, 633; Leffek, K.T.; Matheson, A.F. Can. J. Chem. 1971, 49, 439; Sherrod, S.A.; Boekelheide, V. J. Am. Chem. Soc. 1972, 94, 5513.

82. Halevi, E.A.; Nussim, M.; Ron, M. J. Chem. Soc. 1963, 866; Halevi, E.A.; Nussim, M. J. Chem. Soc. 1963, 876.

83. Sunko, D.E.; Szele, I.; Hehre, W.J. J. Am. Chem. Soc. 1977, 99, 5000; Kluger, R.; Brandl, M. J. Org. Chem. 1986, 51, 3964.

84. Halevi, E.A.; Margolin, Z. Proc. Chem. Soc. 1964, 174. A value for 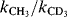of 2.13 was reported for one case: Liu, K.; Wu, Y.W. Tetrahedron Lett. 1986, 27, 3623.

85. Halevi, E.A.; Margolin, Z. Proc. Chem. Soc. 1964, 174.

86. See Caldwell, R.A.; Misawa, H.; Healy, E.F.; Dewar, M.J.S. J. Am. Chem. Soc. 1987, 109, 6869.

87. See Harris, J.M.; Hall, R.E.; Schleyer, P.v.R. J. Am. Chem. Soc. 1971, 93, 2551.

88. For reported exceptions, see Tanaka, N.; Kaji, A.; Hayami, J. Chem. Lett. 1972, 1223; Westaway, K.C. Tetrahedron Lett. 1975, 4229.

89. Shiner, Jr., V.J.; Neumann, A.; Fisher, R.D. J. Am. Chem. Soc. 1982, 104, 354 and references cited therein.

90. Streitwieser, Jr., A.; Jagow, R.H.; Fahey, R.C.; Suzuki, S. J. Am. Chem. Soc. 1958, 80, 2326.

91. Westaway, K.C.; Waszczylo, Z.; Smith, P.J.; Rangappa, K.S. Tetrahedron Lett. 1985, 26, 25.

92. Westaway, K.C.; Lai, Z. Can. J. Chem. 1988, 66, 1263.

93. Werstiuk, N.H.; Timmins, G.; Cappelli, F.P. Can. J. Chem. 1980, 58, 1738.

94. See Alvarez, F.J.; Schowen, R.L. Isot. Org. Chem. 1987, 7, 1; Kresge, A.J.; More O'Ferrall, R.A.; Powell, M.F. Isot. Org. Chem. 1987, 7, 177; Schowen, R.L. Prog. Phys. Org. Chem. 1972, 9, 275;. See Arnett, E.M.; McKelvey, D.R. in Coetzee, J.F.; Ritchie, C.D. cited above, pp. 343–398.

95. Bunton, C.A.; Shiner, Jr., V.J. J. Am. Chem. Soc. 1961, 83, 42, 3207, 3214; Swain, C.G.; Thornton, E.R. J. Am. Chem. Soc. 1961, 83, 3884, 3890. See also, Mitton, C.G.; Gresser, M.; Schowen, R.L. J. Am. Chem. Soc. 1969, 91, 2045.

96. More O'Ferrall, R.A.; Koeppl, G.W.; Kresge, A.J. J. Am. Chem. Soc. 1971, 93, 9.