Chapter 8
Acids and Bases
Two acid–base theories are used in organic chemistry today: the Br nsted theory and the Lewis theory.1 These theories are quite compatible and are used for different purposes.2 However, the Lewis-based idea of electron-donating species (bases) and electron- accepting species (acids) is often the more useful for organic chemistry. Remember also that most organic reactions are not done in an aqueous medium, and focus on electron transfer rather than proton transfer is far more useful.
nsted theory and the Lewis theory.1 These theories are quite compatible and are used for different purposes.2 However, the Lewis-based idea of electron-donating species (bases) and electron- accepting species (acids) is often the more useful for organic chemistry. Remember also that most organic reactions are not done in an aqueous medium, and focus on electron transfer rather than proton transfer is far more useful.
8.A. Brønsted Theory
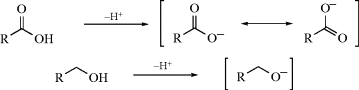
According to this theory, an acid is defined as a proton donor3 and a base as a proton acceptor. However, a base must have a pair of electrons available to share with the proton; this is usually present as an unshared pair, but sometimes is in a π orbital. By this definition, an acid–base reaction is the transfer of a proton from an acid to a base. However, protons do not exist free in solution, but must be attached to an electron pair. In fact, the acid does not “give up” a proton, but rather the base donates electrons to the proton, “pulling it away” to form the conjugate acid. After removal of the proton, the species remaining (the conjugate base) still retains the electron pair to which the proton was formerly attached. The conjugate base, in theory at least, can reacquire a proton and is therefore a base. All acids will generate a conjugate base upon reaction with a suitable base, and all bases will generate a conjugate acid by reaction with a suitable acid. All acid–base reactions fit the equation

No charges are shown in this equation, but an acid always has a charge one positive unit higher than that of its conjugate base.
8.A.i Br nsted Acids
nsted Acids
According to the Br nsted definition, acid strength may be defined as the tendency to give up a proton and base strength as the tendency to accept a proton. All acid–base reactions are reversible, and both an acid and a conjugate acid are present in the equilibrium mixture. In one sense, acid–base reactions occur because the acid and the conjugate acid are not of equal strength (i.e., the equilibrium can be shifted to one side or the other). If an acid, say HCl, is placed in contact with the conjugate base of a weaker acid, say acetate ion, the conjugate acid in this reaction would be acetic acid. Since HCl is a stronger acid than acetic acid (see Table 8.1), the equilibrium lies well to the right. As the reaction is written, if the equilibrium lies to the right (higher concentration of acetic acid and a lower concentration of HCl), HCl is the stronger acid. Likewise, acetate is taken to be a stronger base than the chloride ion. If this is a correct statement, treatment of acetic acid with chloride ion should give essentially no reaction, since the weaker acid already has the proton. This is found to be correct.
nsted definition, acid strength may be defined as the tendency to give up a proton and base strength as the tendency to accept a proton. All acid–base reactions are reversible, and both an acid and a conjugate acid are present in the equilibrium mixture. In one sense, acid–base reactions occur because the acid and the conjugate acid are not of equal strength (i.e., the equilibrium can be shifted to one side or the other). If an acid, say HCl, is placed in contact with the conjugate base of a weaker acid, say acetate ion, the conjugate acid in this reaction would be acetic acid. Since HCl is a stronger acid than acetic acid (see Table 8.1), the equilibrium lies well to the right. As the reaction is written, if the equilibrium lies to the right (higher concentration of acetic acid and a lower concentration of HCl), HCl is the stronger acid. Likewise, acetate is taken to be a stronger base than the chloride ion. If this is a correct statement, treatment of acetic acid with chloride ion should give essentially no reaction, since the weaker acid already has the proton. This is found to be correct.
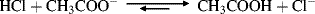
Table 8.1 The pKa Values for Many Types of Acidsa
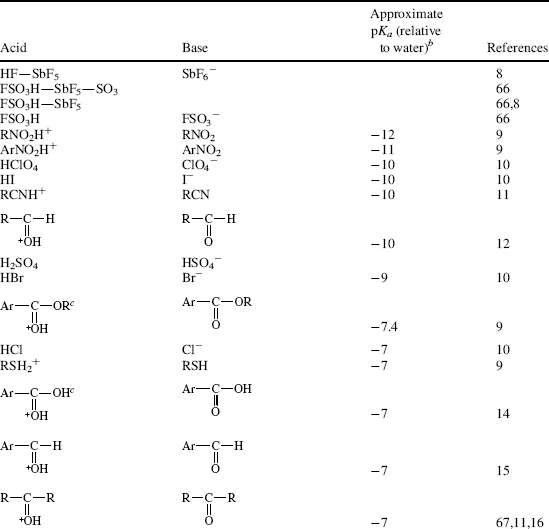
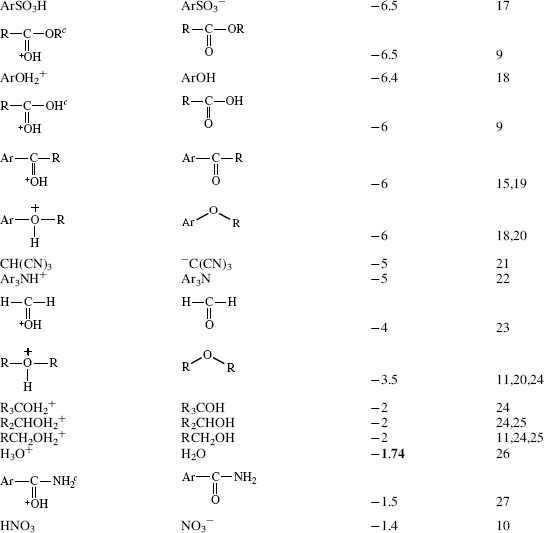


For a comparison of two different acids, the position of the equilibrium in reaction with a common base allows the relative strengths of acids to be determined.4 Likewise, the strength of two different bases will be determined by comparing the equilibrium established when they react with a common acid. By definition, the acid and base are always drawn on the left side of the equation, and the conjugate acid and conjugate base are assumed to be on the right side of the equation.
Of course, if the two acids involved are close to each other in strength, a measurable reaction will occur from both sides. This finding really means that the concentration of acid and base at equilibrium will be close to that of the concentration of the conjugate acid and conjugate base. However, the position of equilibrium will still be over to the side of the weaker acid (unless the acidities are equal within experimental limits). If the concentration of acid and base is higher, the reaction of conjugate acid and conjugate base is more facile, and the compound labeled as the acid is considered to be a weaker acid. If the concentration of the conjugate acid and conjugate base is higher, the reaction of the acid and base is more facile, and the compound labeled as the acid is a stronger acid.
Using these protocols as the definition of acid strength, it is possible to construct a table in which acids are listed in order of acid strength5 (Table 8.1).6 The conjugate base is shown next to each acid in Table 8.1. Using the axiom that a strong acid generates a weak conjugate base and a weak acid will generate a strong conjugate base, it is clear that if the acids in such a table are listed in decreasing order of acid strength, the bases must be listed in increasing order of base strength. The pKa values7 in Table 8.1 are most accurate in the middle of the table.8–67
The pKa values are much harder to measure68 for very strong and very weak acids, and these values must be regarded as approximate. If one did not have the pKa values available, it can be determined experimentally that HClO4 is a stronger acid than H2SO4. A mixture of HClO4 and H2SO4 in 4-methyl-2-pentanone can be titrated to an HClO4 end point without interference by H2SO4.69 Similarly, HClO4 can be shown to be stronger than HNO3 or HCl. However, this is not quantitative, and the value of −10 in the table is not much more than an educated guess. The values for RNO2H+, ArNO2H+, HI, RCNH+ and RSH2+ must also be regarded as highly speculative.70 A wide variety of pKa values have been reported for the conjugate acids of even such simple bases as acetone67 (−0.24 to −7.2), diethyl ether (−0.30 to −6.2), ethanol (−0.33 to −4.8), methanol (−0.34 to −4.9), and 2-propanol (−0.35 to −5.2), depending on the method used to measure them.71 Very accurate values can be obtained only for acids weaker than hydronium ion and stronger than water.
A crystallographic scale of acidity has been developed, including the acidity of C–H compounds. Measuring the mean C–H O distances in crystal structures correlated well with conventional pKa(DMSO) values,72 where DMSO is dimethyl sulfoxide. An ab initio study was able to correlate ring strain in strained hydrocarbons with hydrogen-bond acidity.73 The kinetic acidity of aliphatic hydrocarbons has been determined.74
O distances in crystal structures correlated well with conventional pKa(DMSO) values,72 where DMSO is dimethyl sulfoxide. An ab initio study was able to correlate ring strain in strained hydrocarbons with hydrogen-bond acidity.73 The kinetic acidity of aliphatic hydrocarbons has been determined.74
The bottom portion of Table 8.1 consists of very weak acids (pKa above that of water ≈15.8).75 In most of these acids, the proton is lost from a carbon atom, and such acids are known as carbon acids. The pKa values for such weak acids are often difficult to measure and are known only approximately. The methods used to determine the relative positions of these acids are discussed in Chapter 5.76 The acidity of carbon acids is proportional to the stability of the carbanions that are their conjugate bases (see Sec. 5.B.i).
The extremely strong acids at the top of the table are known as superacids (see Sec. 5.A.ii).77 The actual species present in the FSO3H–SbF5 mixture are probably H[SbF5(SO3F)] and H[SbF2(SO3F)4.66 The addition of SO3 causes formation of the still stronger H[SbF4(SO3F)2], H[SbF3(SO3F)3], and H[(SbF5)2(SO3F)].66 There is a study of electrophilic intermediates that are generated in superacids78 (also see Chapter 10).
By the use of tables (e.g., Table 8.1), it is possible to determine whether a given acid will react with a given base to give reasonable concentrations of the conjugate acid and base. For tables in which acids are listed in order of decreasing strength, the rule is that any acid will react with any base in the table that is below it but not with any above it.79 The greater the separation in the table, the better the reaction. It must be emphasized that the order of acid strength in Table 8.1 separation applies when a given acid and base react without a solvent or, when possible, in water. In other solvents, the order may be greatly different (see Sec. 8.G). In the gas phase, where solvation effects are completely or almost completely absent, acidity orders may also differ greatly.80 For example, in the gas phase, toluene is a stronger acid than water and tert-butoxide ion is a weaker base than methoxide ion81 (see also Sec. 8.G). It is also possible for the acidity order to change with temperature. For example, >50 °C the order of base strength is BuOH > H2O > Bu2O; from 1 to 50 °C the order is BuOH > Bu2O > H2O; while <1 °C the order becomes Bu2O > BuOH > H2O.82
8.A.ii. Br nsted Bases
nsted Bases
Basicity may be measured by a parameter known as proton affinity of an anion. The dissociation of a hydrogen ion for a molecule in the gas phase is called the proton affinity of the conjugate base.83 A hydrogen-bond basicity scale has been developed that can be used to determine the relative basicity of molecules. Table 8.2 gives the pKHB values for several common heteroatom-containing molecules.84 This is obtained from the protonated form (conjugated acid) of the base in question. The larger the number, the more basic is that compound. The basicity of aliphatic amines has been calculated,85 the ion-pair basicity of amines in THF86 and in water87 has been determined, and the basicity of pyridine was examined.88 There are secondary deuterium isotope effects for measuring the basicity of secondary amines, and deuteration was found to increase the basicity.89 Weaker bases have also been examined, and the basicity of carbonyl compounds in carbon tetrachloride has been determined.97 Alkenes are weak bases98 that react with strong acids (e.g., HCl or HBr, Reaction 15-02). Note that extremely twisted amides (Sec. 4.Q.ii) exhibit high basicity.99
Table 8.2 The pKHB Values for Many Types of Bases.
| Base | Approximate pKHB | Reference |
| N-Methyl-2-piperidone | 2.60 | 90 |
| Et2NCONEt2 | 2.43 | 90 |
| N-Methyl-2-pyrrolidinone | 2.38 | 90 |
| PhCONMe2 | 2.23 | 90 |
| HCONMe2 | 2.10 | 90 |
| PhCONHMe | 2.03 | 90 |
| 18-crown-6 | 1.98 | 91 |
| HCONHMe | 1.96 | 90 |
| Aniline | 4.60 | 92 |
| N-methylaniline | 4.85 | 92 |
| PhNHNH2 | 5.27 | 92 |
| Ph(Me)NNH2 | 4.99 | 92 |
| 15-crown-5 | 1.82 | 91 |
| 12-crown-4 | 1.73 | 91 |
| PhOCONMe2 | 1.70 | 90 |
| Et2N–CN | 1.63 | 93 |
| Me2N–CN | 1.56 | 93 |
| δ-Valerolactone | 1.43 | 94 |
| Oxetane | 1.36 | 91 |
| γ-Butyrolactone | 1.32 | 94 |
| THF | 1.28 | 91 |
| Cyclopentanone | 1.27 | 95 |
| t-BuOMe | 1.19 | 91 |
| Acetone | 1.18 | 95 |
| MeCOOEt | 1.07 | 95 |
| 1,4-Dioxane | 1.03 | 91 |
| Et2O | 1.01 | 91 |
| 1,3-Dioxane | 0.93 | 91 |
| 1-Methyloxirane | 0.97 | 91 |
| PhCOOMe | 0.89 | 94 |
| MeOCOOMe | 0.82 | 94 |
| PhCHO | 0.78 | 95 |
| Bu2O | 0.75 | 91 |
| HCOOEt | 0.66 | 94 |
| MeCHO | 0.65 | 95 |
| Me2NO2 | 0.41 | 96 |
| MeNO2 | 0.27 | 96 |
| PhNO2 | 0.30 | 96 |
| Furan | −0.40 | 91 |
A class of organic compounds termed superbases has been developed.100 Vinamidine type or Schwesinger proton sponges (see Sec. 8.F), 1,101 are dubbed superbases and are probably the most powerful organic neutral bases known. The pKa (pKBH+) in MeCN was measure as 31.94. It has been shown that the pKa values of strong neutral organic (super)bases in acetonitrile are well described by the density functional theory.102 The fundamental type of proton sponge is 1,8-bis(dimethylamino)naphthalene (2, see Sec. 8.F), with a pKBH+ of 18.18.103 Other superbase-type compounds include amidinazines [e.g., N1,N1-dimethyl-N2-β-(2-pyridylethyl)-formamidine (3)], pKBH+ in DMSO = 25.1,104 1,8-bis(tetramethylguanidino)naphthalene, (4),105 and quinolino[7,8-h]quinolines (e.g., 5) with a pKBH+ = 12.8.106
It is important to note that organometallic compounds, such as Grignard reagents (RMgX) and organolithium reagents (RLi),107 are powerful bases. The conjugate bases of both of these bases are alkanes, (R–H), which are very weak acids indeed (see Table 8.1).

8.B. The Mechanism of Proton-Transfer Reactions
Proton transfers between a base and an oxygen or nitrogen acid are usually extremely fast.108 Such reactions are generally diffusion controlled in the thermodynamically favored direction.109 In fact, a normal acid is defined110 as one whose proton-transfer reactions are completely diffusion controlled, except when the conjugate acid of the base to which the proton is transferred has a pK value very close (differs by less than ~ 2 pK units) to that of the acid. The normal acid–base reaction mechanism consists of three steps:
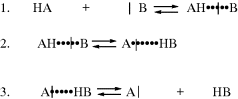
The actual proton transfer takes place in the second step the first step is formation of a hydrogen-bonded complex. The product of the second step is another hydrogen-bonded complex, which dissociates in the third step.
However, not all such proton transfers are diffusion controlled. For example, if an internal hydrogen bond exists in a molecule, reaction with an external acid or base is often much slower.111 In a case such as 3-hydroxypropanoic acid, the −OH ion can form a hydrogen bond with the acidic hydrogen only if the internal hydrogen bond breaks. Therefore only some of the collisions between −OH ions and 3-hydroxypropanoic acid molecules result in proton transfer. In many collisions, the −OH ions will come away “empty-handed”, resulting in a lower reaction rate. Note that this affects only the rate, not the equilibrium. Other systems are capable of hydrogen bonding (e.g., 1,2-diols). In the case of cyclohexane-1,2-diols, hydrogen bonding, ion–dipole interactions, polarizability, and stereochemistry all play a role in determining the acidity.112 The presence of halogen atoms (e.g., chlorine) can lead to hydrogen-bonding effects.113 Another factor that can create lower rates is a molecular structure in which the acidic proton is protected within a molecular cavity (e.g., the in–in and out–in isomers shown in Sec. 4.L). See also the proton sponges mentioned in Section 8.F. Proton transfers between an acidic and a basic group within the same molecule can also be slow, if the two groups are too far apart for hydrogen bonding. In such cases, participation of solvent molecules may be necessary.
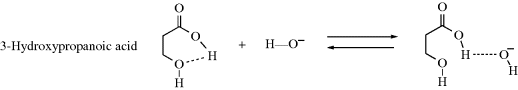
Proton transfers to or from a carbon atom114 in most cases are much slower than those strictly between oxygen or nitrogen atoms. At least three factors can be responsible for this,115 not all of them applying in every case.
 nsted acids known.119
nsted acids known.119In connection with factors 2 and 3, it has been proposed115 that any factor that stabilizes the product (e.g., by resonance or solvation) lowers the rate constant if it develops late on the reaction coordinate, but increases the rate constant if it develops early. This is called the Principle of Imperfect Synchronization.
Mechanisms of proton transfer have been studied for many compounds, including the reactions of acids with lactams,121 amides with various bases,122 and amines with alkoxide bases.123
8.C. Measurements of Solvent Acidity124
When a solute is added to an acidic solvent it may become protonated by the solvent. This effect can lead to an enhancement of acidity, as in the effect of using formic acid rather than methanol.125 An acidity scale has been reported for ionic liquids126 (see Sec. 9.D.iii for a discussion of ionic liquids), and the Lewis acidity of ionic liquids has been established using IR.127 If the solvent is water and the concentration of solute is not very great, then the pH of the solution is a good measure of the proton-donating ability of the solvent. Unfortunately, this is no longer true in concentrated solutions because activity coefficients are no longer unity. A measurement of solvent acidity is needed that works in concentrated solutions and applies to mixed solvents as well. The Hammett acidity function128 is a measurement that is used for acidic solvents of high dielectric constant.129 For any solvent, including mixtures of solvents (but the proportions of the mixture must be specified), a value H0 is defined as
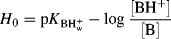
H0 is measured by using “indicators” that are weak bases (B) and so are partly converted, in these acidic solvents, to the conjugate acids BH+. Typical indicators are o-nitroanilinium ion, with a pK in water of −0.29, and 2,4-dinitroanilinium ion, with a pK in water of −4.53. For a given solvent, [BH+]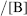 [B] is measured for one indicator, usually by spectrophotometric means and with the known pK in water (
[B] is measured for one indicator, usually by spectrophotometric means and with the known pK in water (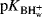 ) for that indicator, H0 can be calculated for that solvent system. In practice, several indicators are used, so that an average H0 is taken. Once H0 is known for a given solvent system, pKa values in it can be calculated for any other acid–base pair.
) for that indicator, H0 can be calculated for that solvent system. In practice, several indicators are used, so that an average H0 is taken. Once H0 is known for a given solvent system, pKa values in it can be calculated for any other acid–base pair.
The symbol H0 is defined as

where 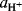 is the activity of the proton and fI and
is the activity of the proton and fI and 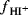 are the activity coefficients of the indicator and conjugate acid of the indicator,130 respectively. The parameter H0 is related to H0 by
are the activity coefficients of the indicator and conjugate acid of the indicator,130 respectively. The parameter H0 is related to H0 by
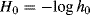
so that H0 is analogous to pH and H0 to [H+], and indeed in dilute aq solution H0 = pH.
The parameter H0 reflects the ability of the solvent system to donate protons, but it can be applied only to acidic solutions of high dielectric constant, mostly mixtures of water with acids (nitric, sulfuric, perchloric, etc.). It is apparent that the H0 treatment is valid only when 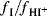 is independent of the nature of the base (the indicator). Since this is so only when the bases are structurally similar, the treatment is limited. Even when similar bases are compared, many deviations are found.131 Other acidity scales132 have been set up, including a scale for C–H acids,133 among them H− for bases with a charge of −1, HR for aryl carbinols,134HC for bases that protonate on carbon,135 and HA for unsubstituted amides.136 It is now clear that there is no single acidity scale that can be applied to a series of solvent mixtures, irrespective of the bases employed.137
is independent of the nature of the base (the indicator). Since this is so only when the bases are structurally similar, the treatment is limited. Even when similar bases are compared, many deviations are found.131 Other acidity scales132 have been set up, including a scale for C–H acids,133 among them H− for bases with a charge of −1, HR for aryl carbinols,134HC for bases that protonate on carbon,135 and HA for unsubstituted amides.136 It is now clear that there is no single acidity scale that can be applied to a series of solvent mixtures, irrespective of the bases employed.137
Although most acidity functions have been applied only to acidic solutions, some work has also been done with strongly basic solutions.138 The H− function, which is used for highly acidic solutions when the base has a charge of −1, can also be used for strongly basic solvents, in which case it measures the ability of these solvents to abstract a proton from a neutral acid (BH).139 When a solvent becomes protonated, its conjugate acid is known as a lyonium ion.
Another approach to the acidity function problem was proposed by Bunnett et al.,140 who derived the equation
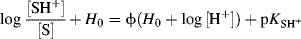
where S is a base that is protonated by an acidic solvent. Thus the slope of a plot of log ([SH+]/[S]) + H0 against H0 + log [H+] is the parameter ϕ, while the intercept is the pKa of the lyonium ion (SH+, referred to infinite dilution in water). The value of ϕ expresses the response of the equilibrium
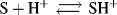
to changing acid concentration. A negative ϕ indicates that the log of the ionization ratio [SH+]/[S] increases, as the acid concentration increases, more rapidly than −H0. A positive ϕ value indicates the reverse. The Bunnett–Olsen equation given above is a linear free–energy relationship (see Sec. 9.C) that pertains to acid–base equilibria. A corresponding equation that applies to kinetic data is
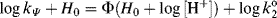
where kψ is the pseudo-first-order rate constant for a reaction of a weakly basic substrate taking place in an acidic solution and 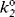 is the second-order rate constant at infinite dilution in water. In this case, ϕ characterizes the response of the reaction rate to changing acid concentration of the solvent. The Bunnett–Olsen treatment has also been applied to basic media, where, in a group of nine reactions in concentrated NaOMe solutions, no correlation was found between reaction rates and either H− or stoichiometric base concentration, but where the rates were successfully correlated by a linear free energy equation similar to those given above.141
is the second-order rate constant at infinite dilution in water. In this case, ϕ characterizes the response of the reaction rate to changing acid concentration of the solvent. The Bunnett–Olsen treatment has also been applied to basic media, where, in a group of nine reactions in concentrated NaOMe solutions, no correlation was found between reaction rates and either H− or stoichiometric base concentration, but where the rates were successfully correlated by a linear free energy equation similar to those given above.141
A treatment partially based on the Bunnett–Olsen treatment is that of Bagno et al.,142 which formulates medium effects (changes in acidity of solvent) on acid–base equilibria. An appropriate equilibrium is chosen as reference, and the acidity dependence of other reactions compared with it, by use of the linear free energy equation
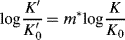
where the K values are the equilibrium constants for the following: K for the reaction under study in any particular medium; K′ for the reference reaction in the same medium; K0 for the reaction under study in a reference solvent; 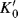 for the reference reaction in the same reference solvent; and m∗ is the slope of the relationship [corresponding to (1 − ϕ) of the Bunnett–Olsen treatment]. This equation has been shown to apply to many acid–base reactions.
for the reference reaction in the same reference solvent; and m∗ is the slope of the relationship [corresponding to (1 − ϕ) of the Bunnett–Olsen treatment]. This equation has been shown to apply to many acid–base reactions.
Another type of classification system was devised by Bunnett143 for reactions occurring in moderately concentrated acid solutions. Log kψ + H0 is plotted against log  , where Kψ is the pseudo-first-order rate constant for the protonated species and
, where Kψ is the pseudo-first-order rate constant for the protonated species and 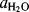 is the activity of water. Most such plots are linear or nearly so. According to Bunnett, the slope of this plot w tells something about the mechanism. Where w is between −2.5 and 0, water is not involved in the rate-determining step; where w is between 1.2 and 3.3, water is a nucleophile in the rate-determining step; where w is between 3.3 and 7, water is a proton-transfer agent. These rules hold for acids in which the proton is attached to oxygen or nitrogen.
is the activity of water. Most such plots are linear or nearly so. According to Bunnett, the slope of this plot w tells something about the mechanism. Where w is between −2.5 and 0, water is not involved in the rate-determining step; where w is between 1.2 and 3.3, water is a nucleophile in the rate-determining step; where w is between 3.3 and 7, water is a proton-transfer agent. These rules hold for acids in which the proton is attached to oxygen or nitrogen.
A new acidity scale has been developed based on calorimetric measurement of N-methylimidazole and N-methylpyrrole in bulk solvents.144 A revised version of this method was shown to give better results in some cases.145 Another scale of solvent acidities was developed based on the hydrogen-bond donor acidities in aq DMSO.146 Note that bond energies, acidities, and electron affinities are related in a thermodynamic cycle, and Fattahi and Kass147 show that by measuring two of these quantities the third can be found.
8.D. Acid and Base Catalysis148
Many reactions are catalyzed by acids or bases. Some are catalyzed by both acids and bases. In such cases, the catalyst is involved in a fundamental way in the mechanism. The first step of such a reaction is nearly always a proton transfer between the catalyst and the substrate.
Reactions can be catalyzed by acid or base in two different ways, called general and specific catalysis. If the rate of an acid-catalyzed reaction run in a solvent (S) is proportional to its conjugate acid [SH+], the reaction is said to be subject to specific acid catalysis, the acid being the lyonium ion (SH+). The acid that is put into the solvent may be stronger or weaker than SH+, but the rate is proportional only to the [SH+] that is actually present in the solution derived from the equilbrium

The identity of HA is important only to the extent that it determines the position of equilibrium, and hence the [SH+]. Most measurements have been made in water, where SH+ is H3O+.
In general acid catalysis, the rate is increased not only by an increase in [SH+], but also by an increase in the concentration of other acids (e.g., in water by phenols or carboxylic acids). These other acids increase the rate even when [SH+] is held constant. In this type of catalysis the strongest acids catalyze best, so that, in the example given, an increase in the phenol concentration catalyzes the reaction much less than a similar increase in [H3O+]. This relationship between acid strength of the catalyst and its catalytic ability can be expressed by the Br nsted catalysis equation149
nsted catalysis equation149
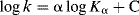
where k is the rate constant for a reaction catalyzed by an acid of ionization constant Kα. According to this equation, when log k is plotted against log Kα for catalysis of a given reaction by a series of acids, a straight line should be obtained with slope and intercept C. Straight lines are obtained in many cases, but not always. The relationship usually fails when acids of different types are compared. For example, it is much more likely to hold for a group of substituted phenols than for a collection of acids that contains both phenols150 and carboxylic acids. The Br nsted equation is another linear free energy relationship (see Sec. 9.C).
nsted equation is another linear free energy relationship (see Sec. 9.C).
Analogously, there are general and specific (S− from an acidic solvent SH) base-catalyzed reactions. The Br nsted law for bases is
nsted law for bases is
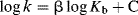
The Br nsted equations relate a rate constant k to an equilibrium constant Ka. In Chapter 6, the Marcus equation was seen to relate a rate term (in that case ΔG‡) to an equilibrium term (ΔG°). When the Marcus treatment is applied to proton transfers151 between a carbon and an oxygen (or a nitrogen), the simplified152 equation (Sec. 6.I)
nsted equations relate a rate constant k to an equilibrium constant Ka. In Chapter 6, the Marcus equation was seen to relate a rate term (in that case ΔG‡) to an equilibrium term (ΔG°). When the Marcus treatment is applied to proton transfers151 between a carbon and an oxygen (or a nitrogen), the simplified152 equation (Sec. 6.I)
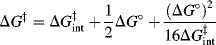
where
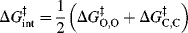
can be further simplified: Because proton transfers between oxygen and oxygen (or nitrogen and nitrogen) are much faster than those between carbon and carbon, 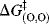 is much smaller than
is much smaller than 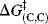 and one can write153
and one can write153
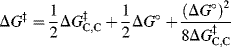
Thus, if the carbon part of the reaction is kept constant and only the A of HA is changed (where A is an oxygen or nitrogen moiety), then ΔG‡ is dependent only on ΔG°. Differentiation of this equation yields the Br nsted α:
nsted α:

The Br nsted law is therefore a special case of the Marcus equation.
nsted law is therefore a special case of the Marcus equation.
A knowledge of whether a reaction is subject to general or specific acid catalysis supplies information about the mechanism. For any acid-catalyzed reaction we can write
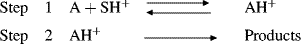
If the reaction is catalyzed only by the specific acid SH+, it means that step 1 is rapid and step 2 is rate controlling. This means that an equilibrium has been rapidly established between A and the strongest acid present in the solution, namely, SH+ (since this is the strongest acid that can be present in S). On the other hand, if step 2 is faster, there is no time to establish equilibrium and the rate-determining step must be step 1. This step is affected by all the acids that may be present, and the rate reflects the sum of the effects of each acid (general acid catalysis). General acid catalysis is also observed if the slow step is the reaction of a hydrogen-bond complex (A HB), since each complex reacts with a base at a different rate. A comparable discussion can be used for general and specific base catalysis.154 Further information can be obtained from the values α and β in the Br
HB), since each complex reacts with a base at a different rate. A comparable discussion can be used for general and specific base catalysis.154 Further information can be obtained from the values α and β in the Br nsted catalysis equations, since these are approximate measures of the extent of proton transfer in the transition state. In most cases, values of α and β are between 1 and 0. A value of α or β near 0 is generally taken to mean that the transition state resembles the reactants; that is, the proton has been transferred very little when the transition state has been reached. A value of α or β near 1 is taken to mean the opposite; that is, in the transition state the proton has been almost completely transferred. However, cases are known in which these generalizations are not followed,155 and their theoretical basis has been challenged.156 In general, the proton in the transition state lies closer to the weaker base.
nsted catalysis equations, since these are approximate measures of the extent of proton transfer in the transition state. In most cases, values of α and β are between 1 and 0. A value of α or β near 0 is generally taken to mean that the transition state resembles the reactants; that is, the proton has been transferred very little when the transition state has been reached. A value of α or β near 1 is taken to mean the opposite; that is, in the transition state the proton has been almost completely transferred. However, cases are known in which these generalizations are not followed,155 and their theoretical basis has been challenged.156 In general, the proton in the transition state lies closer to the weaker base.
8.E. Lewis Acids and Bases
At about the same time that Br nsted proposed his acid–base theory, Lewis put forth a broader theory. A base in the Lewis theory is the same as in the Br
nsted proposed his acid–base theory, Lewis put forth a broader theory. A base in the Lewis theory is the same as in the Br nsted one, namely, a compound with an available pair of electrons, either unshared or in a π orbital. However, a Lewis base donates electrons to an atom other than H or C.157 A Lewis acid is any species with a vacant orbital.158 In a Lewis acid–base reaction, the unshared pair of the base forms a covalent bond with the vacant orbital of the acid, as represented by the general equation
nsted one, namely, a compound with an available pair of electrons, either unshared or in a π orbital. However, a Lewis base donates electrons to an atom other than H or C.157 A Lewis acid is any species with a vacant orbital.158 In a Lewis acid–base reaction, the unshared pair of the base forms a covalent bond with the vacant orbital of the acid, as represented by the general equation
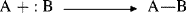
in which charges are not shown, since they may differ. A specific example is
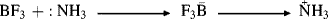
In the Br nsted picture, the acid is a proton donor, but in the Lewis picture the proton itself is the acid since it has a vacant orbital. A Br
nsted picture, the acid is a proton donor, but in the Lewis picture the proton itself is the acid since it has a vacant orbital. A Br nsted acid becomes, in the Lewis picture, the compound that gives up the actual acid. The advantage of the Lewis theory is that it correlates the behavior of many more processes. For example, AlCl3 and BF3 are Lewis acids because they have only six electrons in the outer shell and have room for eight. Lewis acids SnCl4 and SO3 have eight, but their central elements, not being in the first row of the periodic table, have room for 10 or 12. Other Lewis acids are simple cations, like Ag+. The simple reaction
nsted acid becomes, in the Lewis picture, the compound that gives up the actual acid. The advantage of the Lewis theory is that it correlates the behavior of many more processes. For example, AlCl3 and BF3 are Lewis acids because they have only six electrons in the outer shell and have room for eight. Lewis acids SnCl4 and SO3 have eight, but their central elements, not being in the first row of the periodic table, have room for 10 or 12. Other Lewis acids are simple cations, like Ag+. The simple reaction 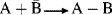 is not very common in organic chemistry, but the scope of the Lewis picture is much larger because reactions of the types shown here, which are very common in organic chemistry, are also Lewis acid–base reactions. In fact, all reactions in which a covalent bond is formed through one species contributing a filled and the other a vacant orbital may be regarded as Lewis acid–base reactions. An ab initio analysis of the factors that determine Lewis versus Lowry–Br
is not very common in organic chemistry, but the scope of the Lewis picture is much larger because reactions of the types shown here, which are very common in organic chemistry, are also Lewis acid–base reactions. In fact, all reactions in which a covalent bond is formed through one species contributing a filled and the other a vacant orbital may be regarded as Lewis acid–base reactions. An ab initio analysis of the factors that determine Lewis versus Lowry–Br nsted acidity–basicity is available.159
nsted acidity–basicity is available.159

When a Lewis acid combines with a base to give a negative ion in which the central atom has a higher than normal valence, the resulting salt is called an ate complex.160 Examples are
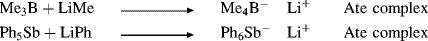
Ate complexes are analogous to the onium salts formed when a Lewis base expands its valence, for example,

Far fewer quantitative measurements have been made of Lewis acid strength compared to that of Br nsted acids.161 A simple table of Lewis acidities based on some quantitative measurement (e.g., that given for Br
nsted acids.161 A simple table of Lewis acidities based on some quantitative measurement (e.g., that given for Br nsted acids in Table 8.1) is not feasible because Lewis acidity depends on the nature of the base and any solvent that can function as a base. For example, lithium perchlorate functions as a weak Lewis acid in ether.162 Qualitatively, the following approximate sequence of acidity of Lewis acids of the type MXn has been suggested, where X is a halogen atom or an inorganic radical: BX3 > AlX3 > FeX3 > GaX3 > SbX5 > SnX4 > AsX5 > ZnX2 > HgX2.
nsted acids in Table 8.1) is not feasible because Lewis acidity depends on the nature of the base and any solvent that can function as a base. For example, lithium perchlorate functions as a weak Lewis acid in ether.162 Qualitatively, the following approximate sequence of acidity of Lewis acids of the type MXn has been suggested, where X is a halogen atom or an inorganic radical: BX3 > AlX3 > FeX3 > GaX3 > SbX5 > SnX4 > AsX5 > ZnX2 > HgX2.
8.E.i Hard–Soft Acids–Bases
The facility with which an acid–base reaction takes place depends, of course, on the strengths of the acid and the base. But it also depends on quite another quality, called the hardness163 or softness of the acid or base.164 Hard and soft acids and bases have these characteristics:
A qualitative listing of the hardness of some acids and bases is given in Table 8.3.165 The treatment has also been made quantitative,166 with the following operational definition:
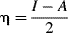
In this equation, η, the absolute hardness, is half the difference between I, the ionization potential, and A, the electron affinity.167 The softness (σ), is the reciprocal of η. Values of η for some molecules and ions are given in Table 8.4.168 Note that the proton, which is involved in all Br nsted acid–base reactions, is the hardest acid listed, with η = ∞ (it has no ionization potential). The above equation cannot be applied to anions, because electron affinities cannot be measured for them. Instead, the assumption is made that η for an anion X− is the same as that for the radical X•.169 Other methods are also needed to apply the treatment to polyatomic cations.169
nsted acid–base reactions, is the hardest acid listed, with η = ∞ (it has no ionization potential). The above equation cannot be applied to anions, because electron affinities cannot be measured for them. Instead, the assumption is made that η for an anion X− is the same as that for the radical X•.169 Other methods are also needed to apply the treatment to polyatomic cations.169
Table 8.3 Hard and Soft Acids and Basesa

a. See Ref. 165.
Once acids and bases have been classified as hard or soft, a simple rule can be given: hard acids prefer to bond to hard bases, and soft acids prefer to bond to soft bases [the HSAB (hard–soft acid–base) principle].170 The rule has nothing to do with acid or base strength but merely says that the product A–B will have extra stability if both A and B are hard or if both are soft. Another rule is that a soft Lewis acid and a soft Lewis base tend to form a covalent bond, while a hard acid and a hard base tend to form ionic bonds.
One application of the first rule given above is found in complexes between alkenes or aromatic compounds and metal ions (see above). Alkenes and aromatic rings are soft bases and should prefer to complex with soft acids. Thus, Ag+, Pt2+, and Hg2+ complexes are common, but complexes of Na+, Mg2+, or Al3+ are rare. Chromium complexes are also common, but in such complexes the chromium is in a low or zero oxidation state (which softens it) or attached to other soft ligands. Another application is the reaction:

The HSAB principle predicts that the equilibrium should lie to the right, because the hard acid CH3CO+ should have a greater affinity for the hard base (RO−) than for the soft base (RS−). Indeed, thiol esters are easily cleaved by RO− or hydrolyzed by dilute base (−OH is also a hard base).171 Another application of the rule is discussed in Section 10.G.ii.172 The HSAB principles have been applied to analyze the reactivity of ketone and ester enolate anions,173 and in analyzing catalyst selectivity in synthesis.174
8.F. The Effects of Structure on the Strengths of Acids and Bases175
The structure of a molecule can affect its acidity or basicity in a number of ways. Unfortunately, in most molecules two or more of these effects (as well as solvent effects) are operating, and it is usually very difficult or impossible to say how much each effect contributes to the acid or base strength.176 Small differences in acidity or basicity between similar molecules are particularly difficult to interpret. It is well to be cautious when attributing them to any particular effect.

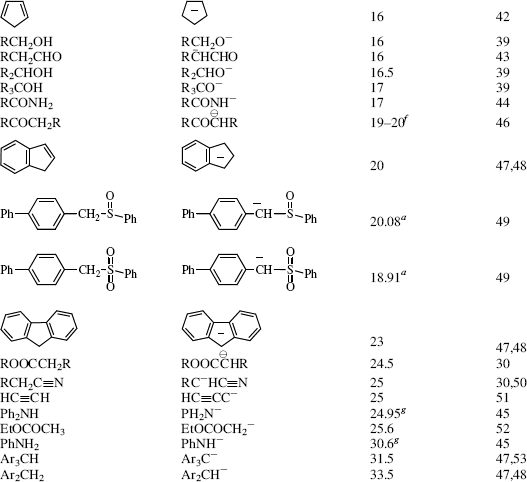
 N group. Thus amides (RCONH2) are more acidic than amines (RCH2NH2); esters (RCH2COOR′) more than ethers (RCH2CH2OR′); and ketones (RCH2COR′) more than alkanes (RCH2CH2R′) (Table 8.1). The effect is enhanced when two carbonyl groups are attached to the same carbon (because of additional resonance and spreading of charge); for example, β-keto esters (see 7) are more acidic than simple ketones or carboxylic esters (Table 8.1). Compounds such as (7) are generically referred to as active methylene compounds (X–CH2–X), where X is an electron-withdrawing groups (a carbonyl, cyano, sulfonyl, etc.).187 The influence of substituents in the α-position of substituted ethyl acetate derivatives has been studied.188 Extreme examples of this effect are found in the molecules tricyanomethane [(NC)3CH], with a pKa of −5 (Table 8.1), and 2-(dicyanomethylene)-1,1,3,3-tetracyanopropene (NC)2C=C[CH(CN)2]2, whose first pKa is below −8.5 and whose second pKa is −2.5.
N group. Thus amides (RCONH2) are more acidic than amines (RCH2NH2); esters (RCH2COOR′) more than ethers (RCH2CH2OR′); and ketones (RCH2COR′) more than alkanes (RCH2CH2R′) (Table 8.1). The effect is enhanced when two carbonyl groups are attached to the same carbon (because of additional resonance and spreading of charge); for example, β-keto esters (see 7) are more acidic than simple ketones or carboxylic esters (Table 8.1). Compounds such as (7) are generically referred to as active methylene compounds (X–CH2–X), where X is an electron-withdrawing groups (a carbonyl, cyano, sulfonyl, etc.).187 The influence of substituents in the α-position of substituted ethyl acetate derivatives has been studied.188 Extreme examples of this effect are found in the molecules tricyanomethane [(NC)3CH], with a pKa of −5 (Table 8.1), and 2-(dicyanomethylene)-1,1,3,3-tetracyanopropene (NC)2C=C[CH(CN)2]2, whose first pKa is below −8.5 and whose second pKa is −2.5.


 nsted acids and bases that differ in the position of an element in the periodic table:
nsted acids and bases that differ in the position of an element in the periodic table:
 RCONH2
RCONH2  RCOCH3.
RCOCH3.


 SnCl4 unit with substituents attached to the carbonyl.213
SnCl4 unit with substituents attached to the carbonyl.213 C−, which has more s character in its unshared pair than CH2=CH− or CH3CH2− (sp vs sp2 vs sp3, respectively), is a much weaker base. This explains the relatively high acidity of acetylenes and HCN. Another example is that alcohol and ether oxygen atoms, where the unshared pair is sp3, are more strongly basic than carbonyl oxygen atoms, where the unshared pair is sp2 (Table 8.1).
C−, which has more s character in its unshared pair than CH2=CH− or CH3CH2− (sp vs sp2 vs sp3, respectively), is a much weaker base. This explains the relatively high acidity of acetylenes and HCN. Another example is that alcohol and ether oxygen atoms, where the unshared pair is sp3, are more strongly basic than carbonyl oxygen atoms, where the unshared pair is sp2 (Table 8.1).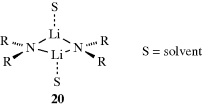
Table 8.4 Some Absolute Hardness Values in Electron Voltsa

Table 8.5 The pK Values for Some Acidsa
a. See Ref. 47.
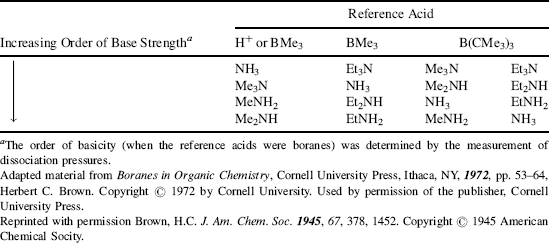
Table 8.6 Bases Listed in Increasing Order of Base Strength when Compared with Certain Reference Acids.
8.G. The Effects of the Medium on Acid and Base Strength
Structural features are not the only factors that affect acidity or basicity. The same compound can have its acidity or basicity changed when the reaction conditions are changed. The effect of temperature (Sec. 8.A) has already been mentioned. More important is the effect of the solvent, which can exert considerable influence on acid and base strengths by differential solvation.234 If a base is more solvated than its conjugate acid, its stability is increased relative to the conjugate acid. For example, Table 8.6 shows that in reactions with a proton, where steric effects are absent, methylamine is a stronger base than ammonia and dimethylamine is stronger still.235 These results are easily explainable if one assumes that methyl groups are electron donating. However, trimethylamine, which should be even stronger, is a weaker base than dimethylamine or methylamine. This apparently anomalous behavior can be explained by differential hydration.236 Thus, NH4+ is much better hydrated (by hydrogen bonding to the water solvent) than NH3 because of its positive charge.237 It has been estimated that this effect contributes ~11 pK units to the base strength of ammonia.238 When methyl groups replace hydrogen, this difference in hydration decreases239 until, for trimethylamine, it contributes only ~6 pK units to the base strength.195 Thus two effects act in opposite directions, the field effect increasing the basicity as the number of methyl groups increases and the hydration effect decreasing it. Taken together, the strongest base is dimethylamine and the weakest is ammonia in solution. If alkyl groups are electron donating, one would expect that in the gas phase,240 where the solvation effect does not exist, the basicity order of amines toward the proton should be R3N > R2NH > RNH2 > NH3, and this has indeed been confirmed, for R = Me, as well as R = Et and Pr.241 Aniline too, in the gas phase, is a stronger base than NH3,242 so its much lower basicity in aqueous solution (pKa of PhNH3+ 4.60 compared with 9.24 for aq NH4+) is caused by similar solvation effects and not by resonance and field electron-withdrawing effects of a phenyl group. Similarly, pyridine243 and pyrrole244 are both much less basic than NH3 in aqueous solution (pyrrole245 is neutral in aqueous solution), but more basic in the gas phase. Care must be taken in attributing relative acidities or basicities to any particular effect. Solvent has a significant influence on the Hammett reaction constant (Sec. 11.D), which influences the acidity of substituted benzoic acids.246
In the case of Lewis acids, protic solvents (e.g., water or alcohol) can strongly influence their reactivity, cause it to react via an alternative path to the one desired, or even cause decomposition. Rare earth metal triflates have been used to develop water tolerant Lewis acids that can be used in many organic reactions.247
For simple alcohols, the order of gas-phase acidity is completely reversed from that in aqueous solution. In solution, the acidity is in the order H2O > MeCH2OH > Me2CHOH > Me3COH, but in the gas phase the order is precisely the opposite.248 Once again solvation effects can be invoked to explain the differences. Comparing the two extremes, H2O and Me3COH, we see that the OH− ion is very well solvated by water while the bulky Me3CO− is much more poorly solvated because the water molecules cannot get as close to the oxygen. Thus in solution H2O gives up its proton more readily. When solvent effects are absent, however, the intrinsic acidity is revealed and Me3COH is a stronger acid than H2O. This result demonstrates that simple alkyl groups cannot be simply regarded as electron donating. If methyl is an electron-donating group, then Me3COH should be an intrinsically weaker acid than H2O, yet it is stronger. A similar pattern is found with carboxylic acids, where simple aliphatic acids (e.g., propanoic) are stronger than acetic acid in the gas phase,249 although weaker in aqueous solution (Table 8.5). The evidence in these and other cases250 is that alkyl groups can be electron donating when connected to unsaturated systems, but may have either no effect or may actually be electron withdrawing in other systems. It appears that the intrinsic gas-phase acidity order of alcohols as well as the basicity order of amines is due to the effect of alkyl groups, because of their polarizability, which can spread both positive and negative charges.251 It has been calculated that even in the case of alcohols the field effects of the alkyl groups are still operating normally, but are swamped by the greater polarizability effects.252 Polarizability effects on anionic centers are a major factor in gas-phase acid–base reactions.253 It has been shown (by running reactions on ions that are solvated in the gas phase) that solvation by even one molecule of solvent can substantially affect the order of basicities.254
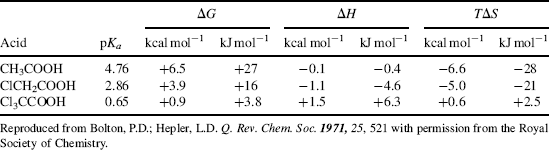
The effect on the orientation of solvent molecules when an acid or base is converted to its conjugate is an important aspect of solvent effects. For example, consider an acid (RCOOH) converted to RCOO− in aqueous solution. The solvent molecules, by hydrogen bonding, arrange themselves around the COO− group in a much more orderly fashion than they had been arranged around the COOH group (because they are more strongly attracted to the negative charge). This leads to a considerable loss of freedom and a decrease in entropy. Thermodynamic measurements show that for simple aliphatic and halogenated aliphatic acids in aqueous solution at room temperature, the entropy (TΔS) usually contributes much more to the total free energy change ΔG than does the enthalpy ΔH.255 Two examples are shown in Table 8.7.256 Resonance and field effects of functional groups therefore affect the acidity of RCOOH in two distinct ways. They affect the enthalpy (electron-withdrawing groups increase acidity by stabilizing RCOO− by charge dispersal), but they also affect the entropy (by lowering the charge on the COO− group and by changing the electron-density distribution in the COOH group, electron-withdrawing groups alter the solvent orientation patterns around both the acid and the ion, and consequently change ΔS).
Table 8.7 Thermodynamic Values for the Ionizations of Acetic and Chloroacetic Acids in H2O at 25°Ca
A change from a protic to an aprotic solvent can also affect the acidity or basicity, since there is a difference in solvation of anions by a protic solvent (which can form hydrogen bonds) and an aprotic one.257 The effect can be extreme: In DMF, picric acid is stronger than HBr,258 though in water HBr is far stronger. This particular result can be attributed to size. That is, the large ion (O2N)3C6H2O− is better solvated by DMF than the smaller ion Br−.259 The ionic strength of the solvent also influences acidity or basicity, since it has an influence on activity coefficients.
In summary, solvation can have powerful effects on acidity and basicity. In the gas phase, the effects discussed in Section 8.F, especially resonance and field effects, operate unhindered by solvent molecules. Electron-withdrawing groups generally increase acidity (and decrease basicity); electron-donating groups act in the opposite way. In solution, especially aqueous solution, these effects still largely persist (which is why pK values in Table 8.5 do largely correlate with resonance and field effects), but in general are much weakened, and occasionally reversed.179
Notes
1. For monographs on acids and bases, see Stewart, R. The Proton: Applications to Organic Chemistry, Academic Press, NY, 1985; Bell, R.P. The Proton in Chemistry, 2nd ed., Cornell University Press, Ithaca, NY, 1973; Finston, H.L.; Rychtman, A.C. A New View of Current Acid–Base Theories, Wiley, NY, 1982.
2. For discussion of the historical development of acid–base theory, see Bell, R.P. Q. Rev. Chem. Soc. 1947, 1, 113; Bell, R.P. The Proton in Chemistry, 1st ed., Cornell University Press, Ithaca, NY, 1959, pp. 7–17.
3. According to IUPAC terminology (Bunnett, J.F.; Jones, R.A.Y. Pure Appl. Chem. 1988, 60, 1115), an acid is a hydron donor. The IUPAC recommends that the term proton be restricted to the nucleus of the hydrogen isotope of mass 1, while the nucleus of the naturally occurring element, which contains ~0.015% deuterium, be called the hydron (the nucleus of mass 2 has always been known as the deuteron). This accords with the naturally occurring negative ion, which has long been called the hydride ion. In this book, however, we will continue to use proton for the naturally occurring form, because most of the literature uses this term.
4. Although equilibrium is reached in most acid–base reactions extremely rapidly (see Sec. 8.B), some are slow (especially those in which the proton is lost from a carbon) and in these cases time must be allowed for the system to come to equilibrium.
5. For a review of stronger Bronsted acids, see Akiyama, T. Chem. Rev. 2007, 107, 5744.
6. Table 8.1 is a thermodynamic acidity scale and applies only to positions of equilibria. For the distinction between thermodynamic and kinetic acidity (see Sec. 8.B).
7. For a first principles calculation of pK values in nonaqueous solution, see Ding, F.; Smith, J.M.; Wang, H. J. Org. Chem. 2009, 74, 2679.
8. Gold,V.; Laali, K.; Morris, K.P.; Zdunek, L.Z. J. Chem. Soc. Chem. Commun. 1981, 769; Sommer, J.; Canivet, P.; Schwartz, S.; Rimmelin, P. Nouv. J. Chim. 1981, 5, 45.
9. Arnett, E.M. Prog. Phys. Org. Chem. 1963, 1, 223, pp. 324–325.
10. Bell, R.P. The Proton in Chemistry, 2nd ed., Cornell University Press, Ithaca, NY, 1973.
11. Deno, N.C.; Gaugler, R.W.; Wisotsky, M.J. J. Org. Chem. 1966, 31, 1967.
12. Levy, G.C.; Cargioli, J.D.; Racela, W. J. Am. Chem. Soc. 1970, 92, 6238. See, however, Brouwer, D.M.; van Doorn, J.A. Recl. Trav. Chim. Pays-Bas 1971, 90, 1010.
13. Carboxylic acids, esters, and amides are shown in this table to be protonated on the carbonyl oxygen. See Smith, C.R.; Yates, K. Can. J. Chem. 1972, 50, 771; Benedetti, E.; Di Blasio, B.; Baine, P. J. Chem. Soc. Perkin Trans. 2 1980, 500; Homer, R.B.; Johnson, C.D. in Zabicky, J. The Chemistry of Amides, Wiley, NY, 1970, pp. 188–197. It has been shown that some amides protonate at nitrogen: see Perrin, C.L. Acc. Chem. Res. 1989, 22, 268. For a review of alternative proton sites, see Liler, M. Adv. Phys. Org. Chem. 1975, 11, 267.
14. Stewart, R.; Granger, M.R. Can. J. Chem. 1961, 39, 2508.
15. Yates, K.; Stewart, R. Can. J. Chem. 1959, 37, 664; Stewart, R.; Yates, K. J. Am. Chem. Soc. 1958, 80, 6355.
16. Lee, D.G. Can. J. Chem. 1970, 48, 1919.
17. Cerfontain, H.; Koeberg-Telder, A.; Kruk, C. Tetrahedron Lett. 1975, 3639.
18. Arnett, E.M.; Wu, C.Y. J. Am. Chem. Soc. 1960, 82, 5660; Koeberg-Telder, A.; Lambrechts, H.J.A.; Cerfontain, H. Recl. Trav. Chim. Pays-Bas 1983, 102, 293.
19. Fischer, A.; Grigor, B.A.; Packer, J.; Vaughan, J. J. Am. Chem. Soc. 1961, 83, 4208.
20. Arnett, E.M.; Wu, C.Y. J. Am. Chem. Soc. 1960, 82, 4999.
21. Boyd, R.H. J. Phys. Chem. 1963, 67, 737.
22. Arnett, E.M.; Quirk, R.P.; Burke, J.J. J. Am. Chem. Soc. 1970, 92, 1260.
23. McTigue. P.T.; Sime, J.M. Aust. J. Chem. 1963, 16, 592.
24. Deno, N.C.; Turner, J.O. J. Org. Chem. 1966, 31, 1969.
25. Chandler, W.D.; Lee, D.G. Can. J. Chem. 1990, 68, 1757.
26. For a discussion, see Campbell, M.L.; Waite, B.A. J. Chem. Educ. 1990, 67, 386.
27. Grant, H.M.; McTigue, P.; Ward, D.G. Aust. J. Chem. 1983, 36, 2211.
28. Bruckenstein, S.; Kolthoff, I.M. in Kolthoff, I.M.; Elving, P.J. Treatise on Analytical Chemistry, Vol. 1, pt. 1, Wiley, NY, 1959, pp. 432–433.
29. Brown, H.C.; McDaniel, D.H.; Häflinger, O. in Braude, E.A.; Nachod, F.C. Determination of Organic Structures by Physical Methods, Vol. 1, Academic Press, NY, 1955, pp. 567–662.
30. Pearson, R.G.; Dillon, R.L. J. Am. Chem. Soc. 1953, 75, 2439.
31. This value includes the CO2 usually present. The value for H2CO3 alone is 3.9 in Bell, R.P. The Proton in Chemistry, 2nd ed., Cornell University Press, Ithaca, NY, 1973.
32. Crampton, M.R. in Patai, S. The Chemistry of the Thiol Group, pt. 1, Wiley, NY, 1974, pp. 396–410.
33. See Bunting, J.W.; Kanter, J.P. J. Am. Chem. Soc. 1993, 115, 11705.
34. Perrin, D.D. Ionisation Constants of Inorganic Acids and Bases in Aqueous Solution, 2nd ed., Pergamon, Elmsford, NY, 1982.
35. Rochester, C.H. in Patai, S. The Chemistry of the Hydroxyl Group, pt. 1, Wiley, NY, 1971, p. 374.
36. Cram, D.J. Chem. Eng. News 1963, 41 (No. 33, Aug. 19), 94.
37. Bowden, K.; Stewart, R. Tetrahedron 1965, 21, 261.
38. Hine, J.; Philips, J.C.; Maxwel, J.I. J. Org. Chem. 1970, 35, 3943. See also, Ang, K.P.; Lee, T.W.S. Aust. J. Chem. 1977, 30, 521.
39. Reeve, W.; Erikson, C.M.; Aluotto, P.F. Can. J. Chem. 1979, 57, 2747.
40. See also, Olmstead, W.N.; Margolin, Z.; Bordwell, F.G. J. Org. Chem. 1980, 45, 3295.
41. Harned, H.S.; Robinson, R.A. Trans. Faraday Soc. 1940, 36, 973.
42. Streitwieser, Jr., A.; Nebenzahl, L. J. Am. Chem. Soc. 1976, 98, 2188.
43. Guthrie, J.P.; Cossar, J. Can. J. Chem. 1986, 64, 2470.
44. Homer, R.B.; Johnson, C.D. in Zabicky, J. The Chemistry of Amides, Wiley, NY, 1970, pp. 238–240.
45. The pKa of acetone in DMSO is reported to be 26.5. See Bordwell, F.G.; Zhang, X.-M. Accts. Chem. Res. 1997, 26, 510.
46. Guthrie, J.P.; Cossar, J.; Klym, A. J. Am. Chem. Soc. 1984, 106, 1351; Chiang, Y.; Kresge, A.J.; Tang, Y.S.; Wirz, J. J. Am. Chem. Soc. 1984, 106, 460.
47. Streitwieser, Jr., A.; Ciuffarin, E.; Hammons, J.H. J. Am. Chem. Soc. 1967, 89, 63.
48. Streitwieser, Jr., A.; Hollyhead, W.B.; Pudjaatmaka, H.; Owens, P.H.; Kruger, T.L.; Rubenstein, P.A.; MacQuarrie, R.A.; Brokaw, M.L.; Chu, W.K.C.; Niemeyer, H.M. J. Am. Chem. Soc. 1971, 93, 5088.
49. Streitwieser, A.; Wang, G.P.; Bors, D.A. Tetrahedron 1997, 53, 10103.
50. For a review of the acidity of cyano compounds, see Hibbert, F. in Patai, S.; Rappoport, Z. The Chemistry of Triple-bonded Functional Groups, pt. 1; Wiley, NY, 1983, pp. 699–736.
51. Cram, D.J. Fundamentals of Carbanion Chemistry, Academic Press, NY, 1965, p. 19. See also, Dessy, R.E.; Kitching, W.; Psarras, T.; Salinger, R.; Chen, A.; Chivers, T. J. Am. Chem. Soc. 1966, 88, 460.
52. Amyes, T.L.; Richard, J.P. J. Am. Chem. Soc. 1996, 118, 3129.
53. Streitwieser, Jr., A.; Hollyhead, W.B.; Sonnichsen, G.; Pudjaatmaka, H.; Chang, C.J.; Kruger, T.L. J. Am. Chem. Soc. 1971, 93, 5096.
54. Buncel, E.; Menon, B. J. Am. Chem. Soc. 1977, 99, 4457.
55. Buncel, E.; Menon, B. J. Organomet. Chem. 1977, 141, 1.
56. Albrech, H.; Schneider, G. Tetrahedron 1986, 42, 4729.
57. Boerth, D.W.; Streitwieser, Jr., A. J. Am. Chem. Soc. 1981, 103, 6443.
58. Streitwieser, Jr., A.; Scannon, P.J.; Niemeyer, H.M. J. Am. Chem. Soc. 1972, 94, 7936.
59. Streitwieser, Jr., A.; Boerth, D.W. J. Am. Chem. Soc. 1978, 100, 755.
60. This value is calculated from results given in Streitwieser, Jr., A.; Caldwell, R.A.; Young, W.R. J. Am. Chem. Soc. 1969, 91, 529. For a review of acidity and basicity of cyclopropanes, see Battiste, M.A.; Coxon, J.M. in Rappoport, Z. The Chemistry of the Cyclopropyl Group, pt. 1, Wiley, NY, 1987, pp. 255–305.
61. See Daasbjerg, K. Acta Chem. Scand. B 1995, 49, 878 for pKa values of various hydrocarbons in DMF.
62. This value is calculated from results given in Streitwieser, Jr., A.; Taylor, D.R. J. Chem. Soc. D 1970, 1248.
63. These values are based on those given in Cram, D.J. Chem. Eng. News 1963, 41 (No. 33, Aug. 19), 94, but are corrected to the newer scale of Streitwieser, A.; Streitwieser, Jr., A.; Scannon, P.J.; Niemeyer, H.M. J. Am. Chem. Soc. 1972, 94, 7936; Streitwieser, Jr., A.; Boerth, D.W. J. Am. Chem. Soc. 1978, 100, 755.
64. Breslow, R. and co-workers report a value of 71 (Breslow, R.; Grant, J.L. J. Am. Chem. Soc. 1977, 99, 7745), but this was obtained by a different method, and is not comparable to the other values in Table 8.1. A more comparable value is 53. See also, Juan, B.; Schwarz, J.; Breslow, R. J. Am. Chem. Soc. 1980, 102, 5741.
65. This table gives average values for functional groups. See Brown, H.C.; McDaniel, D.H.; Häflinger, O. in Braude, E.A.; Nachod, F.C. Determination of Organic Structures by Physical Methods, Vol. 1, Academic Press, NY, 1955; Serjeant, E.P.; Dempsey, B. Ionisation Constants of Organic Acids in Aqueous Solution, Pergamon, Elmsford NY, 1979; Kortüm, G.; Vogel, W.; Andrussow, K. Dissociation Constants of Organic Acids in Aqueous Solution, Butterworth, London, 1961. The index in the 1979 volume covers both volumes. Kortüm, G.; Vogel, W.; Andrussow, K. Pure Appl. Chem. 1960, 1, 190; Arnett, E.M. Prog. Phys. Org. Chem. 1963, 1, 223; Perrin, D.D. Dissociation Constants of Organic Bases in Aqueous Solution, Butterworth, London, 1965, and Supplement, 1972; Collumeau, A. Bull. Soc. Chim. Fr. 1968, 5087; Bordwell, F.G. Acc. Chem. Res. 1988, 21, 456; Perrin, D.D. Ionisation Constants of Inorganic Acids and Bases in Aqueous Solution, 2nd ed., Pergamon, Elmsford NY, 1982; Pure Appl. Chem. 1969, 20, 133.
66. Gillespie, R.J. Acc. Chem. Res. 1968, 1, 202.
67. For discussions of pKa determinations for the conjugate acids of ketones, see Bagno, A.; Lucchini,V.; Scorrano, G. Bull. Soc. Chim. Fr. 1987, 563; Toullec, J. Tetrahedron Lett. 1988, 29, 5541.
68. For a review of methods of determining pKa values, see Cookson, R.F. Chem. Rev. 1974, 74, 5.
69. Kolthoff, I.M.; Bruckenstein, S. in Kolthoff, I.M.; Elving, P.J. Treatise on Analytical Chemistry, Vol. 1, pt. 1, Wiley, NY, 1959, pp. 475–542, p. 479.
70. For reviews of organic compounds protonated at O, N, or S, see Olah, G.A.; White, A.M.; O'Brien, D.H. Chem. Rev. 1970, 70, 561; Olah, G.A.; White, A.M.; O'Brien, D.H. in Olah, G.A.; Schleyer, P.v.R. Carbonium Ions, Vol. 4, Wiley, NY, 1973, pp. 1697–1781.
71. Rochester, C.H. Acidity Functions, Academic Press, NY, 1970. For discussion of the basicity of such compounds, see Liler, M. Reaction Mechanisms in Sulfuric Acid, Academic Press, NY, 1971, pp. 118–139.
72. Pedireddi, V.R.; Desiraju, G.R. J. Chem. Soc. Chem. Commun. 1992, 988.
73. Alkorta, I.; Campillo, N.; Rozas, I.; Elguero, J. J. Org. Chem. 1998, 63, 7759.
74. Streitwieser, A.; Keevil, T.A.; Taylor, D.R.; Dart, E.C. J. Am. Chem. Soc. 2005, 127, 9290.
75. See Reutov, O.A.; Beletskaya, I.P.; Butin, K.P. CH-Acids, Pergamon, NY, 1978; Cram, D.J. Fundamentals of Carbanion Chemistry, Academic Press, NY, 1965, pp. 1–45; Streitwieser, Jr., A.; Hammons, J.H. Prog. Phys. Org. Chem. 1965, 3, 41; Wiberg, K.B. J. Org. Chem. 2002, 67, 1613.
76. See Jones, J.R. Q. Rev. Chem. Soc. 1971, 25, 365; Fischer, H.; Rewicki, D. Prog. Org. Chem. 1968, 7, 116; Reutov, O.A.; Beletskaya, I.P.; Butin, K.P. CH-Acids, Chapter 1, Pergamon, NY, 1978 (an earlier version of this chapter appeared in Russ. Chem. Rev. 1974, 43, 17); Gau, G.; Assadourian, L.; Veracini, S. Prog. Phys. Org. Chem. 1987, 16, 237; in Buncel, E.; Durst, T. Comprehensive Carbanion Chemistry, pt. A, Elsevier, NY, 1980, the reviews by Pellerite, M.J.; Brauman, J.I. pp. 55–96 (gas-phase acidities); and Streitwieser, Jr., A.; Juaristi, E.; Nebenzahl, L. pp. 323–381.
77. See Olah, G.A.; Prakash, G.K.S.; Sommer, J. Superacids, Wiley, NY, 1985; Gillespie, R.J.; Peel, T.E. Adv. Phys. Org. Chem. 1971, 9, 1; Arata, K. Adv. Catal. 1990, 37, 165. For a review of methods of measuring superacidity, see Jost, R.; Sommer, J. Rev. Chem. Intermed. 1988, 9, 171.
78. Prakash, G.K.S. J. Org. Chem. 2006, 71, 3661.
79. These reactions are equilibria. What the rule actually says is that the position of equilibrium will be such that the weaker acid predominates. However, this needs to be taken into account only when the acid and base are close to each other in the table (within ~2 pK units).
80. See Gal, J.; Maria, P. Prog. Phys. Org. Chem. 1990, 17, 159.
81. Bohme, D.K.; Lee-Ruff, E.; Young, L.B. J. Am. Chem. Soc. 1972, 94, 4608, 5153.
82. Gerrard, W.; Macklen, E.D. Chem. Rev. 1959, 59, 1105. For other examples, see Calder, G.V.; Barton, T.J. J. Chem. Educ. 1971, 48, 338; Hambly, A.N. Rev. Pure Appl. Chem. 1965, 15, 87, p. 88.
83. Tal'Rose, V.L.; Frankevitch, E.L. J. Am. Chem. Soc. 1958, 80, 2344; DeKock, R.L. J. Am. Chem. Soc. 1975, 97, 5592; McDaniel, D.H.; Coffman, N.B.; Strong, J.M. J. Am. Chem. Soc. 1970, 92, 6697. For a computational study of the proton affinities of ketones, vicinal diketones and α-keto esters, see Taskinen, A.; Nieminen, V.; Toukoniitty, E.; Murzin, D.Yu.; Hotokka, M. Tetrahedron 2005, 61, 8109.
84. For measnurement of amine basicity via ion pair statibity in ionic liquids (Sec. 9.D.iii), see D'Anna, F.; Renato Noto, R. Tetrahedron 2007, 63, 11681.
85. Caskey, D.C.; Damrauer, R.; McGoff, D. J. Org. Chem. 2002, 67, 5098.
86. Streitwieser, A.; Kim, H.-J. J. Am. Chem. Soc. 2000, 122, 11783; Garrido, G.; Koort, E.; Ràfols, C.; Bosch, E.; Rodima, T.; Leito, I.; Rosés, M. J. Org. Chem. 2006, 71, 9062.
87. Canle, L.M.; Demirtas, I.; Freire, A.; Maskill, H.; Mishima, M. Eur. J. Org. Chem. 2004, 5031.
88. Chmurzynski, L. J. Heterocyclic Chem. 2000, 37, 71.
89. Perrin, C.L.; Ohta, B.K.; Kuperman, J.; Liberman, J.; Erdélyi, M. J. Am. Chem. Soc. 2005, 127, 9641.
97. Carrasco, N.; González-Nilo, F.; Rezende, M.C. Tetrahedron 2002, 58, 5141.
98. A new scale of π-basicity is proposed. See Stoyanov, E.S.; Stoyanova, I.V.; Reed, C.A. Chemistry: European J. 2008, 14, 7880.
99. Ly, T.; Krout, M.; Pham, D.K.; Tani, K.; Stoltz, B.M.; Julian, R.R. J. Am. Chem. Soc. 2007, 129, 1864.
90. Le Questel, J.-Y.; Laurence, C.; Lachkar, A.; Helbert, M.; Berthelot, M. J. Chem. Soc. Perkin Trans. 2 1992, 2091.
91. Berthelot, M.; Besseau, F.; Laurence, C. Eur. J. Org. Chem. 1998, 925.
92. Korzhenevskaya, N.G.; Rybachenko, V.I.; Kovalenko, V.V.; Lyashchuk, S.N.; Red'ko, A.N. Russ. J. Org. Chem. 2007, 43, 1475.
93. Berthelot, M.; Helbert, M.; Laurence, C.; LeQuestel, J.-Y.; Anvia, F.; Taft, R.W. J. Chem. Soc. Perkin Trans. 2 1993, 625.
94. Besseau, F.; Laurence, C.; Berthelot, M. J. Chem. Soc. Perkin Trans. 2 1994, 485.
95. Besseau, F.; Luçon, M.; Laurence, C.; Berthelot, M. J. Chem. Soc. Perkin Trans. 2 1998, 101.
96. Laurence, C.; Berthelot, M.; Luçon, M.; Morris, D.G. J. Chem. Soc. Perkin Trans. 2 1994, 491.
100. For calculated basicities of super bases see Glasovac, Z.; Eckert-Maksi , M.; Maksi
, M.; Maksi , Z.B. New J. Chem., 2009, 33, 588.
, Z.B. New J. Chem., 2009, 33, 588.
101. Schwesinger, R.; Mißfeldt, M.; Peters, K.; von Schnering, H.G. Angew. Chem. Int. Ed. 1987, 26, 1165; Schwesinger, R.; Schlemper, H.; Hasenfratz, Ch.; Willaredt, J.; Dimbacher, T.; Breuer, Th.; Ottaway, C.; Fletschinger, M.; Boele, J.; Fritz, H.; Putzas, D.; Rotter, H.W.; Bordwell, F.G.; Satish, A.V.; Ji, G.Z.; Peters, E.-M.; Peters, K.; von Schnering, H.G. Liebigs Ann. 1996, 1055.
102. Kova evi
evi , B.; Maksi
, B.; Maksi , Z.B. Org. Lett. 2001, 3, 1523.
, Z.B. Org. Lett. 2001, 3, 1523.
103. Alder, R.W.; Bowman, P.S.; Steele, W.R.S.; Winterman, D.R. Chem. Commun. 1968, 723; Alder, R.W. Chem. Rev. 1989, 89, 1215.
104. Raczynska, E.D.; Darowska, M.; Dabkowska, I.; Decouzon, M.; Gal, J.-F.; Maria, P.-C.; Poliart, C.D. J. Org. Chem. 2004, 69, 4023.
105. Raab, V.; Kipke, J.; Gschwind, R.M.; Sundermeyer, J. Chem. Eur. J. 2002, 8, 1682.
106. Krieger, C.; Newsom, I.; Zirnstein, M.A.; Staab, H.A. Angew. Chem. Int. Ed. 1989, 28, 84.
107. Gorecka-Kobylinska, J.; Schlosser, M. J. Org. Chem. 2009, 74, 222.
108. For reviews of such proton transfers, see Hibbert, F. Adv. Phys. Org. Chem. 1986, 22, 113; Crooks, J.E. in Bamford, C.H.; Tipper, C.F.H. Chemical Kinetics, Vol. 8; Elsevier, NY, 1977, pp. 197–250. See Bernasconi, C.F.; Fairchild, D.E.; Montañez, R.L.; Aleshi, P.; Zheng, H.; Lorance, E. J. Org. Chem. 2005, 70, 7721.
109. See Eigen, M. Angew. Chem. Int. Ed. 1964, 3, 1.
110. See, for example, Hojatti, M.; Kresge, A.J.; Wang, W. J. Am. Chem. Soc. 1987, 109, 4023.
111. See Ritchie, C.D.; Lu, S. J. Am. Chem. Soc. 1989, 111, 8542.
112. Chen, X.; Walthall, D.A.; Brauman, J.I. J. Am. Chem. Soc. 2004, 126, 12614.
113. Abraham, M. H.; Enomoto, K.; Clarke, E. D.; Sexton, G. J. Org. Chem. 2002, 67, 4782.
114. See Hibbert, F. in Bamford, C.H.; Tipper, C.F.H. Chemical Kinetics, Vol. 8, Elsevier, NY, 1977, pp. 97–196; Kreevoy, M.M. Isot. Org. Chem. 1976, 2, 1; Leffek, K.T. Isot. Org. Chem. 1976, 2, 89.
115. See Bernasconi, C.F. Tetrahedron 1985, 41, 3219.
116. Houk, R.J.T.; Anslyn, E.V.; Stanton, J.F. Org. Lett. 2006, 8, 3461.
117. Kresge, A.J.; Powell, M.F. J. Org. Chem. 1986, 51, 822; Formosinho, S.J.; Gal, V.M.S. J. Chem. Soc. Perkin Trans. 2 1987, 1655.
118. Not all 1-alkynes behave as normal acids; see Aroella, T.; Arrowsmith, C.H.; Hojatti, M.; Kresge, A.J.; Powell, M.F.; Tang, Y.S.; Wang, W. J. Am. Chem. Soc. 1987, 109, 7198.
119. Juhasz, M.; Hoffmann, S.; Stoyanov, E.; Kim, K.-C.; Reed, C.A. Angew. Chem. Int. Ed. 2004, 43, 5352.
120. See Kurz, J.L. J. Am. Chem. Soc. 1989, 111, 8631.
121. Wang, W.; Cheng, P.; Huang, C.; Jong, Y. Bull. Chem. Soc. Jpn. 1992, 65, 562.
122. Wang, W.-h.; Cheng, C.-c. Bull. Chem. Soc. Jpn. 1994, 67, 1054.
123. Lambert, C.; Hampel, F.; Schleyer, P.v.R. Angew. Chem. Int. Ed. 1992, 31, 1209.
124. For fuller treatments, see Hammett, L.P. Physical Organic Chemistry, 2nd ed., McGraw-Hill, NY, 1970, pp. 263–313; Jones, R.A.Y. Physical and Mechanistic Organic Chemistry, 2nd ed., Cambridge University Press, Cambridge, 1984, pp. 83–93; Arnett, E.M.; Scorrano, G. Adv. Phys. Org. Chem. 1976, 13, 83.
125. Holt, J.; Karty, J.M. J. Am. Chem. Soc. 2003, 125, 2797.
126. Thomazeau, C.; Olivier-Bourbigou, H.; Magna, L.; Luts, S.; Gilbert, B. J. Am. Chem. Soc. 2003, 125, 5264.
127. Yang, Y.-l.; Kou, Y. Chem. Commun. 2004, 226.
128. Hammett, L.P.; Deyrup, A.J. J. Am. Chem. Soc. 1932, 54, 2721.
129. See Rochester, C.H. Acidity Functions, Academic Press, NY, 1970; Cox, R.A.; Yates, K. Can. J. Chem. 1983, 61, 2225; Boyd R.H. in Coetzee, J.F.; Ritchie, C.D. Solute–Solvent Interactions, Marcel Dekker, NY, 1969, pp. 97–218.
130. See Yates, K.; McClelland, R.A. Prog. Phys. Org. Chem. 1974, 11, 323.
131. See Kreevoy, M.M.; Baughman, E.H. J. Am. Chem. Soc. 1973, 95, 8178; García, B.; Leal, J.M.; Herrero, L.A.; Palacios, J.C. J. Chem. Soc. Perkin Trans. 2 1988, 1759; Arnett, E.M.; Quirk, R.P.; Burke, J.J. J. Am. Chem. Soc. 1970, 92, 1260.
132. For lengthy tables of many acidity scales, with references, see Cox, R.A.; Yates, K. Can. J. Chem. 1983, 61, 2225. For an equation that is said to combine the vast majority of acidity functions, see Zalewski, R.I.; Sarkice, A.Y.; Geltz, Z. J. Chem. Soc. Perkin Trans. 2 1983, 1059.
133. See Vianello, R.; Maksi , Z.B. Eur. J. Org. Chem. 2004, 5003.
, Z.B. Eur. J. Org. Chem. 2004, 5003.
134. Deno, N.C.; Berkheimer, H.E.; Evans, W.L.; Peterson, H.J. J. Am. Chem. Soc. 1959, 81, 2344.
135. Reagan, M.T. J. Am. Chem. Soc. 1969, 91, 5506.
136. Edward, J.T.; Wong, S.C. Can. J. Chem. 1977, 55, 2492; Liler, M.; Markovi , D. J. Chem. Soc. Perkin Trans. 2 1982, 551.
, D. J. Chem. Soc. Perkin Trans. 2 1982, 551.
137. Hammett, L.P. Physical Organic Chemistry, 2nd ed., McGraw-Hill, NY, 1970, p. 278; Rochester, C.H. Acidity Functions, Academic Press, NY, 1970, p. 21.
138. For another approach to solvent basicity scales, see Catalán, J.; Gómez, J.; Couto, A.; Laynez, J. J. Am. Chem. Soc. 1990, 112, 1678.
139. See Rochester, C.H. Q. Rev. Chem. Soc. 1966, 20, 511; Rochester, C.H. Acidity Functions, Academic Press, NY, 1970, pp. 234–264; Bowden, K. Chem. Rev. 1966, 66, 119.
140. Bunnett, J.F.; McDonald, R.L.; Olsen, F.P. J. Am. Chem. Soc. 1974, 96, 2855.
141. More O'Ferrall, R.A. J. Chem. Soc. Perkin Trans. 2 1972, 976.
142. Bagno, A.; Scorrano, G.; More O'Ferrall, R.A. Rev. Chem. Intermed. 1987, 7, 313. See also, Cox, R.A. Acc. Chem. Res. 1987, 20, 27.
143. Bunnett, J.F. J. Am. Chem. Soc. 1961, 83, 4956, 4968, 4973, 4978.
144. Catalán, J.; Couto, A.; Gomez, J.; Saiz, J.L.; Laynez, J. J. Chem. Soc. Perkin Trans. 2 1992, 1181.
145. Abraham, M.H.; Taft, R.W. J. Chem. Soc. Perkin Trans. 2 1993, 305.
146. Liu, P.C.; Hoz, S.; Buncel, E. Gazz. Chim. Ital. 1996, 126, 31. See also, Abraham, M.H.; Zhao, Y.J. J. Org. Chem. 2004, 69, 4677.
147. Fattahi, A.; Kass, S.R. J. Org. Chem. 2004, 69, 9176.
148. See Stewart, R. The Proton: Applications to Organic Chemistry, Academic Press, NY, 1985, pp. 251–305; Willi, A.V. in Bamford, C.H.; Tipper, C.F.H. Chemical Kinetics, Vol. 8, Elsevier, NY, 1977, pp. 1–95; Jones, R.A.Y. Physical and Mechanistic Organic Chemistry, 2nd ed., Cambridge University Press, Cambridge, 1984, pp. 72–82; Bender, M.L. Mechanisms of Homogeneous Catalysis from Protons to Proteins, Wiley, NY, 1971, pp. 19–144.
149. See Klumpp, G.W. Reactivity in Organic Chemistry, Wiley, NY, 1982, pp. 167–179; Bell, R.P. in Chapman, N.B.; Shorter, J. Correlation Analysis in Chemistry: Recent Advances, Plenum Press, 1978, pp. 55–84; Kresge, A.J. Chem. Soc. Rev. 1973, 2, 475.
150. See Silva, P.J. J. Org. Chem. 2009, 74, 914.
151. See Marcus, R.A. J. Phys. Chem. 1968, 72, 891; Kresge, A.J. Chem. Soc. Rev. 1973, 2, 475.
152. Omitting the work terms.
153. Albery, W.J. Annu. Rev. Phys. Chem. 1980, 31, 227, p. 244.
154. See Jencks, W.P. Acc. Chem. Res. 1976, 9, 425; Stewart, R.; Srinivasan, R. Acc. Chem. Res. 1978, 11, 271; Guthrie, J.P. J. Am. Chem. Soc. 1980, 102, 5286.
155. See Agmon, N. J. Am. Chem. Soc. 1980, 102, 2164; Murray, C.J.; Jencks, W.P. J. Am. Chem. Soc. 1988, 110, 7561.
156. Pross, A.; Shaik, S.S. New J. Chem. 1989, 13, 427; Lewis, E.S. J. Phys. Org. Chem. 1990, 3, 1.
157. Lewis bases are useful catalysts in organic synthesis. See Denmark, S.E.; Beutner, G.L. Angew. Chem. Int. Ed. 2008, 47, 1560.
158. For a monograph on Lewis acid–base theory, see Jensen, W.B. The Lewis Acid–Base Concept, Wiley, NY, 1980. For a discussion of the definitions of Lewis acid and base, see Jensen, W.B. Chem. Rev. 1978, 78, 1.
159. Rauk, A.; Hunt, I.R.; Keay, B.A. J. Org. Chem. 1994, 59, 6808.
160. For a review of ate complexes, see Wittig, G. Q. Rev. Chem. Soc. 1966, 20, 191.
161. See Satchell, D.P.N.; Satchell, R.S. Q. Rev. Chem. Soc. 1971, 25, 171; Chem. Rev. 1969, 69, 251. See also, Sandström, M.; Persson, I.; Persson, P. Acta Chem. Scand. 1990, 44, 653; Laszlo, P.; Teston-Henry, M. Tetrahedron Lett. 1991, 32, 3837.
162. Springer, G.; Elam, C.; Edwards, A.; Bowe, C.; Boyles, D.; Bartmess, J.; Chandler, M.; West, K.; Williams, J.; Green, J.; Pagni, R.M.; Kabalka, G.W. J. Org. Chem. 1999, 64, 2202.
163. See Ayers, P.W.; Parr, R.G. J. Am. Chem. Soc. 2000, 122, 2010.
164. Pearson, R.G.; Songstad, J. J. Am. Chem. Soc. 1967, 89, 1827. For a monograph on the concept, see Ho, T. Hard and Soft Acids and Bases Principle in Organic Chemistry, Academic Press, NY, 1977; Pearson, R.G. J. Chem. Educ. 1987, 64, 561; Ho, T. Tetrahedron 1985, 41, 1; Pearson, R.G. in Chapman, N.B.; Shorter, J. Advances in Linear Free-Energy Relationships, Plenum Press, NY, 1972, pp. 281–319. For a collection of papers, see Pearson, R.G. Hard and Soft Acids and Bases, Dowden, Hutchinson, and Ross, Stroudsberg, PA, 1973.
165. Taken from Pearson, R.G. J. Chem. Ed. 1968, 45, 581, 643.
166. Pearson, R.G. Inorg. Chem. 1988, 27, 734; J. Org. Chem. 1989, 54, 1423. See also, Orsky, A.R.; Whitehead M.A. Can. J. Chem. 1987, 65, 1970.
167. See Sauers, R.R. Tetrahedron 1999, 55, 10013.
168. Parr, R.G.; Pearson, R.G. J. Am. Chem. Soc. 1983, 105, 7512. Note that there is not always a strict correlation between the values in Table 8.4 and the categories of Table 8.3.
169. Pearson, R.G. J. Am. Chem. Soc. 1988, 110, 7684.
170. For proofs of this principle, see Chattaraj, P.K.; Lee, H.; Parr, R.G. J. Am. Chem. Soc. 1991, 113, 1855.
171. Wolman, Y. in Patai, S. The Chemistry of the Thiol Group, pt. 2, Wiley, NY, 1974, p. 677; Maskill, H. The Physical Basis of Organic Chemistry, Oxford University Press, Oxford 1985, p. 159.
172. See also, Bochkov, A.F. J. Org. Chem. USSR 1986, 22, 1830, 1837.
173. Méndez, F.; Gázguez, J.L. J. Am. Chem. Soc. 1994, 116, 9298.
174. Woodward, S. Tetrahedron 2002, 58, 1017.
175. See Hine, J. Structural Effects on Equilibria in Organic Chemistry, Wiley, NY, 1975; Taft, R.W. Prog. Phys. Org. Chem. 1983, 14, 247; Petrov, E.S. Russ. Chem. Rev. 1983, 52, 1144 (NH acids); Bell, R.P. The Proton in Chemistry, 2nd ed., Cornell Univ. Press, Ithaca, NY, 1973, pp. 86–110. For a monograph on methods of estimating pK values by analogy, extrapolation, and so on, see Perrin, D.D.; Dempsey, B.; Serjeant, E.P. pKa Prediction for Organic Acids and Bases, Chapman and Hall, NY, 1981.
176. The varying degrees by which the different factors that affect gas-phase acidities of 25 acids has been calculated: Taft, R.W.; Koppel, I.A.; Topsom, R.D.; Anvia, F. J. Am. Chem. Soc. 1990, 112, 2047.
177. For a review of the enhancement of acidity by NO2, see Lewis, E.S. in Patai, S. The Chemistry of Functional Groups, Supplement F, pt. 2, Wiley, NY, 1982, pp. 715–729.
178. Filler, R.; Wang, C. Chem. Commun. 1968, 287.
179. See Edward, J.T. J. Chem. Educ. 1982, 59, 354; Schwartz, L.M. J. Chem. Educ. 1981, 58, 778.
180. Headley, A.D.; McMurry, M.E.; Starnes, S.D. J. Org. Chem. 1994, 59, 1863.
181. Wiberg, K.B. J. Org. Chem. 2003, 68, 875.
182. For calculated gas-phase acidities of substituted benzoic acids see Wiberg, K.B. J. Org. Chem. 2002, 67, 4787. Also see Gupta, K.; Giri, S.; Chattaraj, P.K. New J. Chem. 2008, 32, 1945.
183. DeMaria, P.; Fontana, A.; Spinelli, D.; Dell'Erba, C.; Novi, M.; Petrillo, G.; Sancassan, F. J. Chem. Soc. Perkin Trans. 2 1993, 649.
184. Chen, C.-T.; Siegel, J.S. J. Am. Chem. Soc. 1994, 116, 5959. See also, Sotomatsu, T.; Shigemura, M.; Murata, Y.; Fujita, T. Bull. Chem. Soc. Jpn. 1992, 65, 3157.
185. See Exner, O.;  ársky, P. J. Am. Chem. Soc. 2001, 123, 9564. See also, Liptak, M.D.; Shields, G.C. J. Am. Chem. Soc. 2001, 123, 7314.
ársky, P. J. Am. Chem. Soc. 2001, 123, 9564. See also, Liptak, M.D.; Shields, G.C. J. Am. Chem. Soc. 2001, 123, 7314.
186. It has been contended that resonance delocalization plays only a minor role in the increased strength of carboxylic acids compared to alcohols, and the “...higher acidity of acids arises principally because the electrostatic potential of the acidic hydrogens is more positive in the neutral acid molecule...”: Siggel, M.R.; Streitwieser, Jr., A.; Thomas, T.D. J. Am. Chem. Soc. 1988, 110, 8022; Thomas, T.D.; Carroll, T.X.; Siggel, M.R. J. Org. Chem. 1988, 53, 1812. For contrary views, see Exner, O. J. Org. Chem. 1988, 53, 1810; Perrin, D.D. J. Am. Chem. Soc. 1991, 113, 2865. See also, Godfrey, M. Tetrahedron Lett. 1990, 31, 5181.
187. Copper complexes of active methylene compounds show large pKa shifts. See Zhong, Z.; Postnikova, B.J.; Hanes, R.E.; Lynch, V.M.; Anslyn, E.V. Chemistry: European J. 2005, 11, 2385.
188. Goumont, R.; Magnier, E.; Kizilian, E.; Terrier, F. J. Org. Chem. 2003, 68, 6566.
189. See, however, Krygowski, T.M.; Maurin, J. J. Chem. Soc. Perkin Trans. 2 1989, 695.
190. Smith, J.W. in Patai, S. The Chemistry of the Amino Group; Wiley, NY, 1968, pp. 161–204.
191. Liptak, M.D.; Gross, K.C.; Seybold, P.G.; Feldus, S.; Shields, G.C. J. Am. Chem. Soc. 2002, 124, 6421.
192. Taft, R.W. Prog. Phys. Org. Chem. 1983, 14, 247, see Sec. 5.B.i.
193. Note that Lewis acidity decreases, whereas Br nsted acidity increases, going down the table. There is no contradiction here when we remember that in the Lewis picture the actual acid in all Br
nsted acidity increases, going down the table. There is no contradiction here when we remember that in the Lewis picture the actual acid in all Br nsted acids is the same, namely, the proton. In comparing, say, HI and HF, we are not comparing different Lewis acids but only how easily F– and I– give up the proton.
nsted acids is the same, namely, the proton. In comparing, say, HI and HF, we are not comparing different Lewis acids but only how easily F– and I– give up the proton.
194. The effect discussed here is an example of a symmetry factor. For an extended discussion, see Eberson, L. in Patai, S. The Chemistry of Carboxylic Acids and Esters, Wiley, NY, 1969, pp. 211–293.
195. Brown, H.C. J. Am. Chem. Soc. 1945, 67, 378, 1452, Boranes in Organic Chemistry, Cornell University Press, Ithaca, NY, 1972, pp. 53–64. See also, Brown, H.C.; Krishnamurthy, S.; Hubbard, J.L. J. Am. Chem. Soc. 1978, 100, 3343.
196. Hibbert, F.; Simpson, G.R. J. Chem. Soc. Perkin Trans. 2 1987, 243, 613.
197. For a review of the effect of strain on amine basicities, see Alder, R.W. Chem. Rev. 1989, 89, 1215.
198. Staab, H.A.; Saupe, T.; Krieger, C. Angew. Chem. Int. Ed. 1983, 22, 731.
199. Saupe, T.; Krieger, C.; Staab, H.A. Angew. Chem. Int. Ed. 1986, 25, 451.
200. For a review, see Staab, H.A.; Saupe, T. Angew. Chem. Int. Ed. 1988, 27, 865.
201. Howard, S.T. J. Am. Chem. Soc. 2000, 122, 8238.
202. Krieger, C.; Newsom, I.; Zirnstein, M.A.; Staab, H.A. Angew. Chem. Int. Ed. 1989, 28, 84. See also, Staab, H.A.; Zirnstein, M.A.; Krieger, C. Angew. Chem. Int. Ed. 1989, 28, 86.
203. Miyahara, Y.; Goto, K.; Inazu, T. Tetrahedron Lett. 2001, 42, 3097.
204. Ueno, M.; Ishitani, H.; Kobayashi, S. Org. Lett. 2002, 4, 3395.
205. Mathieu, B.; de Fays, L.; Ghosez, L. Tetrahedron Lett 2000, 41, 9651
206. Brown, H.C.; Kanner, B. J. Am. Chem. Soc. 1953, 75, 3865; 1966, 88, 986.
207. Meot-Ner, M.; Smith, S.C. J. Am. Chem. Soc. 1991, 113, 862, and references cited therein. See also, Benoit, R.L.; Fréchette, M.; Lefebvre, D. Can. J. Chem. 1988, 66, 1159.
208. Arnett, E.M.; Harrelson, Jr., J.A. J. Am. Chem. Soc. 1987, 109, 809.
209. For a discussion of why esters and amides are weaker acids than ketones, see Fersner, A.; Karty, J.M.; Mo, Y. J. Org. Chem. 2009, 74, 7245.
210. Wang, X.; Houk, K.N. J. Am. Chem. Soc. 1988, 110, 1870; Wiberg, K.B.; Laidig, K.E. J. Am. Chem. Soc. 1988, 110, 1872.
211. Majewski, M.; Wang, F. Tetrahedron 2002, 58, 4567.
212. Amedjkouh, M. Tetrahedron Asymm. 2004, 15, 577.
213. Gung, B.W.; Yanik, M.M. J. Org. Chem. 1996, 61, 947.
214. Grotjahn, D.B.; Sheridan, P.M.; Al Jihad, I.; Ziurys, L.M. J. Am. Chem. Soc. 2001, 123, 5489.
215. Fressigné, C.; Maddaluno, J.; Giessner-Prettre, C.; Silvi, B. J. Org. Chem. 2001, 66, 6476.
216. Williard, P.G.; Salvino, J.M. J. Org. Chem. 1993, 58, 1. For a study of the oligomer structure of LDA at low ligand concentrations, see Rutherford, J.L.; Collum, D.B. J. Am. Chem. Soc. 2001, 123, 199.
217. Ito, H.; Nakamura, T.; Taguchi, T.; Hanzawa, Y. Tetrahedron Lett. 1992, 33, 3769.
218. Aubrecht, K.B.; Collum, D.B. J. Org. Chem. 1996, 61, 8674.
219. Romesberg, F.E.; Collum, D.B. J. Am.Chem. Soc. 1994, 116, 9198, 9187. For a study of other mixed aggregates, see Thomas, R.D.; Huang, J. J. Am. Chem. Soc. 1999, 121, 11239.
220. Sakuma, K.; Gilchrist, J.H.; Romesberg, F.E.; Cajthami, C.E.; Collum, D.B. Tetrahedron Lett. 1993, 34, 5213.
221. Lucht, B.L.; Collum, D.B. J. Am. Chem. Soc. 1994, 116, 7949.
222. Lucht, B.L.; Collum, D.B. J. Am. Chem. Soc. 1995, 117, 9863. See also, Lucht, B.L.; Collum, D.B. J. Am. Chem. Soc. 1996, 118, 2217, 3529. See Romesberg, F.E.; Bernstein, M.P.; Gilchrist, J.H.; Harrison, A.T.; Fuller, D.J.; Collum, D.B. J. Am. Chem. Soc. 1993, 115, 3475 for the structure in HMPA.
223. Lucht, B.L.; Collum, D.B. J. Am. Chem. Soc. 1994, 116, 6009.
224. Collum, D.B. Acc. Chem. Res. 1993, 26, 227. For NMR studies of LiNEt2 and ring laddering see Rutherford, J.L.; Collum, D.B. J. Am. Chem. Soc. 1999, 121, 10198.
225. Hilmersson, G.; Davidsson, Ö. J. Org. Chem. 1995, 60, 7660. See O'Brien, P. J. Chem. Soc. Perkin Trans. 1 1998, 1439; Sott, R.; Grandander, J.; Dinér, P.; Hilmersson, G. Tetrahedron Asymm. 2004, 15, 267.
226. Arvidsson, P.I.; Hilmersson, G.; Ahlberg, P. J. Am. Chem. Soc. 1999, 121, 183.
227. Carlier, P.R.; Madura, J.D. J. Org. Chem. 2002, 67, 3832.
228. Williard, P. G.; Jacobson, M. A. Org. Lett. 2000, 2, 2753. For the structure and bonding of dilithiodiamines see Pratt, L.M.; Mu, R. J. Org. Chem. 2004, 69, 7519.
229. Sun, C.; Williard, P.G. J. Am. Chem. Soc. 2000, 122, 7829. See also, Pratt, L.M.; Streitwieser, A. J. Org. Chem. 2003, 68, 2830.
230. Jackman, L.M.; Çizmeciyan, D.; Williard, P.G.; Nichols, M.A. J. Am. Chem. Soc. 1993, 115, 6262.
231. Jackman, L.M.; Chen, X. J. Am. Chem. Soc. 1992, 114, 403.
232. Streitwieser, A.; Juaristi, E.; Kim, Y.-J.; Pugh, J.K. Org. Lett. 2000, 2, 3839.
233. Alconcel, L.S.; Deyerl, H.-J.; Continetti, R.E. J. Am. Chem. Soc. 2001, 123, 12675.
234. See Epshtein, L.M.; Iogansen, A.V. Russ. Chem. Rev. 1990, 59, 134; Dyumaev, K.M.; Korolev, B.A. Russ. Chem. Rev. 1980, 49, 1021; Taft, R.W.; Bordwell, F.G. Acc. Chem. Res. 1988, 21, 463; Heemstra, J.M.; Moore, J.S. Tetrahedron 2004, 60, 7287.
235. See Smith, J.W. in Patai, S. The Chemistry of the Amino Group, Wiley, NY, 1968, pp. 161–204.
236. Aue, D.H.; Webb, H.M.; Bowers, M.T. J. Am. Chem. Soc. 1972, 94, 4726; 1976, 98, 311, 318; Mucci, A.; Domain, R.; Benoit, R.L. Can. J. Chem. 1980, 58, 953. See also, Drago, R.S.; Cundari, T.R.; Ferris, D.C. J. Org. Chem. 1989, 54, 1042.
237. For discussions of the solvation of ammonia and amines, see Jones, III, F.M.; Arnett, E.M. Prog. Phys. Org. Chem. 1974, 11, 263; Grunwald, E.; Ralph, E.K. Acc. Chem. Res. 1971, 4, 107.
238. Condon, F.E. J. Am. Chem. Soc. 1965, 87, 4481, 4485.
239. For two reasons: (1) the alkyl groups are poorly solvated by the water molecules, and (2) the strength of the hydrogen bonds of the BH+ ions decreases as the basicity of B increases: Lau, Y.K.; Kebarle, P. Can. J. Chem. 1981, 59, 151.
240. See Liebman, J.F. Mol. Struct. Energ. 1987, 4, 49; Dixon, D.A.; Lias, S.G. Mol. Struct. Energ. 1987, 2, 269; Bohme, D.K. in Patai, S. The Chemistry of Functional Groups, Supplement F, pt. 2, Wiley, NY, 1982, pp. 731–762; Arnett, E.M. Acc. Chem. Res. 1973, 6, 404. See Lias, S.G.; Liebman, J.F.; Levin, R.D. J. Phys. Chem. Ref. Data, 1984, 13, 695. See also, the tables of gas-phase acidities and basicities in the following articles, and their cited references: Meot-Ner, M.; Kafafi, S.A. J. Am. Chem. Soc. 1988, 110, 6297; Headley, A.D. J. Am. Chem. Soc. 1987, 109, 2347; Fujio, M.; McIver, Jr., R.T.; Taft, R.W. J. Am. Chem. Soc. 1981, 103, 4017; Lau, Y.K.; Nishizawa, K.; Tse, A.; Brown, R.S.; Kebarle, P. J. Am. Chem. Soc. 1981, 103, 6291.
241. Briggs, J.P.; Yamdagni, R.; Kebarle, P. J. Am. Chem. Soc. 1972, 94, 5128; Aue, D.H.; Webb H.M.; Bowers, M.T. J. Am. Chem. Soc. 1972, 94, 4726; 1976, 98, 311, 318.
242. Ikuta, S.; Kebarle, P. Can. J. Chem. 1983, 61, 97.
243. Taft, R.W.; Taagepera, M.; Summerhays, K.D.; Mitsky, J. J. Am. Chem. Soc. 1973, 95, 3811.
244. Yamdagni, R.; Kebarle, P. J. Am. Chem. Soc. 1973, 95, 3504.
245. See Catalan, J.; Abboud, J.L.M.; Elguero, J. Adv. Heterocycl. Chem. 1987, 41, 187.
246. Bartnicka, H.; Bojanowska, I.; Kalinowski, M.K. Aust. J. Chem. 1993, 46, 31.
247. Kobayashi, S. Synlett, 1994, 689.
248. Arnett, E.M.; Small, L.E.; McIver, Jr., R.T.; Miller, J.S. J. Am. Chem. Soc. 1974, 96, 5638; Blair, L.K.; Isolani, P.C.; Riveros, J.M. J. Am. Chem. Soc. 1973, 95, 1057; McIver, Jr., R.T.; Scott, J.A.; Riveros, J.M. J. Am. Chem. Soc. 1973, 95, 2706. Also see Bartmess, J.E.; McIver, Jr., R.T. J. Am. Chem. Soc. 1977, 99, 4163.
249. See Caldwell, G.; Renneboog, R.; Kebarle, P. Can. J. Chem. 1989, 67, 611.
250. Brauman, J.I.; Blair, L.K. J. Am. Chem. Soc. 1971, 93, 4315; Laurie, V.W.; Muenter, J.S. J. Am. Chem. Soc. 1966, 88, 2883.
251. Brauman, J.I.; Riveros, J.M.; Blair, L.K. J. Am. Chem. Soc. 1971, 93, 3914; Huheey, J.E. J. Org. Chem. 1971, 36, 204; Radom, L. Aust. J. Chem. 1975, 28, 1; Aitken, E.J.; Bahl, M.K.; Bomben, K.D.; Gimzewski, J.K.; Nolan, G.S.; Thomas, T.D. J. Am. Chem. Soc. 1980, 102, 4873.
252. Taft, R.W.; Taagepera, M.; Abboud, J.M.; Wolf, J.F.; DeFrees, D.J.; Hehre, W.J.; Bartmess, J.E.; McIver, Jr., R.T. J. Am. Chem. Soc. 1978, 100, 7765. For a scale of polarizability parameters, see Hehre, W.J.; Pau, C.; Headley, A.D.; Taft, R.W.; Topsom, R.D. J. Am. Chem. Soc. 1986, 108, 1711.
253. Bartmess, J.E.; Scott, J.A.; McIver, Jr., R.T. J. Am. Chem. Soc. 1979, 101, 6056.
254. Bohme, D.K.; Rakshit, A.B.; Mackay, G.I. J. Am. Chem. Soc. 1982, 104, 1100.
255. Bolton, P.D.; Hepler, L.G. Q. Rev. Chem. Soc. 1971, 25, 521; Gerrard, W.; Macklen, E.D. Chem. Rev. 1959, 59, 1105. See also, Wilson, B.; Georgiadis, R.; Bartmess, J.E. J. Am. Chem. Soc. 1991, 113, 1762.
256. Bolton, P.D.; Hepler, L.G. Q. Rev. Chem. Soc. 1971, 25, 521; p. 529.
257. For a review, see Parker, A.J. Q. Rev. Chem. Soc. 1962, 16, 163.
258. Sears, P.G.; Wolford, R.K.; Dawson, L.R. J. Electrochem. Soc. 1956, 103, 633.
259. Miller, J.; Parker, A.J. J. Am. Chem. Soc. 1961, 83, 117.