1 SZIMMETRIA
2 MOZGÁS
3 ELEMEK
4 SZÍNEK
A képek forrásai
Köszönetnyilvánítás
A LEGEGYSZERŰBB KÉRDÉSEKRE A LEGMÉLYEBB VÁLASZOKAT KERESSÜK
„Micsoda szépség! Láttam felhőket és a távoli, kedves Földre vetett árnyékukat ... A vizek sötétebb, enyhén csillogó foltoknak látszottak ... Amikor a horizont felé pillantottam, láttam a hirtelen, éles átmenetet a Föld fénybe boruló, színes felszíne és a koromfekete égbolt között. Gyönyörködtetett a Föld színeinek változatossága és gazdagsága. A Földet halvány, kék fénykoszorú övezte, amelyik fokozatosan elsötétedett, színe türkizről sötétkékre, lilára, végül koromfeketére változott.
Jurij Gagarin
Ez a könyv a tudományról szól. De mi a tudomány? Jó kérdés, amelyre talán annyiféle válasz adható, ahány tudós él a Földön. Én azt mondanám, a tudomány kísérlet arra, hogy megértsük a természeti világot. A magyarázatok, amelyeket felfedezünk, néha elvontnak tűnnek, és távol esnek attól, amit a józan ész súg, de ez csak a csalóka látszat. A tudomány arról szól, hogy megmagyarázzuk az emberi tapasztalatok apró részleteit is, amelyekkel nap mint nap találkozunk. Miért kék az ég? Miért gömbölyűek a csillagok és a bolygók? Miért forog szakadatlanul a világ? Miért zöldek a növények? Ezeket a kérdéseket egy gyermek is felteheti, de természetesen maguk a kérdések nem gyermetegek, hiszen a válaszok olyan láncolatát indítják meg, amelyek végső soron elvezetnek mai tudásunk határáig.
Ha elég mélyre ásunk, a legtöbb kérdés a bizonytalanságig vezet. A fény és az anyag kölcsönhatásának módja miatt kék az ég, a fény és az anyag kölcsönhatását viszont azok a szimmetriák szabják meg, amelyek kényszerfeltételeket állítanak a természet törvényeiben. Ezekkel a fogalmakkal később még találkozunk a könyvben. Ha azonban valaki még mélyebbre ás, és megkérdezi, mi az oka egy bizonyos szimmetriának, vagy egyáltalán, miért léteznek törvények a természetben, akkor eljutunk azokra a káprázatos, ingoványos területekre, ahol a tudósok élnek és dolgoznak; az ismert és az ismeretlen határmezsgyéjére. Ez a tudományos kutatók világa, de egyben a kíváncsiság és a csodák birodalma.
Az igazán nagy kérdések a félhomályban bújnak meg. Hogyan kezdődött a földi élet? Van-e élet más bolygókon? Mi történt az ősrobbanást követő első pillanatokban? Úgy érezzük, ezek a kérdések mélyek, bonyolultak és megközelíthetetlenek, de az eszközök és a módszerek, amelyekkel ezekre keressük a választ, semmiben sem különböznek azoktól, amelyekkel azt akarjuk kideríteni, miért kék az ég. Ez fontos észrevétel. Ha egy kérdés mélyen szántó, az nem azt jelenti, hogy a választ akkor kaphatjuk meg, ha egy évre elvonulunk a vadonba, ölbe tett kézzel ülünk,
„AZ ELSŐ NAPOKBAN MINDANNYIAN MEGKERESTÜK A HAZÁNKAT. A HARMADIK VAGY NEGYEDIK NAPON CSAK A KONTINENSÜNKRE MUTATTUNK RÁ. AZ ÖTÖDIK NAPON MÁR TUDTUK, HOGY CSAK EGYETLEN FÖLDÜNK VAN.” Sultan Bin Salman Bin Abdulaziz Al-Saud,az űrrepülőgép STS-51G küldetésének űrhajósa
és várjuk, hogy valami történjék. Éppen ellenkezőleg, a válasz gyakran pontosan azokra az alapokra épül, amelyeket az egyszerűbb problémák módszeres és körültekintő felderítésével lefektettünk. Ez könyvünk legfontosabb gondolata. Miközben meg akarjuk érteni hétköznapi világunkat - otthonunk színeit, struktúráit, viselkedését és történetét -, megszerezzük azt a tudást, és kidolgozzuk azokat a módszereket, amelyekkel túlléphetünk a hétköznapi problémákon, és betekinthetünk az azokon túli univerzumba.
„ELÉG KÜLÖNÖS, DE AMIKOR RÁNÉZTEM A FÖLDRE, MINDENT ELSÖPRŐ ÉRZÉS KERÍTETT HATALMÁBA: TE JÓ ISTEN, MILYEN TÖRÉKENY OTT MESSZE AZ AZ APRÓCSKA VALAMI.” Mike Collins, Gemini—10, Apollo—11
A Világegyetemben a legegyszerűbben tanulmányozható hely a Föld bolygó, hiszen ezen élünk, mindamellett még ez a feladat is zavarbaejtően bonyolult. Egyrészt ez az egyetlen bolygó, amelyikről tudjuk, hogy életnek ad otthont. Több mint hétmilliárd ember mellett legalább tízmillió állat- és növényfaj otthona. Felszínének 29 százaléka szárazföld, amelynek 148 326 000 négyzetkilométeres területét az emberek 196 országra osztották fel, bár az utóbbi számot vitatják. Az emberiség 10 000 éves történetét tükrözi, hogy ezen határok közt több mint 4000 vallás alakult ki. Vannak, akik növelni szeretnék az országok számát, mások csökkentenék a vallások sokféleségét. Egy ilyen kis világ esetében, amelyik egy átlagos galaxisban egy közönséges csillag körül kering, ez nem éppen a jól szervezettség jele. Ezt nehéz megérteni, de látásunkat elhomályosítja a szűklátókörűség köde. Csupán alig több mint ötszáz ember jutott elég magasra ahhoz, hogy a világűrből nézhessen le bolygóotthonunkra - erre a kicsiny világra a csillagos égi háttér előtt -, és amikor ezt megteszik, érdekes dolog történik. Felszáll a köd, és attól kezdve nem feldaraboltnak és bonyolultnak, hanem egységesnek és egyszerűnek látják bolygónkat.
„Amikor végre ott vagy a Hold közelében, és visszanézel a Földre, akkor szinte teljesen eltűnnek az országok közötti különbségek és viszályok, és kezd eljutni a tudatodig, hogy talán tényleg ez az egyetlen világunk és hogy a pokolba nem. vagyunk képesek értelmes emberekhez méltó módon együtt élni?” Frank Borman, Gemini—7, Apollo-8
„Ha valaki a repülés előtt megkérdezte volna tőlem: »Szerétnél eljutni oda, és a Holdról felnézni a Földre?«, akkor azt feleltem volna neki: »Nem, semmiképpen.« Amikor azonban a Holdon állva először néztem vissza a Földre, elsírtam magamat.” Alan Shepard, Mercury-3, Apollo-14
Az űrhajósok nem véletlenül tették ezeket a megjegyzéseket. Ezek olyan emberek megjegyzései, akiket a tapasztalat rákényszerített, hogy egyszerűen és más nézőpontból lássák a világot. Magától értetődően egyetlen faj vagyunk, egyetlen bolygót népesítünk be, következésképpen csak kevés esélyünk van, hogy ne tegyük tönkre. Nem lehetünk mindannyian űrhajósok, de tudósok mindannyian lehetünk, és azt hiszem, a tudomány hasonló látásmódot kölcsönöz, mint a távolság. Felemel, bár nem fizikailag, hanem szellemileg, így lehetőségünk van magasból vizslatni az alattunk elterülő tájat. Szabályszerűségeket keresünk, és ha megpillantunk egyet, akkor megpróbáljuk megérteni az eredetét. Scott Carpenter, az Egyesült Államok Haditengerészetének tisztje, a koreai háború veteránja, miután visszatért a világűrből, úgy érezte, hogy nemcsak hazájához kell hűségesnek lennie, hanem az emberiség nagy családjához, bolygónk egészéhez. Az űrrepülés megváltoztatja az emberek szemléletét, akárcsak a tudomány. Minél jobban értjük a természetet, annál gyönyörűbbnek tűnik, és annál jobban felfogjuk, micsoda kiváltság az, ha rövid életünket a felderítésével tölthetjük. Legyünk olyanok, mint a gyerekek! Figyeljünk az apró, jelentéktelen részletekre! Ne hagyjuk, hogy az előítéleteink vezessenek! Senkinek a szavát se fogadjuk el tényként! Figyeljünk és gondolkozzunk! Tegyünk fel egyszerű kérdéseket, és keressünk rájuk egyszerű válaszokat! Erre vállalkozunk ebben a könyvben, és szívből remélem, mire a végére érnek, egyetértenek Scott Carpenterrel.
EZ A BOLYGÓ NEM EGY KEMÉNY VILÁG. ÉRZÉKENY VIRÁG, AMIRŐL GONDOSKODNI KELL. MAGÁNYOS. KICSI. ELSZIGETELT, ÉS NINCS UTÁNPÓTLÁSA. Ml VISZONT CUDARUL BÁNUNK VELE. NYILVÁNVALÓ, HOGY NEM A SAJÁT ORSZÁGUNK, VALLÁSUNK, VÁROSUNK VAGY ÉPPEN SAJÁT MAGUNK IRÁNT KELL A LEGHŰSÉGESEBBEKNEK LENNÜNK, HANEM MÁSODSORBAN AZ EMBERISÉG NAGY CSALÁDJA, ELSŐSORBAN PEDIG BOLYGÓNK EGÉSZE IRÁNT. EZ AZ OTTHONUNK, ÉS EZ MINDEN, AMINK VAN.” Scott Carpenter, Mercury—7
1
SZIMMETRIA
Kedvelem Wilson „Hópehely” Bentley fényképét (lásd a színes melléklet 2. oldalán); félrebillentett fejjel, elégedetten áll, a hidegtől csak a kíváncsiság védi, miközben elmerül a természet finom részleteiben, amelyeket óvatosan, megfeledkezve a kalapjára hulló hóról, a két kezében tart. Kesztyű nélkül. A vermonti Jerichóból származó farmerfiú tizenöt éves korában a havas napokat novembertől áprilisig azzal töltötte, hogy viharvert mikroszkópjával megnézte és lerajzolta a hópelyheket, még mielőtt megolvadtak volna. Csalódással vette tudomásul a jelenség múlékonyságát, a pelyhek túl rövid ideig maradtak meg ahhoz, hogy minden részletüket megörökíthesse. Később fényképezőgéppel kezdett kísérletezni, és 1885. január 15-én a világon először neki sikerült lefényképeznie egy hópihét. Az ezt követő 45 év alatt több mint 5000 felvételt gyűjtött össze. Egész életét annak szentelte, hogy gondosan megfigyelje az esőcseppeket, a hópelyheket és a farmját borító köd cseppjeit.
Ezek a finom részletességű pillanatfelvételek olyan világot mutattak, amelyik bárki számára elérhető, mégis csak ritkán fordul elő, hogy felkelti az átlagemberek érdeklődését. Miért van ez így? A hópelyhek varázslatosak, még ma is, amikor a fényképezés bárki számára magától értetődő. Alig hiszem, hogy ha valaki egy pillantást vet ezekre az alakzatokra, amelyek végtelen változatosságúak és — Darwint idézve —, mindennél gyönyörűbbek, akkor a látvány ne keltené fel a kíváncsiságát. Hogyan alakulnak ki? A természet mely mechanizmusa imitálhatja azt az őrült és türelmetlen szobrászt, aki ontja az egymáshoz hasonló alkotásokat, ám mégsem képes pontosan ugyanazt a mintát kétszer kifaragni?
Ezeket a kérdéseket a természetben előforduló bármely struktúrára vonatkozóan feltehetjük. Az élőlényeket illető kérdésre híressé vált választ adott Darwin A fajok eredete című munkájában. 1898 májusában Bentley cikket jelentetett meg az Appletons Popular Science című folyóiratban, szerzőtársa George Henry Perkins, a Vermonti Egyetem természetrajz-professzora volt. Bentley kifejtette, hogy az általa gyűjtött minták tanúsága szerint nem létezik két egyforma hópihe. „Minden egyes kristály a tervezés mesterműve volt, és egyetlen forma sem ismétlődött soha”, írta. Egyediségük miatt lenyűgözőek és romantikusak, mégis kétségtelenül valamiben hasonlítanak egymásra; közös bennük a „hatosság”. Mi az, ami még ennél is érdekesebb lehet? Ez talán a megfigyelő személyiségén is múlik.
Johannes Kepler nevét általában bolygómozgási törvényei okán ismerjük. Kepler pontosan úgy mélyedt el a dán csillagász, Tycho Brahe nagy pontosságú csillagászati megfigyeléseiben, mint „Hópehely” Bentley a fényképeiben — és Kepler az adatokban valamilyen mintázatot vett észre. Ezek alapján ismerte fel, hogy a bolygók ellipszis alakú pályákon keringenek a Nap körül, az azokat a Nappal összekötő egyenes pedig egyenlő idők alatt egyenlő területeket súrol, továbbá rájött, milyen összefüggés áll fenn a keringési időik és az átlagos naptávolságuk között. Kepler tapasztalati törvényei jelentették azt az alapot, amelyre Newton felépíthette a gravitáció 1687-ben publikált egyetemes törvényét. Vélhetően (bár a magam részéről inkább azt mondanám, vitathatatlanul, de hadd legyenek boldogok a vitázni kívánó történészek) ez volt az első, modern értelemben vett tudományos munka.
Nem sokkal később, mint ahogy Astronomia nova című munkájában közreadta három törvényét, 1610 decemberében, a karácsonyi sötétben Kepler a prágai Károly-hídon sétált, ahol egy hópihe hullott a kabátjára. Az elegáns, fehér, szinte semmiség nyilvánvaló struktúrája felkeltette az érdeklődését, olyannyira, hogy kis könyvecskét írt Strena seu de nive sexangula (A hatszögletű hópehely) címmel. Ez a rövidke tudományos írás időtlenül tanulságos és szórakoztató bepillantást nyújt abba, milyen az, amikor egy zseniális elme játékos kedvében van. A könyv címoldalán a következő ajánlás olvasható: „Matthaus Wacker von Wackenfels úrnak, ő császári fensége tiszteletre méltó udvari tanácsosának, a kitüntetett lovagnak, az írók és filozófusok patrónusának és csekélységem jótevő urának”. Mai nyelvünkből hiányzik ez a dagályosság — bárcsak én is hasonlóan pompás szóvirágokkal kezdhetném ezt a könyvet!
Ha A hatszögletű hópehely modern kutatási javaslat lenne, akkor már az első megmérettetésen elvérezne, hiszen így kezdődik: „Pontosan tudom, mennyire kedvelik Önök a Semmit, nem is elsősorban alacsony ára miatt, hanem a játékos kedvű Passereau elragadó és kifinomult elmejátéka jóvoltából. (Általában elfogadottnak tekintik, hogy Kepler itt a „Passereau” szót szójátékként használja, amellyel a játékos veréb fogalmát kapcsolja össze Jean Passerat francia költő nevével, aki egy újévi verset írt a semmiről. Homályos, de vicces!) Nyugodtan kijelenthetem tehát, hogy egy ajándék annál kedvesebb és örvendetesebb az Önök számára, minél közelebb van a semmihez.” A várható gazdasági előnyöket tehát úgy ecseteli, hogy minél közelebb van a kutatás eredménye a semmihez, annál értékesebb. Jegyezzék ezt fel maguknak...! Keplernek nem sikerült megmagyaráznia a hópelyhek struktúráját - hogyan is sikerülhetett volna? A teljes körű magyarázathoz ismerni kell az atomelméletet és a modern fizika néhány más területét; ezekre majd később térek rá. Sikerült viszont hozzáférhetővé tennie a tudomány örömét; közkinccsé tenni a gondolatot, mely szerint a természet játékos szellemű tanulmányozása óriási érték, függetlenül az eredménytől. Könyvében izgatott kíváncsisággal és elképesztő spekulációkkal tárja az olvasó elé a hópihéket és azok hasonlóságát a természeti világ más szabályos testjeihez: az ötszirmú virágokhoz, a gránátalma magjaihoz és a méhsejtekhez. Oly sok területet érint vibrálva, témáról témára csapongva, hogy végül csodálatos éleselméjűséggel kénytelen visszafogni magát: „Őrületesen elragadtattam magamat, és miközben megpróbáltam a szinte Semmit ajándékként átnyújtani az olvasónak, szinte Semmivé foszlott az egész. Mert ebből a csaknem Semmiből kis híján újjáteremtettem az egész univerzumot, amely mindent magában foglal!” Kepler azonban világos kérdést fogalmazott meg, ami bizonyára mindenkiben felötlik, aki csak megnézi „Hópehely” Bentley rendkívüli fényképeit: hogyan alakulnak ki a látszólag forma nélküli eredetből az olyan szabályos és rendezett struktúrák, mint a hópelyheké? „Minthogy mindannyiszor megtörténik, amikor csak havazni kezd, hogy a hó első pelyhei apró, hatágú csillagokhoz hasonló formákat öltenek, ezért valamilyen meghatározott oknak kell működnie; ha ugyanis ez véletlenszerűen történne, akkor miért mindig hatszögletűek, miért nem alakulnak ki néha öt- vagy hétszögűek, legalábbis amíg különállóak és egymástól távoliak a pelyhek, és még nem olvadnak össze egyetlen zavaros tömeggé?” Kepler tudta, hogy a hópelyhek a megfigyelhető struktúra nélküli vízpárából képződnek. Akkor hát honnan tesz szert a hópihe a szerkezetre? Mit árul el a „hatosságuk” a pihéket felépítő elemekről és az azokat összetartó erőkről? Ez a világ modern szemléletű megközelítése, amint azt minden fizikus felismeri. Évszázadok elteltével is érződik írásából zseniális meglátása és öröme éppúgy, mint csalódottsága, amiért tudása nem elég ahhoz, hogy választ adjon. „Bekopogtattam a kémia ajtaján - írja -, és megtapasztaltam, mennyi mindent kell még elmondani erről a tudományról, mire megtudjuk az okot. Inkább arra lennék kíváncsi, mit szólnak Önök, nagyokosok, ha én most minden további magyarázkodás nélkül kihátrálok a témából. Semmi sem következik tehát. Itt a vége.”
A tudomány örömöt okozó frusztráció. Azokról a kérdésekről szól, amelyekre nincs válasz - talán csak most, de lehet, hogy soha. Arról szól, hogy észrevesszük a szabályszerűségeket, kijelentjük, hogy ezeknek valamilyen természetes magyarázata kell, hogy legyen, és megpróbáljuk megkeresni ezeket a magyarázatokat. Ebben a fejezetben, amelyet Kepler és „Hópehely” Bentley munkája ihletett, megpróbálom megmagyarázni a természet összetett formáit; a méhkaptáraktól a jéghegyekig és a bolygóktól a palack nélkül búvárkodó nagymamákig (komolyan!). Eközben elgondolkozunk azon, miként bukkanhat elő ilyen sokféleség és komplexitás a természet törvényeiből, amelyek egyszerűek, és kevés van belőlük. A fejezet végén még a hópihék szerkezetét is elmagyarázom.
A méheknek trükkös feladatot kell megoldaniuk. Hogyan kell a hosszú, téli hónapokban tárolni a rajnak táplálékot adó mézet? Tudjuk, hogy a méhek erre a célra méhsejteket építenek. Keplert éppen azért érdekelte a méhsejtek struktúrája, mert azokat, mint írja, valamilyen „indítóok” folytán építik. Mivel ő a hópelyheket megformázó „indítóokot” kereste, elhatározta, kideríti, miért építenek a méhek hatszögletű sejteket. Darwin eredményeit ismerve ma már kijelenthetjük, hogy a választ a természetes kiválasztódás adja, ami egyszerű és hatásos elgondolás. Ha valamely örökölt tulajdonság vagy magatartás előnyt jelent abban, amit Darwin a „létért való küzdelemnek” nevezett, akkor ez a tulajdonság a későbbi generációkban uralkodóvá válik, egyszerűen azért, mert nagyobb valószínűséggel adódik tovább az utódoknak. A szervezet fizikai jellemzőinek, viselkedésének és felépítésének összességét fenotípusnak nevezzük, erre vonatkozóan működik a természetes kiválasztódás. Ha a természetes kiválasztódás idézi elő a méhsejt megfigyelt struktúráját, akkor meg kell értenünk, miért előnyös a méhek számára a hatszögletű forma létrehozása.
Charles Darwint bámulatba ejtették a méhek, ezért pontosan követte az útjukat. „Csak eltompult érzékű ember lehet, aki lelkes csodálat nélkül tudja vizsgálni a méhlép finom szerkezetét, amely olyan csodálatosan megfelel rendeltetésének”, írta A fajok eredetében. Élvezem a Viktória-korabeli írások közvetlen stílusát; akinek nem kíváncsiskodik az elméje, az eltompult érzékű ember. Ugyanebben az alapvető művében Darwin leírja azt a kísérletsorozatát, amelyet azért hajtott végre, hogy megismerje a házi méhek sejtépítő ösztönét.
„... eleinte teljesen érthetetlennek látszik, hogy miként dolgozzák ki a szükséges szögeket és lapokat; illetve mi módon állapítják meg, hogy helyesen készítették-e el azokat. De ez a nehézség korántsem oly nagy, mint az első pillantásra tűnik; azt hiszem, kimutatható, hogy ez a szép munka néhány egyszerű ösztönnek az eredménye.”
Ezen egyszerű ösztönök azonosításához a házi méh sejtépítő magatartását Darwin egy testfelépítésében egyszerűbb méhfaj, a Mexikóban honos Melipona domestica viselkedésével hasonlította össze. A Melipona méhek szabályos lépje henger alakú sejtekből áll, amit Darwin egyszerűbb geometriai formának tekintett, nevezetesen a bármilyen struktúrát nélkülöző állapot és a házi méhek hatszög alakú sejtjei közötti átmeneti formának. „Mindebből levonhatjuk azt a következtetést, hogy ha a Melipona már meglevő, önmagukban véve nem is olyan csodálatos ösztöneit kissé módosíthatnánk, akkor ez a méh épp oly rendkívül tökéletes szerkezetű sejteket építene, mint a mézelő méh.”
Hipotézisének ellenőrzése érdekében Darwin barátjával és természetbúvár társával, William Bernhardt Tegetmeierrel közösen kísérletsorozatot hajtott végre. A méhviaszhoz különböző színű festékeket adtak, hogy a látvány alapján követni tudják az építés folyamatát. Megfigyeléseik alapján arra a következtetésre jutottak, hogy a méhek először henger alakú sejteket építenek, amelyeket később alakítanak át hatszögekké. Darwin mindezt a természetes kiválasztódás fogalmaival tudta leírni:
„Ezek alapján úgy gondolom, hogy az ismert ösztönök közül a legcsodálatosabbat, a mézelő méh ösztönét azzal magyarázhatjuk meg, hogy a természetes kiválasztás felhasználta egyszerűbb ösztönöknek számos, egymást követő, apró módosulását; lassú fokozatokon keresztül arra vezette a méheket, hogy kettős rétegben egyforma gömböket írjanak le egymástól adott távolságban, és a viaszt a metsző síkok mentén rakják fel és vájják ki; a méhek természetesen éppoly keveset tudnak arról hogy gömbjeiket egymástól bizonyos határozott távolságra építik, mint a hatoldalú hasábok és a rombusz-alaplapok különböző szögeiről; a természetes kiválasztás folyamatának indító oka ugyanis az volt, hogy a sejtek a lárvák számára megfelelő erősek, megfelelő nagyok és megfelelő alakúak legyenek, és hogy ezt a célt a lehető legnagyobb munka- és viaszmegtakarítással lehessen elérni.
Az a raj boldogult legjobban, amely ilyen módon a legjobb sejteket építette a legkevesebb munkával és a legkevesebb mézet pazarolta el a viasz kiválasztására, és újonnan szerzett ökonómiai ismereteit átörökítette új rajokra, amelyeknek a létért való küzdelemben szintén a legtöbb reményük volt a boldogulásra.” (A Darwintól származó idézetek dr. Mikes Lajos fordításai.)
Darwin arra a következtetésre jutott, hogy ezek a méhek azért építenek hatszög alakú méhsejteket, mert ez az elrendezés adja a méz tárolására rendelkezésükre álló terület leggazdaságosabb kihasználását. A hatszög kialakításához kevesebb viasz kell, márpedig a kevesebb viaszt felhasználó méhek hatékonyabban dolgoznak, ezért valószínűbb a túlélésük, így nagyobb valószínűséggel adják át öröklött viselkedésüket a következő generációnak. Ennek van értelme, mert a méhviaszból álló sejtek építéséhez rendkívül sok mézre van szükség: egyetlen gramm viasz előállításához a méhnek nyolc gramm mézet kell felhasználnia. Ez nyilván hatékonyabb építkezésre ösztönöz, mert minél kevesebb mézet használnak fel viasz készítésére, annál több marad táplálékként. Ez olyan előnyt jelent, ami generációkon átívelően alakítja a mézelő méhek viselkedését.
De vajon helyes-e ez az elképzelés? Kétségtelenül kézenfekvő. Ha a méhek henger alakú sejtekből építenék fel a lépet, akkor a sejtek között hézagok maradnának, vagyis a struktúra egésze kevésbé lenne hatékony. Hasonlóképpen, ötszögek vagy nyolcszögek esetén is rések maradnának, tehát ezek a formák sem kínálnának optimális megoldást. Elképzelhető lenne persze az is, hogy minden egyes méh pontosan olyan alakúra készíti a következő sejtet, hogy az hézagmentesen illeszkedjék a szomszédos sejtekhez. Ebben a „méretre szabott” elrendezésben minden sejt más alakú lenne, de a lépen belüli rések nagyságát a minimumra lehetne szorítani. Ennek a stratégiának viszont az a hátulütője, hogy az egyik méhnek be kell fejeznie a sejt építését, és a másik csak ezután foghat hozzá a szomszédos sejt megépítéséhez. Ez viszont a rendelkezésre álló idő nagyon rossz kihasználását jelentené. Ezért úgy tűnik, az egyetlen olyan, ismétlődő formát kell előnyben részesíteni, amelyik nem hagy réseket. Mindössze három olyan síkidom létezik, amelyekkel a sík hézagmentesen lefedhető: a négyzet, a háromszög és a hatszög. (Ha egynél több fajta síkidomot használunk, akkor a sík sokféleképpen lefedhető. Ezek közül különösen érdekes a Penrose-féle csempézés, ahol a síkot soha nem ismétlődő mintát adó, „aperiodikus” csempék sorozatával fedjük le.)
Miért a hatszöget használják ezek közül a méhek? Valamikor Kr. e. 36 körül adta Marcus Terentius Varro római tudós a méhsejtek alakjára vonatkozó sejtés legrégebbi ismert leírását. Írásában azt állítja, hogy a síkot szabályos hatszögekből álló ráccsal, azaz méhsejtszerkezettel lehet a leghatékonyabban egyenlő területű darabokra (sejtekre) osztani, ha azt akarjuk, hogy a kerületek összege (a felhasznált viasz mennyisége) a lehető legkisebb legyen.
„A MÉHEK TEHÁT TUDJÁK AZT, AMI HASZNOS SZÁMUKRA - VAGYIS AZT, HOGY A HATSZÖG NAGYOBB, MINT A NÉGYZET ÉS A HÁROMSZÖG, ÉS HA MINDEGYIKET UGYANANNYI ANYAGBÓL KÉSZÍTIK EL, AKKOR A HATSZÖGBEN TUDJÁK A LEGTÖBB MÉZET ELRAKTÁROZNI.” Alexandriai Papposz, Kr. u. 340
Bizonyítást nem adott, ezért állítása a következő kétezer évben csak sejtés maradt, amelyet 1999-ben bizonyított be a Michigani Egyetem matematikusa, Thomas Hales. Bizonyítása azt jelenti, hogy a hatszög alakú struktúra a leghatékonyabb mérnöki konstrukció. A természetes kiválasztódás a hatékonyságra törekszik, ezért olyan struktúrákat hoz létre, amelyek az elegáns, a jelenségek lényegét alkotó matematikai törvényszerűséget tükrözik. Milyen gyönyörű válasz ez erre az egyszerű kérdésre.
Nos, ... lehetséges, bár a történetnek ezzel még nincs vége. 2013-ban három mérnök - Karihaloo, Zhang és Wang — „Méhsejtek, avagy hogyan alakulnak át a kör alakú sejtek lekerekített hatszögekké” címmel publikált egy cikket. Állításuk szerint a házi méhek, akárcsak a Melipona méhek, amelyeket Darwin kezdetlegesebb építészeknek minősített, először szintén kör keresztmetszetű sejteket készítenek. A hatszögek azért jelennek meg, mert a méhek testmelege 45 °C-ra melegíti a viaszt. Ezen a hőmérsékleten a viasz kezd megolvadni, és viszkózus folyadékká válik. Ettől kezdve az olvadt viasz kör alakú sejtjei úgy viselkednek, mint a szappanbuborékok, amelyek egymással találkozva 120°-os szögeket alkotva kapcsolódnak egymáshoz. Ha az összes buborék vagy méhsejt azonos méretű és azonos távolságra vannak egymástól, akkor a körkörös szerkezet spontán módon átalakul hatszöges lefedéssé. Karihaloo és munkatársai úgy bizonyították állításukat, hogy füstöléssel félbeszakították a lépet építő házi méhek munkáját, és így kiderült, hogy az utoljára épített sejtek kör alakúak, míg a régebbiek már átalakultak hatszögekké. Az átalakulás hengeresből a hatszögletű struktúrába ugyanolyannak látszik, ahogyan azt Darwin is megfigyelte, de az átalakulás magyarázata eltérő.
A hatszögek kialakulásának alapvető magyarázata továbbra is a természetes kiválasztódás, ám a méheknek nem kell bajlódniuk a sík optimális lefedésének problémájával, elég, ha egyenletes távolságban hasonló nagyságú, kör keresztmetszetű sejteket építenek, majd testük melegének hatására a fizika elvégzi a munka oroszlánrészét. Számomra ez a megoldás az előzőnél is elegánsabb és hatékonyabb: a méhek engedik, hogy a fizika befejezze a munkájukat! Amint a tanulmány szerzői megfogalmazzák: „Nem hagyhatjuk... figyelmen kívül, de nem is kell túlságosan csodálni a méhek szerepét ebben a folyamatban, hiszen a méhek melegítik fel, gyúrják és vékonyítják a viaszt, pontosan ott, ahol erre szükség van.” Ez lenne a megoldás arra a problémára, amely hosszú időn át oly sokak fantáziáját ébresztette fel? A hatszögek eredetéről változatlanul folyik a vita, valószínű tehát, hogy a szakirodalomban nem Karihaloo és munkatársai cikke mondta ki az utolsó szót.
Az imént leírtak annak rendje és módja szerint olyasvalamit illusztrálnak, ami gyakran kimarad a tudomány bemutatásából. A tudományos eredmények mindig csak előzetesek. Egyetlen komoly tudós sem hiheti azt, hogy egy adott témában az övé az utolsó szó. Valamely tudományos eredmény akkor publikálható, ha a szerzők és a dolgozat néhány bírálója úgy gondolják, hogy a leírtak értékes hozzájárulást jelentenek az adott területen folyó kutatáshoz. A lényeg azonban az, hogy a publikálás nem jelenti a leírt megállapítások helyességét, csupán azt, hogy azok nem nyilvánvalóan hibásak. Az a jó, ha a publikáció nem akar lezárni egy kérdést, hanem inkább meglobogtatja a vörös posztót a felajzott kollégák szeme előtt. Mint ahogy átérzem Kepler mérsékelt, de nyilvánvaló örömét, amiért nem találta meg a kielégítő magyarázatot a hópelyhek alakjára, éppily örömmel hallgatnám meg a ti gondolataitokat is, kiváló kollégáim.
Kepler A hatszögletű hópehely című dolgozatának utolsó soraiban szeretetteljes sajnálkozással ír arról, hogy „bekopogtatott a kémia ajtaján”; aminek az lett a következménye, hogy a következő generációk kitárták ezeket az ajtókat. Azt állítja — helyesen -, hogy a hópelyhek alakja legalább részben valamilyen mélyebben fekvő struktúrának vagy alaknak tudható be, de tekintettel arra, hogy az atomelmélet csak a XIX. század elején vált kísérletekkel ellenőrizhető tudománnyá, az atomok belső szerkezetét pedig csak a XX. században fedezték fel, ezért Keplernek semmiképpen sem volt módja arra, hogy kinyissa az ajtót, amelyiken kopogtatott. Ma már tudjuk, hogy a hópelyhek alkotóelemei a vízmolekulák, az egymással kapcsolatba kerülő vízmolekulák pedig rendkívül bonyolult viselkedésre képesek. Ez az állítás talán meglepően hangzik, ha arra gondolunk, hogy a víz színtelen, szagtalan folyadék. De talán nem is olyan meglepő, ha arról sem feledkezünk meg, hogy a vízmolekulák spontán módon összeállva létrehozzák a hópelyhek valószínűtlen formáit és elragadó változatosságát.
Egyetlen vízmolekula nem különösebben bonyolult képződmény. Egymáshoz kapcsolódott hidrogén- és oxigénatomokból áll. Az oxigént elsőként 1774-ben izolálta Joseph Priestley, egy yorkshire-i gyapjúszövő mester fia, míg a hidrogént Henry Cavendish azonosította először 1766-ban. Jean Baptiste Perrin 1926-ban fizikai Nobel-díjat kapott a molekulák fizikailag valóságos létezésének bizonyításáért, amire már alig-alig emlékezünk. Ez azt bizonyítja, milyen nehéz a mikrovilág vizsgálata, és milyen gyorsan alakul át az élenjáró tudomány hétköznapi tudássá.
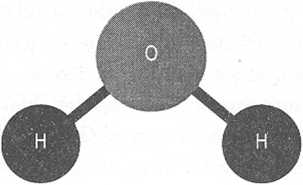
A vízmolekula két hidrogénatomot tartalmaz, amelyek egyetlen oxigénatomhoz kapcsolódnak: H2O (lásd a rajzot). A vízmolekula azonban nem lineáris - a hidrogénatomok iránya 104,5°-os szöget zár be egymással. Ennek az az oka, hogy az oxigénatom átellenes oldalain két extra elektronpár van jelen. Hogy megértsük, miért van ez így, ismerkedjünk meg röviden az atomfizika és a kvantummechanika alapjaival.

A vegyészek szempontjából az atomoknak három alkotórészük van (ennél részletesebben majd később fogunk behatolni az atomokba); a kicsiny és sűrű atommag protonokból és neutronokból áll, ettől nagyon távol elektronok helyezkednek el. Ha az atommag teniszlabda nagyságú lenne, akkor a legkülső elektronok pályája több kilométer lenne. A hidrogén a legegyszerűbb elem, atommagja mindössze egyetlen protonból áll. A következő a hélium, amelynek magját két proton és két neutron alkotja. Az oxigén magjában nyolc proton és nyolc neutron található. Az atommagot elektronok veszik körül, amelyeket a természet négy alapvető kölcsönhatása közül az egyik tart a helyükön: az elektromágnesség. Az elektronok negatív, a protonok pedig pozitív elektromos töltésűek, az elektron negatív töltése pontosan ugyanakkora, csak éppen ellenkező előjelű, mint a proton pozitív töltése. Senki sem tudja, miért pontosan azonos nagyságúak ezek a töltések; ez a fizika alapjainak egyik nagy rejtélye. Minden kémiai elem atomjai elektromosan semlegesek, ami azt jelenti, hogy a magban pontosan ugyanannyi proton található, mint ahány elektron a magot körülveszi. Ennek megfelelően, a hidrogénatomnak egyetlen, míg az oxigénatomnak nyolc elektronja van.
Ezután kissé bele kell kóstolnunk a kvantummechanikába. Az atommag elektromos töltését úgy tudjuk elképzelni mint egy dobozt, amelyikben az elektron csapdába esett. Az elektronok, akárcsak az univerzum többi alapvető építőköve, a kvantummechanika törvényeinek engedelmeskednek; az utóbbiak írják le, hogyan mozognak a részecskék. Kiderült, hogy a kvantumelmélet alapvető szabályai ellentmondanak ösztönös szemléletünknek, és szembemennek a józan ésszel. Ez azonban rendben van így, hiszen semmi okunk sincs feltételezni, hogy a Világegyetemet irányító törvények mindegyikének meg kell felelnie a „józan ész” elvárásainak. A szubatomi részecskék viselkedését leíró szabályok közül a legalapvetőbb értelmében a részecskék soha nincsenek nyugalomban. Nincsenek béklyóba kötve, ezért nagy valószínűséggel elvándorolnak a helyükről, és minél erősebben próbáljuk egy adott helyre odacövekelni őket, annál erőteljesebben akarnak elmenni onnan. Az atommag jelenléte némiképp megszelídíti a zabolátlan elektronokat, mert belekényszeríti őket a „nukleáris dobozba”.
AZ ELEKTRONOK VISELKEDÉSÉT IRÁNYÍTÓ MÁSIK SZABÁLY SZERINT EZEK A RÉSZECSKÉK NEM KÜLÖNÖSEBBEN KEDVELIK EGYMÁS TÁRSASÁGÁT. EZT NEVEZIK PAULI-FÉLE KIZÁRÁSI ELVNEK.
Az elektronok viselkedését irányító másik szabály szerint ezek a részecskék nem különösebben kedvelik egymás társaságát. Ezt nevezik Pauli-féle kizárási elvnek, és ugyancsak a kvantumelmélet törvényeiből következik. Az elektronok ezért úgy rendeződnek el a mag körül, hogy a lehető legtávolabb helyezkedjenek el egymástól. Van azonban még egy feltétel, amelyik fontos az atom felépítésének megértése szempontjából. Az ellentétes spinű elektronok mégiscsak közel kerülhetnek egymáshoz (más szóval „párokat alkothatnak”). Természetesen túl közel nem kerülhetnek, mert azonos az elektromos töltésük, márpedig az azonos töltések taszítják egymást.
A spin a szubatomi részecskék olyan tulajdonsága, amelyet könnyű megnevezni, de annál nehezebb elképzelni. Ha úgy tetszik, az elektronokat apró, pörgő búgócsigáknak képzelhetjük, de ez az analógia több sebből vérzik, ezért jobban tesszük, ha nem folyamodunk hozzá. Ezt előre bocsátva, azt mondhatjuk, hogy a spin annak a mértéke, mennyire forog az elektron - bár éppen egy pont forgása az, amit nem túl könnyű elképzelni. Az elektront és a hozzá hasonló részecskéket „1/2 spinűeknek”, azaz feles spinűek-nek vagy fermionoknak nevezzük. Az ilyen részecskék spinjének csak két értéke lehet, a „felfelé-spin” és a „lefelé-spin”. A spin fogalma közvetlen, bár meglehetősen összetett folyománya Einstein speciális relativitáselmélete és a kvantumelmélet egyesítésének, amit az elektront leíró egyenlet megadásával 1928-ban a fizikus Paul Diracnak sikerült megalkotnia. A részletek témánk szempontjából nem érdekesek, csak az a lényeg, hogy a negatív töltésű elektronok az atommagban lévő pozitív töltésű protonok csapdájába esnek, miközben igyekszenek a lehető legtávolabb maradni egymástól, bár az ellentétes spinű elektronok közelebb kerülhetnek egymáshoz, mint az azonos spinűek. Ez már elég információ ahhoz, hogy megértsük a vízmolekulát. Az oxigénatomnak nyolc elektronja van. Kettő közülük az atommaghoz meglehetősen közel helyezkedik el, ezért ezek lényegében figyelmen kívül hagyhatók, ha a két hidrogénatom kapcsolódását vizsgáljuk. A további hat elektron úgy helyezkedik el a mag körül, ahogyan azt az ábra mutatja. (Nagyon nehéz kiszámítani, hogy egy adott molekulán belül hol helyezkednek el az elektronok. A részletek az atommag által keltett, gömbszimmetrikus potenciálra alkalmazott Schrödinger-egyenletből következnek. Ha további részletekre kíváncsiak, és jobban el szeretnének mélyedni a kvantumelméletben, akkor bővebben olvashatnak ezekről a kérdésekről kollégámmal, Jeff Forshaw-val közösen írott, The Quantum Universe (A kvantumuniverzum) című könyvünkben.)

A vízmolekula szerkezete az oxigén nyolc elektronjával, amelyek közül kettő egy-egy hidrogénatommal osztozik.
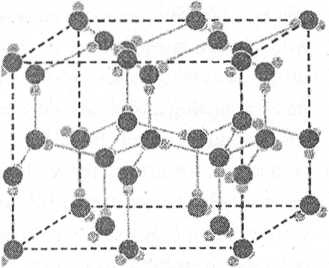
A jég 1h módosulatának hexagonális kristályszerkezete. A vízmolekulákat hidrogénkötések kapcsolják egymáshoz, az egyik molekula oxigénatomja egy másik molekula egyik hidrogénje felé fordul.
A kémia egyik alapvető fogalma, amely ugyancsak a kvantumelmélet alapvető törvényeire vezethető vissza, azt mondja ki, hogy az atomok megosztozhatnak az elektronjaikon. Ennek eredményeképpen jön létre a kémiai kötés. A két hidrogénatom a saját egy-egy elektronját - ha erre lehetőség van - megosztja az oxigénatommal, ezzel betöltik az oxigén atommagja körül üresen maradt két külső helyet; ennek eredményeképpen létrejön a vízmolekula, amely a felső rajzon látható. A 104,5°-os „törést” az okozza, hogy az oxigénatom külső elektronszintjén két további elektronpár is jelen van. Ezek az oxigénatom hidrogénatomokkal ellentétes oldalán helyezkednek el, ez adja meg a vízmolekula jellegzetes alakját és sok különleges tulajdonságát.
A vízmolekula, akárcsak az azt alkotó atomok, elektromosan semleges, de az elektronok egyenetlen eloszlása következtében a molekula „lábain” csekély pozitív többlettöltés mutatkozik, míg a molekula oxigén felőli végén a negatív töltés enyhe túlsúlya tapasztalható. Emiatt a vízmolekula az úgynevezett poláros molekulák közé tartozik - mert a molekulának van egy pozitív és egy negatív vége. Ez a jelenség a bonyolultság új világát nyitja meg előttünk.
A víz polárosságának fontos következménye, hogy a vízmolekulák szívesen tapadnak egymáshoz. A vízmolekula negatív, oxigén felőli vége vonzza a másik molekulák pozitív, hidrogén felőli végét, ezért a molekulák az úgynevezett hidrogénhíd-kötéssel- (hidrogénkötéssel) egymáshoz kapcsolódnak. Ez bizonyos mértékig a folyékony vízben is előfordul, ami meglehetősen nagy és bonyolult struktúrák létrejöttét eredményezi.
A jelenség még drámaibb, amikor a hőmérséklet csökken, a víz pedig megfagy. A vízjég nagyon kísérteties anyag. A jégnek 17 módosulatát ismerjük, amelyek közül a Földön az 1h (Ih, ahol I a sorszáma, a h pedig a hexagonális elrendezésre utal) változat a leggyakoribb (szerkezete az ábrán látható). A szabályos kristályszerkezet eredménye a víz egyik legbizarrabb tulajdonsága: a jég úszik a vízen. Ez rendkívül szokatlan viselkedés. Minden más gyakran előforduló szilárd anyag a szilárd fázisában nagyobb sűrűségű, mint folyékony fázisában, ezért nem úszik saját folyadék állapota tetején. A jég kristályszerkezete azonban olyannyira nyitott, hogy sűrűsége közönséges légköri nyomáson a 0 °C hőmérsékleten 8%-kal kisebb a folyékony vízénél. Ezért úsznak a jéghegyek az óceánokon.
A jelenség érdekes, és a legkevésbé sem magától értetődő. Egyes elképzelések szerint a víz e fontos tulajdonságának létfontosságú szerepe lehetett az evolúcióban és a földi élet fennmaradásában. Ha a jég sűrűbb lenne a folyékony víznél, akkor lesüllyedne az óceánok fenekére. Ebben a helyzetben, különösen a nagy eljegesedések idején, a Föld tavai és óceánjai alulról felfelé, azaz fenékig befagytak volna, és talán tartósan szilárd halmazállapotúak maradtak volna. Ennek katasztrofális következményei lettek volna az élővilágra és a táplálékláncra, amely a tengervízben és az édesvízben egyaránt a vizek fenekén található állati és növényi életen alapul.
A jég komplex struktúrája a kvantumelmélet törvényeiből következik; ezekből a törvényekből nincs túl sok, és ezek a törvények egyszerűek. Mindamellett, az „egyszerű” ebben az esetben nem azt jelenti, hogy a kvantumelméletet egyszerű megtanulni és alkalmazni; ez nem így van. A kvantumelmélet abban az értelemben egyszerű, hogy kevés matematikai szabályt tartalmaz, amelyek viszont a legkülönbözőbb léptékű természeti jelenségek széles körét képesek leírni, az atomok és a molekulák szerkezetétől a Nap belsejében folyó magreakciókig. Emellett az olyan, ma már hétköznapi eszközök működését is leírják, mint például a tranzisztor és a lézer, vagy újabban ezeken alapul az a sokkal egzotikusabb technológia, amelyiken a kvantumszámítógépek működése alapul.
Éppen az a modern természettudomány meghatározó és egyúttal legmeglepőbb sajátossága, hogy milyen gazdaságos a jelenségek leírása. Nem eleve nyilvánvaló az, hogy az alapvető törvények kis csoportjának képesnek kell lennie az univerzumot benépesítő objektumok határtalan komplexitásának leírására, mégis ez az, amit az elmúlt évszázadok során felismertünk. Talán az a helyzet, hogy ha egy univerzum elég szabályos ahhoz, hogy megengedje olyan komplex természetes objektumok létezését, mint amilyen az emberi agy, akkor azt az univerzumot egyszerű törvényeknek kell irányítania, de mivel nem ismerjük a törvények eredetét, ebben nem lehetünk biztosak. Mindenesetre érdekes, hogy a jelenségek mélyén található egyszerűségből ilyen bonyolultság képes kialakulni, amire jó példa a szerény vízmolekula. Aszimmetrikus, „megtört” formája, ami végső soron a jég komplex struktúrájáért felel, a kvantumelmélet törvényeinek következménye, bár ezekbe a törvényekbe nincs beépítve a „törés”. Tulajdonképpen a fizikus kijelentheti, hogy a törvények nagyfokú szimmetriát mutatnak, ezért a hidrogén és az oxigén atommagja is szimmetrikus, így szép, gömb alakú „nukleáris dobozokat” hoznak létre, amelyekben csapdába ejtik az elektronokat. Ha azonban az atomok egymás közelébe kerülnek, aszimmetrikus struktúrát hoznak létre.
A szimmetria fogalma központi helyet foglal el a modern fizikában, ezért ebben a könyvben többször is találkozunk ezzel a fogalommal. Most csak annyit jegyezzünk meg, hogy a vízmolekula aszimmetrikus felépítése annak a következménye, ahogyan az elektronok az oxigénatom magja körül elhelyezkednek. A külső elektronok négy különböző helyre kerülhetnek (kettesével), márpedig az így rendelkezésre álló helyeken az oxigénatom hat külső elektronja csak aszimmetrikus elrendezésben tud elhelyezkedni. Ezért, amikor a két hidrogénatom megközelíti az oxigént, akkor csak ennek az aszimmetrikus elrendezésnek megfelelően tudnak hozzákapcsolódni, így spontán módon megjelenik az aszimmetrikus struktúra. Senkinek sem kellett megterveznie a vízmolekulát, és nem kellett a 104,5°-os törés szögét esztétikai alapon más formákkal szemben előnyben részesítenie! Ez a kvantumelmélet törvényeinek következménye, jóllehet ez az érték sehol sincs önkényesen előírva a törvényekben.
A víz tulajdonságaiért végső soron a molekulái közötti kölcsönhatás a felelős. A vízmolekulák tulajdonságait viszont az azt alkotó hidrogén- és oxigénatomok közötti kölcsönhatások hozzák létre. A hidrogén- és az oxigénatomok tulajdonságait az azokat alkotó részecskék - a protonok, neutronok és elektronok - kölcsönhatásai határozzák meg, amelyeket viszont egyszerű törvények irányítanak. Vajon a végtelenségig folytathatnánk ezt a gondolatmenetet? Milyen messzire juthatunk, milyen mélyre áshatunk, hogy az anyag általános tulajdonságaira minél alapvetőbb magyarázatokat találjunk?