Pontosan ma húsz éve kezdtem a doktori témámon dolgozni (e sorokat 2015. október 1-jén írom). Három évvel később benyújtottam „Kettős diffrakciós disszociáció nagy impulzusátadás esetén” című dolgozatomat. Kutatásaim során a pomeron nevű részecskével foglalkoztam, amelyet Iszaak Pomerancsuk szovjet orosz fizikusról neveztek el. Ezeket a részecskéket a HERA nevű részecskegyorsítóban protonok és elektronok közt létrehozott, nagy energiájú ütközésekben keletkező törmelékben kerestem. A HERA a hadron-elektron gyűrűs gyorsítót (Hadron-Electron Ring Accelerator) jelenti, de a rövidítés egyben Hérára utal, aki a görög mitológiában Zeusz felesége volt. A 6,7 kilométer kerületű berendezés Hamburg északi részén az utcák alatt helyezkedett el. Hamburgban öröm volt diáknak lenni. Télen az Elba befagy, de a jégtörők utat vágnak a kikötő felé, a város pedig érzi a tenger közelségét. Nyaranta Blankenese régi házai alatt a folyópartot szegélyező kis öblök zsúfolásig megtelnek, és a város mediterrán hangulatot áraszt. Az oldhami környezetéből kiszakított huszonéves fiatalembert hajnalonként bármely évszakban elszórakoztatja a Reeperbahn. Meglepő, hogy ilyen körülmények között három évet el lehet tölteni azzal, hogy valaki a protonok és az elektronok nagyenergiájú ütközéseit figyelve a pomeron nevű részecskére vadászik.

Miért érdeklődtem a pomeron iránt? A természet négy alapvető kölcsönhatása közül az egyiket leíró legjobb elméletet akartam ellenőrizni. E kölcsönhatások közül az egyikkel - az elektromágnességgel — korábban már találkoztunk: ez tartja meg az elektronokat az atommag körül, és ez hozza létre a hidrogénhídkötéseket a vízmolekulák között. A pomeronra vonatkozó kutatásaim a négy közül egy másik kölcsönhatásra, az erős kölcsönhatásra vagy más néven erős magerőre irányultak. Ha visszagondolunk az oxigén atommagjának felépítésére, akkor magától értetődő, miért van szükség erre a kölcsönhatásra. Ez az atommag nyolc szorosan összezsúfolt, pozitív töltésű protonból és nyolc, töltés nélküli (semleges) neutronból álló golyó. Az elektromágneses erő egyik alapvető tulajdonsága, hogy az azonos töltések taszítják egymást; akkor viszont kérdés, miért nem repülnek szerteszét az atommagot felépítő részecskék. Azért, mert a protonok közti elektromágneses taszításnál sokkal erősebb kölcsönhatás, a magerő, ami összetartja az atommagot alkotó részecskéket.

A protonok kicsik, mégis testünk tömegének valamivel több mint a felét ezek a részecskék teszik ki. A többit legnagyobb részben neutronok alkotják. Egy átlagos ember testében körülbelül húszezer millió millió millió millió proton található. A tudományos életben ezt a számot 2 • 10²⁸-ként írják le, ami azt jelenti, hogy a kettes után 28 nulla következik. Ezen a szinten tehát meglehetősen egyszerűek vagyunk.

Ha mélyebbre hatolunk a protonok és a neutronok belsejében, akkor a helyzet bonyolultabbá válik. Hétköznapi fogalmainkkal mérve a protonok nagyon kicsik, de napjainkban a tudomány és a technika már olyan fejlett, hogy a belsejükbe is be tudunk pillantani. Erre a feladatra készült a HERA. Ez az eszköz valójában egy gigantikus elektronmikroszkóp, amelyikkel mélyen az anyag részecskéinek belsejébe hatolhatunk. Gondosan ügyelnünk kell arra, mit nevezünk méretnek, hiszen a protonnak nincs szilárd felszíne, de a legújabb mérések szerint a sugara valamivel több mint 0,8 femtométer, vagyis nem egészen 10^-15 méter (utóbbi a méter ezermilliomod milliomod része). (Jelenleg van némi eltérés a proton sugarára vonatkozó különböző mérések eredménye között, ami azt jelezheti, hogy közrejátszhat valamilyen érdekes jelenség, amelyet még nem ismerünk. Lásd például: http://arxiv.org/ pdf/1502.05314.pdf, amelyik szakmai cikk ugyan, mégis azt javaslom, vessenek rá egy pillantást, mert ennek ellenére szépen illusztrálja a modern részecskefizika pontosságát.)

Mivel öregszem, és egyre szentimentálisabbá válok, meg egyébként is, ma már jobbára szavakkal keresem a kenyeremet, megbocsátottam magamnak, hogy könyvembe beillesztettem két ábrát abból a doktori értekezésemből, amelyet húsz évvel ezelőtt Hamburgban írtam. Végső soron ezek voltak az én hópelyheim. Az első rajzot az 1990-es években egy UNIX operációs rendszer alatt működő xfig számítógépes programmal készítettem. Boldog idők! A rajzon az látható, amint egy elektron összeütközik egy protonnal. A modern fizika nyelve első pillantásra felfoghatatlan, amit a disszertációmból vett ábraaláírások szemléltetnek, de ez a nyelv nem azért ilyen érthetetlen, hogy a fizikusok okosabbaknak láttassák magukat. Hogy őszinte legyek, sosem gondoltam, hogy dolgozatomat egy nem fizikus is elolvassa. Minden egyes szóra szükség van, és mindegyik jelent valamit. És ezzel George Orwell is egyetértene. „Valaki rákaphat az ivásra, mert úgy érzi, kudarcba fulladt az élete, aztán még teljesebb kudarcot vallhat, amiért iszik. Nagyjából ugyanez történik az angol nyelvvel. Csúnyává és pontatlanná válik, mert ostobák a gondolataink, de nyelvünk henyesége megkönnyíti, hogy ostoba gondolataink támadjanak.” (George Orwell, Politics and the English Language. [Magyarul: A politika és az angol nyelv in: George Orwell: Az irodalom fölszámolása, Európa Könyvkiadó, Budapest 1990. Válogatta: Takács Ferenc]) A fizika a pontos gondolkodásról szól, amit a nyelv pontossága segít és tesz nyilvánvalóvá.

Az ábra magyarázó szövege szerint a semleges áram azt jelenti, hogy az elektron visszalökődik a protonról, miközben kicserél vele egy elektromosan semleges részecskét — ebben az esetben egy fotont, vagyis a fény részecskéjét. Ez a görög γ betűvel jelölt foton hullámos vonalként látható a rajzon. A DIS rövidítés a „mélyen rugalmatlan szórást” (Deep Inelastic Scattering) jelenti, vagyis azt, hogy a foton eltalál valamit, mélyen a proton belsejében, aminek következtében a proton darabokra szakad. Így írja le egy mai részecskefizikus bármely két részecske kölcsönhatását; a kölcsönhatás az azt szállító valamilyen más részecske „kicserélődését” jelenti a két kölcsönható részecske között. Ebben az esetben a kölcsönhatás az elektromágnesség, az azt hordozó részecske pedig a foton. A vízmolekulák jéggé válásának legalapvetőbb leírása értelmében a vízmolekulákban lévő elektronok fotonokat bocsátanak ki és nyelnek el, aminek az eredménye végül a molekulák összetapadása.

Másként is el lehet képzelni ezt az elektron-proton ütközést. Arra is gondolhatunk, hogy az elektronból kibocsátott foton beleütközik a protonba és feltárja annak belső szerkezetét. Ez a struktúra látható a disszertációmból átvett másik ábrán.

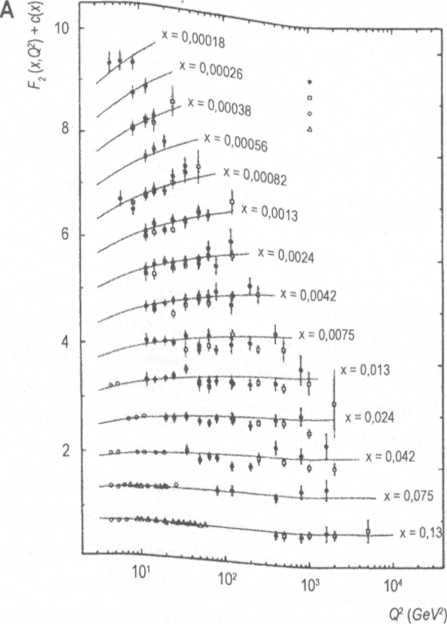
F₂(x,Q²), a HERA-ban mérve, valamint rögzített céltárgyú kísérletekben Q²(a) és x(b) függvényében. A görbék fenomenológiai illesztések H1-gyel végezve. c(x) önkényesen választott függőleges elmozdulás, amelyet az (A) diagramon a jobb áttekinthetőség érdekében minden ponthoz hozzáadtunk, ahol c(x) = 0,6(n - 0,4), n pedig az x tároló sorszáma úgy, hogy n = 1 esetén x = 0,13 legyen.

Engedjék meg, hogy egyetlen bekezdésnyi posztgraduális fizikát is beszúrjak a könyvembe. Két okból bátorkodom ezt megtenni. Az első az, hogy számomra különösen nagy örömöt okoz, ha meg tudok értetni egy bonyolult gondolatot, és ezáltal rá tudok világítani a természet mélyén fekvő egyszerűségre és szépségre. A biológus Edward O. Wilson alkotta meg erre az érzésre a „ión megvilágosodás” fogalmát. A kifejezéssel illetett felismerést Arisztotelész a fizika tudományának alapjait lefektető Thalésznek tulajdonítja, aki Kr. e. 600 körül Ióniában élt. Ezt az eufóriát érezzük, amikor megértünk valamit a természetről, és azt látjuk, hogy a megoldás elegáns. A másik ok az, hogy felidézek egy olyan elképzelést, amelynek kidolgozásába személyesen is bekapcsolódhattam. A tudomány arról szól, hogy gondos megfigyeléseket végzünk, majd megkíséreljük megmagyarázni, amit látunk. Megfigyelésünk tárgya lehet a méhsejtek hatszöges felépítése éppúgy, mint a hópelyhek kicsipkézett szimmetriája, vagy az elektron protonról történő visszalökődésének részletei. A gondos megfigyelések vezettek el a ión megvilágosodáshoz.

A HERA berendezéssel végzett kísérleteinkben azt mértük, milyen irányban és mekkora energiával repül tovább az elektron, miután nekiütközött a protonnak. A mérés egyszerű, és ennek alapján fel tudtuk térképezni azt, amiről az elektron „visszalökődött”- vagyis az anyag szerkezetének bámulatos titkait. Az ábrán a proton belsejét kétféleképpen tettem láthatóvá. Az F₂(x, Q²)-tel jelölt valamit a proton szerkezeti függvényének nevezzük. Lássuk most a helyzetet kicsit alaposabban, ami már némi gondolkodást is igényel. Vessünk egy pillantást az első, az (A) jelű rajzra, azon belül a legalsó, x = 0,13 feliratú görbére.

A görbe pontjai annak a valószínűségét adják meg, hogy az elektron egy olyan objektumról pattan vissza a proton belsejében, amelyik a proton impulzusának 13 százalékát hordozza - ezt jelenti az x = 0,13. A Q² mennyiség a protonba ütköző foton úgynevezett virtualitása. Ezt a mennyiséget például arra jellemzőnek tekinthetjük, milyen felbontással tudja letapogatni a foton a proton belsejét. Ha Q² értéke nagy, akkor a foton hullámhossza rövid, tehát a nagy Q²-tel jellemzett fotonok finomabb részleteket tudnak feltárni. Az x = 0,13 görbe meglehetősen lapos, ami azt jelenti, hogy bármiről verődik is vissza a foton, az a valami úgy viselkedik, mintha a kiterjedése nem lenne érzékelhető. Ezt azért kell így értelmezni, mert azt látjuk, hogy hiába fokozzuk mikroszkópunk felbontóképességét (ami nagyobb Q² értékeknek felel meg), nem tapasztalunk változást. Ez akkor fordul elő, ha a foton a proton belsejében az anyag nagyon kis kiterjedésű csomóiról lökődik vissza. Ezeket a kis csomókat nevezzük kvarkoknak, és amennyire ma meg tudjuk állapítani, ezek a részecskék a Világegyetem legalapvetőbb építőkövei. A bemutatott két ábra együtt leírja, mi van a proton belsejében, úgy, ahogyan az a HERA gyorsítóval dolgozó sok száz tudós előtt többévi kísérletezés eredményeképpen feltárult.

A proton tehát nyüzsgő, pontszerű alkotóelemekből felépülő tömeg, amely az adott kereteken belül folytonosan változik. A belső váz három kvarkból áll; két „fel” kvarkból és egy „le” kvarkból. A kvarkokat az erős kölcsönhatás tartja össze, amelyet a gluonoknak nevezett részecskék közvetítenek, ugyanúgy, ahogyan a fotonok az elektromágneses kölcsönhatás közvetítő részecskéi. A fotonokkal ellentétben azonban a gluonok (további gluonok kicserélésével) egymással is kölcsönhatásra léphetnek, aminek következtében a felbontóképességet növelve, a proton belsejében egyre bonyolultabb szerkezet tárul elénk. A (B) illusztráció ezt a viselkedést mutatja; a görbe emelkedése x kisebb értékei felé arról árulkodik, hogy rengeteg gluon van jelen, amelyek mindegyike csak a proton impulzusának apró töredékét hordozza. Ugyanez az (A) ábráról is leolvasható. Kisebb x értékek esetén a görbék már nem laposak. A szakmai zsargonban ezt a jelenséget „a skálatörvény sérülésének” nevezzük, ami azt jelenti, hogy a felbontóképesség növelésekor a pontszerű alkotórészek egyre nagyobb számban látszanak előtűnni. Más szavakkal, kis felbontás esetén csak a vázat tudjuk felbontani, azaz a három kvarkot, míg nagy felbontással vizsgálva a proton gluonszerkezete a maga teljes pompájában tárul elénk. Durván úgy fogalmazhatunk, hogy a proton impulzusának körülbelül a felét a gluonok hordozzák, mert olyan sok nyüzsög belőlük a kvarkok között. Azokat a görbéket, amelyek ezen a diagramon az adatpontokon keresztül futnak, az erős kölcsönhatás legjobb elmélete, a kvantum-színdinamika, röviden QCD alapján számítottuk ki. A QCD azon szabályok összessége, amelyek annak a valószínűségét adják meg, hogy a kvark kibocsát egy gluont, valamint leírják azt, ahogyan a gluonok más kvarkokkal és gluonokkal kölcsönhatnak. Ez is egy kvantumelmélet - ugyanolyan keretrendszer, mint amilyenre a vízmolekula struktúrájának tárgyalásakor hivatkoztunk. Amikor az elektromos töltésekkel foglalkozunk - például az elektronok és az atommag közötti kölcsönhatással akkor az elektromágnesség kvantumelméletét használjuk, amelyet kvantum-elektrodinamikának, angol nevének rövidítésével QED-nek nevezünk.

Emlékszem, számítógépes programokat írtam, hogy átrágjam magamat az egyes elektron-proton ütközésekből kapott adathalmokon, és előállítsam a fentihez hasonló ábrákat. Az 1990-es években rendelkezésünkre álló számítógépeken ezek a programok napokig futottak. Ha ránézek ezekre a rajzokra, még ma is felvillanyoz az érzés, hogy egy Hamburg alatt működő, 6,7 kilométer kerületű berendezéssel megvizsgáltam ezermilliomod milliomod méter kiterjedésű objektum struktúráját. Egyúttal olyan elmélet volt a kezünkben, amelyikkel megértettük, és le tudtuk írni, mi az, amit látunk. Az ipari méretű mérnöki teljesítmény és a szubatomi világ szépségének teljes összhangját. Ez volt maga a ión megvilágosodás.

A következő ábra pillanatképet mutat a közönséges anyag mély struktúrájáról. Ebből állunk, mi mindannyian, legalábbis azon a szinten, ameddig méréseinkkel eljuthatunk. Kétféle kvark, amelyeket gluonok tartanak össze, protonokat és neutronokat alkotnak, amelyeket viszont további gluonok tartanak össze atommaggá. Az elektronokat fotonok tartják meg az atommagok körül, hogy atomok jöjjenek létre, az atomokat pedig az elektronjaik között kicserélődő fotonok tapasztják össze molekulákká. És így tovább! Ez az egyszerű kép egy évszázadnyi kísérletezés és elméleti kutatás eredményeképpen alakult ki. A mindenség struktúráját néhány alapvető építőelemből kiindulva néhány szabály használatával meg tudjuk magyarázni. Az alapvető építőelemek közül hárommal találkoztunk: a fel-kvarkkal (u-kvark), a le-kvarkkal (d-kvark) és az elektronnal. Két kölcsönhatással is megismerkedtünk: az erős kölcsönhatással és az elektromágneses erővel. Létezik még egy kölcsönhatás, a gyenge, vagy más néven gyenge magerő, amelyik a fel-kvarkot át tudja alakítani le-kvarkká, miközben egy másik részecske, úgynevezett elektron-neutrínó szabadul fel. Ezzel együtt összesen négy anyagi részecskét ismerünk. A gyenge kölcsönhatás közvetítő részecskéi a W- és a Z-bozonok. Létezik továbbá a Higgs-bozon, amit 2012-ben sikerült felfedezni a Genfben működő nagy hadronütköztetőben (LHC, Large Hadron Collider). Ez a részecske ad tömeget az anyag építőelemeinek.

A negyedik és egyben utolsó kölcsönhatás az összes közül a legismertebb - a gravitáció. Ez azonban annyira gyenge, hogy a szubatomi világban még az olyan érzékeny kísérleteinkkel sem vehető észre a hatása, mint amilyen a HERA. Ha ez a kijelentés kissé titokzatosan hangzik, különösen annak, aki már esett le létráról, akkor tegyük félre emlékezetünkben egy időre ezt a gondolatot; a gravitáció hatására később fogunk visszatérni, amikor a bolygók és a galaxisok alakját tárgyaljuk meg.

Ez a négy részecske, a négy kölcsönhatás és a Higgs-bozon elégnek tűnik ahhoz, hogy leírjuk a vízmolekulát, a méhsejtet, az embert vagy a Földet. Elképesztően elegáns és egyszerű rendszer. Valamilyen ok miatt azonban a természet nem elégedett meg ezzel a gazdaságos rendszerrel, hanem két másolatot is készített a fel-kvarkokról, a le-kvarkokról, az elektronokról és az elektron-neutrínókról. Ez a két újabb család minden tekintetben azonos az elsővel, vagyis az eredetivel, azzal az eltéréssel, hogy az ezekbe tartozó részecskék tömege nagyobb, valószínűleg azért, mert másképp lépnek kölcsönhatásba a Higgs-részecskékkel. A három részecskecsalád létezése újabb nagy rejtély, ezért a XXI. század részecskefizikájának egyik legfontosabb feladata éppen annak a kiderítése, miért tűnik úgy, hogy a természet teljesen fölöslegesen ilyen pazarló módon jár el. Természetesen semmi szükség arra, hogy ilyen pazarló legyen. Azt viszont tudjuk, hogy legalább három részecskecsaládnak kell léteznie ahhoz, hogy megvalósulhasson a CP-sértésnek nevezett folyamat, amelyre annak magyarázatához van szükség, hogy ha az univerzum történetének kezdetén egyenlő mennyiségben volt jelen az anyag és az antianyag, akkor miért maradt meg mára valamennyi abból az anyagból, amelyik a csillagokat és az embereket felépíti. Ez sem ad választ azonban a „Miért?” kérdésére, pedig jó lenne biztosan tudni, hogy a bolygók, a csillagok és a galaxisok létezése több a puszta véletlen művénél.

Ezekkel az extra családokkal együtt az anyag 12 alapvető részecskéjét ismerjük, továbbá négy különböző, a kölcsönhatásokat közvetítő részecskét és a Higgs-részecskét. Ez minden, legalábbis mai ismereteink szerint - bár cseppet sem lennék meglepve, ha az elkövetkező években a nagy hadronütköztetőből még kiugrana valami újdonság. Reményemet az táplálja, hogy számos egymástól független csillagászati megfigyelés alapján elfogadható bizonyítékok szólnak amellett, hogy a Világegyetemben az anyag még egy formája, az úgynevezett sötét anyag is jelen van. Tömegét tekintve ebből ötször annyi van a Világegyetemben, mint „közönséges” anyagból, márpedig a sötét anyag nem állhat annak a 12 fajta részecskének egyikéből sem, amelyeket a részecskegyorsítókkal, például a HERA-val vagy az LHC-vel végzett kísérleteinkben megtaláltunk.

A természeti világ alapvető építőelemei, valamint három a természet négy alapvető kölcsönhatása közül: az erős magerőt a gluonok; a gyenge kölcsönhatást a W- és Z-bozonok; az elektromágneses kölcsönhatást pedig a fotonok közvetítik.

Nem áll szándékomban olvasóimat részletekbe menő részecskefizikai tanfolyammal traktálni, bármennyire is szeretném; ebben a fejezetben inkább természeti formákat és mintázatokat mutatnék be, illetve azt, amit ezek a Világegyetem működéséről elárulnak. De ha mindezt előrebocsátva, mégis elkísérnének egy utolsó kiruccanásra a részecskefizika világába, akkor elmondom, hogyan fedezték fel a proton és a neutron belsejében a kvarkokat, mert a történet szép példája annak, ahogyan a fizikusok felfigyelnek valamilyen mintázatra, majd megpróbálják megmagyarázni. Az érdekes azonban az, hogy a kvarkok létezését hamarabb jósolták meg, mint ahogy kísérleti úton felfedezték őket.

Az elméleti előrejelzés, amely szerint a protonok és a neutronok szintje alatt létezik még valamilyen építőelem, 1964-ből, Murray Gell-Manntól és George Zweigtől származik. Előrejelzésük a szubatomi részecskék abban az időben ismert rendszerén alapult. Az 1960-as évek elejére már az elemi részecskék látszólag a végtelenségig gyarapodó sorát sikerült felfedezni, de a rendszer nem volt elegáns, amellett fölösleges elemeket is tartalmazott. A proton és a neutron a részecskéknek abba a nagy családjába tartozik, amelyet barionoknak nevezett részecskék alkotnak; e család további tagjai a lambdák, szigmák, delták, kaszkádok és egy sor további részecske. Van az elemi részecskéknek egy másik nagy családja, az úgynevezett mezonok: a pionok, a kaonok, a ró-mezonok és így tovább. Egyedül a lambda-részecskéknek 13 különböző típusát ismerték, ehhez jött még hozzá a kilencféle szigma és a nyolc kaon. A részecskefizika egyre inkább a botanika szubatomi ágára kezdett hasonlítani. Akkor azonban Gell-Mann és Zweig szép mintázatot vett észre. A részecskéket megfigyelt tulajdonságaik alapján geometriai minták szerint lehetett elrendezni. Az egyik ilyen elrendezést a következő ábra mutatja. Ma ezeket a rendszereket szupermultipletteknek nevezzük.

A barionok „szupermultiplettje", minden egyes barionnál feltüntetve az azt alkotó kvarkokat.

Ahogy már Kepler is gyanította, amikor szemügyre vette a hópelyhek hatszögű szimmetriáját, a természetben megjelenő mintázatok gyakran valamilyen mélyebben fekvő struktúra megnyilvánulásai. A mintákat néha könnyű felismerni, néha nem - Gell-Mann mindenesetre 1969-ben megkapta a fizikai Nobel-díjat az elemi részecskék rendszerének felismeréséért de e mintázatok minden esetben a természet nyelvének megfejtésre váró „rosette-i kövét” képezik. Ebben az esetben az elemi részecskék mintázata azt sugallta Gell-Mann és Zweig számára, hogy a barionoknak három kisebb részecskéből kell felépülniük, amelyeket Gell-Mann kvarkoknak nevezett el. Amikor először észrevették a mintát, akkor három kvarkot építettek be a rendszerükbe: a fel-, a le- és a különös kvarkot. A szupermultiplettek alacsonyabb szintjein a különböző barionok a három építőelem hármas kombinációi. Ha egy negyedik kvarkot — a bájost - is hozzáadtak a rendszerhez, akkor a magasabb szinteket is létre tudták hozni. Az ábra mutatja, hogyan épülnek fel az egyes részecskék a különböző kvarkokból: a Δ⁺⁺ például három fel-kvarkból áll.

Az ábrán a piramis alján látható részecske, az Ω^- (ómega mínusz) történeti szempontból különösen érdekes, mert a létezését Gell-Mann egy 1962-ben a CERN-ben (Európai Részecskefizikai Kutatóközpont) tartott konferencián pusztán a rendszerükben megfigyelhető minta alapján jósolta meg. Ezt követően 1964-ben az Egyesült Államokban, a Brookhaven Nemzeti Laboratóriumban felfedezték a részecskét. Ha egy elmélet megjósol valamilyen újdonságot, majd később ezt sikerül felfedezni, akkor meglehetősen biztosak lehetünk benne, hogy jó nyomon járunk.

A természet négy kölcsönhatása közül hárommal tehát már megismerkedtünk; az atommagban működő erős és gyenge kölcsönhatással, valamint az elektromágnességgel, továbbá találkoztunk a természetet felépítő 12 alapvető részecskével. Ezután az utolsó, a leggyengébb, de a legismertebb kölcsönhatással foglalkozunk, a gravitációval. Vizsgálatához végiggondoljuk azoknak az objektumoknak a méretét és az alakját, amelyeket a gravitáció létrehoz. Ezek nem afféle apróságok, mint a szubatomi részecskék, még csak nem is olyan kicsik, mint egy hópihe, hanem sokkal nagyobb struktúrák: bolygók, csillagok és galaxisok.

Miért gömb alakú a Föld?

Jól ismert a Földről készült, A kék üveggolyó című fénykép. A felvételt 1972. december 7-én készítette a Hold felé tartó Apollo-17 űrhajó legénysége. A téli napfordulóhoz közeledve az Antarktiszon mindenütt süt a nap, a kép közepén pedig Madagaszkár, a makimajmok szigete látható. A sárga sivatagok a kék óceánokkal váltakoznak, a zöld árnyalatai pedig az élet jelei.

A NASA 2012. december 5-én tette közzé a kép párjaként A fekete üveggolyó című felvételt, amelyen a két amerikai kontinens éjszakába burkolózik. Ezen a képen előtűnnek a civilizáció jelei; a fények az ember uralkodásának kora hajnalát adják hírül. Mit látunk ezeken a képeken? Melyik a Föld legalapvetőbb tulajdonsága? Alekszej Leonov, aki 1965. március 18-án végrehajtotta a történelem első űrsétáját, megadta a választ:

„Soha nem tudtam, mit jelent az, hogy kerek a világ, amíg nem láttam a Földet a világűrből.” Alekszej Leonov, Voszhod-2, Szojuz-19/Szojuz-Apollo

Az űrből nézve a Föld csaknem tökéletesen gömb alakú. A Naprendszer összes bolygója, a nagyobb holdak és maga a Nap is ilyen, mint ahogyan a Világegyetem minden csillaga is gömbölyű. Miért? Ha sok különböző test ugyanolyan alakú, akkor erre magyarázatot kell adnunk. Közelebb jutunk a megoldáshoz, ha végiggondoljuk, mi befolyásolhatja egy bolygó, hold vagy csillag alakját. Az összetételüket kizárhatjuk, hiszen a bolygók egészen más anyagokból épülnek fel, mint a csillagok. A Föld nehéz kémiai elemekből áll, például vasból, oxigénből, szilíciumból és szénből. Ezzel szemben a Nap anyagát elsősorban hidrogén és hélium alkotja, egyébként is, a Nap hatalmas plazmagömb, szilárd felszín nélkül. Az óriásbolygók, például a Jupiter inkább a csillagokra hasonlítanak, mintsem a Földhöz, legalábbis ami az összetételüket illeti. Ezek is főként hidrogénből és héliumból állnak. A csillagokban és a bolygókban azonban közös, hogy ugyanaz az erő alakította ki és tartja össze őket - a gravitáció. Ha tehát meg szeretnénk érteni, miért gömb alakú mindegyik, akkor alaposabban meg kell ismernünk a gravitációs erő természetét.

Az év legnagyobb részében Tarragona csendes, mediterrán kikötőváros Spanyolország északkeleti tengerpartján (Katalóniában). Minden szeptemberben azonban felpezsdül az élet a városban, amikor az élénk színű ingekbe öltözött csapatok a tarragonai castells versenyen szembeszállnak a gravitációval. A castell embertornyot jelent, amely akár tíz ember magasságig is emelkedhet. A versengés az erőt, az egyensúlyérzéket, a stratégiát egyaránt próbára teszi, emellett szoros együttműködést igényel a csapat tagjai között. Minden csapat azzal kezdi az embertorony építését, hogy kialakítja a torony alapját (pinya), amelyet akár kétszáz ember is alkothat. Miután összeállt az alap, a felsőbb szinteket alkotó emberek speciálisan megtervezett geometriai elrendezésben, egymás vállára állva próbálnak minél magasabb tornyot építeni. A legsikeresebb csapat a Castellers de Vilafranca, akik 1972 óta már nyolcszor nyerték meg a tarragonai versenyt. A zöld inget viselő versenyzők egymással tökéletes összhangban építik az egyik szintet a másikra, a felsőbb szintekben egyre kevesebb emberrel. Amikor elkészült a stabilan álló embertorony, a legfelső szintet alkotó két gyerek (enxaneta) merészen felmászik a torony tetejére. Az enxaneták általában 6-7 éves gyerekek, akik könnyűek, mozgékonyak és talán nem félősek. Ez az a látvány, amelynek kedvéért a nézősereg összegyűlt. Végül a tornyok összeroskadnak, az emberi építmény ledől, a zuhanást csak az alul állók könyöke, térde, feje és válla csillapítja, ám a leeső emberek többnyire megússzák horzsolásokkal, zúzódásokkal, ütésekkel és néhány foguk elvesztésével. A súlyos sérülések nagyon ritkák.

Magától értetődő, miért zuhannak le az egyensúlyukat vesztő emberek: a gravitáció miatt. De pontosan hogyan viselkednek a testek a gravitáció hatására? A részleteket illetően két elméleti rendszer is létezik, bármelyiket használhatjuk, attól függően, mit szeretnénk kiszámítani. Ez a természettudomány sikerének kulcsát jelentő gondolatot illusztrálja, miszerint a tudományban nincs abszolút igazság! Csak a hasznosság számít; ha egy elmélet bizonyos körülmények között a kísérletek eredményével egyező előrejelzést ad, akkor nyugodtan használhatjuk az elméletet, de tisztában kell lennünk a korlátaival. Az első gravitációelméletet Isaac Newton 1687-ben írta le A természetfilozófia matematikai alapjai (Philosophiae naturalis principia mathematica, röviden Principia) című munkájában. Megalkotásához — legalább részben - kíváncsi ismerősünk, Johannes Kepler munkája adta az ösztönzést.

A gravitáció pontosabb leírását Albert Einstein 1915-ben publikálta. Newton elmélete semmit sem mond arról a mechanizmusról, ahogyan a gravitáció két test között hat, bár lehetővé teszi bárhol a Világegyetemben bármely két test közötti gravitációs erő nagyságának kiszámítását. Einstein pontosabb általános relativitáselmélete magyarázatot is ad a gravitációs erőre. Az anyag és az energia jelenléte torzítja a tér és az idő szerkezetét, a testek pedig ebben a torzult téridőben mozognak egyenes vonalú pályáikon. A téridő torzulása miatt úgy tűnik számunkra, mintha a testekre valamilyen erő hatna, ezt nevezzük gravitációnak. Einstein képe szerint azonban nem lép fel semmilyen erő, hanem a téridő görbül meg, és az a szabály érvényes, hogy ebben a görbült téridőben minden test egyenes vonalú mozgást végez. A téridő fogalmával a 2. fejezetben majd sokkal részletesebben is megismerkedünk.

Visszatérve eredeti kérdésünkhöz, hogy miért gömb alakúak a bolygók, ennek megválaszolásához nincs szükségünk Einstein elegáns, de matematikailag bonyolult általános relativitáselméletére. Fölösleges ágyúval lőni a verébre. Maradjunk tehát Newton egyszerűbb elméleténél, annál is inkább, mert az általános relativitáselmélet ugyanezt a választ adná. Az általános tömegvonzás Newton-féle törvénye így írható fel:

Szavakkal kifejezve az egyenlet azt állítja, hogy bármely két test között F nagyságú erő lép fel, amelynek nagysága egyenesen arányos a két tömeggel, m-mel és M-mel, továbbá fordítva arányos a két test közötti r távolság négyzetével. Ha megkétszerezzük a testek közötti távolságot, akkor a köztük fellépő gravitációs erő a negyedére csökken. A G tényezőt Newton-féle egyetemes gravitációs állandónak nevezzük. Ezt az összefüggésben szerepeltetve fejezhetjük ki számszerűen a gravitációs erő nagyságát. Ha a tömegeket kilogrammban, a távolságot pedig méterben mérjük, a gravitációs erőt pedig newtonban szeretnénk megkapni, akkor G = 6,6738 • 10^-11 m³ kg^-1 s^-2.

A Newton-féle gravitációs állandó egyike a fizika alapvető állandóinak. A Világegyetem egyik olyan tulajdonságát fejezi ki, amely megmérhető, de - legalábbis jelenlegi tudásunk szerint -nem vezethető le semmilyen mélyebb alapelvből. A fizika egyik nagy megválaszolatlan kérdése az, hogy miért ilyen kicsi a gravitációs állandó értéke, ami egyenértékű azzal a kérdéssel, hogy miért ilyen gyenge a két test között ható gravitációs erő. A kölcsönhatások erősségének összehasonlítása nem egyértelmű, mert az erősségük attól függően változik, milyen energián vizsgáljuk őket; jó okunk van például feltételezni, hogy közvetlenül az ősrobbanás után, amikor az úgynevezett Planck-hőmérséklet — azaz 1,417 • 10³² Celsius-fok - uralkodott, akkor a négy kölcsönhatás egyforma erős volt. Ahhoz azonban, hogy ilyen hőmérsékleten le tudjuk írni a fizikát, a gravitáció kvantumelméletére lenne szükségünk, ami azonban egyelőre még nem áll kellő részletességgel a rendelkezésünkre. Azokon az energiákon azonban, amelyekkel a hétköznapi életben van dolgunk, a gravitáció negyven nagyságrenddel gyengébb az elektromágneses erőnél, vagyis, ha le akarnánk írni a két erő arányát kifejező számot, akkor az 1-es után negyven nullát kellene tennünk. Ez az arány képtelenségnek hangzik, ezért magyarázatot igényel. A fizikusok a Világegyetem extra térbeli dimenzióiról spekulálnak, és más, hasonlóan egzotikus ötleteket vetnek fel, de mindeddig nincs olyan kísérleti bizonyítékunk, amelyik közelebb vinne a megoldáshoz. Az egyik lehetőség az, hogy a természet állandói az ősrobbanáskor véletlenszerűen vették fel értékeiket, vagyis kiszámíthatatlan azoknak a konstansoknak az értéke, amelyek megszabják, hogy véletlenül éppen milyen lett az a Világegyetem, amelyikben élünk. De az is lehet, hogy egy szép napon majd rájövünk arra az elméletre, amelyik megmagyarázza, miért éppen akkora az alapvető fizikai állandók értéke, amekkorának tapasztaljuk.

Newton úgy fedezte fel a gravitáció törvényét, hogy egyszerű összefüggést keresett, amelyik leírja a bolygók látszólag bonyolult mozgását a Nap körül. A bolygómozgások három, Keplertől származó, empirikus törvénye levezethető Newton gravitációs törvényéből és mozgástörvényeiből. Ezért tekintjük Newton elméletét elegánsnak, összhangban azzal, amit korábban a kvantumelmélettel kapcsolatban írtam. Newton felfedezett egy egyszerű összefüggést, amelyik a jelenségek széles körének leírására használható: a Földön a tüzérségi lövedékek röppályájának kiszámítására éppúgy, mint a bolygók Nap körüli pályájának leírására, de a Jupiter és a Szaturnusz holdjainak bolygóik körüli vagy a csillagok galaxison belüli mozgását is ezek a törvények szabják meg. Ez volt az elsőként felismert, valóban egyetemes érvényű természeti törvény.

Feltett kérdésünkre, „Miért gömb alakú a Föld?”, tehát valahol Newton egyenletében kell keresnünk a választ, hiszen a Föld a gravitáció hatására alakult ki. A gravitációs erő a bolygók szobrásza. Naprendszerünk egy gáz- és porfelhőből alakult ki, amelyik körülbelül 4,6 milliárd évvel ezelőtt a gravitáció vonzásának hatására összeomlott. Először a Nap jött létre, majd a bolygók. Forgassuk most vissza az idő kerekét, és képzeljük magunk elé azt az állapotot, amikor a frissen megszületett Nap a még bolygók nélküli Naprendszer közepén világít! A fiatal Nap körül annak a gáz- és porfelhőnek a maradványai keringenek, amelyikből a Nap megszületett, és amely anyagban a bolygók elkészítéséhez szükséges minden hozzávaló megtalálható. Ezt az anyagot nevezzük protoplanetáris korongnak. A bolygók kialakulásának apró részletei jelenleg is intenzív kutatás tárgyát képezik, mindenesetre a mechanizmus eltérő lehet a Földhöz hasonló kőzetbolygók, illetve a Jupiterre hasonlító gázóriások esetében. A Föld-szerű bolygóknál a porszemcsék véletlen ütközései körülbelül 1 kilométer átmérőjű objektumok, az úgynevezett planetezimálok összetömörülését eredményezik. Ezek gravitációs vonzásuk révén kisebb kő- és porcsomókat húznak magukhoz, miáltal nő a tömegük és erősödik a gravitációjuk, vagyis egyre több testet vonzanak magukhoz és így tovább. Ez a folyamat a megszaladó anyagbefogás (akkréció). A Newton-törvényeken alapuló számítógépes szimulációk eredménye szerint az egyre nagyobbra hízó planetezimálok sorozatos ütközései következtében a fiatal csillag körül keringő protoplanetáris korongból néhány kőzetbolygó alakul ki.

A bolygókeletkezési modelljeinket fiatal csillagrendszerek távcsöves megfigyelésével ellenőrizni lehet. 2014-ben a chilei ALMA Obszervatórium (Atacama Large Millimeter/submillimeter Array, az Atacama-sivatagban, milliméteres és szubmilliméteres hullámhosszakon működő nagy rendszer) látványos képeket készített egy protoplanetáris korong belsejében éppen kialakuló bolygórendszerről a HL Tauri jelű csillag körül. A rendszer mindössze 100 000 éves, és csak 450 fényévre van a Földtől. Világosan megfigyelhető a korongban koncentrikus gyűrűk sorozata, amelyeket sötét sávok választanak el egymástól. Feltételezik, hogy ezek a sávok azért sötétek, mert ezeket már kitisztították azok a bolygókezdemények, amelyek a csillag körül keringve összegyűjtik a környékükön lévő anyagot - tehát tulajdonképpen a sávok a bolygópályák „árnyékai”. Érdemes megemlíteni, hogy a bolygók kialakulása ebben a nagyon fiatal rendszerben már meglehetősen előrehaladottnak tűnik. A rendszerről készített kép valószínűleg bepillantást enged abba, milyen lehetett a Naprendszerünk mintegy 4,5 milliárd évvel ezelőtt.

„FORCA, EQUILIBRI, VALOR I SENY” (ERŐ, EGYENSÚLY, BÁTORSÁG ÉS JÓZAN ÉSZ)

A kőzetbolygók tehát kis, szabálytalan alakú planetezimálokként kezdik életüket, és csak az idő múlásával fejlődnek gömbökké. Ha meg akarjuk érteni, miért, akkor fel kell figyelnünk arra, hogy a Naprendszerben nem minden égitest gömb alakú. A Mars egyik holdjának, a Phobosnak körülbelül 11 kilométer a sugara. Az égitest egy alaktalan csomó. Még ennél is kisebbek egyes kisbolygók, üstökösmagok és azok a porszemek, amelyek a bolygókkal egy időben keletkeztek. A 67P jelű Csurjumov-Geraszimenko-üstökös magja még az 5 kilométeres nagyságot sem éri el, furcsa alakja súlyzóra emlékeztet. Az e sorok írásakor az üstökös körül keringő Rosetta űrszonda adatainak elemzése azt mutatta, hogy az üstökös magja két nagyobb test kis sebességű összeütközésének eredményeképpen jött létre. Talán az üstökös magja pillanatképet mutat abból a folyamatból, amelyik korábban a sokkal nagyobb égitestek, a bolygók és holdak létrejöttéhez vezetett. A kisebb anyagcsomók a gravitáció hatására összeolvadnak, és ha elég anyag található a közelben, mint ahogyan az a Naprendszer történetének legkorábbi szakaszában lehetett, akkor a testek sok ilyen ütközést szenvednek el, miközben egyre nagyobbra nőnek. De vajon miért nem gömb alakú a 67P üstökös?

Emlékezzünk vissza az embertoronyra! Mi szabja meg a torony maximális magasságát? Képzeljünk el egy olyan helyzetet, ahol az embertorony minden szintjét csak egyetlen ember alkotja, aki az alatta álló vállán áll. Ha a torony csak kétszintes, akkor az alul álló emberre csak a fölötte álló személy súlya nehezedik. Vizsgáljuk meg ezt a helyzetet! Mi a súly? A Föld felszínén mérhető testsúlyunkat Newton formulája adja meg; ez az az erő, amelyet a Föld a testünkre kifejt. Milyen számokat helyettesítsünk az összefüggésbe, ha ki akarjuk számítani az erő nagyságát? Legyen a tömegünk 75 kg. A Föld tömege 5,972 • 10²⁴ kg. Newton gravitációs állandója G = 6,6738 • 10^-11 m³ kg^-1 s^-2. De mit írjunk r helyére? Ez testünk középpontja és a Föld középpontjának távolsága. Ez kissé merészen hangzik. Pontosabban r a Föld tömegközéppontja és testünk tömegközéppontja közötti távolság, de ehelyett Newton formulájában jó közelítéssel a Föld sugarát használhatjuk. Azért, mert a mi magasságunk elhanyagolható a Föld átlagos, 6 371 000 méter sugarához képest, érdemben nem változtat a számítás eredményén, ha testünk tömegközéppontja néhányszor tíz centiméterrel magasabbra vagy alacsonyabbra kerül.

A számokat Newton képletébe helyettesítve azt kapjuk, hogy a Föld felszínén ránk ható erő - vagyis a súlyunk - körülbelül 736 newton (1 newton az az erő, amelynek a hatására 1 kg tömeg 1 m/s² gyorsulással mozog).

Most egy másik Newton-törvényre is szükségünk lesz, méghozzá a harmadik mozgástörvényre, amelyet ugyancsak a Principiában közölt: a hatással mindig egyenlő nagyságú és ellentétes visszahatás áll szemben. Ez azt jelenti, hogy a Föld valamekkora erőt gyakorol ránk, mi pedig ugyanekkora, de ellentétes irányú erőt fejtünk ki a Földre. Most már megérthetjük, mi történik, amikor az embertorony egyre magasabbra nő. Ha valaki a másik ember vállára áll, akkor körülbelül 730 newton erővel nyomja az alatta állót. Ha még egy ugyanekkora tömegű ember felmászik, akkor a legalul álló emberre ható erő megkétszereződik: már 1460 newton lesz. Ha további két ember felmászik, és így a torony már öt emelet magas lesz, akkor a legalul állóra 2920 newton hat és így tovább. Nyilvánvaló, hogy valamikor elérkeznek ahhoz a ponthoz, amikor a legalul álló ember már nem elég erős ahhoz, hogy megtartsa a tornyot, így az összeomlik. Ez az a helyzet, amikor a castellerek ügyessége szóhoz jut. Ha a legalsó szintet sok ember alkotja, akkor szét lehet osztani az erőt az emberek között, így magasabbra lehet építeni a tornyot, még mielőtt a katasztrófa bekövetkezik. Ennek természetesen ára van; a nagyobb alapra nagyobb első szint épülhet, arra nagyobb második és így tovább. A több emberből álló szintek azonban nagyobb erőt fejtenek ki az alattuk lévő szintre. A gravitációs feladvány zseniális geometriai megoldásai a próbálgatás, az ösztönös megérzések és az ügyesség eredményeképpen alakulnak ki - ez az, ami olyan izgalmassá teszi a tarragonai castells versengést. Számunkra azonban az egészből csak az alapelv érdekes. Minél magasabbra épül a torony, annál nagyobb erő hat az aljára, és végül elérnek egy határt.

Talán már sejtik, hová szeretnék kilyukadni. A magas embertornyokat azért nehéz megtartani, mert a torony tömegének növekedésével arányosan nő az aljára ható erő. Ebből érezhetjük, hogy a bolygó felszíne fölé tornyosuló struktúra méretének határt szab a bolygót felépítő kőzetek szerkezeti erőssége, valamint a bolygó tömege, mert az szabja meg a gravitációs vonzás erősségét, következésképpen a struktúra súlyát. A Föld legmagasabb hegye - ha a tengerfenéken elhelyezkedő aljától mérjük - a Hawaii-szigeteken lévő Mauna Kea. A kihunyt tűzhányó 10 kilométer magas, tehát bő egy kilométerrel magasabb a Mount Everestnél. A Mauna Kea lassan süllyed, mert a hegy súlya olyan óriási, hogy azt már az alatta lévő kőzet képtelen megtartani. A Mars ezzel szemben kisebb tömegű bolygó. Tömege mindössze 6,39 • 10²³ kg, ami a Földének körülbelül 10%-a, sugara pedig feleakkora, mint a Földé. Newton gravitációs törvényét felhasználva, gyors számítással azt kapjuk, hogy egy test súlya a Mars felszínén csak 40%-a a földi súlyának. Mivel a Mars a Földéhez hasonló összetételű, a felszínét alkotó kőzetek nagyjából ugyanolyan erősek, amiből az következik, hogy a Mars felszíne nagyobb tömegű hegyeket képes megtartani, mert azoknak ott kisebb a súlyuk - mint ahogy valóban ez a helyzet. A Marson emelkedő Olympus-hegy a legmagasabb hegy a Naprendszerben, több mint 24 kilométer magas, vagyis majdnem annyi, mintha három Everestet raknánk egymás tetejére. Óriási súlya miatt egy ekkora monstrum elképzelhetetlen a Földön, mert a Földnek nagyobb a tömege, ezért erősebb gravitációs vonzást fejt ki a felszínén.

Látjuk tehát, hogy léteznie kell egy határnak, amilyen magasságig egy bolygó felszínén a hegyek emelkedhetnek. Minél nagyobb tömegű a bolygó, annál erősebb a gravitációs vonzás a felszínén, és annál alacsonyabb a legmagasabb struktúra, amelyet a felszíne még képes megtartani. Ahogy a kialakulóban levő bolygók egyre nagyobbá válnak, az erősebb gravitáció következtében úgy lesz egyre simább a felszínük. A kisebb tömegű bolygók felszíne egyenetlenebb. Közeledünk tehát kérdésünk megválaszolásához; megtaláltuk ugyanis azt a mechanizmust, amelyik kisimítja a bolygók felszínét. Már csak arra vagyunk kíváncsiak, miért jelenti ez azt, hogy a felszín éppen gömb alakúvá simul ki.

Képzeljünk el egy hegyet a bolygó felszínén. Magasodjék a hegy, mondjuk, az Északi-sarkon. Ezután lelki szemeink előtt fordítsuk el 90 fokkal a bolygót, így a hegy az Egyenlítőre kerül. Megváltozott ettől valami? A hegy maximális magasságára vonatkozó okoskodásunk változatlanul érvényes, mert a felszínen ható gravitációs erő kizárólag a bolygó tömegétől és sugarától, valamint a hegy tömegétől függ. Newton gravitációs egyenlete semmiféle szögre sem hivatkozik.

Bonyolultabban is fogalmazhatunk persze, és azt is mondhatjuk, hogy Newton gravitációs törvénye szimmetrikus az elforgatásra nézve. Ezen azt értjük, hogy két adott test között ható gravitációs erő nagysága független a testek egymáshoz viszonyított helyzetétől. Ez példa arra, mire gondolnak a matematikusok és a fizikusok, amikor a természet valamelyik törvényének vagy összefüggésének szimmetriájáról beszélnek. Egyben azt is jelenti, hogy ha a Föld bármely pontjára vonatkozóan kiszámítjuk a hegy maximális magasságát, akkor a hegy helyétől függetlenül mindig ugyanazt az eredményt kell kapnunk, mert Newton gravitációs törvénye szimmetrikus az elforgatásra nézve. A gravitációs törvény szimmetriája tükröződik az objektumok formájának szimmetriájában. A gravitáció kisimítja a hegyeket, demokratikusan, szimmetrikusan, mert azok az objektumok, amelyekre elég nagy gravitációs erő hat, legyőzik saját anyaguk szilárdságát, ennek következtében pedig a test végül gömb alakúvá válik. Ez az oka a Föld gömbszimmetrikus alakjának.

Mély gondolat rejtőzik itt, amelyik a modern elméleti fizika lényegét mutatja. Rendkívül hatékony és talán alapvető módszernek bizonyul, ha a szimmetriákból kiindulva gondolkozunk. Nézzük például annak a lehetőségét, hogy a természetben jelen vannak bizonyos szimmetriák, amelyek a Világegyetem alapvető tulajdonságait alkotják. Ezeket a szimmetriákat tükrözik a létrejövő fizikai objektumok. Képzeljünk el például egy olyan univerzumot, amelyik csak a 90 fokos elforgatásokra nézve szimmetrikus természeti törvényeket enged meg. Egy ilyen univerzumban csak olyan objektumok jöhetnek létre, amelyek csakis 90 fokkal történő elforgatás esetén maradnak változatlanok; tehát kockák létezhetnének, gömbök viszont nem. Ez korántsem olyan őrültség, mint amilyennek hangzik. Amennyire tudjuk, a mi Világegyetemünkben is érvényes néhány erőteljesen korlátozó jellegű szimmetria, és ezek a dolgok mélyén fekvő szimmetriák határozzák meg, mely szubatomi részecskék létezhetnek, és közöttük milyen kölcsönhatások működhetnek. (Ezek azonban nem a háromdimenziós tér szimmetriái, mint amilyen például a kocka elforgatásra nézve mutatott szimmetriája, hanem sokkal absztraktabb szimmetriák.) Valójában a természet minden, ma alapvetőnek gondolt törvénye megérthető, ha a szimmetriákból indulunk ki. Természetesen valamilyen nagyon komoly érvnek kellene amellett szólnia, hogy a természet szimmetriáit valóban alapvetőeknek kell tartanunk. Steven Weinberg, a Nobel-díjas fizikus például így fogalmazott: „Szeretnék ehelyütt felvetni valamit, amiben nem vagyok teljesen biztos, de legalábbis a lehetőségek egyikének tartom: talán a kvantummechanika alapelvein kívül nem is kell mást mondanunk a világról, elég, ha meghatározzuk a természet egy szimmetriacsoportját.” Az ugyancsak Nobel-díjas Philip Anderson szerint: „Nem sokat túlozunk, ha kijelentjük, hogy a fizika a szimmetriák tudománya.” A Nobel-díjas David Gross így írt: "Aligha képzelhető el jelentős haladás a természet törvényeinek levezetését illetően bizonyos szimmetriák létezése nélkül... Napjainkban egyre inkább rájövünk arra, hogy a szimmetriaelvek fontosabbak, mintsem gondoltuk - ezek szabják meg, milyenek legyenek a természet törvényei.” Az a komplexitás, amelyet alkalmanként a Világegyetemre pillantva érzékelünk, eltakarja a szemünk elől a mélyen rejtőző szimmetriákat. A modern elméleti fizika egyik célja viszont pontosan az, hogy a komplexitás leplét lerántva, elénk tárja a természet törvényeinek hátterében álló egyszerűséget és szimmetriát.

Visszatérve eredeti problémánkhoz, a bolygók és holdak alakjára vonatkozó fenti gondolatmenet ellenőrizhető előrejelzéshez vezet: eszerint az égitestek akkor gömb alakúak, ha elég nagyok, következésképpen elég nagy tömegűek ahhoz, hogy a felszínükön érvényes gravitációs vonzás legyőzze az őket alkotó kőzetek szerkezeti szilárdságát. A kőzetek szilárdsága végső soron a természet azon kölcsönhatásainak erősségével áll kapcsolatban, amelyek összetartják a kőzeteket alkotó anyagokat - a szilícium-dioxid molekuláit vagy a más molekulákban előforduló vasat és egyéb anyagokat. Ez az elektromágneses erő, mi más lehetne? Mindössze négy kölcsönhatás létezik, ebből kettőnek a működése a hatótávolságuk miatt az atommagra szorítkozik. A nagy objektumok, mint például a bolygók formáját a gravitáció és az elektromágnesség összjátéka szabja meg, az előbbi igyekszik gömbbé simítani a testeket, az utóbbi viszont ellenáll ennek. Kiszámíthatjuk, hozzávetőlegesen mekkora lehet az a legkisebb anyagcsomó, amelyiknek közelítőleg gömb alakúnak kell lennie. Ehhez össze kell hasonlítanunk az égitest felszíne közelében lévő sziklatömb súlyát az alatta elhelyezkedő kőzet mechanikai szilárdságával.

(A gömb alakú kőzettestek legkisebb mérete és a Föld legmagasabb hegyei. Képzeljünk el egy hatalmas kőkockát, egy még nagyobb kőgolyó, például egy bolygó felszínén (kocka helyett bármilyen más formát is választhatnánk, de talán így könnyebb magunk elé képzelni). Ha a kocka túl nagy, akkor súlya alatt megroppan az alatta lévő kőzet, a kocka pedig elsüllyed. Nyilván hatalmas súly kell ahhoz, hogy a kőzet a kocka nyomásának engedve deformálódjék. A gránit például 130 millió newton/m² (vagyis 130 MPa) nyomásnak is ellenáll, ami a légnyomás valamivel több mint ezerszerese. Feltételezzük, hogy a nagy kőgolyónk körülbelül 100 MPa nyomófeszültségig képes ellenállni, ezt a határt P-vel jelöljük. Ezután ki kell számítanunk, mekkora a A magasságú (élhosszúságú) kocka súlya. A súlyt úgy kapjuk meg, hogy a tömegét megszorozzuk (Newton törvénye értelmében) GM/R²-tel, ahol M a nagy gömb tömege, R pedig a sugara. Legyen a kocka sűrűsége a földi kőzetekre jellemző p = 3000 kg/m³, ebben az esetben tömege p • h³. A gömb tömegét hasonló módon az M = 4/3 • 3,14 • R³ • p összefüggéssel kapjuk meg (ahol 3,14 a gömb térfogatának kiszámításához használt π arányossági tényező közelítő értéke). Hozzávetőleges számításunk céljára a 3,14/3 hányadost közelítőleg 1-nek tekinthetjük, ez nem okoz lényeges változást (elvégre csak durva becslést kívánunk végezni, nem tökéletesen pontos számítást). Mindezt figyelembe véve azt kapjuk, hogy a kocka súlya p • h³• G • 4R • p. Ekkora súly nehezedik az alatta lévő kőzetre, ami akkor enged a nyomásnak, ha a súly nagyobb, mint amekkorát az adott nyomófeszültséget elviselő kőzet a kocka alatti területen elbír, vagyis a súly nagyobb, mint P • h². Más szavakkal, a kőzet akkor roppan meg a kocka súlya alatt, ha h³ • G • 4R • p² nagyobb mint P • h². Ebből következik, hogy h-nak kisebbnek kell lennie, mint P/(G4Rp²). Ha ez a h-ra kapott maximális érték kisebb a gömb sugarának 10%-ánál, akkor a kocka ottléte ellenére a gömböt továbbra is gömbnek tekintjük (vagyis a kocka csak kis kidudorodást jelent a nagyobb gömb felszínén). Ha a h/R = 0,1 értéket behelyettesítjük, akkor azt kapjuk, hogy a bolygó sugarának nagyobbnak kell lennie P/(0,1 G4p²) négyzetgyökénél. A további számértékeket behelyettesítve azt kapjuk, hogy a sugár valamivel nagyobb 600 kilométernél. Ezt a számot nem kell szó szerint érteni, hiszen a kőzet sűrűségére és szilárdságára csak hozzávetőleges, átlagos értékeket használtunk, amelyektől az egyes bolygókon, kisbolygókon és üstökösökön a tényleges értékek eltérhetnek. Ez azonban nem kisebbíti kapott eredményünk jelentőségét. Számításunk bebizonyította, hogy a körülbelül 600 kilométernél nagyobb sugarú kőzettömegek meglehetősen sima felületűek igyekeznek lenni, mert a felszínükön előforduló nagy struktúrák alámerülnek, és elnyelődnek a belsejükben. Ha már idáig eljutottunk, akkor gyorsan arra is becslést végezhetünk, mekkorák lehetnek a legmagasabb hegyek a Földön, illetve a Marson. Valójában ezeket az imént már ki is számítottuk. A Földön a hegy lehetséges legnagyobb magassága P/(G4Rp²). A Földön a GM/R² tényezőt (ahol M a Föld tömege, R pedig a sugara) a g gravitációs gyorsulásnak nevezzük, amelynek nagysága jó közelítéssel 10 m/s². Ez azt jelenti, hogy a kocka alakú hegy akkor süllyedne el, ha magasabb lenne, mint Pg/p, ami körülbelül 3,3 kilométernek felel meg. Ha a hegy nem kocka, hanem kúp alakú, akkor az eredmény 3-szor ekkora, vagyis körülbelül kilométer, ami nagyon közel van a Föld legmagasabb hegyeinek magasságához. A Marson, ahol a felszíni gravitáció csak körülbelül 40%-a a földinek, ennek értelmében a legmagasabb hegy 10 km / 40% = 25 kilométer magas lenne, ami nagyjából megfelel az Olympus-hegy magasságának.)

Számításaink helyességét a Naprendszer égitestjeit megfigyelve ellenőrizhetjük. A Phobos megfelel várakozásunknak; közepes sugara alig több 11 kilométernél, tömege pedig mindössze 10¹⁶ kg, vagyis a felszínén túl gyenge a gravitáció ahhoz, hogy legyőzze a kőzetek merevségét, és a felszínt kisimítva, gömbbé formázza a Phobost. Körülbelül 550 kilométeres átmérőjével a Pallas kisbolygó a legnagyobb ismert, nem gömb alakú égitest. A Szaturnusz egyik holdja, a Mimas sugara viszont nem éri el a 200 kilométert, mégis gömb alakú, ez a legkisebb gömbölyű égitest a Naprendszerben. Ez a hold viszont túlnyomórészt jégből áll, amely könnyebben deformálható, mint a kőzet — ez az oka annak, hogy kis mérete ellenére mégis gömb formájú. Becslésünk tehát a helyes mérettartományba esik.

Fontos kitérőként megemlítem, hogy az efféle, „papírcetlin elvégezhető” becslések nagyon fontosak a fizikában; elárulják ugyanis, jó nyomon járunk-e, anélkül, hogy szükségtelenül túl kellene bonyolítanunk a dolgokat. Finomíthattuk volna a számításunkat, ha figyelembe vesszük a különböző égitestek jellemző kémiai összetételét és pontosabban számítjuk ki különböző mélységekben a gravitációs vonzás erősségét. Megpróbálkozhattunk volna azzal is, hogy Newton törvényei helyett az általános relativitáselméletet használjuk, de ezzel sem jutottunk volna sokkal előbbre. A tudományt hivatásszerűen művelőknek meg kell tanulniuk azt, mit lehet elhanyagolni és mit kell figyelembe venni - ezt nevezhetjük fizikai érzéknek. Nincs pontos mérethatár, amely fölött az égitestek gömb alakúak, mert a tényleges határ függ az objektum összetételétől: a jég és kőzetek keverékéből álló testek könnyebben deformálhatok, mint a teljes egészében kőzetekből állók. Általános szabályként mégis kijelenthetjük, hogy a 400 kilométernél nagyobb átmérőjű jeges hold gömb alakúvá válik. A kőzetekből álló testeknek nagyobbaknak kell lenniük, mert alakjuk megváltoztatásához erősebb gravitációra van szükség. Ha egy kőzetekből álló holdnak belső energiaforrása van, például azért, mert a belsejében több radioaktív anyagot tartalmaz, vagy erősebb árapályerők hatnak rá, akkor könnyebben deformálható, és így már kisebb méret esetén is gömb alakú lesz, szemben a kevésbé aktív, hasonló nagyságú holdakkal. A Naprendszerben se szeri, se száma a merevség és a gravitáció összjátékát mutató példáknak, nagyon durva közelítéssel mégis sikerült levezetnünk azt a megállapítást, miszerint a néhány száz kilométert meghaladó sugarú égitesteknek gömb alakúaknak kell lenniük, mert ezeknél a gravitációs erő legyőzi a kőzetek szilárdságát.

Amikor a gravitáció diadalmaskodik, akkor az általa létrehozott objektumok alakja a fizikai törvény mélyén rejtőző szimmetriát tükrözi. Ezért mindig gömb alakúak a nagyméretű és egyedülálló égitestek.

A nagyobb méretek világában azonban változik a helyzet. Legközelebbi nagy galaxisszomszédunk, az Androméda-köd mintegy 400 milliárd csillagból áll, amelyeket a gravitáció alakított ki és tart össze. A galaxis mégsem gömb, hanem korong alakú. Miért?

Azzal érveltünk, hogy a bolygók és a nagy holdak gömb alakúak, mert ha a gravitációs erő elég nagy ahhoz, hogy legyőzze az anyagot szilárd állapotban tartó elektromágneses erőket, akkor a gravitációs kölcsönhatás hátterében álló szimmetria nyilvánul meg a létrehozott objektumok alakjában. Minthogy Newton gravitációs törvénye nem tartalmaz kitüntetett irányt, ezért nincs kitüntetett irány a keletkező égitesteken sem. Ez azonban még a bolygókra sem teljesen igaz, mert az égitestek forognak.

Bolygónk 24 óránként fordul meg a tengelye körül. A forgástengely kijelöl egy speciális irányt, ami azt jelenti, hogy a Föld felszínének pontjai mégsem teljesen egyenértékűek. Aki a Föld Egyenlítőjén áll, az 1670 km/óra kerületi sebességgel mozog, míg Minnesotában ugyanez a sebesség csak 1180 km/óra. A gömbszimmetria tehát sérül - a két pont különbözik egymástól. Amint a 2. fejezetben látni fogjuk, ennek a különbségnek megfigyelhető jelei vannak például a légköri ciklonok forgásának irányára vagy a tüzérségi lövedékek röppályájára. A forgás a Föld alakjának csekély mértékű lapultságát is okozza - a Föld egyenlítői kerülete 40 075 kilométer, míg a poláris (a sarkokon átmenő) kerülete csak 40 008 kilométer. A Föld tehát nem pontosan gömb alakú, hanem forgása következtében lapult ellipszoid. Ha gyorsabban forogna, lapultabb lenne. Amikor a Naprendszer kialakult, akkor a forgása - pontosabban szólva az impulzusmomentuma - az újonnan létrejött Naptól kifelé „adódott át”, elsősorban a protoplanetáris korongban létrejövő ütközések és mágneses kölcsönhatások révén. Ennek eredményeképpen a rendszer korong alakúvá lapult.

Néhány azon tulajdonságok közül, amelyet a Naprendszer korongjában a szimmetria részleges elveszése okoz.

Ha a forgás kifelé, vagyis a középponttól távolodó irányban adódik át, ez egyes galaxisokat lapulttá tesz, ilyen az Androméda-köd is. A gömbhalmazok, például a látványos Messier 80, ezzel szemben gömbszimmetrikusak maradnak, mert szerkezetük túl diffúz ahhoz, hogy az impulzusmomentum át tudjon adódni kifelé. A gravitáció által összetartott objektumok alakja tehát a „forgás” mértékétől és tengelyének irányától függ. A fizikában jártas olvasók számára azt is elárulom, hogy az L impulzusmomentum és az E gravitációs potenciális energia aránya számít. Nagy L/E = korong; kis L/E = gömb.

A jelenség hátterében nagyon fontos gondolat bújik meg. A „szimmetriasértés” fogalmát használtuk annak leírására, hogyan jelöl ki a forgástengely jelenléte egy meghatározott irányt, aminek következtében az objektum nem „tökéletesen” gömb alakú, ami a jelenség hátterében álló természeti törvény - esetünkben a gravitáció - szimmetriáját tükrözné. Korong alakú Naprendszerünk kevésbé szimmetrikus, mint egy gömb, mert csak akkor marad ugyanolyan, ha a tér egy bizonyos tengelye - nevezetesen a forgástengely - körül forgatjuk el. A szimmetria egy része tehát elveszett. Úgy fogalmazhatunk, hogy a Naprendszert létrehozó gravitációs törvény szimmetriáját elrejtette az a körülmény, hogy a térben jelen van egy kitüntetett irány - a forgástengely iránya. Maga a forgás a kezdeti porfelhő csaknem 5 milliárd évvel ezelőtti összeomlásának pontos részleteiből adódott, míg a forgás mennyiségének megoszlása a Nap és a bolygók között az összeomlás pontos sebességétől, a protoplanetáris korong sűrűségétől és rengeteg további, apró részlettől függ, amelyek a Naprendszer keletkezésének történetében szerephez jutottak. Mindez rávilágít a modern természettudomány előtt álló legfontosabb kihívásra: el kell tudni dönteni, hogy a természetben megfigyelt struktúrák mely tulajdonságai a háttérben álló természeti törvények szimmetriájának tükröződései, és melyeket határoznak meg a keletkezés közben előforduló más körülmények. Ezt különösen akkor nagyon nehéz megállapítani, ha bonyolult rendszerekről van szó. A bolygók, bolygórendszerek és galaxisok, bár csillagászati méretűek, mégis könnyebben magyarázhatók, mint némely hétköznapi objektum, amelyekkel nap mint nap találkozunk. Hagyjuk most ott a bolygókat, és egy hatalmas ugrással térjünk át a létező struktúrák közül a legösszetettebbekre - az élőlényekre. Az élő szervezetek szimmetriáinak és struktúrájának felderítésével tovább vizsgálhatjuk azt az elgondolást, amely szerint a fizikai objektumok alakja a fizikai alapelvek és az adott objektumok kialakulásának története közötti komplex összjáték eredménye.

A természet alapvető építőkövei és kölcsönhatásai

Miért gömb alakú a Föld?