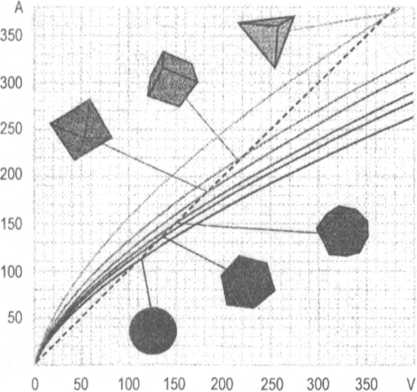
A diagram azt mutatja, hogyan csökken az egyre lekerekítettebb formájú testek esetében a felszín (A) és a felszin/térfogat arány, ha a térfogatot (V) növeljük.
A gravitáció és az elektromágneses kölcsönhatás közötti versengés simítja gömbökké a bolygók és a holdak felszínét, és korlátozza a felszínükön előforduló legnagyobb hegyek magasságát. Könyvem egyik központi gondolata értelmében, amelyet majd a 3. fejezetben fejtek ki részletesen, nincs lényegi különbség az élettelen dolgok, például a bolygók, és az élőlények, például a baktériumok vagy az emberek között; a Világegyetemben minden objektum ugyanazokból az összetevőkből áll, és a természet ugyanazon kölcsönhatásai alakítják ki őket. Ezért arra kell számítanunk, hogy az élőlények formáinak és funkcióinak is határai vannak, amelyeket a természet törvényei kényszerítenek rájuk. Az élő szervezetek felépítését természetesen nem kizárólag a fizika alapvető törvényei határozzák meg, hiszen a háttérben ott működik a természetes kiválasztódás által irányított evolúció, amelyik az idők során úgy alakítja az élőlényeket, hogy azok minél jobban alkalmazkodjanak változó környezetükhöz, a más élőlényekkel való kapcsolataikhoz és a rendelkezésre álló környezeti fülkék sokaságához. Ezt az alkotó összjátékot a fizika törvényeinek kérlelhetetlen determinizmusa és a földi élet nyüzsgő, végtelenül összefonódott és örökké változó genetikai adatbázisa között gyönyörűen ragadja meg Darwin A fajok eredete záró gondolataiban:
„Nagyszerűség van ebben a felfogásban, amely szerint a Teremtő az életet a maga különböző erőivel eredetileg csak néhány vagy csak egyetlen formába lehelte bele; és mialatt bolygónk a nehézkedés megmásíthatatlan törvénye szerint keringett, ebből az egyszerű kezdetből végtelen sok szépséges és csodálatos forma bontakozott ki, s bontakozik ki még most is. (Dr. Mikes Lajos fordítása)
Másik visszatérő témánk a régi korok természettudósai ellentmondást nem tűrő kíváncsiságának méltatása. Izgatott költői stílusban írják le a témába vágó és lényeges elképzeléseiket, előadásmódjuk mégis valahogyan nélkülözi a mai hivatásos természettudomány megkövetelte komolyabb és szabatosabb megfogalmazást. A modern korban is vannak nagyszerű szerzők, akik megragadják a tudomány logikáját, világosságát és csodáit — hirtelen Richard Feynman, Richard Dawkins és Carl Sagan jut az eszembe de mégis van valami szívderítő abban, amikor szavakban látjuk kibontakozni a tudományt. A reneszánsz szerzők korlátai oly gyakran azonosak az egész emberi tudás korlátaival, hogy a szóban forgó vizsgálódások közel valós idejűeknek tekinthetők, nem pedig egy jól kitaposott szellemi ösvény emlékeinek. Talán ez az, ami olyan szívderítően intellektuális hangvételt kölcsönöz a régi korok mesterei írásainak.
Éppen úgy, ahogy a gravitáció megszabja a Föld hegyeinek maximális magasságát, annak is korlátot szab, milyen formákat alakíthat ki a természetes kiválasztódás, mert korlátozza, mekkora lények élhetnek a Föld felszínén. Négyszáz évvel ezelőtt Galilei megvizsgálta, hogy milyen tényezők határozzák meg, mekkora lehet egy állat. Hasonlóan a hópelyhek szerkezetén eltűnődő Keplerhez, ő is a kora tudásának élvonalába tartozó, sőt azokat megelőző munkát végzett. Galilei utolsó könyve a Matematikai érvelések és bizonyítások volt, amelyet házi őrizetben írt. A könyvet 1638-ban jelentette meg a holland Lodewijk Elzevir kiadó, mert az inkvizíció szorításában ezt más országban nem lehetett megtenni. Akármelyik tudós elolvassa ezt a könyvet, ismerősnek fogja találni a kiadó nevét, mert az Elsevier ma is a vezető tudományos könyvkiadók közé tartozik. Galilei három ember, Simplicio, Sagredo és Salviati beszélgetése formájában írta meg a könyvét, akik mindegyike a szerző más-más korú énjét jeleníti meg, a korának megfelelő tudásával. A szereplők négy napig tartó beszélgetésük során egyik kérdést a másik után vetik fel, és minden problémát alaposan megvitatnak, mielőtt áttérnének a következőre. A könyv olyasféle élvezetet nyújt, mintha a parkban kifülelnénk a szomszéd padon ülők beszélgetését - bár a közparkok padjain ritkán szoktak ilyen elmélyült eszmecserét folytatni. Galilei végigvezet a kor fizikájának legfontosabb kérdésein, beleértve Arisztotelész fizikájának kritikáját, a gyorsuló mozgást, a tüzérségi lövedékek mozgását és a végtelen természetét. Vizsgálta az anyagok szilárdságát, azt, milyen korlátokat állítanak a természet törvényei az élő és élettelen struktúrák méretére és alakjára vonatkozóan.
Az eddigiekből már világosan láthatja az olvasó, hogy sem a természetes, sem a mesterséges dolgok nagyságát nem lehet minden határon túl növelni. Hasonlóképpen, nem lehetnek eltúlzott méretűek a hajók, a paloták vagy a templomok úgy, hogy az evezőket, az árbocokat, a gerendáikat és az egészet összetartó vasszegecseiket mind felnagyítjuk. A természet sem alkothat rendkívüli méretű fákat, mert ágaik letörnének a saját súlyuk alatt; ugyanígy lehetetlen lenne az emberek, a lovak vagy más állatok csontvázát óriásira növelni, de közben elvárni, hogy teljesítsék megszokott funkciójukat. A méret növelésével együtt kellene járnia, hogy a szokásosnál keményebb és erősebb anyagokat használunk, vagy pedig annyira megnöveljük a csontok méretét, hogy attól már megváltozik az élőlények alakja, és a lény a megszokottól eltérő képet mutatna.
Galilei ismerte fel és mondta ki elsőként a térfogat és a felület közötti kapcsolatot, amelyet ma négyzetes-köbös törvénynek szoktunk nevezni; eszerint, ha egy test méretét növeljük, akkor a térfogata gyorsabban nő, mint a felszíne. Nézzünk például egy 2 cm élhosszúságú kockát. Ennek a felszíne 6 • 2 • 2 = 24 cm2, térfogata pedig 2 • 2 • 2 = 8 cm3. Ha megkétszerezzük az oldalak hosszát, akkor a felszíne 96 cm2-re nő, a térfogata pedig 64 cm3-re. Ha ismét megkétszerezzük az oldalakat, akkor a felszíne 384 cm2-re, a térfogata pedig 512 cm3-re nő és így tovább.
Ez azt jelenti, hogy ha egy állat teste nagyobbra nő, akkor a térfogata és ezzel együtt a tömege gyorsabban nő, mint a testfelülete és mint a csontjai keresztmetszete. Ennek az a következménye, hogy egy lényt nem lehet egyszerűen csak „felnagyítani”. Az egér nem növelhető elefánt nagyságúra, mert a csontváza összeroppanna a súlya alatt - ezért vannak az elefántnak a testméretéhez viszonyítva vastagabb lábai, mint az egérnek. Ez a körülmény végül határt szab annak, mekkorára nőhet a szárazföldön élő állatok teste; a csontok vagy a fák esetében a fa anyagának teherbírása ugyanúgy határt szab a szervezet tömegének, mint ahogy a Föld kérgét alkotó kőzetek szilárdsága határt szab a hegyek magasságának. A Marson viszont az elefántoknak vékonyabb lábaik lehetnének.
Galilei arra is rájött, hogy van egy kivétel ezen szabály alól. Miközben a gravitáció határt szab a szárazföldi állatok méretének és alakjának, addig a fizikai törvények szabta korlátok egészen másfélék a vízben. A tengeri állatok lebegnek a vízben, ami azt jelenti, hogy a gravitáció hatása figyelmen kívül hagyható. Testsúlyuk megtartásához nincs szükségük erős csontokra, ezért ennek a feltételnek nincs hatása testük alakjára. Így beszélget erről Simplicio, Sagredo és Salviati az elképzelt kerti padon. Nem tehetek róla, de hallgatva őket, nekem óhatatlanul Pete és Dud jeleneteinek háromszereplős reneszánsz változata jut az eszembe.
Simplicio: Ezt az állítást fölöttébb könnyű cáfolni: gondoljunk csak arra, milyen hatalmas halakat ismerünk; a bálna példáid, ha jól tudom, akkorára is megnőhet, mint tíz elefánt, mégsem esik széjjel.
Salviati: Ellenvetése éles elmére vall, de mielőtt válaszolnék, engedjen meg egy kérdést: megfigyelte-e már, hogy a halak, ha akarják, mozdulatlanul lebegnek a vízben, nem süllyednek le és nem jönnek fel a felszínre, és mindezt a legcsekélyebb erőkifejtés, úszás nélkül?
Salviati: A vízben élő állatoknál tehát éppen fordított a helyzet, mint a szárazföldieknél: ezeknél az a feladat hárul a csontokra, hogy saját súlyukat és a hús súlyát is megtartsák, amazoknál viszont a hús megtartja saját magát, sőt még a csontokat is. Ennek ismeretében most már nem csodálkozhatunk azon, hogy a vízben létezhetnek igen hatalmas állatok, a földön, tehát a levegőben viszont nem.
Simplicio: Meggyőzött; talán csak annyit fűznék hozzá, hogy ezeket a szárazföldieknek nevezett állatokat voltaképpen helyesebb lenne légi állatoknak nevezni, hiszen levegőben élnek, levegő veszi körül őket, és levegőt lélegeznek.
Sagredo: Élveztem a Simplicio úrral folytatott vitát, a kérdést és a választ is; egyébként könnyen el tudom képzelni, hogy ha ezeket az irdatlan halakat a szárazföldre vonszolnánk, nem sokáig maradnának egyben: a csontjaik közötti ízesülések meglazulnának, és összeroppanna a testük. (Dávid Gábor fordítása)
Megszabadulva a gravitáció zsarnoki uralmától, a vízi állatok nagyobbra nőhetnek szárazföldi rokonaiknál, ám azok sem függetleníthetik magukat teljesen a fizika törvényeitől.
Telente a Floridát körülvevő meleg tengerek adnak otthont a természet szemmel láthatóan egyik legkevésbé elegáns teremtményének. Fontos erre felhívnunk a figyelmet, mert a lomha kinézetű lamantin (karibi manátusz) ugyanolyan jól alkalmazkodott saját környezetéhez, mint a leggyönyörűbb pillangók. A nyugat-indiai lamantin a tengeritehenek (Sirenia) rendjének legnagyobb élő képviselője, egy teljes mértékben vízi életmódot folytató, növényevő emlős. A rendszertanilag nem teljesen pontos, mindamellett jó leírás alapján az állatot 4 méter hosszú, lábatlan, tengerben élő tehénként képzelhetjük el, amely komótosan legelészi a floridai partok mentén lassan áramló tengerben tenyésző tengeri füvet.
A nyári hónapokban a lamantinok északra vándorolnak, egészen Massachusetts magasságáig, de amikor beköszönt a hűvösebb évszak, akkor vissza kell térniük a melegebb tengerekbe.
A 20 °C-nál alacsonyabb hőmérsékletű vízben nem tudnak hosszabban életben maradni. Mivel télen is igénylik a meleg vizet, ezért a lamantinok nagyobb csoportokba verődnek a Florida partjai mentén feltörő meleg források környékén, ahol a tengervíz hőmérséklete egész évben 22 °C fölött marad. Élvezik az emberi tevékenység előnyeit is, szívesen időznek az erőművek kifolyóinál Apollo Beach és Fort Myers környékén. A lamantin tényleg különös állat; közelebbi rokona az elefántnak, mint bármely tengeri állatnak - közös ősük körülbelül 60 millió évvel ezelőtt élt, tehát nem sokkal a dinoszauruszok kihalása után. Ez a közös ős a mai szirti borzokra hasonlíthatott. Ez a körülbelül 50 cm hosszú állat sem az elefántokra, sem a tengeri tehenekre nem hasonlít; ám 60 millió év elég hosszú idő ahhoz, hogy a természetes kiválasztódás rostáján csak az az állat maradjon fenn, amelyik képes kihasználni saját ökológiai fülkéjének előnyeit.
Az elefánt ökológiai fülkéjét az jelenti, hogy ez a legnagyobb testű szárazföldi állat, ami kétségkívül előnyös a ragadozókkal szemben, külleme azonban magán viseli a gravitációval való viaskodás anatómiai jeleit. A négyzetes-köbös törvénynek megfelelően az elefántoknak rendkívül vastag lábuk alakult ki, hogy hordozni tudják jelentős súlyukat. Ne feledkezzünk meg a test hűtéséről sem; a szervezetben termelődő hő a test felszínén keresztül távozik. Minél nagyobb az állat testének térfogata, annál több hőt termel, testének felülete azonban a négyzetes-köbös összefüggés értelmében csak kisebb arányban nő. Ez a szárazföldi állatok számára problémát jelent, az elefánt azonban úrrá lett a helyzeten, mert zseniális hűtőrendszert fejlesztett ki - a nagy füleit.
A lamantin viszont egy másik ökológiai fülkét töltött be. A tengerparton élő szárazföldi állat átalakult vízi emlőssé, mellső végtagjai uszonyokká fejlődtek, bár az ősi, ujjcsontokat és körmöt tartalmazó felépítés megőrződött. Hátsó végtagjai egyetlen hatalmas, evező alakú farokúszóvá alakultak át; ezt a fokozatos evolúciós változást ragyogóan dokumentálják a fosszíliák. Az egykori ős végtagjai az elefántnál megvastagodtak, hogy ellenálljanak a gravitációnak, a lamantinnál viszont áramvonalassá váltak, így az állat akár 12 km/óra sebességgel is tud úszni. A lamantin mélyre le tud merülni, és akár 20 percig is a víz alatt maradhat, de mivel tüdővel lélegző emlősről van szó, ezért időnként a felszínre kell jönnie lélegzetet venni. Annak érdekében, hogy minél hosszabb ideig maradhasson a víz alatt, lelassítja a szívverését és az anyagcseréjét, csökkenti az oxigénszükségletét, de ezen a ponton a biológia már összeütközésbe kerül a fizikával. A lassú anyagcsere korlátozott hőtermelést jelent, a víz azonban nagyon hatékonyan vezeti el a test hőjét, ezért fennáll a test kihűlésének a veszélye. Az állat magától értetődő módon, a természetes kiválasztódás útján felfedezte a kompromisszumos megoldást: nagyobb testűvé fejlődött, miáltal csökkent a felszín/térfogat arány, ezért csökkent az egységnyi térfogatra jutó hőveszteség. További csökkenést eredményezett, hogy a test gömbölydedebbé alakult (lásd az ábrát).
A diagram azt mutatja, hogyan csökken az egyre lekerekítettebb formájú testek esetében a felszín (A) és a felszin/térfogat arány, ha a térfogatot (V) növeljük.

Nagyszerű példát láttunk tehát arra, amikor a természetes módon kifejlődő forma a mélyebb matematikai valóságot tükrözi. A gömb az a háromdimenziós alakzat, amelyiknél a legkisebb a felszín/térfogat arány. Ha nagy térfogatban sok hőt akarunk fejleszteni, de a testfelületen a lehető legkevesebbet szeretnénk elveszíteni, akkor gömb alakú testre van szükségünk - és valóban, a lamantin a Föld leginkább gömb alakú emlőse. Micsoda nagyszerű dolog ez, hacsak nem csillagász valaki. A csillagász Fritz Zwickyről tudjuk, hogy kollégái egy csoportját szférikus korcsoknak nevezte, mert bármilyen irányból nézett rájuk, minden oldalról elfajzottnak látszottak. Ez viszont visszavezet bennünket a szimmetria kérdéséhez. Ha egy fizikusnak kellene megterveznie a lamantin testét, akkor az állat gömb alakú lenne. A szimmetrikus formák, például a bolygók alakja általában a szimmetrikus természeti törvények működésének a következménye, hacsak nincs valamilyen különleges ok a szimmetria sérülésére. A biológiában a nagyméretű szervezetek soha nem tökéletesen szimmetrikusak. Miért?
Leonardo da Vinci Vitruvius-tanulmányában lerajzolt ember talán a történelem leghíresebb emberábrázolása. Az ember egy kör és egy négyzet belsejében két különböző testtartást egymásra rajzolva helyezkedik el. Az arányokat Leonardo gondosan kiszámította, mert az Ember testfelépítése mélyén rejlő tökéletességet akarta bemutatni, illetve közvetlenül összekapcsolni az univerzummal. Da Vincit az egyik legjelentősebb klasszikus mű, az ókori római építész Vitruvius De architectura (Az építészetről) című munkája ihlette. Az emberi test alakjának a körhöz és a négyzethez viszonyítása azokat az ókori elképzeléseket tükrözi, amelyek Platón, Püthagorasz és mások misztikus hagyományaiig nyúltak vissza, amelyek kapcsolatot próbáltak teremteni a természet és a geometria között. Kepler korai, a bolygók mozgásáról írott munkája is szilárdan ebben a hagyományban gyökerezett. Kezdetben úgy gondolta, hogy a bolygók pályái a tökéletes „platóni” testekbe illeszkedően írhatók le, és ezt az elképzelését csak akkor vetette el, amikor a megfigyelési adatok alapján arra a következtetésre kényszerült, hogy a bolygók pályái nem körök, hanem ellipszisek. Érdemes utalni arra a körülményre, hogy a bolygók mozgásának leírása sokkal szebb és elegánsabb, mint ahogyan azt Kepler a geometriai tökéletesség alapján remélte. Amint láttuk, valójában a Naprendszerben az összes bolygó és hold mozgása, sőt a Világegyetem összes bolygórendszerének mozgásai Newton mozgástörvényei és gravitációs törvénye alkalmazásával írhatók le. Ezek olyan egyszerűséget sugallnak, ami bizonyára tetszett volna Keplernek, korábban pedig Platónnak, hiszen Newton törvényei megtestesítik a „tökéletes” gömbszimmetriát, ami rejtve bár, de mégis nyilvánvalóan a törvények alapján létrehozott minden struktúrában jelen van.
Hasonlóképpen, mai szemmel nézve, az emberi test formáját illetően nem a szimmetriája az érdekes, hanem az, hogy ez a szimmetria csak részleges. Amint már említettem, a gömb a tökéletesen szimmetrikus, háromdimenziós forma, hiszen minden irányból nézve ugyanolyannak látszik. Az embereknek - hasonlóan a legtöbb, de nem az összes nagy testű emlőshöz - a testük egyik végén a fejük, a másik végén a végbélnyílásuk helyezkedik el, amelyek az értelmes egyedek többségénél rendkívül eltérő funkciót töltenek be. Az emberi test úgynevezett kétoldalas szimmetriát mutat, legalábbis külsőleg. Ez azt jelenti, hogy fejünk búbjától a talpunkig szimmetriasík húzódik, amelyre nézve testünk tükörszimmetrikus; vagyis van egy bal és egy jobb felünk. Miért?
Ennek a könyvnek egy televíziós sorozat az alapja. Az elvont tudományos fogalmakat elmagyarázni szándékozó dokumentumfilmek készítésekor az egyik problémát annak megtervezése jelenti, hogy az egyes jelenetekben mit mutasson meg a kamera. Rég elmúltak azok az idők, amikor a nézők megelégedtek a felvevőgép hordozható fülkéjében ülő, torzonborz frizurájú, középkorú, kezében méretes tolltartót szorongató tudós látványával. A magam részéről sajnálom, hogy így van, mert én 1968-ban születtem, eredendően kócos a hajam, és nagy tolltartóm is van. Valakinek a BBC-nél ragyogó ötlete támadt, mert úgy gondolta, hogy az élőlények szimmetriájának sokféleségét a Dél-Korea déli partvidéke előtt fekvő Mara-szigeten lenne érdemes bemutatni, ahol a palack nélkül merülő búvárnők élnek.
Koreának ebben a tartományában évszázados hagyomány, hogy a nők légzőfelszerelés nélkül merülnek le a tenger mélyére, ahol összegyűjtik ehető csigákból, kagylókból, tengeri sünökből és polipokból álló értékes zsákmányukat. Munkájuk olyan fontos, hogy Mara vált a világon ritka matriarchális társadalmak egyikévé; hagyományosan az asszonyok dolgoznak a tengeren, miközben a férfiak nevelik a gyerekeket és vezetik a háztartást. A Kelet-Kínai-tenger hideg vizében nem könnyű búvárnőnek (henjo, haenyeo, azaz tengeri nő) lenni. A lányok már 11 éves koruk körül elkezdik a mesterség elsajátítását, majd miután profikká válnak, egész életükben ezzel keresik a kenyerüket. Nem tudjuk, hogyan alakult ki ez a hagyomány, de biológiai szempontból van értelme; ugyanis a nők a férfiaknál jobban tudnak alkalmazkodni a hideg tengervízben végzett munkához. A búvárruhák elterjedése előtt a henjók testét alig valami védte merülés közben, ezért a nők testében található több zsírszövet előnyt jelenthetett. A búvárok gyakran órákon át a vízben maradnak, merülésükkor akár két percig is a víz alatt tudnak maradni, miközben 20 méter mélyre merülnek. Napjainkban a henjók átlagéletkora 65 év, de a búvárnők közül sokan a 80-as éveikben járnak. Ez a demográfiai torzulás változó világunk tükörképe. Ma már a henjók száma nem éri el a kétezret, míg valaha ötvenezren is voltak. A XXI. századi generáció számára már kevésbé vonzó a tenger mélyének gazdagsága, bár a henjókat még ma is nagy megbecsülés övezi a koreai kultúrában, a turisták pedig távoli vidékekről is tömegesen özönlenek a szigetre, hogy lássák a lemerülő búvárnőket, és megkóstolják a tenger mélyéről felhozott finomságokat.
Az óceánokat a különböző testfelépítésű lények legváltozatosabb példányai lakják. A tengeri csillagok, a tengeri rózsák és a medúzák sugaras szimmetriát mutatnak, legalábbis a felületes szemlélő számára; van tetejük és aljuk, amit a szájuk elhelyezkedése alapján azonosíthatunk, de nincs „bal” és „jobb” oldaluk. A medúza teste tengelyesen teljesen forgásszimmetrikus (hengerszimmetrikus), míg az ötkarú tengeri csillag a középpontja körüli 72 fokos elforgatással vihető át önmagába. A polipok, hozzánk hasonlóan, kétoldalas szimmetriát mutatnak, vagyis testük egy centrális síkra nézve szimmetrikus, eltekintve attól a körülménytől, hogy nyolc karjuk van. Egyes szivacsok teste ezzel szemben minden szimmetriát nélkülöz. Mi lehet az oka annak, hogy az élőlényeknél a szimmetriák ilyen széles skálája figyelhető meg? Érdekes kérdés, amelyre jelenleg is keresik a választ a kutatók. A legidősebb, széles körben elfogadott fosszília, amelyik bizonyítottan kétoldalas szimmetriát mutat, egy 555 millió éves, meztelen csigára hasonlító teremtmény, az úgynevezett kimberella. Ennek az egykor köveken élő lénynek a megkövesedett maradványát először Dél-Ausztráliában, később sokkal nagyobb számban az oroszországi Fehér-tengerben találták meg. A kimberella még közvetlenül a kambriumi robbanás előtti időkben élt. Kambriumi robbanásnak a ma élő állatok őseinek hirtelen megjelenését és az élővilág rohamos diverzifikációját nevezzük a földtörténeti kambrium kor elején. Az első soksejtű szervezetekre vonatkozó fosszilis bizonyítékok viszont ősibbek, 600 millió évesek, tehát az ediakara faunát képviselik.
A legszélesebb körben elfogadott nézet szerint a kétoldalas szimmetria előnyös a forgásszimmetriával szemben, mert a szervezetek hatékonyabb mozgását teszi lehetővé. Gondoljunk például a cápákra. Nem véletlen, hogy a tengeralattjárók ezekre az állatokra hasonlítanak, hiszen mindkettőnek ugyanazt a feladatot kell megoldania: gyorsan és hatékonyan kell a víz alatt mozogniuk. Nem építünk forgásszimmetrikus, gyors mozgású tengeralattjárókat, hanem inkább a cápák testfelépítését utánozzuk. Amikor az élőlények elkezdték érzékelni a környezetüket, és egyre bonyolultabb mozgásokat kezdtek végezni benne, akkor a központi idegrendszer befogadása számára a jobb és a bal, illetve a fent és a lent megkülönböztetését lehetővé tevő testfelépítés volt az előnyös, mert így volt biztosítható a ragadozók és zsákmányaik kialakuló világában a szükséges gyorsaság.
Van azonban egy másik lehetőség is. A medúzák is kétoldalas szimmetriát mutatnak, de csak a testükön belül. Evolúciós szempontból ez fontos körülmény. Arra utalhat, hogy a kétoldalas szimmetria eredetileg azért alakulhatott ki, mert így tökéletesíthető volt a szervezet belsejének működése; lehetővé vált például a zsigerek és a légzőrendszer hatékony szétválasztása. Továbbá, a kétoldalasan szimmetrikus élőlények kifejlődéséért felelős gének a medúzákban és a tengeri rózsákban is megtalálhatók. Ezt arra vonatkozó bizonyítéknak tekintjük, hogy közös ősünket kétoldalas szimmetria jellemezhette, az egyes komplex, soksejtű lényeknél külsőleg megfigyelhető sugaras szimmetria pedig későbbi evolúciós fejlemény.
Még egy példát említhetünk a tudomány fejlődésének csodálatos tempójára és örökké változó természetére. A tegnap tankönyveiben olvasható magyarázatok holnapra történelmi érdekességgé válhatnak, és ennek pontosan azért kell így lennie, mert a természeti világra vonatkozó ismereteink hiányosak, de folyamatosan gyarapodnak. A tudomány fejlődéséből következik, hogy tegnap kevesebbet értettünk a világból, mint ma. Ennek fényében vitathatatlan és csodálatos arra gondolni, hogy őseinket geológiai korokon át követni tudjuk, mintegy félmilliárd évvel ezelőttig, amikor az az ősünk élt, amelyik velünk együtt minden, ma a Földön élő soksejtű állatnak a közös őse volt, és valahogy úgy nézhetett ki, mint a kimberella.
Fejezzük be ott, ahol elkezdtük ezt a fejezetet, és foglaljuk össze mindazt, amit megtudtunk, hogy válaszolhassunk Kepler kérdésére a hópelyhek egyediségére és kollektív szimmetrikus szépségére vonatkozóan. A hópihe kialakulását attól a pillanattól követjük, amikor a magasan lebegő felhőben megszületik, egészen addig, amíg leérkezik a földre. A hópelyhek a közvetlenül jéggé kondenzálódó vízpárából jönnek létre. Nem fagyott esőcseppek, hanem kristályok, amelyek a felhőben fokozatosan egyre nagyobbra híznak.
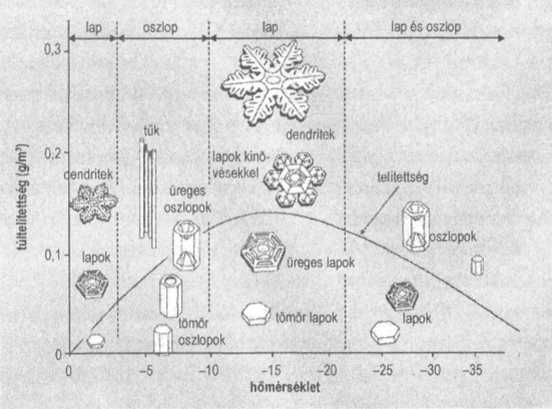
A hópehelyformák különféle körülmények (hőmérséklet és légnedvesség) közti megjelenését mutató morfológiai diagram.
A jégkristályok struktúráját a Földön előforduló hőmérsékleteken és légnyomásokon az úgynevezett morfológiai diagram mutatja. A hatszöges kristályszerkezetet a szabad vízmolekula két kötése közötti 104,5 fokos szög okozza, ami viszont a kvantumelmélet törvényeinek következménye. Ez áll a hópelyhek hatos szimmetriájának hátterében. A hatszögek egyértelműen felismerhetők „Hópehely” Wilson fényképein. A hópihék tökéletlen árnyai annak a „tökéletesebb” formának, amelyet a jég kristályrácsa mutat; ez utóbbi maga is a vízmolekula belső szerkezetének következménye, vagyis a molekulát létrehozó alapvető természeti törvényeknek - az erős, a gyenge és az elektromágneses kölcsönhatások kvantumelméletének - fizikai megnyilvánulása. Ha ránézünk egy hópihére, a Világegyetem elsődleges struktúráját látjuk.
Mégis, a háttérben álló egyszerűség ellenére, minden egyes hópihe különböző. Miért? Azért, mert kialakulásuk története egyedi. Amint a bolygók, a galaxisok esetében láttuk, a természet egyszerű törvényei a formák végtelen sokaságát képesek létrehozni, mert a kezdeti feltételek és a formálódás története soha nem pontosan azonosak. A törvények szimmetriáját elrejti a keletkezés tényleges története, az viszont már a tudósok feladata, hogy a történet torzító lencséjén keresztül meglássák a valóságot. Annak elképzeléséhez, hogyan hajtható ez végre a hópelyhek esetében, némi támpontot ad az úgynevezett morfológiai diagram. Ez a diagram megmutatja, miként változik a hópihék struktúrája a hőmérséklet és a levegő nedvességének függvényében.
A diagram függőleges tengelyén a nedvesség látható, tehát annak a felhőnek a páratartalma, amelyben a hópihe megszületik. A vízszintes tengelyen a hőmérsékletet ábrázoltuk. A nagy, laza szerkezetű hópelyhek, amelyek bonyolult, ágas-bogas szerkezetűek, a nagy nedvességtartalmú felhőkben keletkeznek, ha a hőmérséklet -10 és -20 °C közötti. Alacsonyabb hőmérséklet és nedvesség esetén a hópelyhek kisebb, elágazások nélküli hatszögek. Magasabb hőmérsékleten viszont tűk és hasábok formálódnak. A bonyolult és változatos felépítésű hópelyhek keletkezéséhez magas páratartalom szükséges. A diagram azt is érzékelteti, hogyan lehetnek a hópelyhek egymáshoz hasonlóak, de mégis egyediek. Az adatokat ilyen módon ábrázolva látható, hogy az eltérő időjárási körülmények és a keletkezési (kristálynövekedési) történetek a kristályok különböző mintázatait hozzák létre.
Hogy mindez világosabb legyen, meg kell értenünk a kristályok növekedésének folyamatát. A folyamatot, amelynek során a vízmolekula geometriája átvivődik a hópihe alakjába, kristályfelületek képződésének (fazettásodásnak) nevezzük. A felhőben létrejövő parányi jégkristály azért hízik, mert további vízmolekulák ütköznek neki, amelyeket a hidrogénhíd-kötések a jégszemcséhez kötnek. A sík kristályfelületek azért képződnek, mert a kristály durva, egyenetlen részein több hely van, ahol az újonnan érkező vízmolekulák megtapadhatnak; a sima felületeken viszont kevesebb. Ez azt jelenti, hogy a kezdeti kristály göröngyösebb részei gyorsabban nőnek, miközben kisimulnak, mert az egyenetlen felület gödrei kitöltődnek. A sík kristályfelületek képződésének eredményeképpen hatszög alakú hasábok jönnek létre, amelyeket a morfológiai diagramon „tömör lapokként” jelöltünk. Ezek a lemezek azért síkok, mert a vízmolekulák szívesebben kapcsolódnak a vékony, hatszögletű kerülethez, mint hatszög alsó és felső sík felületeihez, amelyeket alapfazettáknak nevezünk. Alacsony légnedvesség esetén ez a kristályok növekedésének uralkodó módja, ezért maradnak ilyenkor a hópelyhek kevés finom elágazást mutató, nagyjából sík hatszög alakúak. Ha még egyszer megnézzük „Hópehely” Bentley fényképeit a színes mellékletben, akkor ott a felső sor közepén lévő, 780-as számmal jelölt hópihe tartozik ebbe a típusba.
A bonyolult szerkezet másik oka a kristálynövekedés elágazási instabilitásnak nevezett tulajdonsága. Ha a kristály felületén kis kidudorodás alakul ki, akkor a dombocska tetején nagyobb valószínűséggel tapadnak meg az újabb vízmolekulák, mert az jobban belenyúlik a nedves levegőbe. Emiatt a dudor gyorsabban nő a környezeténél, ezért nevezzük instabilitásnak. Ha csak kevés vízmolekula van jelen, akkor az elágazás és a sík kristályfelületek képződése között versengés alakul ki, ezért bonyolultabb szerkezetű hópihe jön létre. Az elágazási instabilitás a hatszögletű hasábok csúcsain is kialakul — a csúcsok gyorsabban nőnek, mint a közöttük lévő egyenes oldalak, ami konkáv struktúra kialakulásához vezet. Ennek viszont ellenáll a sík kristályfelületek képződése, mert az élek közötti konkáv felületeken több hely van új kötések létrehozására. Ezekben a pontokban több vízmolekula jelenik meg, de valószínűbb, hogy a molekulák inkább az így kialakuló görbék közepén telepszenek meg. A két folyamat verseng egymással az újabb vízmolekulák megszerzéséért. Ha a levegő nedves, akkor bőséges az utánpótlás vízmolekulákból, ezért az elágazások dominálnak, mert az instabilitások növekedési sebessége felülmúlja azt, amilyen ütemben a molekulák a diffúzió révén eljutnak a struktúrában mélyebben fekvő, sík kristályfelületig. Így a hatszög alakú hasábok csúcsai általában gyorsabban nőnek, ami bonyolult, csillagszerű elágazásokat hoz létre. Ha viszont a levegő kevésbé nedves, akkor az ágak növekedési üteme elmarad a diffúzió sebességétől, ezért a sík kristályfelületek képződése dominál, a kifejlődő kristály pedig simább, egyszerűbb alakú lesz.
A növekedő hópehely a felhő különböző részeibe sodródik, ahol eltérő fizikai körülmények uralkodnak, helyenként nedvesebb, másutt szárazabb a levegő, és a hőmérséklet is eltérő. Minden egyes ilyen tartomány a növekedés más típusát részesíti előnyben, néha a sík kristályfelületek képződése dominál, máskor inkább az elágazások fejlődnek. Nézzük végig még egyszer „Hópehely” Bentley fényképeit! Belülről kifelé haladva, minden egyes hópihe fejlődésének történetét nyomon követhetjük. Mindegyik kis hatszöggel kezdődik, mert amikor kicsik, akkor mindig a sík kristályfelületek képződése a nyerő folyamat. Ha nedvesebb levegőbe jutnak, akkor az elágazások rohamosan egyre bonyolultabbá teszik a struktúrát. Ezután a hópihe a felhő csekélyebb nedvességtartalmú részére sodródhat, így újra a sík kristályfelületek képződése lesz a jellemző folyamat. Ez az oka annak, hogy minden egyes hópihe különbözik a többitől. Mindegyik egyedi útvonalat jár be a felhő belsejében, és ennek az útvonalnak minden apró részlete beleíródik a struktúrájába.
A hópelyhek megőriznek valamit a kristály képződésének hátterében álló szimmetriából, mert a felhőben néhány centiméteres távolságon belül — ez a hópelyhek jellemző mérete - a körülmények nem változnak számottevően. Következésképp a hópehely minden csúcsa pontosan ugyanolyan körülményeket tapasztal, ezért a struktúra növekedése minden irányban ugyanolyan. Ha a hópihe egyik oldala a másiktól lényegesen eltérő körülmények közé kerül - például nekiütközik egy másik pihének -, akkor a szimmetria elvész. Természetesen rengeteg olyan hópihe fordul elő, amelyek megrongált, aszimmetrikus formában érnek földet, de ezeket nem szoktuk lefényképezni!
Fizikusként kénytelen vagyok a hópelyheket négydimenziós objektumokként szemlélni; felépítésük csak a történetük vonatkozásában értelmezhető, történetük viszont látható módon kódolva van a struktúrájukban. A hópehelyből úgy olvashatunk, mint egy történelemkönyvből. Pontosan ugyanez a megállapítás érvényes az élőlényekre is. Képtelenség megérteni a lamantin testfelépítését, ha nem ismerjük a faj evolúciós történetét. Miért vannak a lamantin uszonyaiba ujjcsontok ágyazódva? Azért, mert az uszonyok egy kistermetű, szárazföldi ősének a lábaiból fejlődtek ki. Az élőlények pillanatképet alkotnak, egy nagyszabású, négydimenziós történet időbeli vetületét; így testfelépítésükben kódolva tartalmazzák a földi élet egész négymilliárd éves történetét. A test a történet minden mozzanatát hűen feljegyzi.
A természet egyszerű, szimmetrikus törvényei és a hosszú, zűrös történelem közti összjáték alakítja ki azt a bonyolult világot, amelyben élünk. A modern természettudomány diadala éppen annak köszönhető, hogy ezt a két tényezőt szét tudjuk választani, ami mérhetetlen horderejű felfedezéseket tett lehetővé. Ennek a megközelítésnek a csíráival már Kepler évszázadokkal ezelőtti írásaiban is találkozhatunk. „Minthogy mindannyiszor megtörténik, amikor csak havazni kezd, hogy a hó első pelyhei apró, hatágú csillagokhoz hasonló formákat öltenek, ezért valamilyen meghatározott oknak kell működnie; ha ugyanis ez véletlenszerűen történne, akkor miért mindig hatszögletűek, miért nem alakulnak ki néha öt- vagy hétszögűek...?”, tette fel a kérdést Kepler. Íme a válasz: azért, mert a természet gyönyörű és mély, mi pedig be szeretnénk pillantani abba a mélyen fekvő szépségbe. Ne gyanítgassunk! Ne találgassunk! Gondolkozzunk, észleljünk, kísérletezzünk, figyeljünk, keressünk hasonlóságokat és különbségeket a természeti világban, és próbáljuk megérteni azokat! Ami pedig a legfontosabb, érezzük jól magunkat, örüljünk, derüljünk jókedvre, amikor szembesülünk az ismeretlennel, és rászánjuk az időnket, hogy felderítsük az azon túli, végtelen területeket. Ha elég gondosan szemügyre vesszük, akkor a legegyszerűbb dolgokban is minden képzeletünket felülmúló kincseket találhatunk.
A HÓPELYBŐL ÚGY OLVASHATUNK, MINT EGY TÖRTÉNELEMKÖNYVBŐL. PONTOSAN UGYANEZ A MEGÁLLAPÍTÁS ÉRVÉNYES AZ ÉLŐLÉNYEKRE IS.
2
MOZGÁS
Emlékeznek egy tökéletes nyári napra? Nem pontosan arra, hol és mikor történt, hanem a bágyasztó melegre, a fűszerek illatára, a csiklandozó füvekre, a levegőben szálló termésekre és a döngicsélő rovarokra. A nagy művészek a jelen élményeként idézik fel a ködbe vesző múltat, mert az emlékeink maradandóak. Claude Monet gyermekkori nyári délutánok ezreinek a hangulatát sűrítette Pipacsvirágzás (Les Coquelicots) című képébe. Az Argenteuil közeli, falusi tájat ábrázoló festmény Monet egyik legkedvesebb és legismertebb képének bizonyult.
Monet 1873 nyarán és őszén hasonló képek sorozatát festette meg. Nem tudjuk, pontosan melyik napon és hány órakor festette a képet, de Argenteuil környékén a pipacsok május végén és június elején borulnak virágba, a ragyogó égbolt és az árnyékok hiánya pedig azt jelzi, hogy a kép dél körül készülhetett. Illessen meg most azonban minket is a művészi szabadság joga, és határozzuk meg azt a pillanatot, amikor a kisfiú édesanyjával a pipacsok közt sétált, Monet pedig gondos mérlegelés után egy piros pöttyöt helyezett el a készülő festményen. Tegyük fel, hogy mindez 1873. május 26-án délben történt, a franciaországi Argenteuil közelében elterülő réten. Másfél évszázad elteltével ez a nap már a feledés homályába merült, és csak Monet festményén létezik. A hely még ma is megtalálható, de a pillanat elszállt. Legalábbis ezt súgja a hóbortos józan eszünk, de vajon helyesen gondoljuk?
Albert Einstein 1905-ben tette közzé speciális relativitás-elméletét, amelyik a nevezetes E - mc2 összefüggést is tartalmazza. Vigasztal a tudat, hogy létezik egy ilyen híres formula, mert lehetőséget ad arra, hogy azt képzeljem, egy villanás erejéig bevilágítok a populáris kultúra mindent elborító sötétségébe.
„A HOLDKORONG PEREME MÖGÜL HIRTELEN, LASSÚ, BÁMULATOSAN MÉLTÓSÁGTELJES MOZGÁSSAL FELBUKKAN EGY KÉK ÉS FEHÉR SZIPORKÁZÓ DRÁGAKŐ, EGY FÉNYES, POMPÁS ÉGSZÍNKÉK GÖMB, AMELYET LASSAN ÖRVÉNYLŐ, FEHÉR FÁTYLAK ÉKESÍTENEK. APRÓ GYÖNGYSZEMKÉNT FOKOZATOSAN EMELKEDIK A FEKETE TITOKZATOSSÁG MÉLY TENGERÉBE. HOSSZÚ PILLANATOK MÚLTÁN JUT EL A TUDATOMIG, HOGY EZ A FÖLD... AZ OTTHON.” Edgar Mitchell, Apollo— 14, a Hold körüli keringés közben, 1971. február
A speciális relativitáselmélet pillanatokkal, pontosabban szólva, eseményekkel foglalkozik. Esemény az, ami a tér egy bizonyos helyén valamely megadott pillanatban történik. Amikor Monet vásznát az ecsetével megérintve elhelyezte azt a bizonyos piros pöttyöt, az egy esemény. Ismerjük a helyét, és tudjuk, mikor történt. Einstein elmélete megadja, hogyan kell megmérnünk két esemény távolságát, és mit kell gondolnunk két esemény kapcsolatáról. Mert a speciális relativitáselmélet a tér és az idő elmélete.
Mi az idő? Hétköznapi tapasztalatunk értelmében az idő olyasvalami, ami múlik, és amit az óráinkkal mérhetünk. Ha mindenki pontosan beállítja az óráját, és az órák mechanikai szempontból tökéletesek, akkor azt gondolhatnánk, hogy mindenki mindig ugyanazt az időt fogja mérni. Mi a jelenben élünk, ezért számunkra kényelmes a jelen pillanatát „mostként” definiálni. Mivel mindannyian egyetértünk abban, mi az idő, ezért egyet kell értenünk abban is, mit jelent a „most”. Következésképpen a múlt elszállt, emlékét csak a vászonra festett kép őrzi meg korokon át, a jövő pedig az, ami majd elérkezik.
Mi a tér? A teret olyan színpadnak érezzük, amelyen az események megtörténnek; hatalmas doboznak, amely magában foglalja a Földet, a Holdat, a Napot, a bolygókat és a csillagokat. Két ember egy megbeszélt és tökéletesen szinkronizált óráikkal rögzített időpontban pontosan kalibrált méterrúdjaikkal megmérheti a Föld és a Hold távolságát, és így ugyanazt a távolságot fogják kapni.
Ebben a fejezetben Einstein nyomdokain haladva majd rájövünk, hogy az előző két bekezdés magától értetődőnek tűnő állításai hibásak, felfedezzük, hogy a tér és az idő nem az, aminek látszik. Ez egészen addig a meghökkentő lehetőségig vezet el bennünket, mely szerint Monet varázslatos nyári pillanata talán az öregedő vásznon kívül is létezhet. Amint a híres fizikus és matematikus Hermann Weyl megfogalmazta: „Az objektív világ egyszerűen csak van, nem pedig történik. Csak a testem életútján keresztül előkúszó tudatosságom tekintete az, ami az időben folytonosan változó, tünékeny képként életre kelti azt.”
Érdemes azonban az elején kezdeni a történetet, ezért nézzük alaposan végig, miként változott a fizika történetében a térbeli távolságokról és az időtartamokról alkotott képünk. A tér és az idő modern felfogása felé tett első lépés azonos volt a modern tudomány felé tett első lépéssel. Ezért történetünk a XVII. században Galileivel, Newtonnal, valamint a bolygók mozgásának és a Föld Naprendszeren belüli helyének tanulmányozásával kezdődik.
Élet egy forgó és keringő bolygón
A mozgás tanulmányozása hosszú és ellentmondásos történet, amely sok ezer évvel ezelőttre nyúlik vissza. Első pillanatban nehéz elképzelni, hogyan lehetett valaha is a mozgás vizsgálata ellentmondásos; mert az egész olyan egyszerűnek tűnik. Az ellentmondás eredete részben annak a körülménynek tudható be, hogy egy forgó bolygón élünk, amelyik eközben a Nap körül száguld. Ez az állítás még Newton korában is problematikusnak számított, részben a jól ismert teológiai okok miatt, de azért is, mert mi magunk valójában nem érezzük ezt a mozgást. A józan eszünk azt súgja, hogy egy helyben állunk, és az a közkeletű felfogás, amely szerint „semmit sem tudok a tudományról, azt viszont tudom, mit gondolok, és mit érzek”, még a XXI. században is erőteljesen negatív hatással van a közfelfogásra - nem is beszélve a XVII. századról. Ha valóban helytálló lenne az az érzés, mely szerint az univerzum középpontjában egy nyugvó bolygón egy helyben állunk, akkor Galilei és sokan mások számos.„kellemetlenségtől” kímélhették volna meg magukat.
Néha a figyelemre méltó gondolatok oly mélyen beivódnak a kultúra szövetébe, hogy már nem is tűnnek figyelemre méltónak egyszerűen azért, mert annyira közismertek. Kitűnő példa erre a Föld Nap közüli mozgásának rejtélye és az égi dinamika igazi, de rejtőzködő vadsága, amelyeket a természet elrejteni igyekszik a szemünk elől. Legtöbbünk nem sokat törődik azzal, mi is történik a lábunk alatt, mert arra tanítottak, hogy a bonyolult fogalmakat vakmerő szellemi hanyagsággal kezeljük. A művelt ember valószínűleg tudja, hogy mi mindannyian egy 40 000 km egyenlítői kerületű és 6000 millió millió millió tonna tömegű gömb felszínén járkálunk, amely 24 óránként körbefordul hetykén félrebillent tengelye körül, miközben az egész forgó mindenség másodpercenként 30 kilométert megtéve száguld a Nap körül, hogy 940 millió kilométer hosszú pályáján egy év alatt körbe tudja járni azt. Az ilyen ember valószínűleg nem találja hihetetlennek, hogy ezeket a mozgásokat a legkevésbé sem vesszük észre. Mindez mégis szédítő érzés.
Nagy oka van annak, hogy ezt a mozgást nem vesszük észre, és ennek megértéséhez pontosan meg kell vizsgálnunk, mit is értünk mozgáson. A XVII. század előtt széles körben elfogadott nézet szerint a testek akkor mozognak, ha valami előrehajtja őket, és ha ez a hatás megszűnik, akkor a test megáll. Általában Arisztotelésznek tulajdonítják, hogy kimondta ezt az ösztönös meglátást, amely azon az elképzelésen alapul, hogy minden történésnek valamilyen oka kell, hogy legyen. Mivel a mozgás olyasvalami, ami megtörténik, beleértve azt, hogy bizonyos időintervallum alatt megváltozik a mozgó test helye, ezért ennek is okának kell lennie. Ha ezt az okot megszüntetjük, akkor a mozgásnak meg kell szűnnie. Talán ösztönösen nézve jónak tűnik ez a kép, de mégis hibás.
Az igaz, hogy ha egy asztalon álló tárgyat meglökünk, akkor az mozgásba jön, ha pedig abbahagyjuk a mozgatását, akkor megáll. Ez azért van így, mert a tárgy és az asztal közötti súrlódás lefékezi a tárgy mozgását. Ha nem lenne súrlódás, és meglökünk egy testet, akkor a mozgásállapota mindaddig úgy marad, amíg újra hozzá nem érünk. Ezt a tehetetlenség elvének nevezzük, ami, ha jobban belegondolunk, igen jelentős megállapítás.
A senki máshoz nem fogható Richard Feynman Nobel-díjas fizikus leírta, hogyan ismertette meg őt apja a tehetetlenség fogalmával, amikor felfigyelt egy érdekes jelenségre, miközben az asztalon egy kisautóval és egy golyóval játszott.
„Figyelj csak, Apa, észrevettem valamit. Ha meghúzom az autót, a golyó a hátuljába gurul, amikor tovább húzom, utána pedig hirtelen megállítom, akkor a golyó az autó elejébe gurul. Miért van ez így?”
„Ezt senki sem tudja - mondta. - Az általános elv az, hogy a mozgó testek továbbra is mozogni akarnak, az álló testek pedig továbbra is állni akarnak, és ez csak akkor változik, ha jól meglököd őket. A testeknek ezt a törekvését tehetetlenségnek nevezzük, azt azonban senki sem tudja, miért van ez így.”
Alapos magyarázat volt. Nem elégedett meg azzal, hogy megmondta a jelenség nevét.
Kedvelem ezt a történetet, mert valami fontosat mutat meg. Vannak olyan, a természetre vonatkozó kérdések, amelyekre az a válasz, hogy „azért, mert ilyen a Világegyetemünk.” Kell ilyen válaszoknak is lenniük, mert még ha tudnánk is, hogyan kell az összes természeti törvényt levezetni valamilyen „első alapelvekből”, akkor is tudnunk kellene, melyek ezek az első alapelvek. A tehetetlenség törvénye, ahogyan azt Feynman apja elmagyarázta, mai tudásunk szerint egyike ezeknek az alapelveknek. A modern fizikában az egyik legnehezebb dolog azt eldönteni, hogy a Világegyetem tulajdonságai közül melyek valóban alapvetőek, és melyek következnek valamilyen mélyebb elvből vagy törvényből. Ez az egész könyv a „Miért?” kérdéséről szól. Néha a válasz egyszerűen az, hogy „csak”. Ez néha tévedésnek bizonyulhat - kiderülhet, hogy valaminek mégiscsak van mélyebb oka, amelyet korábban még nem ismertünk, de a válasz semmiképpen sem felületes.
Isaac Newton a tehetetlenség elvét három mozgástörvénye közül az elsőben fogalmazta meg. Ezeket a törvényeket az 1687-ben megjelent A természetfilozófia matematikai alapjai, vagy röviden Principia című könyvében adta közre. Manapság lényegében mindenki szó szerint el tudja mondani ezt a törvényt, vagy legalábbis emlékszik iskolai tanulmányaira, amikor még tényleg tudta:
„Minden test megmarad nyugalmi állapotában vagy egyenletes és egyenes vonalú mozgásában, hacsak külső erő nem kényszeríti ennek az állapotnak a megváltoztatására.”
Ebben a kijelentésben azonban el van rejtve egy finom részlet. Ha kijelentjük, hogy valamely test mozog, akkor azt is meg kell kérdeznünk, „mihez képest mozog ez a test?” Newton természetesen elgondolkozott ezen a kérdésen, és csaknem helyes választ adott. A témáról szóló írásai tanulságosak, a tér és az idő kérdésének lényegét érintik, és rávilágítanak, milyen kapcsolatban állnak a mozgással. Törvényeit illetően Newton világosan megfogalmazta ezeket a feltételeket.
„Az abszolút, valóságos és matematikai idő önmagában véve, és természeténél fogva, minden külső vonatkozás nélkül egyenletesen múlik...”
„AZ ABSZOLÚT, VALÓSÁGOS ÉS MATEMATIKAI IDŐ ÖNMAGÁBAN VÉVE, ÉS TERMÉSZETÉNÉL FOGVA, MINDEN KÜLSŐ VONATKOZÁS NÉLKÜL EGYENLETESEN MÚLIK...” Isaac Newton
Ez az a józan észen alapuló kép, amely szerint az idő múlik, és múlása ütemét mindenki azonosnak érzékeli.
„Az abszolút tér saját lényegénél fogva, külsőleg egyáltalán semmihez sem viszonyítva, mindenkor egyenlő és változatlan marad...”
„Az abszolút mozgás a testnek egyik abszolút helyről a másikra való helyváltoztatása. ”
(Heinrich László fordításai)
Ez Newton arra vonatkozó kijelentése, hogy létezik valamiféle óriási doboz, és ezen belül történik minden. Kicsit továbbléphetünk, és elképzelhetjük a rácsvonalak sorozatát, amelyek keresztül-kasul szelik a doboz belsejét, és amelyekhez viszonyítva megadhatjuk a Világegyetemben található bármely objektum helyét. Ezután az abszolút mozgást úgy definiálhatjuk, mint elmozdulást az ezen univerzális rácshálózathoz képest, amely hálózatot az abszolút térben nyugalomban lévőnek tételezünk fel. Ez a hatalmas rács példa arra, amit a továbbiakban vonatkoztatási rendszernek fogunk nevezni. Az abszolút mozgás definiálásához Newton feltételezte, hogy létezik egy nagyon speciális vonatkoztatási rendszer: az, amelyik megfelel az előbbi, az abszolút térhez képest nyugalomban lévő, univerzális rácsnak, amelyhez minden mozgást viszonyítunk.
Ezután Newton egy további bámulatos megfigyelést tesz:
„Azonban a mozgás és a nyugalom, amint általában tárgyaljuk, csak viszonylagosan különbözik egymástól.
Nem mindig vannak nyugalomban azok a testek, amelyeket a mindennapi életben nyugalomban levőknek tekintünk.” (Heinrich László fordítása)
Newton kijelentése értelmében lehetetlen megkülönböztetni, hogy egy test „ténylegesen” egyenes vonalú mozgást végez, vagy „ténylegesen” nyugalomban van. Talán nem vagyunk „ténylegesen nyugalomban”, ahogy ő fogalmaz, de ezt nem tudjuk eldönteni. Ez az oka annak, miért nem érezzük a Föld felszínén állva a Nap körüli mozgásunkat; perces időfelbontásban figyelve, csaknem állandó sebességgel és jó közelítéssel egyenes irányban mozgunk. Newton helyesen jegyezte meg, hogy ha ez a helyzet, akkor nem érezzük a mozgásunkat; valójában nyugodtan kijelenthetjük, hogy nyugalomban vagyunk, még akkor is, ha az ő szavaival élve nem vagyunk „ténylegesen nyugalomban”.
Tegyünk most egy látszólag filozófiai kitérőt, amelynek azonban fontos következményei vannak Einstein relativitáselméletének kifejlődésére. Ha - legalábbis elvben - lehetetlen eldönteni, hogy mozgunk-e vagy sem, akkor mi értelme van az abszolút tér fogalmának? Talán a valóságban nem is létezik olyan kitüntetett vonatkoztatási rendszer, amelyikhez minden mozgást viszonyíthatunk? Esetleg meg kellene szabadulnunk az egész fogalomtól? Igen, pontosan így van, meg kellene szabadulnunk, de Newton ezt nem tette meg. Az a szép az egészben, hogy Newton mozgástörvényei csak relatív mozgásokkal foglalkoznak, tehát nem támaszkodnak annak a kitüntetett vonatkoztatási rendszernek feltételezésére, amelyikhez minden mozgást viszonyítani lehet. Az egyenleteit helyesen írta fel, ezután azonban az értelmezésüket megterhelte az abszolút tér szükségtelen filozófiai ballasztjával. Mindez a lényeget nem érintő szőrszálhasogatásnak tűnhet, pedig nem az. Az a kényelmes, de fölösleges ötlet, amely szerint a tér az a rögzített színpad, amelyen „a dolgok megtörténnek”, határozottan veszélyes a természet megértése szempontjából. Einstein megszabadult ettől a fogalomtól, ami lehetővé tette számára, hogy megalkossa a tér és az idő gyökeresen újszerű elméletét, amely a természeti világnak Newton törvényeinél pontosabb leírását adja.
Ez nem azt jelenti, hogy ki akarnánk dobni a vonatkoztatási rendszer fogalmát - a legkevésbé sem! Valamire rájöttem a fizikával kapcsolatban azokban az években, amikor megpróbáltam a magam számára megérteni és másoknak elmagyarázni. Az igazán mélyértelmű fogalmak gyakran tökéletes szőrszálhasogatásnak tűnnek. Ez a fizika és a filozófia közti néhány hasonlóság egyike. Jó példa erre alapos bevezetésünk a vonatkoztatási rendszerek tárgyalásához; úgy tűnhet, mintha túlságosan is gondosak lettünk volna, de muszáj gondosaknak lennünk, ha meg akarjuk érteni azokat a néha titokzatos megjegyzéseket, amelyeket már eddig is Einstein speciális relativitáselméletének következményeihez fűztünk. Ezt szem előtt tartva, tegyünk rövid kitérőt, és vegyük még részletesebben szemügyre a vonatkoztatási rendszereket! Megéri az erőfeszítést!
Fontos kitérő: a vonatkoztatási rendszer
Képzeljük el, hogy felrajzoljuk az egész Világegyetemet átfogó rácsvonalak rendszerét, pontosan úgy, ahogyan azt Newton tette. Ettől kezdve az objektumok helyét ezekhez a rácsvonalakhoz viszonyítva határozhatjuk meg. A hálózat jelenti a vonatkoztatási rendszerünket.
A vonatkoztatási rendszerek persze többek, mint egymáshoz kapcsolódó méterrudak sokasága. Mérnünk kell az időt is. Képzeljük el, hogy azonos órákat helyezünk el a Világegyetem különböző pontjaiban. Az egyes órák a rácshoz képest rögzített helyzetűek. Ezután már hozzáfoghatunk, és megmérhetjük, hol és mikor történt egy esemény. Az események mindig a tér valamely pontjában (a méterrudak rendszerével pontosan meg tudjuk adni, hol) és egy meghatározott időpontban történnek (az eseményhez legközelebbi óráról le tudjuk olvasni, pontosan mikor).
Nem túlzás azt állítani, hogy az egész fizika visszavezethető a különböző események közötti kapcsolatok megértésére. Ezért bajlódunk a vonatkoztatási rendszer felállításával (a szó szoros értelmében), amelyet fel tudunk használni az események helyének és időpontjának megadásához. Szükséges az elővigyázatosság: nagyon pontosan tisztában kell lennünk azzal, hogyan mérjük az események időpontját.
Ennek a fontosságát úgy szemléltethetjük, hogy elképzelünk egy meghatározott eseményt: egy tűzijáték rakétájának a felrobbanását. A robbanás időpontját a rakéta felrobbanásának helyéhez legközelebbi óráról olvashatjuk le a robbanás időpontjában. Ez azonban nem azonos azzal az idővel, amelyet az eseményt biztonságos távolságból figyelő ember észlel, mert a fényfelvillanásnak valamekkora időre van szüksége, mire elér a megfigyelőhöz. A fény egy nanoszekundum, vagyis a másodperc milliárdod része alatt körülbelül 30 centimétert tesz meg. (Gyakran gondolok arra, hogy ha létezik a Teremtő, akkor ő minden bizonnyal angolszász mértékegységeket használ, mert ez majdnem pontosan 1 lábnak felel meg.) Más módon is megérthetjük, miért kell nagyon gondosan eljárnunk: azért, mert semmilyen feltevést sem kell tennünk arra vonatkozóan, milyen ütemben járnak az óráink. Megbeszéltük, hogy az órák azonos felépítésűek, ezért joggal bízhatunk abban, hogy azonos tempóban járnak. Ez azonban csak feltételezés, és amint hamarosan látni fogjuk, hibás. Ezért kell nagyon pontosan tisztáznunk, hogyan mérjük az időt.
A vonatkoztatási rendszerrel a saját nézőpontunkat is meghatározzuk, vagyis azt, hogy milyen perspektívából figyeljük meg a Világegyetemet. Saját vonatkoztatási rendszerünket szabadon választhatjuk meg, míg valaki más ugyancsak szabadon választhatja meg az ő elképzelt vonatkoztatási rendszerét. Általánosságban azt mondhatjuk, hogy két vonatkoztatási rendszer mozoghat egymáshoz képest (képzeljük el a mérőrudak és órák két rendszerét, amelyek egymáshoz képest mozognak). A lehetséges vonatkoztatási rendszerek száma korlátlan, de a speciális relativitáselméletében Einstein kitünteti a vonatkoztatási rendszerek egy csoportját. Nevezetesen, bevezeti az „inerciális vonatkoztatási rendszer” vagy röviden inerciarendszer fogalmát.
Akkor vagyunk nyugalomban egy inerciarendszerben, ha azt látjuk, hogy valamilyen különálló objektum vagy nyugalomban van, vagy pedig állandó sebességgel egyenes vonalú mozgást végez. A forgó vonatkoztatási rendszerek, például amelyet a forgó Földhöz rögzítünk, nem inerciarendszerek. Sok olyan jelenség létezik, amelyeket az életünkben magától értetődőnek tekintünk, a viharrendszerektől az árapályig, de ezek a jelenségek a forgásunk következtében jelentkeznek, még ha ezt a forgást nem is érezzük, következésképpen ezek a jelenségek egy inerciarendszerben nem fordulnának elő. A jelenség pontos működését akkor fogjuk megérteni, amikor alaposabban szemügyre vesszük az óceánokon fellépő árapályt és a viharrendszerek viselkedését.
Mint már említettem, nem létezik egyetlen „kitüntetett” inerciarendszer, mert az inerciarendszerek mind egyformán jók, azaz egyenértékűek egymással. Ha egy inerciarendszerben vagyunk, akkor kijelenthetjük, hogy nyugalomban vagyunk, és egyetlen olyan mérés sem létezik, amelyikkel ennek az ellenkezőjét lehetne bizonyítani. Minthogy a Föld felszínén jó közelítéssel inerciarendszerben vagyunk, ezért nem érezzük percről percre az elmozdulásunkat.
Einstein az összes inerciarendszer egyenértékűségének megkövetelését az alapelvek rangjára emelte. Ez azt jelenti, hogy a különböző inerciarendszerekben végrehajtott azonos kísérletek mindig azonos eredményt adnak. Másként fogalmazva azt is kijelenthetjük, hogy a természet törvényei nem változnak meg attól, hogy egyik vagy másik inerciarendszerből vizsgáljuk azokat; ha ugyanis ettől megváltoznának, akkor meg tudnánk különböztetni egymástól az inerciarendszereket! Nem szeretném már a fejezet elején lelőni a poént, de ez az inerciarendszerek között érvényesülő tökéletes demokrácia, amint hamarosan ki fog derülni, komoly kényszerfeltételt ad a természet törvényeire nézve: előírja, hogy egyrészt Newton törvényei, másrészt az elektromosság és mágnesség törvényei nem lehetnek egyidejűleg érvényesek. Ez talán első hallásra nem tűnik túlságosan ijesztőnek, de a 4. fejezetben látni fogjuk, hogy az elektromosság és a mágnesség törvényei a fizika egyik legfontosabb pillérét alkotják - Newton törvényei mellett. Előbbiek rengeteg olyan jelenséget írnak le, amelyeket a hétköznapi életünkben magától értetődőnek tekintünk; az elektromos generátoroktól és villanymotoroktól kezdve a szivárvány létrejöttén keresztül a lencsék és az internetet az otthonainkba továbbító optikai szálak működéséig, illetve a kvantummechanikával történő egyesítése után az atomok és molekulák felépítéséig; de a listát szinte a végtelenségig folytathatnánk. Elképzelhetetlen, hogy az a rendszer, amelyet a természet négy alapvető kölcsönhatása egyikének leírására használunk, összeegyeztethetetlen legyen a mozgások leírására használt elméleti kerettel. Ez az ellentmondás sarkallta Einsteint a tér és az idő új elméletének megalkotására. Ezt később majd látni fogjuk. Egyelőre vizsgáljuk meg világunkat különböző nézőpontokból, vagyis különböző vonatkoztatási rendszereket használva, de a newtoni kereteken belül. Ily módon megértjük az évszakok múlását, a ciklonok forgását és az óceánok árapályát.