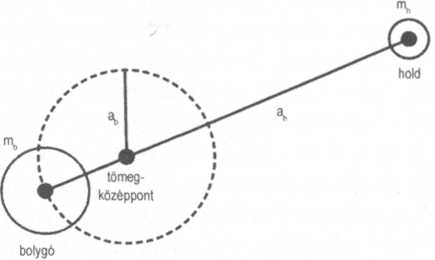
A tömegközéppont.
Az árapály
Az apály és a dagály szakadatlan váltakozása drámai mértékű, ismétlődő és gyors változásokat okoz a Föld tengerpartjain. Kis türelemmel és egy kényelmes nyugággyal felszerelve bárki, saját szemével is megfigyelheti a táj változását. Ne gondoljanak geológiai időskálán lejátszódó jelenségekre. Az árapály következtében a Kanada északi részén fekvő Fundy-öbölben a legnagyobb a vízszint ingadozása: a Burntcoat Head-i Kanadai Hidrográfiai Szolgálat feljegyzései szerint 56 láb (17 méter). Örömömre szolgál, hogy ezt az adatot a kulturális sokszínűség dicséretére, lábban kifejezve adhatom meg.
Az árapály eredete ősi rejtély. Az árapály és a holdfázisok közötti kapcsolat már több mint 2000 éve ismert, de sem a minta felismeréséhez, sem pedig az apály, a dagály és a szökőár időpontjának és magasságának előrejelzéséhez nincs szükség a jelenség hátterében álló fizikai folyamat ismeretére. Ha csupán hajózni akarunk, akkor nem kell ismernünk a miértet, elég, ha tudjuk, mikor. Amikor a XVI. században megjelent a Naprendszer heliocentrikus modellje, a kor csillagászai kitüntetett figyelmet fordítottak az árapály magyarázatára, hiszen olyan földi jelenségről volt szó, amelyik nyilvánvaló módon kapcsolatban állt a Föld, a Hold és a Nap egymáshoz viszonyított mozgásával. Johannes Kepler azt állította, hogy az árapályt a Hold által a földi óceánokra kifejtett vonzóerő kelti, de az erő magyarázatára nem tudta megadni a megfelelő mechanizmust. Galilei nem értett egyet ezzel a nézettel, és egy egyre inkább sértődött hangvételű párbeszédben fejtette ki ellenérvet, amely szerint az árapály a Föld forgásának és Nap körüli keringésének a következménye:
„De mindazok közt a jelentős tudósok között, akik ezeknek a csodálatos természeti jelenségeknek szentelték figyelmüket, jobban csodálkozom Kepleren, mint bárki máson. Hogyan is tudott egy olyan szabadgondolkozású és átható éleslátással megáldott ember, mikor a Föld mozgásáról szóló tan már a kezében volt, eltűrni és méltányolni olyan dolgokat, mint a Hold uralma a víz felett, s a rejtett tulajdonságok, melyek nem egyebek gyermekségeknél?"
(Galilei: Dialogo; M. Zemplén Jolán fordítása)
A „gyermekség” szó helyett szándékosan használom gyakrabban az „együgyűséget”. Galilei az 1616-ban írt, Discorso del flusso e reflusso del mare (Értekezés az árapályról) című munkájában a Föld óceánjainak mozgását ahhoz hasonlította, ahogyan a víz egy vázában lötykölődik. Azzal érvelt, hogy mivel a váza helyzete és gyorsulása torzítja a víz elhelyezkedését az edényben, ugyanígy torzítja az óceánok mozgását a Föld helyzete és gyorsulása. Olyan mechanizmust gondolt ki, amelyben pozitív és negatív gyorsulásokkal magyarázta az árapály során fellépő ide-oda mozgást. Ezt az elméletét sokan „élete nagy tévedésének” tekintik. A sors fintora, hogy Galileinek és Keplernek is csak részben volt igaza. Az alábbiakban elolvashatják az árapály jelenségének valódi magyarázatát.
Keplernek igaza volt abban, hogy az árapályt a Hold gravitációs vonzása okozza, amelyet a Földre gyakorol. Ezt természetesen nem így fogalmazta meg, mert akkor még nem jelent meg Newton egyetemes gravitációelmélete. Galileinek viszont abban volt igaza, hogy a Föld valóban gyorsul. Ő csak azt nem tudta megmondani, merrefelé.
Fogadjuk el, hogy az árapálynak valami köze van a Holdhoz; amelynek pályáját pontosan ugyanúgy lehet leírni, ahogyan a Föld Nap körüli pályáját. A Holdat a gravitációs erő folyamatosan a Föld felé húzza, mégsem közeledik felénk, mert eközben - a tehetetlenség elvének megfelelően - folyamatosan egyenes vonalban próbál továbbhaladni.
Most fel kell idéznünk Newton harmadik, egyben utolsó mozgástörvényét, amelyik így hangzik: A hatással mindig egyenlő nagyságú és ellentétes visszahatás áll szemben.
Ez azt jelenti, hogy az erők mindig párosával lépnek fel. Ha a Eöld gravitációs vonzást fejt ki a Holdra, akkor a Hold ugyanolyan nagyságú, de ellentétes irányú gravitációs erővel vonzza a Földet. Ez azt jelenti, hogy a Földnek a Hold felé kell zuhannia, mégpedig úgy, hogy gyorsulását a középpontjaikat összekötő egyenes irányában ható gravitáció idézi elő. Miért nem zuhan rá ez esetben a Föld a Holdra? Pontosan ugyanazért, amiért a Hold sem zuhan rá a Földre - mert zuhanása közben mindig odébb megy. Tehát a Földnek is keringenie kell! De mi körül? A válasz az, hogy kicsit trehányul fejezzük ki magunkat, amikor azt mondjuk, hogy a Hold a Föld körül kering. A kijelentés jó közelítéssel igaz ugyan, de valójában keringését a Föld középpontjától kicsit távolabb lévő pont körül végzi, amely pontot a Föld-Hold-rendszer közös tömegközéppontjának nevezzük. Ha jobban meg akarjuk érteni, mi történik, képzeljünk el két, egyenlő tömegű holdat, amelyek kör alakú pályáikon egymás körül keringenek. Minden tökéletesen szimmetrikus, ezért mindkét test a középpontjaiktól egyenlő távolságban lévő pont körül kering. Ezt a pontot nevezzük a rendszer tömegközéppontjának. Ha az egyik hold nagyobb tömegű a másiknál, akkor a tömegközéppont közelebb lesz a nagyobb tömegű holdhoz, és mindkettő ezen eltolódott helyzetű pont körül kering. A Föld 81-szer akkora tömegű, mint a Hold, ezért a tömegközéppont, amelyik körül a két égitest kering, nagyon közel van a Föld középpontjához, bár nem esik pontosan egybe azzal. Távolsága a Föld középpontjától 4700 kilométer, ami a Föld-Hold-távolságnak körülbelül 1/81-ed része. Ezért közelítőleg elfogadható, bár nem teljesen pontos azt állítani, hogy a Hold a Föld körül kering. Az állítás azért csak közelítőleg tekinthető észszerűnek, mert pontosan azt a kérdést kerüli el, hogyan gyorsul a Föld a Hold felé és - amint annak lennie kell - hogyan kerüli el mégis, hogy belézuhanjon!
Az a tény, hogy a Föld a Föld-Hold-rendszer tömegközéppontja körül kering, döntő fontosságú, ha meg akarjuk érteni az árapály jelenségét. A kulcs a nézőpont, vagyis a vonatkoztatási rendszer, pontosan abban az értelemben, ahogyan a Coriolis-erőt és a viharrendszerek kialakulására gyakorolt hatását vizsgáltuk. Ezúttal is ide-oda ugrálunk a vonatkoztatási rendszerek között, hogy megkeressük a fellépő tehetetlenségi erőket - a fizikusok gyakran folyamodnak ehhez a trükkhöz, mert kegyetlenül hasznos tud lenni, feltéve, ha tudjuk, hogyan kell csinálni! (Lásd a tömegközéppontra vonatkozó ábrát.)
Képzeljük el, mi történik a Föld középpontjában csücsülő megfigyelő szemszögéből nézve. Ez az a pont, amelyik a Föld-Hold-rendszer tömegközéppontja körül kering. Feltételezhetjük, hogy a Föld középpontja tökéletes kört ír le, ami jó közelítéssel igaz is. A vonatkoztatási rendszerünk ebben az esetben nem tehetetlenségi rendszer, hiszen forog, éppen ezért számítanunk kell a tehetetlenségi erők felbukkanására. De melyekre? Ezúttal nem a Coriolis-erőre, amelyik akkor lép fel, ha a testek a forgó vonatkoztatási rendszerben mozognak, hanem a centrifugális erőre. Milyen hatása van ennek az erőnek? A Fold középpontjában ülő megfigyelő szempontjából a gravitációs erő a Földet - Newton gravitációs törvényének megfelelően - egyenes vonalban a Hold középpontja felé gyorsítja. A Föld ennek ellenére nem közeledik a Holdhoz — ha kör alakú pályán kering a Föld—Hold-rendszer tömegközéppontja körül, akkor távolsága az utóbbitól változatlan marad.

A tömegközéppont.
Ez azt jelenti, hogy a Föld középpontjában tartózkodó megfigyelőnek a Hold gravitációs vonzásával azonos nagyságú, de ellentétes irányú erőt kell érzékelnie, hogy a két erő pontosan kiegyenlítse egymást. Ezt az erőt, amelyik a gravitációs erővel azonos nagyságú, de azzal ellentétes irányú, nevezzük centrifugális erőnek. Ez nem más, mint az a jól ismert erő, amelyet akkor érzünk, amikor egy gyorsan forgó körhintán ülünk. Valami kifelé lök bennünket, és ha a megfelelő típusú körhintát választottuk, akkor az ülésünk kifelé lendülve felemelkedik, ahogy nő a sebesség, egyre magasabbra. Ez a centrifugális erő hatása.
Nagyszerű! De mi köze van ennek az árapályhoz? Emlékezzünk vissza arra, hogy a Föld kis sugarú pályán kering a Föld-Hold-rendszer tömegközéppontja körül. A Föld középpontjában a Hold gravitációs vonzását pontosan kiegyenlíti a centrifugális erőnek nevezett tehetetlenségi erő. Képzeljünk most el egy pontot a Föld felszínén, közvetlenül a Hold alatt. A Hold gravitációs vonzása a Föld felszínének a Hold alatti pontjában erősebb, mint a Föld középpontjában, mert a Föld felszínének ez a pontja közelebb van a Holdhoz, mint a Föld középpontja. A felszín közvetlenül a Hold alatti részén valamivel erősebb a gravitációs vonzás, és ez a többletgravitáció torzítja az óceánok felszínének alakját, vagyis ez okozza a dagályt a Hold alatt.

Az árapály jelensége.
Vizsgáljuk meg most, mi a helyzet a Föld átellenes oldalán! Ott a Hold gravitációs vonzása kisebb, mint a Föld középpontjában, ami irt is azt eredményezi, hogy az óceánok vize távolabbra kerül a szilárd felszíntől, vagyis dagálypúp alakul ki. Ezért van a Földön mindenütt naponta kétszer dagály — az egyik a Hold alatt, a másik pedig bolygónk átellenes oldalán.
Az árapályerők tehát a Hold gravitációs vonzása következtében lépnek fel, és ennek látványos megnyilvánulása, a tengerjárás ami annak a következménye, hogy a Föld a Föld-Hold-rendszer tömegközéppontja körül kering. Bár az árapály jelenségét általában a tengerfelszín jelentős mértékű deformációjaként érzékeljük, az árapályerők elég nagyok ahhoz, hogy a Föld szilárd kérgében is mérhető nagyságú deformációt okozzanak: a kőzetek nap mint nap akár fél méterrel is elmozdulhatnak. Ez az eltolódás nem túl jelentős, de a GPS-rendszereket úgy szabályozzák be, hogy figyelembe vegyék a Föld gravitációs terében a kőzetekben az árapály miatt bekövetkező változásokat. A geológusok eközben a szilárd földkéregben megjelenő árapály hatását követik a törésvonalak mentén, illetve azt vizsgálják, mennyiben válthatnak ki ezek a változások földrengéseket vagy vulkánkitöréseket.
Az örvénylő viharrendszerekre és az árapályra adott magyarázatok véleményem szerint azért szépek és elegánsak, mert megtestesítik könyvünk egyik központi gondolatát, mely szerint a természetben előforduló, látszólag bonyolult és egymástól független jelenségek ugyanannak az egyszerű, alapvető, esetünkben Newton gravitációs törvényéből és mozgástörvényeiből álló rendszernek a segítségével magyarázhatók. Nem hiszem, hogy különösebb okra lenne szükségünk, amiért magyarázatot keresünk ezekre a jelenségekre, azon a tényen túlmenően, hogy ez a munka érdekes és szórakoztató. Mindamellett az árapály és a viharok magyarázata azért is előnyös volt számunkra, mert lehetővé tette, hogy átugráljunk egyik vonatkoztatási rendszerből a másikba, vagyis különböző nézőpontokból szemléljük ugyanazokat a fizikai jelenségeket. Ez a gondolat lesz a kiindulópontunk ahhoz, hogy mélyebbre hatoljunk a fizika világában. Amint a fejezet elején már kifejtettem, Albert Einsteintől származik az az alapelv szintjére emelt gondolat, miszerint a természet törvényeinek minden vonatkoztatási rendszerben ugyanolyan alakúaknak kell lenniük. Világegyetemünk ennek az alapelvnek megfelelően épül fel. Ezt a követelményt alkalmazva arra a következtetésre jutott, hogy kénytelen elvetni Newton törvényeit, és átírni a térről és az időről alkotott ösztönös képünket, a természeti jelenségeknek azt a hatalmas színpadát, amelyet hajlamosak vagyunk adottnak tekinteni.
A mozgások témaköre meglepően gazdag. A finomságok már Newton Principiájában is nyilvánvalóak. Miután általánosságban foglalkozott a testek mozgásával, és kidolgozott számos olyan eszközt, amelyek létezése napjaink fizikusai számára magától értetődő, Newton figyelme a bolygók Nap körüli mozgására irányult, hogy megoldjon olyan, a tudósokat ősidők óta foglalkoztató problémákat, mint az árapály kérdése, vagy a napok, a hónapok és az évek múlása. Pontosan tudta, hogy ehhez elengedhetetlen a tér és az idő természetének megértése, ezért különös gonddal fogalmazta meg az abszolút tér és az abszolút idő létezésére vonatkozó feltevéseit. Newton szükségét érezte, hogy feltevésként jelentse ki az abszolút idő létezését. Ez számomra egyértelműen bizonyítja, milyen zseniális fizikus volt. Newton úgy kezelte ezt a feltevést, mint ahogyan ma a tehetetlenség törvényét kezeljük; olyan axiómának tekintette, amely összhangban van a kor megfigyeléseivel, de nem bizonyítható valamilyen első alapelvekből kiindulva. Figyelemreméltó, hogy nemcsak azonosította ezt a feltevést, hanem említésre érdemesnek tartotta, jóllehet a XVII. században - és bizonyára a legtöbb ember fejében ma is — az idő olyan jelentéktelen apróság volt, amelyre nem érdemes több szót vesztegetni annak kijelentésénél, hogy abszolút érvényű és egyenletesen múlik. Ezzel viszont visszaérkeztünk oda, amikor fejezetünk elején arról tűnődtünk, hogy Monet pipacsokkal borított rétje az évek múlásával - talán örökre — eltűnt. Most viszont már abban a helyzetben vagyunk, hogy alaposan szemügyre vehetjük ezt a zavarba ejtő „talán”-t.
Miért cserélte le Einstein Newton mozgástörvényeit?
A mozgások felderítésében kulcsfontosságú fogalom a tehetetlenségi/inerciális vonatkoztatási rendszer, vagy röviden inerciarendszer. Ha viszont már ráuntak erre a fogalomra, akkor emlékeztetném önöket arra a korábbi javaslatomra, hogy igyanak meg egy pohár bort. Ha megteszik, még a minőségi borok és az emlékek közötti kapcsolatra is rátalálhatnak.
A lényeg mégis az, hogy lehetetlen eldönteni, melyik inerciarendszerben vagyunk, mert ezek a rendszerek mind tökéletesen egyenértékűek egymással, a „nyugalom” fogalma pedig mindig viszonylagos. Egyszerűbben fogalmazva ez azt jelenti, hogy nem tudjuk megmondani, mozgunk-e vagy sem. Ha gyorsulunk, akkor egészen más a helyzet, mert olyankor megjelennek a tehetetlenségi erők. Albert Einstein nagyon mélyen elgondolkozott ezeken a problémákon - véleményem szerint mindenki másnál mélyebben. Einstein a fésületlen, zoknit nem hordó zseni őstípusa. Élete későbbi szakaszában úgy nézett ki, mintha nem is ebben a világban élne, hanem egy, csak az elméletein keresztül elérhető, a földi ügyes-bajos dolgainkon túli, absztrakt térben. Ez természetesen közhely, Einstein jelentős fizikus volt, de a megértés „királyi útját” ő sem fedezte fel, mert ilyen út nem létezik. Keményen dolgozott, elmélyülten gondolkozott és megtanulta, hogyan kell összegzéseket készíteni. Mindamellett két relativitáselmélete kétségtelenül az emberiség legjelentősebb eredményei közé tartozik. Több mint egy évszázad telt el mióta megjelentek, és azóta is a modern fizika alapját képezik.
Einstein abból kiindulva jött rá a speciális relativitáselméletére, hogy a legfontosabb alapelvek szintjére emelve axiómának, a Világegyetem alapvető tulajdonságának tekintette azt a gondolatot, amely szerint az inerciarendszerek mind egyenértékűek. Ez a gondolat volt a vezérlő csillaga. Ha meg akarjuk érteni, miért volt ez ilyen fontos Einstein számára, akkor fel kell idéznünk a szimmetriának az 1. fejezetben megtárgyalt fogalmát.
Az a kijelentés, miszerint minden inerciarendszer egyenértékű, egy szimmetriára vonatkozó állítás. Ha még emlékszünk rá, a szimmetria a matematikában és a fizikában azt jelenti, hogy valamit megteszünk, aminek az az eredménye, hogy semmi sem változik. Egy négyzet bizonyos szimmetriája például azt jelenti, hogy ha megváltoztatjuk a nézőpontunkat, és 90 fokkal elfogatva szemléljük a négyzetet, akkor ugyanolyannak látjuk, mint korábban. Hasonló kérdéseket tehetünk fel a fizikai törvényeket, például Newton mozgástörvényeit illetően is. Vajon ezek a törvények is változatlanok maradnak, ha más nézőpontból vesszük szemügyre azokat? Az egyik ilyen szimmetria a következő kérdésre vonatkozik: ugyanolyannak látszanak-e a természet törvényei az összes inerciarendszerből?
Íme, a dolgok egy másik lehetséges szemléletmódja. A fizika törvényei a valóságos dolgokat és azok viselkedését írják le. Newton törvényei, amint láttuk, kimondják, hogy a guruló golyó mindaddig egyenes vonalú mozgást végez, amíg valamilyen külső erőhatás nem lép fel. Ha viszont fellép egy erőhatás, akkor az F = ma összefüggés adja meg, mi történik a golyóval. Képzeljük el, hogy egy guruló golyó mozgását figyeljük, miközben hirtelen úgy döntünk, hogy egy másik nézőpontból szeretnénk látni ezt a mozgást, ezért átugrunk egy másik inerciarendszerbe. Olyan vonatkoztatási rendszert választunk, amelyik a golyó felé, annak mozgásával szembe repül, miközben arra vagyunk kíváncsiak, hogyan változik meg ettől az események általunk adott leírása. Jól jegyezzük meg, hogy „az események általunk adott leírása” tulajdonképpen más szavakkal „a természet törvényeit” fejezi ki, tehát valójában azt szeretnénk megtudni, hogyan változnak meg a természeti törvények. Továbbra is úgy látjuk, hogy a golyó egyenes vonalú mozgást végez, hiszen semmilyen erő sem hat rá, sebességét viszont eltérőnek érzékeljük. Ha például 20 m/s sebességgel repülünk a golyó felé, és korábbi vonatkoztatási rendszerünkben a golyó sebességét 10 m/s-nak mértük, akkor a józan ész azt diktálja, hogy az új vonatkoztatási rendszerben a golyó 30 m/s sebességgel gurul felénk. Ha ily módon adjuk össze a sebességeket, akkor Newton törvényeit használjuk, és azt tapasztaljuk, hogy előrejelzésünk helyesnek bizonyul. A jelenség fizikájáról adott leírásunk változatlan maradt, annak ellenére, hogy közben megváltoztattuk a nézőpontunkat. Ez Newton törvényeinek szimmetriáját tükrözi; a törvények változatlan alakúak maradnak, miközben átugrunk egyik inerciarendszerből a másikba, az összes objektum sebességének megváltozását pedig egyszerűen és a józan ész diktálta módon követjük.
Érdemes itt megemlíteni egy szakkifejezést: ha a fenti módon számítjuk ki a sebesség megváltozását, akkor ezt az eljárást Galileo Galilei tiszteletére Galilei-transzformációnak nevezzük. Minden tekintetben a fizika szakkifejezéseit használva azt állíthatjuk, hogy Newton törvényei invariánsak a Galilei-transzformációra nézve - ami a Newton-törvények szimmetriája.
Most gondoljuk végig a viharokra és az árapályra adott magyarázatainkat. Ezek olyan helyzetek, amelyekben a Newton-törvények nem maradnak változatlanok, amikor átváltunk egy másik vonatkoztatási rendszerre. A forgó rendszerben a golyó pályája elgörbül, vagyis a Coriolis-erő megjelenése következtében nem folytatja egyenes vonalú mozgását. Erről Newton második törvényének a forgó vonatkoztatási rendszerre történő módosításával adhatunk számot. A törvény a továbbiakban nem az F = ma alakot ölti. Ehelyett a következőképpen változik: F + FCor = ma, ahol FCor jelöli a Coriolis-erőt. Hasonlóképpen, az árapály eredetére gondolva olyan, a Földdel együtt forgó vonatkoztatási rendszerre váltunk át, amelyik a Föld-Hold-rendszer közös tömegközéppontja körül kering. Ebben az esetben az F = ma összefüggés F + Fcen = ma alakúra módosul, ahol Fcen a centrifugális erőt jelöli. A forgó vonatkoztatási rendszerek esetében tehát azt tapasztaltuk, hogy Newton törvénye egyik esetben sem marad változatlan, mert megjelentek a „tehetetlenségi erők”. Szakszerűen úgy fogalmazhatunk, hogy Newton törvényei nem invariánsuk arra a transzformációra nézve, amikor egy inerciarendszerről átváltunk egy forgó vonatkoztatási rendszerre. Egyébként mindkét esetben a centrifugális erő és a Coriolis-erő egyaránt jelen van, de az árapály létrejötte szempontjából a Coriolis-erő hatása nem jelentős, míg a ciklonok és anticiklonok kialakulásakor a centrifugális erő hatása hagyható figyelmen kívül.
Azért töltöttünk el némi időt ezeknek a gondolatoknak a megvitatásával, mert ezeknek kiemelkedően fontos szerepük van a modern fizikában - különösen akkor, ha meg akarjuk érteni, miért dolgozta ki Einstein a relativitáselméletét.
Einstein volt az első, aki komolyan vett egy nagyon fontos, de első pillantásra meglehetősen furcsa tényt. Newton törvényeivel ellentétben, az elektromosság és a mágnesség törvényei nem invariánsak a Galilei-transzformációra nézve. Nem ugyanolyan alakúak az összes inerciarendszerben, ha úgy változtatjuk meg a sebességeket, ahogyan azt akkor tettük, amikor a Newton-törvényeket akartuk más nézőpontból megvizsgálni. Ez azt jelenti, hogy Newton törvényei nem állnak összhangban (nem konzisztensek) az elektromosság és a mágnesség törvényeivel. Ez volt a helyzet, amellyel Einsteinnek 1905-ben szembe kellett néznie.
Egyszerű oka van annak, amiért az elektromosság és a mágnesség törvényei gondot okoznak, de ennek megértéséhez röviden vissza kell pillantanunk a fizika történetébe. A XIX. században az elektromosság és a mágnesség kutatása a fizika élvonalát jelentette. Sok tudós emlékét őrizték meg az elektromosság területén ma is használt fogalmak: André-Marie Ampére-ről nevezték el ampernek az áramerősség mértékegységét, míg a feszültség egysége, a volt, Alessandro Voltáról kapta a nevét. A legjelentősebb kísérleti áttörést 1831-ben és 1832-ben érték el, amikor a londoni Királyi Intézetben és a Királyi Természettudományi Társaságban (Royal Society) végrehajtott kísérletsorozatával Michael Faraday felfedezte az elektromágneses indukciót, majd ennek nyomán feltalálta az elektromos generátort, amivel lefektette a modern világunk alapjait.
Az 1860-as években James Clerk Maxwell skót fizikus rájött, hogyan lehet egységes elméleti leírást adni az elektromos és a mágneses jelenségekről. Maxwell egyenletei az emberi szellem legjelentősebb alkotásai közé tartoznak. Einstein később úgy jellemezte Maxwell munkásságát, mint „a legalapvetőbb és leggyümölcsözőbb korszak a fizika történetében Newton óta”. Az egyenletek egyszerűen gyönyörűek, ezért nem tehetem meg, hogy ne mutassam meg önöknek. Pokolba azokkal, akik szerint minden közölt egyenlet csökkenti az ismeretterjesztő könyvek eladható példányszámát. Íme, Maxwell egyenletei:

Az egyenletekben E és B az elektromos, illetve a mágneses térerősséget jelöli, amelyek az elektromos és mágneses jelenségek Maxwell-féle leírásának alapfogalmai. Az ebben a formában felírt egyenletek csak két további fizikai mennyiséget tartalmaznak: t az időt, c pedig a fénysebességet jelöli. (A nem említett szimbólumok különböző matematikai műveleteket jelentenek - a szerkesztő megjegyzése.) Ez az a kulcs, amely Einstein számára kitárta a kaput. A fény sebessége Maxwell egyenleteiben állandóként jelenik meg, vagyis olyan alapvető számként, amelynek nem változik az értéke. Ez a Világegyetem felépítésének egyik axiómája, alapvető építőköve. Ez az a sebesség, amelyik mindenki számára ugyanakkora, függetlenül attól, milyen vonatkoztatási rendszerben dolgozik az illető. A felismerés megrázó, és katasztrofális hatásúnak látszik a fizika egészére nézve. Hogyan fordulhat elő, hogy mindenki ugyanakkorának méri a fény sebességét, függetlenül attól, milyen vonatkoztatási rendszerben dolgozik? Emlékezzünk vissza arra a példánkra, amikor a guruló golyó megfigyelése közben átváltottunk egyik vonatkoztatási rendszerről a másikra. Csak annyit kellett tennünk, hogy a józan ész diktálta és a Galilei-transzformációval kifejezett módon összeadtuk a sebességeket, és máris minden rendben volt. Maxwell azonban lerombolta ezt az elképzelést.
Képzeljünk el valakit, aki egy zseblámpát tart a kezében. A fény fénysebességgel hagyja el a zseblámpát, azaz másodpercenként 299 792 458 métert tesz meg. Képzeljük el azt is, hogy valaki ezt a jelenetet egy másik inerciális vonatkoztatási rendszerből figyeli, amely rendszer a fénysebesség felével közeledik a lámpa felé. Azt várnánk, hogy a sebességeket a Galilei-transzformációnak megfelelően összeadva, bármelyik rendszerben le tudjuk írni a helyzetet. A lámpa felé közeledő megfigyelő arra a következtetésre jutna, hogy a fénysugár 450 000 000 m/s sebességgel suhan el mellette - ami c + 1/2 c sebességnek felel meg. Maxwell egyenletei azonban az állítják, hogy nem ez a helyzet, hanem mindkét megfigyelő pontosan 299 792 458 m/s-nak méri a fény sebességét. A fény sebessége soha nem változik, teljesen mindegy, honnan nézzük. A fénysebesség állandó - a természet egyik alapvető jellemzője.
Ha ez kísértetiesnek hangzik, nem csoda, mert az is. Nem tudok más magyarázatot adni erre, csak azt, hogy a Világegyetemünk így van megalkotva. Maxwell egyenletei helyesek. Az a kijelentés, hogy a fény sebessége minden inerciarendszerben ugyanaz az állandó, ugyanolyan szilárd alapokon áll, mint a tehetetlenség elve. Azért van így, mert így van.
Einstein éleselméjűsége - vagy nevezzük inkább zsenialitásának - abban áll, hogy készpénznek vette Maxwell egyenleteit, ezért kitartott amellett, hogy hiába ugrunk át egyik inerciarendszerből a másikba, a fénysebesség ugyanakkora marad. Nem adhatjuk tehát úgy össze a sebességeket, ahogyan eddig tettük; az a módszer egyszerűen hibás. A Galilei-transzformáció hibás, és ennek értelmében ugyancsak hibásak Newton törvényei, amelyek azt a szimmetriát mutatják, amelyet a Galilei-transzformáció jelent.
Ezek után megpróbálhatjuk mindezeket a gondolatokat összehozni. Einstein úgy építette újjá a fizikát a semmiből, hogy két axiómához ragaszkodott, amelyeket Einstein-féle posztulátumoknak nevezünk. Közülük az elsőt már valóban jól ismerjük.
A fizika törvényei minden inerciarendszerben azonosak.
A második posztulátum abból ered, hogy szó szerint veszi a Maxwell-egyenleteket:
A fénysebesség vákuumban bármely inerciarendszerben ugyanakkora.
Ha fizikatankönyvet írnék, akkor most sorra venném ennek a két posztulátumnak az összes következményét, miközben olyan kincsekre bukkannánk, mint az E = mc2 összefüggés - vagyis arra a kijelentésre, amely szerint a tömeg és az energia egyenértékű. Ez a könyv azonban nem tankönyv. Ezért itt Einstein két posztulátumának egyetlen, de nagyon sajátos következményét akarjuk megvizsgálni: azt a gondolatot, amely szerint a tér és az idő nem az, aminek látszanak.
Térjünk most vissza a kezdetekhez; ahhoz a pillanathoz, amikor Argenteuil határában Monet leült a pipacsoktól pirosló rét szélére, tüdejét elárasztotta a késő tavaszi délután illata, ő pedig egy apró, piros foltot pöttyintett a vásznára. A relativitáselmélet nyelvén a piros festékpötty térbeli helyét és megjelenésének idejét eseménynek nevezzük. Mivel háromdimenziós térben élünk, a vászonra festett pipacs helyének megadásához három számra van szükségünk. Ez a három szám például a pipacsföldön álló festőállvány földrajzi szélessége, hosszúsága és a vászon tengerszint feletti magassága lehet. Ez a három szám megadja, hol történt az esemény. Meg kell adnunk azt is, mikor történt az esemény: 1873. május 26-án délben. Az esemény térbeli és időbeli helyének megadásához tehát négy koordinátára van szükségünk; három meghatározza a térbeli helyét, egy pedig az időpontját.
Gondoljunk most egy másik eseményre! Amint a fények elhalványodnak, Monet a hóna alá csapja a félkész vásznat, visszaballag a faluban lévő szobájába, és magára zárja az ajtót. A zár kattanása egy másik eseményt jelent, amelyiknek más a földrajzi szélessége, hosszúsága, a tengerszint feletti magassága, és az órája is más időpontot mutat. 1873. május 26-án este 8 órát.
Képzeljük el, hogy Monet elhatározta, hogy megméri a festőállványa és a szobája ajtaja közötti távolságot, amelyet pontosan 2 kilométernek talál, a két hely tengerszint fölötti magassága pedig azonos. Ez a két esemény térbeli távolsága. A két esemény között Monet órája szerint 8 óra telt el.
Newton, akárcsak Einstein színre lépése előtt bárki más, egyetértett volna azzal a józan ész sugallta megállapítással, amely szerint bármely megfigyelő, aki elhatározza, hogy megméri Monet festőállványának a távolságát a szobája ajtajától, valamint a piros pötty lefestése és az ajtózár kattanása között eltelt időt, Monet-ével teljesen azonos eredményt kapott volna, feltéve, hogy mérőrúdjaik és óráik pontosak és egymással szinkronban vannak. Einstein azonban rájött, hogy ha két posztulátumát alkalmazza, akkor nem ez a helyzet. A különböző megfigyelők nem egymáséval egyező eredményeket kapnak az események térbeli távolságára és a köztük eltelt időtartamra. Írjuk le pontosabban a helyzetet! Képzeljük el, hogy egy vállalkozó szellemű francia pilóta, aki egy jövőt idéző repülőgépet vezet, 1873. május 26-án a fénysebesség felével elrepül Monet mellett. A pilóta a pipacsot ábrázoló pont vászonra kerülése és az ajtózár kattanása közt eltelt időt 9 óra 14 percnek méri, a pipacsföldön álló festőállvány és az ajtó távolságát viszont 1,73 kilométernek találja. Ezt az eltérést nem az a módszer okozza, ahogyan a távolságot és az időt méri, mint ahogyan az sem, milyen formájú mérőeszközt használ.
Ráadásul sem Monet, sem a pilóta nem hibázott a méréskor; mindketten tökéletesen bizonyosak abban, hogy mérésüket helyesen hajtották végre. Továbbá, Einstein rájött, hogy a valóságban nem létezik sem abszolút idő, sem pedig abszolút tér. Ismételjük meg ezt, mert nagyon különös. A pilóta szemszögéből nézve Monet ideje lassabban múlik az övénél, ami azt jelenti, hogy Monet lassabban öregszik, mint a pilóta, Monet pedig valóban csak 1,73 kilométert tesz meg, amíg hazaér. Ennek a fordítottja is igaz. Ha Monet felnéz az égre, és látja elrepülni a repülőgépet, akkor azt tapasztalja, hogy pilóta órája lassabban jár az övénél, következésképpen a pilóta lassabban öregszik, mint ő. Egyúttal azt is megállapítja, hogy a repülőgép 0,866-szor rövidebb, mint amilyennek a pilótája méri. Persze, ha ez a valóságban megtörtént volna, akkor Monet minden bizonnyal abbahagyta volna a pipacsos rét lefestését, de nem ez a lényeg, hanem az, hogy mindez nem csupán elméleti lehetőség, mert a jelenség valóságos. A mozgó órák lelassulását idődilatációnak nevezzük, a mozgó tárgyak megrövidülését pedig Lorentz-kontrakciónak.
Ha önök jártasak a matematikában, akkor a „Monet és a pilóta” című szakaszban megtalálják annak a levezetését, miért és mennyivel látja lassabban járni Monet óráját a pilóta. A következtetés egyenes folyománya Einstein két posztulátumának, az érvelés pedig meglehetősen egyszerű, követéséhez nincs szükség a Pitagorasz-tételnél bonyolultabb matematikai ismeretekre. Ha viszont önök e szakasz áttanulmányozása nélkül is hisznek nekem, akkor nyugodtan folytassák az olvasást!
Az okot, amiért Einstein elmélete azt állítja, hogy a különböző vonatkoztatási rendszerekben mért térbeli távolságok és időtartamok nem azonosak, Einstein két posztulátumában kell keresnünk - vagyis annak megkövetelésében, hogy a természet törvényei minden inerciális vonatkoztatási rendszerben ugyanolyanok legyenek, illetve a fénysebesség minden inerciarendszerben ugyanakkora legyen. E két posztulátumból következik, hogy a mozgó órák lassabban járnak, amint azt az említett szakaszban majd bebizonyítjuk. Szabatosabban fogalmazva azt mondhatjuk, hogy Einstein a két inerciális vonatkoztatási rendszer közötti áttérést leíró Galilei-transzformációt kénytelen volt a Lorentz-transzformációnak nevezett egyenletekkel helyettesíteni. A Lorentz-transzformáció változatlanul hagyja a fénysebességet, amint azt a második posztulátum megköveteli. Ennek azonban borzalmas ára van: a Lorentz-transzformáció hatására megváltoznak a térbeli távolságok és az időtartamok, vagyis a mozgó méterrudak összezsugorodnak, a mozgó órák járása pedig lelassul!
Mit jelent mindez a számunkra? Rájöttünk, hogy a tér és az idő nem az, aminek látszanak, legalábbis, ha elfogadjuk, hogy a fénysebességnek minden megfigyelő számára állandónak kell lennie. Nem létezik az abszolút tér, mert az egymáshoz képest különböző sebességgel mozgó megfigyelők az események közti távolságot megmérve, nem ugyanazt az eredményt kapják. Nem tartható fenn a Világegyetemnek az a kellemes képe, amely hatalmas dobozhoz hasonlítja, amelyben minden csillagnak, bolygónak és galaxisnak meghatározott helye van, mert a csillagok, bolygók és galaxisok közötti távolságokat nem tudjuk egyértelműen definiálni. Hasonlóképpen, nem létezik az abszolút idő sem, mert nem lehet egyértelműen meghatározni a különböző események közt eltelt időtartamot.
Ez szórakoztató és furcsa, de egyúttal súlyos problémát jelent a fizika egésze számára. A problémát Einstein első posztulátuma jelenti, amely szerint a fizika törvényei minden inerciarendszerben azonosak. A fizika törvényei azok az eszközök, amelyek segítségével előre tudjuk jelezni a valóságos világban elvégzett kísérleteink eredményét; mert ezek adják a természet leírását. Ha ezeknek minden inerciarendszerben azonosaknak kell lenniük, akkor ebből az következik, hogy olyan mennyiségeket kell tartalmazniuk, amelyek ugyancsak azonosak minden inerciarendszerben. A fizika törvényei azonban, amelyeket az iskolában megtanultunk, vonalzóval mért távolságokat és órával mért időtartamokat tartalmaznak. Gondoljunk például Newton második törvényére, az F = ma összefüggésre, amely megadja, mekkora a gyorsulással mozog az m tömegű test F erő hatására. A gyorsulást m/s2-ben mérjük, tehát ez a fizikai mennyiség a bizonyos idő alatt megtett út változását fejezi ki. Minthogy azonban felfedeztük, hogy a távolságok és az időtartamok nem azonosak a különböző vonatkoztatási rendszerekben, ebből az következik, hogy Newton törvényei sem maradhatnak változatlan alakúak! Ez pedig maga lenne a katasztrófa.
Szerencsére nem ez a helyzet, mert Einstein megtalálta a kivezető utat. Rájött, hogy miközben két esemény térbeli távolsága, akárcsak a közöttük eltelt időtartam hossza megváltozhat, van egy olyan mennyiség, amelyik nem változik akkor sem, amikor áttérünk egyik inerciarendszerről a másikra: a térben és időben egyidejűleg, a kettő speciális kombinációjaként mért távolság.
Ha Monet festőállványa és a háza ajtaja közti távolságot Δx-szel, a piros pötty lefestése és a zár kattanása között eltelt időt pedig Δt-vel jelöljük, akkor a két esemény közötti változatlanul maradó „távolság” Δs2 = c2Δt2 — Δx2 lesz. A Δs távolság nagyságában Monet és a pilóta egyetértenek, jóllehet Δt-t és Δx-et egyaránt különbözőnek mérik. A Δs mennyiséget a két esemény téridőbeli távolságának nevezzük. A c fénysebesség körmönfont módon kerül bele a képletbe, ezzel kell megszorozni a Δt időkülönbséget. Miért? Egy dolgot máris biztosan kijelenthetünk: valamiféle sebességnek biztosan meg kell jelennie az összefüggésben, hogy a téridőbeli távolság értelmes legyen. Tegyük fel, hogy a Δt időkülönbséget másodpercben, a Δx térbeli távolságot méterben mérjük. Nem vonhatunk ki egy másodpercekben mért mennyiséget egy méterben mértből - éppúgy, ahogy nem lehet tíz narancsból öt almát elvenni. Ha viszont a másodpercekben mért időkülönbséget megszorozzuk egy méter/másodperc egységű sebességgel, akkor gond nélkül folytathatjuk a számolást, és ki tudjuk vonni belőle Δx-et. Ez az érvelés nem árulja el, milyen értéket kell c-nek felvennie, csak azt, hogy valamilyen sebességnek kell lennie.
Egy alsóbb évfolyamokra járó egyetemistáknak tartott fizikaelőadáson most annak taglalásával folytathatnánk, miként kezeli a speciális relativitáselmélet az energiát és az impulzust, majd bebizonyíthatnánk, hogy ez a speciális sebesség éppen a tömeg nélküli (azaz nulla nyugalmi tömegű) részecskék sebességeként értelmezhető. Véletlenül, mint tudjuk, a fotonok nyugalmi tömege nulla, ezért éppen a speciális c sebességgel mozognak - ezért nevezzük ezt az állandót fénysebességnek.
Az a körülmény, hogy a téridőben a távolságokat minden megfigyelő ugyanakkorának méri, felveti azt az ötletet, hogy esetleg a Δs és a hozzá hasonló mennyiségek alapján újjávarázsolhatnánk Newton törvényeit. Pontosan ezt tette Einstein, aki nemcsak Newton törvényeit, hanem a jól ismert fizikai mennyiségeket, például az energiát és az impulzust is azok téridőbeli változatára cserélte. Ebből adódik az E = mc2 összefüggés. Úgy gondolom, megnyugtató, hogy a természet ily módon van megalkotva. Végül is az események jelentik életünk történetét. Emlékeinket nem tudjuk különválasztani térbeli és időbeli összetevőre. Emlékszem egy tökéletes nyári napra 1972 augusztusában, amikor a sárgán ragyogó Nap elpárologtatta a gyep illatát, a méhek zümmögése pedig elnyomta a város zaját. Szüleink kertjében húgommal felállítottuk a lubickolómedencét, és addig pancsoltunk a vízben, amíg kidörzsölődött a combunk. Minderre egyetlen eseményként emlékszem, nem pedig különálló földrajzi szélességként, hosszúságként és dátumbélyegzőként.
A fotókon én vagyok, azon a bizonyos, verőfényes 1972. augusztusi napon a kerti medencében, illetve 2009. szeptember 2-án, filmforgatás közben, Etiópiában.


Saját téridődiagramom az oldhami Királyi Kórházban ülő Albert szemszögéből nézve.
Létezik egy ötletes módszer - az úgynevezett téridődiagram amellyel látványosan szemléltethetők az efféle gondolatok. Felrajzolásához az események térbeli helyét a vízszintes, időpontját pedig a függőleges tengelyen ábrázoljuk, amint az a következő ábrán látható. Két térbeli dimenziót az egyszerűség és áttekinthetőség kedvéért figyelmen kívül hagytunk, ezek gondolatmenetünk szempontjából amúgy is közömbösek, arról nem is beszélve, milyen körülményes lenne a sík papírlapon megkonstruálni egy négydimenziós diagramot. A téridődiagramon saját életutamat szeretném ábrázolni. Mindenekelőtt pontosan tisztázni kell, milyen vonatkoztatási rendszert használunk a téridődiagram elkészítésekor. Esetemben az oldhami Királyi Kórház lesz a vonatkoztatási rendszer kiindulópontja (amelyet inerciarendszernek tételezünk fel), ott láttam meg ugyanis a napvilágot 1968. március 3-án. Ez azt jelenti, hogy létrehozzuk az oldhami mérőrudak és az oldhami stopperórák rendszerét, amelyik nyugalomban van a Királyi Kórházhoz képest. Megállapodunk abban, hogy az órák születésem pillanatában nullát mutatnak, és mivel az oldhami Királyi Kórházban születtem, ezért születésem mint esemény koordinátái x = 0 és ct = 0 lesznek, ahol x az oldhami Királyi Kórháztól mért távolság, t pedig az x = 0 helyen található oldhami stopperóra által mért idő. Nos, jelöljük ezt az eseményt az „1968. március 3.” felirattal - ez lesz téridődiagramunk origója, azaz kezdőpontja.
Ezek után további eseményeket is elhelyezhetünk a diagramon. 1972 augusztusában a pancsolómedencénkben négy kilométerre voltam az oldhami Királyi Kórháztól. Abban a pontban az ott lévő oldhami óra 4 1/2 évet mutatott. 1989. március 3-án az olaszországi Firenzében jártam, ahol a svéd Europe rockegyüttes előzenekaraként a Dare nevű együttesünkkel autóbuszos turnén vettünk részt. Tudom, akkor az oldhami óra 21 évet mutatott, én pedig körülbelül 2000 kilométerre voltam az oldhami Királyi Kórháztól. Még egy eseményt említek. 2009. szeptember 2-án a számomra egyik legkedvesebb országban, Etiópiában jártam, ahol a Wonders of the Solar System (A Naprendszer csodái) című sorozat jeleneteit vettük fel az Erta Ale lávatónál, kedves, afar törzsbeli kísérőmmel.
Ily módon életem minden eseményét ábrázolni tudom az oldhami órákkal mért időpont és az oldhami Királyi Kórháztól való távolságuk alapján. A téridődiagramon így kapott vonalat az életem világvonalának nevezzük. Ez életem minden eseményét megjeleníti, ahogy azok időpontját az oldhami órák alapján, helyét pedig az oldhami méterrudakkal megállapítjuk. Gondoljunk csak Hermann Weyl emlékezetes kijelentésére: „Csak a tudatomnak a testem életútját végigkísérő tekintete számára kel életre a térben tovasuhanó és az időben folyvást változó képként ennek a világnak egy szelete.” Ez az, amire Weyl gondolt.
Van a téridődiagramnak még egy sajátossága, amelyet meg kell említeni: az 1968. március 3-i ponton áthaladó átlós vonalak. Ezek alkotják az úgynevezett fénykúpot, márpedig a fénykúpnak nagyon fontos szerepe van a relativitáselméletben. Ennek megértéséhez képzeljük el azt, hogy valaki születésem pillanatában egy fényjelet küldött ki Oldhamből a Világegyetembe - talán ünneplésként, ki tudja? Egy másodperc elteltével a fénysugár 1 fénymásodperc utat tett meg. Jelöljük meg eseményként a téridőnek azt a pontját, ameddig a fényjel az első másodperc végéig eljutott, vagyis az időtengelyen és a tértengelyen is az 1 másodperc * c koordinátákkal jellemzett pontot. Két másodperc elteltével a fényjel már 2 fénymásodperc távolságot tett meg és így tovább. Eszerint a fénykúp nem más, mint annak a fénysugárnak a világvonala, amelyik a diagram origójából - születésem eseményétől - indult ki. Ez a vonal mindvégig 45 fokos szögben halad a diagramon. Az én világvonalam a fénykúp belsejében vándorol, aminek azért kell egészen bizonyosan így lennie, mert semmi sem mozoghat a fénynél gyorsabban. Ennek belátásához nézzük meg a diagramon az „X”-szel jelölt pontot! Ez egy nagyon távol történt eseményt jelöl. Képzeljük el, hogy ez az esemény nem más, mint hogy egy földönkívüli fiúcska az 50 fényév távolságban lévő bolygóján a kerti medencéjében pancsol, mégpedig az oldhami órák tanúsága szerint pontosan akkor, amikor az én 1972-es kerti medencés eseményem is történt. Kijelenthetjük, hogy az oldhami vonatkoztatási rendszerben a két esemény egyidejű. Ha valaki jelen volt a születésemkor, akkor a fénynél sokkal gyorsabban kellene mozognia, hogy odaérjen a másik eseményhez — 4 1/2 év alatt 50 fényév távolságot kellene megtennie, márpedig ez nem lehetséges, mert semmi sem mozoghat a fénynél gyorsabban. Ezt bizonyára sokszor hallották már, és bizonyára fúrja az oldalukat, miért van így. Woody Allen szerint: „Lehetetlen a fény sebességénél gyorsabban utazni, de természetesen nem is kívánatos, mert folyton lerepülne a kalapunk.” Hamarosan ténylegesen meg fogjuk látni, miért nem lehetséges.
A fénykúpnak a diagram felső részébe eső részét a születésemre vonatkozó fénykúp jövőjének nevezzük, mert ez a téridőnek azt a tartományát jelöli ki, amelynek meglátogatására vagy befolyásolására lehetőségem van. A fénykúpon kívül eső eseményekre viszont semmilyen módon sem tudok hatással lenni, mert a fénysebességnél gyorsabban kellene utaznom, hogy odaérjek.
A diagram alsó felében, vagyis a születésem előtti időben is látunk egy fénykúpot. Ez a születésemhez viszonyított múltbeli fénykúp. A szüleim világvonalainak például valahol az én múltbeli fénykúpom belsejében kell lennie, hiszen magától értetődően hatásuk volt a megszületésemre. Sőt mi több, minden egyes ősöm világvonalának az én múltbeli fénykúpom belsejében kell lennie, egészen a földi élet 4 milliárd évvel ezelőtti kezdetéig visszamenőleg. A múltbeli fénykúpomon kívül elhelyezkedő események közül egyik sem lehetett hatással a születésemre, mert az azok által kibocsátott jelek csak a fénysebességnél gyorsabban haladva érkezhettek volna meg Oldhambe 1968. március 3-án.
Tegyünk most fel egy kérdést! Hogyan nézne ki ugyanez a diagram az elszánt francia pilótánk szemszögéből, aki állandó sebességgel repül? Azt már tudjuk, hogy a pilóta az oldhami órákat lassabban járni, az oldhami méterrudakat pedig összehúzódni látná, ezért az ő téridődiagramján az én világvonalam eseményei másutt lennének.
Az egyszerűség kedvéért tételezzük fel, hogy a pilóta születésem pillanatában a saját óráját hozzáigazítja az oldhami órákhoz, és elfogadja azt is, hogy az oldhami Királyi Kórház jelentse a nulla helyet az ő téridődiagramja tértengelyén. Másképp fogalmazva, a két diagram origója a t=0 pillanatban egybeesik.
Bár az oldhami Királyi Kórházban ülő megfigyelő nem fog egyetérteni a pilótával a világvonalamon előforduló események közötti térbeli, illetve időbeli távolság nagyságában, azonban az események közötti, a Δs2 = c2Δt2 - Δx2 összefüggéssel meghatározott, téridőbeli távolságot mindketten ugyanakkorának találják. Ez azt jelenti, hogy Δx és Δt tetszőleges módon változhat, de csak úgy, hogy Δs mindig változatlan maradjon. A pilóta téridődiagramja a következő ábrán látható. Vegyük észre, hogy - összhangban

A téridődiagram a pilóta szemszögéből nézve, aki hozzám képest +x irányban nagy sebességgel repül. A tengelyeket ct'-vel és x'-vel jelöltem, hogy hangsúlyozzam; a pilóta vonatkoztatási rendszerében eltérőek a tér- és az időkoordináták. Az origóban lévő esemény - a születésem amelyet az 1968. március 3. felirat jelöl, továbbra is az origóban marad, mert megegyeztünk abban, hogy a t = t' = 0 pillanatban a két vonatkoztatási rendszer origója egybeesik.
Ennek a görbének minden ponlja a téridőben azonos távolságra van az „1968. március 3.” eseménytől
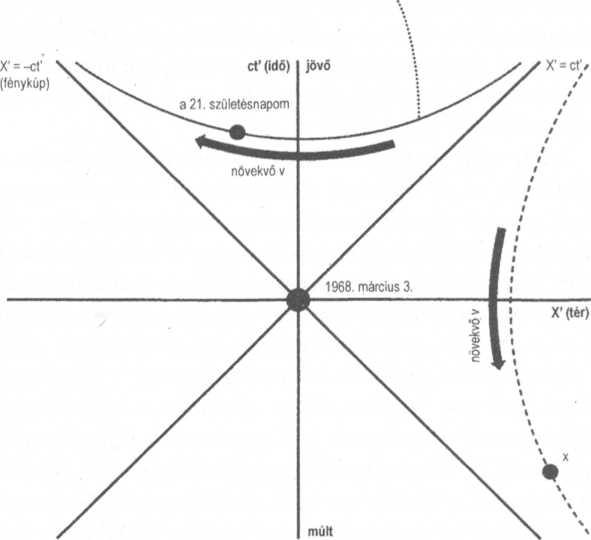
Einstein második posztulátumával - a fénykúpok változatlanok. A pilótának és az oldhami megfigyelőnek egyet kell értenie abban, hogy milyen gyorsan terjed a fény. Most lássuk, hová került a 21. születésnapomat jelentő esemény! Tudjuk, hogy a pilóta órája más ütemben jár, mint az oldhami óra, továbbá a pilóta mérőrúdjai az oldhamiektől eltérő hosszúságúak. Azt is tudjuk azonban, hogy bármekkora távolságot és időkülönbséget is mér a pilóta az „1968. március 3-i esemény” és a „21. születésnap” esemény között, a két értéknek engedelmeskednie kell annak a szabálynak, amely szerint az események közti Δs távolság ugyanakkora marad. A 21. születésnapom eseményének összes lehetséges helyét a pilóta téridődiagramján görbeként ábrázolhatjuk. A tényleges hely, amelyet a pilóta a görbén megjelöl, attól függ, mekkora sebességgel és milyen irányban repül. Ezúttal azt tételeztük fel, hogy a pilóta a fényéhez közeli sebességgel repül az oldhami pozitív x irányban. Egy érdekesség azonnal nyilvánvaló. A 21. születésnapom mindig a születésemkor kezdődő, jövőbeli fénykúp belsejében marad. Ennek így is kell lennie, hiszen a születésem volt a 21. születésnapom kiváltó oka! Bajban lennénk, ha valaki másnak a nézőpontjából a 21. születésnapom a fénykúpon kívülre csúszna, és így a születésem nem lehetne hatással rá!
Eddig tehát rendben is volnánk! Nézzük meg azonban most közelebbről az „X” eseményt - a földönkívüli kisfiú a medencéjében pancsol -, amelyik a születésem fénykúpján kívülre esik. Ennek az eseménynek is meg kell tartania téridőbeli távolságát 1968. március 3-tól, ehhez azonban eltérő útvonalat kell bejárnia. Döntő jelentőségű, hogy nem szükségszerűen marad a jövőmben. A pilóta és Oldham bizonyos relatív sebességei esetén a pilóta számára úgy tűnik, mintha az esemény a múltamban lenne! Ez bizony megérdemel egy felkiáltójelet. A pilóta szemszögéből nézve megváltozott az X esemény és a születésem időbeli sorrendje. Tényleg Einstein gyönyörű elmélete az, amelyik ezt a képtelen eredményt produkálja? Valóban igaz lehet, hogy a téridő különböző eseményeinek időrendjét a különböző megfigyelők különbözőnek látják? Igen, a megállapítás igaz, de ez nem okoz problémát, mert az X esemény mindig az én múltbeli és jövőbeli fénykúpomon kívül marad. Ez azt jelenti, hogy sem az X esemény nem lehetett befolyással az én megszületésemre, sem pedig a születésem nem gyakorolhatott hatást az X eseményre. A két esemény oksági szempontból független. Ez azt jelenti, hogy érdektelen, milyen időbeli sorrendet tulajdonítunk két ilyen eseménynek (amelyeket „térszerűen elválasztott” eseményeknek nevezünk), mert még elvben sem gyakorolhatnak egymásra bármiféle hatást. Nézzünk meg egy konkrét példát, hogy mindez érthetőbb legyen!
Képzeljük el, hogy pontosan a születésem pillanatában az én vonatkoztatási rendszeremben óriási robbanás történt a Napon. A Nap távolsága nyolc fényperc, ami azt jelenti, hogy a robbanás legalább nyolc percen keresztül semmilyen földi eseményre sem lehet hatással, mert ennyi idő alatt ér el a fény a Naptól a Földig. Az ilyen eseményeket „térszerűen elválasztottaknak” nevezzük, vagyis egy mellettünk nagy sebességgel elrepülő űrhajós a robbanást akár a születésem előtt, akár azt követően is láthatta. A két esemény időrendje felcserélődne. De kit érdekel? Mi változna ettől? Az égvilágon semmi, mert a két esemény nem lehet hatással egymásra.
Vegyük észre azonban, hogy nyolc perc elteltével a robbanás lökéshulláma elérheti a Földet, elpusztíthatja Oldhamet, és ahogyan a helyi szlengben mondani szokták, „akkor nekem annyi”. Ne felejtsük el azonban, hogy a téridőben lejátszódó eseményekről beszélünk. A születésem az egyik esemény, a robbanás egy másik, ám a születésem kívül esik a robbanás fénykúpján, ezért a robbanás nem tudja megakadályozni, hogy a világra jöjjek. Szerencsétlen pusztulásom nyolc perccel később viszont már egy másik esemény, amelyik a robbanás fénykúpján belül van. Senki sem láthatja időben fordított sorrendben ezeket az eseményeket. Azokat az eseményeket, amelyek egymás múltbeli vagy jövőbeli fénykúpján belülre esnek, „időszerűen elválasztott” eseményeknek nevezzük, és ezek időrendje nem változtatható meg.
Ne feledjük, Hogy minden működik, ha mégoly bonyolult módon is. Van azonban egy bökkenő. Gondoljunk újra a születésem eseményére - „1968. március 3.” -, és az X eseményre. Az oldhami vonatkoztatási rendszerben az X esemény az én jövőmben következik be. Egy másik vonatkoztatási rendszerben az X esemény a születésemmel egyidejűleg történhet, a pilóta vonatkoztatási rendszerében pedig a múltamban. Eszerint az egyik vonatkoztatási rendszerben véletlenül egyszerre bekövetkező események valamely másik vonatkoztatási rendszerben nem egyidejűek. Bár ez nem okoz problémát, mint láttuk, mégis felvet egy érdekes kérdést. Ha nem különböztethető meg egymástól egyértelműen a múlt és a jövő, és ha egy bizonyos esemény az egyik megfigyelő szerint valakinek a jövőjében, egy másik megfigyelő szerint viszont ugyanezen személy múltjában következik be, akkor mit jelent valójában a múlt és a jövő fogalma? Amikor megszülettem, akkor az X esemény már megtörtént, vagy még nem? Szerintem még nem. A pilóta szerint viszont már igen. Ez arra enged következtetni, hogy a relativitáselméletben az események a mi múltról, jelenről és jövőről alkotott fogalmainkon túl is léteznek.
Tegyük ezt még szemléletesebbé! Emlékezzünk vissza arra, hogy az X esemény azt jelenti, hogy egy földönkívüli kisfiú a Földtől 50 fényévre lévő bolygón a kerti medencéjében pancsol. Az oldhami vonatkoztatási rendszerben ez az esemény az én 1972-es nyári napommal egyidejűleg történt. Most pillantsunk a pilóta téridődiagramjára, hogyan érzékeli ezt az eseményt a hozzám képest nagy sebességgel repülő pilóta. Léteznek olyan vonatkoztatási rendszerek, amelyekben a földönkívüli kisfiú pancsolómedencéje az én múltamban található, az én egész életem pedig, benne az én pancsolásommal, az ő jövőjében van. Az én nyári napom az ő számára nem történt meg. Valahol ott lebeg a téridőben, az ő jövőjében, bár a téridőnek az a tartománya számára hozzáférhetetlen. Az én nézőpontomból viszont az én 1972-es kerti medencém az én saját emlékem, amire szeretettel gondolok vissza. Tehát bizonyosan végleg elmúlt, vagy nem?
Ha Einstein relativitáselméletét szó szerint értjük, akkor nincs értelme annak, hogy a múlt már megtörtént, a jövő pedig majd csak ezután fog megtörténni. Egy térszerűen elválasztott esemény az egyik nézőpontból valakinek a múltjában, más nézőpontból viszont a jövőjében lehet. Mindegy, mert ezek az események nem lehetnek egymásra hatással, feltéve, hogy semmi sem haladhat a fénynél gyorsabban. Ezért olyan fontos a relativitáselméletben a fénysebesség mint univerzális sebességhatár. Ez gondoskodik az oksági viszonyok megőrzéséről. Ez a viselkedése azonban azt a kérdést veti fel, hogy az összes esemény, amely megtörténhet vagy megtörtént a Világegyetem történetében, bizonyos értelemben „odakint” van-e. Ezt az elgondolást tömbuniverzum (block universe) elméletként ismerjük. A téridő négydimenziós buborékként ábrázolható, amelyen belül mozgunk, miközben találkozunk a világvonalunkon levő eseményekkel. A buborékban kénytelenek vagyunk fénysebességgel mozogni, ami a mi személyes perspektívánkból azt jelenti, hogy másodpercenként 1 másodperc sebességgel haladunk a jövő felé. (Ezt a téridőbeli távolság definíciója alapján láthatjuk be. Legyen Δx = 0, mert mi a saját vonatkoztatási rendszerünkben vagyunk, és vegyük észre, hogy Δs / Δt = c.) A téridő geometriája következtében öregszünk.
Hangsúlyozni kell, hogy bár a tömbuniverzum-elmélet a relativitáselmélet folyománya, ennek ellenére nem szükségszerűen helyes. Tudjuk, hogy a relativitáselmélet nem teljesen konzisztens a kvantumelmélettel, mindamellett a legtöbb fizikus reméli, hogy valamikor majd sikerül kidolgozni a téridő kvantumelméletét. Azt viszont nem tudjuk, hogy ez az elmélet a józan ész számára könnyebben felfogható képet alkot-e a múltról és a jövőről. Soha nem szabad elfelejtenünk, hogy a fizikai elméletek, például a relativitáselmélet, a valóság modelljei, amelyek a kísérletek eredményeivel egyező előrejelzéseket adnak - ez az elméletek ellenőrzésének az a gyakorlati próbája, amelyet mind a speciális, mind pedig az általános relativitáselmélet az elmúlt több mint egy évszázad alatt oly diadalmasan teljesített. Vajon a tömbuniverzum valóságos, vagy csupán Einstein modelljének a folyománya? Ki tudja? Én azonban azt gondolom, hogy következményei legalábbis megfontolásra érdemesek. Az elképzelés hátulütője, hogy a tömbuniverzumban nem létezik szabad akarat. Jövőnk összes eseménye „létezik”, és várja, hogy a világvonalunk mentén haladva belebotoljunk. Személy szerint engem nem különösebben érdekel, van-e szabad akaratom. Ez semmit sem jelent számomra. Az érem másik oldalát azonban csodálatosnak találom. A tömbuniverzumban a múlt is ott van valahol „odakint”. Az 1972-es idilli nyári délutánom Anyával, Apával és a húgommal nem csak az emlékeimben létezik. Nem szállt el örökre, bár én már soha többé nem tudom elérni. De mégis ott van; ugyanúgy, ahogy minden ember, minden pillanat valahol a téridőben mindig és örökké létezik. Imádom ezt a gondolatot.