References
  1. 1.
    B. Afsari, R. Tron, R. Vidal, On the convergence of gradient descent for finding the Riemannian center of mass. SIAM J. Contr. Opt.51 (3), 2230–2260 (2013)
  2. 2.
    M. Agueh, G. Carlier, Barycenters in the Wasserstein space. Soc. Indus. Appl. Math.43 (2), 904–924 (2011)
  3. 3.
    M. Agueh, G. Carlier, Vers un théorème de la limite centrale dans l’espace de Wasserstein? C.R. Math.355 (7), 812–818 (2017)
  4. 4.
    A. Ahidar-Coutrix, T. Le Gouic, Q. Paris, Convergence rates for empirical barycenters in metric spaces: curvature, convexity and extendable geodesics. Probab. Theory Relat. Fields (2019). https://​link.​springer.​com/​article/​10.​1007%2Fs00440-019-00950-0
  5. 5.
    M. Ajtai, J. Komlós, G. Tusnády, On optimal matchings. Combinatorica4 (4), 259–264 (1984)
  6. 6.
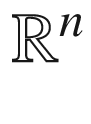
    G. Alberti, L. Ambrosio, A geometrical approach to monotone functions in $$\mathbb R^n$$ . Math. Z.230 (2), 259–316 (1999)
  7. 7.
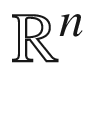
    S. Alesker, S. Dar, V. Milman, A remarkable measure preserving diffeomorphism between two convex bodies in $$\mathbb R^n$$ . Geometriae Dedicata74 (2), 201–212 (1999)
  8. 8.
    P.C. Álvarez-Esteban, E. del Barrio, J.A. Cuesta-Albertos, C. Matrán, Uniqueness and approximate computation of optimal incomplete transportation plans. Ann. Inst. Henri Poincaré Probab. Stat.47 (2), 358–375 (2011)
  9. 9.
    P.C. Álvarez-Esteban, E. del Barrio, J.A. Cuesta-Albertos, C. Matrán, A fixed-point approach to barycenters in Wasserstein space. J. Math. Anal. Appl.441 (2), 744–762 (2016)
  10. 10.
    L. Ambrosio, N. Gigli, A user’s guide to optimal transport, inModelling and Optimisation of Flows on Networks (Springer, Berlin, 2013), pp. 1–155
  11. 11.
    L. Ambrosio, A. Pratelli, Existence and stability results in theL 1 -theory of optimal transportation, inOptimal Transportation and Applications (Springer, Berlin, 2003), pp. 123–160
  12. 12.
    L. Ambrosio, N. Gigli, G. Savaré,Gradient Flows in Metric Spaces and in the Space of Probability Measures . Lectures in Mathematics. ETH Zürich, 2nd edn. (Springer, Berlin, 2008)
  13. 13.
    Y. Amit, U. Grenander, M. Piccioni, Structural image restoration through deformable templates. J. Amer. Stat. Assoc.86 (414), 376–387 (1991)
  14. 14.
    E. Anderes, S. Borgwardt, J. Miller, Discrete Wasserstein barycenters: optimal transport for discrete data. Math. Meth. Oper. Res.84 (2), 1–21 (2016)
  15. 15.
    J. Backhoff-Veraguas, J. Fontbona, G. Rios, F. Tobar, Bayesian learning with Wasserstein barycenters (2018). arXiv:1805.10833
  16. 16.
    A. Bandeira, P. Rigollet, J. Weed, Optimal rates of estimation for multi-reference alignment (2017). arXiv:1702.08546
  17. 17.
    M. Beiglböck, W. Schachermayer, Duality for Borel measurable cost functions. Trans. Amer. Math. Soc.363 (8), 4203–4224 (2011)
  18. 18.
    M. Beiglböck, M. Goldstern, G. Maresch, W. Schachermayer, Optimal and better transport plans. J. Func. Anal.256 (6), 1907–1927 (2009)
  19. 19.
    D.P. Bertsekas,Nonlinear Programming (Athena Scientific, Belmont, 1999)
  20. 20.
    R. Bhatia,Positive Definite Matrices (Princeton University Press, Princeton, 2009)
  21. 21.
    P.J. Bickel, D.A. Freedman, Some asymptotic theory for the bootstrap. Ann. Stat.9 (6), 1196–1217 (1981)
  22. 22.
    J. Bigot, T. Klein, Characterization of barycenters in the Wasserstein space by averaging optimal transport maps. ESAIM: Probab. Stat.22 , 35–57 (2018)
  23. 23.
    J. Bigot, R. Gouet, T. Klein, A. López, Upper and lower risk bounds for estimating the Wasserstein barycenter of random measures on the real line. Electron. J. Stat.12 (2), 2253–2289 (2018)
  24. 24.
    P. Billingsley,Convergence of Probability Measures , 2nd edn. (Wiley, New York, 1999)
  25. 25.
    S. Bobkov, M. Ledoux,One-Dimensional Empirical Measures, Order Statistics and Kantorovich Transport Distances , vol. 261, no. 1259 (Memoirs of the American Mathematical Society, Providence, 2019). https://​doi.​org/​10.​1090/​memo/​1259
  26. 26.
    V.I. Bogachev, A.V. Kolesnikov, The Monge–Kantorovich problem: achievements, connections, and perspectives. Russ. Math. Surv.67 (5), 785–890 (2012)
  27. 27.
    E. Boissard, T. Le Gouic, On the mean speed of convergence of empirical and occupation measures in Wasserstein distance. Ann. Inst. H. Poincaré. Probab. Stat.50 (2), 539–563 (2014)
  28. 28.
    E. Boissard, T. Le Gouic, J.-M. Loubes, Distribution‘s template estimate with Wasserstein metrics. Bernoulli21 (2), 740–759 (2015)
  29. 29.
    F. Bolley, A. Guillin, C. Villani, Quantitative concentration inequalities for empirical measures on non-compact spaces. Prob. Theory Rel. Fields137 , 541–593 (2007)
  30. 30.
    N. Bonneel, J. Rabin, G. Peyré, H. Pfister, Sliced and radon Wasserstein barycenters of measures. J. Math. Imag. Vis.51 (1), 22–45 (2015)
  31. 31.
    Y. Brenier, Polar factorization and monotone rearrangement of vector-valued functions. Commun. Pure Appl. Math.44 (4), 375–417 (1991)
  32. 32.
    L.A. Caffarelli, The regularity of mappings with a convex potential. J. Amer. Math. Soc.5 (1), 99–104 (1992)
  33. 33.
    G. Carlier, I. Ekeland, Matching for teams. Econ. Theory42 (2), 397–418 (2010)
  34. 34.
    A. Chakraborty, V.M. Panaretos, Functional registration and local variations: Identifiability, rank, and tuning (2017). arXiv:1702.03556
  35. 35.
    V. Chernozhukov, A. Galichon, M. Hallin, M. Henry, Monge–Kantorovich depth, quantiles, ranks and signs. Ann. Stat.45 (1), 223–256 (2017)
  36. 36.
    P. Clément, W. Desch, An elementary proof of the triangle inequality for the Wasserstein metric. Proc. Amer. Math. Soc.136 (1), 333–339 (2008)
  37. 37.
    J.A. Cuesta-Albertos, C. Matrán, Notes on the Wasserstein metric in Hilbert spaces. Ann. Probab.17 (3), 1264–1276 (1989)
  38. 38.
    J.A. Cuesta-Albertos, L. Rüschendorf, A. Tuero-Diaz, Optimal coupling of multivariate distributions and stochastic processes. J. Multivar. Anal.46 (2), 335–361 (1993)
  39. 39.
    J.A. Cuesta-Albertos, C. Matrán-Bea, A. Tuero-Diaz, On lower bounds for theL 2 -Wasserstein metric in a Hilbert space. J. Theor. Probab.9 (2), 263–283 (1996)
  40. 40.
    J.A. Cuesta-Albertos, C. Matrán, A. Tuero-Diaz, Optimal transportation plans and convergence in distribution. J. Multivar. Anal.60 (1), 72–83 (1997)
  41. 41.
    D.J. Daley, D. Vere-Jones,An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure (Springer, Berlin, 2007)
  42. 42.
    E. del Barrio, J.-M. Loubes, Central limit theorems for empirical transportation cost in general dimension. Ann. Probab.47 (2), 926–951 (2019). https://​projecteuclid.​org/​euclid.​aop/​1551171641
  43. 43.
    E. del Barrio, E. Giné, C. Matrán, Central limit theorems for the Wasserstein distance between the empirical and the true distributions. Ann. Probab.27 (2), 1009–1071 (1999)
  44. 44.
    D. Dowson, B. Landau, The Fréchet distance between multivariate normal distributions. J. Multivar. Anal.12 (3), 450–455 (1982)
  45. 45.
    I.L. Dryden, K.V. Mardia,Statistical Shape Analysis , vol. 4 (Wiley, Chichester, 1998)
  46. 46.
    R.M. Dudley, The speed of mean Glivenko–Cantelli convergence. Ann. Math. Stat.40 (1), 40–50 (1969)
  47. 47.
    R.M. Dudley,Real Analysis and Probability , vol. 74 (Cambridge University Press, Cambridge, 2002)
  48. 48.
    N. Dunford, J.T. Schwartz, W.G. Bade, R.G. Bartle,Linear Operators (Wiley-Interscience, New York, 1971)
  49. 49.
    R. Durrett,Probability: Theory and Examples (Cambridge University Press, Cambridge, 2010)
  50. 50.
    J. Edmonds, R.M. Karp, Theoretical improvements in algorithmic efficiency for network flow problems. J. ACM19 (2), 248–264 (1972)
  51. 51.
    F. Ferraty, P. Vieu,Nonparametric Functional Data Analysis: Theory and Practice (Springer, Beriln, 2006)
  52. 52.
    A. Figalli,The Monge–Ampère Equation and Its Applications (European Mathematical Society, Zürich, 2017)
  53. 53.
    J. Fontbona, H. Guérin, S. Méléard, Measurability of optimal transportation and strong coupling of martingale measures. Electron. Commun. Probab.15 , 124–133 (2010)
  54. 54.
    N. Fournier, A. Guillin, On the rate of convergence in Wasserstein distance of the empirical measure. Probab. Theory Rel. Fields162 (3–4), 707–738 (2015)
  55. 55.
    M. Fréchet, Les éléments aléatoires de nature quelconque dans un espace distancié. Ann. Inst. Henri Poincaré10 (4), 215–310 (1948)
  56. 56.
    M. Fréchet, Sur la distance de deux lois de probabilité. C.R. Hebd. Seances Acad. Sci.244 (6), 689–692 (1957)
  57. 57.
    D.H. Fremlin,Measure Theory, Vol. 4: Topological Measure Theory (Torres Fremlin, Colchester, 2003)
  58. 58.
    B. Galasso, Y. Zemel, M. de Carvalho, Bayesian semiparametric modelling of phase-varying point processes (2018). arXiv:1812.09607
  59. 59.
    W. Gangbo, R.J. McCann, The geometry of optimal transportation. Acta Math.177 (2), 113–161 (1996)
  60. 60.
    W. Gangbo, A. Świȩch, Optimal maps for the multidimensional Monge–Kantorovich problem. Comm. Pure Appl. Math.51 (1), 23–45 (1998)
  61. 61.
    T. Gasser, A. Kneip, Searching for structure in curve samples. J. Amer. Statist. Assoc.90 (432), 1179–1188 (1995)
  62. 62.
    M. Gelbrich, On a formula for theL 2 -Wasserstein metric between measures on Euclidean and Hilbert spaces. Math. Nachr.147 (1), 185–203 (1990)
  63. 63.
    D. Gervini, T. Gasser, Self-modelling warping functions. J. Roy. Stat. Soc.: Ser. B66 (4), 959–971 (2004)
  64. 64.
    D. Gervini, T. Gasser, Nonparametric maximum likelihood estimation of the structural mean of a sample of curves. Biometrika92 (4), 801–820 (2005)
  65. 65.
    C.R. Givens, R.M. Shortt, A class of Wasserstein metrics for probability distributions. Mich. Math. J.31 (2), 231–240 (1984)
  66. 66.
    J.C. Gower, Generalized Procrustes analysis. Psychometrika40 (1), 33–51 (1975)
  67. 67.
    D. Groisser, On the convergence of some Procrustean averaging algorithms. Stochastics: An Inter. J. Probab. Stoch. Process.77 (1), 31–60 (2005)
  68. 68.
    H. Heinich, J.-C. Lootgieter, Convergence des fonctions monotones. C. R. Acad. Sci. ser. 1 Mathé322 (9), 869–874 (1996)
  69. 69.
    T. Hildebrandt, Integration in abstract spaces. Bull. Amer. Math. Soc.59 (2), 111–139 (1953)
  70. 70.
    L. Horváth, P. Kokoszka,Inference for Functional Data with Applications , vol. 200 (Springer, Berlin, 2012)
  71. 71.
    T. Hsing, R. Eubank,Theoretical Foundations of Functional Data Analysis, with an Introduction to Linear Operators (Wiley, Hoboken, 2015)
  72. 72.
    G.M. James, Curve alignment by moments. Ann. Appl. Stat.1 (2), 480–501 (2007)
  73. 73.
    H.E. Jones, N. Bayley, The Berkeley growth study. Child Dev.12 (2), 167–173 (1941)
  74. 74.
    R. Jordan, D. Kinderlehrer, F. Otto, The variational formulation of the Fokker–Planck equation. SIAM J. Math. Anal.29 (1), 1–17 (1998)
  75. 75.
    O. Kallenberg,Random Measures , 3rd edn. (Academic, Cambridge, 1983)
  76. 76.
    O. Kallenberg,Foundations of Modern Probability (Springer, Berlin, 1997)
  77. 77.
    L.V. Kantorovich, On the translocation of masses. (Dokl.) Acad. Sci. URSS37 (3), 199–201 (1942)
  78. 78.
    H. Karcher, Riemannian center of mass and mollifier smoothing. Commun. Pure Appl. Math.30 (5), 509–541 (1977)
  79. 79.
    A. Karr,Point Processes and Their Statistical Inference , vol. 7 (CRC Press, Boca Raton, 1991)
  80. 80.
    H.G. Kellerer, Duality theorems for marginal problems. Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete67 (4), 399–432 (1984)
  81. 81.
    B. Kloeckner, A generalization of Hausdorff dimension applied to Hilbert cubes and Wasserstein spaces. J. Topol. Anal.4 (2), 203–235 (2012)
  82. 82.
    A. Kneip, J.O. Ramsay, Combining registration and fitting for functional models. J. Amer. Stat. Assoc.103 (483), 1155–1165 (2008)
  83. 83.
    M. Knott, C.S. Smith, On the optimal mapping of distributions. J. Optim. Theory Appl.43 (1), 39–49 (1984)
  84. 84.
    A. Kroshnin, V. Spokoiny, A. Suvorikova, Statistical inference for Bures–Wasserstein barycenters (2019). arXiv:1901.00226
  85. 85.
    H.W. Kuhn, The Hungarian method for the assignment problem. Nav. Res. Log. Quart.2 , 83–97 (1955)
  86. 86.
    H. Le, Locating Fréchet means with application to shape spaces. Adv. Appl. Probab.33 (2), 324–338 (2001)
  87. 87.
    T. Le Gouic, J.-M. Loubes, Existence and consistency of Wasserstein barycenters. Prob. Theory Relat. Fields168 (3–4), 901–917 (2017)
  88. 88.
    E.L. Lehmann, A general concept of unbiasedness. Ann. Math. Stat.22 (4), 587–592 (1951)
  89. 89.
    D.G. Luenberger, Y. Ye,Linear and Nonlinear Programming (Springer, Berlin, 2008)
  90. 90.
    J.S. Marron, J.O. Ramsay, L.M. Sangalli, A. Srivastava, Functional data analysis of amplitude and phase variation. Stat. Sci.30 (4), 468–484 (2015)
  91. 91.
    V. Masarotto, V.M. Panaretos, Y. Zemel, Procrustes metrics on covariance operators and optimal transportation of Gaussian processes. Sankhyā A81 , 172–213 (2019) (Invited Paper, Special Issue on Statistics on non-Euclidean Spaces and Manifolds)
  92. 92.
    D.M. Mason, A weighted approximation approach to the study of the empirical Wasserstein distance, in ed. by C. Houdré, D.M. Mason, P. Reynaud-Bouret, J. Rosiński,High Dimensional Probability VII (Birkhäuser, Basel, 2016), pp. 137–154
  93. 93.
    R.J. McCann, A convexity principle for interacting gases. Adv. Math.128 (1), 153–179 (1997)
  94. 94.
    R.J. McCann, Exact solutions to the transportation problem on the line. Proc. R. Soc. London, Ser. A: Math. Phys. Eng. Sci.455 (1984), 1341–1380 (1999)
  95. 95.
    G. Monge, Mémoire sur la théorie des déblais et des remblais. Histoire de l’Académie R. des Sci. de Paris177 , 666–704 (1781)
  96. 96.
    J. Munkers, Algorithms for the assignment and transportation problems. J. Soc. Indust. Appl. Math.5 , 32–38 (1957)
  97. 97.
    R.B. Nelsen,An Introduction to Copulas (Springer, Berlin, 2013)
  98. 98.
    I. Olkin, F. Pukelsheim, The distance between two random vectors with given dispersion matrices. Linear Algebra Appl.48 , 257–263 (1982)
  99. 99.
    F. Otto, The geometry of dissipative evolution equations: the porous medium equation. Comm. Part. Differ. Equ.26 , 101–174 (2001)
  100. 100.
    V.M. Panaretos, Y. Zemel, Amplitude and phase variation of point processes. Ann. Stat.44 (2), 771–812 (2016)
  101. 101.
    V.M. Panaretos, Y. Zemel, Statistical aspects of Wasserstein distances. Annu. Rev. Stat. Appl.6 , 405–431 (2019)
  102. 102.
    B. Pass, Optimal transportation with infinitely many marginals. J. Funct. Anal.264 (4), 947–963 (2013)
  103. 103.
    G. Peyré, M. Cuturi, Computational optimal transport. Found. Trends Mach. Learn.11 (5–6), 355–607 (2019). https://​www.​nowpublishers.​com/​article/​Details/​MAL-073
  104. 104.
    D. Pollard.Convergence of Stochastic Processes (Springer, Berlin, 2012)
  105. 105.
    A. Pratelli, On the sufficiency ofc -cyclical monotonicity for optimality of transport plans. Mathe. Zeitschrift258 (3), 677–690 (2008)
  106. 106.
    S.T. Rachev, The Monge–Kantorovich mass transference problem and its stochastic applications. Theory Probab. Appl.29 (4), 647–676 (1985)
  107. 107.
    S.T. Rachev, L. Rüschendorf,Mass Transportation Problems: Volume I: Theory, Volume II: Applications (Springer, Berlin, 1998)
  108. 108.
    J. Ramsay, X. Li, Curve registration. J. Roy. Stat. Soc.: Ser. B (Stat. Methodol.)60 (2), 351–363 (1998)
  109. 109.
    J.O. Ramsay, B.W. Silverman,Applied Functional Data Analysis: Methods and Case Studies , vol. 77 (Citeseer, 2002)
  110. 110.
    J.O. Ramsay, B.W. Silverman,Functional Data Analysis , 2nd edn. (Springer, Berlin, 2005)
  111. 111.
    J.O. Ramsay, H. Wickham, S. Graves, G. Hooker,FDA: Functional Data Analysis , R package version 2.4.8 (2018)
  112. 112.
    R.T. Rockafellar, Characterization of the subdifferentials of convex functions. Pac. J. Math.17 (3), 497–510 (1966)
  113. 113.
    R.T. Rockafellar,Convex Analysis (Princeton University Press, Princeton, 1970)
  114. 114.
    C.A. Rogers, Covering a sphere with spheres. Mathematika10 (2), 157–164 (1963)
  115. 115.
    B.B. Rønn, Nonparametric maximum likelihood estimation for shifted curves. J. Roy. Stat. Soc.: Ser. B (Stat. Methodol.)63 (2), 243–259 (2001)
  116. 116.
    L. Rüschendorf, Onc -optimal random variables. Stat. Probab. Lett.27 (3), 267–270 (1996)
  117. 117.
    L. Rüschendorf, S.T. Rachev, A characterization of random variables with minimumL 2 -distance. J. Multivar. Anal.32 (1), 48–54 (1990)
  118. 118.
    H. Sakoe, S. Chiba, Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech Signal Process.26 (1), 43–49 (1978)
  119. 119.
    F. Santambrogio,Optimal Transport for Applied Mathematicians , vol. 87 (Springer, Berlin, 2015)
  120. 120.
    W. Schachermayer, J. Teichmann, Characterization of optimal transport plans for the Monge–Kantorovich problem. Proc. Amer. Math. Soc.137 (2), 519–529 (2009)
  121. 121.
    E.M. Stein, R. Shakarchi,Real Analysis: Measure Theory, Integration & Hilbert Spaces . (Princeton University Press, Princeton, 2005)
  122. 122.
    R. Tang, H.-G. Müller, Pairwise curve synchronization for functional data. Biometrika95 (4), 875–889 (2008)
  123. 123.
    J.D. Tucker, W. Wu, A. Srivastava, Generative models for functional data using phase and amplitude separation. Comput. Stat. Data Anal.61 , 50–66 (2013)
  124. 124.
    C. Villani,Topics in Optimal Transportation (American Mathematical Society, Providence, 2003)
  125. 125.
    C. Villani,Optimal Transport: Old and New (Springer, Berlin, 2008)
  126. 126.
    M.J. Wainwright,High-Dimensional Statistics: A Non-Asymptotic Viewpoint (Cambridge University Press, Cambridge, 2019)
  127. 127.
    J.-L. Wang, J.-M. Chiou, H.-G. Müller, Functional data analysis. Annu. Rev. Stat. Appl.3 , 257–295 (2016)
  128. 128.
    K. Wang, T. Gasser, Alignment of curves by dynamic time warping. Ann. Stat.25 (3), 1251–1276 (1997)
  129. 129.
    K. Wang, T. Gasser, Synchronizing sample curves nonparametrically. Ann. Stat.27 , 439–460 (1999)
  130. 130.
    J. Weed, F. Bach, Sharp asymptotic and finite-sample rates of convergence of empirical measures in Wasserstein distance. Bernoulli25 (4A), 2620–2648 (2019). https://​projecteuclid.​org/​euclid.​bj/​1568362038
  131. 131.
    J. Wrobel, V. Zipunnikov, J. Schrack, J. Goldsmith, Registration for exponential family functional data. Biometrics75 , 48–57 (2019)
  132. 132.
    S. Wu, H.-G. Müller, Z. Zhang, Functional data analysis for point processes with rare events. Stat. Sinica23 (1), 1–23 (2013)
  133. 133.
    W. Wu, A. Srivastava, Analysis of spike train data: Alignment and comparisons using the extended Fisher–Rao metric. Electron. J. Stat.8 , 1776–1785 (2014)
  134. 134.
    Y. Zemel, V.M. Panaretos, Fréchet means and Procrustes analysis in Wasserstein space. Bernoulli25 (2), 932–976 (2019)
  135. 135.
    Y. Zemel, V.M. Panaretos, Supplement to “Fréchet means and Procrustes analysis in Wasserstein space” (2019)