Interlude 3: Partial Differentiation

“Look out there, Lenny. Ain’t those hills and valleys pretty?”

“Yeah George. Can we get a place over there when we get some money? Can we?”

George squinted. “Exactly where are you looking Lenny?”

Lenny pointed. “Right over there George. That local minimum.”

Partial Derivatives

The calculus of multivariable functions is a straightforward generalization of single-variable calculus. Instead of a function of a single variable t, consider a function of several variables. To illustrate, let’s call the variables x, y, z, although these don’t have to stand for the coordinates of ordinary space. Moreover, there can be more or fewer than three. Let us also consider a function of these variables, V(x, y, z). For every value of x, y, z, there is a unique value of V(x, y, z) that we assume varies smoothly as we vary the coordinates.

Multivariable differential calculus revolves around the concept of partial derivatives. Suppose we are examining the neighborhood of a point x, y, z, and we want to know the rate at which V varies as we change x while keeping y and z fixed. We can just imagine that y and z are fixed parameters, so the only variable is x. The derivative of V is then defined by

(1)

where Δ V is defined by

(2)

Note that in the defininition of Δ V, only x has been shifted; y and z are kept fixed.

The derivative defined by Eq. (1) and Eq. (2) is called the partial derivative of V with respect to x and is denoted

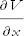
or, when we want to emphasize that y and z are kept fixed,

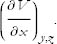
By the same method we can construct the partial derivative with respect to either of the other variables:

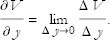
A shorthand notation for the partial derivatives of V with respect to y is

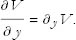
Multiple derivatives are also possible. If we think of 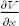as itself being a function of x, y, z, then it can be differentiated. Thus we can define the second-order partial derivative with respect to x:

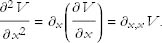
Mixed partial derivatives also make sense. For example, one can differentiate ∂ _y V with respect to x:

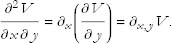
It’s an interesting and important fact that the mixed derivatives do not depend on the order in which the derivatives are carried out. In other words,

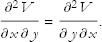
Exercise 1: Compute all first and second partial derivatives—including mixed derivatives—of the following functions.

Stationary Points and Minimizing Functions

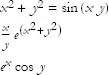
Let’s look at a function of y that we will call F (see Figure 1).

Figure 1: Plot of the function F(y).

Notice that there are places on the curve where a shift in y in either direction produces only an upward shift in F. These points are called local minima. In Figure 2 we have added dots to indicate the local minima.

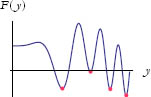
Figure 2: Local minima.

For each local minimum, when you go in either direction along y, you begin to rise above the dot in F(y). Each dot is at the bottom of a little depression. The global minimum is the lowest possible place on the curve.

One condition for a local minimum is that the derivative of the function with respect to the independent variable at that point is zero. This is a necessary condition, but not a sufficient condition. This condition defines any stationary point,

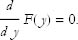
The second condition tests to see what the character of the stationary point is by examining its second derivative. If the second derivative is larger than 0, then all points nearby will be above the stationary point, and we have a local minimum:

If the second derivative is less than 0, then all points nearby will be below the stationary point, and we have a local maximum:

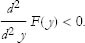
See Figure 3 for examples of local maxima.

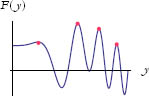
Figure 3: Local maxima.

If the second derivative is equal to 0, then the derivative changes from positive to negative at the stationary point, which we call a point of inflection:

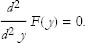
See Figure 4 for an example of a point of inflection.

Figure 4: Point of inflection.

These are collectively the results of a second-derivative test.

Stationary Points in Higher Dimensions

Local maxima, local minima, and other stationary points can happen for functions of more than one variable. Imagine a hilly terrain. The altitude is a function that depends on the two coordinates—let’s say latitude and longitude. Call it A(x, y). The tops of hills and the bottoms of valleys are local maxima and minima of A(x, y). But they are not the only places where the terrain is locally horizontal. Saddle points occur between two hills. You can see some examples in Figure 5.

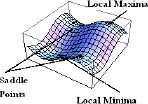
Figure 5: A function of several variables.

The very tops of hills are places where no matter which way you move, you soon go down. Valley bottoms are the opposite; all directions lead up. But both are places where the ground is level.

There are other places where the ground is level. Between two hills you can find places called saddles. Saddle points are level, but along one axis the altitude quickly increases in either direction. Along another perpendicular direction the altitude decreases. All of these are called stationary points.

Let’s take a slice along the x axis through our space so that the slice passes through a local minimum of A, see Figure 6.

Figure 6: A slice along the x axis.

It’s apparent that at the minimum, the derivative of A with respect to x vanishes, we write this:

On the other hand, the slice could have been oriented along the y axis, and we would then conclude that

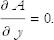
To have a minimum, or for that matter to have any stationary point, both derivatives must vanish. If there were more directions of space in which A could vary, then the condition for a stationary point is given by:

(3)

for all x_i.

There is a shorthand for summarizing these equations. Recall that the change in a function when the point x is varied a little bit is given by

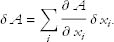
The set of Equations (3) are equivalent to the condition that

(4)

for any small variation of x.

Suppose we found such a point. How do we tell whether it is a maximum, a minimum, or a saddle. The answer is a generalization of the criterion for a single variable. We look at the second derivatives. But there are several second derivatives. For the case of two dimensions, we have

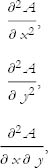
and

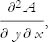
the last two being the same.

These partial derivatives are often arranged into a special matrix called the Hessian matrix.

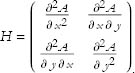
Important quantities, called the determinant and the trace, can be made out of such a matrix. The determinant is given by

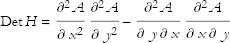
and the trace is given by

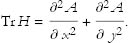
Matrices, determinants, and traces may not mean much to you beyond these definitions, but they will if you follow these lectures to the next subject—quantum mechanics. For now, all you need is the definitions and the following rules.

If the determinant and the trace of the Hessian are positive then the point is a local minimum.

If the determinant is positive and the trace negative the point is a local maximum.

If the determinant is negative, then irrespective of the trace, the point is a saddle point.

However: One caveat, these rules specifically apply to functions of two variables. Beyond that, the rules are more complicated.

None of this is obvious for now, but it still enables you to test various functions and find their different stationary points. Let’s take an example. Consider

F(x, y) = sin x + sin y.

Differentiating, we get

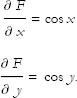
Take the point 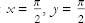. Since 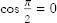, both derivatives are zero and the point is a stationary point.

Now, to find the type of stationary point, compute the second derivatives. The second derivatives are

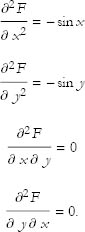
Since we see that both the determinant is positive,

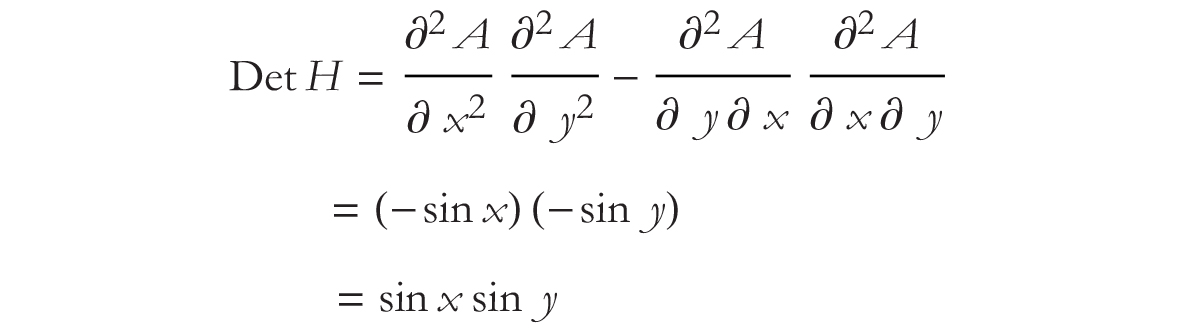
and the trace of the Hessian is negative.

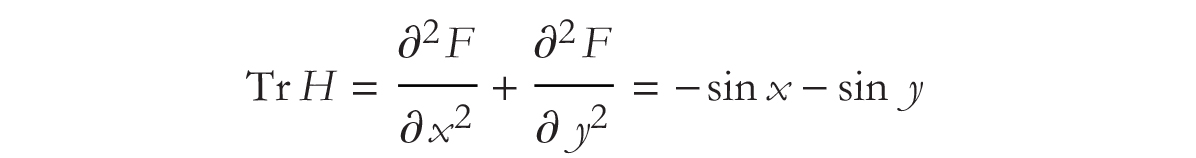
So the function at the point , is

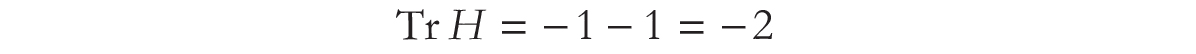
thus we have a positive determinant and a negative trace, the point is a maximum.

Exercise 2: Consider the points 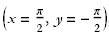, , 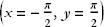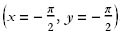. Are these points stationary points of the following functions? Is so, of what type?.