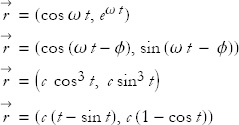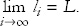
Lenny complained, “George, this jumpy stroboscopic stuff makes me nervous. Is time really so bumpy? I wish things would go a little more smoothly.”
George thought for a moment, wiping the blackboard. “Okay, Lenny, today let’s study systems that do change smoothly.”
In this book we will mostly be dealing with how various quantities change with time. Most of classical mechanics deals with things that change smoothly—continuously is the mathematical term—as time changes continuously. Dynamical laws that update a state will have to involve such continuous changes of time, unlike the stroboscopic changes of the first lecture. Thus we will be interested in functions of the independent variable t.
To cope, mathematically, with continuous changes, we use the mathematics of calculus. Calculus is about limits, so let’s get that idea in place. Suppose we have a sequence of numbers, l1, l2, l3, . . ., that get closer and closer to some value L. Here is an example: 0.9, 0.99, 0.999, 0.9999, . . . . The limit of this sequence is 1. None of the entries is equal to 1, but they get closer and closer to that value. To indicate this we write
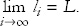
In words, L is the limit of li as i goes to infinity.
We can apply the same idea to functions. Suppose we have a function, f(t), and we want to describe how it varies as t gets closer and closer to some value, say a. If f(t) gets arbitrarily close to L as t tends to a, then we say that the limit of f(t) as t approaches a is the number L. Symbolically,
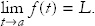
Let f(t) be a function of the variable t. As t varies, so will f(t). Differential calculus deals with the rate of change of such functions. The idea is to start with f(t) at some instant, and then to change the time by a little bit and see how much f(t) changes. The rate of change is defined as the ratio of the change in f to the change in t. We denote the change in a quantity with the uppercase greek letter delta, Δ. Let the change in t be called Δt. (This is not Δ × t, this is a change in t.) Over the interval Δt, f changes from f(t) to f(t + Δt). The change in f, denoted Δf, is then given by
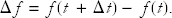
To define the rate of change precisely at time t, we must let Δt shrink to zero. Of course, when we do that Δf also shrinks to zero, but if we divide Δf by Δt, the ratio will tend to a limit. That limit is the derivative of f(t) with respect to t,
|
(1) |
A rigorous mathematician might frown on the idea that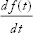 
is the ratio of two differentials, but you will rarely make a mistake this way.
Let’s calculate a few derivatives. Begin with functions defined by powers of t. In particular, let’s illustrate the method by calculating the derivative of f(t) = t2. We apply Eq. (1) and begin by defining f(t + Δt):
We can calculate (t + Δt)2 by direct multiplication or we can use the binomial theorem. Either way,
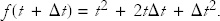
We now subtract f(t):
The next step is to divide by Δt:
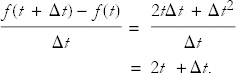
Now it’s easy to take the limit Δt → 0. The first term does not depend on Δt and survives, but the second term tends to zero and just disappears. This is something to keep in mind: Terms of higher order in Δt can be ignored when you calculate derivatives. Thus
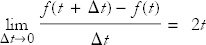
So the derivative of t2 is
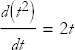
Next let us consider a general power, f(t) = tn. To caclulate its derivative, we have to calculate f(t + Δt) = (t + Δt)n. Here, high school algebra comes in handy: The result is given by the binomial theorem. Given two numbers, a and b, we would like to calculate (a + b)n. The binomial theorem gives
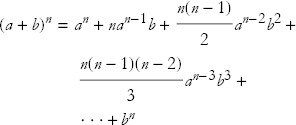
How long does the expression go on? If n is an integer, it eventually terminates after n+1 terms. But the binomial theorem is more general than that; in fact, n can be any real or complex number. If n is not an integer, however, the expression never terminates; it is an infinite series. Happily, for our purposes, only the first two terms are important.
To calculate (t + Δt)n, all we have to do is plug in a = t and b = Δt to get
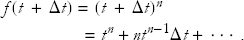
All the terms represented by the dots shrink to zero in the limit, so we ignore them.
Now subtract f(t) (or tn),
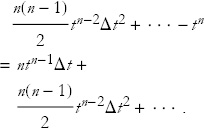
Now divide by Δt,
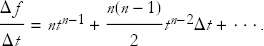
and let Δt → 0. The derivative is then
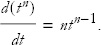
One important point is that this relation holds even if n is not an integer; n can be any real or complex number.
Here are some special cases of derivatives: If n = 0, then f(t) is just the number 1. The derivative is zero—this is the case for any function that doesn’t change. If n = 1, then f(t) = t and the derivative is 1—this is always true when you take the derivative of something with respect to itself. Here are some derivatives of powers
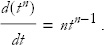
For future reference, here are some other derivatives:
|
(2) |
One comment about the third formula in Eq. (2), 
. The meaning of et is pretty clear if t is an integer. For example, e3 = e × e × e. Its meaning for non-integers is not obvious. Basically, et is defined by the property that its derivative is equal to itself. So the third formula is really a definition.
There are a few useful rules to remember about derivatives. You can prove them all if you want a challenging exercise. The first is the fact that the derivative of a constant is always 0. This makes sense; the derivative is the rate of change, and a constant never changes, so
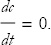
The derivative of a constant times a function is the constant times the derivative of the function:
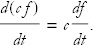
Suppose we have two functions, f(t) and g(t). Their sum is also a function and its derivative is given by
This is called the sum rule.
Their product of two functions is another function, and its derivative is
Not surprisingly, this is called the product rule.
Next, suppose that g(t) is a function of t, and f(g) is a function of g. That makes f an implicit function of t. If you want to know what f is for some t, you first compute g(t). Then, knowing g, you compute f(g). It’s easy to calculate the t-derivative of f:
This is called the chain rule. This would obviously be true if the derivatives were really ratios; in that case, the dg’s would cancel in the numerator and denominator. In fact, this is one of those cases where the naive answer is correct. The important thing to remember about using the chain rule is that you invent an intermediate function, g(t), to simplify f(t) making it f(g). For example, if
and we need to find 
, then the t3 inside the logarithm might be a problem. Therefore, we invent the intermediate function g = t3, so we have f(g) = ln g. We can then apply the chain rule.
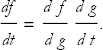
We can use our differentiation formulas to note that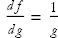 
and 
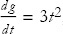, so
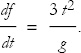
We can substitute g = t3, to get
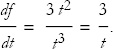
That is how to use the chain rule.
Using these rules, you can calculate a lot of derivatives. That’s basically all there is to differential calculus.
Exercise 2: The derivative of a derivative is called the second derivative and is written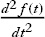 
. Take the second derivative of each of the functions listed above.
Exercise 3: Use the chain rule to find the derivatives of each of the following functions.
Exercise 4: Prove the sum rule (fairly easy), the product rule (easy if you know the trick), and the chain rule (fairly easy).
Exercise 5: Prove each of the formulas in Eq.s (2). Hint: Look up trigonometric identities and limit properties in a reference book.
The concept of a point particle is an idealization. No object is so small that it is a point—not even an electron. But in many situations we can ignore the extended structure of objects and treat them as points. For example, the planet Earth is obviously not a point, but in calculating its orbit around the Sun, we can ignore the size of Earth to a high degree of accuracy.
The position of a particle is specified by giving a value for each of the three spatial coordinates, and the motion of the particle is defined by its position at every time. Mathematically, we can specify a position by giving the three spatial coordinates as functions of t: x(t), y(t), z(t).
The position can also be thought of as a vector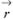 
(t) whose components are x, y, z at time t. The path of the particle—its trajectory—is specified by 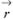(t). The job of classical mechanics is to figure out 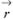(t) from some initial condition and some dynamical law.
Next to its position, the most important thing about a particle is its velocity. Velocity is also a vector. To define it we need some calculus. Here is how we do it:
Consider the displacement of the particle between time t and a little bit later at time t + Δt. During that time interval the particle moves from x(t), y(t), z(t) to x(t + Δt), y(t + Δt), z(t + Δt) or, in vector notation, from 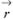(t) to 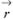(t + Δt). The displacement is defined as
or
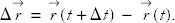
The displacement is the small distance that the particle moves in the small time Δt. To get the velocity, we divide the displacement by Δt and take the limit as Δt shrinks to zero. For example,
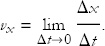
This—of course—is the definition of the derivative of x with respect to t.
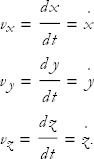
Placing a dot over a quantity is standard shorthand for taking the time derivative. This convention can be used to denote the time derivative of anything, not just the position of a particle. For example, if T stands for the temperature of a tub of hot water, then Ṫ will represent the rate of change of the temperature with time. It will be used over and over, so get familiar with it.
It gets tiresome to keep writing x, y, z, so we will often condense the notation. The three coordinates x, y, z are collectively denoted by xi and the velocity components by vi:
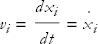
where i takes the values x, y, z, or, in vector notation
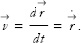
The velocity vector has a magnitude 
,
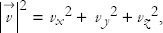
this represents how fast the particle is moving, without regard to the direction. The magnitude is called speed.
Acceleration is the quantity that tells you how the velocity is changing. If an object is moving with a constant velocity vector, it experiences no acceleration. A constant velocity vector implies not only a constant speed but also a constant direction. You feel acceleration only when your velocity vector changes, either in magnitude or direction. In fact, acceleration is the time derivative of velocity:
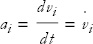
or, in vector notation
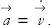
Because vi is the time derivative of xi and ai is the time derivative of vi, it follows that acceleration is the second time derivative of xi,
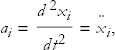
where the double-dot notation means the second time derivative.
Suppose a particle starts to move at time t = 0 according to the equations
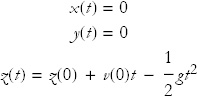
The particle evidently has no motion in the x and y directions but moves along the z axis. The constants z(0) and v(0) represent the initial values of the position and velocity along the z direction at t = 0. We also consider g to be a constant.
Let’s calculate the velocity by differentiating with respect to time.
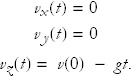
The x and y components of velocity are zero at all times. The z component of velocity starts out at t = 0 being equal to v(0). In other words, v(0) is the initial condition for velocity.
As time progresses, the −gt term becomes nonzero. Eventually, it will overtake the initial value of the velocity, and the particle will be found moving along in the negative z direction.
Now let’s calculate the acceleration by differentiating with respect to time again.
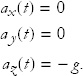
The acceleration along the z axis is constant and negative. If the z axis were to represent altitude, the particle would accelerate downward in just the way a falling object would.
Next let’s consider an oscillating particle that moves back and forth along the x axis. Because there is no motion in the other two directions, we will ignore them. A simple oscillatory motion uses trigonometric functions:
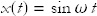
where the lowercase greek letter omega, ω, is a constant. The larger ω, the more rapid the oscillation. This kind of motion is called simple harmonic motion (see Figure 1).
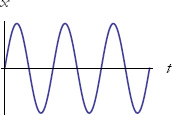
Figure 1: Simple harmonic motion.
Let’s compute the velocity and acceleration. To do so, we need to differentiate x(t) with respect to time. Here is the result of the first time derivative:
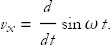
We have the sine of a product. We can relabel this product as b = ωt:
Using the chain rule,
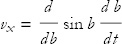
or
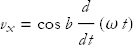
or
We get the acceleration by similar means:
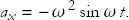
Notice some interesting things. Whenever the position x is at its maximum or minimum, the velocity is zero. The opposite is also true: When the position is at x = 0, then velocity is either a maximum or a minimum. We say that position and velocity are 90° out of phase. You can see this in Figure 2, representing x(t), and Figure 3, representing v(t).
Figure 2: Representing position.
Figure 3: Representing velocity.
The position and acceleration are also related, both being proportional to sin ω t. But notice the minus sign in the acceleration. That minus sign says that whenever x is positive (negative), the acceleration is negative (positive). In other words, wherever the particle is, it is being accelerated back toward the origin. In technical terms, the position and acceleration are 180° out of phase.
Exercise 6: How long does it take for the oscillating particle to go through one full cycle of motion?
Next, let’s consider a particle moving with uniform circular motion about the origin. This means that it is moving in a circle at a constant speed. For this purpose, we can ignore the z axis and think of the motion in the x, y plane. To describe it we must have two functions, x(t) and y(t). To be specific we will choose the particle to move in the counterclockwise direction. Let the radius of the orbit be R.
It is helpful to visualize the motion by projecting it onto the two axes. As the particle revolves around the origin, x oscillates between x = − R and x = R. The same is true of the y coordinate. But the two coordinates are 90° out of phase; when x is maximum y is zero, and vice versa.
The most general (counterclockwise) uniform circular motion about the origin has the mathematical form
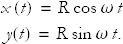
Here the parameter ω is called the angular frequency. It is defined as the number of radians that the angle advances in unit time. It also has to do with how long it takes to go one full revolution, the period of motion—the same as we found in Exercise 6:
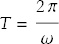
Now it is easy to calculate the components of velocity and acceleration by differentiation:
|
(3) |
This shows an interesting property of circular motion that Newton used in analyzing the motion of the moon: The acceleration of a circular orbit is parallel to the position vector, but it is oppositely directed. In other words, the acceleration vector points radially inward toward the origin.
Exercise 7: Show that the position and velocity vectors of the previous section are orthogonal.
Exercise 8: Calculate the velocity, speed, and acceleration for each of the following position vectors. If you have graphing software, plot each position vector, each velocity vector, and each acceleration vector.
