(1)
“Old timer, what are you looking for under the locomotive?”
Lenny loved the big steam locomotives, so now and then, on their days off, George took him down to the train yard. Today, they found a confused old man who looked as if he had lost something.
“Where’s the horse that pulls this thing?” the old timer asked George.
“We’ll, it don’t need no horse. Here, I’ll show you how it works. You see this place over here,” he said, pointing. “That’s the fire box where they burn the coal to get out the chemical energy. Then this, right next to it, is the boiler where the heat boils the water to make steam. The steam pressure does work against the piston in this here box. Then, the piston pushes against these rods, and they make the wheels turn.” The old timer grinned, shook George’s hand, and took his leave.
Lenny had been standing aside while George explained the locomotive. Now, with a look of sheer admiration, he came over to George and said, “George, I loved the way you explained things to that guy. And I understood all of it. The fire box, the boiler, the piston. Just one thing I didn’t get.”
“What’s that, Lenny?”
“Well, I was just wondering. Where’s the horse?”
One often learns that there are many forms of energy (kinetic, potential, heat, chemical, nuclear, . . . ) and that the sum total of all of them is conserved. But when reduced to the motion of particles, classical physics really has only two forms of energy: kinetic and potential. The best way to derive the conservation of energy is to jump right into the formal mathematical principles and then step back and see what we have.
The basic principle—call it the potential energy principle— asserts that all forces derive from a potential energy function denoted V({x}). Recall that {x} represents the entire set of 3N coordinates—the configuration space—of all particles in the system. To illustrate the principle, let’s begin with the simplest case of a single particle moving along the x axis under the influence of a force F(x). According to the potential energy principle, the force on the particle is related to the derivative of the potential energy, V(x):
|
(1) |
In the one-dimensional case, the potential energy principle is really just a definition of V(x). In fact, the potential energy can be reconstructed from the force by integrating Eq. (1):
|
(2) |
We can think of Eq. (1) in the following way: The force is always directed in a way that pushes the particle toward lower potential energy (note the minus sign). Moreover, the steeper V(x), the stronger the force. The slogan that captures the idea is Force pushes you down the hill.
Potential energy by itself is not conserved. As the particle moves, V(x) varies. What is conserved is the sum of potential energy and kinetic energy. Roughly speaking, as the particle rolls down the hill (in other words, as it moves toward lower potential energy), it picks up speed. As it rolls up the hill, it loses speed. Something is conserved.
Kinetic energy is defined in terms of the velocity v and mass m of the particle. It is denoted by T:
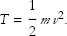
The total energy E of the particle is the sum of the kinetic and potential energies:
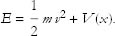
As the particle rolls along the x axis, the two types of energy individually vary, but always in such a way that the sum is conserved. Let’s prove it by showing that the time derivative of E is zero.
First let’s calculate the rate of change of the kinetic energy. The mass is assumed constant, but v2 can vary. The time derivative of v2 is
|
(3) |
Exercise 1: Prove Eq. (3). Hint: Use the product rule for differentiation.
It follows that the time derivative of the kinetic energy is
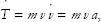
where the time derivative of the velocity has been replaced by the acceleration.
Next, let’s calculate the rate of change of potential energy. The key is to realize that V(x) changes with time because x changes. Here is the formula that expresses this:
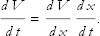
(It's okay to think of derivatives as ratios and to cancel the factors of d x in the numerator and denominator.) Another way to write this equation is to replace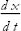 
with the velocity v:
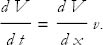
(Be careful to not confuse V and v.)
Now we can calculate the rate of change of the total energy:
Note that since both terms contain a factor of v, we can factor it out:
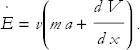
Now look at the expression in parentheses. Use the fact that the derivative of V is related to the force. Recalling the minus sign in Eq. (1), we see that the rate of change of E is given by
We now have what we need to prove energy conservation: Newton’s law, F = m a, is exactly the condition that the factor in parentheses vanishes, which in turn tells us that the total energy is constant.
One point before we go on to many-dimensional motion. We have shown that energy is conserved, but why is it that momentum is not conserved in this case? After all, in the previous chapter we showed that for an isolated system of particles, Newton’s third law implies that total momentum does not change. The answer is that we have left something out of the system—namely, the object that exerts the force on the one-dimensional particle. For example, if the problem has to do with a particle falling in a gravitational field, the gravitational force is exerted by the Earth. When the particle falls, its momentum changes, but that change is exactly compensated for by a tiny change in the motion of the Earth.
It is a fact that the components of force are derivatives of potential energy, but it is not a definition. This is so when there is more than one x to worry about—because space has more than one dimension, or because there is more than one particle, or both. It is quite possible to imagine force laws that do not come from differentiating a potential energy function, but nature does not make use of such nonconservative forces.
Let’s be a little more abstract than we have so far been. Call the coordinates of configuration space xi (remember, configuration space is the same as position space). For now, the subscript i will not refer to which particle we are talking about or which direction of space. It runs over all these possibilities. In other words, for a system of N particles there are 3N values of i. Let’s forget where they come from; we are simply considering a system of abstract coordinates labeled i.
Now let’s write the equations of motion:
|
(4) |
For each coordinate, there is a mass mi and a component of force Fi. Each component of force can depend on all positions {x}.
We have seen in the one-dimensional case that the force is minus the derivative of the potential energy, as in Eq. (1). This was a definition of V, not a special condition on the force. But when there is more than one dimension, things get more complicated. It is generally not true that if you have a set of functions Fi({x}), that they can all be derived by differentiating a single function V({x}). It would be a brand-new principle if we asserted that the components of force can be described as (partial) derivatives of a single potential energy function.
Indeed this principle is not hypothetical. It is a basic mathematical expression of one of the most important principles of physics:
For any system there exists a potential V({x}) such that
|
(5) |
What law of nature does Eq. (5) represent? You may have already guessed that it is the conservation of energy. We’ll see that shortly, but first let’s try to visualize what it means.
Picture a terrain with the function V({x}) representing the height or altitude at each point. First of all, the minus sign in Eq. (5) means that the force points in the downhill direction. It also says that the force is greater along directions where the slope is steeper. For example, on a contour map, there is no force pushing along the contour lines. The force vector points perpendicular to the contours.
Now let’s come back and derive energy conservation. To do that, we plug Eq. (5) into the equations of motion (4):
|
(6) |
The next step is to multiply each of the separate equations in Eq. (6) by the corresponding velocity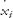 
and sum them all,
|
(7) |
Now we have to manipulate both sides of the equation in the same way that we did in the one-dimensional example. We define the kinetic energy to be the sum of all the kinetic energies for each coordinate:
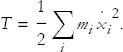
Here is what the two sides of Eq (7) give. First the left-hand side:
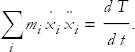
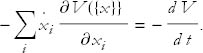
Thus we can rewrite Eq. (7) as
|
(8) |
Precisely as in the one-dimensional case, Eq. (8) says that the time derivative of the total energy is zero—energy is conserved.
To picture what is going on, imagine that the terrain has a ball rolling on it with no energy being lost to friction. Whenever the ball rolls toward a lower altitude it picks up speed, and whenever it rolls uphill it loses speed. The calculation tells us this happens in a special way that conserves the sum of the kinetic and potential energies.
You might wonder why the forces of nature are always gradients (derivatives) of a single function. In the next chapter we will reformulate classical mechanics using the principle of least action. In this formulation, it is “built in” from the very beginning that there is a potential energy function. But then why the principle of least action? Ultimately, the answer can be traced to the laws of quantum mechanics and to the origin of forces in field theory—subjects that, for the moment, are still out of range for us. So, why quantum field theory? At some point we have to give up and say that’s just the way it is. Or, not give up and push on.
Exercise 2: Consider a particle in two dimensions, x and y. The particle has mass m. The potential energy is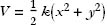 
. Work out the equations of motion. Show that there are circular orbits and that all orbits have the same period. Prove explicitly that the total energy is conserved.
Exercise 3: Rework Exercise 2 for the potential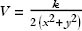 
. Are there circular orbits? If so, do they all have the same period? Is the total energy conserved?
Before moving on to the principle of least action, I want to list a few of the different kinds of energy that we talk about in physics, and review how they fit into the picture. Let’s consider
Some, but not all, of these distinctions are a bit old-fashioned. Mechanical energy usually refers to the kinetic and potential energy of large visible objects such as planets or weights being hoisted by a crane. It often refers to gravitational potential energy.
The heat contained in a gas or other collection of molecules is also kinetic and potential energy. The only difference is that it involves the large and chaotic motion of so many particles that we don’t even try to follow it in detail. Chemical energy is also a special case: The energy stored in chemical bonds is a combination of the potential energy and kinetic energy of the constituent particles that make up the molecules. It’s harder to understand because quantum mechanics has to replace classical mechanics, but nonetheless, the energy is the potential and kinetic energy of particles. The same goes for atomic and nuclear energy.
Electrostatic energy is just another word for the potential energy associated with the forces of attraction and repulsion between electrically charged particles. In fact, apart from gravitational energy, it is the primary form of potential energy in the ordinary, classical world. It is the potential energy between charged particles in atoms and molecules.
Magnetic energy is tricky, but the force between the poles of magnets is a form of potential energy. The tricky part comes when we think about the forces between magnets and charged particles. Magnetic forces on charged particles are a new kind of beast called velocity-dependent forces. We will come back to this later in the book.
Finally, there is the energy stored in electromagnetic radiation. It can take the form of heat from the sun, or the energy stored in radio waves, laser light, or other forms of radiation. In some very general sense, it is a combination of kinetic and potential energy, but it is not the energy of particles (not until we get to quantum field theory, anyway) but, of fields. So we will set electromagnetic energy aside until a later book.
