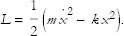
Doc was sitting at the bar drinking his usual—a beer milk shake—and reading the paper, when Lenny and George walked in. “What are you reading about, Doc?”
Doc looked up at Lenny over his glasses. “I see where this guy Einstein says, ‘Insanity is doing the same thing over and over and expecting different results.’ What do you think about that?”
Lenny thought for a minute. “You mean like every time I eat here I order chili, and then I get a stomachache?”
Doc chuckled, “Yeah, that’s the idea. I see you’re beginning to understand Einstein.”
You may wonder what happened to energy conservation and whether it fits the pattern relating symmetries to conservation laws. Yes, it does, but in a slightly different way than the examples in Lecture 7. In all of those examples the symmetry involved shifting the coordinates qi. For instance, a translation is a symmetry that simultaneously shifts the Cartesian coordinates of all the particles in a system by the same amount. The symmetry connected with energy conservation involves a shift of time.
Imagine an experiment involving a closed system far from any perturbing influences. The experiment begins at time t0 with a certain initial condition, proceeds for a definite period, and results in some outcome. Next, the experiment is repeated in exactly the same way but at a later time. The initial conditions are the same as before, and so is the duration of the experiment; the only difference is the starting time, which is pushed forward to t0 + Δt. You might expect that the outcome will be exactly the same, and that the shift Δt would make no difference. Whenever this is true, the system is said to be invariant under time translation.
Time-translation invariance does not always apply. For example, we live in an expanding universe. The effect of the expansion on ordinary laboratory experiments is usually negligible, but it’s the principle that counts. At some level of accuracy, an experiment that begins later will have a slightly different outcome than one which begins earlier.
Here is a more down-to-earth example. Suppose the system of interest is a charged particle moving in a magnetic field. If the magnetic field is constant then the motion of the particle will be time-translation invariant. But if the current that generates the field is being slowly increased, then the same initial condition for the particle—but starting at different times—will result in a different outcome. The description of the particle will not be time-translation invariant.
How is time-translation symmetry, or the lack of it, reflected in the Lagrangian formulation of mechanics? The answer is simple. In those cases where there is such symmetry, the Lagrangian has no explicit dependence on time. This is a subtle point: The value of the Lagrangian may vary with time, but only because the coordinates and velocities vary. Explicit time dependence means that the form of the Lagrangian depends on time. For example, take the harmonic oscillator with Lagrangian
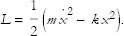
If m and k are time-independent then this Lagrangian is time-translation invariant.
But one can easily imagine that the spring constant k might, for some reason, change with time. For example, if the experiment took place in a changing magnetic field, this could have a subtle effect on the atoms of the spring, which in turn could cause k to vary. In that case, we would have to write
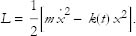
This is what we mean by an explicit time dependence. More generally, we can write
|
(1) |
where the t dependence is due to the time variation of all the parameters controlling the behavior of the system.
With this idea in hand, we can now give a very succinct mathematical criterion for time-translation symmetry: A system is time-translation invariant if there is no explicit time dependence in its Lagrangian.
Let’s consider how the actual value of the Lagrangian, Eq. (1), changes as a system evolves. There are three sources of time dependence of L. The first and second are due to the time dependence of the coordinates q and the velocities 
. If that were all, we would write
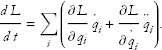
But if the Lagrangian has explicit time dependence, then there is another term:
|
(2) |
Let’s examine the various terms in Eq. (2) using the Euler-Lagrange equations of motion. The first type of term, 
, can be written
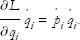
The second type of term,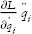 
, takes the form
If we combine everything, we get
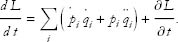
The first two terms can be simplified. We use the identity
|
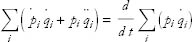
(3) |
Notice that even if there is no explicit time dependence in L, the Lagrangian will nevertheless depend on time through the first term 
. The upshot is that there is no such thing as conservation of the Lagrangian.
Inspection of Eq. (3) reveals something interesting. If we define a new quantity H by
|
(4) |
then Eq. (3) has a very simple form:
|
(5) |
The steps leading to Eq. (5) may seem a bit complicated, but the result is very simple. The new quantity H varies with time only if the Lagrangian has an explicit time dependence. An even more interesting way to say it is if a system is time-translation invariant, then the quantity H is conserved.
The quantity H is called the Hamiltonian, and, as you might expect, it is important because (among other reasons) it is the energy of a system. But it is more than important; it is the central element in an entirely new formulation of mechanics called the Hamiltonian formulation. But for now, let’s consider its meaning by returning to a simple example, the motion of a particle in a potential. The Lagrangian is
|
(6) |
and the canonical momentum is just the usual momentum
|
(7) |
Let’s plug Eq. (6) and Eq. (7) into Eq. (4), the definition of H:
Notice what happens: Two terms proportional to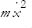 
combine to give the usual kinetic energy, and the potential term becomes + V(x). In other words, H just becomes the usual total energy, kinetic plus potential.
This is the general pattern that you can check for any number of particles. If the Lagrangian is kinetic energy minus potential energy, then
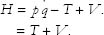
There are systems for which the Lagrangian has a more intricate form than just T − V. For some of those cases, it is not possible to identify a clear separation into kinetic and potential energy. Nonetheless, the rule for constructing the Hamiltonian is the same. The general definition of energy for these systems is Energy equals Hamiltonian.
Moreover, if there is no explicit time dependence in the Lagrangian, then the energy H is conserved.
If, however, the Lagrangian is explicitly time-dependent, then Eq. (5) implies that the Hamiltonian is not conserved. What happened to the energy in that case? To understand what is going on, let’s consider an example. Suppose that a charged particle, with unit electric charge, is moving between the plates of a capacitor. The capacitor has a uniform electric field ∊ due to the charges on the plates. (The reason we are using ∊ for electric field, instead of the more conventional E, is to avoid confusing it with energy.) You don’t have to know anything about electricity. All you need to know is that the capacitor creates a potential energy equal to ∊ x. The Lagrangian is
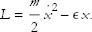
As long as the field is constant, the energy is conserved. But suppose the capacitor is being charged up so that ∊ is also ramping up. Then the Lagrangian has an explicit time dependence:
Now the energy of the particle is not conserved. Depending on the momentary location x of the particle, the energy varies according to
Where did that energy come from? The answer is that it came from the battery that was charging the capacitor. I won’t go into details, but the point is that when we defined the system to consist of just the particle, we narrowed our focus to just a part of a bigger system that includes the capacitor and the battery. These additional items are also made of particles and therefore have energy.
Consider the entire experiment, including the battery, capacitor, and particle. The experiment begins with an uncharged capacitor and a particle at rest, somewhere between the plates. At some moment we close a circuit, and current flows into the capacitor. The particle experiences a time-dependent field, and, at the end of the experiment, the capacitor is charged and the particle is moving.
What if we did the entire experiment an hour later? The outcome, of course, would be the same. In other words, the entire closed system is time-translation invariant, so the entire energy of all items is conserved. If we treated the entire collection as a single system, it would be time-translation invariant, and the total energy would be conserved.
Nevertheless, it is often useful to divide a system into parts and to focus on one part. In that case, the energy of part of the system will not be conserved if the other parts are varying with time.
The Hamiltonian is important because (among other reasons) it is the energy. But its significance is far deeper: It is the basis for a complete revamping of classical mechanics, and it is even more important in quantum mechanics.
In the Lagrangian—or action—formulation of mechanics, the focus is on the trajectory of a system through the configuration space. The trajectory is described in terms of the coordinates q(t). The equations are second-order differential equations, so it is not enough to know the initial coordinates; we also have to know the initial velocities.
In the Hamiltonian formulation, the focus is on phase space. Phase space is the space of both the coordinates qi and the conjugate momenta pi. In fact, the q’s and p’s are treated on the same footing, the motion of a system being described by a trajectory through the phase space. Mathematically, the description is through a set of functions qi(t), pi(t). Notice that the number of dimensions of phase space is twice that of configuration space.
What do we gain by doubling the number of dimensions? The answer is that the equations of motion become first-order differential equations. In less technical terms, this means that the future is laid out if we know only the initial point in phase space.
The first step in constructing the Hamiltonian formulation is to get rid of the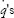 
and replace them with the p's. The goal is to express the Hamiltonian as a function of q's and p’s. For particles in ordinary Cartesian coordinates, the momenta and velocities are almost the same thing, differing only by a factor of the mass. As usual, the particle on a line is a good illustration.
We start with the two equations
When we replace the velocity with p / m the Hamiltonian becomes a function of p and x:
|
(8) |
One last point before we write the equations of motion in Hamiltonian form: The partial derivative of H with respect to x is just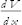 
, or minus the force. Thus the equation of motion (F = m a) takes the form
|
(9) |
We noted earlier that in the Hamiltonian formulation, the coordinates and momenta are on the same footing. From that you might guess that there is another equation similar to Eq. (9), with p and x interchanged. That is almost true, but not quite. The correct equation is
|
(10) |
with a plus sign instead of a minus sign.
To see why Eq. (10) is true, just differentiate the expression for H with respect to p. From Eq. (8) we get
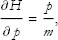
which from the first equation is just 
.
So now we see a very simple symmetric packaging of the equations. We have two equations of motion instead of one, but each is of first-order:
|
(11) |
These are Hamilton’s equations for a particle on a line. Soon we will derive the general form for any system, but for now I will tell you what it is. We start with a Hamiltonian that is a function of all the q’s and p’s:
H = H(qi, pi).
We can use this to generalize Equations (11),
|
(12) |
So we see that for each direction in phase space, there is a single first-order equation.
Let’s stop to consider how these equations are related to the very first chapter of this book, in which we described how deterministic laws of physics predict the future. What Equations (12) say is this:
If at any time you know the exact values of all the coordinates and momenta, and you know the form of the Hamiltonian, Hamilton’s equations will tell you the corresponding quantities an infinitesimal time later. By a process of successive updating, you can determine a trajectory through phase space.
The harmonic oscillator is by far the most important simple system in physics. It describes all sorts of oscillations in which some degree of freedom is displaced and then oscillates about an equilibrium position. To see why it is so important, let’s suppose a degree of freedom q has a potential energy V(q) that has a minimum. The minimum describes a stable equilibrium, and when the degree of freedom is displaced, it will tend to return to the equilibrium position. Without any real loss of generality, we can locate the minimum at q = 0. The generic function that has a minimum at this point can be approximated by the quadratic function
V(q) = V(0) + c q2. |
(13) |
where V(0) and c are constants. The reason why there is no linear term proportional to q is that the derivative 
must be zero at the minimum. We can also drop the term V(0) since adding a constant to the potential energy has no effect.
The form of Eq. (13) is not very general; V could contain terms of all orders—for example, q3 or q4. But as long as the system deviates from q = 0 by only a small amount, these higher-order terms will be negligible compared to the quadratic term. This reasoning applies to all sorts of systems: springs, pendulums, oscillating sound waves, electromagnetic waves, and on and on.
I will write the Lagrangian in what may seem like a special form involving a single constant called ω:
|
(14) |
Exercise 1: Start with the Lagrangian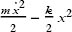 
and show that if you make the change in variables 
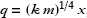, the Lagrangian has the form of Eq. (14). What is the connection among k, m, and ω?
Exercise 2: Starting with Eq. (14), calculate the Hamiltonian in terms of p and q.
The Hamiltonian corresponding to Eq. (14) is very simple:
|
(15) |
It was in order to get H into such a simple form that we changed variables from x to q in Exercise 1.
One of the hallmarks of the Hamiltonian formulation is how symmetric it is between the q’s and p’s. In the case of the harmonic oscillator, it is almost completely symmetric. The only asymmetry is a minus sign in the first of Equations (12). For a single degree of freedom, Hamilton’s equations are Equations (11). If we plug our Hamiltonian, Eq. (15), into Equations (12), we get,
|
(16) |
How do these two equations compare with Lagrange’s equations that we would derive from Eq. (14)? First of all, there is only one Lagrangian equation:
|
(17) |
Second, this equation is second-order, meaning that it involves second time derivatives. By contrast, the Hamiltonian equations are each first-order. This somehow means that two first-order equations are equivalent to one second-order equation. We can see this by differentiating the second equation in Equations (16) with respect to time,
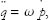
and then using the first equation in Equations (16). This enables us to replace ṗ with −ω q, which gives us Eq. (17): The Euler-Lagrange equation of motion.
Is one formulation better than the other? Did Lagrange have the final word or did Hamilton? You can decide for yourself, but wait a while before you do. We still have a couple of courses on relativity and quantum mechanics before the real meanings of the Lagrangian and Hamiltonian become completely clear.
Let’s return to Equations (16). We usually “think” in configuration space. The harmonic oscillator is a system that moves back and forth along a single axis. But it is also an excellent starting point for getting used to “thinking” in phase space. Phase space (for the oscillator ) is two-dimensional. It is easy to see that the trajectories of the oscillator in phase space are concentric circles about the origin. The argument is very simple. Go back to the expression for the Hamiltonian, Eq. (15). The Hamiltonian, being the energy, is conserved. It follows that q2 + p2 is constant with time. In other words, the distance from the origin of phase space is constant, and the phase point moves on a circle of fixed radius. In fact Eq.s (16) is the equation for a point moving with constant angular velocity ω about the origin. Especially interesting is the fact that the angular velocity in phase space is the same for all orbits, independent of the energy of the oscillator. As the phase point circles the origin, you can project the motion onto the horizontal q axis, as shown in Figure 1. It moves back and forth in an oscillatory motion, exactly as expected. However, the two-dimensional circular motion through phase space is a more comprehensive description of the motion. By projecting onto the vertical p axis, we see that the momentum also oscillates.
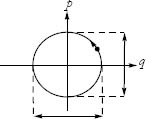
Figure 1: The harmonic oscillator in phase space.
The harmonic oscillator is especially simple. In general, the motion of a system through phase space is more complicated and less symmetric. But the fact that the phase point stays on a contour of constant energy is universal. Later we will discover more general properties of motion in phase space.
Let’s complete a piece of business that we left unfinished: the general derivation of Hamilton’s equations. The Lagrangian is some general function of the coordinates and velocities,
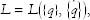
and the Hamiltonian is
The change in the Hamiltonian is
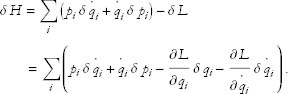
Now if we use the definition of pi, namely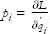 
, we see that the first and last terms exactly cancel, leaving
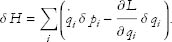
Let’s compare this with the general rule for a small change in a function of several variables:
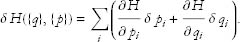
By matching the terms proportional to δ qi and δ pi, we arrive at
|
(18) |
There is only one last step, and that is to write Lagrange’s equations in the form
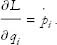
Inserting this in the second of Equations (18) we get Hamilton’s equations,
|
(19) |
