30

Gaussian Elimination is Not Optimal (1969)

Volker Strassen

Matrix multiplication is such a simple operation that it is hard to imagine there is anything left to learn about it. To multiply two n × n matrices A and B and get an n×n product matrix C, compute the n² dot products of rows of A with columns of B. Each of those dot products involves n multiplications of numbers and n − 1 additions, for a total of n³ number multiplications and n²(n − 1) additions. What else could there be to say?

A great deal, it turns out. The German mathematician Volker Strassen (b. 1936) may have been trying to prove a lower bound, that n³ multiplications are necessary as well as sufficient, when he discovered this algorithm. The paper entails two remarkable ideas. The first is that a divide-and-conquer, recursive algorithm might beat the conventional algorithm, if there is a way to compute the product of 2 × 2 matrices with fewer than 8 multiplications. Even after seeing this proved, it still seems surprising that the overhead of implementing the recursion is asymptotically repaid. The other amazing discovery is that two 2 × 2 matrices can be multiplied with only 7 multiplications. Any high school student might have figured that out scribbling on a pad of paper between classes; in the centuries that people have been multiplying matrices, nobody noticed because nobody had a reason to try. (An analogous algorithm for integer multiplication, due to Karatsuba and Ofman (1962), was already known. It recursively computes the product of two 2n-bit numbers by three multiplications of n-bit numbers, thus yielding a O(n^{log₂ 3}) ≈ n^1.58 time algorithm for n-bit multiplications, better than the conventional Θ(n²) algorithm.)

Strassen’s algorithm is tricky to implement both correctly and efficiently, but its utility under a good implementation is not merely theoretical. The discovery that n × n matrices can be multiplied using n^{log₂ 7} ≈ n^2.8 multiplications led to the still unsolved problem of how much smaller the exponent can be. As of this writing, the answer is no more than 2.373, but no lower bound greater than 2 is known; these more exotic algorithms are not practically useful, however.

This paper, alongside Karatsuba and Ofman (1962), established the divide-and-conquer technique as a tool for a variety of algorithmic problems. The implications for efficiently solving systems of linear equations—which give the paper its title—are remarkable in their own right.

---

30.1

BELOW we will give an algorithm which computes the coefficients of the product of two square matrices A and B of order n from the coefficients of A and B with less than 4.7 · n^{log 7} arithmetical operations (all logarithms in this paper are for base 2, thus log 7 ≈ 2.8; the usual method requires approximately 2n³ arithmetical operations). The algorithm induces algorithms for inverting a matrix of order n, solving a system of n linear equations in n unknowns, computing a determinant of order n etc. all requiring less than const n^{log 7} arithmetical operations.

This fact should be compared with the result of Klyuev and Kokovkin-Shcherbak (1965) that Gaussian elimination for solving a system of linear equations is optimal if one restricts oneself to operations upon rows and columns as a whole. We also note that Winograd (1968) modifies the usual algorithms for matrix multiplication and inversion and for solving systems of linear equations, trading roughly half of the multiplications for additions and subtractions. It is a pleasure to thank D. Brillinger for inspiring discussions about the present subject and S. Cook and B. Parlett for encouraging me to write this paper.

30.2

We define algorithms α_{m, k} which multiply matrices of order m2^k, by induction on k: α_{m, 0} is the usual algorithm for matrix multiplication (requiring m³ multiplications and m²(m − 1) additions). α_{m, k} already being known, define α_{m, k+1} as follows:

If A, B are matrices of order m2^k+1 to be multiplied, write

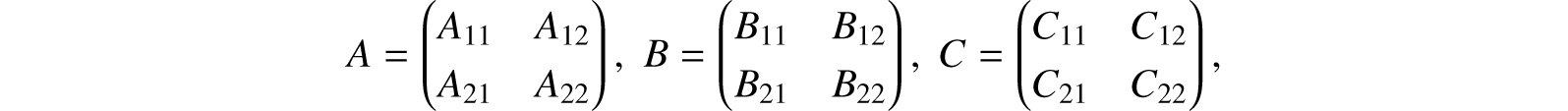
where the A_ik, B_ik, C_ik are matrices of order m2^k. Then compute

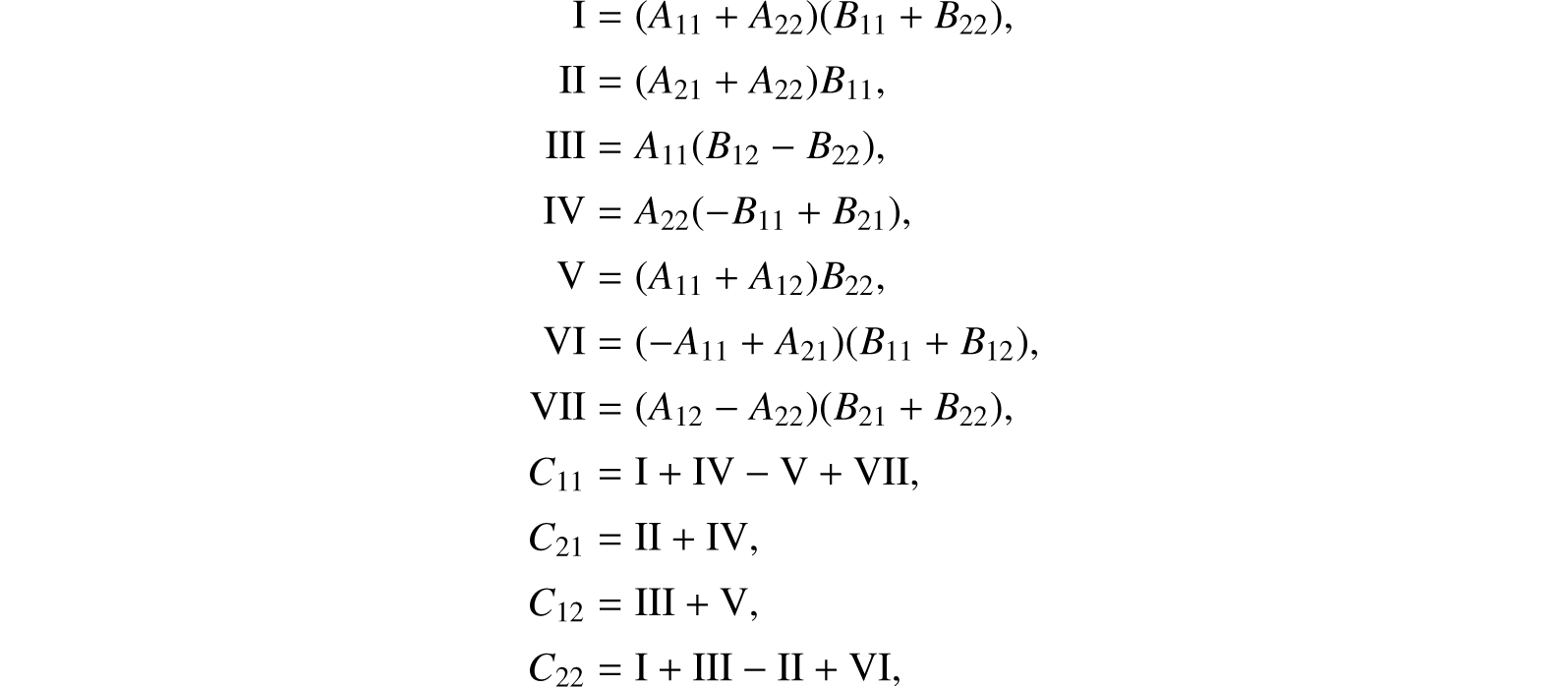
using α_mk for multiplication and the usual algorithm for addition and subtraction of matrices of order m2^k.

By induction on k one easily sees

Fact 1. α_{m, k} computes the product of two matrices of order m2^k with m³7^k multiplications and (5 + m)m²7^k − 6(m2^k)² additions and subtractions of numbers.

Thus one may multiply two matrices of order 2^k with 7^k number multiplications and less than 6 · 7^k additions and subtractions.

Fact 2. The product of two matrices of order n may be computed with < 4.7n^{log 7} arithmetical operations.

Proof. Put k = ⌊log n − 4⌋, m = ⌊n2^−k⌋ + 1; then n ≤ m2^k. Imbedding matrices of order n into matrices of order m2^k reduces our task to that of estimating the number of operations of α_m,k. By Fact 1 this number is

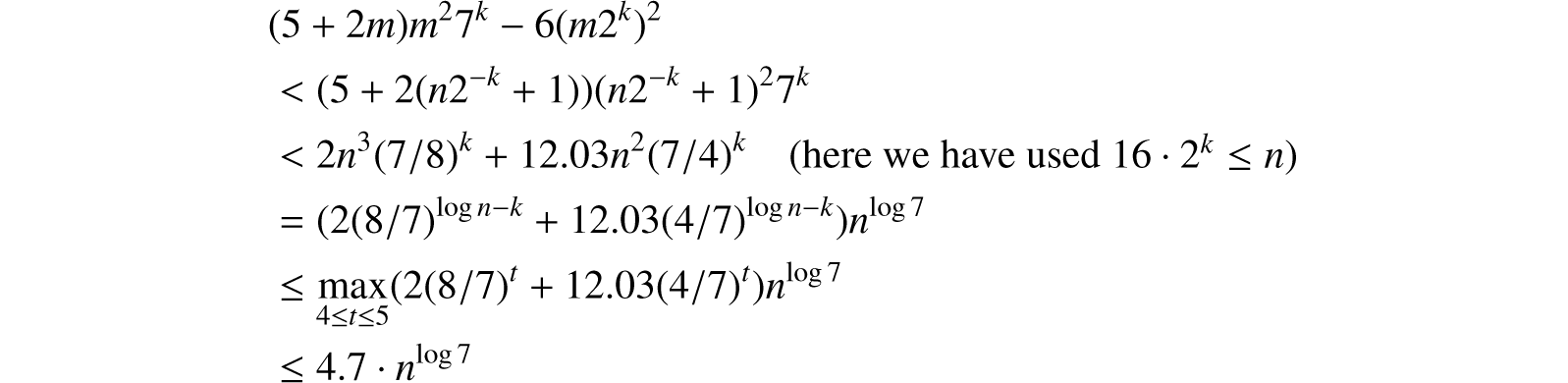
by a convexity argument.

We now turn to matrix inversion. To apply the algorithms below it is necessary to assume not only that the matrix is invertible but that all occurring divisions make sense (a similar assumption is of course necessary for Gaussian elimination).

We define algorithms β_{m, k} which invert matrices of order m2^k, by induction on k: β_m,0 is the usual Gaussian elimination algorithm. β_{m, k} already being known, define β_{m, k+1} as follows:

If A is a matrix of order m2^k+1 to be inverted, write

where the A_ik, C_ik are matrices of order m2^k. Then compute

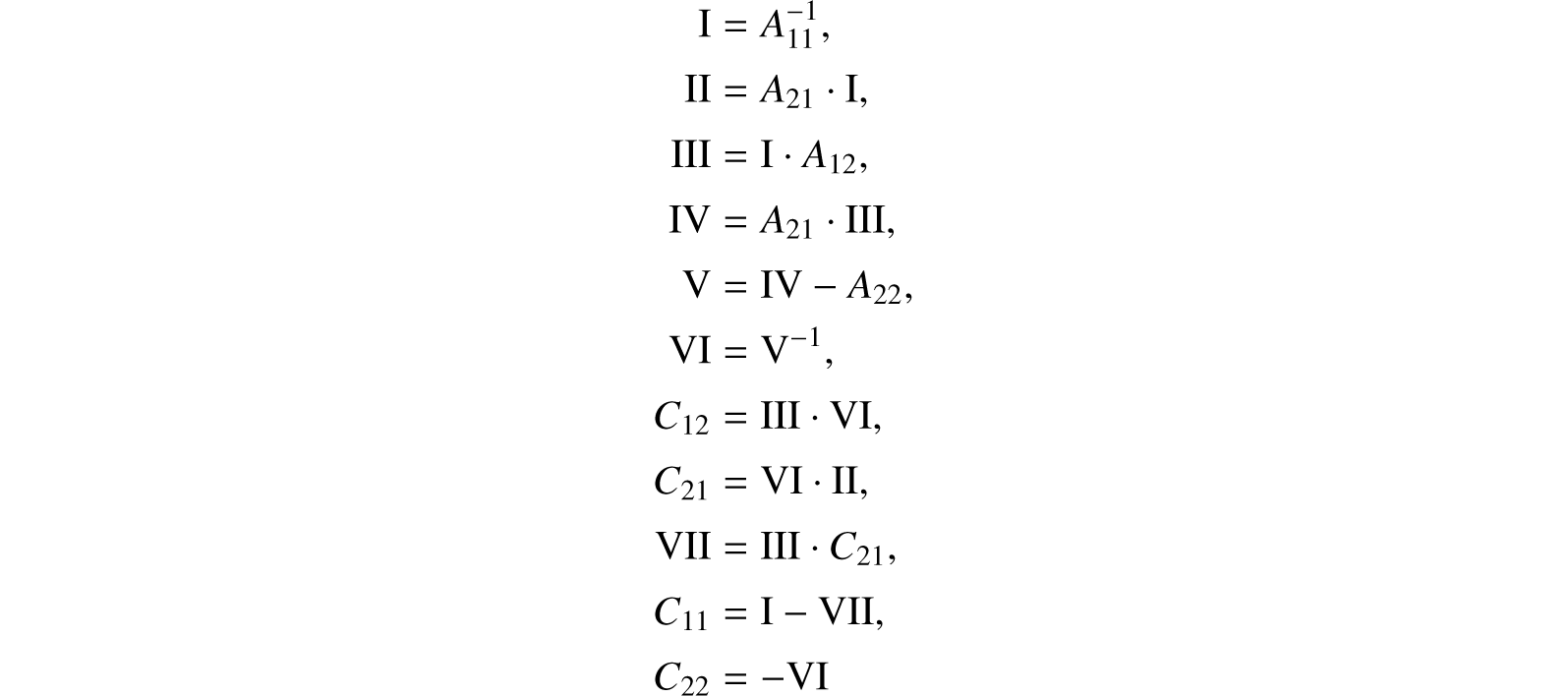
using α_{m, k} for multiplication, β_{m, k} for inversion and the usual algorithm for addition or subtraction of two matrices of order m2^k.

By induction on k one easily sees

Fact 3. β_{m, k} computes the inverse of a matrix of order m2^k with m2^k divisions, multiplications and additions and subtractions of numbers. The next Fact follows in the same way as Fact 2.

Fact 4. The inverse of a matrix of order n may be computed with < 5.64 · n^{log 7} arithmetical operations.

Similar results hold for solving a system of linear equations or computing a determinant (use ).

1. Reprinted from Strassen (1969), with permission from Springer.