5
Mathematical Problems (1900)
David Hilbert
Nothing is more important to the progress of science than knowing what question to ask. The great German mathematician David Hilbert (1862–1943) of the University of Göttingen used the occasion of the International Congress of Mathematicians at the turn of the twentieth century to characterize mathematical problems and their solutions generally, and to challenge his colleagues with a list of 23 unsolved problems. Several problems were solved quickly, but the tenth problem took seventy years to resolve, and the resolution came in a form—a demonstration of recursive unsolvability—that Hilbert could not have articulated in 1900. The eighth problem, the Riemann hypothesis, is still unresolved; the status of other more ambiguously worded problems is arguable.
In the year 2000, the Clay Mathematics Institute updated Hilbert’s list with a list of seven Millennium Prize problems, offering a $1 million dollar reward for the solution of each (Clay Mathematics Institute, 2000). To date, only one—the Poincaré conjecture—has been solved. The Riemann hypothesis is on the Millennium list; so is the 𝒫 = 𝒩𝒫 problem (chapter 34).
No precise notion of an algorithm was known in 1900, much less of recursive unsolvability. And yet Hilbert’s address is full of hints of things to come: his references to processes with a “finite number of steps,” and to “the impossibility of the solution under the given hypotheses, or in the sense contemplated”—for which he gives as an example the ancient proof of the irrationality of 
. In the late nineteenth century, the logical revolution foreshadowed by Boole developed into the field of metamathematics, the program to construct solid mathematical foundations for the conduct of mathematics itself. Gottlob Frege (1879) provided the first rigorous axiomatization of modern logic with the publication of Begriffsschrift, and Whitehead and Russell (1910) published the first part of their massive Principia Mathematica, an attempt to completely formalize all of mathematics. Leibniz’s dream seemed within reach.
Yet as the attempts to formalize mathematics became more robust, several inconsistencies and paradoxes emerged. Hilbert, troubled by the shaky ground on which his optimism was founded, challenged the mathematical community to “dispose of the foundational questions in mathematics as such once and for all” (Hilbert, 1928; Van Heijenoort, 1967). This challenge became known as Hilbert’s program, and only once the challenge was posed was it possible to imagine that it might not be achievable.
In Hilbert’s 1900 address, there is not much thinking about such an impossibility. The tone is uplifting and encouraging. Every problem can be solved, one way or another. There is no ignorabimus (literally, no “we shall not know”—that is, no giving up on finding the answer).
In fact this spirit informed much of human culture at the time. The turn of the twentieth century was a moment of general positivity in the world. Wars were limited and of manageable scale. The Industrial Revolution had brought prosperity and progress, at least to the Western world. Fifty million people visited the Exposition Universelle (World Fair) in Paris to see first-hand the wonders of the modern world. Romantic, swirly artworks in the art nouveau (“new art”) style spoke to the general feelings that life was gentle, beautiful, flourishing organically, and could only get better.
We excerpt the prefatory remarks of Hilbert’s address. Of the 23 problems, we include only the second and the tenth. The tenth is the problem of determining whether a diophantine equation is solvable over the integers. These are equations of the form p(x1, …, xk) = 0, where p is a polynomial in which the terms are integer constants multiplied by products of the variables raised to integer powers—for example, 
. The requirement that the values of x1, …, xk be integers turns what looks like an algebraic problem into a combinatorial problem. The decades-long efforts of Martin Davis, Hilary Putnam, Julia Robinson, and Yuri Matiyasevich eventually demonstrated the unsolvability of the general problem of determining whether such an equation has a solution, with Matiyasevich contributing the number-theoretic coup de grâce in 1970 (Matiyasevich, 1993).
Fifteen years after Hilbert’s address, Europe was in the depths of a bloody, seemingly senseless and endless war. Literature turned ironic and cynical; dark and violent themes emerged in the visual arts. As though reflecting the pessimistic shift, between the two World Wars Gödel and Turing demonstrated the unexpected consequences of formalizing symbolically the idea of a finite process of discrete steps. Formal systems themselves have their limits, it seemed.
Hilbert’s health declined during the 1920s, and the great school of mathematicians that had grown around him at Göttingen was all but dissolved when the Nazis purged it of Jewish professors. Hilbert’s gravestone bears (in German) his brave words, “We must know. We shall know.” He had said this in 1930, on the day before Kurt Gödel announced a result in a line of inquiry stimulated by Hilbert’s second problem, about the independence and consistency of axioms. Gödel proved that in any recursively axiomatizable consistent logical system strong enough to axiomatize basic arithmetic, some true propositions could not be proved—thus confounding any attempt at a simple answer to the question of what can be known.
And yet, in closing one door, Gödel and Turing opened countless others. Gödel’s proof that mathematics can never be a single closed system also meant that its possibilities are limitless. Turing, in defining what an algorithm is in order to prove what algorithms cannot do, opened the study of algorithms to scientific analysis, both theoretical and practical, and ushered in the computational world of today.
WHO of us would not be glad to lift the veil behind which the future lies hidden; to cast a glance at the next advances of our science and at the secrets of its development during future centuries? What particular goals will there be toward which the leading mathematical spirits of coming generations will strive? What new methods and new facts in the wide and rich field of mathematical thought will the new centuries disclose?
History teaches the continuity of the development of science. We know that every age has its own problems, which the following age either solves or casts aside as profitless and replaces by new ones. If we would obtain an idea of the probable development of mathematical knowledge in the immediate future, we must let the unsettled questions pass before our minds and look over the problems which the science of today sets and whose solution we expect from the future. To such a review of problems the present day, lying at the meeting of the centuries, seems to me well adapted. For the close of a great epoch not only invites us to look back into the past but also directs our thoughts to the unknown future.
The deep significance of certain problems for the advance of mathematical science in general and the important role which they play in the work of the individual investigator are not to be denied. As long as a branch of science offers an abundance of problems, so long is it alive; a lack of problems foreshadows extinction or the cessation of independent development. Just as every human undertaking pursues certain objects, so also mathematical research requires its problems. It is by the solution of problems that the investigator tests the temper of his steel; he finds new methods and new outlooks, and gains a wider and freer horizon.
It is difficult and often impossible to judge the value of a problem correctly in advance; for the final award depends upon the gain which science obtains from the problem. Nevertheless we can ask whether there are general criteria which mark a good mathematical problem. An old French mathematician said: “A mathematical theory is not to be considered complete until you have made it so clear that you can explain it to the first man whom you meet on the street.” This clearness and ease of comprehension, here insisted on for a mathematical theory, I should still more demand for a mathematical problem if it is to be perfect; for what is clear and easily comprehended attracts, the complicated repels us.
Moreover a mathematical problem should be difficult in order to entice us, yet not completely inaccessible, lest it mock at our efforts. It should be to us a guide post on the mazy paths to hidden truths, and ultimately a reminder of our pleasure in the successful solution. The mathematicians of past centuries were accustomed to devote themselves to the solution of difficult particular problems with passionate zeal. They knew the value of difficult problems. I remind you only of the “problem of the line of quickest descent,” proposed by John Bernoulli. Experience teaches, explains Bernoulli in the public announcement of this problem, that lofty minds are led to strive for the advance of science by nothing more than by laying before them difficult and at the same time useful problems, and he therefore hopes to earn the thanks of the mathematical world by following the example of men like Mersenne, Pascal, Fermat, Viviani and others and laying before the distinguished analysts of his time a problem by which, as a touchstone, they may test the value of their methods and measure their strength. The calculus of variations owes its origin to this problem of Bernoulli and to similar problems.
Fermat had asserted, as is well known, that the diophantine equation
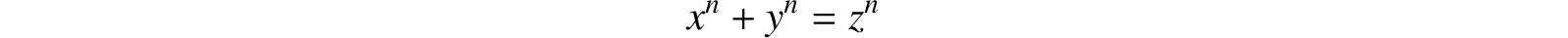
(x, y and z integers) is unsolvable—except in certain self-evident cases. The attempt to prove this impossibility offers a striking example of the inspiring effect which such a very special and apparently unimportant problem may have upon science. For Kummer, incited by Fermat’s problem, was led to the introduction of ideal numbers and to the discovery of the law of the unique decomposition of the numbers of a circular field into ideal prime factors—a law which today, in its generalization to any algebraic field by Dedekind and Kronecker, stands at the center of the modern theory of numbers and whose significance extends far beyond the boundaries of number theory into the realm of algebra and the theory of functions.
To speak of a very different region of research, I remind you of the problem of three bodies. The fruitful methods and the far-reaching principles which Poincaré has brought into celestial mechanics and which are today recognized and applied in practical astronomy are due to the circumstance that he undertook to treat anew that difficult problem and to approach nearer a solution.
The two last mentioned problems—that of Fermat and the problem of the three bodies—seem to us almost like opposite poles—the former a free invention of pure reason, belonging to the region of abstract number theory, the latter forced upon us by astronomy and necessary to an understanding of the simplest fundamental phenomena of nature.
But it often happens also that the same special problem finds application in the most unlike branches of mathematical knowledge. So, for example, the problem of the shortest line plays a chief and historically important part in the foundations of geometry, in the theory of curved lines and surfaces, in mechanics and in the calculus of variations. And how convincingly has F. Klein, in his work on the icosahedron, pictured the significance which attaches to the problem of the regular polyhedra in elementary geometry, in group theory, in the theory of equations and in that of linear differential equations. …
It remains to discuss briefly what general requirements may be justly laid down for the solution of a mathematical problem. I should say first of all, this: that it shall be possible to establish the correctness of the solution by means of a finite number of steps based upon a finite number of hypotheses which are implied in the statement of the problem and which must always be exactly formulated. This requirement of logical deduction by means of a finite number of processes is simply the requirement of rigor in reasoning. Indeed the requirement of rigor, which has become proverbial in mathematics, corresponds to a universal philosophical necessity of our understanding; and, on the other hand, only by satisfying this requirement do the thought content and the suggestiveness of the problem attain their full effect. A new problem, especially when it comes from the world of outer experience, is like a young twig, which thrives and bears fruit only when it is grafted carefully and in accordance with strict horticultural rules upon the old stem, the established achievements of our mathematical science. …
Some remarks upon the difficulties which mathematical problems may offer, and the means of surmounting them, may be in place here.
If we do not succeed in solving a mathematical problem, the reason frequently consists in our failure to recognize the more general standpoint from which the problem before us appears only as a single link in a chain of related problems. After finding this standpoint, not only is this problem frequently more accessible to our investigation, but at the same time we come into possession of a method which is applicable also to related problems. The introduction of complex paths of integration by Cauchy and of the notion of the IDEALS in number theory by Kummer may serve as examples. This way for finding general methods is certainly the most practicable and the most certain; for he who seeks for methods without having a definite problem in mind seeks for the most part in vain.
In dealing with mathematical problems, specialization plays, as I believe, a still more important part than generalization. Perhaps in most cases where we seek in vain the answer to a question, the cause of the failure lies in the fact that problems simpler and easier than the one in hand have been either not at all or incompletely solved. All depends, then, on finding out these easier problems, and on solving them by means of devices as perfect as possible and of concepts capable of generalization. This rule is one of the most important levers for overcoming mathematical difficulties and it seems to me that it is used almost always, though perhaps unconsciously.
Occasionally it happens that we seek the solution under insufficient hypotheses or in an incorrect sense, and for this reason do not succeed. The problem then arises: to show the impossibility of the solution under the given hypotheses, or in the sense contemplated. Such proofs of impossibility were effected by the ancients, for instance when they showed that the ratio of the hypotenuse to the side of an isosceles right triangle is irrational. In later mathematics, the question as to the impossibility of certain solutions plays a preeminent part, and we perceive in this way that old and difficult problems, such as the proof of the axiom of parallels, the squaring of the circle, or the solution of equations of the fifth degree by radicals have finally found fully satisfactory and rigorous solutions, although in another sense than that originally intended. It is probably this important fact along with other philosophical reasons that gives rise to the conviction (which every mathematician shares, but which no one has as yet supported by a proof) that every definite mathematical problem must necessarily be susceptible of an exact settlement, either in the form of an actual answer to the question asked, or by the proof of the impossibility of its solution and therewith the necessary failure of all attempts. Take any definite unsolved problem, such as the question as to the irrationality of the Euler-Mascheroni constant C, or the existence of an infinite number of prime numbers of the form 2n + 1. However unapproachable these problems may seem to us and however helpless we stand before them, we have, nevertheless, the firm conviction that their solution must follow by a finite number of purely logical processes.
Is this axiom of the solvability of every problem a peculiarity characteristic of mathematical thought alone, or is it possibly a general law inherent in the nature of the mind, that all questions which it asks must be answerable? For in other sciences also one meets old problems which have been settled in a manner most satisfactory and most useful to science by the proof of their impossibility. I instance the problem of perpetual motion. After seeking in vain for the construction of a perpetual motion machine, the relations were investigated which must subsist between the forces of nature if such a machine is to be impossible; and this inverted question led to the discovery of the law of the conservation of energy, which, again, explained the impossibility of perpetual motion in the sense originally intended.
This conviction of the solvability of every mathematical problem is a powerful incentive to the worker. We hear within us the perpetual call: There is the problem. Seek its solution. You can find it by pure reason, for in mathematics there is no ignorabimus. …
2. THE COMPATIBILITY OF THE ARITHMETICAL AXIOMS
When we are engaged in investigating the foundations of a science, we must set up a system of axioms which contains an exact and complete description of the relations subsisting between the elementary ideas of that science. The axioms so set up are at the same time the definitions of those elementary ideas; and no statement within the realm of the science whose foundation we are testing is held to be correct unless it can be derived from those axioms by means of a finite number of logical steps. Upon closer consideration the question arises: Whether, in any way, certain statements of single axioms depend upon one another, and whether the axioms may not therefore contain certain parts in common, which must be isolated if one wishes to arrive at a system of axioms that shall be altogether independent of one another.
But above all I wish to designate the following as the most important among the numerous questions which can be asked with regard to the axioms: To prove that they are not contradictory, that is, that a finite number of logical steps based upon them can never lead to contradictory results. …
10. DETERMINATION OF THE SOLVABILITY OF A DIOPHANTINE EQUATION
Given a diophantine equation with any number of unknown quantities and with rational integral numerical coefficients: To devise a process according to which it can be determined by a finite number of operations whether the equation is solvable in rational integers. …
Reprinted from Hilbert (1902).