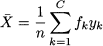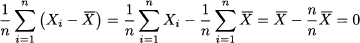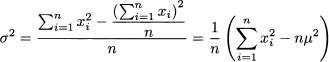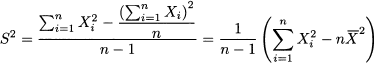Chapter 4
Descriptive Statistics: On the Way to Elementary Probability
Some fundamental concepts of descriptive statistics, like frequencies, relative frequencies, and histograms, have been introduced informally in Chapter 1. Here we want to illustrate and expand those concepts in a slightly more systematic way. Our treatment will be rather brief since, within the framework of this book, descriptive statistics is essentially a tool for building some intuition paving the way for later chapters on probability theory and inferential statistics.
We introduce basic statistical concepts in Section 4.1, drawing the line between descriptive and inferential statistics, and illustrating the difference between sample and population, as well as between qualitative and quantitative variables. Descriptive statistics provides us with several tools for organizing and displaying data, some of which are outlined in Section 4.2. While displaying data graphically is useful to get some feeling for their distribution, we typically need a few numbers summarizing their essential features; quite natural summary measures such as mean and variance are dealt with in Section 4.3. Then, in Section 4.4 we consider measures of relative standing such as percentiles, which are a less obvious but quite important tool used to analyze data. We should mention that basic descriptive statistics does not require overly sophisticated concepts, and it is rather easy to understand. However, sometimes concepts are a bit ambiguous, and a few subtleties can be better appreciated when armed with a little more formal background. Percentiles are a good case in point, as there is no standard definition and software packages may compute them in different ways; yet, they are a good way to get some intuitive feeling for probabilistic concepts, like quantiles, that are relevant in many applications in logistics and finance. Finally, in Section 4.5 we move from data in a single dimension to data in multiple dimensions. We limit the discussion to two dimensions, but the discussion here is a good way to understand the need for the data reduction methods discussed in Chapter 17.
4.1 WHAT IS STATISTICS?
A rather general answer to this question is that statistics is a group of methods to collect, analyze, present, and interpret data (and possibly to make decisions). We often consider statistics as a branch of mathematics, but this is the result of a more recent tendency. From a historical perspective, the term “statistics” stems from the word “state.” Originally, the driving force behind the discipline was the need to collect data about population and economy, something that was felt necessary in the city states of Venice and Florence during Renaissance. Many governments did the same in the following centuries. Then, statistics got a more quantitative twist, mainly under the impulse of French mathematicians. As a consequence, statistics got more intertwined with the theory of probability, a tendency that was not free from controversy.
Over time, many statistical tools have been introduced and they are often looked at as a bunch of cookbook recipes, which may result in quite some confusion. In order to bring some order, a good starting point is drawing the line between two related subbranches:
- Descriptive Statistics consists of methods for organizing, displaying, and describing data by using tables, graphs, and summary measures.
- Inferential Statistics consists of methods that use sampling to help make decisions or predictions about a population.
To better understand the role of sampling, we should introduce the following concepts.
DEFINITION 4.1 (Population vs. sample) A population consists of all elements (individuals, items, etc.) whose characteristics are being studied. A sample is a portion of the population, which is selected for study.
To get the point, it suffices to reflect a bit on the cost and the time required to carry out a census of the whole population of a state, e.g., to figure out average household income. A much more common occurrence is a sample survey. For the study to be effective, the sample must be representative of the whole population. If you sample people in front of a big investment bank, you are likely to get a misleading picture, as the sample is probably biased toward a very specific type of individual.
Example 4.1 One of the best-known examples of bad sample selection is the 1936 presidential election poll by the Literary Digest. According to this poll, the Republican governor of Kansas, Alf Landon, would beat former president Franklin Delano Roosevelt by 57–43%. The sample size was not tiny at all, as the Digest mailed over 10 million questionnaires and over 2.3 million people responded. The real outcome was quite different, as Roosevelt won with 62%. One of the reasons commonly put forward to explain such a blunder is that many respondents were selected from lists of automobile and telephone owners. Arguably, a selection process like that would be correct nowadays, but in the past the sample was biased towards relatively wealthy people, which in turn resulted in a bias towards republican voters.
A sample drawn in such a way that each element in the target population has a chance of being selected is called a random sample. If the chance of being selected is the same for each element, we speak of a simple random sample.1
Household income is an example of a variable. A variable is a characteristic of each member of the population, and below we discuss different types of variable we might be interested in. Income is a quantitative variable, and we may want some information about average income of the population. The average income of the population is an example of a parameter. Typically, we do not know the parameters characterizing a whole population, and we have to resort to some form of estimate. If we use sampling, we have to settle for the average income of the sample, which is a statistic. The statistic can be used to estimate the unknown parameter.
If sampling is random, whenever we repeat the experiment, we get different results, i.e., different values of the resulting statistic. If the results show wide swings, any conclusion that we get from the study cannot be trusted. Intuition suggests that the larger the sample, the more reliable the conclusions. Furthermore, if the individuals in the population are not too different from one another, the sample can be small. In the limit, if all of the individuals were identical, any one of them would make a perfect sample. But if there is much variability within the population, a large sample must be taken. In practice, we need some theoretical background to properly address issues related to the size of the sample and the reliability of the conclusions we get from sampling, especially if such conclusions are the basis of decision making. In Chapter 9, on inferential statistics, we will consider such issues in detail. On the contrary, basic descriptive statistics does not strictly rely on quite sophisticated concepts. However, probability theory is best understood by using descriptive statistics as a motivation. Descriptive statistics is quite useful when conducting an exploratory study, i.e., if we want to analyze data to see if an interesting pattern emerges, suggesting some hypothesis or line of action. However, when a confirmatory analysis is carried out, to check a hypothesis, inferential statistics comes into play.
4.1.1 Types of variable
If we are sampling a population to figure out average household income, we are considering income as the variable of interest.
DEFINITION 4.2 (Variables and observations) A variable is a characteristic under study, which assumes different values for different elements of a population or a sample. The value of a variable for an element is called an observation or measurement.
This definition is illustrated in Table 4.1, where hypothetical data are shown. An anonymous person is characterized by weight, height, marital status, and number of children. Variables are arranged on columns, and each observation corresponds to a row. We immediately see differences between those variables. A variable can be
Table 4.1 Illustrating types of variable.

- Quantitative, if it can be measured numerically
- Qualitative or categorical, otherwise
Clearly, weight and number of children are quantitative variables, whereas marital status is not. Other examples of categorical variables are gender, hair color, or make of a computer.
If we look more carefully at quantitative variables in the table, we see another difference. You cannot have 2.1567 children; this variable is restricted to a set of discrete values, in this case integer numbers. On the contrary, weight and height can take, in principle, any value. In practice, we truncate those numbers to a suitable number of significant digits, but they can be considered as real numbers. Hence, quantitative variables should be further classified as
- Discrete, if the values it can take are countable (number of cars, number of accidents occurred, etc.)
- Continuous, if the variable can assume any value within an interval (length, weight, time, etc.)
In this book we will generally associate discrete variables with integer numbers, and continuous variables with real numbers, as this is by far the most common occurrence. However, this is not actually a rule. For instance, we could consider a discrete variable that can take two real values such as ln(18) or 2π. We should also avoid the strict identification of “a variable that can take an infinite number of values” with a continuous variable. It is true that a continuous variable restricted to a bounded interval, e.g., [2,10], can assume an infinite number of values, but a discrete variable can take an infinite number of integer values as well.2 For instance, if we consider the number of accidents that occurred on a highway in one month, there is no natural upper bound on them, and this should be regarded as a variable taking integer values i = 1,2,3, …, even though very large values are (hopefully) quite unlikely.
The classification looks pretty natural, but the following examples show that sometimes a little care is needed.
Example 4.2 (Dummy and nominal variables) Marital status is clearly a qualitative variable. However, in linear regression models (Chapters 10 and 16) it is quite common to associate them with binary values 1 and 0, which typically correspond to yes/no or true/false. In statistics, such a variable is often called “dummy.” The interpretation of these numerical values is actually arbitrary and depends on modeler’s choice. It is often the case that numerical values are attached to categorical variables for convenience, but we should consider these as nominal variables. A common example are the Standard Industrial Classification (SIC) codes.3 You might be excited to discover that SIC code 1090 corresponds to “Miscellaneous Metal Ores” and 1220 to “Bituminous Coal & Lignite Mining.” No disrespect intended to industries in this sector and, most importantly, no one should think that the second SIC code is really larger than the first one, thereby implying some ranking among them.
The example above points out a fundamental feature of truly numerical variables: They are ordered, whereas categorical variables cannot be really ordered, even though they may be associated with numerical (nominal but not ordinal) values. We cannot double a qualitative or a nominal variable, can we? But even doubling a quantitative variable is trickier than we may think.
Example 4.3 Imagine that, between 6 and 11 a.m., temperature on a day rises from 10°C to 20°C. Can we say that temperature has doubled? It is tempting to say yes, but imagine that you measure temperature by Fahrenheit, rather than Celsius degrees. In this case, the two temperatures are 50°F and 68°F, respectively,4 and their ratio is certainly not 2.
What is wrong with the last example is that the origin of the temperature scale is actually arbitrary. On the contrary, the origin of a scale measuring the number of children in a family is not arbitrary. We conclude this section with an example showing again that the same variable may be used in different ways, associated with different types of variable.
Example 4.4 (What is time?) Time is a variable that plays a fundamental role in many models. Which type of variable should we use to represent time?
Time as a continuous variable. From a “philosophical” point of view, time is continuous. If you consider two time instants, you can always find a time instant between them. Indeed, time in physics is usually represented by a real number. Many useful models in finance are also based on a continuous representation of time, as this may result in handy formulas.5
Time as a discrete variable. Say that we are in charge of managing the inventory of some item, that is ordered at the end of each week. Granted, time is continuous, but from our perspective what really matters is demand during each week. We could model demand by a variable like dt, where subscript t refers to weeks 1,2,3, …. In this model, time is discretized because of the structure of the decision making process. We are not interested in demand second by second. In the EOQ model (see Section 2.1) we treated time as a continuous variable, because demand rate was constant. In real life, demand is unlikely to be constant, and time must be discretized in order to build a manageable model. Indeed, quite often time is discretized to come up with a suitable computational procedure to support decisions.6
Time as a categorical variable. Consider daily sales at a retail store. Typically, demand on Mondays is lower than the average, maybe because the store is closed in the morning. Demand on Fridays is greater, and it explodes on Saturdays, probably because most people are free from their work on weekends. We observe similar seasonal patterns in ratings of TV programs and in consumption of electrical energy.7 We could try to analyze the statistical properties of dmon, dfri, etc. In this case, we see that “Monday” and “Friday” subscripts do not correspond to ordered time instants, as there are different weeks, each one with a Monday and a Friday. A time subscript in this case is actually related to categorical variables.
Table 4.2 Raw data may be hard to interpret.
Time can be modeled in different ways, and the choice among them may depend on the purpose of the model or on computational conveniency.
4.2 ORGANIZING AND REPRESENTING RAW DATA
We have introduced the basic concepts of frequencies and histograms in Section 1.2.1. Here we treat the same concepts in a slightly more systematic way, illustrating a few potential difficulties that may occur even with these very simple ideas.
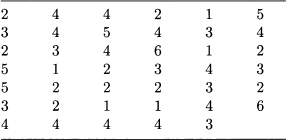
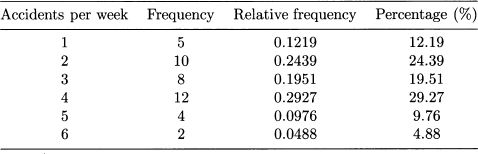
Imagine a car insurance agent who has collected the weekly number of accidents occurred during the last 41 weeks, as shown in Table 4.2. This raw representation of data is somewhat confusing even for such a small dataset. Hence, we need a more systematic way to organize and present data. A starting point would be sorting the data in order to see the frequency with which each of the values above occurs. For instance, we see that in 5 weeks we have observed one accident, whereas two accidents have been observed in 12 cases. Doing so for all of the observed values, from 1 to 6, we get the second column of Table 4.3, which shows frequencies for the raw data above.
An even clearer picture may be obtained by considering relative frequencies, which are obtained by taking the ratio of observed frequencies and the total number of observations:
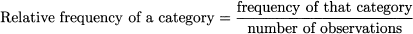
For instance, two accidents have been observed in 10 cases out of 41; hence, the relative frequency of the value 2 is 10/41 = 0.2439 = 24.39%. Relative frequencies are also displayed in Table 4.3. Sometimes, they are reported in percentage terms. What is really essential to notice is that relative frequencies should add up to 1, or 100%; when numbers are rounded, a small discrepancy can occur.
Table 4.3 Organizing raw data using frequencies and relative frequencies.
Frequencies and relative frequencies may be represented graphically in a few ways. The most common graphical display is a bar chart, like the one illustrated in Fig. 4.1. The same bar chart, with a different vertical axis would represent relative frequencies.8 A bar chart can also be used to illustrate frequencies of categorical data. In such a case, the ordering of bars would have no meaning, whereas for quantitative variables we have a natural ordering of bars. A bar chart for quantitative variables is usually called a histogram. For qualitative variables, we may also use an alternative representation like a pie chart. Figure 4.2 shows a pie chart for answers to a hypothetical question (answers can be “yes,” “no,” and “don’t know”). Clearly, a pie chart does not show any ordering between categories.
Fig. 4.2 A pie chart for categorical data.

Table 4.4 Frequency and relative frequencies for grouped data.
| Average travel time to work (minutes) | Frequency | Percentage (%) |
| < 18 | 7 | 14 |
| 18–21 | 7 | 14 |
| 21–24 | 23 | 46 |
| 24–27 | 9 | 18 |
| 27–30 | 3 | 6 |
| ≥ 30 | 1 | 2 |
A histogram is naturally suited to display discrete variables, but what about continuous variables, or discrete ones when there are many observed values? In such a case, it is customary to group data into intervals corresponding to classes. As a concrete example, consider the time it takes to get to workplace using a car. Time is continuous in this case, but there is little point in discriminating too much using fractions of seconds. We may consider “bins” characterized by a width of three minutes, as illustrated in Table 4.4. To formalize the concept, each “bin” corresponds to an interval. The common convention is to use closed-open intervals.9 This means, for instance, that the class 18–21 in Table 4.4 includes all observations ≥ 18 and < 21 or, in other words, it corresponds to interval [18,21). To generalize, we use bins of the following form:
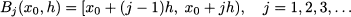
where x0 is the origin of this set of bins and should not be confused with an observation, and h is the bin width. Actually, h need not be the same for all of the bins, but this may be a natural choice. The first bin, B1(x0, h), corresponds to interval [x0, x0 + h); the second bin, B2(x0, h), corresponds to interval [x0 + h, x0 + 2h), and so on. For widely dispersed data it might be convenient to introduce two side bins, i.e., an unbounded interval (-∞, xl) collecting the observations below a lower bound xl, and an unbounded interval [xu, +∞) for the observations above an upper bound xu.
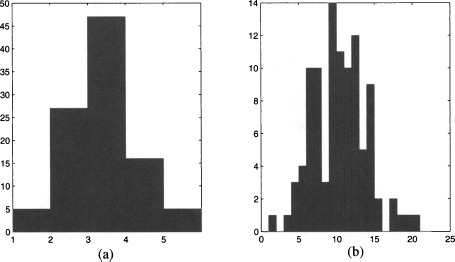
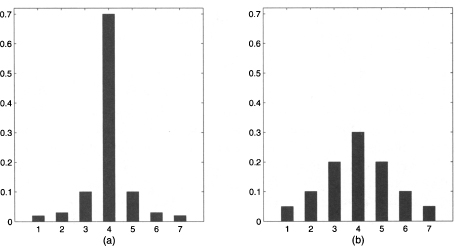
Histograms are a seemingly trivial concept, that can be used to figure out basic properties of a dataset in terms of symmetry vs. skewness (see Fig. 1.5), as well as in terms of dispersion (see Fig. 1.6). In practice, they may not be as easy to use as one could imagine. A first choice we have to make concerns the bin width h and, correspondingly, the number of bins. The same dataset may look differently if we change the number of bins, as illustrated in Fig. 4.3. Using too few bins does not discriminate data enough and any underlying structure is lost in the blur [see histogram (a) in Fig. 4.3]; using too many may result in a confusing jaggedness, that should be smoothed in order to see the underlying pattern [see histogram (b) in Fig. 4.3]. A common rule of thumb is that one should not use less than 5 bins, and no more than 20. A probably less obvious issue is related to the choice of origin x0, as illustrated by the next example.
Fig. 4.3 Bar charts illustrating the effect of changing bin width in histograms.
Example 4.5 Consider the dataset in Table 4.5, reporting observed values along with their frequency. Now let us choose h = 0.2, just to group data a little bit. Figure 4.4 shows three histograms obtained by setting x0 = 54.9, x0 = 55.0, and x0 = 55.1, respectively. At first sight, the change in histogram shape due to an innocent shift in the origin of bins is quite surprising. If we look more carefully into the data, the source of the trouble is evident. Let us check which interval corresponds to the first bin in the three cases. When x0 = 54.9, the first bin is [54.9,55.1) and is empty. When x0 = 55.0, the first bin is changed to [55.0, 55.2); now two observations fall into this bin. Finally, when x0 = 55.1, the first bin is changed to [55.1, 55.3), and 2 + 4 = 6 observations fall into this bin. The point is that, by shifting bins, we change abruptly the number of observations falling into each bin, and a wild variation in the overall shape of the histogram is the result.10
Table 4.5 Data for Example 4.5.

The example above, although somewhat pathological, shows that histograms are an innocent-looking graphical tool, but they may actually be dangerous if used without care, especially with small datasets. Still, they are useful to get an intuitive picture of the distribution of data. In the overall economy of the book, we should just see that the histogram of relative frequencies is a first intuitive clue leading to the idea of a probability distribution.
We close this section by defining two concepts that will be useful in the following.
DEFINITION 4.3 (Order statistics) Let X1, X2, …, Xn be a sample of observed values. If we sort these data in increasing order, we obtain order statistics, which are denoted by X(1), X(2), …, X(n). The smallest observed value if X(1) and the largest observed value is X(n).
DEFINITION 4.4 (Outliers) An outlier is an observation that looks quite apart from the other ones. This may be a very unlikely value, or an observation that actually comes from a different population.
Example 4.6 Consider observations
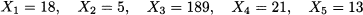
Ordering these values yields the following order statistics:
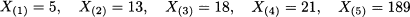
The last value is quite apart from the remaining ones and is a candidate outlier.
Spotting an outlier is a difficult task, and the very concept looks quite arbitrary. There are statistical procedures to classify an outlier in a sensible and objective manner, but in practice we need to dig a bit deeper into data to figure out why a value looks so different. It may be the result of a data entry error or a wrong observation, in which case the observation should be eliminated. It could be just an unlikely observation, in which case eliminating the observation may result in a dangerous underestimation of the actual uncertainty. In other cases, we may be mixing observations from what are actually different populations. If we take observations of a variable in small towns and then we throw New York into the pool, an outlier is likely to result.
4.3 SUMMARY MEASURES
A look at a frequency histogram tells us many things about the distribution of values of a variable of interest within a population or a sample. However, it would be quite useful to have a set of numbers capturing some essential features quantitatively; this is certainly necessary if we have to compare two histograms, since visual perception can be misleading. More precisely, we need a few summary measures characterizing, e.g., the following properties:
- Location, i.e., the central tendency of the data
- Dispersion
- Skewness, i.e., lack of symmetry
4.3.1 Location measures: mean, median, and mode
We are all familiar with the idea of taking averages. Indeed, the most natural location measure is the mean.
DEFINITION 4.5 (Mean for a sample and a population) The mean for a population of size n is defined as
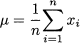
The mean for a sample of size n is
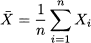
The two definitions above may seem somewhat puzzling, since they look identical. However, there is an essential difference between the two concepts. The mean of the population is a well-defined number, which we often denote by μ. If collecting information about the whole population is not feasible, we take a sample resulting in a mean  . But if we take two different samples, possibly random ones, we will get different values for the mean. In later chapters, we will discover that the population mean is related to the concept of expected value in probability theory, whereas the sample mean is used in inferential statistics as a way to estimate the (unknown) expected value. The careful reader might also have noticed that we have used a lowercase letter xi when defining the mean of a population and an uppercase letter Xi for the mean of a sample. Again, this is to reinforce the conceptual difference between them; in later chapters we will use lowercase letters to denote numbers and uppercase letters to denote random variables. Observations in a random sample are, indeed, random variables.
. But if we take two different samples, possibly random ones, we will get different values for the mean. In later chapters, we will discover that the population mean is related to the concept of expected value in probability theory, whereas the sample mean is used in inferential statistics as a way to estimate the (unknown) expected value. The careful reader might also have noticed that we have used a lowercase letter xi when defining the mean of a population and an uppercase letter Xi for the mean of a sample. Again, this is to reinforce the conceptual difference between them; in later chapters we will use lowercase letters to denote numbers and uppercase letters to denote random variables. Observations in a random sample are, indeed, random variables.
Example 4.7 We want to estimate the mean number of cars entering a parking lot every 10 minutes. The following 10 observations have been gathered, over 10 nonoverlapping time periods of 10 minutes: 10, 22, 31, 9, 24, 27, 29, 9, 23, 12. The sample mean is
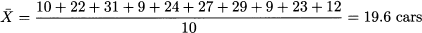
Note that the mean of integer numbers can be a fractional number. Also note that a single small observation can affect the sample mean considerably. If, for some odd reason, the first observation is 1000; then
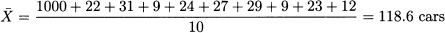
The previous example illustrates the definition of mean, but when we have many data it might be convenient to use frequencies or relative frequencies. If we are given n observations, grouped into C classes with frequencies fi, the sample mean is
Here, yk is a value representative of the class. Note that yk need not be an observed value. In fact, when dealing with continuous variables, yk might be the midpoint of each bin; clearly, in such a case grouping data results in a loss of information and should be avoided. When variables are integer, one single value can be associated with a class, and no difficulty arises.
Example 4.8 Consider the data in Table 4.6, which contains days of unjustified absence per year of a group of employees. Then:  410 + 430 + 290 + 180 + 110 + 20 = 1440, and
410 + 430 + 290 + 180 + 110 + 20 = 1440, and
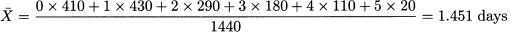
If relative frequencies pk = fk/n are given, the mean is calculated as
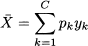
where again yk is the value associated with class k. It is easy to see that this is equivalent to Eq. (4.1). In this case, we are computing a weighted average of values, where weights are nonnegative and add up to one.
The median, sometimes denoted by m, is another measure of central tendency. Informally, it is the value of the middle term in a dataset that has been ranked in increasing order.
Table 4.6 Data for Example 4.8.
| Days of absence | Frequency |
| 0 | 410 |
| 1 | 430 |
| 2 | 290 |
| 3 | 180 |
| 4 | 110 |
| 5 | 20 |
Example 4.9 Consider the dataset: 10, 5, 19, 8, 3. Ranking the dataset (3,5,8,10,19), we see that the median is 8.
More generally, with a dataset of size n the median should be the order statistic
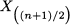
An obvious question is: What happens if we have an even number of elements? In such a case, we take the average of the two middle terms, i.e., the elements in positions n/2 and n/2 + 1.
Example 4.10 Considered the ordered observations
We have n = 12 observations; since (n + 1)/2 = 6.5, we take the average of the sixth and seventh observations:
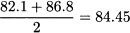
The median is less sensitive than the mean to extreme data (possibly outliers). To see this, consider the dataset (4.2) and imagine substituting the smallest observation, X(1) = 74.1, with a very small number. The mean is likely to be affected significantly, as the sample size is very small, but the median does not change. The same happens if we change X(12), i.e., the largest observation in the sample. This may be useful when the sample is small and chances are that an outlier enters the dataset. Generally speaking, there are statistics that may be more robust than other ones, and they should be considered when we have a small dataset that is sensitive to outliers.
The median can also be used to measure skewness. Observing the histograms in Fig. 4.5, we may notice that:
Fig. 4.5 Bar charts illustrating right- and left-skewed distributions.

- For a perfectly symmetric distribution, mean and median are the same.
- For a right-skewed distribution [see histogram (a) in Fig. 4.5], the mean is larger than the median (and we speak of positively skewed distri-butions); this happens because we have rather unlikely, but very high values that bias the mean to the right with respect to the median.
- By the same token, for a left-skewed distribution [see histogram (b) in Fig. 4.5], the mean is smaller than the median (and we speak of negatively skewed distributions).
In descriptive statistics there is no standard definition of skewness, but one possible definition, suggested by K. Pearson, is
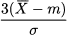
where m is the median and σ is the standard deviation, a measure of dispersion defined in the next section. This definition indeed shows how the difference between mean and median can be used to quantify skewness.11
Finally, another summary measure is the mode, which corresponds to the most frequent value. In the histograms of Fig. 4.5 the mode corresponds to the highest bar in the plot. In some cases, mean, mode, and median are the same. This happens in histogram (a) of Fig. 4.6. It might be tempting to generalize and say that the three measures are the same for a symmetric distribution, but a quick glance at Fig. 4.6(b) shows that this need not be the case.
Fig. 4.6 Single and bimodal distributions.

Example 4.11 The histogram in Fig. 4.6(b) is somewhat pathological, as it has two modes. A more common occurrence is illustrated in Fig. 4.7, where there is one true mode (the “globally maximum” frequency) but also a secondary mode (a “locally maximum” frequency). A situation like this might be the result of sampling variability, in which case the secondary mode is just noise. In other cases, it might be the effect of a complex phenomenon and just “smoothing” the secondary mode is a mistake. We may list a few practical examples in which a secondary mode might result:
Fig. 4.7 A bimodal distribution.

- The delivery lead time from a supplier, i.e., the time elapsing between issuing an order and receiving the shipment. Lead time may feature a little variability because of transportation times, but a rather long lead time may occur when the supplier runs out of stock. Ignoring this additional uncertainty may result in poor customer service.
- Consider the repair time of a manufacturing equipment. We may typically observe ordinary faults that take only a little time to be repaired, but occasionally we may have a major fault that takes much more time to be fixed.
- Quite often, in order to compare student grades across universities in different countries, histograms are prepared for each university and they are somehow matched in order to define fair conversion rules. Usually, this is done by implicitly assuming that there is a “standard” grade, to which some variability is superimposed. Truth is that the student population is far from uniform; we may have a secondary mode for the subset more skilled students, which actually constitute a different population than ordinary students.12
4.3.2 Dispersion measures
Location measures do not tell us anything about dispersion of data. We may have two distributions sharing the same mean, median, and mode, yet they are quite different. Figure 4.8, repeated from Chapter 1 (Fig. 1.6), illustrates the importance of dispersion in discerning the difference between distributions sharing location measures. One possible way to characterize dispersion is by measuring the range X(n) – X(1), i.e., the difference between the largest and the smallest observations. However, the range has a couple of related shortcomings:
Fig. 4.8 Bar charts illustrating the role of dispersion: mean, median, and mode are the same, but the two distributions are quite different.
1. It uses only two observations of a possibly large dataset, with a corresponding potential loss of valuable information.
2. It is rather sensitive to extreme observations.
An alternative and arguably better idea is based on measuring deviations from the mean. We could consider the average deviation from the mean, i.e., something like
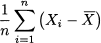
However, it is easy to see that the above definition is useless, as the average deviation is identically zero by its very definition:
The problem is that we have positive and negative deviations canceling each other. To get rid of the sign of deviations, we might consider taking absolute values, which yields the mean absolute deviation (MAD):
(4.4) 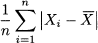
As an alternative, we may average the squared deviations, which leads to the most common measure of dispersion.
DEFINITION 4.6 (Variance) In the case of a population of size n, variance is defined as
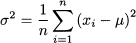
In the case of a sample of size n, variance is defined as
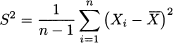
These definitions mirror the definition of mean for populations and samples. However, a rather puzzling feature of the definition of sample variance S2 is the division by n - 1, instead of n. A convincing justification will be given in Section 9.1.2 within the framework of inferential statistics. For now, let us observe that the n deviations (Xi -  ) are not independent, since identity of Eq. (4.3) shows that when we know the sample mean and the first n - 1 deviations, we can easily figure out the last deviation.13 In fact, there are only n - 1 independent pieces of information or, in other words, n - 1 degrees of freedom. Another informal argument is that since we do not know the true population mean μ, we have to settle for its estimate
) are not independent, since identity of Eq. (4.3) shows that when we know the sample mean and the first n - 1 deviations, we can easily figure out the last deviation.13 In fact, there are only n - 1 independent pieces of information or, in other words, n - 1 degrees of freedom. Another informal argument is that since we do not know the true population mean μ, we have to settle for its estimate  , and in estimating one parameter we lose one degree of freedom (1 df). This is actually useful as a mnemonic to help us deal with more complicated cases, where estimating multiple parameters results in the loss of more degrees of freedom.
, and in estimating one parameter we lose one degree of freedom (1 df). This is actually useful as a mnemonic to help us deal with more complicated cases, where estimating multiple parameters results in the loss of more degrees of freedom.
Variance is more commonly used than MAD. With respect to MAD, variance enhances large deviations, since these are squared. Another reason, that will become apparent in the following, is that variance involves squaring deviations, and the function g(z) = z2 is a nice differentiable one. MAD involves an absolute value h(z) = |z|, which is not that nice. However, taking a square does have a drawback: It changes the unit of measurement. For instance, variance of weekly demand should be measured in squares of items, and it is difficult to assign a meaning to that. This is why a strictly related measure of dispersion has been introduced.
DEFINITION 4.7 (Standard deviation) Standard deviation is defined as the square root of variance. The usual notation, mirroring Definition 4.6, is σ for a population and S for a sample.
The calculation of variance and standard deviation is simplified by the following shortcuts:
Example 4.12 Consider the sample:
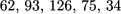
We have
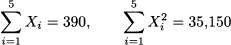
Hence, sample variance is
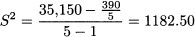
and sample standard deviation is
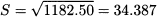
It is quite instructive to prove the above formulas. We consider here shortcut of Eq. (4.5), leaving the second one as an exercise:
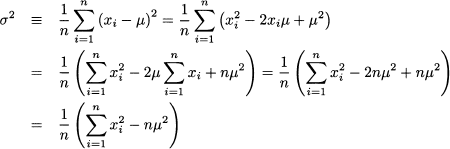
These rearrangements do streamline calculations by hand or by a pocket calculator, but they can be computationally unfortunate when dealing with somewhat pathological cases.
Example 4.13 Consider the dataset in Table 4.7. The first column shows the raw data; the second column shows the corresponding centered data, which are obtained by subtracting the mean from the raw data. Of course, variance is the same in both cases, as shifting data by any amount does not affect dispersion. If we use the definition of variance, we get the correct result in both cases, S2 = 229.17. However, if we apply the streamlined formula of Eq. (4.6), on a finite precision computer we get 0 for the raw data. This is a consequence of numerical errors, and we may see it clearly by considering just two observations with the same structure as the data in Table 4.7:
Table 4.7 Computing variance with raw and centered data.
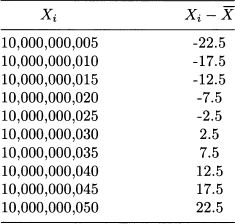

where  1 and
1 and  2 are much smaller than α. For instance, in the table we have α = 10,000,000,000,
2 are much smaller than α. For instance, in the table we have α = 10,000,000,000,  1 = 5, and
1 = 5, and  2 = 10. Then
2 = 10. Then
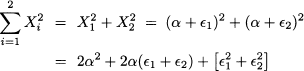
and
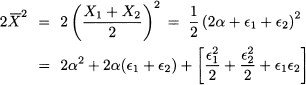
We see that the two expressions are different, but since  1 and
1 and  2 are relatively small and get squared, the terms in the brackets are much smaller than the other ones. With a finite-precision computer arithmetic, they will be canceled in the calculations, so that the difference between the two expressions turns out to be zero. This is a numerical error due to truncation. In generel when taking the difference of similar quantities, a loss of precision may result. If we subtract the mean α + (
2 are relatively small and get squared, the terms in the brackets are much smaller than the other ones. With a finite-precision computer arithmetic, they will be canceled in the calculations, so that the difference between the two expressions turns out to be zero. This is a numerical error due to truncation. In generel when taking the difference of similar quantities, a loss of precision may result. If we subtract the mean α + ( 1 +
1 +  2)/2, we compute variance with centered data:
2)/2, we compute variance with centered data:
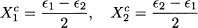
which yields the correct result
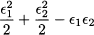
with no risk of numerical cancelation. Although the effects need not be this striking in real-life datasets, it is generally advisable to work on centered data.
We close this section by pointing out a fundamental property of variance and standard deviation, due to the fact that they involve the sum of squares.
PROPERTY 4.8 Variance and standard deviation can never be negative; they are zero in the “degenerate” case when there is no variability at all in the data.
4.4 CUMULATIVE FREQUENCIES AND PERCENTILES
The median m is a value such that 50% of the observed values are smaller than or equal to it. In this section we generalize the idea to an arbitrary percentage. We could ask which value is such that 80% of the observations are smaller than or equal to it. Or, seeing things the other way around, we could ask what is the relative standing of an observed value. In Section 1.2.1 we anticipated quite practical motivations for asking such questions, which are of interest in measuring the service level in a supply chain or the financial risk of a portfolio of assets. The key concept is the set of cumulative (relative) frequencies.
DEFINITION 4.9 (Cumulative relative frequencies) Consider a sample of n observations Xi, i = 1, …, n, and group them in m classes, corresponding to each distinct observed value yk, k = 1, …, m. Classes are sorted in increasing order with respect to values: yk < yk+1. If fk is the frequency of class k, the cumulative frequency of the corresponding value is the sum of all the frequencies up to and including that value:
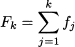
By the same token, given relative frequencies pk = fk/n, we define cumulative relative frequencies:
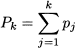
For the sake of simplicity, when no ambiguity arises, we often speak of cumulative frequencies, even though we refer to the relative ones.
Example 4.14 Consider the data in Table 4.8, which displays frequencies, relative frequencies, and cumulative frequencies for a dataset of 47 observations taking values in the set {1, 2, 3, 4, 5}. If we cumulate frequencies, we obtain cumulative frequencies:
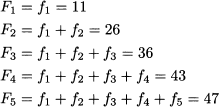
Table 4.8 Illustrating cumulative frequencies.

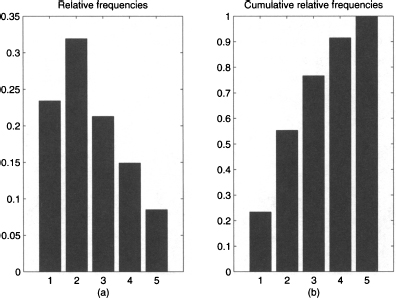
Fig. 4.9 Bar charts of relative frequencies and cumulative relative frequencies for the data in Table 4.8.
Cumulative relative frequencies are computed by adding relative frequencies:
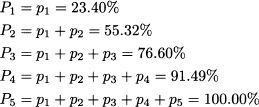
Since relative frequencies add up to 1, the last cumulative frequency must be 1 (or 100%). Since relative frequencies cannot be negative, cumulative frequencies form an increasing sequence; this is also illustrated in Fig. 4.9. Incidentally, the percentages in the first two rows of Table 4.8 may look wrong. If we add up the first two relative frequencies, 23.40% and 31.91%, we obtain 55.31%, whereas the second cumulative relative frequency in the last column of the table is 55.32%. This is just the effect of rounding; indeed, such apparent inconsistencies are common when displaying cumulative frequencies.
Cumulative frequencies are related with a measure of relative standing of a value yk, the percentile rank. A little example illustrates why one might be interested in percentile ranks.
Example 4.15 In French universities, grades are assigned on a numerical scale whose upper bound is 20 and the minimum for sufficiency is 10. A student has just passed a tough exam and is preparing to ask her parents for a well-deserved bonus, like a brand-new motorcycle, or a more powerful flamethrower, or maybe a trip to visit museums abroad. Unfortunately, her parents do not share her enthusiasm, as her grade is just 16, whereas the maximum is 20. Since this is just a bit above the midpoint of the range of sufficient grades (15), they argue that this is just a bit above average. She should do much better to earn a bonus! How can she defend her position?
As the saying goes, everything is relative. If she got the highest grade in the class, her claim is reasonable. Or maybe only 2 colleagues out of 70 earned a larger grade. What she needs to show is that she is near the top of the distribution of grades, and that a large percentage of students earned a worse grade.
The percentile rank of an observation Xi could be defined as the fraction of observations which are less than or equal to Xi:
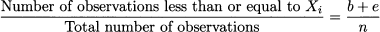
where b is the number of observations below and e the number of observations equal to Xi, respectively. This definition is just based on the cumulative relative frequency corresponding to value Xi. However, there might be a little ambiguity. Imagine that all of the students in the example above have received the same grade, 16 out of 20. Using this definition, the percentile rank would be 100%. This is the same rank that our friend would get if she were the only student with a 16 out of 20, with everyone lagging far behind. A definition which does not discriminate between these two quite different cases is debatable indeed. We could argue that if everyone has received 16 out of 20, then the percentile rank for everyone should be 50%. Hence, we could consider the alternative definition of the percentile rank of Xi as
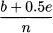
which accounts for observations equal to Xi in a slightly different way. Some well-known spreadsheets use still another definition, which eliminates the number of observations equal to Xi:
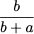
where b is the number of observations strictly below Xi, as before, and a is the number of observations strictly above Xi. We see that, sometimes, descriptive statistics is based on concepts that are a bit shaky; however, for a large dataset, the above ambiguity is often irrelevant in practice.
Now let us go the other way around. Given a value, we may be interested in its percentile rank, which is related to a cumulative frequency. Given a relative frequency, which is a percentage, we may ask what is the corresponding value. Essentially, we are inverting the mapping between values and cumulative frequencies. Values corresponding to a percentage are called percentiles. For instance, the median is just the 50% percentile, and we want to generalize the concept. Unfortunately, there is no standard definition of a percentile and software packages might yield slightly different values, especially for small datasets. In the following, we illustrate three possible approaches. None is definitely better than the other ones, and the choice may depend on the application.
Approach 1. Let us start with an intuitive definition. Say that we want to find the kth percentile. What we should do, in principle, is sort the n observations to get the order statistics X(j), j = 1, …, n. Then, we should find the value corresponding to position kn/100. Since this ratio is not an integer in general, we might round it to the nearest integer. To illustrate, consider again the dataset (4.2), which we repeat here for convenience:
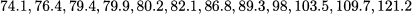
What is the 42nd percentile? Since we have only 12 observations, one possible approach relies on the following calculation:
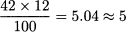
so that we should take the 5th element (80.2). Sometimes, it is suggested to add 1/2 to the ratio above before rounding. Doing so, we are sure that at least 42% of the data are less than or equal to the corresponding percentile. Note that in the sample above we have distinct observed values. The example below illustrates the case of repeated values.
Example 4.16 Let us consider again the inventory management problem we considered in Section 1.2.1. For convenience, let us repeat here the cumulative frequencies of each value of observed demand:
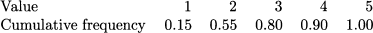
Imagine that we want to order a number of items so that we satisfy the whole demand in at least 85% of the cases. If we trust the observed data, we should find a 85% percentile. Since we have 20 observations, we could look at the value X(j), where j = 85 x 20/100 = 17. Looking at the disaggregated data, we see that X(17) = 4, and there is no need for rounding. However, with large datasets it might be easier to work with cumulative frequencies. However, there is no value corresponding to a 85% cumulative frequency; what we may do, however, is take a value such that its cumulative frequency is at least 85%, which leads us to order four items. This example has two features:
- We want to be “on the safe side.” We have a minimal service level, the probability of satisfying all customers, that we want to ensure. Hence, it makes sense to round up values. If the minimal service level were 79%, then j = 79 x 20/100 = 15.8; looking at the order statistics, we see that X(15) = 3 and X(16) = 4, but we should order four items to be on the safe side.
- Percentiles in many cases, including this one, should correspond to decisions; since we can only order an integer number of items, we need a percentile that is an integer number.
Approach 2. Rounding positions may be a sensible procedure, but it is not consistent with the definition of median that we have considered before. For an even number of observations, we defined the median as the average of two consecutive values. If we want to be consistent with this approach, we may define the kth percentile as a value such that:
1. At least kn/100 observations are less than or equal to it.
2. At least (100 - k)n/100 observations are greater than or equal to it.
For instance, if n = 22 and we are looking for the 80% percentile, we want a value such that at least 80 x 22/100 = 17.6 observations are less than or equal to it, which means that we should take X(18); on the other hand, at least (100 - 80) x 22/100 = 4.4 values should be larger than or equal to it. Also this requirement leads us to consider the 18th observation, in ascending order. Hence, we see that in this case we just compute a position and then we round up. However, when kn/100 is an integer, two observations satisfy the above requirement, Indeed, this happens if we look for the 75% percentile and n = 32. Both X(24) and X(25) meet the two requirements stated above. So, we may take their average, which is exactly what happens when calculating the median of an even number of observations.
Approach 3. Considering the two methods above, which is the better one? Actually, it depends on our aims. Approach 2 does not make sense if the percentile we are looking must be a decision restricted to an integer value, as in Example 4.16. Furthermore, with approach 1 we are sure that the percentile will be an observed value, whereas with approach 2 we get a value that has not been observed. This is critical with integer variables, but if we are dealing with a continuous variable, it makes perfect sense. Indeed, there is still a third approach that can be used with continuous variables and is based on interpolating values, rather than rounding positions. The idea can be summarized as follows:
1. The sorted data values are taken to be the 100(0.5/n), 100(1.5/n), …, 100([n - 0.5]/n) percentiles.
2. Linear interpolation is used to compute percentiles for percent values between 100(0.5/n) and 100([n - 0.5]/n).
3. The minimum or maximum values in the dataset are assigned to percentiles for percent values outside that range.
Let us illustrate linear interpolation with a toy example.
Example 4.17 We are given the dataset
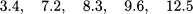
According to the procedure above, 3.4 is taken as the 10% percentile, 7.2 is taken as the 30% percentile, and so on until 12.5, which is taken as the 90% percentile. If we ask for the 5% percentile, the procedure yields 3.4, the smallest observation. If we ask for the 95% percentile, the procedure yields 12.5, the largest observation.
Things are more interesting for the 42% percentile. This should be somewhere between 7.2, which corresponds to 30%, and 8.3, which corresponds to 50%. To see exactly where, in Fig. 4.10 we plot the cumulative frequency as a function of observed values, and we draw a line joining the two observations. How much should we move along the line from value 7.2 toward value 8.3? The length of the line segment is
Fig. 4.10 Finding percentiles by interpolation.
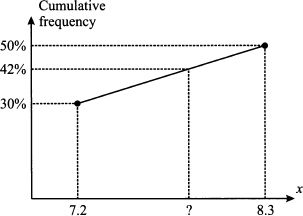
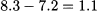
and we should move by a fraction of that interval, given by
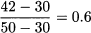
Hence, the percentile we are looking for is
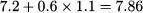
The above choice of low and high percentiles might look debatable, but it reflects the lack of knowledge about what may happen below X(1) and above X(n). Note that if we have a large dataset, X(1) will be taken as a lower percentile than in the example, reflecting the fact that with more observations we are more confident about the lowest value that observations may take; however, we seldom can claim that a value below X(1) cannot be observed. Similar considerations apply to X(n). In fact, there is little we can do about extreme values unless we superimpose a theoretical structure based on probability theory.
In practice, whatever approach we use, provided that it makes sense for the type of variable we are dealing with and the purpose of the analysis, it will not influence significantly the result for a large dataset. In the following chapters, when dealing with probability theory and random variables, we will introduce a strictly related concept, the quantile, which does have a standard definition.
4.4.1 Quartiles and boxplots
Among the many percentiles, a particular role is played by the quartiles, denoted by Q1, Q2, and Q3, corresponding to 25%, 50%, and 75%, respectively. Clearly, Q2 is simply the median. A look at these values and the mean tells a lot about the underlying distribution. Indeed, the interquartile range
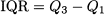
has been proposed as a measure of dispersion, and an alternative measure of skewness, called Bowley skewness, is
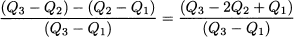
The three quartiles are the basis of a common graphical representation of data, the boxplot (also known as a “whisker diagram”). A boxplot is shown in Fig. 4.11. In the picture you may notice a box. The line in the middle of the box corresponds to the median, whereas the two edges of the box correspond to the lower and upper quartiles. Dashed lines are drawn connecting the box to two fences. The two fences should be two bounds on the “normal” values of the observed variable. Any point beyond those fences is a potential outlier.
Fig. 4.11 A boxplot with outliers.

You will not be surprised to learn that there are alternative definitions of fences, and several variations on boxplots. One possible choice is to tentatively place the lower and upper fences at points

respectively. Points beyond such fences are regarded as outliers and are represented by a cross. If there is no outlier above the upper fence, this is placed corresponding to the largest observation; the lower fence is dealt with similarly. In Fig. 4.11 a dataset consisting of positive values is represented; since no observation is flagged as an outlier on the left part of the plot, the lower fence corresponds to the smallest observation, which is close to zero.
4.5 MULTIDIMENSIONAL DATA
So far, we have considered the organization and representation of data in one dimension, but in applications we often observe multidimensional data. Of course, we may list summary measures for each single variable, but this would miss an important point: the relationship between different variables.
We will devote all of Chapter 8 to issues concerning independence, correlation, etc. Here we want to get acquainted with those concepts in the simplest way. To begin with, let us consider bidimensional categorical data. To represent data of this kind, we may use a contingency table.
Example 4.18 Consider a sample of 500 married couples, where both husband and wife are employed. We collect information about yearly salary. For each person in the sample, we collect categorical information about the gender. The quantitative information about salary is transformed into categorical information by asking: Is salary less or more than $30,000? We could express this as “high” and “low” income. We should not just disaggregate couples into two separate samples of 500 males and 500 females, as we could miss some information about the interactions between the two categorical variables. The contingency table in Table 4.9 is able to capture information about interactions. Armed with the contingency table, we may ask a few questions:
Table 4.9 Contingency table for qualitative data

- What is the probability that a randomly selected female is high-income? We have 500 wives in the sample, and 36 + 54 = 90 are high-income. Then, the desired probability14 is
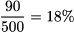
- What is the probability that a randomly selected person, of whatever gender, is low-income? Note that we have 500+500 persons, since there are 500 pairs in the sample. We have 212 pairs in which both members are low-income, and 198 + 36 pairs in which one of them is low-income. Hence, we should take the following ratio:
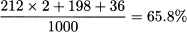
- If we pick a couple at random, what is the probability that the wife is low-income, assuming that the husband is low-income? Apparently, this is a tough question, but we may find the answer using a little intuition. There are 212 + 36 = 248 pairs in which the husband is low-income. We should restrict the sample to this subset and take the ratio
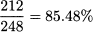
since the wife is low-income in 212 out of these 248 pairs.
- If we pick a couple at random, what is the probability that the wife is low-income, assuming that the husband is high-income? Using the same idea as the previous question, we get

In Section 5.3 we will see how the last two questions relate to the fundamental concept of conditional probability.
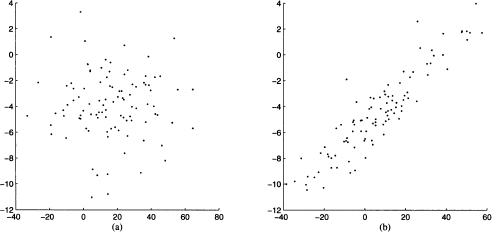
If we need to represent pairs of quantitative variables, we might aggregate them in classes and prepare corresponding contingency tables. A possibly more useful representation is the scatterplot, which is better suited to investigate the relationships between pairs of variables. In a bidimensional scatterplot, points are drawn corresponding to observations, which are pairs of values; coordinates are given by the values taken by the two variables in each observation. In Fig. 4.12 two radically different cases are illustrated. In scatterplot (a), we can hardly claim that the two variables have a definite relationship, since no pattern is evident; points look completely random. Scatterplot (b) is quite another matter, as it seems that there is indeed some association between the two variables; we could even imagine drawing a line passing through the data. This is what we do in Chapter 10, where we take advantage of this kind of association by building linear regression models.
Fig. 4.12 Two scatterplots illustrating data dependence.
Contingency tables and scatterplots work well in two dimensions, but what if we have 10 or even more dimensions? How can we visualize data in order to discern potentially interesting associations and patterns? These are challenging issues dealt with within multivariate statistics. One possibility is trying to generalize the analysis for two dimensions. For instance, we may arrange several scatterplots according to a matrix, one plot for each possible pair of variables. As you may imagine, these graphical approaches can be useful in low-dimensional cases but they are not fully satisfactory. More refined alternatives are based, e.g., on the following approaches:
- We can reduce data dimensionality by considering combination of variables or underlying factors.
- We can try to spot and classify patterns by cluster analysis.
Data reduction methods, including principal component analysis, factor analysis, and cluster analysis, are dealt with in Chapter 17.
Problems
4.1 You are carrying out a research about how many pizzas are consumed by teenagers, in the age range from 13 to 17. A sample of 20 boys/girls in that age range is taken, and the number of pizzas eaten per month is given in the following table:
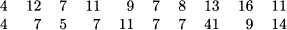
- Compute mean, median, and standard deviation.
- Is there any odd observation in the dataset? If so, get rid of it and repeat the calculation of mean and median. Which one is more affected by an extreme value?
4.2 The following table shows a set of observed values and their frequencies:

- Compute mean, variance, and standard deviation.
- Find the cumulated relative frequencies.
4.3 You observe the following data, reporting the number of daily emergency calls received by a firm providing immediate repair services for critical equipment:

- Compute mean, mode, and quartiles.
- Find the cumulated relative frequencies.
4.4 Management wants to investigate the time it takes to complete a manual assembly task. A sample of 12 workers is timed, yielding the following data (in seconds):
- Find mean and median; do you think that the data are skewed?
- Find the standard deviation.
- What is the percentile rank of the person who took 20.1 seconds to complete the task?
- Find the quartiles, using the second approach that we have described for the calculation of percentiles.
- Suppose that management want to define an acceptable threshold, based on the 90% percentile; all workers taking more than this time are invited to a training session to improve their performance. Find this percentile using the interpolation method.
4.5 Professors at a rather unknown but large college have developed a habit of heavy drinking to forget about their students. The following data show the number of hangovers since the beginning of semester, disaggregated for male and female professors:

- Given that the professor is a female, what is the probability that she had a hangover twice or more during the semester?
- What is the probability that a professor is a male, given that he had a hangover once or less during the semester?
For further reading
- All introductory books on statistics offer a treatment of the essentials of descriptive statistics; a couple of examples are Refs. [3] and [4], which have also inspired some of the examples in this chapter.
- We did not cover at all the issues involved in designing and administering questionnaires for population surveys; they are dealt with at an introductory level in the text by Curwin and Slater [1].
- The graphical representation of multivariate data is dealt with, e.g., in the book by Härdle and Simar [2].
- Example 4.13 is based on H. Pottel, Statistical flaws in Excel. This unpublished paper may be downloaded from a few Webpages, including http://www.mis.coventry.ac.uk/~nhunt/pottel.pdf.
REFERENCES
1. J. Curwin and R. Slater, Quantitative Methods for Business Decisions, 6th ed., Cengage Learning EMEA, London, 2008.
2. W. Härdle and L. Simar, Applied Multivariate Statistical Analysis, 2nd ed., Springer, Berlin, 2007.
3. M.K. Pelosi and T.M. Sandifer, Elementary Statistics: From Discovery to Decision, Wiley, New York, 2003.
4. S.M. Ross, Introduction to Probability and Statistics for Engineers and Scientists, 4th ed., Elsevier Academic Press, Burlington, MA, 2009.
1 In practice, to obtain acceptable results with a small sample, we resort to stratification, i.e., we build a sample that reflects the essential features of overall population. In this book we will only deal with simple random samples.
2 Intervals and real vs. integer numbers are introduced in Section 2.2. We will avoid considering pathological cases such as the sequence xk = 1 - 1/k, k = 1,2,3, …, where a countably infinite number of values is contained in a bounded interval.
3 See http://www.sec.gov/info/edgar/siccodes.htm
4 The formula used to convert Celsius degrees to Fahrenheit is F = (9/5) x C + 32.
5 Actually, too handy a formula may be dangerous if not properly understood and misused. A notable example is the celebrated Black–Scholes–Merton formula for pricing options.
6 That applies to physics, too; computational procedures to simulate physical systems are always based on some form of discretization, including discretization of time.
7 Time series, including seasonal ones, are dealt with in Chapter 11.
9 See Section 2.2.2 for the definition of open and closed intervals.
10 To avoid these abrupt changes we can smooth data using so-called kernel density functions; this is beyond the scope of this book, and we refer the reader, e.g., to Chapter 1 of Ref. [2].
11 There are alternative definitions of skewness in descriptive statistics. Later, we will see that there is a standard definition of skewness in probability theory; see Section 7.5.
12 Indeed, one of the most abject uses of statistics is using it to enforce some pattern on students’ grades. As someone put it a while ago, there are lies, damned lies, and statistics.
13 The careful reader will find this line of reasoning somewhat unconvincing, as the same observation could be applied to population variance. The true reason is that sample variance is used as an estimator of the true unknown variance, and the estimator is biased, i.e., is subject to a systematic error, if we divide by n rather than n - 1, as we prove in Section 9.1.2.
14 Formally, we have not introduced probabilistic concepts yet, but we already know that relative frequencies may be interpreted as intuitive probabilities.