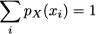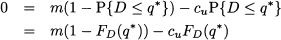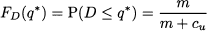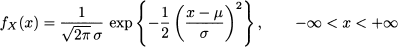Chapter 7

Continuous Random Variables

In the previous chapter we have gained the essential intuition about random variables in the discrete setting. There, we introduced ways to characterize the distribution of a random variable by its PMF and CDF, as well as its expected value and variance. Now we move on to the more challenging case of a continuous random variable. There are several reasons for doing so:

• Some random variables are inherently continuous in nature. Consider the time elapsing between two successive occurrences of an event, like the request for service or a customer arrival to a facility. Time is a continuous quantity and, since this timespan cannot be negative, the support of a random variable modeling this kind of uncertainty is [0, +∞).
• Sometimes, continuous variables are used to model variables that are actually integers. As a practical example, consider demand for an item; a low-volume demand can be naturally modeled by a discrete random variable. However, when volumes are very high, it might be convenient to approximate demand by a continuous variable. To see the point, imagine a demand value like d = 2.7; in discrete manufacturing, you cannot sell 2.7 items, and rounding this value up and down makes a big difference; but what about d = 10,002.7? Quite often this turns out to be quite a convenient simplification, in both statistical modeling and in decision making.1
• Last but not least, in the next chapters on statistical applications, the most common probability distribution is, by far, the normal (or Gaussian) distribution, which is a continuous distribution whose support is the whole real line = (-∞, +∞). As we will see, there are several reasons why the normal distribution plays a pivotal role in statistics.

This chapter extends the concepts that we have introduced for the discrete case, and it also presents a few new ones that are better appreciated in this broader context. The mathematical machinery for a full appreciation of continuous random variables is definitely more challenging than that required in the discrete case. However, an intuitive approach is adequate to pursue applications to business management. Cutting a few corners, the essential difficulty in dealing with continuous random variables is that we cannot work with the probability P(X = x), as this is always zero for a continuous random variable. Unlike the discrete case, the probability mass is not concentrated at a discrete set of points, but it is distributed over a continuous set, which contains an infinite number of points even if the distribution support is a bounded interval like [a, b]. The role of the PMF is played here by a probability density function (PDF for short). Furthermore, the sums we have seen in the discrete context should be replaced by integrals.

Integrals were introduced in Section 2.13; we do not really need any indepth knowledge, as integrals can be just interpreted as areas. In Section 7.1 we pursue an intuitive approach to see the link between such areas and probabilities. Then, we introduce density functions in Section 7.2, where we also see that the concept of cumulative distribution function (CDF) needs no adjustment when moving from discrete to continuous random variables. We see how expected values and variances are applied in this context in Section 7.3. Then, we expand our knowledge about the distribution of random variables by considering their mode, median, and quantiles in Section 7.4, and higher-order moments, skewness, and kurtosis in Section 7.5. All of these concepts apply to discrete random variables as well, but we have preferred to treat them once in the most general setting. As you can imagine, there is a remarkable variety of continuous distributions that can be applied in practice; we may use theoretical distributions whose parameters may be fit against empirical data, or we may just come up with an empirical distribution reflecting the data. In Section 7.6 we outline the main theoretical distributions – uniform, beta, triangular, exponential, and normal distributions – and we hint at how empirical distributions can be expressed. In Section 7.7 we take a first step toward statistical inference by considering sums of independent random variables; this will also lead us to the cornerstone central limit theorem, as well as a few more distributions that can be obtained from the normal and also play a pivotal role in inferential statistics; we will also have a preview of the often misunderstood law of large numbers. We illustrate a few applications in Section 7.8, with emphasis on quantiles of the normal distribution; what is remarkable, is that the very same concepts can be put to good use in diverse fields such as supply chain management and financial risk management. Finally, we consider sequences of random variables in time, i.e., stochastic processes, in Section 7.9. Section 7.10 can be skipped by most readers, as it has a more theoretical nature: Its aim is to clarify a point that we did not really investigate in the previous chapter, when we defined a random variable, i.e., the relationship between the random variable and the event structure of the underlying probability space.

7.1 BUILDING INTUITION: FROM DISCRETE TO CONTINUOUS RANDOM VARIABLES

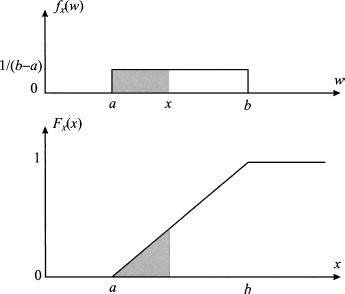
The most natural way to characterize a discrete distribution is by its PMF, which can be depicted as a set of bars whose height is the probability of each value. What happens when we consider a random variable that may take any real value on an interval? A starting point to build intuition is getting back to descriptive statistics and relative frequency histograms. Imagine taking a sample of values, which are naturally continuous, and plotting the corresponding histogram of relative frequencies. The appearance of the histogram depends on how large the bins are. If they are rather coarse intervals, the histogram will look extremely jagged, like the one in Fig. 7.1(a). If we shrink the bins, we get thinner bars, looking like the histogram (b) in the figure. Please note that all of the histograms in Fig. 7.1 refer to the same set of data. You may also notice that the relative frequencies in the second case are lower than in the first one; this happens because there are more bins, and we assign fewer outcomes to each one. In the limit, if the bins get smaller and smaller and the sample size is large, we will get something like histogram (c) in the figure. This looks much like a continuous function, describing where sampled values are more likely to fall, whereas the PMF is just a set of values on a discrete set of points.

To make this idea a bit more precise, let us consider a continuous uniform distribution, which is arguably the simplest distribution we can think of. We got acquainted with the discrete uniform distribution in Section 6.5.2. If we consider a continuous uniform variable on the interval [a, b], we should have a “uniform probability” over that interval, as depicted in Fig. 7.2. Given a point x in the interval, what is the probability that the random variable X takes that value, i.e., P(X = x)? Whatever this value is, it must be the same for all of the points in the interval. We know from Section 6.5.2 that in the discrete case p = 1/n, where n is the number of values in the support, but here we have an infinite number of values within the bounded interval [a, b]. Intuitively, if n → +∞, then p = 1/n → 0. Moreover, if we assign any strictly positive value to p, the sum of probabilities will go to infinity, but we know that probabilities should add up to 1. It is tempting to think that the root of the trouble is that we are dealing with a support consisting of infinitely many possible values. However, this is not really the case. In Section 6.5.6, we considered the Poisson distribution, which does have an infinite support. However, since probabilities vanish for large values of the random variable, their sum does converge to 1. This is not possible here, as we are considering a uniform variable. It seems that there is no way to assign a meaningful probability value to a single outcome in the continuous case.

Fig. 7.1 Frequency histograms for shrinking bin widths.

Fig. 7.2 A uniform distribution on the interval [a, b].

However, there is a way out of the dilemma. We can assign sensible probabilities to intervals, rather than single values. To be concrete, consider a uniform random variable on the interval [0, 10], which is denoted by X ~ U(0, 10). Common sense suggests the following results:

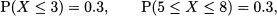
as in both cases we are considering an interval whose length is 3, i.e., 30% of the whole support. Notice that this probability depends on the width of the interval we consider, not on its location; indeed, this is what makes a distribution uniform, after all. More generally, it seems that if we consider an interval of width w included in [0, 10], the probability that X falls there should be the ratio between w and the width of the whole support: w/10. By the way, we recall from elementary geometry that a point has “length” zero; hence, we begin to feel that in fact P(X = x) = 0 for any value x.

So far, so good, but what about a nonuniform distribution, like that in Fig. 7.3? If we consider several intervals of the same width, we cannot associate the same probability with them. Probability should be related to the height of the distribution, which is not constant. Hence, the length of subintervals will not do the trick. Nevertheless, to keep the shape of the distribution duly into account, we may associate probability of an interval with the area under the distribution, over that interval. The concept is illustrated in Fig. 7.4. If we shift the interval [a, b] in the uniform case, we always get the same area, provided that the interval is a subset of the whole support; if we do the same in the bell-shaped case, we get quite different results. We start seeing that probabilities in the continuous case

Fig. 7.3 A bell-shaped, nonuniform distribution.

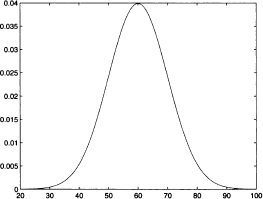
Fig. 7.4 Linking probability to areas.

1. Are distributed, whereas they are concentrated at a discrete set of points in the discrete case; we cannot work with a probability mass function associating single values x with the probability P(X = x) = 0.

2. May be associated with areas below a function that replaces the PMF, but plays a similar role; this function is the probability density function (PDF). We will denote the PDF of random variable X as fX(x).

To wrap up our intuitive reasoning, we should state one fundamental property of the PDF. When dealing with discrete variables, we know that probabilities add up to 1:

(7.1)

For continuous variables, it must be the case that

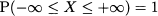
implying that the overall area below the PDF must be 1. But we also recall from Section 2.13 that this area can be expressed by an integral. Therefore, condition (7.1) should be replaced by

(7.2)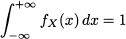

If we are dealing with a uniform variable with support [a, b], then

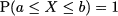
This is just a condition on the area of a rectangle with one edge of length (b - a), and the other one corresponding to the value of the PDF. Therefore:

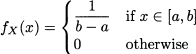
If the support is the interval [0, 10], then

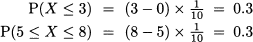
as expected. With more general distributions, we have some more technical difficulties in calculating areas, but there are plenty of statistical tables and software packages taking care of this task for us.

7.2 CUMULATIVE DISTRIBUTION AND PROBABILITY DENSITY FUNCTIONS

A full characterization of discrete random variables can be given in terms of PMF or CDF. They are related, as the CDF can be obtained from the PMF by summing, and we can go the other way around by taking differences. For the reasons we have mentioned, in the continuous case the role of the PMF is assumed by a probability density function, whereas the CDF is defined in exactly the same way:2

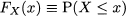
As we have pointed out, the PDF is a nonnegative function fX(x) that does not give the probability of a single value, but can be used to evaluate probabilities of intervals:

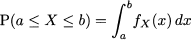
Then, it is easy to see the link between PDF and CDF:

(7.3)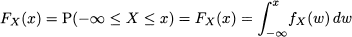

Since the PDF is nonnegative, the CDF is a nondecreasing function:

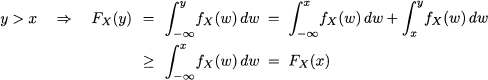
Furthermore

The last property is just another way to express the normalization condition on the PDF:

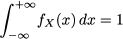
We may observe a few similarities between CDFs of discrete and continuous random variables:

• The CDF is a nondecreasing function ranging from 0 to 1.
• We obtain CDF by summing probabilities expressed by the PMF of discrete random variables, and by integrating the PDF of continuous random variables; since the integral is, in a sense, a sort of continuous sum, this is not surprising.

The main difference is that, unlike the discrete case, the CDF of a continuous random variable is a continuous function, as illustrated in the following example.

Example 7.1 To illustrate the link between CDF and PDF, consider the PDF of a uniform distribution:

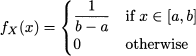
Clearly, the event {X ≤ a} has zero probability; hence, we should expect that FX(x) = 0 x ≤ a. Indeed

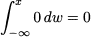
For a ≤ x ≤ b, we have

(7.4)

Finally, FX(x) = 1 for x ≥ b. Both PDF and CDF of a uniform distribution are illustrated in Fig. 7.5.

Fig. 7.5 From PDF to CDF in the case of a uniform distribution.

From the example, we see that since the CDF is the integral of the PDF, it is a continuous function, even if the PDF has some kinky point. On the contrary, the CDF in the discrete case jumps because the probability mass is concentrated at a discrete set of points, rather than being distributed on a continuous support.

We may also better understand why the probability of any specific value is zero for continuous random variables:

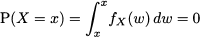
As a consequence, in the continuous case, we obtain

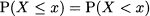
Another point worth mentioning is that

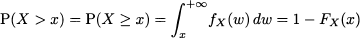
As a final remark, we recall that in the discrete case we may go from CDF to PMF by taking differences. With continuous random variables, the equivalent operation is taking the derivative of the CDF. Indeed, we may also write P(a ≤ X ≤ b) as

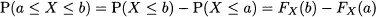
which implies

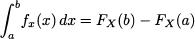
Recalling the fundamental theorem of calculus,3 we conclude that

(7.5)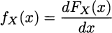

7.3 EXPECTED VALUE AND VARIANCE

Given a continuous random variable X and its PDF fX(x), its expected value is defined as follows:

(7.6)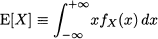

Quite often, we use the short-hand notation μX = E[X]. Again, this is a straightforward extension of the discrete case, where E[X] = ΣixipX(xi).

Example 7.2 As an illustration, let us consider the expected value of a uniform random variable on [a, b]. Symmetry suggests that the expected value should be the midpoint of the support. Indeed

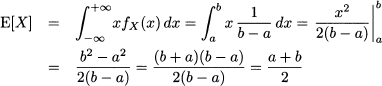
By the same token, we define variance of a continuous random variable as:

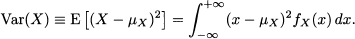
Common shorthand notations for variance are σ2 and σX2; its square root σX is standard deviation. More generally, we define the expected value of a function g(X) of a random variable as

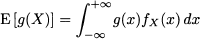
The considerations we made about expected values of discrete random variables apply here as well. Since integration is a linear operator,4 just like the sum, expectation is linear in the continuous case, too. All of the properties of expectation and variance, that we have introduced for the discrete case, carry over to the continuous case. In particular, we recall the following very useful properties:

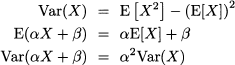
where α; and β are arbitrary real numbers.

7.4 MODE, MEDIAN, AND QUANTILES

In the chapter on descriptive statistics, we have introduced concepts like mode, median, and percentiles. We have also remarked that some concepts, in particular the percentiles, are somewhat shaky in the sense that there are slightly different definitions and ways of calculating them using observed data. In this section we examine probabilistic counterparts of these concepts, and how they are related to discrete and continuous random variables.

Fig. 7.6 A bimodal PDF.

7.4.1 Mode

The mode of a probability distribution is a point at which the PMF or the PDF is maximized. The concept is easy to grasp, but we should point out that the mode for a continuous random variable is not the value with maximum probability, since probabilities of all possible values are just zero. On the contrary, the interpretation for discrete variables is closer to the intuitive concept that we introduced along with descriptive statistics.

The mode need not be unique in principle, as multiple maxima are possible. Most of the theoretical distributions we examine later in this chapter have a single mode, but, in practice, we may find multimodal distributions in the sense illustrated in Fig. 7.6. We have a well-defined mode, but there is a secondary local maximum. If the distribution is built by fitting against empirical data, it may be the case that the secondary mode is just sampling noise. However, we should never discard the possibility that we really need a sort of mixed distribution to model different dynamics of a phenomenon.

7.4.2 Median and quantiles for continuous random variables

Roughly speaking, the median is a value splitting a dataset into two equal parts. When dealing with continuous random variables, we find that the median is a value mX such that

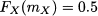
Geometrically, the median splits the PDF in two parts with an area equal to 0.5. In descriptive statistics, the median can be regarded as a specific case of percentile that corresponds to a 50% probability. In probability theory, the term is usually replaced by quantiles.

DEFINITION 7.1 (Quantiles of continuous random variable) Given the CDF FX (x) of a continuous random variable and a probability level α;

Fig. 7.7 Probability and quantiles for a continuous random variable.

[0, 1], we define the quantile xα of the distribution as the number satisfying the equation

(7.7)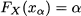

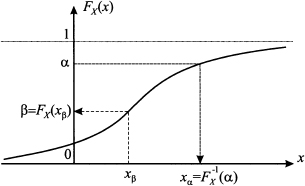
Geometrically, the quantile xα is a number leaving an area α; to its left, under the PDF. Conceptually, computing a quantile requires inversion of the CDF, as illustrated in Fig. 7.7. Be sure to understand this figure, as quantiles play a prominent role in many applications to follow:

1. Given a value xβ, we may find the corresponding probability β = P {X ≤ xβ} by evaluating the CDF FX(xβ).

2. Given a probability α, we may find the corresponding quantile α; = F−1 X(α), which is a value, by inverting the CDF.

A natural question is if the CDF is in fact an invertible function. In most cases, when dealing with continuous random variables, the CDF is a strictly increasing and continuous function; hence, inverting the function poses no difficulty. When support is infinite, we cannot really find quantiles corresponding to probabilities 0 and 1, and we should set x0 = - ∞ and x1 = +∞. There is no guarantee of finding a unique quantile, as the CDF may be a nondecreasing function that is constant on certain intervals, rather than a strictly increasing function. This may happen if the support of the distribution consists of disjoint intervals.

Example 7.3 Consider values xa < xb < xc < xd and a continuous random variable X whose support consists of the disjoint intervals [xa, xb] and [xc, xd]. Since X cannot assume values between xb and xc, the CDF is constant on the interval [xb, xc], and FX(xb) = FX(xc) = α, for some probability value α. Clearly, the quantile xα seems undefined, since the function is noninvertible on that interval.

The example may look somewhat pathological, but in fact this is what happens with discrete random variables. This is why quantiles need to be defined in a more general way.

Table 7.1 PMF and CDF for the discrete probability distribution of Example 7.4.

7.4.3 Quantiles for discrete random variables

Computing quantiles for a discrete random variable by applying Definition 7.1 would require inverting the CDF. However, this is a piecewise constant function, featuring jumps at each value of the distribution support, which makes its inversion impossible in general.

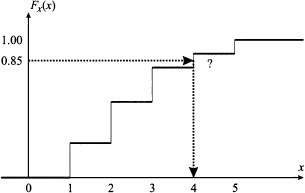
Example 7.4 Consider random demand for a spare part, sold in low volumes, over the next time period. There is no inventory at present, and we must determine the purchased quantity, in such a way that the probability of satisfying the whole demand is above a minimal threshold. Assume that randomness in demand can be modeled by the PMF of Table 7.1, and that we would like to meet demand with a probability of 0.85. In the parlance of supply chain management, we should say that our service level is 85%.5 The purchased amount should correspond to the quantile with 0.85 probability level. A look at Table 7.1 shows that there is no value of x such that FX(x) = 0.85. Indeed, the function is not invertible, as illustrated in Fig. 7.8. What would one do in practice? The sensible solution, since x = 3 gives only a 80% service level, is to select x = 4 to meet the required constraint.

Fig. 7.8 The CDF for a discrete random variable is not invertible.

What we have done in the example above makes sense: The quantile is related to a decision, and we make it in such a way to stay on the safe side. In fact, Definition 7.1 can be generalized as follows.

DEFINITION 7.2 (Generalized definition of quantiles) Let FX(x) be the CDF of random variable X. Given a probability level α; [0, 1], we define the quantile xα of the distribution as the smallest number xα such that FX(xα) ≥ α. Formally

(7.8)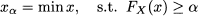

We immediately see that if the CDF is invertible, this definition boils down to the previous one. Indeed, Eq. (7.8) corresponds to the so-called generalized inverse function. The reader is urged to check that applying this definition, we do find the decision we chose in Example 7.4. Unlike percentiles, quantiles of probability distributions have a precise definition that makes perfect sense, as we will see in the applications described later in Section 7.8. Before proceeding with theoretical concepts, it is worth pausing a little and check a remarkable example.

7.4.4 An application: the newsvendor problem again

In Example 6.9 we have considered and solved numerically a hypothetical instance of the newsvendor problem. The procedure was based on brute force and did not provide us with any valuable insight into the structure of the problem itself. Furthermore, if we approximate the distribution of demand by a continuous distribution, which makes sense for high sale volumes, we cannot try any possible value. An analytical solution would definitely be more elegant and useful. An easy way to find it is based on marginal analysis.6 Say that we have purchased q - 1 items. Should we buy one more?

We recall that profit margin of one sold unit is given by m = s - c, i.e., selling price minus purchasing cost. If a unit remains unsold at the end of the sale time window, we incur a cost cu = c - su, i.e., purchasing cost minus markdown price, the cost of unsold items. If we buy unit number q, we might incur a cost cu; if we do not buy it, we might miss the profit margin m. We should figure out if we expect that this marginal unit is profitable or not. To attach probabilities to events, observe that the marginal unit will contribute m if demand D is at least q; otherwise, it will reduce profit by cu. Hence, the expected marginal profit is

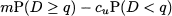
Note that if demand is a discrete random variable, we should be careful with the inequalities, as in that case the probability P(D ≥ q) is different from P(D > q); if demand has continuous distribution, we may be sloppy with the inequalities. If the expected marginal profit is positive, we should buy one more item; otherwise, we should not. Hence, we must find an optimal quantity q* such that

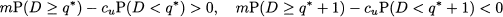
The task is considerably simplified by assuming that demand is a continuous random variable. Then, expected marginal profit can be regarded as the first-order derivative of expected profit, and the optimal solution can be found by enforcing the first-order necessary condition for optimality:

(7.9)

where FD (·) is the CDF of demand. This in turn implies that

(7.10)

To be precise, we should also check the second-order derivative, since stationarity alone cannot tell a minimum from a maximum. We may recall that the derivative of the CDF is just the PDF. Hence, if we differentiate Eq. (7.9), we obtain

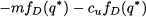
which is certainly negative, since the PDF is positive.7

By using Eq. (7.10), it is not only easy to find the optimal ordering quantity; we also gain a fundamental insight into the problem structure:

1. First we compute the ratio m/(m + cu), which can be interpreted as the probability of satisfying the whole demand, i.e., the service level.

2. Then we find the quantile corresponding to that service level.

We should note that, since m and cu are positive, the ratio is bounded by the interval [0, 1]. Since the CDF is monotonically increasing, we order more (and raise the service level) when m is large with respect to cu. We order less when profit margin is small, or when the cost of unsold items is too large. This is not too surprising and explains the different patterns that we observe at different retail shops, depending on what they sell. An obvious question is: When is it optimal to order the expected value of demand? If the distribution is symmetric, the expected value is just the median. We will order the median if the optimal service level is 50%, which happens when m = cu.

Example 7.5 Let us solve Example 6.9 by assuming, this time, a continuous uniform distribution on the interval [5, 15]. With the data of the problem, we have m = 25 - 20 = 5 and cu = 20 - 0 = 20. Hence, the optimal service level is 5/(5 + 20) = 20%. Using Eq. (7.4) for the CDF of the continuous uniform distribution, we find

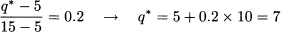
By sheer luck, we get the same integer solution we found by brute force in the discrete case. In general, the value q* is not integer, and we have to check whether it is optimal to round it up or down.

The classical newsvendor problem has an easy and elegant solution, but we should not forget the limitations of the underlying model:

• We are assuming that any leftover item can be sold at the markdown price su, independently of the amount of unsold items; in practice, mark-down management procedures may be necessary.8
• We are assuming that the expected value of profit is a sensible objective. While this might make sense in the long run, sometimes risk aversion should be taken into account (see Section 13.2).

Despite all of these limitations, the basic newsvendor model is am extremely useful model for building intuition and can be generalized in many ways. A rather surprising fact is that the reasoning above, based on marginal analysis, can be applied in completely different settings.

Example 7.6 We consider here the simplest model for revenue management in the airline industry (we considered overbooking strategies in Example 6.13). This model is known as Littlewood’s two-class, single-capacity control model.9 Assume that we may sell tickets at two different prices, p1 and p2, with p1 > p2. The two prices correspond to two different classes of customers: Class 2 consists of passengers reserving their flight well in advance, maybe because they are planning their holidays. Class 1 consists of business travelers, flying because of business engagements that might pop up at the last minute. Business travelers are typically willing to pay much more for a flight, and this is why they are charged a higher price. Clearly, we are uncertain about the’ two demands for seats, but we imagine that a probability distribution for the two demands is known (we also assume that demands of the two classes are independent random variables). According to our assumptions, the demand D2 from passengers of class 2 is realized before demand D1 from class 1. If we satisfy all of the requests of class 2 (up to capacity C of the aircraft), we may regret our decision if it turns out that

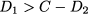
In such a case, had we reserved more seats to class 1 by rejecting demand from class 2 beyond some threshold level, we would have made more money by selling some seats at a price p1 > p2. Hence, we can define a &#x201C;protection level,&#x201D; which is the capacity reserved for passengers of class 1. Of course, if the protection level is set too high, we could regret our decision as well, if we turn down too many requests from class 2, only to find later that demand D1 is low and seats are left empty.

Rather surprisingly, the problem can be tackled much along the lines of the newsvendor problem by marginal analysis. Let us denote the reservation level by y1, i.e., the number of seats reserved to class 1. Let us also denote by F1(·) the CDF for demand from class 1. Say that a customer of class 2 requests a seat when the remaining capacity is y1. Should we accept or reject the offer? To answer the question, we should trade off a sure revenue p2 against an uncertain revenue p1. This revenue is uncertain, because we will make p1 only if demand D1 is at least y1. We should accept the request if

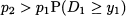
and we should reject it otherwise. If we assume a continuous distribution for D1 the optimal protection level y*1 is exactly where the two amounts above are the same:

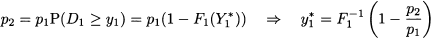
To check the solution, observe that y*1 is large when p2 is small with respect to p1; in the limit, if p2/p1 goes to zero, the protection level is the aircraft capacity and all of the requests from class 2 will be rejected.

We should stress that both basic newsvendor and Littlewood’s models are rather crude simplifications of reality. Nevertheless, they do provide us with essential intuition and can be extended to cope with more realistic models of actual problems.

7.5 HIGHER-ORDER MOMENTS, SKEWNESS, AND KURTOSIS

Expected value and variance do not tell us the whole story about a random variable. To begin with, they do not say anything about the possible lack of symmetry. From descriptive statistics, we know that to characterize symmetry of a distribution, or lack thereof, we need a coefficient measuring its skewness. Furthermore, we may have distributions according to which extreme events, like huge losses due to a stock market crash, are pretty rare, and distributions in which they are not that unlikely. The probability of extreme realizations of random variables depends on the probability mass associated with the tails of the distribution. Needless to say, when dealing with risk management we do need measures taking these features into account. They all rely on the definition of a more general concept, moments of a random variable.

DEFINITION 7.3 (Moments of a random variable) The moment of order k of random variable X is defined as E[Xk]. The central moment of order k is defined as E[(X - μx)k].

We immediately see that expected value is just the first-order moment, whereas variance is the second-order central moment. To characterize deviations with respect to the expected value, we need an even-order moment, to avoid cancelation between positive and negative deviations. But in order to capture lack of symmetry, we need just that, which is captured by a central moment of odd order. Furthermore, in order to capture fat tails, we need higher-order moments than just the second one. This motivates the following definitions.

DEFINITION 7.4 (Skewness and kurtosis) Skewness is defined as

(7.11)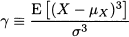

Kurtosis is defined as

(7.12)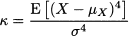

Looking at these definition, one could wonder why we should divide the moment of order k = 3, 4 by a corresponding power of the standard deviation σ. The point is that the above properties should not depend on change of scale or shifts in the underlying distribution: If we define a random variable Y = α; + βX, its skewness and kurtosis should be the same as X. It is easy to see that skewness is not changed by this linear affine transformation:

The same applies to kurtosis. In Fig. 7.9 we illustrate two asymmetric distributions. The PDF on the left is skewed to the right and has positive skew; in such a case, the median is smaller than the expected value. The PDF

Fig. 7.9 Schematic representation of positive and negative skewness.

on the right is skewed to the left and has negative skew. Figure 7.10 shows two distributions with different tail behavior. The distribution with kurtosis k = 9 has fatter tails and a corresponding lower mode. This makes sense, as the overall area below any PDF must always be 1; if tails are fatter, some probability mass is removed from the central portion of the distribution.

Fig. 7.10 Schematic representation of kurtosis.

7.6 A FEW USEFUL CONTINUOUS PROBABILITY DISTRIBUTIONS

In the following sections we describe some continuous probability distributions. The main criterion of classification is theoretical vs. empirical distributions. The former class consists of distributions that are characterized by a very few parameters; indeed, they can also be labeled as parametric distributions. Theoretical distributions will never fit empirical data exactly, but they provide us with very useful tools, as they can be justified by some assumption about the underlying randomness. Furthermore, they have PDFs in analytical form, which may help us in finding analytical solutions to a wide set of problems. On the contrary an empirical distribution will, of course, fit observed data very well, but there is a hidden danger in doing so: We might overfit the distribution, obtaining a PDF or a CDF that does fit the peculiarities of the observed sample, but does not describe the properties of the population very well.

Empirical distribution will be the last example we cover here. First we consider the few main theoretical distributions, to provide the reader with the essential feeling for them. We start from the simplest case, the uniform distribution; then we consider the triangular and the beta distributions, which may be used as rough-cut models when little information is available on the underlying uncertainty. Then we describe the exponential and the normal distributions. They play a central role in probability theory because of their properties and because they can be used as building blocks to obtain other distributions. We defer the treatment of a few distributions obtained from the normal to Section 7.7.2, as they require some background on sums of random variables.

7.6.1 Uniform distribution

We have already met the uniform distribution in Section 7.1, where we specified its PDF and CDF. To say that a random variable X is uniformly distributed on the interval [a, b], the notation X ~ U(a, b) is used. We have already shown that the expected value is the midpoint on the support:

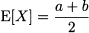
Since the uniform distribution is symmetric, the median and the expected value are the same, and skewness is zero. It can be shown that variance is

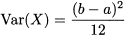
A peculiarity of the uniform distribution is that it has no well defined mode, since the PDF is constant. All of the remaining theoretical distributions have a single mode.

It is reasonable to say that the uniform distribution is a very dry model of uncertainty, as it just provides us with bounds on the possible realizations of X. It is often stated that the uniform distribution should be used whenever we have no idea about the underlying uncertainty. Actually this is a bit debatable, and the following argument has been proposed to counter this view. Suppose that the only thing we know about variable X is that it can take values between 0 and 1. Apparently, a uniform distribution U(0, 1) is an obvious choice. But now consider the variable Y = Xα, for some value α; > 0. We cannot say anything about Y, either, and the variable is bounded between 0 and 1. However, we cannot say that both X and Y are uniformly distributed. Indeed, representing almost complete ignorance is not as easy as it may seem. Nevertheless, a uniform distribution is often used in Bayesian statistics as a noninformative prior.10 Another quite relevant application of a U(0, 1) distribution is random-number generation for Monte Carlo simulation.11 When we have to simulate randomness by a computer program, we first generate a U(0, 1) variable, which is then transformed to whatever we need to model uncertainty.

7.6.2 Triangular and beta distributions

Triangular distribution is a possible model of uncertainty when limited knowledge is available. Three parameters characterize it: the extreme points of the support [a, b] and that the mode c, where a ≤ c ≤ b. The PDF for a triangular random variable is depicted in Fig. 7.11. The expected value and variance for a triangular distribution are

Fig. 7.11 PDF of a triangular distribution.

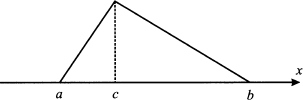
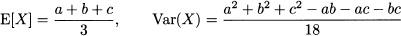
respectively.

Imagine a project planning problem, which involves tasks of quite uncertain duration. If we are able to assign the support, i.e., lower and upper bound on the time to complete a task, and a mode, we might consider using a triangular distribution. A distribution that is widely used in such applications, but featuring a better academic pedigree, is the beta distribution. This distribution has support on the interval [0, 1] and depends on two parameters, α1 and α2. Its PDF is

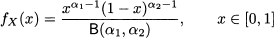
To be precise, when α1, α2 < 1, the support is the open interval (0, 1), as PDF goes to infinity at its extreme points. In the following, we will just consider the case α1, α2 > 1. The definition of the PDF involves a normalization factor B(α1, α2), the beta function, defined as

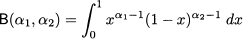
The beta distribution can be adapted to many practical cases by shifting and scaling, which results in an arbitrary support [a, b]. The expected value and variance are

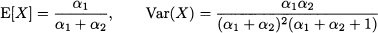
respectively. The mode, for α1, α2 > 1, is

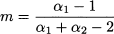
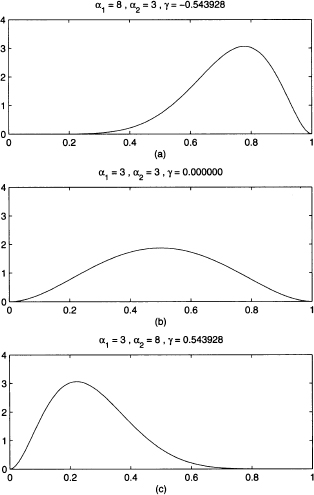
Figure 7.12 shows three examples of beta distributions, for different settings of its parameters. Looking at the PDF, we see that the distribution is symmetric when α1 = α2. Indeed, skewness is expressed as follows:

Fig. 7.12 PDF of symmetric and skewed beta distributions.

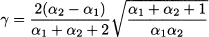
7.6.3 Exponential distribution

The exponential distribution is one the main tools used to model uncertainty, and it is related to other distributions, as well as to an important family of stochastic processes that we will investigate later. An exponential random variable can only take nonnegative values, i.e., its support is [0, +∞), and it owes its name to the functional form of its density:

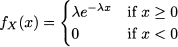
Here λ > 0 is a given parameter, and the notation X ~ exp(λ) is often used.12 Straightforward integration13 yields the CDF

(7.13)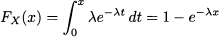

and the expected value is

It is worth noting that the expected value is quite different from the mode, which is zero. It can be shown that variance for the exponential distribution is 1/λ2, implying that the coefficient of variation is cX = 1. Figure 7.13 shows the PDF and the CDF for an exponential distribution with parameter λ = 2.

Fig. 7.13 PDF and CDF of an exponential distribution with λ = 2.

Unlike the uniform distribution, there are typically good physical reasons for adopting this distribution to model a random quantity. A common use of exponential distribution is to model time elapsing between two random events, e.g., the interarrival time between two consecutive service requests. Note that λ is, within this interpretation, a rate at which events occur, e.g., average number of service requests per unit time; the mean interarrival time is 1/λ. In fact, we often speak of exponential random variables with rate λ. There are a few important points worth mentioning:

• The exponential distribution is linked to the Poisson distribution, which we covered in Section 6.5.6. Imagine that the successive interarrival times of service requests are independent14 and exponentially distributed with rate λ, and count the number of such requests arriving during a time interval of length t. Then, the number of requests we count is a discrete random variable following a Poisson distribution with parameter λt. In Section 7.9 we will see that this phenomenon corresponds to a common stochastic process, which is unsurprisingly known as the Poisson process.
• If we sum n independent exponential variables with rate λ, we obtain a new probability distribution that is called Erlang. This distribution is also widely used in applications to model time between events.
• Probably the most important feature of an exponential random variable is its &#x201C;lack of memory.&#x201D; We will consider this property in more detail in Section 8.5.2, but we can realize its intuitive meaning and its practical relevance by considering the waiting time for the arrival of a bus at a bus stop. If we know that the time between two consecutive arrivals is uniformly distributed between, say, 2 and 10 minutes, and we have been waiting for 9 minutes, we may have a pretty clear idea about the time we still have to wait. The more we have waited in so far, the less we are supposed to wait in the future. On the contrary, if this time is exponentially distributed, the fact that we waited for a long time does not change the distribution; the distribution when we get to the bus stop and the distribution after waiting 20 minutes are the same. A full understanding of this requires concepts about independence and conditional distributions, which are provided in Chapter 8, but it is important to see the practical implication of this property. Imagine that we use the exponential distribution to model time between failures of an equipment. Lack of memory implies that even if the machine has been in use for a long time, this does not mean that it is more likely to have a failure in the near future. Note again the big difference with a uniform distribution. If we know that time between failures is uniformly distributed between, say, 50 and 70 hours, and we also know that 69 hours have elapsed since the last failure, we must expect the next failure within one hour. If the time between failures is exponentially distributed and 69 hours have elapsed, we cannot conclude anything, since from a probabilistic point of view the machine is brand new. If we think of purely random failures, due to bad luck, the exponential distribution may be a plausible model, but definitely it is not if wear is the main driving factor of failures.

7.6.4 Normal distribution and its quantiles

The normal distribution is by far the most common, and misused, distribution in the theory of probability. It is also known as Gaussian distribution, but the term &#x201C;normal&#x201D; illustrates its central role quite aptly. Its PDF has a seemingly awkward form

(7.14)

depending on two parameters, μ and σ2. Actually, we met such a function a while ago,15 and we noted its peculiar bell shape. Figure 7.14 shows two PDFs for μ = 0, and σ = 1, σ = 3. Actually, it is quite easy to interpret the PDF (7.14):

Fig. 7.14 PDF of two normal distributions.

• The initial factor is just a normalization factor, and its role is only to ensure that the area below the PDF is 1.
• The expected value is just the parameter μ; indeed, this parameter has the effect of shifting the PDF left and right.
• The variance is just the parameter σ2; indeed, this parameter has the effect of changing the scale, i.e., spreading or concentrating the bell, as we can see in Fig. 7.14.

We often use the notation X ~ N(μ, σ2) to indicate that X has normal distribution; note that the second parameter corresponds to variance, rather than standard deviation. It is very easy to see that for the normal distribution expected value (mean), mode, and median are just the same. The PDF is clearly symmetric with respect to the expected value, so skewness is zero. On the contrary, a somewhat surprising fact is that kurtosis for a normal variable is κ = 3, and it does not depend on the specific value of the parameters.

Indeed, in some books the definition of kurtosis, which we gave in Definition 7.4, is replaced by

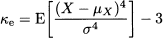
This is a surprising definition for the uninitiated, and we prefer the alternative one. The point is that the tail behavior of the normal distribution is a sort of benchmark, and it may be useful to express kurtosis of other distribution with reference to this base case. The appropriate name for is excess kurtosis.

The last point shows that all of the possible normal distributions are essentially the same in terms of tail behavior. In fact, there is something more to notice. We can transform any normal random variable into any other normal variable, with different parameters, just by a linear affine transformation. Consider a generic normal X ~ N(μ, σ2), and consider the variable

(7.15)

In terms of PDF, we are just shifting the graph and changing its scale, without changing its basic form. Using the familiar rules concerning expected values and variance, we observe the following:

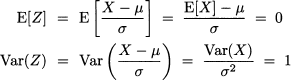
A normal variable Z ~ N(0, 1), with zero expected value and unit variance is called standard normal. The transformation (7.15) is called standardization. Actually, it applies to any distribution, as it yields a variable with zero expected value and unit variance, but it plays an important role for the normal distribution. We may also go the other way around: Given a standard normal Z, we may invert (7.15) to get an arbitrary normal by destandardization:

(7.16)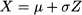

The normal distribution has many nice properties, which we will discover in the following text and justify its popularity. One unpleasing feature, though, is that its CDF cannot be calculated analytically. As we know from chapter 2, integrating the density (7.14) requires finding its antiderivative. As it turns out, this is impossible and we must resort to numerical methods to evaluate the integral and, therefore, the CDF. This poses no practical difficulty as plenty of software is available to carry out this task efficiently and with more than adequate precision. We should mention that, traditionally, any text involving probability and statistics provides the reader with tables to carry out calculations by hand.16 The trouble is that we cannot have a set of tables for any possible normal distribution. However, we can easily carry out the job once, for the standard normal, and then apply standardization and destandardization to work with an arbitrary normal.17 Tables for the standard normal provide us with values of the following CDF:

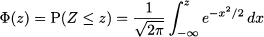
Sometimes, only the right area is tabulated:

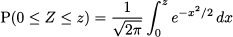
Of course, this does not change anything because of the symmetry of the PDF. Given a way to compute , we can deal with probabilities for an arbitrary normal variable X ~ N(μ, σ2). To find the probability P(X ≤ β), we should just apply standardization:

Example 7.7 Consider X ~ N(3, 16), i.e., a normal variable with expected value 3 and standard deviation 3. Let us compute P(2 < X < 7):

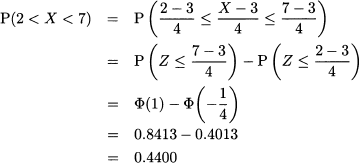
When using statistical tables, we cannot carry out the above calculation directly, as typically we are provided with values π(z) only for z ≥ 0. However, we may easily to take advantage of symmetry to compute π(- 1/4):

1. We need the area of the PDF to the left of z = -1/4.

2. Because of symmetry with respect to the expected value E[Z] = 0, this is just the area to the right of z = 1/4.

3. But this is just the probability:

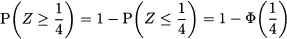
4. Hence:

The kind of gimmicks of the example above are not required anymore, if you have a decent piece of software, but they are still worth learning to really know the ropes of working with normal variables. This is also important because one of the most common tasks in statistics is the use of quantiles of normal distributions. Numerical inversion of the CDF for the standard normal, or reading statistical tables the other way around, yields the quantiles:

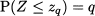
for a probability level q (0, 1). Actually, the usual notation in statistical applications is z1-α, where α; is a rather small number, like 0.1 or 0.05; geometrically, the quantile z1-α leaves an area 1 - α; of PDF to its left, and α; is the area of the right tail. This is illustrated in Fig. 7.15. From the figure, we also see that if we want to leave two symmetric tails on the left and on the right, such that their total area is α, we should consider quantile z1-α/2 and observe that

Fig. 7.15 Using quantiles of the standard normal distribution.

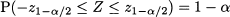
Now, we know that there is a way to find quantiles zq for the standard normal, but how can we find a quantile xq for a generic normal variable? The quick-and-dirty recipe mirrors destandardization:

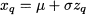
To see why this works, observe the following:

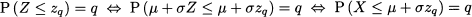
Example 7.8 Consider a normal variable X with expected value μ = 100 and standard deviation σ = 20. What is its 95% quantile? We are looking for a number x0.95 such that

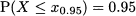
Statistical software provides us with the corresponding quantile for the standard normal distribution: z0.95 = 1.6449. Hence

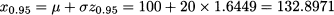
Example 7.9 (A well-known rule for the normal distribution) Given a normal variable X ~ N(μ, σ2), we might wonder how many realizations are expected to fall in an interval of the form μ ± kσ. We find

1. P(μ - σ ≤ X ≤ μ + σ) ≊ 68.26%

2. P(μ - 2σ ≤ X ≤ μ + 2σ) ≊ 95.44%

3. P(μ - 3σ ≤ X ≤ μ + 3σ) ≊ 99.74%

We see that almost all of the realizations are expected to fall &#x201C;within three standard deviations of the mean.&#x201D; In other words, the width of the interval including almost all of them is six standard deviations; indeed, a managerial philosophy has been called six sigma because of this.

This also shows that the normal distribution has rather thin tails, and this is why it serves as a benchmark in terms of kurtosis. If we observe events that go much beyond the three-sigma wall we should question the applicability of a model based on the normal distribution. A well-known example is the stock market crash of October 19, 1987. This date did deserve the name of &#x201C;Black Monday,&#x201D; as the Dow Jones Industrial Average index dropped from 2246 to 1738, a decline of almost 25% in one day. Fitting a normal distribution against index returns shows that this event was about 20 standard deviations below average. In fact, it is rather common to observe such extreme events on financial markets. On the one hand, alternative distributions have been proposed, with fatter tails, to better account for such phenomena. On the other hand, more radical approaches have been proposed, modeling the dynamic behavior of stock market participants, which are not completely rational decisionmakers. The very applicability of probability modeling to this kind of system have been questioned.18

Fig. 7.16 The CDF for an empirical distribution.

7.6.5 Empirical distributions

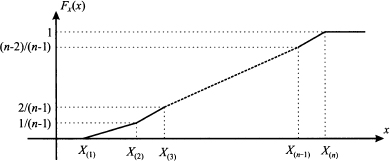
Sometimes, no theoretical distribution seems to fit available data, and we resort to an empirical distribution. A standard way to build an empirical distribution is based on order statistics, i.e., sorted values from a sample. Assume that we have a sample of n values and order statistics X(i), i = 1, …, n, where X(i) ≤ X(i+1). The value X(1) is the smallest observation and X(n) is the largest one.

Assume that we want to rule out values above and below the observed range. Then, we can write

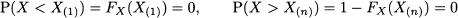
The last condition implies Fx(X(n)) = 1. Note that this is rather arbitrary; sometimes, small tails are appended to the extreme points of the observed range in order to avoid overfitting. This is, however, an arbitrary and ad hoc procedure. To assign values of the CDF for intermediate order statistics, we may simply divide the range from 0 to 1 in equal intervals, which results in the following rule:

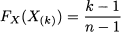
For values falling between order statistics, linear interpolation is the simplest choice and results in a CDF like the one illustrated in Fig. 7.16. Given the CDF, the PDF is obtained. Clearly, choosing linear interpolation results in a kinky CDF with nondifferentiable points. In order to get a smoother curve, we could also interpolate with higher-order polynomials.19

Once again, we should remark that fitting an empirical distribution has some hidden traps. It is easy to trust available data too much and to obtain a distribution that reflects peculiarities in the sample, which do not necessarily carry over to the whole population. Furthermore, it is sometimes possible to come up with mixtures of theoretical distributions that do fit the data and eliminate the need for arbitrary choices, e.g., as far as the support and the tail behavior are concerned.

Example 7.10 One standard reason for rejecting simple theoretical distributions is that empirical frequencies may display multiple modes. Then, it is tempting to fit whatever we have observed, but this may result in a poor understanding of the underlying phenomena. Consider, for instance, the time needed to complete surgical operations. If we take statistics about these times, quite likely we will observe multiple modes. But this might be linked to the different kinds of operations being executed, which may range from quite simple to very complex ones. It is much better to fit discrete probabilities against the different classes of operations, and then to model the variability of the time within each class around the expected value for each one.

7.7 SUMS OF INDEPENDENT RANDOM VARIABLES

A recurring task in applications is summing random variables. If we have n random variables Xi, i = 1, …, n, we may build another random variable

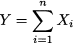
What can we say about the distribution of Y? The answer depends on two important features of the terms in the sum:

• Is the distribution of all of the Xi the same?
• Are the involved variable independent?

We will clarify what we mean by &#x201C;independent random variables&#x201D; formally in Chapter 8, but what we know about independent events and conditional probabilities is enough to get the overall idea: Two variables are independent if knowing the realization of one of them does not help us in predicting the realization of the other one.

DEFINITION 7.5 (i.i.d. variables) We say that the variables Xi, i = 1, …, n, are i.i.d. if they are independent and identically distributed.

Arguably, the case of i.i.d. variables is the easiest we may think of. Unfortunately, even in this case, characterizing the distribution of the sum on random variables is no trivial task. It might be tempting to think that the distribution of Y should, at least qualitatively, similar to the distribution of the Xi, but a simple counterexample shows that this is not the case.

Fig. 7.17 Sampling the sum of two i.i.d. uniform variables.

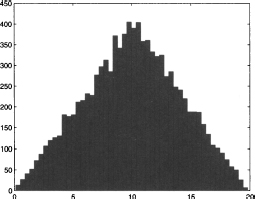
Example 7.11 Consider two independent random variables, uniformly distributed between 0 and 10: U1, U2 ~ U(0, 10). The support of their sum, Y = U1 + U2, is clearly the interval [0, 20], but what about the distribution? The analytical answer would require a particular form of integral, but we may guess the answer by sampling this distribution with the help of statistical software. Figure 7.17 shows the histogram obtained by sampling 10,000 observations of the sum. A look at the plot suggests a triangular distribution. In fact, it can be shown that the distribution of Y is triangular, with support on interval [0, 20] and mode m = 10.

By the same token, if we sum two i.i.d. exponential variables, we do not get an exponential. There is an important case in which distribution is preserved by summing.

PROPERTY 7.6 The sum of jointly normal random, variables is a normal random variable.

It is important to note that this property does not assume independence: It applies to normal variables that are not independent and have different parameters. The term &#x201C;jointly&#x201D; may be puzzling, however. The point is that characterizing the joint distribution of random variables is not as simple as it may seem. It is not enough to specify the distribution of each single variable, as this provides us with no clue about their joint behavior. The term above essentially says that we are dealing with a multivariate normal distribution, which we define later, in Section 8.4.

So, the results concerning the general distribution of the sum of random variables are somewhat discouraging, but we recall that something more can be said if we settle for the basic features of a random variable, i.e., expected value and variance. We stated a couple of properties when dealing with discrete random variables, that carry over to the continuous case.

PROPERTY 7.7 (Expected value of a sum of random variables) The expected value of the sum of random variables is the sum of their expected values, assuming that they exist:

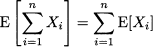
PROPERTY 7.8 (Variance of a sum of independent random variables) The variance of the sum of independent random variables is the sum of their variances, assuming that they exist:

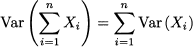
It is important to notice that the two properties above do not require variables to be identically distributed. The property about variance does require independence, however.

Example 7.12 Consider two independent normal variables, X1 ~ N(10, 25) and X2 ~ N(-8, 16). Then, the sum Y = X1 + X2 is a normal random variable, with expected value

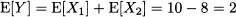
and standard deviation

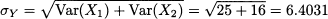
Note that we cannot add standard deviations; doing so would lead to a wrong result (5 + 4 = 9).

The example illustrates the fact that, when variables are independent, we may sum variances, but not standard deviations:

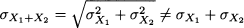
Another important remark concerns the sum and the difference between independent random variables. The property implies Var (X + Y) = Var (X) + Var (Y), but what about their difference? We must apply the property care-fully:

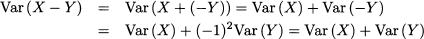
We see that the variance of a difference is not the difference of the variance; it is also worth noting that this would easily lead to nonsense, as by taking differences of variances we could find a negative variance.

7.7.1 The square-root rule

Consider a sequence of i.i.d. random variables observed over time, Xt, t = 1,..., T. Let μ and σ be the expected value and standard deviation of each Xt, respectively. Then, if we consider the sum over the T periods, Y = Σt=1T Xt, we havez

(7.17)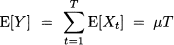

(7.18)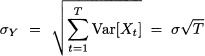

We see that the expected value scales linearly with time, whereas the standard deviation scales with the square root of time. Sometimes students and practitioners are confused by the result concerning standard deviations. It is important to draw the line between the sum of T random variables and the product of T and one random variable.

Example 7.13 Consider demand for an item, over a time interval consisting of T time buckets, say, weeks. The time interval could be delivery lead time, i.e., the time elapsing between the instant at which we issue a replenishment order and the time instant at which we receive the corresponding shipment from the supplier. In practice, demand during lead time is a relevant variable for inventory management decisions. Say that μ and σ are expected value and standard deviation of weekly demand, respectively, and assume that demands in different weeks are independent.

Then, the expected value of demand during lead time is Tμ, but its standard deviation is and not Tσ. The typical way to get the wrong result is by considering demand during lead time as a random variable

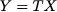
where X is a random variable corresponding to demand during one week. It is true that Var(Y) = T2Var(X), but this is the wrong reasoning; by doing so, we assume that demand during a week is realized, and then it is replicated for T weeks. But this does not correspond to the real phenomenon.

The square-root rule shows that, if T is very small, then the volatility term dominates the expected value term, as the square root of T goes to zero more slowly than T itself does, when the latter goes to zero. This has some implications for measuring financial risk, as we shall see later, but there is another hidden trap here. It is tempting to apply the rule by considering fractional values of T, but this may lead to nonsense. An example will illustrate the point.

Example 7.14 Let us assume that the yearly demand for an item is normally distributed with expected value 1000 and standard deviation 250. If the lead time is 2 months, what is the distribution of lead time demand DLT? If we assume that the year consists of 12 identical months of 30 days, and we assume that demands in different months are independent, we could consider the application of the above rules with T = 2/12 = 1/6. In terms of expected value and standard deviation, this would imply

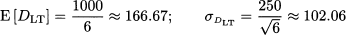
This might make some sense, but can we say that lead time distribution is normally distributed? If we recall the three-sigma rule, we note that

In fact, if we assume normality, the probability of negative demand is far from negligible. This example shows that if we assume normality of monthly demand, we may deduce normality of demand during a year, but we cannot go the other way around.

7.7.2 Distributions obtained from the normal

As we pointed out, if we sum i.i.d. random variables, we may end up with a completely different distributions, with the normal as a notable exception. However, there are ways to combine independent normal random variables that lead to new distributions that have remarkable applications, among other things, in inferential statistics. In fact, statistical tables are available for the random variables we describe below, providing us with quantiles we need to carry out statistical tests, as we will see in later chapters.

The chi-square distribution Consider a set of independent standard normal variables Zi, i = 1, …, n. Consider random variable X defined as

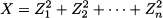
Obviously, X cannot have normal distribution, as it cannot take negative values. This distribution is called chi-square, with n degrees of freedom. This is often denoted as X ~ χn2. The following results can be proved:

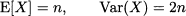
Figure 7.18 shows the PDF for chi-quare variables with 4 and 8 degrees of freedom. The second one corresponds to the PDF with the lower mode, and the higher expected value and variance.

Fig. 7.18 PDF of two chi-square variables, χ42 and χ82.

Student’s t distribution Consider a standard normal variable Z and a chi-square variable χn2 with n degrees of freedom. Also assume that they are independent. Then, the random variable

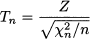
has Student’s t distribution with n degrees of freedom.20 We can show that

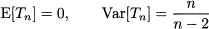
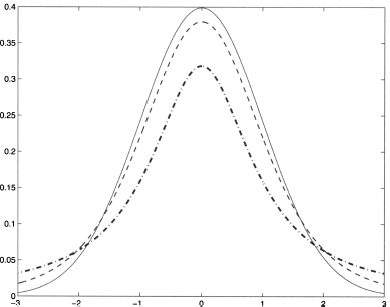
incidentally, we see that variance need not be always defined, as it may go to infinity. Figure 7.19 shows the PDFs of T1 and T5 variables, along with the PDF of standard normals. The PDF with the highest mode, drawn with a continuous line, corresponds to the standard normal; T1, represented with a dash-dotted line, features the lowest mode and the fattest tails. Indeed, the t distribution does look much like a standard normal, but it has fatter tails. When the number of degrees of freedom increases, the t distribution gets closer and closer to the standard normal. To see this quantitatively, we observe that kurtosis for the t distribution is

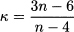
when n goes to infinity, kurtosis tends to 3, which is the kurtosis for a normal variable. Indeed, traditional statistical tables display quantiles for t variables up to n = 30, suggesting the use of quantiles for the standard normal for larger values of n. This approximation is not needed anymore, but it is useful to keep in mind that t distribution does tend to the standard normal for large values of n.

Fig. 7.19 Comparing the PDFs of two t distributions, T1 and T5 against the standard normal.

The F distribution Consider two independent random variables with chi-square distributions χn12 and χn22, respectively. The random variable

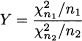
is said to have F distribution with n1 and n2 degrees of freedom, which is denoted by Y ~ F(n1, n2). Note that the degrees of freedom cannot be interchanged, as the former refers to the denominator of the ratio, the latter to its denominator.

There is a relationship between F and t distributions, which can be grasped when considering a F(1, n) variable. This involves a χ12 variable, with 1 degree of freedom, which is just a standard normal squared. Hence, what we have is

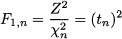
i.e., the square of a t variable with n degrees of freedom. Furthermore, when n2 is large enough, we get a Fn, ∞ variable. By the law of large numbers, that we will state precisely later, when n2 goes to infinity, the ratio χn22/n2 variable converges to the numerical value 1. Hence a Fn, ∞ variable is just a χn2 variable divided by n:

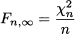
Figure 7.20 shows the PDF of a F random variable with 5 and 10 degrees of freedom. After this list of weird distributions obtained from the standard normal, the reader might well wonder why one should bother. The answer will be given when dealing with inferential statistics and linear regression, but we can offer at least some intuition:

Fig. 7.20 PDF of a F(5, 10) random variable.

• We know from descriptive statistics that the sample variance involves squaring observations; when the population is normally distributed, this entails essentially squaring normal random variables, and the distribution of sample variance is linked to chi-square variables.
• Furthermore, when we standardize a normal random variable, we take a normal variable (minus the expected value), and we divide it by its standard deviation; this leads to the t distribution.
• Finally, a common task in inferential statistics is comparison of two variances. A typical way to do this is to take their ratio and check whether it is small or large. When variances come from sampling normal distributions, we are led to consider the ratio of two chi-square variables.

Comparing the PDFs of the three distributions, we see that the t distribution is symmetric, whereas the other two have nonnegative support. This should be kept in mind when working with quantiles from these distributions.

The lognormal distribution Unlike the previous distributions, the lognormal does not stem from statistical needs, but it is worth mentioning anyway because of its role in financial applications, among others. A random variable Y is lognormally distributed if log Y is normally distributed; put another way, if Y is normal, then eY is lognormal. Since the exponential is a nonnegative function, a lognormal random variable cannot take negative values. In fact, it has often been used (and misused) as a model of random stock prices since, unlike the normal, it cannot yield negative prices.21 Another noteworthy feature of lognormal random variables is that a product of lognormals is a lognormal variable; this is a consequence of the similar property of sums of normal variables and the properties of logarithms.

The following formulas illustrate the relationships between the parameters of a normal and a lognormal distribution. If X ~ N(μ, σ2) and Y = eX, then

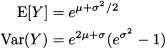
In particular, we see that

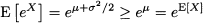
Since the exponential is a convex function, this is a consequence of Jensen’s inequality.22 Figure 7.21 shows the PDF of a lognormal variable with parameters μ = 0 and σ = 1.

7.7.3 Central limit theorem

As we noted, it is difficult to tell which distribution we obtain when summing a few i.i.d. variables. Surprisingly, we can tell something pretty general when we sum a large number of such variables. We can get a clue by looking at Fig. 7.22. We see the histogram obtained by sampling the sum of independent exponential random variables with rate λ = 0.5 or, in other words, expected value 2; the sample size is 10,000. In plot (a) we see the histogram for just one exponential variable; we observe the exponential shape that we expect. Plot (b) shows the histogram when n = 10 independent exponentials are summed; finally, plot (c) shows what happens for n = 100. The last histogram looks suspiciously like a normal density. Indeed, the celebrated central limit theorem confirms the intuition.

Fig. 7.22 Histograms obtained by sampling the sum of n independent exponentials with rate λ = 0.5, for n = 1,10, 100.

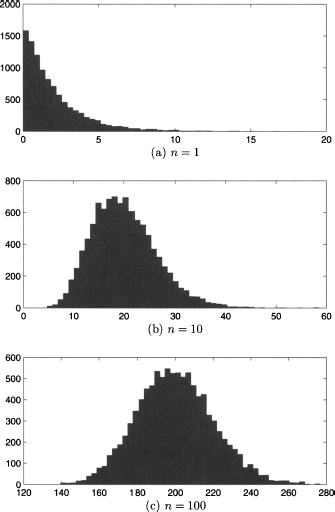
THEOREM 7.9 (Central limit theorem) Let X1 X2, …, Xn, be a sequence of i.i.d. random variables with expected μ, and standard deviation σ.

Fig. 7.21 PDF of a lognormal variable with parameters μ = 0 and σ = 1.

Then, for n large, the following holds:

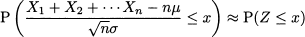
where Z is standard normal.

This theorem essentially states that the sum of n i.i.d. variables tends to a normal distribution with expected value nμ and standard deviation 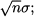by standardization we get Z.23 The central limit theorem contributes to explain why the normal distribution plays a pivotal role: When we sum many random contributions, we tend to end up with a normal distribution. For instance, demand for items sold in high volumes can often be modeled by a normal distribution, resulting from the sum of many individual demands, whereas this model is inappropriate for low-volume items.

7.7.4 The law of large numbers: a preview

The sample mean plays a key role in descriptive statistics and, as we shall see, in inferential statistics as well. In this section we take a first step to characterize its properties and, in so doing, we begin to appreciate an often cited principle: the law of large numbers.

Consider a sample consisting of i.i.d. variables Xi, i = 1, …, n, with expected value μ and variance σ2. The sample mean

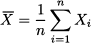
is a random variable and it is natural to wonder what is its distribution. From what we have seen, we know that a general answer does not exist. However, if the sample comes from a normal population, the sample mean is normally distributed, because the sum of normals is normal as well. Furthermore, we can rely on the central limit theorem to conclude that sample mean will tend to be normal when the sample is large enough.

Another intuitive property of the sample mean is that it should get closer and closer to the true expected value μ, when n progressively increases. Indeed, on the basis of the properties of sums of random variables, we obtain

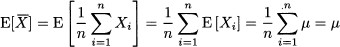
Furthermore, relying on the independence assumption, we also see that

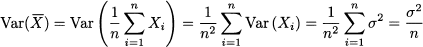
This is a remarkable result: The larger the sample size, the lower the variance of the sample mean. In the limit, this variance goes to zero; but a random variable with zero variance is just a number. Then, we may suspect that we should write something like this:

(7.19)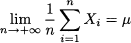

This gets close to a precise statement of the law of large numbers. Actually, stating this law precisely requires to specify all of the hidden assumptions as well. Furthermore, the limit above has no clear meaning: What is the limit of a sequence of random variables? How can a random variable tend to a number? A sound statement of the law of large numbers requires some concepts of stochastic convergence. We will outline these concepts in the advanced Section 9.8; however, most readers may skip the involved technicalities.

7.8 MISCELLANEOUS APPLICATIONS

In this section we outline a few applications from logistics and finance. The three examples will definitely look repetitive, and possibly boring, but this is exactly the point: Quantitative concepts may be applied to quite different situations, and this is why they are so valuable. In particular, we explore here three cases in which quantiles from the normal distributions are applied.

7.8.1 The newsvendor problem with normal demand

We know from Section 7.4.4 that the optimal solution of a newsvendor problem with continuous demand is the solution of the equation

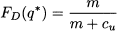
i.e., the quantile of demand distribution, corresponding to probability m/(m + cu). If we assume normal demand, with expected value μ and standard deviation σ, then the optimal order quantity (assuming that we want to maximize expected profit) is

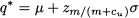
Assume that items are purchased from a supplier for $10 per item and then are sold at $15, and that the salvage value of unsold items is $3. The expected value of demand over the sales window is 10,000 items, and its standard deviation is 2000 items. Then we find

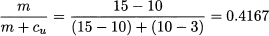
Note that service level is lower than 50%, so the corresponding quantile from the standard normal distribution is negative, and we should buy less than expected demand. Indeed, statistical software yields

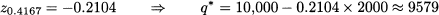
Note that, since the profit margin is low with respect to the cost of unsold items, we should be conservative; the larger the risk, measured by standard deviation, the less we buy.

7.8.2 Setting the reorder point in inventory control

Say that we are in charge of managing the inventory of a component, whose supply lead time is 2 weeks. Weekly demand is modeled by a normal random variable with expected value 100 and standard deviation 20 (let us pretend that this makes sense). If we apply a reorder point policy based on the EOQ model, we should order a fixed quantity whenever the inventory level falls below a reorder point R.24 How can we set R in order to achieve a 95% service level?

The service level in this case is the probability of not having a stockout during the delivery lead time. Note that we may run out of stock during the time window between the instant at which we issue the order to our supplier and the time instant at which items are received and inventory is replenished. Hence, we should consider the probability that demand during lead time does not exceed the reorder point R, which should be set in such a way that

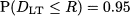
If we assume that weekly demand is normal, then we should just compute a quantile from the normal distribution again. If demands in two consecutive weeks are independent, then the distribution of the demand during lead time is normal with parameters

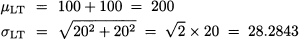
Since z0.95 = 1.6449, we should set

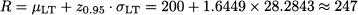
Note that, if there were no risk, we would just set R = 200. The additional 47 items we keep on stock are a safety stock. To reduce safety stock, and save money related to holding inventory, we should reduce demand uncertainty and/or lead time. This is precisely one of the cornerstones of the so-called Toyota approach, which was originally applied within the automotive industry to car manufacturing; its extension to other industries resulted in the well-known just-in-time philosophy.

7.8.3 An application to finance: value at risk (VaR)

Most financial investments entail some degree of risk. Imagine a bank holding a portfolio of assets; the bank should set aside enough capital to make up for possible losses on the portfolio. To determine how much capital the bank should hold, precise guidelines have been proposed, e.g., by the Basel committee. Risk measures play a central role in such regulations, and a commonly proposed risk measure is value at risk [VaR; please note the capitalization of letters to avoid ambiguity with variance (Var)]. It must be mentioned that bank regulation has been the subject of quite some controversy, in the wake of financial disasters following the subprime mortgage crisis of 2007–2008. In particular, VaR has been criticized as an inadequate risk measure, offering a false sense of security. It has even been suggested that VaR should not be taught at all in business schools.25 However, like it or not, VaR is used; hence, students and practitioners should be fully aware of what it is and what it is not. We will investigate VaR and its limitations further in Section 13.2.3. The first step, however, is understanding VaR in a simple setting.

Informally, VaR allows to say something like

We are X percent sure that we will not lose more than V dollars over the next N days.

We immediately see that VaR is actually a quantile of the distribution of losses. To clarify the idea, consider a portfolio consisting of a single stock: We own $10 million in Microsoft shares, and we want to estimate one-day VaR, with 99% confidence level. The simplest textbook calculation goes like this: Assume that the daily return of the stock is normally distributed. We know from the square-root rule of Section 7.7.1 that, in such a short times-pan, volatility (standard deviation) dominates drift (expected return). Then, assume that daily return is a normal variable with expected value 0% and standard deviation σd = 2%. Daily profits and losses can be expressed as the daily variation δW in our wealth:

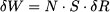
where N is the number of stocks, S their initial price, and δR the random return. We have a loss when δR < 0. If we plot the PDF of profit, losses correspond to the left tail; if we plot the PDF for loss, they are on the right tail; in the case of the normal distribution, given its symmetry, this makes no real difference. To find VaR, we need to solve the equation

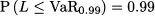
where L = -δW is loss. Given what we have seen repeatedly about quantiles of the normal distribution, we see that we should compute

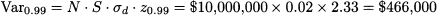
Now what about the 10-day VaR? The following reasoning is often proposed: Since volatility scales with the square root of time, it follows that

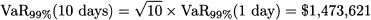
Obviously, this reasoning assumes independence in daily returns, which should certainly not be taken for granted. Furthermore, when we consider time horizons, the drift should not be neglected. More generally, we know that the normal distribution has thin tails and should not be considered a safe model of uncertainty in finance. So, the above calculation should be regarded just as a starting point. Nevertheless, it proves our point: Quantitative concepts can be used (and misused) in a variety of unrelated settings.

7.9 STOCHASTIC PROCESSES

So far, we have considered a single random variable. However, more often than not, we have to deal with multiple random variables. There are two cases in which we have to do so:

• We might observe different random variables, say, Xi, i = 1, …, n, at the same time. In such a case, we speak of cross-sectional data. As practical examples, think of the return of several financial assets over an investing horizon; alternatively, consider the demand for several items, which could be complementary or substitute goods.
• We might observe a single random variable, over multiple time periods, say, Xt, t = 1, …, T. In such a case, we speak of longitudinal data. For instance, we may observe the weekly return of a financial asset over a timespan of a few months, or daily demand for an item.

In practice, we may also have the two views in combination, i.e., multiple variables observed over a timespan of several periods. In such a case, we speak of panel data. Given the scope of this book, we will not consider panel data. If we observe cross-sectional data, and the corresponding random variables are independent, then we may just study one variable at a time, and that’s it. However, this is just a very special and simple case. We need more sophisticated tools to deal with dependence, which is the topic of the next chapter. In this section, we want to consider random variables over time.

DEFINITION 7.10 (Stochastic process) A time-indexed collection of random variables is called a stochastic process. If time is discretized, we have a discrete-time process:

(7.20)

If time is continuous, we have a continuous-time (also known as continuous-parameter) process:

(7.21)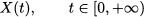

In general, one could consider a collection of random variables depending on space, rather than time. Then, we could speak of discrete- or continuous-parameter processes. In the applications we consider in the book, the parameter will always be time. In some loose sense, the stochastic process is a generalization of deterministic functions of time, in that for any value of t it yields a random variable (which is a function itself) rather than a number. If we observe a sequential realization of the random variables over time, we get a sample path of the process. In this introductory book, we will essentially deal with discrete-time processes, but it is a good idea to consider at least a simple example of a relevant continuous-time process.

Example 7.15 (Poisson process) The Poisson process is an example of a counting process, i.e., a stochastic process N(t) counting the number of events that occurred in the time interval [0, t]. Such a process starts from zero and has unit increments over time. We may use such a process to model order or customer arrivals. The Poisson process is obtained when we make specific assumptions about the interarrival times of customers. Let Xk, k = 1, 2, 3, 4, …, be the interarrival time between customer k - 1 and customer k; by convention, X1 is the arrival time of the first customer after the start time t = 0. We obtain a Poisson process if we assume that variables Xk are mutually independent and all exponentially distributed with parameter λ, which is in this case the arrival rate, i.e., the average number of customers arriving per unit time. A sample path is illustrated in Fig. 7.23; we see that the process &#x201C;jumps&#x201D; whenever a customer arrives, so that sample paths are piecewise constant.

Fig. 7.23 Sample path of the Poisson process.

We have already mentioned the link between Poisson and exponential distributions and the Poisson process. If we consider a time interval [t1, t2], with t1 < t2, then the number of customers who arrived in this interval, i.e., N(t2) - N(t1), has Poisson distribution with parameter λ(t2 - t1). Furthermore, if we consider another time interval [t3, t4], where t3 < t4, which is disjoint from the previous one, i.e., (t2 < t3), then the random variables N(t2) - N(t1) and N(t4) - N(t3) are independent. We say that the Poisson process has stationary and independent increments.

The Poisson process is a useful model for representing the random arrival of customers who have no mutual relationships at all. This is a consequence of the lack of memory of the exponential distribution.

The model can be generalized to better fit reality. For instance, if we observe the arrival process of customers at a big retail store, we easily observe variations in the arrival rate. If we introduce a time-varying rate λ(t), we get the so-called inhomogeneous Poisson process. Furthermore, if we consider not only customer (or order) arrivals, but the demanded quantities as well, we see the opportunity of associating another random variable, the quantity per order, with each customer. The cumulative quantity demanded D(t) in the time interval [0, t] is another stochastic process, which is known as a compound Poisson process. The sample paths of this process would be qualitatively similar to those in Fig. 7.23, but the size of the jumps would be random. This is a possible model for demand, when sale volumes are not large enough to warrant use of a normal distribution.

Naive thinking would draw us to the conclusion that, in order to characterize a stochastic process, we should give the distribution of Xt for all the relevant time instants t. This is what we call the marginal distribution. The following example shows that marginal distributions do not tell the whole story.

Example 7.16 (A Gaussian process) A common class of stochastic processes consists of sequences of random variables whose marginal distribution is normal, which is why they are termed Gaussian processes. To be precise, we should say that a Gaussian process requires that the random variables Xt1, Xt2, …, Xtm have a jointly normal distribution for any possible choice of time instants t1, t2, …, tm, but for the sake of simplicity we will put in the same bag any process for which the marginal distribution of Xt is normal. However, it is important to realize that in doing so we are considering processes that may be very different in nature. Consider the stochastic process

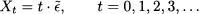
where is standard normal variable. In our loose sense, we may say that this is a Gaussian process, since Xt is normal with expected value 0 and variance t2. However, it is a somewhat degenerate process, since uncertainty is linked to the realization of a single random variable. If we know the value of Xt for a single time instant, then we can figure out the whole sample path. Figure 7.24 illustrates this point by showing a few sample paths of this process. A quite different process is obtained if all variables Xt are normal with parameters μ and σ2 and mutually independent. Figure 7.25 shows a sample path of the process . However, the marginal distributions of the individual random variables Xt are exactly the same for both processes.

Fig. 7.24 Sample paths of the stochastic process .

Fig. 7.25 Sample path of process , where .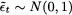

The example shows that we really need some way to characterize the interdependence of jointly distributed random variables, which is the topic of next chapter. Discrete-time stochastic processes will be discussed further in Chapter 11 on time series models.

7.10 PROBABILITY SPACES, MEASURABILITY, AND INFORMATION

Successful investing in stock shares is typically deemed a risky and complex endeavor. However, the following piece of advice seems to offer a viable solution:26

Buy a stock. If its price goes up, sell it. If it goes down, don’t buy it.

In this section we dig a little deeper into concepts related to measurability of random variables and their relationship to the flow of information and its impact on decisions. Despite their more theoretical character,27 the concepts we consider here are often met when reading books on quantitative finance, where it is common to read about filtrations and adapted processes. We will not try a full and rigorous treatment, which would require a quite sophisticated machinery; still, we will be able to understand what is wrong with the above suggestion from a probabilistic perspective, and the concepts that we illustrate should look less intimidating after getting an intuitive feel for them.

We pointed out that a random variable is actually a mapping

from a set Ω of outcomes of a random experiment to the set of real numbers . Indeed, random variables are often denoted by X(ω) to emphasize this point. However, not all conceivable mappings are legitimate random variables. To see this, we need to clarify the concept of probability space.

DEFINITION 7.11 (Probability space) A probability space is a triple, usually denoted by (Ω, F, P), where Ω, is the sample space, consisting of outcomes of a random experiment; F is a family of subsets of Ω, the events, with suitable closure properties; and P is a probability measure mapping events into the interval [0, 1].

To fully get the message behind this definition, we should observe that for a given sample space we may define different probability measures, which is not surprising, but we may also define different families of events. If we roll a die, the obvious sample space is Ω = {1,2,3,4,5,6}, and we may consider a family of events obtained by arbitrary combinations of set operations like union, complement, and intersection. This would make a rather large family of all subsets of size 1, 2, etc., also including Ω itself and its complement, the empty set π:

(7.22)

However, we may constrain events a bit in order to reflect information or lack thereof. For instance, we might consider the following family of events:

(7.23)

It is easy to check that if we try taking complements and unions of elements in F2, we still get an element of F2. Since intersection is just a combination of these two operations, we see that F2 is closed under elementary set operations. This family of events, with respect to F1, is definitely less rich, and this reflects lack of information. It is the set of events we would deal with if the only information available about the roll of the die were &#x201C;even&#x201D; or &#x201C;odd.”

When assigning a probability measure to subsets of Ω, we need to make sure that we are able to do the same for any event that we may obtain by elementary set operations. In other words, we should not get a subset that is not an event. This requirement may be expressed by requiring that F be a field.

DEFINITION 7.12 (Field) A family F of subsets of Ω is called a field if the following conditions hold:

1.

2.

3.

A field is also called an algebra of sets. The conditions in the definition state that F is closed under elementary set operations. Note that the first and second conditions imply that the empty set θ belongs to the field F.

Example 7.17 Given Ω = {1, 2, 3, 4}, consider the family of subsets

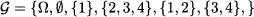
This is not a field since, for instance

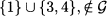
Actually, to cope with continuous random variables and more generally with probability distributions with infinite support, a stronger concept is needed: a σ-field, also called a σ-algebra. To define this stronger concept, the third condition is extended to a countable union of events:

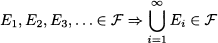
Indeed, whenever the concept infinity comes into play, pathological cases can occur. The very concept of σ-field is necessary to avoid weird cases in which it is impossible to assign a probability measure to an event. We will not be concerned with these anomalies, since we limit our treatment to a finite sample space.

Even describing a finite field by enumerating all of its subsets may be a daunting task. However, we may describe it implicitly by considering a finite partition P of Ω, i.e., a finite family of subsets Ei, i = 1, …, n, such that

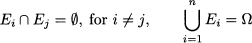
Given a partition P, we may consider the σ-field σ(P) generated by combining subsets in the partition in any possible way. In the case of (7.22), the partition consists of all singleton sets, whereas in the case of (7.23) we have the two subsets of even and odd outcomes.

Let us now turn to random variables. Given a probability space, we may define random variables as mappings of outcomes into real numbers, but we should clarify how we associate a measure probability with a random variable. Actually, we associate a probability measure with underlying events. Indeed, the probability that we assign to random variables should be associated with the underlying events in the field F. Consider a discrete random variable X and numeric value a. How can we define the probability P(X = a)? We should consider the subset of outcomes ω Ω such that X(ω) = a, which essentially amounts to inverting the function X(ω):28

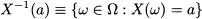
Then, the probability we seek is just the probability measure of the subset X−1(a). However, this is only possible if any such subset is an event in the σ-field F.

Example 7.18 Consider the sample space Ω = {1, 2, 3, 4} and a partition

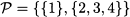
Let F = σ(P) be the field generated by this partition and define the mapping X(ω):

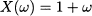
This mapping is not a random variable with respect to the field F. In fact, we cannot assign the probability P(X = 3), since

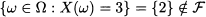
To be a random variable, a mapping Y(ω) should be constant for the three outcomes in {2, 3, 4}. For instance

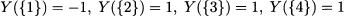
is a legitimate random variable.

What is wrong with Example 7.18 is not the mapping X(ω) per se; it is its association with the field F. If we had a richer field, generated by the partition of Ω into its singletons, there would be no issue. Technically speaking, we say that X is not F-measurable.

DEFINITION 7.13 (Measurable random variable) We say that a random variable X(ω) is F-measurable if

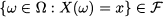
for all values of x.

In other words, the inverse function for any value x must be an event in the field F, so that we may associate a probability measure with it. This can be done or not depending on the random variable and the richness of the field of events F. If we go back to dice throwing, it is clear that if our field is given by (7.23), we can assign only one value to all even outcomes, and another value to all odd outcomes. The field is, in a sense, smaller than F1, since all the events in F2 are events in F1, but the converse is not true; this represents a limitation in the available information.

The link between event fields, measurability, and information can be further clarified if we consider a dynamic problem. Let us consider a stochastic process in the form of the event tree depicted in Fig. 7.26. To be concrete, let us interpret this as a stochastic process describing the price of a stock share. At time t = 0, the stock price is X0 = 10. Then, the price may go up or down, resulting in a stochastic process Xt, t = 0,1,2,3. In this case the sample space consists of outcomes ωi, i = 1,2, …, 8, and each outcome corresponds to a scenario, i.e., a possible path of stock prices. For instance, outcome ω3 is associated with scenario (10, 12, 11, 13). If we are at any terminal node in the scenario tree, we know which scenario has occurred, since we can observe the whole history of stock prices. However, if we are, e.g., on node n4, we do not know whether we are observing scenario ω3 or ω4, since they cannot be distinguished. Nevertheless, we do have some information, since by observing the past history of stock prices we can rule out any other scenario. In the root node n0 we have the least information, since any scenario is possible.

Fig. 7.26 An event tree.

All of this is reflected in the event fields with which random variables Xt, t = 0,1,2,3, are associated. We can capture information by suitable partitions of the sample space

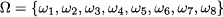
At time t = 0 we cannot say anything, and our field of events is

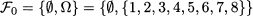
At time t = 1 we can at least rule out half of the scenarios. This is reflected by the more refined partition

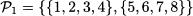
which generates the field

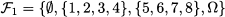
At time t = 2, there is a further branching, refining the partition

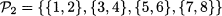
which generates an even richer field:

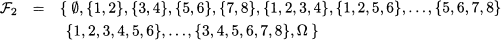
Finally, at time t = 3, we have the finest partition, consisting of singletons

which generates the richest field F3, consisting of all possible subsets Ω. We note that, as time goes by, we get larger and larger fields.

DEFINITION 7.14 (Filtration) An increasing sequence of σ-fields

defined on a common sample space ω, is called a filtration.

A filtration defines precisely how information is collected by observing a stochastic process. This concept can be defined for continuous-time processes with a continuous state space, and it requires a sophisticated mathematical machinery. However, the essential message is quite simple:

The sequence of decisions we make by observing the stochastic process at times t = 0, 1, 2, … must reflect the available information and cannot be anticipative.

The piece of advice with which we have opened this section is clearly not implementable: It would require knowledge of the future. From a technical perspective, consider decision variables Ztb and Zts representing the number of stock shares that we buy and sell, respectively, at time t. At time t = 0 we have a unique decision, since we can just buy or sell here and now. Seen from time t = 0, the variables for the next time instants are random variables, as they depend on the decision that we will make on the basis of the observed path of the stochastic process and our expectations for the future, which are represented by the scenario tree. The random variables at time t must be Ft-measurable. If we are at node n4 in the event tree of Fig. 7.26, we cannot say &#x201C;buy if scenario is ω3&#x201D; and &#x201C;do not buy if scenario is ω4.&#x201D; The decision, whatever it is, must be the same for the two scenarios. Otherwise, the random variable corresponding to the decision at that node would not be constant on the event {ω3, ω4}, and it would not be measurable; we would be in trouble just as in Example 7.18. Technically speaking, we say that decisions must be adapted to the filtration Ft. The piece of financial advice we have considered, unfortunately, is not adapted to the filtration and would require clairvoyance to be practically implementable.

Problems

7.1 A random variable X has normal distribution with μ = 250 and σ = 40. Find the probability that X is larger than 200.

7.2 Consider a normal variable with μ = 250 and σ = 20, and find the probability that X falls in the interval between 230 and 260.

7.3 We should set the reorder point R for an item, whose demand during lead time is uncertain. We have a very rough model of uncertainty – the lead time demand is uniformly distributed between 5000 and 20000 pieces. Set the reorder point in such a way that the service level is 95%.

7.4 You are working in your office, and you would like to take a very short nap, say, 10 minutes. However, every now and then, your colleagues come to your office to ask you for some information; the interarrival time of your colleagues is exponentially distributed with expected value 15 minutes. What is the probability that you will not be caught asleep and reported to you boss?

7.5 A friend of yours is an analyst and is considering a probability model to capture uncertainty in monthly demand of an item featuring high-volume sales. He argues that the central limit applies and, after a thorough check of data, proposes a normal distribution with expected value 12,000 and standard deviation 7000 items. Is this a reasonable model?

7.6 Let X be a normal random variable with expected value μ = 6 and standard deviation σ = 1. Consider random variable W = 3X2. Find the expected value E[W] and the probability P(W > 120).

7.7 You have just issued a replenishment order to your supplier, which is not quite reliable. You have ordered 400 items, but what you will receive is a normal random variable with that expected value, and standard deviation 40 (let us assume that using a continuous random variable is a sensible approximation of the discrete random variable modeling the integer number of received items). After receiving the shipment, you will have to serve a number of customer requests. The amount that your customers ask for is a random variable with expected value 3 and standard deviation 0.3. How many customer requests should you receive in order to have a probability of stockout larger than 10%?

7.8 Let X ~ χn2 be a chi-square variable with n degrees of freedom. Prove that E[X] = n.

7.9 You work for a manufacturing firm producing items with a limited time window for sale. Items are sold by a distributor facing uncertain demand over the time window, which we model by a normal distribution with expected value 10,000 and standard deviation 2500. The distributor decides how many items to order using a newsvendor model. From the distributors perspective, each item costs $10 and is sold at the recommended price of $14. Unsold items are bought back by the manufacturer. Assume that the manufacturer would like to see at least 15,000 items on the shelves (in order to promote her brand name); at what price should she be willing to buy unsold items back?

7.10 You are in charge of deciding the purchased amount of an item with limited time window for sales and uncertain demand. The unit purchase cost is $10 per item, the selling price is $16, and unsold items at the end of the sales window have a salvage value of $7 per item. Demand is also influenced by the level of competition. If there is none, demand is uniformly distributed between 1200 and 2200 items. However, if a strong competitor enters the game, demand is uniformly distributed between 100 and 1100 items.

• If the probability that the competitor enters the market is assumed to be 50%, how many items should you order to maximize expected profit? (Let us assume that selling prices are the same in both scenarios.)
• What if this probability is 20%? Does purchased quantity increase or decrease?

7.11 In some applications we are interested in the distribution of the maximum among a set of realization of random variables. Let us consider a set of n i.i.d. variables Ui, i = 1, …, n, with uniform distribution on the unit interval [0, 1]. Let X be their maximum: X = max {U1, U2, …, Un}. Prove that the CDF of X is FX(x) = xn.

For further reading

Most useful references for this chapter are essentially the same as in the previous chapter, some of which are repeated here just for readers’ convenience.

• For an elementary introduction to continuous random variables, see Ref. [14] or [13]. The first reference also illustrates the link between probability theory and statistics, whereas the second one is more concerned with probability theory, including stochastic processes.
• At a more advanced level is Ref. [16]. Stochastic processes are dealt with at a reasonably sophisticated level in Ref. [7], which is accompanied by Ref. [6].
• Issues in measurability of random variables are dealt with in Refs. [5], [12], and [15], which definitely make more challenging reading.
• On the application side, the link between probability theory and mathematical finance is well illustrated in Ref. [11]. A useful reading on value at risk is provided in Ref. [9].
• The role of stochastic models in manufacturing is well documented in Ref. [8]; applications to supply chain management are also described at an elementary level in Ref. [4]; see Ref. [1] or [18] for a more advanced treatment.

REFERENCES

1. S. Axsäter, Inventory Control, 2nd ed., Springer, New York, 2006.

2. J.C. Bogle, Black Monday and black swans, Financial Analysts Journal, 64(2):30–40, 2008.

3. R. Bookstaber, A Demon of Our Own Design: Markets, Hedge Funds, and the Perils of Financial Innovation, Wiley, New York, 2008.

4. P. Brandimarte and G. Zotteri, Introduction to Distribution Logistics, Wiley, New York, 2007.

5. M. Capiński and T. Zastawniak, Probability through Problems, Springer-Verlag, Berlin, 2000.

6. G. Grimmett and D. Stirzaker, One Thousand Exercises in Probability, Oxford University Press, Oxford, 2003.

7. G. Grimmett and D. Stirzaker, Probability and Random Processes, 3rd ed., Oxford University Press, Oxford, 2003.

8. W. Hopp and M. Spearman, Factory Physics, 3rd ed., McGraw-Hill, New York, 2008.

9. P. Jorion, Value at Risk: The New Benchmark for Controlling Derivatives Risk, McGraw-Hill, New York, 1997.

10. R.L. Phillips, Pricing and Revenue Optimization, Stanford University Press, Stanford, CA, 2005.

11. S.R. Pliska, Introduction to Mathematical Finance: Discrete Time Models, Blackwell Publishers, Maiden, MA, 1997.

12. S.I. Resnick, A Probability Path, Birkhäuser, Boston, 1999.

13. S.M. Ross, Introduction to Probability Models, 8th ed., Academic Press, San Diego, 2002.

14. S.M. Ross, Introduction to Probability and Statistics for Engineers and Scientists, 4th ed., Elsevier Academic Press, Burlington, MA, 2009.

15. S.M. Ross and E.A. Peköz, A Second Course in Probability, Probability Bookstore, Boston, 2007.

16. D. Stirzaker, Elementary Probability, 2nd ed., Cambridge University Press, Cambridge, UK, 2003.

17. K.T. Talluri and G.J. Van Ryzin, The Theory and Practice of Revenue Management, Springer, New York, 2005.

18. P.H. Zipkin, Foundations of Inventory Management, McGraw-Hill, New York, 2000.

1 We will appreciate this point when dealing with linear programming models in Chapter 12.

2 Introductory treatments of random variables start from mass and density functions, as they are more intuitive and related to frequency histograms. However, a sound treatment should start from the CDF, which is a more general concept.

3 See Theorem 2.22.

4 See Property 2.23.

5 This is just one possible definition of service level, related to the probability of not having a stockout; one can also refer to the size of the stockout; see, e.g., Chapter 5 of Ref. [4].

6 See Chapter 5 of Ref. [4] for a more rigorous analysis and for some generalizations of the basic newsvendor model.

7 Clearly, we are ruling out the pathological case in which the PDF is zero. Negative profit margin or cost of unsold items would make no sense. By writing expected profit explicitly, we could check that it is a concave function; hence, stationarity is a necessary and sufficient condition for optimality.

8 See, e.g, Chapter 10 of Ref. [10].

9 See Chapter 2 of Ref. [17] for more information and extensions.

10 See Section 14.7.

11 See Section 9.7.

12 Note that this notation refers to the parameter characterizing the distribution, rather than to the expected value.

13 See Example 2.43; the example also shows that the area below the PDF of the exponential distribution is actually 1.

14 We did not cover independence between random variables yet: however, recalling the concept of independent events, the concept should be rather clear.

15 See Example 2.10.

16 This book is an exception, since tables are a heritage of the past, and software tools are easier to use in practice, not to mention much more precise. Some tools, like R, are freely available on the Web (see http://www.r-project.org). Nevertheless, statistical tables are offered on the book Webpage for the readers’ convenience.

17 The idea is also helpful when designing numerical algorithms to compute or invert the CDF of the normal; we just need one procedure, for the standard normal, and a simple transformation of its output provides us with what we need.

18 We will outline a few related issues in Chapter 14. There are many interesting accounts of what happened on the Black Monday and the hard lessons that were learned on that infamous day; see, among others, Refs. [2] and [3].

19 A common choice is based on cubic splines, which are third-order polynomials associated with each interval, selected in such a way that the function is continuous, as well as its first-and second-order derivative.

20 Just in case you are wondering about a professor called Student, this is actually a pseudonym used in 1908 by William Sealy Gosset to publish his results about this distribution. Gosset’s employer, the Guinness brewery, forbade members of its staff to publish scientific papers, for fear of trade secret leaks.

21 We recall that stock shares are limited liability assets; hence, they cannot take negative values. In other words, the worst-case return is -100%.

22 See Theorem 6.8.

23 From a theoretical perspective, we should say that we have convergence in distribution. We outline the fundamental concepts of stochastic convergence in Section 9.8; many readers, however, may ignore the related subtleties.

24 This is a rather imprecise statement, as ordering decisions should consider backorders and on-order inventory See, e.g., Ref. [4] for a complete treatment.

25 See N.N. Taleb and P. Triana, Bystanders to this financial crime were many, Financial Times Dec. 8, 2008.

26 In his history of the Great Crash of 1929, John K. Galbraith attributes this fundamental advice to an American comedian; see J.K. Galbraith, The Great Crash 1929, originally published in 1954, reprinted by Mariner Books, 2009.

27 This supplement may be safely skipped. The only section in which we use related concepts is Section 13.4, where we illustrate multistage stochastic linear programming models.

28 The careful reader will immediately guess that what we are saying works only for a discrete random variable, since for continuous random variables the probability of observing a specific value is zero. Indeed, in a rigorous treatment we should consider events {ω Ω: X(ω) ≤ a}, but to keep things as intuitive as possible, we will refrain from doing so.