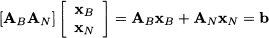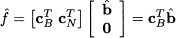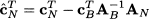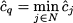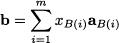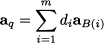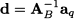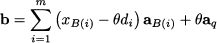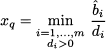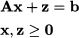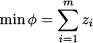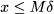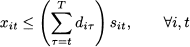12.6.1 Simplex method

The simplex method is the standard algorithm to solve LP problems and is based on the following observations:

• An LP problem is a convex problem; hence, if we find a locally optimal solution, we have also found a global optimizer.
• An LP problem is a concave problem, too; hence, we know that we may restrict the search for the optimal solution to the boundary of the feasible set, which is a polyhedron. Actually, it can be shown that there is an optimal solution corresponding to a vertex, or extreme point, of the polyhedron.
• So, we need a clever way to explore extreme points of the feasible set. Geometrically, we may imagine moving from a vertex to a neighboring one, trying to improve the objective function. When there is no neighboring vertex improving the objective, we have found a local optimizer, which is also global.

It is useful to visualize this process, by referring to Fig. 1.3. Imagine starting from a trivially feasible solution, the origin M0. We may improve this production plan by moving along the edges of the polyhedron; one possible path is (M0, M1, M2, M3); another path is (M0, M4, M3). Both paths lead to the optimizer, even though one seems preferable, as it visits less vertices. In large-scale problems, only a small subset of vertices is actually visited to find an optimizer.

Now, in order to obtain a working algorithm, we should translate this geometric intuition into algebraic terms. The first step is transforming the LP problem in standard form,

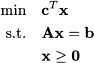
where 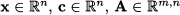, and . Clearly, the problem makes sense only if the matrix A has less rows than columns, i.e., if m < n. If so, the set of equality constraints, regarded as a system of linear equations, has an infinite set of solutions, which may be considered as ways of expressing the right-hand side vector b as linear combinations of columns of A. Let us express A in terms of its column vectors aj, j = 1, …, n:

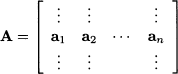
where aj m. There are n columns, but a subset B of m columns suffices to express b as follows:

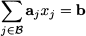
To be precise, we should make sure that this subset of columns is a basis, i.e., that they are linearly independent; in what follows, we will cut a few corners and assume that this is the case. A solution of this system, in which n - m variables are set to zero, and only m are allowed to assume a nonzero value is a basic solution. Hence, we can partition the vector x into two subvectors: the subvector xB m of the basic variables and the subvector xN n-m of the nonbasic variables. Using a suitable permutation of the variable indices, we may rewrite the system of linear equations

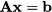
as

(12.81)

where AB m,m is nonsingular and AN m,n-m. However, in the LP model we have a nonnegativity restriction on variables. A basic solution where xB ≥ 0 is called a basic feasible solution. The simplex algorithm relies on a fundamental result, that we state loosely and without proof: Basic feasible solutions correspond to extreme points of the polyhedral feasible set of the LP problem.

Solving an LP amounts to finding a way to express b as a least-cost linear combination of at most m columns of A, with nonnegative coefficients. Assume that we have a basic feasible solution x; we will consider later how to obtain an initial basic feasible solution. If x is basic feasible, it may be written as

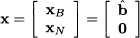
where

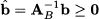
The objective function value corresponding to x is

(12.82)

Now we should look for neighboring vertices improving this value. Neighboring vertices may be obtained by swapping a column in the basis with a column outside the basis. This means that one nonbasic variable is brought into the basis, and one basic variable leaves the basis.

To assess the potential benefit of introducing a nonbasic variable into the basis, we should express the objective function in terms of nonbasic variables. To this aim, we rewrite the objective function in (12.82), making its dependence on nonbasic variables explicit. Using Eq. (12.81), we may express the basic variables as

(12.83)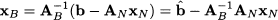

Then we rewrite the objective function in terms of nonbasic variables only

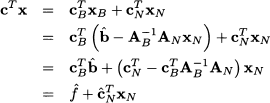
where

(12.84)

The quantities 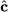N are called reduced costs, as they measure the marginal variation of the objective function with respect to the nonbasic variables. If 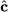N ≥ 0, it is not possible to improve the objective function; in such a case, bringing any nonbasic variable into the basis at some positive value cannot reduce the overall cost. Therefore, the current basis is optimal if 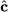N ≥ 0. If, on the contrary, there exists a q N such that $cCq < 0, it is possible to improve the objective function by bringing xq into the basis. A simple strategy is to choose q such that

(12.85)

This selection does not necessarily result in the best performance of the algorithm; we should consider not only the rate of change in the objective function, but also the value attained by the new basic variable. Furthermore, it may happen that the entering variable is stuck to zero and does not change the value of the objective. In such a case, there is danger of cycling on a set of bases; ways to overcome this difficulty are well explained in the literature.

When xq is brought into the basis, a basic variable must “leave” the basis in order to maintain Ax = b. To spot the leaving variable, we can reason as follows. Given the current basis, we can use it to express both b and the column aq corresponding to the entering variable:

(12.86)

(12.87)

where B(i) is the index of the ith basic variable (i = 1, …, m), aB(i) is the corresponding column, and

(12.88)

If we multiply Eq. (12.87) by a number θ and subtract it from Eq. (12.86), we obtain

(12.89)

From Eq. (12.89) we see that θ is the value of the entering variable in the new solution and the values of the current basic variables are affected in a way depending on the sign of di. If di ≤ 0, xB(i) remains nonnegative when xq increases. But if there is an index i such that di > 0, then we cannot increase xq at will, since there is a limit value for which a currently basic variable becomes zero. This limit value is attained by the entering variable xq, and the first current basic variable that gets zero leaves the basis:

(12.90)

If d ≤ 0, there is no limit on the increase of xq, and the optimal solution is unbounded.

In order to start the iterations, an initial basis is needed. One possibility is to introduce a set of auxiliary artificial variables z in the constraints:

(12.91)

The artificial variables can be regarded as residuals, in the same vein as residuals in linear regression. Assume also that the equations have been rearranged in such a way that b ≥ 0. Clearly, a basic feasible solution of the system (12.91) where z = 0 is also a basic feasible solution for the original system Ax = b. In order to find such a solution, we can introduce and minimize an auxiliary function π as follows

(12.92)

using the simplex method itself. Finding an initial basic feasible solution for this artificial problem is trivial: z = b. If the optimal value of (12.92) is π* = 0, we have found a starting point for the original problem; otherwise, the original problem is infeasible.

The reader is urged to keep in mind that what we have stated here is only the principle of the simplex method. Many things may go wrong with such a naive idea, and considerable work is needed to make it robust and efficient. Indeed, even though the simplex method dates back to 1947, it is still being improved today. We leave these refinement of the simplex method to the specialized literature and illustrate its application to the familiar optimal mix problem.32

Example 12.23 A first step, which is actually carried out by good solvers, is to preprocess the formulation eliminating redundant constraints. This results in the streamlined problem

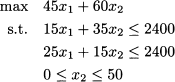
We should rewrite it in standard form, by introducing three slack variables s1,s2,s3 ≥ 0:33

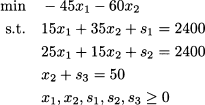
In matrix terms, we have:

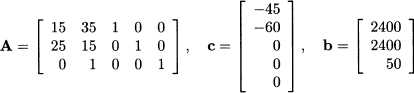
Finding an initial feasible solution is easy; as a starting basis, we consider {s1, s2, s3}, which corresponds to a production plan where x1 = x2 = 0, i.e., the origin M0 in Fig. 1.3. The corresponding basis matrix is AB = I, i.e., a 3 x 3 identity matrix. Using the notation we introduced, we have

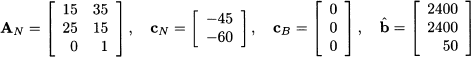
Since the cost coefficients of the basic variables are zero, application of Eq. (12.84) yields the reduced costs [-45, -60]. To improve the mix, according to Eq. (12.85) we should bring x2 into the basis. Geometrically, we move vertically along an edge of the polyhedron, from M0 to M1. By the way, this is sensible as item 2 has the largest contribution to profit, but we observe that this is not necessarily the best choice, as we start moving along the longer of the two paths that lead to the optimal solution M3; in fact, selecting the nonbasic variable with the most negative reduced cost is not the strategy of choice of modern solvers. Now we should apply Eq. (12.90) to find the variable leaving the basis. Since the matrix of basic columns is the identity matrix, applying (12.88) is easy:

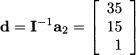
and

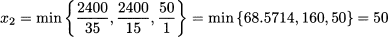
We see that the slack variable s3 leaves the basis, as x2 reaches its upper bound.

Now, let us avoid terribly boring calculations and cut a long story short. Repeating these steps, we would bring x1 into the basis, making one capacity constraint binding by driving to zero the corresponding slack variable. We know that both capacity constraints are binding at the optimal solution M3. Let us just check that this is indeed the optimal solution. The extreme point M3 corresponds to the basis {x1, x2, x3}; therefore, we have

Finding the corresponding basic feasible solution requires solving a system of linear equations. Formally:

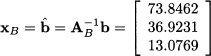
Now we need the reduced costs of s1 and s2

As both reduced costs are positive, we have indeed found the optimal basis. We note that in practice no matrix inversion is required; we may just solve systems of linear equations using by the Gaussian elimination process of Section 3.2.2.

In closing this example, the very careful reader might notice that the reduced costs above are exactly the shadow prices of capacity constraints that we have seen in Example 12.21. Indeed, there is a connection, which we cannot pursue here; we just notice that the simplex method yields shadow prices as a very useful by-product.

12.6.2 LP-based branch and bound method

When dealing with a MILP, the simplex method cannot guarantee an integer solution; more often than not, we obtain a fractional solution. There is an even more troubling fact, which is essentially due to the lack of convexity. In fact, if some magical oracle hands over the optimal solution of a continuous LP, we know how to verify its optimality by checking reduced costs. Unfortunately there is no such condition for integer LPs; to find the optimal solution, we should explore the whole set of feasible solutions, at least in principle. Enumerating the whole set of solutions is conceptually easy for a pure binary program, such as the knapsack problem of Section 12.4.1. It is natural to consider a search tree like the one depicted in Fig. 12.20. At each node, we branch on a variable generating two subproblems. At the root node in the figure, we branch on x1, defining a left subproblem in which x1 = 0 (i.e., item 1 is not included in the knapsack), and a right subproblem in which x1 = 1 (i.e., item 1 is not included in the knapsack). At each level of the tree we branch on a different variable, and the leaves of the tree correspond to a candidate solution. Not all of the leaves correspond to feasible solutions, because of the budget constraint. Hence, many solutions will be excluded from the search process. Yet, it is easy to see that this is not a very practical solution approach. If there are n binary variables, there are potentially 2n solutions to check, resulting in a combinatorial explosion. We say that this enumeration process has exponential complexity in the worst case.

Fig. 12.20 Search tree for a pure binary programming problem.

Things would definitely look brighter, if we could find a way to “prune” the tree by eliminating some of its branches. We may avoid branching at a node of the tree if we are sure that the nodes beneath that one cannot yield an optimal solution; but how can we conclude this without considering all of these nodes? We have already observed that if we relax the integrality requirements in a MILP and solve the corresponding continuous LP, we obtain a bound on the optimal value of the MILP.34 In the familiar production mix example, solving the continuous LP we get an optimal contribution to profit 5538.46. This is an optimistic estimate on the true optimal contribution to profit, 5505, which we obtain when requiring integrality of the decision variables. In the case of a maximization problem, the optimistic estimate is an upper bound U B on the optimal objective value (in a minimization problem, the optimistic estimate is a lower bound). Such bounds may be calculated at any node of the search tree for a MILP by relaxing the free integer decision variables to continuous values; free variables are those that have not been fixed to any value by previous branching decisions. This is called continuous relaxation or LP-based relaxation.

Now suppose that in the process of exploring the search tree we find a feasible (integer), though not necessarily optimal solution. Then, its value is a lower bound LB on the optimal objective value for a maximization problem, since the optimal profit cannot be lower than the value of any feasible solution (a feasible solution yields an upper bound for a minimization problem). It is easy to see that by comparing lower and upper bounds, we may eliminate certain nodes from the search tree. For instance, imagine that we know a feasible solution of a knapsack problem, such that its value is 100; so, we have a lower bound LB = 100 on the value of the optimal knapsack. Say that the LP relaxation at a node in the search tree yields an upper bound UB = 95. Then, we observe that LB > UB and immediately conclude that this node can be safely eliminated: We do not know what is the value of the best solution in the branches below that node, but we know that it cannot be better than the feasible solution we already know. The roles of lower and upper bounds are reversed for a minimization problem. The following example shows in detail LP-based branch and bound for a knapsack problem.35

Example 12.24 Consider the knapsack problem

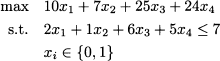
We first solve the root problem of the tree (P0 in Fig. 12.21), which is the continuous relaxation of the binary problem, obtained by relaxing the integrality of decision variables and requiring 0 ≤ xi ≤ 1. Solving the problem, we get the solution

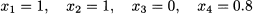
Fig. 12.21 Search tree for the knapsack problem of Example 12.24.

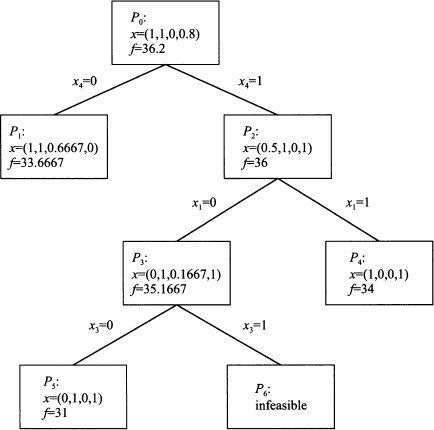
with objective value 36.2. This is an upper bound and, since all of the problem data are integers, we can immediately conclude that the optimal value cannot exceed 36. We observe that the last variable is fractional, and we branch on it, generating two more subproblems: In P1 we set x4 = 0, and in P2 we set x4 = 1. Note that we are free to branch on other variables as well, but this choice seems to make more sense; there is the possibility of obtaining an integer solution before reaching the bottom level of the tree. Solving P1 yields

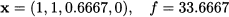
whereas P2, yields

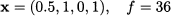
It is important to notice that both upper bounds are smaller than the bound obtained at the root node. This makes sense, because we are adding constraints, and the value of the optimal continuous solution cannot increase by doing so. Now we should choose which branch of the tree (i.e., which subproblem) to explore first. One possible rule is to look down the most promising branch. Hence, we generate two more subproblems from P2, branching on the fractional variable x1. Setting x1 = 0 results in subproblem P3, whose solution yields

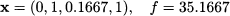
Setting x1 = 1 results in subproblem P4, whose solution yields our first integer solution

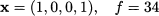
Note that we have found an integer solution without reaching a leaf node; when this happens, i.e., when the continuous relaxation yields an integer solution, there is no point in further branching at that node. Having found our first integer solution, we also have a lower bound (34) on the optimal value. Comparing this with the root bound, we could conclude that the optimal value must either be 34, 35, or 36. Actually, checking the bound on the lower-level, still-active nodes, we may immediately conclude that the optimal value must be either 34 or 35, the bound we obtain from node P3. Subproblem P1 may be immediately eliminated, as its upper bound is lower than the value of our feasible solution. We say that the subproblem has been “fathomed,” or that the tree “has been pruned.” Clearly, the earlier we prune the tree, the more subproblems we eliminate.

We are not done, though, because node P3 looks promising. There, we branch on the fractional variable x3. Setting x3 = 0 results in subproblem P4, whose solution yields a new integer solution

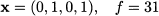
This solution is worse than the first one; yet, it is the best we can do down that branch, so we may prune the node. Setting x3 = 1 results in the infeasible subproblem P4; indeed, if we try putting both items 1 and 3 into the knapsack, we exceed its capacity (2 + 6 > 7). Now we may report solution x = (1, 0, 0, 1) as optimal. We have explored a fair amount of nodes, but many of them have been eliminated in the process.

Let us generalize the above scheme a bit. The idea of branching consists of taking a problem P(S), with feasible set S, and generating a set of suproblems by partitioning S into a collection of subsets S1, …, Sq such that

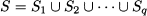
Then, for a minimization problem, we have

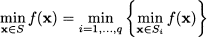
The rationale behind this decomposition of the feasible set is that solving the problems over smaller sets should be easier; or, at least, the bounds obtained by solving the relaxed problems should be tighter. For efficiency reasons it is advisable, but not strictly necessary, to partition the set S in such a way that subsets are disjoint:

Of course, in a MILP model involving binary and continuous variables, we branch only on binary variables. But what about general integer variables? It is clearly unreasonable to create a branch for each possible integer value. The standard strategy is again to generate only two subproblems, branching on a fractional variable as follows. Assume that an integer variable xj takes a noninteger value 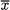j in the optimal solution of the relaxed subproblem. Then two subproblems are generated; in the downchild we add the constraint36

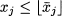
to the formulation; in the upchild we add

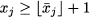
For instance, if 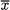j = 4.2, we generate two subproblems with the addition of constraints xj ≤ 4 (for the downchild) and xj ≥ 5 (for the upchild).

Now we may state a branch and bound algorithm in fairly general terms. To fix ideas, we refer to a minimization problem; it is easy to adapt the idea to a maximization problem. Given subproblem P(Sk), let v[P(Sk)] denote the value of its optimal solution, and let β[P(Sk)] be a lower bound:

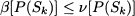
Note that P(Sk) can be fathomed only by comparing the lower bound β[P(Sk)] with an upper bound on v[P(S)]. It is not correct to fathom P(Sk) on the basis of a comparison with a subproblem P(Si) such that

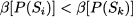
Fundamental branch and bound algorithm

1. Initialization. The list of open subproblems is initialized to P(S); the value of the incumbent solution v* is set to +∞. At each step, the incumbent solution is the best integer solution found so far.

2. Selecting a candidate subproblem. If the list of open subproblems is empty, stop: The incumbent solution x*, if any has been found, is optimal; if v* = +∞, the original problem was infeasible. Otherwise, select a subproblem P(Sk) from the list.

3. Bounding. Compute a lower bound β(Sk) on v[P(Sk)] by solving a relaxed problem . Let be the optimal solution of the relaxed subproblem.

4. Prune by optimality. If $xBk is feasible, prune subproblem P(Sk). Furthermore, if , update the incumbent solution x* and its value v*. Go to step 2.

5. Prune by infeasibility. If the relaxed subproblem 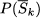is infeasible, eliminate P(Sk) from further consideration. Go to step 2.

6. Prune by bound. If β(Sk) ≥ v*, eliminate subproblem P(Sk) and go to step 2.

7. Branching. Replace P(Sk) in the list of open subproblems with a list of child subproblems P(Sk1), P(Sk2), …, P(Skq), obtained by partitioning Sk; go to step 2.

A thorny issue is which variable we should branch on. Similarly, we should decide which subproblem we select from the list at step 2 of the branch and bound algorithm. As it is often the case, there is no general answer; software packages offer different options to the user, and some experimentation may be required to come up with the best strategy.

Many years ago, the ability of branch and bound methods to solve realistically sized models was quite limited. Quite impressive improvements have been made in commercial branch and bound packages and these, together with the availability of extremely fast and cheap computers, have made branch and bound a practical tool for business management. Nevertheless, many practical problems remain, for which finding the optimal solution requires a prohibitive computational effort. Domain-dependent heuristics have been developed, but we should note that the above branch and bound scheme can be twisted to yield high-quality heuristics by a simple trick. We should just relax the condition β(Sk) ≥ v* as follows:

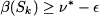
where is a given threshold representing the minimal absolute improvement over the incumbent that we require to explore a branch. Doing so, we might miss the true optimal solution, but we might prune many additional branches, with the guarantee that the difference between the best integer solution found and the optimal solution is bounded by . If we prefer to state the threshold in relative terms, we can prune a node when

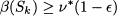
In this case, is related to a guarantee on the maximum percentage suboptimality. If = 0.01, we know that maybe we missed the optimal solution, but this would improve the best integer solution we found by at most 1%. It is up to the user to find the best tradeoff between computational effort and solution quality. Another interesting way to reduce computational effort is by reformulating the model in order to improve its solvability, as we illustrate next.

12.6.3 The impact of model formulation

We have seen that commercial branch and bound procedures compute bounds by LP-based (continuous) relaxations. Given a MILP problem

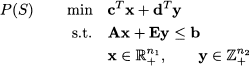
where S denotes its feasible set, the continuous relaxation is obtained by relaxing the integrality constraints, which yields the relaxed feasible set $SB and the relaxed problem:

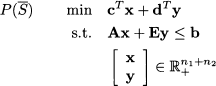
If we could find the convex hull of S, which is a polyhedron, the application of LP methods on that set would automatically yield an integer solution. Unfortunately, apart from a few lucky cases, finding the convex hull is as hard as solving the MILP problem. A less ambitious task is to formulate a model in such a way that its relaxed region $SB is as close as possible to the convex hull of S; in fact, the smaller $SB, the larger the lower bound (for a minimization problem) and we know that tighter bounds make pruning more effective. In the following example, we show how careful model formulation may help.

Example 12.25 (Plant location reformulation of lot-sizing problems) When modeling fixed-charge problems, we link a continuous variable x and a binary variable δ by the big-M constraint

(12.93)

where M is any upper bound on x. In principle, M may be a very large number, but to get a tight relaxation, we should make it as small as possible. To see why, consider Fig. 12.22, where we illustrate the feasible region associated with constraint (12.93). The feasible set consists of the origin and the vertical line corresponding to δ - 1 and x ≥ 0. When we solve the continuous relaxation, we drop the integrality constraint on δ and replace it by δ [0, 1]. This results in the shaded triangles in the figure, whose area depends on a line with slope M. It is easy to see that if M is large, the resulting feasible set for the relaxed problem is large as well. In fact, models with big-M constraints are notoriously hard to solve, and the lot-sizing problem is a well-known example. However, sometimes we may improve the tightness of bounds by resorting to clever reformulations. We illustrate the idea for the minimum-cost version (12.53) of the model.

Fig. 12.22 The impact of big-M on a continuous relaxation.

The naive model formulation is based on production variables xit, representing how much we produce of item i during time bucket t. This continuous variable is related to a binary setup variable δit by a fixed-charge constraint such as

(12.94)

Here, the big-M is given by the total demand of item i, over the time buckets from t to T. One way to reduce this big-M is to disaggregate the production variable xit, introducing a set of decision variables yitp, which represent the amount of item i produced during time bucket t to satisfy the demand during time bucket p ≥ t. This new variable represents a disaggregation of the original variable xit, since

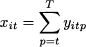
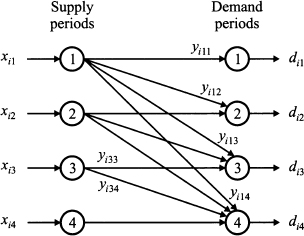
This reformulation is related to a sort of plant location problem, whereby locations are “in time,” rather than “in space.” This is illustrated in Fig. 12.23. If we “open the plant” in time bucket 1, we pay the setup cost; then material can flow outside that supply period in order to meet demand at destination nodes. Clearly, if we open a plant in time bucket t, we may only use its outflow to meet demand at later time buckets p ≥ t.

Fig. 12.23 Interpreting the plant location reformulation of lot sizing problems.

Doing so, we introduce more decision variables, but now the link between continuous and binary setup variables is

(12.95)

This constraint involves a much smaller big-M; indeed, if we sum constraints (12.95) over p, we find the aggregate constraint (12.94). Now we may also get rid of inventory variables; the amount corresponding to yitp is held in inventory for (p - t) time buckets; hence the corresponding holding cost is

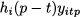
Finally, we obtain the following model:

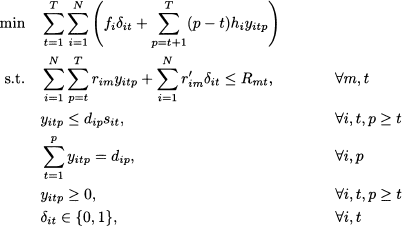
It is also worth noting that this model formulation allows us to consider perishable items in a quite natural way. If the shelf life of an item is, say, 3 time buckets, we will not define variables yitp for p - t > 3; you may visualize the idea by just dropping some arcs in Fig. 12.23.

The reformulation we have just considered may look a bit counter-intuitive, and it is not always easy to find a suitable model reformulation like this one. Luckily, many tricks to strengthen a model formulation may be automated.

Example 12.26 (Cover inequalities) Let us consider the knapsack problem of Example 12.24 again:

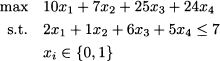
If we observe the budget constraint, it is easy to see that items 1 and 3 cannot be both selected, as their total weight is 8, it exceeds the available budget. Hence we might add the constraint

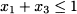
which is obviously redundant in the discrete domain, but is not redundant in the continuous relaxation. By the same token, we could add the following constraints

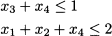
Such additional constraints are called cover inequalities and may contribute to strengthen the bound from the LP relaxation, cutting the CPU time considerably. Solving the strengthened model formulation results in the search tree depicted in Fig. 12.24. We may notice that the root subproblem P0 yields a stronger bound than the plain knapsack model (34.66667 < 36.2). What is more striking is that, if we branch on x1, we immediately get two integer solutions and the search process can be stopped.

Fig. 12.24 Search tree for the knapsack problem with cover inequalities.

Cover inequalities may be automatically generated and are only one of the types of cuts that have been introduced in state-of-the-art software packages implementing branch and bound. The term “cuts” stems from the fact that these additional constraints cut portions of the polyhedron of the continuous relaxation, strengthening bounds. Moreover, clever and effective heuristics have also been devised to generate good integer solutions as soon as possible in the search tree. This generates good upper bounds that help in further pruning the tree. Indeed, the improvement in commercial branch and bound packages over the last 10 years or so has been dramatic, allowing the solution of problems that were intractable a while ago.

Problems

12.1 Assume that functions fi(x), i = 1, …, m, are convex. Prove that the function

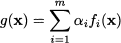
where αi > 0, is convex.

12.2 Is the function f(x) = xe2x convex? Does the function feature local minima? What can you conclude?

12.3 Consider the domain defined by the intersection of planes:

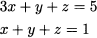
Find the point on this domain which is closest to the origin.

12.4 Solve the optimization problem

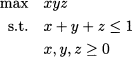
How can you justify intuitively the solution you find?

12.5 Consider the constrained problem:

• Is the objective function convex?
• Apply the KKT conditions; do we find the true minimizer?

12.6 In Example 12.12 we considered a single-period blending problem with limited availability of raw materials. In practice, we should account for the possibility of purchasing raw materials at a time-varying cost and storing them.

• Extend the model to a multiperiod decision model with purchase decisions, assuming that you know the future prices of raw materials and that storage capacity is unlimited. (Note: of course, assuming that future prices are known may be unrealistic; however, commodity derivatives could be used to eliminate uncertainty.)
• Assume that raw materials must be stored in separate tanks, which are available in a limited number. Hence, you may only store up to a given number of raw material types. How can you model this additional constraint?

12.7 Extend the production planning model (12.27) in order to take maintenance activities into account. More precisely, we have M resource centers, and each one must be shut down for exactly one time bucket within the planning horizon. Furthermore, since the maintenance department has quite limited personnel, we can maintain at most two resource centers per time bucket.

12.8 Extend the knapsack problem to cope with logical precedence between activities. For instance, say that activity 1 can be selected only if activities 2, 3, and 4 are selected. Consider alternative model formulations in terms of branch and bound efficiency.

12.9 In Section 12.4.2 we have illustrated a few ways to represent logical constraints. Suppose that activity i must be started if and only if both activities j and k are started. By introducing customary binary variables, it is tempting to write a constraint like xi = xjxk; unfortunately, this is a bad nonlinear constraint. How can we express this logical constraint linearly? Generalize the idea and find a way to linearize the product $PIi=1n xi of n binary variables.

12.10 In the minimum cost lot-sizing problem, we assumed that demand must be satisfied immediately; by a similar token, in the maximum profit lot-sizing model, we assumed that any demand which is not satisfied immediately is lost. In other words, in both cases we assumed that customers are impatient.

• Write a model for cost minimization, assuming that customers are willing to wait, but there is a penalty. More precisely, backlog is allowed, which can be represented as “negative inventory holding.” Clearly, the backlog cost bi, must be larger than the holding cost hi. Build a model to minimize cost.
• Now assume that customers are indeed patient, but they are willing to wait only for two time buckets; after two time buckets, any unsatisfied demand is lost. Build a model to maximize profit.
• In the classical lot-sizing model, we implicitly assume that each customer order may be satisfied by items that were produced in different batches. In some cases, this is not acceptable; one possible reason is due to lot tracing; another possible reason is that there are little differences among batches (e.g., in color), that customers are not willing to accept. Then, we should explicitly account for individual order sizes and due dates. Build a model to maximize profit.
• As a final generalization, assume that customers are impatient and that they order different items together (each order consists of several lines, specifying item type and quantity). If you cannot satisfy the whole order immediately, it is lost. Build a model to maximize profit.

12.11 In the portfolio optimization models that we considered in this chapter, risk is represented by variance or standard deviation of portfolio return. An alternative is using MAD (mean absolute deviation):

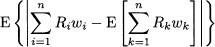
where Ri is the random return of asset i and wi is its portfolio weight. Suppose that we do not trust any probability distribution for return, but we have a time series of historical data. Let rit be the observed return of asset i in time bucket t, t = 1, …, T.

• Build a MILP model to find the minimum MAD portfolio subject to the following constraints:

  — Short selling is not allowed.

  — Expected return should not be below a given target.

  — To avoid a fragmented portfolio, no more than k < n assets can be included in the portfolio, and if an asset is included, there is a lower bound on its weight.

  — Assets are partitioned according to industrial sectors (e.g., banks, energy, chemicals, etc), as well as according to geographic criteria (Asia, Europe, etc.). For each set of assets, overall lower and upper bounds are to be satisfied.

• What is the danger of this modeling approach, based on observed time series?

12.12 A telecommunication network is a set of nodes and directed arcs on which data packets flow. We assume that the flow between each pair of nodes is known and constant over time; please note that the matrix of such flows need not be symmetric, and that packets labeled with a source/destination pair (s, d) are a commodity on their own. Nodes are both source and destination of data packets to and from other nodes, respectively; they can be also used as intermediate nodes for routing, as some pairs of nodes may not be connected directly. Both arcs and nodes are subject to a capacity constraint in terms of packets that they can transport and route over a time frame.

From an operational point of view, we would like to route all of the traffic, in such a way that no network element (node or arc) is congested. For the sake of simplicity, let us assume that a network element is congested when its traffic load exceeds 90% of its nominal capacity (in practice, congestion is a nonlinear phenomenon). We measure network congestion by the number of network elements whose traffic load exceeds this limit.

• Build a model to minimize network congestion, which has an impact on quality of service.
• Extend the model to include capacity expansion opportunities. For each network element, we may expand capacity either by 25% or by 70%; each expansion level is associated with a fixed cost. Build a MILP model to find a tradeoff between quality of service and network cost.

For further reading

• We have been far from rigorous in stating and proving optimality conditions. Readers looking for a more complete treatment, including second-order conditions and handy criteria to check convexity, may refer to Ref. [10] or [11].
• A good reference on linear programming, including alternatives to the classical simplex method, is Ref. [12]. An in-depth treatment of nonlinear programming can be found in Ref. [2], which also illustrates many solution algorithms; see also Ref. [7].
• Integer programming is thoroughly dealt with in Ref. [15]. We just mentioned powerful methods based dynamic column generation; see Ref. [6] for an extensive treatment and many examples.
• We did not cover at all heuristic methods for integer programming models and discrete optimization, but there is a huge literature on ad hoc methods. Each variant of problem may be tackled by a specific approach. To avoid getting lost, it is useful to have a grasp of general principles that can be tailored to specific problems. For instance, tabu search is described in Ref. [8], and Ref. [9] is devoted to genetic algorithms.
• The bibliography on optimization methods is quite rich, but unfortunately the same cannot be said with respect to model building. A welcome exception is the text by Williams [14], which shows well-crafted examples taken from a wide range of application domains. The same author has also written a book on model solving, Ref. [13], from which Example 12.4 has been taken.
• It is also useful to have a look at books illustrating the application of optimization modeling to specific domains. Readers interested in optimization models for manufacturing management may consult Ref. [3]; models for distribution logistics are described in Ref. [4]. Optimization models in finance are treated at an introductory level in Ref. [1], which also describes nonlinear programming algorithms. At a more advanced level, Refs. [5] and [16] are useful readings.
• From a practical perspective, optimization modeling is of no use if it is not complemented by a working knowledge of commercial optimization software. There is a wide array of both solvers and modeling tools. Solvers are the libraries implementing solution methods, which may be hard to use without a suitable interface enabling the user to express the model in a natural way. I definitely suggest having a look at

  http://www.gurobi.com

  http://www.ampl.com

  Other useful links are

  http://www.informs.org

  http://www.gams.com

  http://www.lindo.com

  http://www.solver.com

  http://www.maximal-usa.com

REFERENCES

1. M. Bartholomew-Biggs, Nonlinear Optimization with Financial Applications, Kluwer Academic Publishers, New York, 2005.

2. M.S. Bazaraa, H.D. Sherali, and C.M. Shetty, Nonlinear Programming. Theory and Algorithms, 2nd ed., Wiley, Chichester, West Sussex, UK, 1993.

3. P. Brandimarte and A. Villa, Advanced Models for Manufacturing Systems Management, CRC Press, Boca Raton, FL, 1995.

4. P. Brandimarte and G. Zotteri, Introduction to Distribution Logistics, Wiley, New York, 2007.

5. G. Cornuejols and R. T$uUt$uUnc$uU, Optimization Methods in Finance, Cambridge University Press, New York, 2007.

6. G. Desaulniers, J. Desrosiers, and M.M. Solomon, eds., Column Generation, Springer, New York, 2005.

7. R. Fletcher, Practical Methods of Optimization, 2nd ed., Wiley, Chichester, West Sussex, UK, 1987.

8. F.W. Glover and M. Laguna, Tabu Search, Kluwer Academic, Dordrecht, The Netherlands, 1998.

9. Z. Michalewicz, Genetic Algorithms + Data Structures = Evolution Programs, Springer-Verlag, Berlin, 1996.

10. C.P. Simon and L. Blume, Mathematics for Economists, W.W. Norton, New York, 1994.

11. R.K. Sundaram, A First Course in Optimization Theory, Cambridge University Press, Cambridge, UK, 1996.

12. R.J. Vanderbei, Linear Programming: Foundations and Extensions, Kluwer Academic, Dordrecht, The Netherlands, 1996.

13. H.P. Williams, Model Solving in Mathematical Programming, Wiley, Chichester, 1993.

14. H.P. Williams, Model Building in Mathematical Programming, 4th ed., Wiley, Chichester, 1999.

15. L.A. Wolsey, Integer Programming, Wiley, New York, 1998.

16. S. Zenios, Practical Financial Optimization, Wiley-Blackwell, Oxford, 2008.

1 See Sections 2.11 and 3.9.

2 See Section 1.1.2.

3 See Section 2.1.

4 From a theoretical point of view, feasible regions with closed boundaries are always preferred, as otherwise we cannot even be sure that a minimum or a maximum exists. To see this, consider the problem min x, subject to the bound x > 2. It is tempting to say that its solution is x* = 2; however, this point is not feasible, as the inequality is strict. In fact, the problem has no solution. We may find the solution x* = 2 if we consider the problem inf x, which has a slightly different meaning that we leave to theoretically inclined treatments. By the same token, you may find sup rather than max. A theorem due to Weierstrass ensures that if a function is continuous, and the feasible set is closed and bounded, the function attains its maximum and minimum within that set. We will steer away from such technical complications.

5 See Section 2.11.

6 See Fig. 1.3 for an illustration in the product mix case.

7 Example 12.4 is taken from Williams [13].

8 See Section 3.8.

9 See Section 8.3.2.

10 See Section 2.11.

11 The theorem can be stated in a less restrictive way, considering the function on an open convex subset of n, but we prefer a simplified formulation to grasp the basic message.

12 See Fig. 2.28.

13 See Example 2.34.

14 See problem 2.9.

15 Integrality requirements make the feasible set discrete; more precisely, we get disconnected subsets, possibly consisting of isolated points. Clearly, lines joining such points do not belong to the feasible set, which makes it nonconvex. Furthermore, it is not obvious how to define local optimality here, since there is no neighborhood in the sense of Definition 2.13. The bottom line is that, as a general rule with a very few exceptions, integrality requirements make an optimization problem much harder than a continuous one.

16 See Section 13.3.1.

17 If we do not want to disregard assembly cost, we may substitute selling price by contribution to profit from assembling and selling an item.

18 Note that, to be uniform with the way we denote the set of time buckets, we explicitly enumerate product types, rather than defining a set I and writing i I, like we did in the ATO case. In practice, the two notations are equivalent and we may choose what we feel more comfortable with, case by case.

19 See also Section 2.13.4.

20 These decisions may be also subject to bounds on certain food amounts, in order to avoid a very unpleasing diet.

21 Some readers might find this way of working with sets a bit abstract. In practice, optimization models are expressed using special languages, like AMPL, that describe the structure of an optimization model. This structure is matched against data to produce a specific problem instance that is passed to a solver. These languages have quite powerful set manipulation tools, allowing for the expression of quite complicated models in a remarkably transparent way.

22 To be precise, when dealing with an undirected network, we should speak of vertices and edges, rather than nodes and arcs.

23 See Section 10.1.1.

24 Often we speak of Pareto efficiency, in honor of Italian economist Vilfredo Pareto (1848–1923), who studied the allocation of goods among economic agents in these terms. It is worth noting that although he is best remembered as an economist, he had a degree in engineering. Later, in the 1950s, many scholars who eventually made a big name in economics also worked on inventory management and workforce planning. Maybe, this lesson in interdisciplinarity has been forgotten in times of over-specialization and “publish or perish” (or is it publish and perish?) syndrome plaguing academia.

25 On the other hand, we should also mention that sometimes the model resulting from a convex combination of objectives may be easier to solve from a computational perspective.

26 See Section 3.5.

27 In fact, this is an alternative norm to the Euclidean one, which squares differences. Sometimes the norm based on absolute values is referred to as L1 norm, whereas the Euclidean norm is the L2 norm.

28 Differentiability is an obvious requirement, since if it does not hold, we cannot take the derivatives involved in the condition. The “regularity” conditions are known in the literature as constraint qualification conditions and assume many forms. One such condition is that the gradients of functions hj are linearly independent at x*. That this condition makes some sense is not too difficult to understand. The stationarity condition in Theorem 12.10 states that the gradient of the objective can be expressed as a linear combination of the gradient of the constraints. There are cases in which this is impossible; one such case occurs if the gradients of the constraints are parallel, as shown later in Example 12.17.

29 Once again, this line of reasoning is not quite correct, and it should be taken only as an intuitive justification. A correct proof requires a bit of hard work.

30 Another common name for Lagrange multipliers is “dual variables,” as opposed to the original variables x of the problem which are referred to as “primal.” This alternative name is related to the theory of duality in mathematical programming.

31 The change in sign is not really relevant, as it depends on how we build the Lagrangian function, but differentiability of the value function q(b) is not guaranteed in general.

32 In LP textbooks, calculations are efficiently organized in a tableau. The tableau is an excellent tool, if the purpose is torturing students by forcing them to solve toy LP problems using pencil, paper, and pocket calculators. I refrain from doing so, as I prefer to emphasize the link between the simplex method and the linear algebraic concepts we have used in describing it.

33 In practice, the simplex method works with simple bounds in a different way, but this is beyond the scope of the book.

34 See also Example 12.4.

35 We should mention that there are specific branch and bound approaches for the knapsack problem, exploiting its structure, but our aim is illustrating a more general idea in the simplest case.

36 The notation [x] corresponds to the “floor” operator, which rounds a fractional number down: [4.7] = 4.