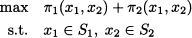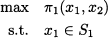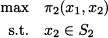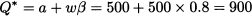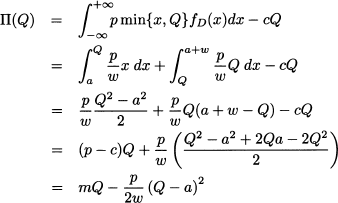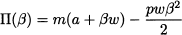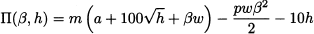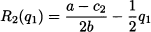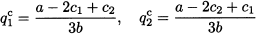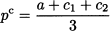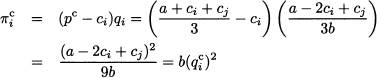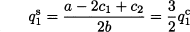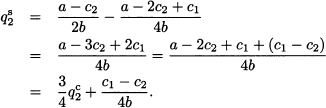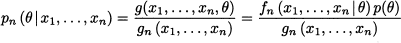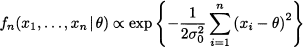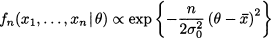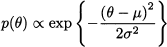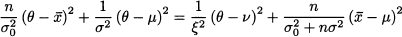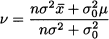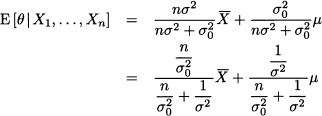Chapter 14
Multiple Decision Makers, Subjective Probability, and Other Wild Beasts
The previous chapters have presented a rather standard view of quantitative modeling. When dealing with probabilities, we have often taken for granted a frequentist perspective; our approach to statistics, especially in terms of parameter estimation, has been an orthodox one. Actually, these are not the only possible viewpoints. In fact, probability and statistics are a branch of mathematics at the boundary with philosophy of science, and as such they are not free from heated controversy. This might sound like a matter of academic debate, but it is not. The “death of probability” was invoked in the wake of the 2008 financial turmoil, when the quantitative modeling approach in finance has been blamed as one of the root causes of the disaster. Of course, truth always lies somewhere between extremes, but this is reason enough to see the need for an eye opening chapter, illustrating alternative views that have been put forward, like subjective probabilities and Bayesian statistics. A similar consideration applies to the chapters on decision models. There, we have also followed a standard route, implicitly assuming that decisions are made by one person keeping all problem dimensions under direct control. We have hinted at some difficulties in trading off multiple and conflicting objectives, when dealing with multiobjective optimization in Section 12.3.3. However, we did not fully address the thorny issues that are raised when multiple decision makers are involved. On the one hand, they can be interested in different objectives; on the other one, they may behave without coordinating their decisions with other actors. Decisions involving not necessarily cooperative actors are the subject of game theory. Rather surprising results are obtained when multiple players interact, possibly leading to suboptimal decisions; here, we do not mean suboptimal only for a single decision maker, but, for the whole set of them. Finally, standard models assume that uncertainty is exogenous, whereas there are many practical situations in which decisions do influence uncertainty, such as big trades on thin and illiquid financial markets or inventory management decisions affecting demand. When all of the above difficulties compound, multiple decision makers can influence one another through decisions, behavior, and information flows, possibly leading to instability due to vicious feedbacks. Such mechanisms have been put forward as an explanation of some major financial crashes.
We are certainly in no position to deal with such demanding topics extensively. They all would require their own (voluminous) book and the technicalities involved are far from trivial. However, I strongly believe that there must be room for a chapter fostering critical thinking about quantitative models. This is not to say that what we have dealt with so far is useless. On the contrary, it must be taken with a grain of salt and properly applied, keeping in mind that we could be missing quite important points, rendering our analysis irrelevant or even counterproductive. Unlike the rest of the book, the aim of this chapter is not to provide readers with working knowledge and ready-to-use methods; rather, a sequence of simple and stylized examples will hopefully stimulate curiosity and further study.
In Section 14.1 we discuss general issues concerning the difference between decision making under risk, the topic of the previous chapter, and decision making under uncertainty, which is related to a more radical view. In Section 14.2 we begin formalizing decision problems characterized by the presence of multiple noncooperative decision makers, setting the stage for the next sections, where we discuss the effects of conflicting viewpoints and introduce game theory. In Section 14.3 we illustrate the effect of misaligned incentives in a stylized example involving two decision makers in a supply chain. The two stakeholders aim at maximizing their own profit, and this results in a solution that does not maximize the overall profit of the supply chain. Such noncooperative behavior is the subject of game theory, which is the topic of Section 14.4. We broaden our view by outlining fundamental concepts about equilibrium, as well as games with sequential or simultaneous moves. Very stylized examples will illustrate the ideas, but this section is a bit more abstract than usual. Therefore, in Section 14.5, we show a more practical example related to equilibrium in traffic networks; this example, known as Braess’ paradox, shows that quite counterintuitive outcomes may result from noncooperative decision making. In Section 14.6 we discuss how the dynamic interaction among multiple actors may lead to instability and, ultimately, to disaster, by analyzing a couple of real-life financial market crashes. Finally, we close the chapter by providing the reader with a scent of Bayesian statistics in Section 14.7. Bayesian learning is related to parameter estimation issues in orthodox statistics; there, the basic concept is that parameters are unknown numbers; within this alternative framework, we may cope with probabilistic knowledge about parameters, possibly subjective in nature. As a concrete example, we outline the Black–Litterman portfolio optimization model, which can be interpreted as a Bayesian approach.
14.1 WHAT IS UNCERTAINTY?
When we flip a fair coin, we are uncertain about the outcome. However, we are pretty sure about the rules of the game: The coin will either land head or tail, and to all practical purposes we assume that the two outcomes are equally likely. However, what about an alien who has never seen a coin and does not take our probabilities for granted? Probably, it would face a more radical form of uncertainty, where the probabilities themselves are uncertain, and not only the outcome of the flip.1 By a similar token, sometimes we have plenty of reliable and relevant data about a random phenomenon, possibly featuring significant variability, which suggests the application of a frequentist concept of probability. Again, coming up with a good decision in such a setting may be far from trivial, but at least we might feel confident about our representation of uncertainty. Unfortunately, we are not always so lucky. Sometimes, we do not have relevant data, as we are facing a brand-new situation, as is the case when launching a truly innovative product. In other cases, the situation is so risky that we cannot have blind faith in statistical data analysis. How about an event with a very low probability, but potentially catastrophic?
Example 14.1 Suppose that we are interested in investigating the safety of an airport, in terms of its ability to manage the takeoff–landing traffic. Apparently, we should consider the statistics of accidents that may be blamed on the airport. However, hopefully, data on such accidents are so scarce that they are hardly relevant. In such a case, we should also consider the near misses, i.e., events that did not actually result in a disaster, but indicate that something is not working as it should. By the same token, car insurance companies are also interested in the driving habits of a potential customer, and not only in his accident track record.
This example shows that sometimes past statistics are not quite relevant because of lack of data. In other cases, even if we have plenty of data, a structural change in the phenomenon may make them irrelevant. In Chapter 5 we have pointed out that there are different interpretations of probabilities. Indeed, the cases above illustrate both the classical concept of probability, based on the idea that there are underlying equally likely outcomes, and the frequentist concept. However, probability may also be a measure of belief in a scientific theory, possibly including subjective elements. Some have even questioned the use of probability as a model of uncertainty. Alternative frameworks have been proposed, like fuzzy sets. We will stick to a probabilistic framework, but it is important to understand a few basic issues, with reference to Fig. 14.1. There, we use a familiar scenario tree (or fan) to represent uncertainty. We have to make a decision here and now, but its ultimate consequence depends on which future scenario will occur. According to a simple probabilistic view, each scenario Si is associated with a well-known probability πi, i = 1, 2, 3. Unfortunately, things are not always that easy.
Fig. 14.1 Schematic illustration of different kinds of uncertainty.

14.1.1 The standard case: decision making under risk
Let us compare two random experiments: fair coin flipping and the draw of a multidimensional random variable, with a possibly complicated joint probability density. The two cases may look quite different. The first one can be represented by a quite simple Bernoulli random variable, and calculating expected values of whatever function of the outcome is pretty straightforward. On the contrary, calculating an expectation in the second case may involve a possibly awkward multidimensional integral. However, the difference is more technical and computational than conceptual, as in both cases we assume that we have a full picture of uncertainty. The important point is that the risk we are facing is linked to the realization of a random variable, which is perfectly known from a probabilistic perspective. With reference to Fig. 14.1, we are pretty sure about:
1. The possible future scenarios, since we know exactly what might possibly happen, and there is no possibility unaccounted for.
2. The probabilities of these scenarios, whatever meaning we attach to them.
Hence, we have a full picture of the scenario tree. This standard case has been labeled as decision under risk, to draw the line between this and more radical views about uncertainty. Risk may be substantial; to see this, consider a one-shot decision when there is a very dangerous, but very unlikely scenario. Which decision model is appropriate to cope with such a case? There is no easy answer, but, at least, we have no uncertainty about our description of uncertainty itself.
14.1.2 Uncertainty about uncertainty
If we are about to launch a brand-new product, uncertainty about future sales is rather different from that in the previous case. Maybe, we know pretty well what may happen, so that the scenarios in Fig. 14.1 are known. However, it is quite hard to assess their probabilities. The following definitions, although not generally accepted, have been proposed:
- Risk is related to uncertainty about the realization of a random variable whose distribution is known.
- Uncertainty, in the strict sense, is related to:
— The parameters of a probability distribution whose qualitative form is known
— A probability distribution whose shape itself is unknown
We see that there are increasing levels of uncertainty. We may be pretty sure that the probability distribution of demand is normal, but we are not quite sure about its parameters; this is where we started feeling the need for inferential statistics and parameter estimation. Nonparametric statistics comes into play when we even question the type of probability distribution we should use. But even if we are armed with a formidable array of statistical techniques, we may lack the necessary data to apply them. Probability in this setting tends to be subjective and based on expert opinion.
Whatever the level of uncertainty, if the probabilities πi are not reliable, a more robust decision making model is needed, as we pointed out in Section 13.5.1; however, there may be something more at play, such as prior opinions and their revision by a learning mechanism. In Chapters 9 and 10 we have taken an orthodox view of statistics, based on the fundamental assumption that parameters are unknown numbers. Then, we try to estimate unknown parameters using estimators; estimators are random variables, and their realized value, the estimate, depends on data collected by random sampling. Given this framework, there are two consequences:
1. There is no probabilistic knowledge associated with parameters, and we never speak about the probability distribution of a parameter.2
2. There is no room for subjective opinions, and collected data are the only sensible information that we should use.
However, when facing new decision making problems, relying on subjective views may be not only appropriate, but also necessary. This is feasible within a Bayesian framework, whereby parameters are regarded as random variables themselves. Within this framework, the distribution that we associate with a parameter depicts our limited state of knowledge, possibly subjective in nature. As we outline in Section 14.7, in the Bayesian approach we start with a prior distribution, which reflects background information and subjective knowledge, or lack thereof; as new information is collected by random sampling, this is reflected by an update of the prior distribution, leading to a posterior distribution by the application of Bayes’ theorem.
Issues surrounding orthodox and Bayesian statistics are quite controversial, but one thing is sure: The probabilities πi in Fig. 14.1 may not be reliable, and we might move move from decision making under risk to decision-making under uncertainty.
14.1.3 Do black swans exist?
The most troublesome case is when some scenarios are particularly dangerous, yet quite unlikely. How can we trust estimates of very low probabilities? To get the message, consider financial risk management. Here we need to work with extreme events (stock market crashes, defaults on sovereign debt, etc.), whose probabilities can be very low and very difficult to assess, because of limited occurrence of such events in the past. Can we trust our ability to estimate the probability of a rare event? And what if we are missing some scenarios completely?
Example 14.2 (Barings Bank and Kobe earthquake) Barings bank was founded in 1762 and it had a long and remarkable history, which came to an abrupt end in 1995, when it was purchased by another bank for the nominal price of £1. The bank went bankrupt as a consequence of highly leveraged3 and risky positions in derivatives, taken by a rogue trader who managed to hide his trading activity behind some glitches in the internal risk management system of the bank. These strategies lead to disaster when Nikkei, the Tokyo stock market index, went south. When does a stock market crash? This can be the result of real industrial or economical problems, or maybe the financial distress of the banking system. Risk management models should account for the uncertainty in such underlying factors, and even unlikely extreme scenarios should enter the picture, when taking very risky positions. However, many have attributed that drop in the Nikkei index to swinging market mood after an earthquake stroke Kobe. Luckily, the earthquake was not hard enough to cause a real economic crisis; yet, its effect was pretty concrete on Barings, which had to face huge losses, ultimately leading to its demise.
Very sophisticated models have been built for financial applications, accounting for a lot of micro- and macro-economic factors, but it must take much imagination to build one considering the potential impact of an earthquake.
Indeed, the most radical form of uncertainty is when we cannot even trust our view about the possible scenarios. To reinforce the concept, imagine asking someone about the probability of a subprime mortgage crisis twenty years before 2007. In Fig. 14.1 we have depicted a black scenario with which it is impossible to associate a probability, for the simple reason that we do not even know beforehand that such a scenario may occur. In common parlance, these scenarios are referred to as “black swans.”4 When black swans are involved, measuring risk is quite difficult if not impossible. The term Knightian uncertainty was proposed much earlier to refer to unmeasurable uncertainty, after the economist Frank Knight drew the line between risk and uncertainty.5 It is quite difficult to assess the impact of unmeasurable uncertainty on a decision model, of course; maybe, there are cases in which we should just refrain from making decisions that can lead to disaster, however small its probability might look like (if nothing else, because of ethical reasons).
14.1.4 Is uncertainty purely exogenous?
The scenario tree of Fig. 14.1 may apply, e.g., to a two-stage stochastic programming problem. In a multistage stochastic programming model we have to make a sequence of decisions; a multistage scenario tree, like the one shown in Fig. 13.11, may be used to depict uncertainty. Even if we take for granted that sensible probabilities can be assigned and that no black swan is lurking somewhere, how can we be sure that our sequence of decisions will not affect uncertainty?
Example 14.3 Setting inventory levels at a retail store is a rather standard decision making problem under risk. Typically, the task requires choosing a model of demand uncertainty, which is an input to the decision procedure. However, which comes first: Our decision or demand uncertainty? Indeed, our very decision may affect uncertainty. Marketing studies show that the amount of items available on the shelves may affect demand. To see why, imagine buying the very last box of a product on a shelf, when there is plenty of a similar item just below. In this case, consumers’ psychology plays an important role, but even in a strict business-to-business problem, which need not involve such issues, an array of stockouts may be fatal to your customer demand. A naive newsvendor model may suggest a low service level because of low profit margins; since the order quantity should be the corresponding quantile of the probability distribution of demand, it will be very low as well, resulting in frequent stockouts. What such a model disregards is that the distribution itself will change as a consequence of our decision, if we offer a consistently low service level and keep disappointing customers. Even worse, this is likely to have an impact on the demand for other items as well. In practice, if a firm offers a catalogue of 1,000 items, it may well be the case that only 10% of them are profitable; the remaining ones are needed nonetheless, to support sales of profitable items.
The line we are drawing here is between endogenous and exogenous uncertainty. Standard decision models may fail to consider how decisions affect uncertainty, which is clearly relevant for sequential decision making. These issues may be exacerbated by the presence of multiple actors, possibly influencing each other by means of actions and information flows, giving rise to feedback effects. A quite relevant example of such nasty mechanisms is represented by financial markets instability and liquidity crises. We consider a couple of such stories in Section 14.6. But even if we disregard risk and uncertainty, the presence of multiple actors may have a relevant impact, as we illustrate in the next sections.
14.2 DECISION PROBLEMS WITH MULTIPLE DECISION MAKERS
Consider the decision problem
The objective function (14.1) can be interpreted in terms of a profit depending on two decision variables, x1 and x2, which must stay within feasible sets S1 and S2, respectively. Note that, even though the constraints on x1 and x2 are separable, we cannot decompose the overall problem, since the two decisions interact through the two profit functions π1(x1, x2) and π2(x1, x2). Nevertheless, using the array of optimization methods of Chapter 12, we should be able to find optimal decisions, x1* and x2*, yielding the optimal total profit
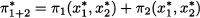
In doing so, we assume that there is either a single stakeholder in charge of making both decisions, or a pair of cooperative decision makers, in charge of choosing x1 and x2, respectively, but sharing a common desire to maximize the overall sum of profits. But how about the quite realistic case of two noncooperative decision makers, associated with profit functions π1(x1, x2) and π2(x1, x2), respectively?
Decision maker 1 wishes to solve the problem
whereas decision maker 2 wishes to solve the problem
Unfortunately, these two problems, stated as such, make no sense. Which value of x2 should we consider in problem (14.2)? Which value of x1 should we consider in problem (14.3)? We must clarify how the two decision makers make their moves.
1. One possibility is that the two decision makers act sequentially. For instance, decision maker 1 might select x1  S1 before decision maker 2 selects x2
S1 before decision maker 2 selects x2  S2. In this case, we may say that decision maker 1 is the leader, and decision maker 2 is the follower. In making her choice, decision maker 1 could try to anticipate the reaction of decision maker 2 to each possible value of x1.
S2. In this case, we may say that decision maker 1 is the leader, and decision maker 2 is the follower. In making her choice, decision maker 1 could try to anticipate the reaction of decision maker 2 to each possible value of x1.
2. Another possibility is that the two decisions are made simultaneously. Unfortunately, the conceptual tools that we have developed so far do not help us in making any sensible prediction about the overall outcome of such a simultaneous decision.
In Section 14.3 we illustrate the first case with a concrete, although stylized, example. Then, in section 14.4 we consider the second case as well, introducing a general theory of noncooperative games. Game theory aims at finding a sensible prediction of an equilibrium solution (x1e, x2e), which depends on the precise assumptions that we make about the structure of the game. Whatever equilibrium solution we obtain, it cannot yield an overall profit larger than π1+2* as the following inequality necessarily holds:
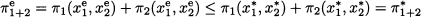
If this inequality were violated, (x1*, x2*) would not be the optimal solution of problem (14.1). This means that if decentralize decisions, the overall system is likely to lose something.
14.3 INCENTIVE MISALIGNMENT IN SUPPLY CHAIN MANAGEMENT
The last point that we stressed in the previous section is the potential difficulty due to the interaction of multiple noncooperative, if not competitive, decision makers. The example we consider is a generalization of the newsvendor model:6
1. Unlike the basic model, there are two decisions to be made. The ordering decision follows the same logic as the standard case, but there is another one, related to product quality, which influences the probability distribution of demand.
2. Since there are two decisions involved, we should distinguish two cases:
- In the integrated supply chain, there is only one decision maker in charge of both decisions.
- In the disintegrated supply chain, there are two decision makers; a producer, who is in charge of setting the level of her product quality, and a distributor, who is in charge of deciding his order quantity.
In order to be able to find analytical solutions, we depart from the usual assumption of normal demand, and we suppose a uniform distribution, say, between 500 and 1000. We will rely on the following notation; the lower bound of the distribution support is denoted by a and its width by w; hence, the expected value is a + w/2. In the numerical example, a = 500 and w = 1000 - 500 = 500. The item has a production cost of c = €0.20 and sells at a price p = €1.00. To keep things as simple as possible, we suppose that the unsold items are just scrapped, and there is no salvage value. With the numbers above, we see that service level should be7
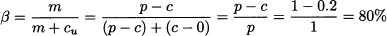
where m = p - c is the profit margin and cu = c is the cost of unsold items, when there is no salvage value. The optimal order quantity is
Since the probability distribution is uniform, we may easily compute the expected profit. This requires calculating fairly simple integrals involving the constant demand density
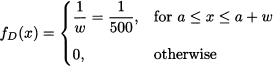
The expected profit depends on Q and it amounts to the expected revenue minus cost:
This expression of expected profit may be interpreted as profit related to the purchased quantity, minus the expected lost revenue due to unsold items.8 To get an intuitive feeling for Eq. (14.5), we may refer to Fig. 14.2, where lost revenue is plotted against demand, for a given order quantity Q. When demand is at its lower bound, D = a, lost revenue is p(Q - a); when demand is D = Q, lost revenue is 0. For intermediate values of demand, lost revenue is a decreasing function of demand and results in the triangle illustrated in the figure. To evaluate the expected value of lost revenue, we should integrate this function, multiplied by the probability density 1/w. But this is simply the area of the triangle in Fig. 14.2, P(Q - a)2/2, times 1/w, which in fact yields the second term in Eq. (14.5). With our numerical data, the optimal expected profit is
Fig. 14.2 A geometric illustration of Eq. (14.5).

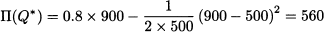
We may also express the expected profit as a function of the service level β, by plugging Eq. (14.4) into Eq. (14.5):
So far, we have always assumed that a demand distribution cannot be influenced by the producer. However, she could improve the product or adopt marketing strategies to change the distribution a bit. The result depends on the effort she spends, which in turn has a cost. Let us measure the amount of effort by h, with unit cost 10. To model the effect of h on demand, we make the following assumptions:
1. For the sake of simplicity, we assume a pure shift in the uniform distribution of demand. Its lower bound a is shifted, but its support width w does not change.9
2. The shift in a should be a concave function of h, to represent the fact that effort is decreasingly effective for increasing levels (diminishing marginal return). One possible building block that we can use is the square-root function.
Hence, we represent the lower extreme of the distribution support by the following function of h:
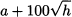
For instance, with our numerical parameters, if h = 1 the lower bound a shifts from 500 to 600. Using Eq. (14.6), we see that, if we include the effort h, the expected profit becomes
Note that the optimal service level does not change, according to our model, since we do not change either the unit cost of the item or its selling price. To find the optimal effort, we should take the first-order derivative of expected profit (14.7) with respect to h and set it to 0:
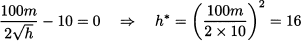
We notice that this condition equates the marginal increase of expected profit contribution from production and sales with the marginal cost of the effort. With this effort, the new probability distribution is uniform between 900 and 1400, the optimal produced quantity increases to Q* = 1300, and by applying Eq. (14.7) the new total expected profit is
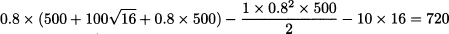
This is the optimal profit resulting from the joint optimal decisions concerning effort level h and purchased amount Q.
The above calculations are formally correct, but potentially flawed: They rely on the assumption that there is one decision maker maximizing overall expected profit and in control of both decisions. What if we have a supply chain with different stakeholders in charge of each decision, with possibly conflicting objectives? To see the impact of misaligned incentives, let us assume that there are two stakeholders:
1. The producer, who is in charge of determining the quality of the product and its potential for sales, through the effort h
2. The distributor, who is in charge of determining the order quantity Q, depending on the probability distribution of demand and the prices at which he can buy and sell
We cannot analyze such a system if we do not clarify not only who is in charge of deciding what, but also when and on the basis of what information. So, to be specific, let as assume the following:
- The producer is the leader and the distributor is the follower, in the sense that the producer decides her effort level h first, and then the distributor will select his order quantity Q. It must be stressed that, in deciding the effort level h, the producer should somehow anticipate how her choice will influence the choice of Q by the distributor.
- The producer is also the leader in the sense that she is the one in charge of pricing decisions, which we assume given. She keeps the selling price fixed at €1.00 and sells each item to the distributor for a price of €0.80, which is the purchase cost from the viewpoint of the distributor. Please note that the profit margin for the distributor is just €0.20; furthermore, he is the one facing all of the risk, as items have no salvage value and there is no buyback agreement in case of unsold items.
- Last but not least, everything is common knowledge, in the sense that the producer knows how the distributor is going to make his decision and both agree on the probability distribution of demand and how this is affected by the effort level h.
The last point implies that when the producer makes her decision, she can anticipate what the optimal decision of the distributor is going to be; hence, she can build a reaction function, also known as best response function, describing how the order quantity Q is influenced by her effort level h. From the point of view of the follower, i.e., the distributor, once the effort h is decided by the leader, the only thing he can do is to determine the order quantity as a function of h. Under our simple assumption of a pure shift in the demand distribution, we have
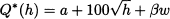
This expression look just the same as before but there is a fundamental difference. Under our assumptions, the production cost and the selling price do not change, but now, since the profit margin is shared, the optimal service level for the distributor is only
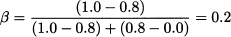
There is a remarkable reduction in the service level, from 80% to 20%, because of the high price at which the distributor buys from the producer. Indeed, the split of the profit is €0.60 to the producer and €0.20 to the distributor. Plugging numbers, the optimal order quantity is
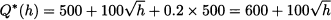
This is how the producer can anticipate the effect of her choice of h on the decision of the distributor, which in turn influences her profit. The profit from the point of view of the producer is
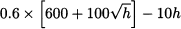
Applying the first-order optimality condition, we obtain the optimal effort, and then the optimal order quantity:
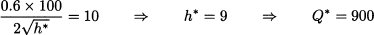
The new optimal order quantity depends on the fact that the shifted probability distribution of demand, with that level of effort, is uniform between 800 and 1300, and optimal service level is just 20%. A first observation that we can make is that both effort and order quantity are reduced when supply chain management is decentralized. This implies that consumers will receive a worse product and a reduced service level. What is also relevant, though, is the change in profit for the two players. The profit of the producer is
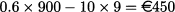
This profit is considerably reduced with respect to expected profit for the producer when she also manages distribution, which is €720. Of course, this is not quite surprising, since the producer has given up a fraction of her profit margin, leaving it to the distributor. Unlike the producer, the distributor faces an uncertain profit. Its expected value can be obtained from Eq. (14.5), after adjusting the parameters to reflect the reduced profit margin
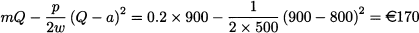
The expected profit for the distributor is less than the (certain) profit of the producer, but this is no surprise after all, considering how margins are split between the two parties. Last but not least, the total profit for the disintegrated supply chain is
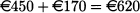
which is €100 less than the total profit for the fully integrated supply chain. Again, this is reasonable, in light of the concepts of Section 14.2.
These observations raise a couple of points:
1. One might well wonder why the producer should delegate distribution to someone else. Actually, there is a twofold answer:
- Her profit now is a certain amount and not an expected value, since the whole risk is transferred to the distributor.
- We did not consider fixed costs related to distribution; they may not impact optimal decisions at the tactical or operational level, but they do have an impact on the bottom line and on strategic decisions.
We may also add further considerations concerning the fact that a distributor is probably better equipped at making demand forecasts and has a better incentive to offer additional services to the customer.
2. In splitting profit margins and decentralizing decisions, something has been lost for everyone: the producer, the distributor, and, last but not least, the customers, who receive less quality and less service. In principle, we could try to find the “optimal split” of profit margins, i.e., the allocation of margins that maximizes the total profit. Of course, this is hardly feasible in practice, as it would require cooperation between the two stakeholders; furthermore, in general, the overall profit will remain suboptimal, anyway. There are practical ways to realign the incentives by shifting fixed amounts of money between the parties, as a lump payment does not affect the above decisions, since it is a constant amount and does not affect the calculation of the derivatives that are involved in the optimality conditions. An alternative is to redistribute risks by introducing buyback contracts;10 if risk is shared between the two stakeholders, the optimal service level for the distributor is increased. The best strategy depends on the specific problem setting, as well as on the relative strengths of the parties involved.
In closing this section, we should note that, although this supply chain problem involves uncertainty in demand, this is not the key point. Coordination issues arise in purely deterministic problems, like the ones we show in Sections 14.4 and 14.5.
14.4 GAME THEORY
In the previous section we have considered a case in which two stakeholders, a producer and a distributor, make their decisions in a specific order. The producer (leader) determines product quality, as well as the probability distribution of demand as a consequence; the distributor (follower) chooses the order quantity. In other cases, however, decisions are taken simultaneously, at least in principle. In fact, the term “simultaneously” need not be taken literally; the point is that no player has any information about what others have previously chosen and cannot use this as an input for her decision. Predicting the outcome of the joint decisions is no easy task in general, and it is the aim of game theory. There is no hope to treat this challenging subject adequately in a few pages, but for our purposes it is quite enough to grasp a few fundamental concepts; these will be illustrated by very stylized examples in this section; in the next one, we consider a paradoxical result in traffic networks, which is a result of noncooperation between decision makers, namely, drivers in that case.
For the sake of simplicity, we consider a very stylized setting:
- There are only two decision makers (players); each player has an objective (payoff) that she wants to maximize and there is no form of cooperation.
- Only one decision has to be made; hence, we do not consider sequential games in which multiple decisions are made over time.
- We assume complete information and common knowledge.11 Formalizing these concepts precisely is not that trivial, but (very) loosely speaking they mean that there is no uncertainty about the data of the problem nor about the mechanisms that map decisions into payoffs. The two players agree on their view of the world, the rules of the game, and know the incentives of the other party; furthermore, each player knows that the other one has all of the relevant information.
There are different ways to represent a game. The best way to understand the basic concepts is by considering the situation in which players must choose within a very small and discrete set of available actions, and the game is represented in normal form.
14.4.1 Games in normal form
The standard example to illustrate the normal form representation of a simple game is the prisoner’s dilemma, which is arguably the prototypical example of a two-player game. The prisoner’s dilemma has been phrased in many different ways;12 in the next example we use what is closest to a business management setting.
Example 14.4 (Prisoner’s dilemma) Consider two firms, say, A and B, which have to set the prices at which their products are sold. The products are equivalent, so price is a major determinant of sales. On the one hand, firm A would like to keep its price high, to keep revenues high as well; on the other one, if the competitor firm B lowers its price, it will erode the market share of firm A. Indeed, sometimes a price war erupts, reducing profits for both firms. To represent the problem, let us assume that there are only two possible prices, low and high. Hence, we consider only a discrete set of possible actions: it is also possible to formalize a game with a continuum of actions represented by real numbers. The following outcomes could result, depending on firms’ actions:
- If firm A sets a high price and firm B sets a low price, firm A will be wiped off the market and firm B will get a huge reward; we obtain a symmetric outcome if we swap firms’ actions.
- If both firms set a low price, the result of this price war will be a fairly low profit for both firms.
Table 14.1 Representation of prisoner’s dilemma in normal form.
| Firm B | ||
| Firm A | Low | High |
| Low | (1, 1) | (3, 0) |
| High | (0, 3) | (2, 2) |
- If firms collude and both of them set a high price, the result will be a fairly high profit for both of them.
Depending on the action selected by all of the players, they will receive a payoff. Unlike the optimization models that we have described in Chapters 12 and 13, the payoff for each player is a function of the decisions of all of the players. Representing the game in normal form requires to specify the payoff to each player, for any combination of actions. The normal form of prisoner’s dilemma is illustrated in Table 14.1. Firm A is the row player and firm B is the column player. Each cell in the table shows the payoff to firms A and B, respectively; the first number is the payoff for the row player, and the second number is the payoff to the column player:
- If both firms play high, the payoff is 2 for both of them.
- If firm A plays high, but firm B plays low, the payoff is 0 for the former and 3 for the latter; these payoffs are swapped if firm A plays low, but firm B plays high.
- If both firms play low, the ensuing price war results in a payoff 1 for each firm.
Actions are selected simultaneously, and we need a sensible way of predicting the result of the game.
It is easy to see that the normal form of a game is appropriate for a small and nonsequential game, and different representations might be more suitable in other cases. In particular, sequential games involve the selection of multiple actions by each player; each action, in general, may depend on the previous choices by the other players. When there is a discrete set of actions available at each stage of the game, this can be represented in extensive form by a tree, much like the decision trees of Section 13.1. Indeed, decision trees may be regarded as a multistage game between the decision maker and nature, which randomly selects an outcome at each chance node. Solving a decision tree requires the specification of a strategy, i.e., a selection of a choice for each decision node. By a similar token, a multistage game requires the specification of a strategy for each player, i.e., a mapping from each state/node in the tree to the set of available actions of the player that must make a choice at that stage of the game. We will not consider the extensive form of a game in this book. Furthermore, we consider only pure strategies, whereby one action is selected by a player. In mixed strategies, each action is selected with a certain probability. Even though we neglect these more advanced concepts, we see that actions are only the building blocks of strategies. Therefore, in the following text we will use the latter term, even though in our very simple examples actions and strategies coincide.
Now we are able to formalize a simple game involving n players; to specify such a game we need:
- The set of available strategies Si for each player, i = 1, …, n; in other words, we need the set of available strategies for each player.
- The set of payoff functions πj(s1, s2, …, sn) for each player j = 1, …, n; the payoff depends on the set of strategies si
 Si selected by all of the players, within the respective feasible set Si.
Si selected by all of the players, within the respective feasible set Si.
Note that, given a set of strategies, the payoff is known, as there is no uncertainty involved; furthermore, each player knows the set of available strategies of the other players, as well as their payoff functions. Hence, all of the players have a clear picture of the incentives of the other players and there is no hidden agenda. Clearly, this is only the simplest kind of game one can consider; partial information and uncertainty are involved in more realistic models. Now the problem is to figure out which outcome should be expected as a result of the game, where by outcome we mean a vector of strategies  , one per player.
, one per player.
14.4.2 Equilibrium in dominant strategies
Sometimes, it is fairly easy to argue which outcome is to be expected. If we consider the strategies for firm A in Table 14.1, we see that:
- If firm B plays high, firm A is better off by playing low, since the payoff 3 is larger than 2.
- If firm B plays low, firm A is better off by playing low, since the payoff 1 is larger than 0.
So, whatever firm B plays, firm A is better off by playing low. The symmetry of the game implies that the same consideration applies to firm B, which will also play low. If there is a single strategy that is preferred by a player, whatever the other players do, it is fairly easy to predict her move. A formalization of this observation leads to the concept of dominant strategy.13
DEFINITION 14.1 (Strictly dominant strategy) A strategy sia strictly dominates strategy sib for player i if
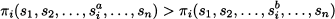
for any possible combination of strategies selected by the other players. There is a strictly dominant strategy si* for player i if it strictly dominates all of the alternatives:
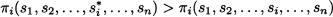
for all alternative strategies si ≠ si* of player i and for all possible strategies sj of players j ≠ i.
In the above definition we only consider strict domination, which involves strict inequalities. For the sake of brevity, in the following we will often just speak of dominant or dominated strategies, leaving the “strict” qualifier aside; actually, some results in game theory do require strict dominance, but we will not be too precise. Clearly, dominant strategies need not exist, but if one exist for a player, it is an easy matter to predict her behavior. It is also important to notice that, in such a case, the prediction assumes only player’s rationality, and there is no overly stringent requirement concerning what she knows or assumes to know about the other players. Furthermore, if there is a dominant strategy for each player, it is also easy to predict the overall outcome of the game.
DEFINITION 14.2 (Equilibrium in dominant strategies) An outcome ($sT1, $sT2, …, $sTn) is an equilibrium in dominant strategies if $sTi  Si is a dominant strategy for each player i, i = 1, …, n.
Si is a dominant strategy for each player i, i = 1, …, n.
If an outcome is an equilibrium in dominant strategies, given that no rational player will play a dominated strategy, it is sensible to predict that this outcome will be the result of the game. In the prisoner’s dilemma, the strategy low is dominant for both players, and we may argue that the outcome will indeed be (low, low). An important observation is that the resulting payoff for the firms is (1, 1); if the two firms selected (high, high), the payoff would be (2, 2), which is higher for both players. Using the terminology of multiobjective optimization,14 the second outcome would be preferred by both players and is Pareto-dominant. However, the lack of coordination between players results in a lower payoff to both of them. The problem with the outcome (low, low) is that it is an unstable equilibrium. Incidentally, we observe that certain firms are often prone to collude on prices, and this is exactly why anti-trust authorities have been set up all around the globe; hence, one could wonder if the above prediction makes empirical sense. The key issue here is that we are considering only a one-shot game. Collusion may be the outcome of more complicated, as well as more realistic, multistage models that capture strategic interaction between firms.
Table 14.2 Battle of the sexes.
| Romeo | ||
| Juliet | Horror | Shopping |
| Horror | (1, 3) | (0, 0) |
| Shopping | (0, 0) | (3, 1) |
It is reasonable to expect that an equilibrium in dominant strategies may only be found in trivial games. The following is a classical example in which no equilibrium in dominant strategies exists.
Example 14.5 (Battle of the sexes) After a long week of hard work, Romeo and Juliet have to decide how to spend their Saturday afternoon. There are two choices available:
1. Attending a horror movie festival, which we denote as strategy horror and is much preferred by Romeo.
2. Going on a shoe shopping spree, which we denote as strategy shopping and is much preferred by Juliet.
Despite their differences in taste, Romeo and Juliet are pretty romantic lovers, so they would prefer to spend their time together anyway. Their preferences may be represented by the payoffs in Table 14.2. We note that if the two players select different strategies, the payoff is zero to both of them, as they will be alone. If the outcome is (shopping, shopping), the resulting payoff will be 3 to Juliet, who would be very happy, and 1 to Romeo, who at least will spend his time and more with his sweetheart. Payoffs are reversed for outcome (horror, horror). The game is simple enough, and in practice it can be seen as a stylized model of two firms that should agree on a standard to make their respective products compatible; these games are called coordination games. However, it is easy to see that there is no dominant strategy for either player. For instance, Romeo would play horror, if he knew that Juliet is about to play horror; however, if he knew that Juliet is going to play shopping, he would change his mind.
Equilibrium in dominant strategies is based on a very restrictive requirement, but we may try to guess the outcome in a slightly more elaborated way, by assuming that all players are rational and that everything is common knowledge. The idea is iterated elimination of dominated strategies and is best illustrated by an example.
Table 14.3 Predicting an outcome by iterated elimination of dominated strategies.

Example 14.6 Consider the game in Table 14.3. Table 14.3(a) describes the game in normal form; note that the row player 1 has two possible strategies, top and bottom, whereas the column player 2 has three available strategies, left, center, and right. Let us compare strategies center and right from the viewpoint of player 2. Checking her payoffs, we see that, whatever the choice of player 1, it is better for player 2 to choose center rather than right, as 2 > 1 and 1 > 0; indeed, center dominates right. Eliminating the dominated strategy from further consideration, we obtain Table 14.3(b). By a similar token, from the viewpoint of player 1, we see that strategy bottom is dominated by top, since 1 > 0. Eliminating the dominated strategy, we get Table 14.3(c). Now, we see that the payoff to player 1 is 1 in any case, whereas player 2 will definitely play center, since 2 > 0. Then, we predict the outcome (top, center).
The procedure above sounds quite reasonable. However, a few considerations are in order.
- We should wonder whether the resulting outcome, if any, depends on the sequence that we follow in eliminating dominated strategies. However, it can be shown that strict dominance makes sure that whatever sequence we take, we will find the same result.
Table 14.4 Can you trust your opponent’s rationality?
| Player 2 | ||
| Player 1 | Left | Right |
| Top | (1, 0) | (1, 1) |
| Bottom | (-1000, 0) | (2, 1) |
- We may fail to find a prediction, when strict dominance does not apply.
- We have to assume that all players are rational and that everything is common knowledge. This, for instance requires that each of the two players knows that the other one is rational, that she knows that the other one knows that she is rational, and so on. As we pointed out, formalizing the intuitive idea of common knowledge is not quite trivial, but the following example shows that this assumption may be critical.
Example 14.7 Trusting the other player’s rationality can be dangerous indeed. Consider the game in Table 14.4. If player 2 is rational, she should choose the strictly dominant strategy right, because it ensures a payoff 1 > 0, whatever the choice of player 1 is. If we eliminate left, it is easy to see that the outcome should be (bottom, right), since by playing bottom player 1 gets a payoff 2 > 1. However, playing bottom is quite risky for player 1 since, if player 2 makes the wrong choice, his payoff will be -1000.
14.4.3 Nash equilibrium
The concepts that we have used so far make sense, but they are a bit too restrictive and limit the set of games for which we may make reasonable predictions. A better approach, in a sense that we should clarify, is Nash equilibrium. Before formalizing the concept, imagine a game in which there is one sensible prediction of the outcome. If the prediction makes sense, all players should find it acceptable, in the sense that they would not be willing to deviate from the prescribed strategy, if no other player deviates as well: The equilibrium should be stable.
DEFINITION 14.3 (Nash equilibrium) An outcome (s1*, s2*, …, sn*) is a Nash equilibrium if no player would gain anything by choosing another strategy, provided that the other players do not change their strategy; in other words, no player i has an incentive to deviate from strategy si*. Let us denote the set of strategies played by all players but i as
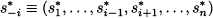
This can be used to streamline notation as follows:
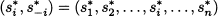
Then, for any player i, si* is the best response to s-i*:
(14.8) 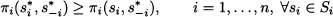
The best way to grasp Nash equilibria is by a simple example, in which we also illustrate a possible way to find them for two-players games with discrete sets of actions.
Table 14.5 Finding Nash equilibrium for the game in Table 14.3. Player 2 Player 1 Left Center Right

Example 14.8 To find a Nash equilibrium, we can:
1. Consider each player in turn, and find her best strategy for each possible strategy of the opponent; for the row player, this means considering each column (strategy of the column player) and find the best row (best response of row player) by marking the corresponding payoff; rows and columns are swapped for the column player.
2. Check if there is any cell in which both payoffs are marked; all such cells are Nash equilibria.
Let us apply the idea to the game in Table 14.3; the results are shown in Table 14.5. If we start with row player 1, we see that her best response to left is top, as 1 > 0; then we underline the payoff 1 in the top-left cell; by the same token, player 1 should respond with top to center, and with bottom to right. Then we proceed with column player 2; we notice that her best response to top is center, since 2 = max{0, 2, 1}; if player 1 plays bottom, player 2 should choose left. In this game, there is no need to break ties, as for each row there is exactly one payoff preferred by the column player, and for each column there is exactly one payoff preferred by the row player. The outcome (top, center) is the only cell with both payoffs marked, and indeed it is a Nash equilibrium. To better grasp what Nash equilibrium is about, note that no player has an incentive to deviate from this outcome, if the other player does not.
We see that the Nash equilibrium in the example is the same outcome that we predicted by iterated elimination of (strongly) dominated strategies. Indeed, it can be proved that:
- If iterated elimination of (strictly) dominated strategies results in a unique outcome, then this is a Nash equilibrium.
- If a Nash equilibrium exists, it is not eliminated by the iterated elimination of (strictly) dominated strategies.
We should note that Nash equilibria may not exist,15 and they need not be unique (see problem 14.1). However, they are a more powerful tool than elimination of dominated strategies, as they may provide us with an answer when the use of dominated strategies fail, without contradicting the prediction of iterated elimination, when this works. In other words, since Nash equilibria are based on less restrictive assumptions than iterated elimination, it fails less often.16 Last but not least, the prediction suggested by Nash equilibria makes sense and sounds plausible enough.
Now it is natural to wonder about more complicated settings, like the case in which each player has a continuum of strategies at her disposal. To this aim, it is useful to interpret Nash equilibria in terms of best response functions.
DEFINITION 14.4 (Best response function) The best response function for each player i is a function
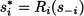
mapping the strategies of the other players into the strategy si* maximizing the payoff of i in response to s-i.
We immediately see that a Nash equilibrium is a solution of a system of equations defined by the best response functions of all players. For a two-player game, we should essentially solve the following system of two equations
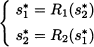
14.4.4 Simultaneous vs. sequential games
In this section we consider Nash equilibrium for the case in which a continuum of infinite actions is available to each player. To be specific, we analyze the behavior of two firms competing with each other in terms of quantities produced. Both firms would like to maximize their profit, but they influence each other since their choices of quantities have an impact on the price at which the product is sold on the market. This price is common to both firms, as we assume that they produce a perfectly identical product and there is no possibility of differentiating prices. This kind of competition is called Cournot competition; the case in which firms compete on prices is called Bertrand competition, but it will not be analyzed here. We start with the case of simultaneous moves, which leads to the Cournot–Nash equilibrium.17 Then we will consider sequential moves.
To clarify these concepts it is useful to tackle a simple model, in which we assume that each firm has a cost structure involving only a variable cost:
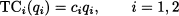
Here, TCi denotes total cost for firm i, ci is the variable cost, and qi is the amount produced by firm i - 1, 2. The total amount available on the market is Q = q1 + q2, and it is going to influence price. In Section 2.11.5 we introduced the concepts of demand and inverse demand functions, relating price and demand. There, we assumed the simplest relationship, i.e., a linear one. By a similar token, we assume here that there is a linear relationship between total quantity produced and price:

Incidentally, this stylized model assumes implicitly that all produced items are sold on the market. Then, the profit for firm i is
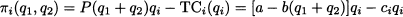
Note that the profit of each firm is influenced by the decisions of the competitor. Assuming that the two firms make their decisions simultaneously, it is natural to wonder what the Nash equilibrium will be. Note that we assume complete information and common knowledge, in the sense that each player has all of the above information and knows that the other player has such information. We can find the equilibrium by finding the best response function Ri(qj) for each firm, i.e., a function giving the profit-maximizing quantity qi* for firm i, for each possible value of qj set by firm j. Enforcing the stationarity condition for the profit of firm 1, we find
(14.9) 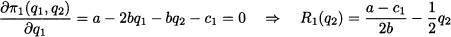
By the same token, for firm 2 we have
To solve the problem, we should find where the two response functions intersect; in other words, we should solve the system of equations
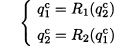
where we use the superscript “c” to denote Cournot equilibrium. In our case, we are lucky, since response functions are linear. In particular, both response functions are downward-sloping lines, as illustrated in Fig. 14.3. Hence, to find the Nash equilibrium we simply solve the system of linear equations
Fig. 14.3 Finding a Nash equilibrium in Cournot competition.

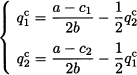
which yields
The resulting equilibrium price turns out to be
and the profit of each firm is
It is interesting to note that if a firm manages to reduce its cost, it will increase its produced quantity and profit as well. We leave this check as an exercise. It is also worth noting that if the firms have the same production technology (i.e., c1 = c2), then we have a symmetric solution q1c = q2c, as expected.
So far, we have assumed that the two competing firms play simultaneously. In the supply chain management problem of Section 14.3, since there are two different types of actions, it is more natural to assume that one of the two players moves first. Hence, we may also wonder what happens in the quantity game of this section if we assume that firm 1, the leader, sets its quantity q1 before firm 2, the follower. Unlike the simultaneous game, firm 2 knows the decision of firm 1 before making its decision; thus, firm 2 has perfect information. The analysis of the resulting sequential game leads to von Stackelberg equilibrium. Firm 1 makes its decision knowing the best response function for firm 2, as given in Eq. (14.10). Hence, the leader’s problem is
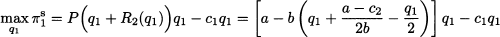
where the superscript “s” refers to von Stackelberg competition. Applying the stationarity condition yields
We see that firm 1 produces more in this sequential game than in the Cournot game. If we plug this value into the best response function R2(q1), we obtain
We see that the output of firm 2 is a fraction of that of the Cournot game, plus a term that is positive if firm 1 is less efficient than firm 2. Now it would be interesting to compare the profits for the two firms under this kind of game. This is easy to do when marginal production costs are the same; we illustrate the idea with a toy numerical example.
Example 14.9 Two firms have the same marginal production cost, c1 = c2 = 5, and the market is characterized by the price/quantity function
In this example we compare three cases:
1. The two firms collude and work together as a cartel. We may also consider the two firms as two branches of a monopolist firm. Note that if the two marginal costs were different, one of the two branches would be just shut down (assuming infinite production capacity, as we did so far).
2. The firms do not cooperate and move simultaneously (Cournot game).
3. The firms do not cooperate and move sequentially (von Stackelberg game).
In the first case, we just need to work with the aggregate output Q. The monopolist solves the problem
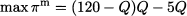
where superscript “m” indicates that we are referring to the monopolist case. We solve the problem by applying the stationarity condition

which yields the following market price and profit:
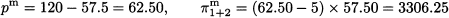
In the second case, the solution given by (14.11) is symmetric:
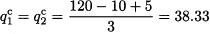
The overall output and price are

respectively. The profit for each firm is
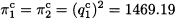
Note that the total overall profit is
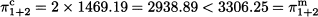
In fact, the monopolist would restrict output to increase price, resulting in a larger overall profit than with the Cournot competition. So, collusion results in a larger profit than competition, which is no surprise.
Let us consider now the von Stackelberg sequential game. Using (14.14) and (14.15), we see that
Table 14.6 Battle of the sexes, alternative version.
| Romeo | ||
| Morticia | Cinema | Restaurant |
| Cinema | (5, -100) | (0, 1) |
| Restaurant | (0, 1) | (5, -100) |
from which we see that, with respect to the simultaneous game, the output of firm 1 is increased whereas the output of firm 2 is decreased. The total output and price are

respectively. The price is lower than in both previous cases, and the distribution of profit is now quite asymmetric:
The overall profit for the sequential game is lower than for the simultaneous one; however, the leader has a definite advantage and its profit is larger in the sequential game.
The toy example above shows that the privilege of moving first may yield an advantage to the leader. Given the structure of the game, it is easy to see that the leader of the sequential game cannot do worse than in the simultaneous game; in fact, she could produce the same amount as in the Cournot game, anyway. However, this need not apply in general. In particular, when there are asymmetries in information or things are random, the choice of the leader, or its outcome when there is uncertainty, could provide the follower with useful information. The following example shows that being the first to move is not always desirable.
Example 14.10 (Battle of the sexes, alternative versions) Let us consider again the battle of the sexes of Example 14.5, where now we assume that Juliet has the privilege of moving first. Given the payoffs in Table 14.2, she knows that, whatever her choice, Romeo will play the move that allows him to enjoy her company. Hence, she will play shopping for sure. In this case, Juliet does not face the uncertainty due to the presence of two Nash equilibria in Table 14.2 and is certainly happy to move first. The situation is quite different for the payoffs in Table 14.6. In this case, Romeo is indifferent between going to cinema or restaurant. What he really dreads is an evening with Morticia. It is easy to see that this game has no Nash equilibrium, as one of the two players has always an incentive to deviate. An equilibrium can be found if we admit mixed strategies, in which players select a strategy according to a probability distribution, related to the uncertainty about the move of the competitor. We do not consider mixed strategies here, but the important point in this case is that no player would like to move first.
We noted that the first version of the battle of the sexes is a stylized coordination game for two firms that should adopt a common standard; in this second version, one firm wants to adopt the same standard as the competitor, whereas the other firm would like to select a different one.
14.5 BRAESS’ PARADOX FOR TRAFFIC NETWORKS
The result of the collective interaction of noncooperative players may be occasionally quite surprising. We illustrate here a little example of the Braess’ paradox for traffic networks.18 Imagine a traffic network consisting of links such as road segments, bridges, and whatnot. Most of us had some pretty bad experiences with traffic jams. Intuition would suggest that adding a link to the network should improve the situation or, to the very least, should not make things worse.
Consider the network in Fig. 14.4.19 In Fig. 14.4(a) we have a four-node
Fig. 14.4 An example of the Braess’ paradox.
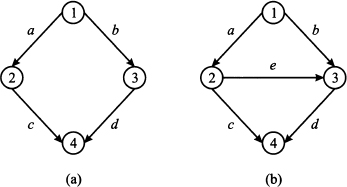
directed network, where the following costs are associated with each arc:
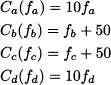
The meaning of these costs should be clarified: They are the traveling costs for an individual driving along each arc, where the flows fa, fb, fc, and fd are the total number of drivers using the corresponding arc. Keep in mind that in game theory the payoff to each player depends on the decisions of the other players as well, and players do not cooperate. In fact, the paradox applies to a problem where drivers have to choose a path independently of each other, but they interact through the level of congestion. This is not a classical network flow problem, where a centralized planner optimizes the overall flow minimizing total cost. Each driver selects a route in a noncooperative way, and we should look for an equilibrium. Traffic equilibrium is beyond the scope of the book, but we may take advantage of the symmetry of the example above. Imagine that the total travel demand is 6, i.e., there are six drivers that must go from node 1 to node 4. There are two possible paths, i.e., sequences of arcs: P1 = (a, c) and P2 = (b, d). Let us denote by fP1* and fP2* the traffic flows along each path at equilibrium. The cost for path P1 is
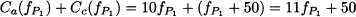
But this happens to be the same as the cost for path P2:
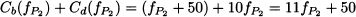
Since the problem is symmetric, intuition suggests that, at equilibrium, the total travel demand is split in two: fP1* = fP2* = 3. Then, the cost of each path for each driver is
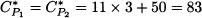
No single driver has an incentive to deviate, because if a driver switches to the other path, her cost would rise to 11 x 4 + 50 = 94. Hence, this is a Nash equilibrium.
Now consider the network 14.4(b), where arc e has been added, whose cost is
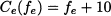
Now, we have an additional path P3 = (a, e, d). Having opened a new route, some drivers have an incentive to deviate. For instance, if a driver moves from path P1 to path P3, her cost would be
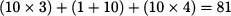
What new equilibrium will emerge? Let us try a symmetric solution again: xP1* = xP2* = xP3* = 2. At this level of flow, the costs of the three paths are
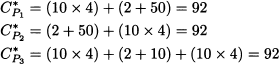
We observe that the three costs are the same, and no one has an incentive to deviate. However, with this equilibrium, every driver is worse off!
The peculiarity of the example above might suggest that this kind of problem is too pathological to actually arise. However, real-life cases have been reported in the literature, where closing a link in a network has improved the situation or adding a new one has created a congestion.20 The crux of the problem, once again, is the collective behavior of several noncooperative decision makers. In business management, this is a common occurrence that should not be dismissed.
14.6 DYNAMIC FEEDBACK EFFECTS AND HERDING BEHAVIOR
Game theory in its simplest form does not consider dynamics, as it revolves around a static equilibrium concept: It posits a situation such that no player has an incentive to deviate. But how is that equilibrium reached dynamically? And what about the disorderly interaction of many stakeholders, maybe stockholders in financial markets? Addressing such issues is beyond the scope of this book, but we illustrate their relevance with two real-life examples; they show that the effects of such interactions may be quite nasty and that uncertainty may not always be adequately represented by an exogenous probability distribution.
Example 14.11 (Long-Term Capital Management) Many financial equilibrium models, like CAPM, assume that no player is big enough to influence markets. However, in specific conditions, players may turn out to be so big that their actions on thin or illiquid markets are significant, with perverse effects. Long-Term Capital Management (LTCM) was a successful hedge fund, which has become famous for its demise.21 The fund took hugely leveraged positions, betting on spreads between securities, such as bonds. A simplified explanation of the strategy is the following:
- The required yield on bonds depends on many factors, including the credit standing of the issuer. If you do not trust the ability of the issuer to repay its debt, you require a higher interest rate to buy its bond, whose price is reduced. If the balance sheet of the issuer is rock solid, you settle for a lower yield, implying a higher price. The difference in required yields is the spread.
- If a bond issuer is in trouble, but you believe that its difficulties are overstated by the market and that it will recover, you could buy its bonds (which are cheaper than they should) and take a short position in high-quality bonds (selling them short), because sooner or later, according to your view, the two bond prices will converge.22
In 1998, the strategy backfired because of a default on Russian bonds; markets got nervous and everyone rushed to sell risky bonds to buy safe ones. This “flight to quality” widened the spreads, resulting in huge losses for LTCM. In such a case, if your positions are leveraged, your creditors get nervous as well, and start asking you to repay your debt; in financial parlance, you get a margin call. This implies that you should liquidate some of the securities in your portfolio to raise some cash. Unfortunately, this exacerbates your trouble, since prices are further depressed by your sales. In normal times, a small trade on a very liquid market should not move prices too much. But if troubled markets get illiquid and you try unloading a huge position in an asset, you get a nasty vicious circle: The more you sell, the more money you lose, the more margin calls you get, the more you should sell. In the end, a committee of bankers had to rescue and bail out the fund in order to avoid a dangerous market crash.
Example 14.12 (The Black Monday crash of 1987) Portfolio insurance is a portfolio management strategy that aims at keeping the value of a portfolio of assets from falling below a given target. The idea is to create a synthetic put option by proper dynamic trading. To cut a long story short, the idea is that when asset value falls, one should sell a fraction of the assets in well-determined proportions. On Monday, 19 October, 1987, stock markets around the world crashed. In what has been aptly named the Black Monday, the Dow Jones Industrial Average index dropped by 22.61%. An explanation of this crash was put forward, which blames portfolio insurance. The idea is rather simple; the market goes south and you start selling to implement dynamic portfolio insurance. Unfortunately, you are not alone, as many other players do the same; hence, there is a further drop in prices that in turn triggers further sales. The result is a liquidity and feedback disaster, exacerbated by the use of automated, computer-based trading systems.23
The above stories, and all of the similar ones, are controversial; there is no general agreement that portfolio insurance has caused the Black Monday crash. Whatever your opinion is, feedback effects and the partial endogenous character of uncertainty cannot be disregarded.
14.7 SUBJECTIVE PROBABILITY: THE BAYESIAN VIEW
In all the preceding chapters concerning probability and statistics we took a rather standard view. On the one hand, we have introduced events and probabilities according to an axiomatic approach. On the other hand, when dealing with inferential statistics, we have followed the orthodox approach: Parameters are unknown numbers, that we try to estimate by squeezing information out of a random sample, in the form of point estimators and confidence intervals. Since parameters are numbers, when given a specific confidence interval, we cannot say that the true parameter is contained there with a given probability; this statement would make no sense, since we are comparing only known and unknown numbers, but no random variable is involved. So, there is no such a thing as “probabilistic knowledge” about parameters, and data are the only source of information; any other knowledge, objective or subjective, is disregarded. The following example illustrates the potential difficulties induced by this view.24
Example 14.13 Let X be a uniformly distributed random variable, and let us assume that we do not know where the support of this distribution is located, but we know that its width is 1. Then, X ~ U[μ - 0.5, μ + 0.5], where μ is the unknown expected value of X, as well as the midpoint of the support. To estimate μ we take a sample of n = 2 independent realizations X1 and X2 of the random variable. Now consider the order statistics

and the confidence interval
What is the confidence level of I, i.e., the probability P{μ  I}? Both observations have a probability 0.5 of falling to the left or to the right of μ. The confidence interval will not contain μ if both fall on the same half of the support. Then, since X1 and X2 are independent, we have
I}? Both observations have a probability 0.5 of falling to the left or to the right of μ. The confidence interval will not contain μ if both fall on the same half of the support. Then, since X1 and X2 are independent, we have
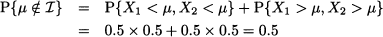
So, the confidence level for I is the complement of this probability, i.e., 50%. Now suppose that we observe X1 = 0 and X2 = 0.6. What is the probability that μ is included in the confidence interval I resulting from Eq. (14.16), i.e., P{0 ≤ μ $le; 0.6}? In general, this question does not make any sense, since μ is a number. But in this specific case, we have some additional knowledge leading to the conclusion that the expected value is included in the interval [0, 0.6] with probability 1. In fact, if X(1) = 0, we may conclude μ ≤ 0.5; by the same token, if X(2) = 0.6, we may conclude μ ≥ 0.1. Since the confidence interval I includes the interval [0.1, 0.5], we would have good reasons to claim that P{0 ≤ μ ≤ 0.6} = 1. But again, this makes no sense in the orthodox framework. By a similar token, if we get X1 = 0 and X2 = 0.001, we would be tempted to say that such a small interval is quite unlikely to include μ, but there is no way in which we can express this properly, within the framework of orthodox statistics.
On one hand, the example illustrates the need to make our background knowledge explicit. In the Bayesian framework, it can be argued that unconditional probabilities do not exist, in the sense that probabilities are always conditional on background knowledge and assumptions. On the other hand, we see the need of a way to express subjective views, which may be revised after collecting empirical data. Bayesian estimation has been proposed to cope with such issues.
14.7.1 Bayesian estimation
Consider the problem of estimating a parameter θ, characterizing the probability distribution of a random available X. We have some prior information about θ, that we would like to express in a sensible way. We might assume that the unknown parameter lies anywhere in the unit interval [0, 1], or we might assume that it is close to some number μ, but we are somewhat uncertain about it. Such a knowledge or subjective view may be expressed by a probability density p(θ), which is called the prior distribution of θ. In the first case, we might associate a uniform distribution with θ; in the second case the prior could be a normal distribution with expected value μ and variance σ2. Note that this is the variance that we associate with the parameter, which is a random variable rather than a number, and not the variance of the random variable X itself.
In Bayesian estimation, the prior is merged with experimental evidence by using Bayes’ theorem. Experimental evidence consists of independent observations X1, …, Xn from the unknown distribution. Here and in the following we mostly assume that random variable X is continuous, and we speak of densities; the case of discrete random variables and probability mass functions is similar. We also assume that the values of the parameter θ are not restricted to a discrete set, so that the prior is a density as well. Hence, let us denote the density of X by f(x | θ), to emphasize its dependence on parameter θ. Since a random sample consists of independent random variables, their joint distribution, conditional on θ, is
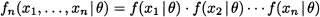
The conditional density fn(x1, …, xn | θ) is also called the likelihood function, as it is related to the likelihood of observing the data values x1, …, xn, given the value of the parameter θ; also notice the similarity with the likelihood function in maximum likelihood estimation.25 Note that what really matters here is that the observed random variables X1, …, Xn are independent conditionally on θ. Since we are speaking about n + 1 random variables, we could also consider the joint density
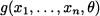
but this will not be really necessary for what follows. Given the joint conditional distribution fn(x1, …, xn | θ) and the prior p(θ), we can find the marginal density of X1, …, Xn by applying the total probability theorem:26
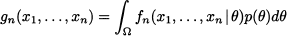
where we integrate over the domain Ω on which θ is defined, i.e., the support of the prior distribution. Now what we need is to invert conditioning, i.e., we would like the distribution of θ conditional on the observed values Xi = xi, i = 1, …, n, i.e.
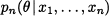
This posterior density should merge the prior and the density of observed data conditional on the parameter. This is obtained by applying Bayes’ theorem to densities, which yields
Note that the posterior density involves a term gn(x1, …, xn) which does not really depend on θ. Its role is to normalize the posterior distribution, so that its integral is 1. Sometimes, it might be convenient to rewrite Eq. (14.17) as
(14.18) 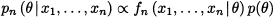
where the symbol α means “proportional to.” In plain English, Eq. (14.17) states that the posterior is proportional to the product of the likelihood function fn (x1, …, xn | θ) and the prior distributionp(θ):
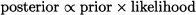
What we are saying is that, given some prior knowledge about the parameter and the distribution of observations conditional on the parameter, we obtain an updated distribution of the parameter, conditional on the actually observed data.
Example 14.14 (Bayesian learning and coin flipping) We tend to take for granted that coins are fair, and that the probability of getting head is 1/2. Let us consider flipping a possibly unfair coin, with an unknown probability θ of getting head. In order to learn this unknown value, we flip the coin repeatedly, i.e., we run a sequence of independent Bernoulli trials with unknown parameter θ.27 If we do not know anything about the coin, we might just assume a uniform prior

If we flip the coin N times, we know that the probability of getting H heads is related to the binomial probability distribution
(14.19) 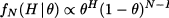
This is our likelihood function. If we regard this expression as the probability of observing H heads, given θ, this should actually be the probability mass function of a binomial variable with parameters θ and N, but we are disregarding the binomial coefficient [see Eq. (6.16)], which does not depend on θ and just normalizes the distribution. If we multiply this likelihood function by the prior, which is just 1, we obtain the posterior density for θ, given the number of observed heads:
Equations (14.19) and (14.20) look like the same thing, because we use a uniform prior, but they very different in nature. Equation (14.20) gives the posterior density of θ, conditional on the fact that we observed H heads and N - H tails. If we look at it this way, we recognize the shape of a beta distribution, which is a density, rather than a mass function. To normalize the posterior, we should multiply it by the appropriate value of the beta function.28 Again, this normalization factor does not depend on θ and can be disregarded.
In Fig. 14.5 we display posterior densities, normalized in such a way that their maximum is 1, after flipping the coin N times and having observed H heads. The plot in Fig. 14.5(a) is just the uniform prior. Now imagine that the first flip lands head. After observing the first head, we know for sure that θ ≠ 0; indeed, if θ were zero, we could not observe any head. The posterior is now proportional to a triangle:
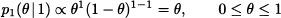
Fig. 14.5 Updating posterior density in coin flipping.

This triangle is shown in Fig. 14.5(b). If we observe another head in the second flip, the updated posterior density is a portion of a parabola, as shown in Fig. 14.5(c):
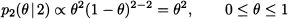
If we get tail at the third flip, we rule out θ = 1 as well. Proceeding this way, we get beta distributions concentrating around the true (unknown) value of θ. Incidentally, the figure has been obtained by Monte Carlo simulation of coin flipping with θ = 0.2.
Armed with the posterior density, there are different ways of obtaining a Bayes’ estimator. Figure 14.5 would suggest taking the mode of the posterior, which would spare us the work of normalizing it. However, this need not be the most sensible choice. If we consider the expected value for the posterior distribution, we obtain
There are different ways of framing the problem, that are a bit beyond the scope of the book,29 but one thing that we can immediately appreciate is the challenge we face. The estimator above involves what looks like an intimidating integral, but our task is even more difficult in practice, because finding the posterior density may be a challenging computational exercise as well. In fact, given a prior, there is no general way of finding a closed-form posterior; things can really get awkward when multiple parameters are involved. Moreover, there is no guarantee that the posterior distribution pn(θ | x1, …, xn) will belong to the same family as does the prior p(θ). However, there are some exceptions. A family of distributions is called a conjugate family of priors if, whenever the prior is in the family, the posterior is too. The following example illustrates the idea.
Example 14.15 (A normal prior) Consider a sample (X1, …, Xn) from a normal distribution with unknown expected value θ and known variance σ02. Then, given our knowledge about the multivariate normal, and taking advantage of independence among observations, we have the following likelihood function:
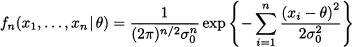
Let us assume that the prior distribution of θ is normal, too, with expected value μ and σ:
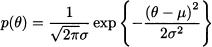
To get the posterior, we may simplify our work by considering in each function only the part that involves θ, wrapping the rest within a proportionality constant. In more detail, the likelihood function can be written as
We may simplify the expression further, by observing that
where  is the average of xi, i = 1, …, n. Then, we may include terms not depending on θ into the proportionality constant and rewrite (14.22) as
is the average of xi, i = 1, …, n. Then, we may include terms not depending on θ into the proportionality constant and rewrite (14.22) as
By a similar token, we may rewrite the prior as
Multiplying Eqs. (14.23) and (14.24), we obtain the posterior
(14.25) 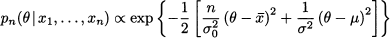
Again, we should try to include θ within one term; to this aim, we use a bit of tedious algebra30 and rewrite the argument of the exponential as follows:
where
(14.28) 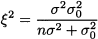
Finally, this leads to
(14.29) 
Disregarding the normalization constant, we immediately recognize the familiar shape of a normal density, with expected value v. Then, given an observed sample mean  and a prior μ, Eq. (14.27) tells us that the Bayes’ estimator of θ can be written as
and a prior μ, Eq. (14.27) tells us that the Bayes’ estimator of θ can be written as
Eq. (14.30) has a particularly nice and intuitive interpretation: The posterior estimator is a weighted average of the sample mean  (the new evidence) and the prior μ, with weights that are inversely proportional to σ02/n, the variance of sample mean, and σ2, the variance of the prior. The more reliable a term, the larger its weight in the average.
(the new evidence) and the prior μ, with weights that are inversely proportional to σ02/n, the variance of sample mean, and σ2, the variance of the prior. The more reliable a term, the larger its weight in the average.
In the example, it may sound a little weird to assume that the variance σ02 of X is known, but not its expected value. Of course, one can extend the framework to cope with estimation of multiple parameters, but there are cases in which we are more uncertain about expected value than variance, as we see in the following section.
14.7.2 A financial application: The Black–Litterman model
We considered portfolio optimization in Example 12.5 and in Section 13.2.2. For the sake of convenience, let us reconsider the problem here. We must allocate our wealth among n risky assets and a risk-free one. The returns of the risky assets are a vector of random variables with expected value μ and covariance matrix Σ; let rf be the return of the risk-free asset. Let w0 be the weight of the risk free asset in the portfolio, whereas the weights of the risky assets are denoted by wi, i = 1, …, n, collected into vector w 
 n. We assume that short sales and cash borrowing are possible; hence, we do not enforce any nonnegativity restriction on portfolio weights. Then, the expected value of portfolio return is
n. We assume that short sales and cash borrowing are possible; hence, we do not enforce any nonnegativity restriction on portfolio weights. Then, the expected value of portfolio return is
and its variance is wT Σw. Note that w0 does not affect variance. If we assume a quadratic utility function, we are essentially lead to consider a mean-variance objective, with risk aversion coefficient λ, resulting in the following quadratic programming problem:
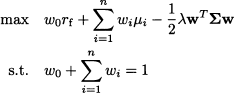
The factor 1/2 is not really essential, as it may be included in the risk aversion coefficient, but it simplifies the derivatives we take below. This constrained optimization problem may be transformed into an unconstrained one by eliminating w0. Plugging
into the objective, we obtain
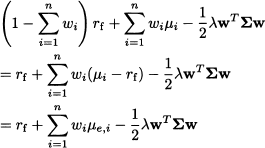
where  is the expected excess return of asset i. Since the leading rf term is inconsequential, the portfolio choice problem can be restated as
is the expected excess return of asset i. Since the leading rf term is inconsequential, the portfolio choice problem can be restated as
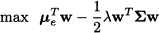
which is a convex optimization problem. Then, to find optimal portfolio weights, we just enforce stationarity conditions:
Solving a system of linear equations is easy enough, and we can find the optimal portfolio weights wi, i = 1, …, n, for the risky assets; then, using Eq. (14.31) we also get the weight of the risk-free asset. One of the difficulties of this simple framework is the estimation of problem inputs,31 such as the vector of expected returns μ and the covariance matrix Σ. Practical experience shows that if we take a simplistic approach and use straightforward sample estimates of these parameters, quite unreasonable portfolios are obtained.
Indeed, they may include very large positions in a few assets, possibly with large short positions as well.
Example 14.16 Consider a universe consisting of seven assets. The correlations among their excess returns, over an investment horizon, are given by the following symmetric table:32
Let us assume that the vector of volatilities is
Based on these data, we may easily build the covariance matrix Σ. If the risk aversion coefficient λ is set to 2.5 and the expected excess return is 7% for each asset, the resulting portfolio weights are

This solution might look unreasonable because weights do not add up to 1, but we should remember that there is a weight w0 for the risk free asset, and therefore
The portfolio looks a bit extreme, as there are quite large weights. This is partially a consequence of a relatively small risk aversion; experience suggests that λ can be in the range from 2 to 4. In practice, by forbidding short sales and adding policy constraints bounding portfolio weights, we might get a more sensible portfolio, but doing so essentially means that we are shaping our strategy using constraints.
A very surprising finding is the dramatic effect of changing estimates of expected excess returns on portfolio weights. Let us assume that the vector of expected (excess) returns is changed to
This could be a way to translate an investor’s view, feeling that some assets will outperform other assets. The new portfolio is

The change in portfolio composition is illustrated in Fig. 14.6. For each asset we display a pair of bars corresponding to portfolio weights; the second port-folio is associated with the right (white) bar within each pair. The dramatic change in the portfolio weights is rather evident and can be explained by the change in expected return of asset 3, 4, and 6, with respect to the first port-folio choice problem. But is this change justified, or is just due to estimation errors? The problem that we are highlighting is that an error in the estimate of expected value may have a significant impact on portfolio choice.
Fig. 14.6 Portfolio instability with respect to estimates of expected return.
It is a common opinion that estimating expected return is even more troublesome than estimating covariances, in the sense that it has a stronger effect on optimized portfolios. A cynical view states that portfolio optimization is the best way to maximize the effect of estimation errors. Even if we refrain from being so drastic, it is certainly true that most financial analysts would feel comfortable only with the estimation of a few expected returns, for those market segments on which they have the most experience. In practice, analysts would not just estimate a parameter based on past observations; what about predicting an expected return for the future? There is no doubt that portfolio management should look forward, rather than backward, but again, analysts may do this for limited market segments. For the rest, they might just share the market consensus and go for a passive management strategy. We also recall that a passive management strategy is a consequence of the capital asset pricing model (CAPM).33 According to a passive strategy, one should just hold the market portfolio, i.e., a portfolio with stock share weights shaped after market capitalization of the corresponding firms. If we accept the validity of CAPM, we may even find expected excess returns implied by the market portfolio. According to CAPM, for each asset i = 1, …, n, we have
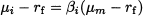
where μm is the expected return of the market portfolio, which can be approximated by a broad index. This relationship may be restated in terms of expected excess returns:
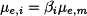
We also note that expected excess returns can be interpreted as risk premia, as they state by how much the expected return of a risky asset exceeds the risk-free return rf. The coefficient βi looks much like the slope of a linear regression, as it is given by
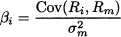
where the numerator is the covariance between the return of asset i and the return of the market portfolio, and σm2 is the variance of market portfolio return. If we denote by wm the weights of the market portfolio, its return is
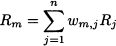
Hence, we have
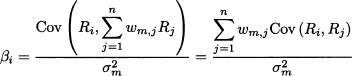
Thus, we may collect the “asset betas” βi into vector β and rewrite CAPM as
where the constant
(14.34) 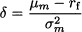
trades off the risk premium (μm - rf) against squared market volatility. Incidentally, a comparison between Eqs. (14.32) and (14.33) suggests some link between δ and an average risk aversion coefficient. The important contribution of Eq. (14.33) is that it yields a consensus market view of the expected excess returns, implied by equilibrium. This might be considered as a starting point of an estimation process, which is not just backward-looking and based on historical data, but also forward-looking.
If we look forward, rather than backward, we are immediately lead to a question: How can we include subjective views that an investor might have? For instance, an investor could think that an asset will outperform another one by, say, 5%. Black and Litterman proposed an approach whereby expected returns are estimated based on two primary inputs:
- A forecast implied by market equilibrium
- A set of subjective views on expected returns
The way the two ingredients are blended depends on the uncertainty that is associated with each of them, and can be interpreted as a Bayesian estimate blending subjective expectations with an outside input.34
One way of stating the model is the following:
1. The vector of expected excess returns is considered as a vector of random variables θ with multivariate normal distribution:
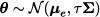
where μe is implied by market equilibrium and Σ is the estimated co-variance matrix. Note that we are trusting the estimate of covariance matrix in providing us the covariance matrix τΣ of the prior distribution; in fact, one of the main difficulties of the Bayesian framework is specifying sensible multivariate priors. The rationale here is that if assets are correlated, the error in estimating their risk premia will be as well. The parameter τ can be used to fine tune the degree of confidence in the market view.
2. Subjective views about risk premia and expected returns can be expressed as linear relationships. For instance, say that we believe that asset 2 will outperform asset 5 by 2%. Then, we could write a condition such as
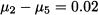
In this case, using expected return or risk premia is inconsequential. Several similar views could be expressed in terms of excess returns and collected in the following matrix form:
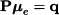
The view above would correspond to a row in matrix P, with elements set to 1 in columns 2 and 5, zero otherwise; the corresponding element in vector q would be 0.02. Of course, subjective views are uncertain as well, and we might express this as
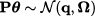
where Ω is typically a diagonal matrix whose elements are related to the confidence in subjective views.
The Black-Litterman model, relying on Bayesian estimation, yields the following estimate of risk premia:
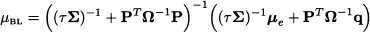
The proof of this relationship is definitely beyond the scope of the book, but it is quite instructive to note its similarity with Eq. (14.30). The interpretation is again that the estimate blends subjective views and objective data, in a way that reflects their perceived reliability.35 Several variations of the Black–Litterman model have been proposed, but the essential message is that subjective and more or less objective views may be blended within a Bayesian framework. In fact, Bayesian approaches have also been proposed in marketing, where they are most relevant to cope with brand-new products and markets, where past data are quite scarce or irrelevant.
Problems
14.1 Find the Nash equilibria in the games in Tables 14.2 and 14.4. Are they unique?
14.2 Consider the Cournot competition outcome of Eqs. (14.12) and (14.13). Analyze the sensitivity of the solution with respect to innovation in production technology, i.e., how a reduction in production cost cj for firm i affects equilibrium quantities, price, and profit.
14.3 Two firms have the same production technology, represented by the cost function:
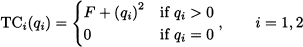
The cost function involves a fixed cost F and a squared term implying a diseconomy of scale; a firm will produce only when its profit is positive. The two firms compete on quantity, and price is related to total quantity Q = q1 + q2 by the linear function P(Q) = 100 - Q. Find the maximum F such that both firms engage in production, assuming a Cournot competition.
14.4 Two firms have a production technology involving a fixed cost and constant marginal cost, as represented by the cost function:
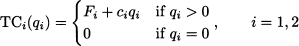
Analyze the von Stackelberg equilibrium when firm 1 is the leader and the two firms compete on quantities.
14.5 Consider the data of the Braess’ paradox example in Section 14.5, but imagine that a central planner can assign routes to drivers, in order to minimize total travel cost. Check that adding the new link e, as in Fig. 14.4(b), cannot make the total cost worse.
14.6 Consider again the Bayesian coin flipping experiment of Example 14.14, where the prior is uniform. If we use Eq. (14.21) to find the Bayesian estimator, what is the estimate of θ after the first head? And after the second head?
14.7 Consider the fraction θ of defective items in a batch of manufactured parts. Say that the prior distribution of θ is a beta distribution with parameters α1 = 5 and α2 = 10 (see Section 7.6.2 for a description of the beta distribution). A new batch of 30 items is manufactured and two of them are found defective. What is the posterior estimate of θ, if we use Eq. (14.21)?
14.8 Prove the identity in Eq. (14.26).
For further reading
- Game theory is dealt with at an introductory level in books on industrial organization, such as Refs. [4] and [22]. See Ref. [11] for a thorough introduction and Ref. [10] for an advanced treatment.
- For Bayesian statistics, you may see Ref. [6] or the more recent version [7]. These books, like the text by Casella and Berger [5], deal with Bayesian statistics within a framework that is compatible with the orthodox view. A more radical approach is advocated by Jaynes in Ref. [16]. An intermediate treatment can be found in Ref. [17].
- For a scientific perspective on Bayesian data analysis, see the treatise by Sivia and Skilling [23].
- The Black–Litterman portfolio management approach was introduced in Ref. [1]; see also Chapter 9 of Ref. [8], or Refs. [13] and [21].
- Interesting and instructive accounts of some financial mishaps can be found in Refs. [2] and [15]. For discussions on black swans, as well as the meaning and the role of probabilities and quantitative modeling in finance, you may refer, e.g., to Refs. [9], [14], and [20].
REFERENCES
1. F. Black and R. Litterman, Global portfolio optimization, Financial Analysts Journal 48:28–43, 1992.
2. R. Bookstaber, A Demon of Our Own Design: Markets, Hedge Funds, and the Perils of Financial Innovation, Wiley, New York, 2008.
3. D. Braess, A. Nagurney, and T. Wakolbinger, On a paradox of traffic planning, Transportation Planning, 39:446–450, 2005.
4. L.M.B. Cabral, Introduction to Industrial Organization, MIT Press, Cambridge, MA, 2000.
5. G. Casella and R.L. Berger, Statistical Inference, 2nd ed., Duxbury, Pacific Grove, CA, 2002.
6. M.H. DeGroot, Probability and Statistics, Addison-Wesley, Reading, MA, 1975.
7. M.H. DeGroot and M.J. Schervish, Probability and Statistics, 3rd ed., Addison-Wesley, Boston, 2002.
8. F.J. Fabozzi, S.M. Focardi, and P.N. Kolm, Quantitative Equity Investing: Techniques and Strategies, Wiley, New York, 2010.
9. S.M. Focardi and F.J. Fabozzi, Black swans and white eagles: on mathematics and finance, Mathematical Methods of Operations Research, 69:379–394, 2009.
10. D. Fudenberg and J. Tirole, Game Theory, MIT Press, Cambridge, MA, 1991.
11. R. Gibbons, Game Theory for Applied Economists, Princeton University Press, Princeton, NJ, 1992.
12. I. Gilboa, Theory of Decision Under Uncertainty, Cambridge University Press, New York, 2009.
13. G. He and R. Litterman, The Intuition Behind Black–Litterman Model Portfolios, Technical report, Investment Management Research, Goldman & Sachs Company, 1999. A more recent version can be downloaded from http://www.ssrn.org.
14. Glyn A. Holton, Defining risk, Financial Analysts Journal, 60:19–25, 2004.
15. L.L. Jacque, Global Derivative Debacles: From Theory to Malpractice, World Scientific, Singapore, 2010.
16. E.T. Jaynes, Probability Theory: The Logic of Science, Cambridge University Press, Cambridge, UK, 2003.
17. P.M. Lee, Bayesian Statistics: An Introduction, 3rd ed., Oxford University Press, New York, 2004.
18. R. Lowenstein, When Genius Failed: The Rise and Fall of Long-Term Capital Management, Random House Trade Paperbacks, New York, 2001.
19. V.G. Narayanan and A. Raman, Hamptonshire Express, Harvard Business School. 2002, Business Case no. 9–698–053.
20. R. Rebonato, Plight of the Fortune Tellers: Why We Need to Manage Financial Risk Differently, Princeton University Press, Princeton, NJ, 2007.
21. S. Satchell and A. Scowcroft, A demystification of the Black–Litterman model: managing quantitative and traditional portfolio construction, Journal of Asset Management, 1:138–150, 2000.
22. O. Shy, Industrial Organization: Theory and Applications, MIT Press, Cambridge, MA, 1995.
23. D.S. Sivia and J. Skilling, Data Analysis: A Bayesian Tutorial, 2nd ed., Oxford University Press, Oxford, 2006.
1 We illustrate a Bayesian framework to learn such probabilities in Example 14.14.
2 Sometimes, it is stated that a confidence interval contains the uncertain parameter with a given probability; this is correct if we refer to an interval estimator, i.e., a pair of random variables. On the contrary, it is plain wrong if we refer to an interval estimate, i.e., to a pair of numbers realized after random sampling. See the discussion in Section 9.2.2.
3 A leveraged position is a trade in which you borrow money to invest in risky positions. If things turn out well, this has the effect to enhance your gain; in case of loss, this is magnified, possibly leading to bankruptcy.
4 A few centuries ago, in Europe, it was common wisdom that all swans were white, for the simple reason that no one ever observed a black one. The picture changed after 1697, when one was found in Australia. See N.N. Taleb, The Black Swan: The Impact of the Highly Improbable, 2nd ed., Random House Trade Paperbacks, 2010.
5 See F.H. Knight, Risk, Uncertainty, and Profit, Houghton Mifflin, Boston, 1921.
6 This example has been inspired by the Harvard Business School (HBS) case [19], to which we refer for additional questions and issues.
7 See Section 7.4.4.
8 There is a potential source of confusion here, as we may lose potential revenue because of a stockout, i.e., when demand is larger than the available inventory. We refer here to revenue that we lose because of unsold items, i.e., when demand is smaller than the available inventory.
9 Earlier in this chapter we insisted on the potential effect of our decisions on uncertainty. In this case, we assume that the effort decision affects only the location of the demand distribution, but not its dispersion. Nevertheless, uncertainty is indeed partially endogenous in our stylized example.
10 See Problem 7.9.
11 Since we do not consider multistage games, we do not deal with perfect information. Perfect information means that each player knows which moves have been played by the other players in the previous stages of the game. Complete information refers to the structure of the game and the payoffs of the other players.
12 In the literal statement of the dilemma, two prisoners are kept in separate cells and are invited to confess their crime, in exchange for a reduction in punishment; if both refuse to confess, they will be released, but if only one prisoner confesses, the other one will be severely punished.
13 In our simple context of nonsequential games, we could speak of dominant actions.
14 See Section 12.3.3.
15 To be precise, for the simple games that we consider here, featuring finite sets of possible actions, they do exist if we allow for mixed strategies, but this is outside the scope of the book.
16 Actually, they never fail in relatively simple games, if we allow for mixed strategies.
17 It is interesting to note that the Cournot duopoly model anticipated Nash equilibrium by more than one century, although in a limited setting.
18 For a full treatment of the Braess’ paradox see Ref. [3]. The numerical example in this section has been taken from a presentation by A. Nagurney, which can be downloaded from http://supernet.som.umass.edu/ (CMS 2010 plenary presentation).
19 See Section 12.2.4 for an introduction to network flow optimization.
20 See http://supernet.som.umass.edu/facts/braess.html
21 Two Nobel Laureates, Robert Merton and Myron Scholes, were involved in the fund, and this has contributed to the fame of this case. In fact, it is often written that they founded LTCM, which is false in many respects. For a full account of the story, see Ref. [18].
22 The practical implementation of this strategy is not that simple, and it may require the use of financial derivatives.
23 This explanation is very simplified. For a much better account see, e.g., Ref. [2].
24 This example is taken from Ref. [12], page 45, which in turn refers back to Ref. [6].
25 See Section 9.9.3.
26 Here we strain a bit some concepts related to conditional densities, which we just outlined in Chapter 8, but the intuition should be clear.
27 This example is based on Chapter 2 of the text by Sivia and Skilling [23].
28 See Section 7.6.2.
29 One way to frame the problem is by introducing a loss function that accounts for the cost of a wrong estimate. It can be shown that Eq. (14.21) yields the optimal estimator when the loss function has a certain quadratic form.
30 See Problem 14.8.
31 See Example 9.21.
32 The numerical data have been taken from [13].
33 See Example 9.21.
34 See Ref. [21] for a detailed proof.
35 There is also an alternative way of interpreting Black–Litterman model in terms of robust “shrinkage” estimators; see, e.g., Chapter 9 of Ref. [8].