Our Philosophy of History
History and theory
Subsequent chapters contain selective histories of thoughts and events that pertain to managing the coinage. We present only a sample from a vast record of thoughts and events. Our model helped us select it, so our sample is biased. Because we are prejudiced observers, we tell the reader what we watched for in the historical record and how our model directed our search.
Clues identified by our model
Our model assumes that coins of a given denomination circulate by tale. The intervals between the minting points and melting points permit gaps between valuations by tale and by weight. That feature of our model implies a range of indeterminacy for the initial exchange rate e, the price of large denomination coins in terms of small denomination coins. Thus, recall our finding that if both coins are to circulate in a two-coin world, the price level p must satisfy
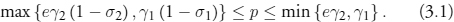
It follows that if both coins are to circulate, the exchange rate must satisfy
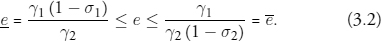
The bound on the right side of (3.2) is attained if the exchange rate aligns the melting point for dollars with the minting point for pennies. The bound on the left side is attained if the exchange rate is set to align the minting point of dollars with the melting point of pennies.
There is a corresponding range of indeterminacy for the initial price level. In the notation of chapter 2, when there are no “within the interval” shortages of small coins, the price level must satisfy
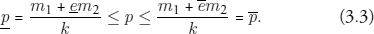
These indeterminacies concern the initial exchange rate and price level. Given an initial e, our model determines the exchange rate and price level over time.
At given settings for the γi’s and σi’s, inequalities (3.2) limit the increases that can occur in the exchange rate due to “within the interval” shortages caused by a binding penny-in-advance constraint. Once the exchange rate is at the upper bound, the only way that further increases in the exchange rate can occur is through an increase in γ1 (a debasement of the penny) or a decrease in γ2 (an enhancement of the dollar).
The theoretical model of chapters 2 and 21 describes how movements in endowments or preferences can cause shortages of small coins even when the price level is within the distinct intervals bracketed by the minting points and melting points for all coins. The consequence of a shortage is to drive both the exchange rate and the price level upward. But in general, the price level may rise more or less than proportionately with the exchange rate. This opens two possibilities, each of which exacerbate the basic problem, but in different ways:
1. If the price level rises less than proportionately with the exchange rate, it brings the price level closer to the point at which dollars will be minted. When that happens, it makes the small change shortage worse by raising m2, which raises the ratio of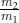 
. In chapter 22, we make precise how an increase in this ratio worsens the shortage problem.
2. If the price level rises more than proportionately with the exchange rate, it makes it more likely that pennies will soon be melted, because the price level is brought relatively closer to the melting point for pennies. That will obviously exacerbate the shortage.
In addition to identifying the cause of shortages of small change, the model identifies cures.
1. Debase the small coins. For fixed parameters σ1, σ2 controlling the lengths of the intervals, a debasement of pennies and a simultaneous resetting of the exchange rate shifts the interval for pennies to the left, promoting minting and inhibiting melting.
Cure 1 repairs a shortage by shifting an interval of fixed size for the small coin to the right. But when σ1 and σ2 are kept small to insure narrow intervals, movements in endowments and other exogenous variables that influence the demand for the quantity of real balances and its composition by denomination, the kit’s from chapter 2, will eventually cause shortages of small coins to recur under the item 1 solution. Maintaining narrow intervals exposes the system to threats of recurrent shortages of either large or small denomination coins. Our model points to a longer lasting but risky cure:
2. Widen the intervals. Debase the small denomination coin (by raising γ1) to move its melting point far to the right, and widen its interval by raising σ1, moving the minting point far to the left. Then mint the small denomination coin on government account in limited amounts to forestall shortages.
Cure 2 proposes to diminish the standing of the small coin as a commodity money, and to use some method other than a narrow interval to regulate its supply. A wide interval creates two sorts of problems. First, a low value of the minting point γ1(1 – σ1) means that people might rarely have an incentive to bring metal to the mint to buy coins. Second, a high value of the melting point means that the automatic upper limit on the price level coming from the money supply mechanism is lost. A government could solve the first problem by minting coins on its own account. But to solve the second problem requires that the government restrain itself not to issue too much on its own account.
The remaining chapters of this book contain our history of how technologies and prevailing ideas for a long time combined to forestall the standard formula; and then how during the Renaissance improvements in the machines for making coins and more sophistication in monetary theory led to policy experiments that sharpened theorists’ understanding of the elements of the standard formula.
We begin in early medieval times and describe how scholastics, secular lawyers, and eventually economists discussed whether coins should be exchanged by weight or by tale, and how a widespread preference for valuation by weight eroded slowly over the centuries. The strength of a writer’s preference for circulation by weight influenced whether he thought that the seigniorage rate σi should be set above or below production costs. Some wrote that a narrow band was just. Others said that what counted was price level stability, which they said could be achieved with valuation by tale. Their discussions clarified the distinction between value by weight and value by tale. Authorities recognized that narrow bands deterred counterfeiters but that they also limited the government’s seigniorage.
We recount many examples in which the exchange rate (the price of large coins in units of small coins) sporadically drifted upward over time (see fig. 2.1). During periods of rapid increases in the exchange rate there were also often shortages of the small coins. The authorities often responded to those shortages by debasing the small coins, a remedy that our model identifies. When the domestic authorities were slow to debase, the market sometimes accomplished an “endogenous debasement” by importing lighter small denomination coins that were being minted by neighboring states.
In time the monetary authorities learned that if a government could monopolize a superior technology for making token coins, it could deter counterfeiting, widen the bands, and increase seigniorage. An important instance occurred when advisors to the king of Castile recommended using the open market operation described by (2.13) to generate royal revenues like (2.14). The king did. But eventually discipline broke: the authorities stopped open market operations in silver and replaced them with pure deficits financed by token coins. The price level rose, and the experiment was abandoned when Castile returned to a full-bodied coinage. From the wreckage of that experiment and other similar ones, theorists later constructed the quantity theory of money, cast in terms of subsidiary coins.
Especially in England, private enterprises again discovered the profitability of open market operations like (2.13) and (2.16). Private citizens could obtain interest-free loans by issuing convertible tokens. Private tokens flourished until the government reclaimed the monopoly for coin issue. The British government implemented the standard formula during the nineteenth century. Later in the nineteenth century, the standard formula triumphed completely when France and the United States adopted it at nearly the same time that they abandoned bimetallism.
This book blends histories of ideas, technologies, and monetary policies. Our theoretical model supplies us a glue that we use to bind together these different aspects of the problem of small change and its solution. In the following three chapters, which compose part II of this book, we describe the technologies and theoretical ideas that were available to guide historical monetary authorities as they encountered and struggled to manage the problem of small change. Part III will then describe in detail how those monetary authorities put these technologies and ideas to work.
