Advances in Tb/s Superchannels
S. Chandrasekhar and Xiang Liu, Bell Labs, Alcatel-Lucent, 791 Holmdel-Keyport Road, Holmdel, NJ 07733, USA
Acknowledgments
The authors are especially grateful to their colleagues working in this field in Bell Laboratories, Alcatel-Lucent, for fruitful collaborations and valuable discussions. Among them are L.L. Buhl, E.C. Burrows, R. Essiambre, A.H. Gnauck, and P.J. Winzer. The authors also wish to thank A.R. Chraplyvy, R.W. Tkach, and P.J. Winzer for their support.
3.1 Introduction
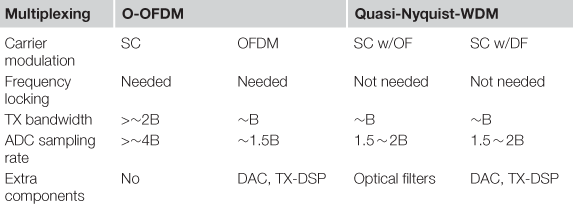
To satisfy the ever-increasing capacity demand in optical fiber communications, the data rate carried by each wavelength channel in wavelength-division multiplexing (WDM) systems has been increasing exponentially [1–3]. The dramatic increase in serial interface rates and WDM capacities of optical networks is shown in Figure 3.1[3]. 100-Gb/s per-channel data rates have been available in commercial systems since mid-2010 [3], and 200-Gb/s per channel data rates have been recently demonstrated. With the introduction of optical superchannels, which avoid the electronic bottleneck via optical parallelism, optical transmission with per-channel data rates beyond 100 Gb/s and up to several Terabits/s (Tb/s) has been experimentally demonstrated [4–7]. The term “superchannel” was first coined by Chandrasekhar and X. Liu et al. [4] for multiple single-carrier-modulated signals arranged under the orthogonal frequency-division multiplexing (OFDM) conditions [8,9], although the use of optical OFDM (O-OFDM) to group multiple modulated bands together was previously demonstrated in the context of OFDM signals [5,6] and in the context of 2-carrier transmission [10]. The superchannel concept was later generalized to any collection of optical signals that are (1) modulated and multiplexed together with high spectral efficiency (SE) at a same originating site, (2) transmitted and routed together over a same optical link, and (3) received at a same destination site. To achieve high-SE multiplexing, “Nyquist-WDM,” “quasi-Nyquist-WDM,” and offset quadrature amplitude modulation (o-QAM) [11–18] have been introduced as promising alternatives of O-OFDM, as we will describe later.
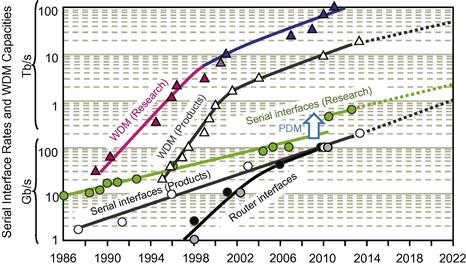
Figure 3.1 Serial interface rates and WDM capacities of optical networks versus year. Courtesy of P.J. Winzer [3].
There are five key benefits of using superchannels in WDM systems as follows:
1. Higher per-channel data rate, to meet the demand of ever-increasing serial interface rates, by avoiding the electronic bottleneck imposed by opto-electronic converters (O/E), electro-optical converters (E/O), digital-to-analog converters (DAC), and analog-to-digital converters (ADC).
2. Higher spectral efficiency in WDM transmission, especially in transparent optical networks based on reconfigurable optical add/drop multiplexers (ROADMs), by reducing the percentage of wasted optical spectrum between channels.
3. Increased efficiency in digital signal processing (DSP), by processing the subchannels within each superchannel separately.
4. Better leverage of photonic integrated circuits (PICs) and application-specific integrated circuits (ASICs).
5. Supporting software-defined optical transmission, enabled by DSP at both transmitter and receiver, to improve system throughput and flexibility.
Tb/s superchannels have also led to a rethinking of spectral bandwidth allocation beyond the current fixed grid architectures, leading to the so-called flexible grid architecture that allows for more efficient utilization of the optical spectrum. In this chapter, we review recent progress on Tb/s superchannel transmission and discuss and compare various superchannel implementations based on O-OFDM and Nyquist WDM. This chapter is organized as follows. Section 3.2 describes the superchannel principle and various terminologies used for superchannels. Section 3.3 presents common modulation schemes used to form a superchannel. Section 3.3 presents two main multiplexing schemes, O-OFDM and quasi-Nyquist WDM. Section 3.5 discusses the detection schemes for receiving a superchannel. Section 3.6 addresses the transmission performance of superchannels based on different modulation formats. Section 3.7 briefly discusses the network implications of using Tb/s superchannels with various optical bandwidths. Finally, Section 3.8 concludes this chapter, with an outlook of future perspectives on superchannel-enabled optical transmission systems and networks.
3.2 Superchannel Principle
Over the last several decades, the field of WDM transmission has evolved from sparsely populated channels, as in coarse WDM (CWDM), to very high density WDM, as in the case of superchannel transmission. It is therefore instructive to classify WDM systems based on the channel bandwidth allocation (or channel spacing) Δf relative to the modulation symbol rate of the channel B. In Table 3.1, different classes of WDM systems are thus defined. One can clearly see that the recent progress in high spectral efficiency systems using advanced modulation formats with coherent detection has opened new regimes, identified as “quasi-Nyquist” WDM (for 1 ≤ Δf/B ≤ 1.2), “Nyquist-WDM” (for Δf/B = 1), and “super-Nyquist” WDM (for Δf/B < 1), respectively. Here, the term “Nyquist” is borrowed from the well-known Nyquist-Shannon sampling theorem, named after Nyquist [19] and Shannon [20], which essentially states that if a function x(t) contains no frequencies higher than B/2 Hz, then it is completely determined by giving its ordinates at a series of points spaced 1/B seconds apart [20]. This is a fundamental result in the field of inforly, Nyquist-WDM here means that the optical spectral bandwidth of an optical signal modmation theory, particularly in telecommunications and signal processing. More specificalulated at a symbol rate of B can be limited to B without losing its fidelity, and similar such signals can be packed at a frequency spacing equal to B in the ideal case, or Δf/B = 1. Packing two signals closer than the Nyquist frequency, termed as “super-Nyquist” WDM or “faster-than-Nyquist” WDM [21], will cause crosstalk, which can be compensated, albeit with added DSP complexity and reduced optical signal-to-noise (OSNR) performance [14]. The definition makes no assumptions on how a channel is modulated, or any physical impairment associated with placing channels close together, such as crosstalk from overlapping spectral content. As an example, optical prefiltering has been employed to mitigate crosstalk in the demonstration of “quasi-Nyquist” WDM [12] and “super-Nyquist” WDM [14]. Alternatively, electronic pre-filtering has also been employed for such demonstrations [16,17].
Table 3.1
Definitions of various classes of WDM.
| Definition | Condition (Δf/B) | Example |
| Coarse WDM | >50 | 10 Gb/s on 20 nm |
| WDM | >5 | 10 Gb/s on 100 GHz |
| DWDM | 1.2 < Δf/B ≤ 5.0 | 28-Gbaud PDM-QPSK on 50 GHz |
| “Quasi-Nyquist” WDM | 1.0 < Δf/B ≤ 1.2 | 28 -Gbaud PDM-16QAM on 33 GHz |
| “Nyquist” WDM | Δf/B = 1 | 28-Gbaud PDM-QPSK on 28 GHz |
| “super-Nyquist” WDM | Δf/B < 1 | 28-Gbaud PDM-QPSK on 25 GHz |
Δf is the allocated channel bandwidth (or channel spacing) and B is the channel symbol rate.
A special case of “Nyquist” WDM is the one that additionally satisfies the O-OFDM conditions, as described below, allowing for crosstalk-free reception of symbol-rate spaced channels without using optical or electrical pre-filtering [4,8,22–25]. The O-OFDM conditions that must be met for multiplexing multiple modulated carriers to form a superchannel can be enumerated [8] as follows.
1. The carrier spacing must equal the symbol rate with sufficient accuracy (inversely proportional to the duration of each processing block at the receiver). This implies that the carriers on which the modulation is imprinted need to be frequency locked. Experimental evidence for such a need is illustrated later in Section 3.4.2.1 under seamless multiplexing.
2. The modulated symbols on the carriers need to be time aligned at the point of de-multiplexing. (This follows from Figure 2 in Ref. [8].)
3. Typically, the frequency-domain response of the modulated symbols is a sinc function. This implies that sufficient bandwidth is needed at the transmitter and the receiver to modulate each subcarrier. At the receiver, there must also be sufficient oversampling speed to capture most of the sinc function for each of the modulated subcarriers.
The transmitter and receiver bandwidth requirements for meeting the O-OFDM conditions can be relaxed by using OFDM to modulate each signal [26], which effectively reduces the bandwidth of each orthogonal optical subcarrier. In this case, one has Ne electronic subcarriers for each of the No optical subcarriers. The bandwidth requirements can also be relaxed by introducing a guard interval (GI) between adjacent modulated symbols, albeit at the expense of reduced WDM SE [27]. While O-OFDM requires that the orthogonality conditions be met by the modulated signals that construct a superchannel, quasi-Nyquist-WDM relaxes the multiplexing requirement by allocating a guard band (GB) between adjacent modulated signals, albeit at the expense of reduced SE.
Generally, the synthesis of Terabit/s superchannels is a two-step process involving both modulation and multiplexing. In the first step (for modulation), one needs to pick a modulation format with the appropriate optical and electronic hardware to realize what we term a single-band transmitter (SB-TX), generating a signal, whose data rate is usually limited by the electronic bottleneck, e.g. resulting from limited bandwidth of components such as optical modulator, modulator driver, photo-detector, trans-impedance amplifier (TIA), DAC, and ADC. Here SB means that there is no optical frequency domain parallelization. In the second step (for multiplexing), the outputs of the SB-TXs are multiplexed in parallel to generate a superchannel having a desired total data rate. The multiplexing can be based on O-OFDM or Nyquist-type WDM. The detection of a superchannel can be categorized as multi-step detection [26] and single-step detection [28,29]. In multi-step detection, a superchannel is divided into multiple subchannels that are detected separately, e.g. via multiple digital coherent detection front-ends. The details on the modulation, multiplexing, and detection schemes will be presented in the following sections.
3.3 Modulation
There are three common modulation schemes used to construct a SB-TX for high-level constellations, as shown in Figure 3.2[30]. The first scheme (a) uses an array of PDM I/Q modulators (PDM-IQMs) that are driven by binary drive signals. To generate a PDM-n-QAM signal, log2(n)/2 PDM-IQMs are needed, together with two 1:log2(n)/2 variable power splitters (VPSs) [31]. The second scheme (b) uses a single PD-IQM that is driven by four analog drive signals, corresponding to the I and Q components of two polarization states of the signal. Four DACs are needed. Digital signal processing (DSP) may be used for pre-equalization and pulse shaping at the transmitter. The third scheme (c) is based on OFDM with QAM subcarrier modulation, which additionally requires OFDM DSP.
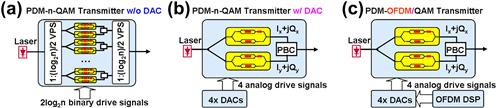
Figure 3.2 Three common types of single-band transmitters (SB-TX). VPS: variable power splitter; DAC: digital-to-analog converter; DSP: digital signal processor.
It is of value to compare the above high-SE transmission schemes. Table 3.2 compares the three SB-TX schemes. SB-(a) has benefits of (1) not requiring a DAC, (2) not requiring DSP, and (3) generating signals with low peak-to-average-power ratio (PAPR) and with low optical loss. However, it requires more than one PD-IQM for n > 4, so photonic integration of multiple PDM-IQMs would make this scheme more attractive. SB-(b) and SB-(c) have the advantage of needing only one PD-IQM, but they require high-speed DACs. Hybrid options are possible as well to trade DAC complexity with parallel-optics complexity. Compared to SB-(c), SB-(b) offers lower PAPR but prefers a slightly higher DAC sampling speed. For single-carrier modulation, DSP can also be applied to tightly confine the signal spectrum through Nyquist filtering with small roll-off factors. With tight spectral filtering, the PAPR of a single-carrier modulated signal increases as compared to the unfiltered case. The high PAPR in SB-(c) can be reduced by the discrete Fourier transform (DFT)-spread technique [32–35].
Table 3.2
Comparison among modulation schemes.
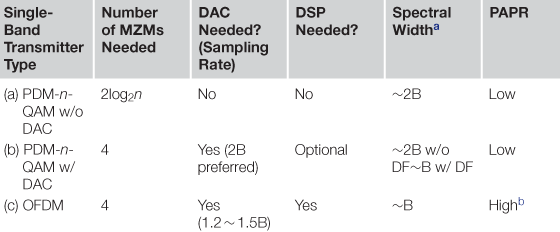
aThe spectral width is measured as null-to-null bandwidth.
bThe high PAPR of OFDM can be reduced by more DSP, e.g. via DFT-spread-OFDM. TX: transmitter; B: signal baud; DF: digital filter.
There are two emerging modulation formats worth mentioning. The signal tolerance to inter-symbol interference (ISI) can be improved by offsetting the in-phase and quadrature components of a quadrature-amplitude modulation (QAM)-based subcarrier by half modulation period in time, leading to the offset-QAM format (o-QAM) [18,36,37]. When the OFDM subcarriers are modulated on a one-dimensional constellation, e.g. via BPSK, the subcarrier spacing can be half of the modulation symbol rate, resulting in the fast-OFDM scheme [38], which uses inverse discrete cosine transforms rather than inverse discrete Fourier transform for subcarrier multiplexing. Fast-OFDM recently found interesting applications in intensity-modulation and direct-detection systems [39].
3.4 Multiplexing
3.4.1 Overview of multiplexing schemes
There are three common schemes for constructing a multi-band transmitter (MB-TX) that consists of multiple SB-TXs, as shown in Figure 3.3[30]. The first scheme (a) is based on O-OFDM, which requires a set of frequency-locked carriers [4–7]. The second scheme (b) is to use optical filters (OFs) to perform the filtering needed to support quasi-Nyquist-WDM [11,12]. The third scheme (c) is to use digital filters (DFs), instead of OFs, to perform the filtering needed to support quasi-Nyquist-WDM [16,17]. In the third scheme, DSP and DAC are both needed. The implementation of the DF can be a root-raised-cosine (RRC) filter. In a more general sense, the inverse fast Fourier transform (IFFT) used in OFDM modulation can also be regarded as a DF that naturally produces a well-confined square-like signal spectrum with a sharp roll-off.
Figure 3.3 Three common types of multi-band transmitters (MB-TX). DMUX: wavelength de-multiplexer; OF: optical filter; DF: digital filter. After Ref. [30]. © 2011 OSA.
Table 3.3 compares several common multiplexing schemes. Single-carrier modulation in conjunction with the orthogonality conditions described earlier, as used in Ref. [4], does not require DAC and transmitter DSP, but requires the sampling speed of the receive-side ADC to be much larger than the modulation speed of each modulated carrier. On the other hand, OFDM modulation on each optical carrier, combined with seamless band multiplexing, as used in Refs. [5,6,26], has the benefits of (1) not requiring the tight OFs and (2) lower requirements on transmitter bandwidth and ADC speed. Quasi-Nyquist multiplexing has the advantage of not requiring frequency-locked carriers, so independent lasers can be used. Confinement of the signal spectrum using DF has the advantage of not requiring bulky optical filters, although a moderate amount of additional DSP is needed to implement the DF at the transmitter. Also, DF usually produces sharper spectrum roll-offs than OF, thereby allowing the modulated carriers to be packed closer. Overall, the use of digital filtering to tightly confine the signal spectrum to enable high-SE multiplexing in the superchannel formation is becoming a preferred solution.
3.4.2 Seamless multiplexing
3.4.2.1 O-OFDM with single-carrier-modulated signals
One common type of seamless multiplexing is based on packing single-carrier-modulated signals under the O-OFDM condition [4,8,9]. This type of multiplexing was also referred to as no-guard-interval (NGI) coherent optical OFDM [10], alluding to the aspect that there is no time-domain guard interval (GI) added after the multiplexing, and all-optical OFDM [40,41], alluding to the aspect that no digital signal processing (e.g. digital FFT/IFFF) is used for the multiplexing. A GI can be added at the modulation stage to mitigate the negative impact of limited modulator bandwidth [42], but at the expense of reduced power efficiency and spectral utilization. The need to have frequency locked multi-carriers spaced closely at the symbol rate, as previously defined for a superchannel, is experimentally confirmed and shown in Figure 3.4,where the measured Q2, at full optical signal-to-noise ratio (OSNR), is plotted as a function of the frequency separation of the carriers for three superchannels, respectively, with 2, 3, and 5 carriers, each modulated with 12.5-Gbaud PDM-QPSK. As the number of carriers increases, the carrier separation frequency has to be locked to the symbol rate very precisely.
Figure 3.4 Measured Q2 (at full OSNR) as a function of the frequency separation of the carriers for a 2-, 3-, and 5-carrier NGI-CO-OFDM system with 12.5-Gbaud PDM-QPSK modulation on each carrier [9].
A superchannel transmitter design based on O-OFDM of multiple single-carrier-modulated signals is shown in Figure 3.5. A group of frequency-locked carriers is first separated by a wavelength demultiplexer (DMUX), before being individually modulated with PDM-OFDM by an I/Q modulator array (I/Q modulators followed by polarization-beam combiners). To achieve orthogonality among the modulated carriers, all the carriers, in addition to being spaced at the modulation symbol rate, need to be synchronously modulated or symbol aligned. With orthogonality among the carriers, no frequency guard band is needed between adjacent carriers. The modulated carriers are then combined by an optical coupler. The optical spectra right after the laser, the multi-carrier generator, and the coupler are also illustrated in the insets (a), (b), and (c), respectively, of Figure 3.5. An extension of the scheme shown in Figure 3.5 is to include DACs in the drive path to the data modulators to generate superchannels with high-level modulation formats. Suitable DSP is needed to map the binary data stream intended for transmission to the constellation of the selected modulation format. Photonic integration of all or most of the optical elements in the multi-carrier transmitter is expected to be essential to enable future cost-effective generation of such Tb/s superchannels.
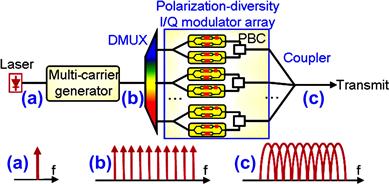
Figure 3.5 Schematic of a multi-carrier superchannel transmitter based on O-OFDM of multiple single-carrier-modulated signals. Optical spectra at locations (a)–(c) are illustrated. DMUX: wavelength de-multiplexer; PBC: polarization beam combiner [9].
Figure 3.6 shows the measured optical spectrum of a 1.2-Tb/s superchannel based on O-OFDM of 24 PDM-QPSK signals [4]. The spectrum of the 24 frequency-locked optical carriers before modulation is also shown. The penalty associated with the seamless multiplexing was shown to be negligible. This 1.2-Tb/s superchannel was transmitted over a record transmission distance of 7200 km with a mean bit error ratio (BER) of <3 × 10–3, a typical threshold of hard-decision (HD) forward-error correction (FEC) codes.
Figure 3.6 Measured optical spectrum of a 1.2-Tb/s superchannel based on O-OFDM of 24 PDM-QPSK signals [4].
3.4.2.2 O-OFDM with OFDM-modulated signals
Another common type of seamless multiplexing is based on packing OFDM-modulated signals under the O-OFDM condition [5–7,26]. In essence, each OFDM-modulated signal can be seen as a set of subcarriers that satisfy the O-OFDM condition with a subcarrier spacing ΔfSC, and multiple such OFDM signals can be arranged to maintain the O-OFDM condition, by synchronizing the OFDM symbols in these signals and putting the GB between any two adjacent OFDM signals to be m·ΔfSC, where m is a positive integer. When m is set to 1, the GB between two adjacent OFDM signals becomes exactly the subcarrier spacing of the OFDM signals, leading to seamless multiplexing of the OFDM signals, or zero-wasted spectrum in the multiplexing process.
In conventional OFDM [43–47], a time-domain GI, e.g. in the form of a cyclic prefix (CP), is inserted in the time domain between adjacent OFDM symbols to accommodate for fiber chromatic dispersion (CD) induced inter-symbol interference (ISI). The larger the chromatic dispersion, the longer is the GI needed, leading to an increased overhead and a reduced spectral efficiency. Recently, reduced-GI OFDM (RGI-OFDM) was proposed to reduce the needed GI in the presence of large CD, by digitally compensating the CD effect prior to the receiver-side OFDM signal processing scheme [26,48]. The RGI-OFDM can be efficiently implemented by a reconfigurable static frequency-domain equalizer as the CD effect is determined by the fiber link and can be viewed as stationary in practice as long as the fiber link is unchanged. Also, the CD effect causes a well-defined quadratic phase response on the signal, which can be readily equalized. A much reduced GI or CP between adjacent OFDM symbols is used to accommodate ISI with short memory, such as that induced by transmitter bandwidth limitations or polarization-mode dispersion (PMD). This approach enables the reduction of the GI from >20% for conventional OFDM to only ∼2% for RGI-OFDM in a typical long-haul 100-Gb/s OFDM system [26].
Figure 3.7 shows an exemplary transmitter setup for forming a superchannel based on O-OFDM of multiple RGI-OFDM signals in a lab context [48]. An external cavity laser (ECL) at 1548.3 nm with a linewidth of ∼100 kHz was used as the laser source. Twenty frequency-locked optical carriers with 6.46-GHz spacing were generated by cascading a 5-comb generator, based on a Mach-Zehnder modulator (MZM) driven by a 25.94-GHz sine-wave with ∼3Vπ amplitude, and a 4-comb generator, based on a nested MZM whose two branches were respectively driven by 3.24 and 9.73-GHz sine-waves with ∼1Vπ amplitudes. A wavelength-selective switch (WSS) was configured to have a 3-dB bandwidth of 120 GHz to reject the unwanted harmonics generated by the 5-comb generator. The 20 frequency-locked carriers were then modulated by a PDM-IQM to generate a PDM-32QAM-OFDM superchannel. The x- and y-polarization components of the PDM signal were independently modulated to better emulate a real transmitter. Four independent drive patterns were stored in two synchronized arbitrary waveform generators (AWGs), each having two 10-GS/s DACs. Pseudo-random bit sequences (PRBS) of length 215 – 1 were used as the payload data. The IFFT size used for OFDM was 128, and the GI was two samples, resulting in a small GI-overhead of 1.56%. Each polarization component of an OFDM symbol contained 78 32-QAM data subcarriers (SCs), four pilot SCs, one unfilled DC SC, and 45 unfilled edge SCs. The spectral bandwidth of each modulated subchannel was 6.48 GHz (=83/128 × 10 GHz), and the 20 frequency-locked 6.48-GHz-spaced input carriers enabled seamless superchannel formation with a total bandwidth of 130 GHz, as shown in inset (f). Three correlated dual-polarization training symbols (TSs) [49] were used for every 697 payload OFDM symbol, resulting in a small TS-overhead of 0.43%. Excluding 7% overhead for forward-error correction, the net payload data rate of the superchannel was 1.12 Tb/s (=10 GHz × 10 b/s/Hz × 78/130 × 697/700 × 20/1.07), corresponding to a net intra-channel SE (ISE, defined later in Section 3.6) of 8.61 b/s/Hz (=1.12 Tb/s/129.7 GHz). This superchannel could likely be put on a 150-GHz grid with <–40 dB crosstalk to neighbors, as indicated in inset (f), to achieve a WDM SE of 7.43 b/s/Hz.
Figure 3.7 Schematic of the experimental setup of a 1.12-Tb/s superchannel transmitter based on seamless multiplexing of multiple OFDM signals under the O-OFDM condition. Insets (a–f) show the schematic outputs (in the frequency domain) and the measured optical spectra at different stages in the transmitter. EDFA: Erbium-doped fiber amplifier; PBC: polarization-beam combiner. After Ref. [48]. © 2011 OSA.
3.4.3 Multiplexing with guard band
3.4.3.1 Multiplexing OFDM-modulated signals with guard band
Seamless multiplexing requires frequency-locked optical carriers, which may be difficult to generate with high tone-to-noise ratio and with low unwanted harmonics. In addition, these frequency-locked carriers need to be separated before modulation by independent modulators. Spectral guard-bands (GBs) can be introduced between OFDM signals to allow for frequency-unlocked independent lasers to be the carriers of a superchannel, at the expense of slightly reduced SE. Figure 3.8 shows the optical spectrum of a superchannel based on multiplexing of eight OFDM-modulated signals with guard band. For each OFDM signal, the FFT size, the sampling rate, and the spectral bandwidth of the filled subcarriers are 128, 30 GS/s, and 19.5 GHz, respectively. The GB used is 1 GHz, representing a spectral overhead of ∼5%, yielding a Δf/B of 1.05, a “quasi-Nyquist” WDM superchannel. The subcarrier modulation is PDM-16QAM. The arrangements of the OFDM subcarriers and symbols are similar to that described in the previous section. The net payload data rate of the superchannel is 1.07 Tb/s (=30 GHz × 8b/s/Hz × 78/130 × 697/700 × 8/1.07), and the overall spectral bandwidth of the superchannel is ∼165 GHz. It is feasible to transmit such 1-Tb/s superchannels on a 175-GHz grid (or a 200-GHz grid to allow ROADM filtering) to achieve a WDM SE of ∼5.7 b/s/Hz (or 5 b/s/Hz).
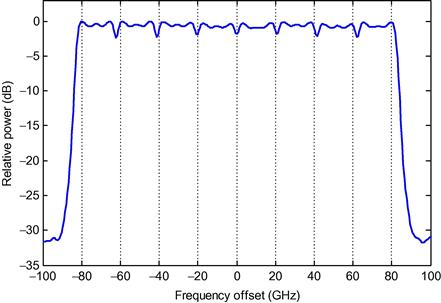
Figure 3.8 Measured optical spectrum of a 1.07-Tb/s superchannel that multiplexes eight OFDM signals with a GB of 1 GHz.
It is important to estimate the crosstalk penalty as a function of the GB bandwidth for various FFT sizes and modulation formats. Figure 3.9 shows the experimentally measured BER performance of one of the eight OFDM signals of the 1.07-Tb/s superchannel (in the back-to-back configuration) as a function of the GB width. For comparison, the BER performance of O-OFDM-based seamless multiplexing by using frequency-locked carriers is also shown (as the dashed line). When the guard band is larger than ∼1 GHz, or ∼5% of the OFDM signal bandwidth, the performance of the superchannel with guard-banded multiplexing becomes better than that with O-OFDM-based seamless multiplexing, which we attribute to the worse back-to-back OSNR of the O-OFDM case due to the high loss of the frequency-comb generator used, resulting in a reduced signal OSNR.
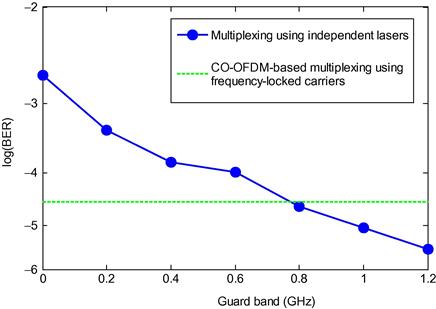
Figure 3.9 Measured BER performance of one of the OFDM signals of the 1.07-Tb/s superchannel as a function of the guard band width.
The crosstalk penalty in guard-banded multiplexing of OFDM signals can be analytically estimated. For each OFDM subcarrier, we have a square pulse in the time domain and hence a sinc waveform in the frequency domain. The edge subcarriers of an OFDM signal are most contaminated by the non-orthogonal subcarriers of other OFDM signals. The amount of the worst-case crosstalk imposed on these edge subcarriers can be expressed as
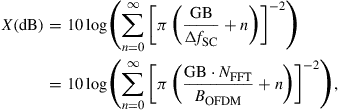(3.1)
where ΔfSC, NFFT, and BOFDM are the OFDM subcarrier spacing, FFT/IFFT size used in OFDM, and the spectral bandwidth of the OFDM signal, respectively. Figure 3.10 shows the crosstalk as a function of the ratio between the GB width and the OFDM signal bandwidth (GB/BOFDM). The crosstalk-induced penalty depends on modulation format and the targeted BER. A comprehensive study on this subject has recently been reported by Winzer et al. [50]. To limit the OSNR penalty at BER = 10–3 to be within 3 dB, the allowed crosstalk amounts are approximately 10 dB, 17.5 dB, and 24 dB for QPSK, 16-QAM, and 64-QAM, respectively. Assuming that we can allow the worst-case edge subcarriers to have 3-dB OSNR penalty at BER = 10–3, the GB-to-bandwidth ratio GB/BOFDM needs to be larger than ∼1.2%, ∼5%, and ∼20% for QPSK, 16-QAM, and 64-QAM subcarrier modulation, respectively. This indicates that for OFDM signals with NFFT > 128 and with n-QAM subcarrier modulation where n ≤ 16, spectrally efficient multiplexing of these OFDM signals with only ∼5% spectral overhead is feasible. For higher-level QAM formats such as 64-QAM, larger GB or additional spectral shaping of the OFDM signal to suppress its sidebands is needed.
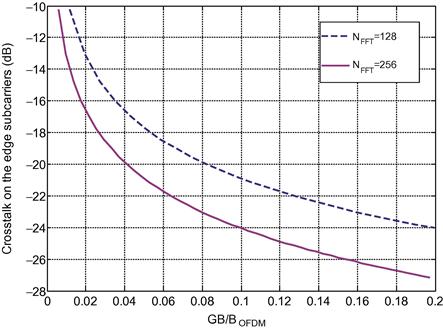
Figure 3.10 Calculated worst-case crosstalk on the edge subcarriers of an OFDM signal as a function of the ratio between the GB width and the OFDM signal bandwidth.
The above analysis can be also applied to estimate the needed GB between superchannels that are based on O-OFDM of single-carrier-modulated signals, by replacing NFFT with the number of single-carrier-modulated signals and replacing BOFDM with the superchannel bandwidth. Obviously, when the number of single-carrier-modulated signals is reduced, the GB-to-bandwidth ratio needs to be increased, as recently shown through numerical simulations by Bosco [51].
3.4.3.2 Multiplexing Nyquist-filtered single-carrier signals with guard band
As discussed previously, quasi-Nyquist-filtered single-carrier signals can have well-confined spectra with a small roll-off factor, β, commonly defined as the ratio between the excess signal bandwidth and the Nyquist bandwidth of the signal (B/2). Without considering laser frequency drift, the needed GB to avoid crosstalk between adjacent Nyquist-filtered signals is thus β·B/2. Smaller roll-off is desired to multiplex signals at higher SE, but the smaller the roll-off, the larger the DSP complexity as longer filters are needed to perform the Nyquist filtering. A numerical study on the robustness of a Nyquist-WDM-based superchannel to optical filtering and to crosstalk induced by adjacent superchannels has been reported [51]. In a recent Nyquist-WDM experiment, a roll-off factor as small as 0.01 has been demonstrated, leading to a record single-mode fiber capacity of 102.3 Tb/s [52].
DFT-spread OFDM [32–35] is also commonly known as single-carrier frequency-division multiple access (SC-FDMA) [53], in which discrete Fourier transform (DFT) and inverse discrete Fourier transform (IDFT) are used to perform the spectral shaping. In SC-FDMA, the modulation is done in the time domain while the equalization is performed in the frequency domain. Multiple SC-FDMA signals can be multiplexed to form a superchannel, and the needed GB to confine the crosstalk penalty to a certain level can be estimated by using the analysis presented in the previous section.
3.5 Detection
In conventional WDM systems, wavelength channels are first de-multiplexed before being received. For superchannels, however, the modulated carriers inside each superchannel are typically too closely spaced to be separated by WDM filters without incurring a filtering penalty. As sharp filtering functions can be readily generated in the digital domain, digital coherent detection enables banded-detection of a superchannel [4,26,54–56], which consists of the following steps:
1. Splitting the superchannel into M copies;
2. Mixing these M copies in M polarization-diversity optical hybrids with M different optical local oscillators (OLOs);
3. Performing digital coherent detection of each of the M copies, with an RF bandwidth that is slightly larger than half of the occupied optical spectral bandwidth of the modulated carrier(s) intended for detection;
4. Digitally filtering each modulated carrier and recovering the data carried by that carrier.
Note that the tight confinement of the spectral content of each modulated carrier in a superchannel, e.g. through transmitter DF, is very beneficial as it reduces the oversampling ratio requirement at the receiver, leading to relaxed ADC sampling speed requirement and more efficient digital signal processing for channel recovery.
It is possible to simultaneously detect more than one carrier per digital sampling at the receiver. At 112 Gb/s, a 2-carrier signal was shown to be detected with low-sampling-rate ADC to reduce both hardware complexity and receiver DSP load [54]. It was also shown that an oversampling factor, defined as the ratio between the sampling rate and the symbol rate of the carrier modulation, as small as 1.4 is sufficient [55]. In Refs. [4] and [56], the simultaneous detection of two and three subcarriers, in the presence of all 24 subcarriers, was demonstrated, respectively.
Figure 3.11 shows the schematic of the banded detection of a superchannel containing N single-carrier-modulated signals. There are M (M < N) detection bands, each of which contains more than one modulated signal to be recovered. The inset illustrates the detection of a 10-carrier superchannel with five detection bands, each containing two modulated carriers. Note that the needed optical hardware (including the optical hybrids and OLOs) is reduced in proportion to the number of carriers per detection band, by the use of faster ADCs and DSPs. In the case of the reception of a 448-Gb/s superchannel based on O-OFDM of ten RGI-OFDM signals [26], two banded detections were used to recover all the ten signals, corresponding to an oversampling ratio of 1.67. It was also shown that multi-carrier superchannels can be detected with oversampling ratios below two with negligible penalties. Figure 3.12 shows the schematic of the DSP block diagram for recovering the (N/M) carriers when detecting the first band of an N-carrier signal using M equally sized detection bands [4]. First, electronic dispersion compensation (EDC) is performed, e.g. by using the well-known frequency-domain equalization approach. Then, carrier separation is conducted by shifting each carrier to the baseband and passing each shifted carrier through two cascaded T/2 and T/4 delay-and-add filters, where T is the modulation symbol period. Constant modulus algorithm (CMA)-based blind equalization with a 15-tap T/4-spaced adaptive FIR filter can be used for polarization demultiplexing and further signal equalization. Other DSP processes include frequency estimation (FE), phase estimation (PE), and data recovery. Finally, the bit error ratio (BER) of each of the detected carriers is measured.
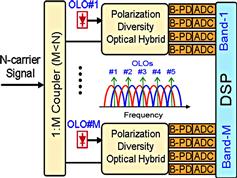
Figure 3.11 Schematic of the banded detection of a multi-carrier signal. Inset: illustration of the detection of a 10-carrier signal with five detection bands, each containing two modulated carriers. B-PD: balanced photo-detector [9].
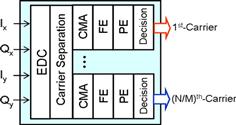
Figure 3.12 Schematic of the DSP block diagram for recovering the (N/M) carriers when detecting the 1st band of an N-carrier signal using M equally sized detection bands. EDC: electronic dispersion compensation; CMA: constant-modulus algorithm-based channel compensation; FE: frequency estimation and compensation; PE: phase estimation and compensation [9].
For a superchannel with OFDM-modulated signals, the DSP at the receiver is strongly linked to the DSP at the transmitter, particularly with the frame structure, training symbols, and pilot subcarriers. Concepts such as correlated dual-polarization (CDP) training symbols [49,57] and intra-symbol frequency-domain averaging (ISFA) [58] have enabled reliable and efficient reception of OFDM signals after long-distance transmission. OFDM-based superchannels are well suited for banded detection for the following reasons. First, when OFDM modulation is used, a square-like optical spectrum with sharp roll-off is naturally obtained, reducing the needed guard band compared to quasi-Nyquist WDM if independent lasers are used as the multiplexing scheme. Second, when CO-OFDM multiplexing is used, the orthogonality among the modulated carriers can be exploited to achieve crosstalk-free demultiplexing of these carriers. Finally, the banded detection makes the frequency range to be covered in the subsequent receiver signal processing much smaller than the bandwidth of the superchannel. This dramatically reduces the complexity of electronic CD compensation, as the size of the CD equalizer scales quadratically with the processing frequency range. In effect, the banded processing of a superchannel increases the overall receiver DSP efficiency. A novel filter-bank-based efficient processing of RGI-OFDM signals and Nyquist-WDM signals was recently proposed by Tolmachev and Nazarathy [59,60].
3.6 Superchannel Transmission
A useful parameter that specifies the spectral efficiency of the superchannel is the intrachannel SE (ISE). For a superchannel whose carriers are multiplexed by PDM n-point quadrature-amplitude modulation (n-QAM), the maximum ISE that can be achieved without a coherent crosstalk penalty is
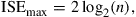(3.2)
where the factor of 2 on the right-hand side accounts for PDM. The actual ISE for an OFDM-based superchannel can be expressed as
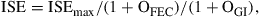(3.3)
where OFEC is the overhead used for forward error correction (FEC) and OGI is the OFDM signal processing related overhead, used for guard intervals, training symbols, and/or pilot subcarriers.
3.6.1 Transmission based on single-carrier modulation and O-OFDM multiplexing
Table 3.4 shows the transmission performance reported for various superchannels in experimental demonstrations. An early demonstration [22], called coherent wavelength division multiplexing (CoWDM), was based on non-return-to-zero (NRZ) signaling, with 42.66-GHz carrier spacing and 42.66-Gb/s on-off keyed (OOK) data modulation on the carriers, with appropriate phase control applied to minimize crosstalk. Subsequently, two-carrier optical OFDM was demonstrated [40] where differential quadrature phase shift keying (DQPSK) was used to generate a 100-Gb/s superchannel, with the two carriers spaced 25-GHz apart, and each modulated at 25 Gbaud. A variant of this approach with four carriers, each modulated using the duobinary format, was also reported [61]. All three of the above demonstrations used direct detection (DD) to recover information from each carrier. All subsequent demonstrations have used coherent detection. O-OFDM using two carriers, each modulated with single-carrier PDM-QPSK, was demonstrated for 100-Gb/s long-haul transmission [54]. The underlying O-OFDM principles elucidated in [8] were used to demonstrate 1.2-Tb/s 24-carrier superchannel generation, detection, and transmission [4]. This was also the first time ultra-large area fiber (ULAF) was used for Terabit/s superchannel transmission. The ULAF had an average fiber loss, dispersion, and dispersion slope at 1550 nm of 0.185 dB/km, 19.9 ps/nm/km, 0.06 ps/nm2/km, respectively. The effective area was 120 μm2, which allowed for high signal launch powers without suffering very much from fiber nonlinearities. As can be seen in Table 3.4, several multi-level modulation formats (QPSK, 8-QAM, and 16-QAM) have been used to synthesize superchannels, and a wide range of ISEs have been demonstrated.
Table 3.4
Experimental demonstrations of superchannels based on single-carrier modulation and O-OFDM.
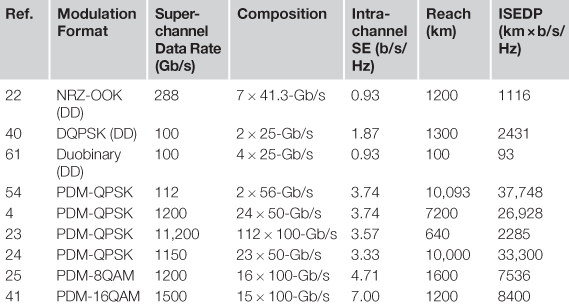
In Table 3.4, we also compare another figure of merit, namely, the intrachannel spectral efficiency and distance product (ISEDP). Large ISEDP values reflect the superior transmission characteristics of high SE superchannels. As the complexity of a modulation format increases, the ISEDPs have correspondingly reduced due to higher OSNR requirements. Record ISEDP values have been achieved by using PDM-QPSK modulation with ISEs ranging from 3.33 to 3.74 b/s/Hz.
3.6.2 Transmission based on OFDM modulation and O-OFDM multiplexing
In Table 3.5, we list experimental demonstrations of superchannels using RGI-OFDM formats as well as quasi-Nyquist filtered single-carrier formats, using digital signal processing techniques at the transmitter as described earlier. It is evident that achieving ISEs beyond 5 b/s/Hz is generally easier using either RGI-OFDM or the quasi-Nyquist-filtering based modulation as compared to unfiltered single-carrier modulation. In addition, the demonstrated ISEDP values in Table 3.5 are generally larger for approximately the same ISE as compared to the values demonstrated in Table 3.5. The reason for both these observations is related to the relative ease of generating high-quality crosstalk-free subcarriers that are multi-level modulated when DAC and transmitter-side signal processing are used. For quasi-Nyquist WDM, the intentionally allocated guard bands between channels alleviate crosstalk impairments, albeit at the expense of slightly reduced SE.
Table 3.5
Experimental demonstrations of superchannels based on OFDM for the O-OFDM optical subcarriers, as well as quasi-Nyquist-WDM and guard-banded OFDM.
We illustrate the performance of RGI-OFDM superchannels with the experiment reported in Ref. [63] and depicted in Figure 3.13. The same setup was successfully used to demonstrate three different modulation formats, show optical parallelization concepts, demonstrate banded detection of the entire superchannel with one digital sampling, and evaluate the concatenation performance of reconfigurable optical add/drop multiplexers (ROADMs). A brief description follows.
Figure 3.13 Schematic of the experimental setup [63]. Insets: (a) OFDM frame structure; (b) optical spectra of three 485-Gb/s WDM channels before and after 4800-km transmission; (c) block diagram of the receiver offline DSP.
At the transmitter, three 100-GHz-spaced 485-Gb/s superchannels based on RGI-OFDM modulation and CO-OFDM multiplexing were generated. The WDM channels were launched into a transmission loop consisting of four Raman-amplified 100-km ULAF spans. To assess the signal performance in optically routed networks with ROADMs, we used a 100-GHz WSS in the loop to separate and recombine the even and odd channels. For each WSS passband, the 0.1-dB and 35-dB bandwidths were ∼72 and ∼125 GHz, respectively. The optical spectra of the three WDM channels, measured by an optical spectrum analyzer with 0.1-nm resolution before and after 4800-km transmission, are shown as inset (b) in Figure 3.12. Evidently, no optical filtering-induced spectral clipping is observed, even after 12 WSS passes. At the receiver, each WDM channel was sequentially filtered out by a second 100-GHz WSS for performance evaluation. An optical local oscillator (OLO) was tuned to the center frequency of the channel under test. With the use of four 80-GS/s ADCs with 32.5-GHz RF bandwidth, each 485-Gb/s signal with an optical bandwidth of 64.8 GHz can be completely sampled through a single coherent detection, without having to resort to banded detection. The digitized waveforms were processed offline. The DSP blocks are shown in inset (c) of Figure 3.13.
With the use of transmitter DSP, the modulation format used for subcarrier modulation in OFDM can be easily changed, leading to a so-called software-defined transmission link. Figure 3.14 shows the recovered constellations of the OFDM subcarriers when modulated by 16-QAM [63], 32-QAM [28], and 64-QAM [29], achieving superchannel data rates of 485, 606, and 728 Gb/s, respectively. The distances transmitted over ULAF fiber with all-Raman amplification were 4800, 1600, and 800 km, respectively.
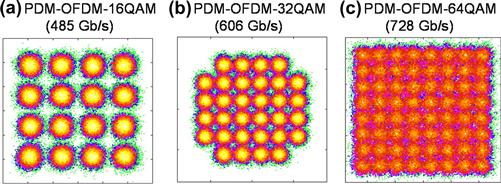
Figure 3.14 Constellations of the OFDM subcarriers (recovered in the back-to-back configuration) when modulated by 16-QAM [63], 32-QAM [28], and 64-QAM [29], respectively, achieving superchannel data rates of 485, 606, and 728 Gb/s.
It is interesting to note that the three formats had a spectral occupancy of between 60 and 65 GHz, demonstrating the adaptive nature of multilevel formats to support high data rates without sacrificing optical spectrum.
With the prevalence of soft-decision forward error correction (SD-FEC) in next generation transport systems, it is important not just to look at pre-FEC error rates (as is permissible for hard-decision FEC if errors are uncorrelated) but also to investigate the probability density function (pdf) of the signal after transmission to see if the noise distribution is, in fact, Gaussian, as the net coding gain (NCG) for the FEC is typically derived using the additive white Gaussian noise (AWGN) assumption [65]. Figure 3.15a shows the pdf of the I and Q components of both polarizations of the center 485-Gb/s PDM-16QAM RGI-CO-OFDM superchannel in the back-to-back configuration, which closely follows the Gaussian distribution. Figure 3.15b shows the pdf after 4800-km transmission at the optimal signal power, which also closely follows the Gaussian distribution. In addition, careful analysis of the pdfs for all 16 constellation points showed that all pdfs are identical and individually obey circularly symmetric complex Gaussian statistics. This indicates that soft-decision FEC can be effective, even in the nonlinear transmission regime, for OFDM-based superchannel transmission.
Figure 3.15 (a) Probability density function (pdf) of the signal distortion in the back-to-back configuration; (b) pdf after 4800-km transmission at 1 dBm per superchannel [63].
More recently, a guard-banded OFDM superchannel with 1.5-Tb/s net data rate, consisting of eight all-electronically-generated 30-Gbaud PDM-OFDM-16QAM signals spaced at 32.8 GHz, was transmitted over 56 100-km ULAF spans (5600 GHz km), achieving a record spectral-efficiency-distance product of over 32,000 km b/s/Hz for terrestrial Tb/s-class superchannel transmission with >5 b/s/Hz net spectral efficiency [64]. Soft-decision forward error correction was implemented using offline processing as an inner code, resulting in a corrected bit-error ratio below the threshold of an outer hard-decision (HD) FEC decoder. This demonstration was enabled by high-speed 50-GS/s DACs and ADCs allowing for a record 233-Gb/s all-electronically-generated and detected OFDM signal, low-nonlinearity ULAF, Raman amplification, low-overhead OFDM, optimized one-step-per-span nonlinear compensation, and SD-FEC.
3.6.3 Transmission based on Nyquist-WDM
The transmission performance of Tb/s Nyquist-WDM superchannels has been studied experimentally [12,13] and numerically [15,66]. Bosco et al. comprehensively studied the transmission performance of Tb/s Nyquist-WDM with PDM-BPSK, PDM-QSPK, PDM-8QAM, and PDM-16QAM formats through numerical simulations [66]. Figure 3.16 shows the maximum reach of Nyquist-WDM superchannels at BER ≤ 4 × 10–4 as a function of capacity in the C-band and as a function of spectral efficiency for PM-BPSK, PM-QPSK, PM-8QAM, and PM-16QAM. (Although this study was done using a BER threshold of 4 × 10–3, longer reaches are achievable when the FEC threshold is higher, as in current generation SD-FEC.) For a given modulation format, the reach decreases as the frequency spacing between the Nyquist-filtered signals approaches the modulation symbol rate (27.75 GHz). For the same modulation format and the same frequency spacing, the transmission distance in standard single-mode fiber (SSMF) is longer than that in non-zero dispersion-shifted fiber (NZDF) due to the larger dispersion and smaller nonlinear coefficient of SSMF. More remarkably, as the constellation size doubles, e.g. from BPSK to QPSK or from 8-QAM to 16-QAM, the transmission distance is almost halved. This observation was also reported by Essiambre et al. in 2010 [67]. There are several other observations from the study. At the optimum transmitted power, the value of the maximum reachable distance is approximately equal to 2/3 of the maximum reachable distance in the linear regime, for all formats and fibers, and the OSNR penalty due to fiber nonlinearity at the optimal signal launch power is ∼1.76 dB. The optimal signal power spectral density is essentially independent of the modulation format. This is also consistent with the simulation results presented in Ref. [67]. These observations can be explained by analyses to be presented in the following section.
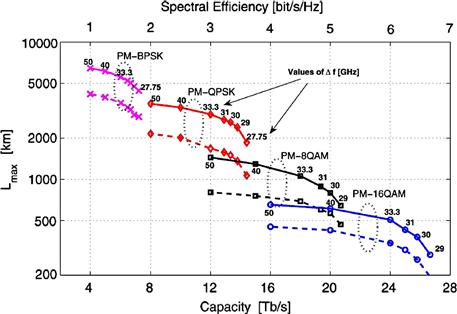
Figure 3.16 Maximum reach with BER ≤ 4 × 10–3 versus capacity in the C-band (bottom axis) and spectral efficiency (top axis) for Nyquist-WDM superchannel with 27.75-Gbaud PM-BPSK (crosses), PM-QPSK (diamonds), PM-8QAM (squares), and PM-16QAM (circles). Lines are obtained connecting simulation results. Solid lines refer to SSMF and dashed lines refer to NZDSF. The corresponding values of Δf in GHz are shown at the SSMF points. (After Ref. [66]. © 2011 IEEE.) Note that longer transmission distances are feasible when the BER threshold is increased, e.g. by using stronger forward error correction codes.
3.6.4 Optimization of the spectral-efficiency-distance-product
For future optical transport systems, it is desirable to increase the SE for higher network capacity. On the other hand, higher SE leads to less tolerance to linear and nonlinear impairments and thus shorter transmission distances, as shown experimentally and numerically in the previous sections. What really matters in many cases is the cost per end-to-end transported information bit (CPB), which is preferred to be as low as possible. A useful metric that closely relates to the CPB is the spectral-efficiency-distance-product (SEDP), because the SEDP is linked to the number of transponders used in a system: usually the higher the SEDP, the less need for optical-to-electronic-to-optical (O/E/O) conversion, and thus the lower the CPB (assuming that O/E/O conversion cost is the major portion of the system cost, which is usually true in WDM systems). In this section, we compare the commonly used PDM-n-QAM modulation formats based on their respective achievable SEDPs. We present simple closed-form expressions for the achievable SEDP. Given the popular use of digital signal processing at both the transmitter and receiver of a Tb/s superchannel link, the optimal format that provides the highest SEDP for a given optical link could be readily implemented.
Assuming that the signal distortions are Gaussian distributed, which is a reasonably accurate assumption for dispersion-uncompensated high-speed transmission links [68–71] we define an effective signal-to-noise ratio (SNR) as the ratio between the signal power and the sum of the linear noise resulting from ASE and the nonlinear noise, given by
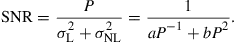(3.4)
where P,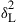 
, and 
are respectively the signal power, linear noise power, and nonlinear noise power, and a and b are parameters that depend on link conditions. The SNR is maximized to
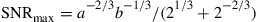(3.5)
at the optimum power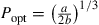 
. Evidently, the SNR penalty due to fiber nonlinearity (as compared to the case without fiber nonlinearity) at the optimal signal launch power is –10log(2/3) ≈ 1.76 dB. This is in good agreement with that obtained through numerical simulations for dispersive coherent transmission [66].
Assuming that the transmission link consists of uniform fiber spans with the same physical characteristics and seamless O-OFDM multiplexing of signals with the same modulation format, the maximum effective SNR can be expressed by [69]
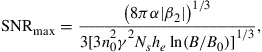(3.6)
where α, β2, and γ are the fiber coefficients for loss, dispersion, and nonlinearity, respectively, Ns is the number of fiber spans of the optical link, n0 is the power spectral density of the optical amplified spontaneous (ASE) noise, which is proportional to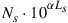 
(where Ls is the length of each fiber span), B is the bandwidth of the WDM signals, B0 is the larger of the CD-induced walk-off bandwidth and the phase estimation bandwidth and he is the nonlinear multi-span noise enhancement factor [70]. The maximum SNR is obtained at the optimum signal power spectral density
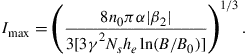(3.7)
For dispersion-uncompensated optical transmission (DUMT) or dispersion compensation module (DCM) free transmission, which is a popular approach enabled by the capability of electronic dispersion compensation in digital coherent receivers, he ≈ 1, we have
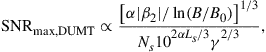(3.8)
and
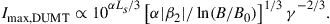(3.9)
The maximum signal qualify factor (Q2) of a signal with n-QAM modulation format has the following dependence on link parameters
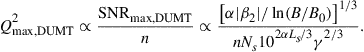(3.10)
The maximum achievable SE obtained by using PDM-n-QAM for the link is achieved by setting the maximum signal quality factor equal to the quality factor corresponding to the underlying FEC threshold,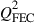 
,
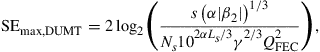(3.11)
where s is a scaling factor. The above analytical results suggest the following key transmission characteristics in DUMT.
1. To increase spectral efficiency by 2 bit/s/Hz, the dispersion coefficient (|β2|) needs to be increased by a factor of 8, the nonlinear coefficient (γ) needs to be decreased by a factor of 21.5 (or ∼2.83), or the number of fiber spans (Ns) needs to be reduced by a factor of 2 [69]. These analytical findings are in reasonable agreement with those obtained through numerical simulation [72].
2. The optimum signal power spectral density is dependent on fiber parameters, but is independent of the transmission distance and the modulation format [66].
3. The optimum signal quality factor Q2 scales inversely proportional to the transmission distance. The physical reason behind this is that in DUMT, the nonlinear noises (or distortions) generated by the fiber spans are de-correlated [71], so the accumulation of the nonlinear noise during transmission scales the same way as the linear noise resulting from the ASE. Reducing the FEC threshold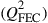 
by 3 dB leads to doubled transmission distance, showing the importance of using powerful FEC codes with higher coding gains, e.g. soft-decision (SD) FEC codes, to enable longer transmission distance.
The above findings from the analytical study are in reasonably good agreement with the results obtained by experiments and numerical simulations for DUMT of superchannels based on O-OFDM and Nyquist-WDM [66]. It is useful to find the SE or modulation format that provides the minimum CPB of a transmission system of a given size. When the system cost is dominated by the optical transponders or the O/E/O conversion, the minimum CPB is achieved when the SEDP of the transmission system is maximized. The effective SEDP of a maximum system length LLink using PDM-n-QAM modulation can be expressed as [73]
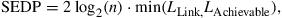(3.12)
where LAchievable is the transmission distance that is achievable by the signal based on fiber parameters of the transmission system and can be written as
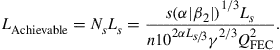(3.13)
Figure 3.17 shows the calculated SEDP as a function of SE in systems using superchannels based on PDM-n-QAM modulation and 100-km ULAF spans [63]. The calculation is based on Eqs. (3.11) and (3.12), and the scaling factor s in Eq. (3.11) was obtained using the results reported in Ref. [63]. The FEC BER threshold and the overall spectral overhead (for FEC and multiplexing) are assumed to be 2 × 10–2 and 29%, respectively [63]. The key implications from the results are (i) there is an optimum SE, SEopt, at which the system SEDP is maximized (for lowest CPB); (ii) the SEopt depends on the system size Llink; and (iii) for long-haul systems where Llink > 1000 km, the SEopt is smaller than 10. A useful takeaway message is that for core optical networks with long-haul reach, there is not much value (in terms of CPB) to push the SE beyond 10 by using superchannels modulated with a constellation size larger than PDM-64QAM. Moreover, when the implementation penalty of higher-level QAM and practical system margin are taken into consideration, the optimum system SE is expected to be pushed downwards, e.g. to be between 4 and 8 b/s/Hz.
Figure 3.17 Calculated SEDP as a function of SE in systems using superchannels and 100-km ULAF spans. The FEC BER threshold and the overall spectral overhead (for FEC and multiplexing) are assumed to be 2 × 10–2 and 29%, respectively.
The above analysis is based on several assumptions, such as homogeneous fiber spans, negligible signal-to-noise nonlinear interaction, and ideal transceivers having zero implementation penalty. More general and comprehensive studies on the ultimate capacities of fiber transmission systems can be found in Refs. [67,72,74–76].
3.7 Networking Implications
In modern dense WDM (DWDM) systems, transparent optical routing based on ROADMs is an essential technology that enables network flexibility and efficiency. In current DWDM systems, a fixed channel grid, as defined by the International Telecommunications Union (ITU), is used. The channel spacing is typically 50 GHz, as shown in Figure 3.18a. For future systems with 1-Tb/s and 400-Gb/s superchannels, the optical bandwidth needed for each channel is expected to be more than 50 GHz. This calls for a new DWDM channel allocation scheme where the channel bandwidth is flexible, or adjustable in order to support these high-data-rate superchannels, as illustrated in Figure 3.18b. This new type of DWDM can be called flexible DWDM or elastic DWDM [77–79]. In the recent 448-Gb/s RGI-OFDM demonstration [26], it has been shown that the superchannel is capable of passing five 80-GHz-grid ROADMs with negligible filtering penalty. For maximum system SE, the center of these superchannels may not coincide with the ITU 50-GHz grid because of their nonstandard optical bandwidth requirements. On the other hand, it may cause too much architectural changes to completely abandon the well-established ITU grid. So, a plausible compromise would be to use a finer ITU grid, e.g. the 25-GHz grid or the 12.5-GHz grid, but allow the channel bandwidth to be flexible, e.g. ranging from 50 to 350 GHz, to efficiently support 100-Gb/s, 400-Gb/s, and 1-Tb/s channels [9,80].
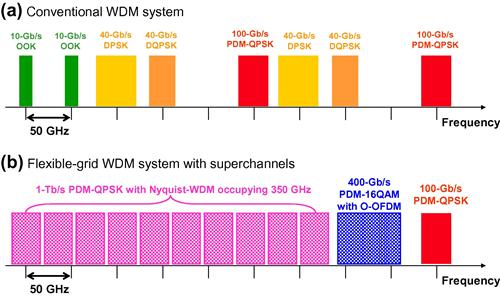
Figure 3.18 Illustrations of a conventional WDM channel allocation (a) and a flexible-grid WDM channel allocation suitable for supporting future 1-Tb/s and 400-Gb/s superchannels (b). The data rates labeled are for net information bit rates.
Currently, a flexible WDM grid architecture with a bandwidth granularity of 12.5 GHz and a center frequency granularity of 6.25 GHz has been standardized by the International Telecommunication Union (ITU) as the ITU G.694.1 standard [81] and illustrated in Figure 3.19. According to the new ITU standard, the allowed frequency slots have a nominal central frequency (in THz) defined by: 193.1 + n × 0.00625, where n is a positive or negative integer including 0, and 0.00625 is the nominal central frequency granularity in THz, and a slot width defined by: 12.5 × m, where m is a positive integer and 12.5 is the slot width granularity in GHz. Any combination of frequency slots is allowed as long as no two frequency slots overlap [81]. The reason that the nominal central frequency granularity needs to be 6.25 GHz is to be able to place a slot that has a width of an even multiple of 12.5 GHz next to one with a width of an odd multiple of 12.5 GHz without a spectral gap or guard band. The flexible WDM architecture is also supported by the recent availability of flexible bandwidth WSSs [82].
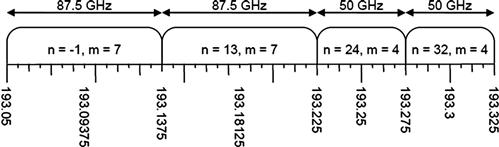
Figure 3.19 A flexible grid allocation example in accordance with the ITU G.694.1 standard. After Ref. [81].
The benefits of the flexible WDM grid architecture on the networking layer have also been studied recently [83–87]. It was shown that the introduction of the elasticity and adaptation in the optical domain yields significant spectral savings and leads to increased network capacity and enhanced survivability in the 400-Gb/s and 1-Tb/s era [83]. The blocking performance of spectrum efficient superchannels in dynamic flexible grid networks was studied, and the results demonstrate that increased spectral efficiency and flexible superchannel assignment do translate into network efficiency gains [84]. The energy efficiency of flexible-grid WDM networks has also been studied [85–87]. It is expected that the flexible-grid WDM architecture would become a popular choice for future Tb/s-per-channel optical networks.
Another key benefit of superchannels is that it efficiently leverages the advances in large-scale photonic integrated circuits (PICs) to reduce optical circuit complexity, as compared to using discrete optical components, and offers maximum flexibility for an engineering design [88–90]. A compact coherent-receiver front end consisting of an integrated 4 × 40 arrayed waveguide grating (AWG) array following a polarization-diversity optical hybrid was recently demonstrated and used for complete demodulation of a 1.12-Tb/s multi-carrier superchannel having ten 112-Gb/s PDM-QPSK signals [91]. Figure 3.20 shows the schematic of the compact superchannel coherent receiver. The cyclic feature of the AWG array allows the receiver to receive modulated carriers that are not adjacently spaced. The scheme can be extended to multi-carrier signals whose carriers are closely spaced, e.g. under the O-OFDM condition, for high-spectral-efficiency Tb/s transmission applications [91]. Large-scale photonic circuit integration [92], both at the transmitter and at the receiver, are needed to enable efficient superchannel synthesis and reception. Furthermore, superchannel architectures can advantageously leverage the advances in large-scale application-specific integrated circuits (ASIC) capable of high-speed parallel signal processing [93], especially when PICs are used to increase the intimacy between photonics and electronics [90].
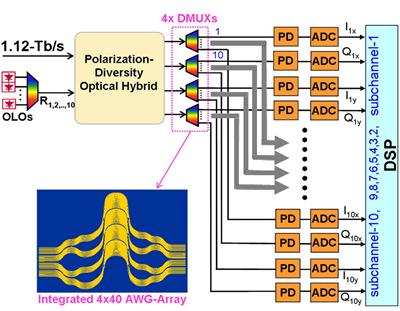
Figure 3.20 Schematic of a compact coherent receiver based on large-scale PICs for receiving a 1.12-Tb/s superchannel with 10 112-Gb/s PDM-QPSK signals [91]. Inset: layout of an integrated 4 × 40 AWG array. DMUX: wavelength demultiplexer; PD: photo-detector; OLO: optical local oscillator; DSP: digital signal processor.
More recently, there has been vigorous research in the field of space division multiplexing (SDM) [94] to explore capacity enhancement using spatial modes/cores in fiber as another dimension. In that context, concepts of “spatial superchannels” have been proposed and demonstrated [95], opening opportunities for further expanding the application of superchannels.
3.8 Conclusion
We have reviewed the principle and recent progress of superchannel transmission with per-channel data rates of Tb/s and beyond. The generation, detection, nonlinear transmission, and networking of Tb/s-per-channel-class superchannels have been discussed. Superchannel transmission offers several key benefits such as higher serial interface rates, higher spectral efficiency and WDM capacity, increased efficiency in digital signal processing, and better leverage of large-scale PICs and ASICs. Enabled by digital signal processing at both transmitters and receivers, high spectral efficiency modulation based on Nyquist-filtered single-carrier and OFDM, together with multiplexing based on Nyquist-WDM and O-OFDM, can be realized. Software-defined optical transmission to optimize the system throughput depending on the link conditions also becomes feasible. The presence of Tb/s superchannels with different spectral bandwidths in a WDM system has led to the introduction of flexible grid WDM architectures to achieve more efficient utilization of the optical spectrum. It is expected that with the further advances in PICs, ASICs, efficient digital signal processing, flexible-bandwidth ROADM and WSS, and network-layer provisioning of flexible bandwidth WDM channels, Tb/s-per-channel-class superchannel transmission will play an important role in future high-capacity optical fiber networks, offering both increased performance and lowered cost per bit to meet the ever-increasing capacity demands of the Internet era.
Glossary
ADC: analog-to-digital conversion (converter)
ASIC: application-specific integrated circuit
BPSK: binary phase-shift keying
CMA: constant modulus algorithm
DAC: digital-to-analog converter
DSP: digital signal processor (processing)
EDC: electronic dispersion compensation
IFWM: intrachannel four-wave mixing
OFDM: orthogonal frequency-division multiplexing
OSNR: optical signal-to-noise ratio
PIC: photonic integrated circuit
PMD: polarization-mode dispersion
QAM: quadrature amplitude modulation
QPSK: quadrature phase-shift keying
ROADM: reconfigurable optical add/drop multiplexer
WDM: wavelength-division multiplexing
WSS: wavelength selective switch
References
1. A.R. Chraplyvy, The coming capacity crunch, in: ECOC Plenary Talk, 2009.
2. Tkach RW. Scaling optical communications for the next decade and beyond. Bell Labs Tech J. 2010;14:3–10.
3. Winzer PJ. Beyond 100G Ethernet. IEEE Commun Mag. 2010;48(7):26–30.
4. S. Chandrasekhar, X. Liu, B. Zhu, D.W. Peckham, Transmission of a 1.2-Tb/s 24-carrier no-guard-interval coherent OFDM superchannel over 7200-km of ultra-large-area fiber, in: ECOC’09, Post-deadline paper PD2.6.
5. Y. Ma, Q. Yang, Y. Tang, S. Chen, W. Shieh, 1-Tb/s per channel coherent optical OFDM transmission with subwavelength bandwidth access, in: OFC’09, Post-deadline paper PDPC1.
6. R. Dischler, F. Buchali, Transmission of 1.2 Tb/s continuous waveband PDM-OFDM-FDM signal with spectral efficiency of 3.3 bit/s/Hz over 400 km of SSMF, in: Proceedings of OFC 2009, March 22–26, 2009, Paper PDPC2.
7. Zhu B, Liu X, Chandrasekhar S, Peckham DW, Lingle Jr R. Ultra-long-haul transmission of 1.2-Tb/s multicarrier no-guard interval CO-OFDM superchannel using ultra-large-area fiber. IEEE Photon Technol Lett. 2010;22:826–828.
8. Chandrasekhar S, Liu X. Experimental investigation on the performance of closely spaced multi-carrier PDM-QPSK with digital coherent detection. Opt Express. 2009;17:12350–12361.
9. S. Chandrasekhar, X. Liu, Terabit superchannels for high spectral efficiency transmission, in: Proceedings of ECOC’10, 2010, Paper Tu.3.C.5.
10. Sano A, Yamada E, Masuda H, et al. No-guard-interval coherent optical OFDM for 100-Gb/s long-haul WDM transmission. J Lightwave Technol. 2009;27:3705–3713.
11. G. Gavioli et al., Investigation of the impact of ultra-narrow carrier spacing on the transmission of a 10-carrier 1 Tb/s superchannel, in: Proceedings of OFC 2010, March 21–25, 2010, Paper OThD3.
12. Gavioli G, Torrengo E, Bosco G, et al. Ultra-narrow-spacing 10-channel 1.12 Tb/sD-WDM long-haul transmission over uncompensated SMF and NZDSF. IEEE Photon Technol Lett. 2010;22(19):1419–1421.
13. E. Torrengo et al., Transoceanic PM-QPSK Terabit superchannel transmission experiments at baud-rate subcarrier spacing, in: Proceedings of ECOC 2010, September 19–23, 2010, Paper We.7.C.2.
14. J.-X. Cai et al., Transmission of 96 × 100 G pre-filtered PDM-RZQPSK channels with 300% spectral efficiency over 10 608 km and 400% spectral efficiency over 4 368 km, in: Proceedings of OFC 2010, March 21–25, 2010, Post-deadline Paper PDPB10.
15. Bosco G, Carena A, Curri V, Poggiolini P, Forghieri F. Performance limits of Nyquist-WDM and CO-OFDM in high-speed PM-QPSK systems. IEEE Photon Technol Lett. 2010;22:1129–1131.
16. X. Zhou et al., 1200 km tansmission of 50 GHz spaced, 5 × 504-Gb/s PDM-32-64 hybrid QAM using electrical and optical spectral shaping, in: OFC 2012, Paper OM2A.2.
17. T. Kobayashi et al., 45.2 Tb/s C-band WDM transmission over 240 km using 538 Gb/s PDM-64QAM single carrier FDM signal with digital pilot tone, in: ECOC 2011, PD Th.13.C.6.
18. S. Randel, A. Sierra, X. Liu, S. Chandrasekhar, P. Winzer, Study of multicarrier offset-QAM for spectrally efficient coherent optical communications, in: ECOC 2011, Paper Th.11.A.
19. Nyquist H. Certain topics in telegraph transmission theory. Trans Am Inst Electr Eng. 1928;47:617–644.
20. Shannon CE. Communication in the presence of noise. Proc Inst Radio Engineers. 1949;37(1):10–21 Reprint as classic paper in Proc. IEEE 86(2) (1998).
21. Colavolpe G, Foggi T, Modenini A, Piemontese A. Faster-than-Nyquist and beyond: how to improve spectral efficiency by accepting interference. Opt Express. 2011;19:26600–26609.
22. A.D. Ellis, F.C.G. Gunning, B. Cuenot, T.C. Healy, E. Pincemin, Towards 1 TbE using coherent WDM, in: Proceedings of OECC/ACOFT 2008, Sydney, Australia, 2008, Paper WeA-1.
23. J. Yu et al., Generation, transmission and coherent detection of 11.2 Tb/s (112 × 100 Gb/s) single source optical OFDM superchannel, in: OFC’2011, PDPA6.
24. T.J. Xia et al, 10,000-km enhanced long-haul transmission of 1.15-Tb/s superchannel using SSMF only, in: OECC 2011, PD1.
25. Y.-K. Huang et al., Terabit/s optical superchannel with flexible modulation format for dynamic distance/route transmission, in: OFC’2012, Paper OM3H.4.
26. Liu X, Chandrasekhar S, Zhu B, Winzer P, Gnauck A, Peckham D. 448-Gb/s reduced-guard-interval CO-OFDM transmission over 2000 km of ultra-large-area fiber and five 80-GHz-grid ROADMs. J Lightwave Technol. 2011;29(4):483–490.
27. Hillerkuss D, et al. 26 Tbit s–1 line-rate super-channel transmission utilizing all-optical fast Fourier transform processing. Nat Photon. 2011;5:364–371.
28. X. Liu et al., Single coherent detection of a 606-Gb/s CO-OFDM signal with 32-QAM subcarrier modulation using 4 × 80-Gsamples/s ADCs, in: ECOC2010 PD2.6.
29. X. Liu et al., 728-Gb/s CO-OFDM transmission over 800-km ULAF using 64-QAM subcarrier modulation and single-step coherent detection with 4 × 80-Gsamples/s ADCs, in: ACP 2010 PD1.
30. X. Liu, S. Chandrasekhar, High spectral-efficiency transmission techniques for systems beyond 100 Gb/s, in: 2011 OSA Summer Topical Meeting on Signal Processing in Photonics Communications (SPPCom), 2011, Paper SPMA1.
31. X. Liu, X. Wei, US patent 7,558,487, filed on September 25, 2005.
32. Tang Y, Shieh W, Krongold B. DFT-spread OFDM for fiber nonlinearity mitigation. IEEE Photon Technol Lett. 2010;22:1250.
33. Chen X, Li A, Gao G, Shieh W. Experimental demonstration of improved fiber nonlinearity tolerance for unique-word DFT-spread OFDM systems. Opt Express. 2011;19:26198–26207.
34. Yang Q, He Z, Yang Z, Yu S, Yi X, Shieh W. Coherent optical DFT-Spread OFDM transmission using orthogonal band multiplexing. Opt Express. 2012;20:2379–2385.
35. A. Li, X. Chen, G. Gao, W. Shieh, B.S. Krongold, Transmission of 1.63-Tb/s PDM-16QAM unique-word DFT-spread OFDM signal over 1,010-km SSMF, in: Optical Fiber Communication Conference, OSA Technical Digest, Optical Society of America, 2012, Paper OW4C.1.
36. S. Randel, S. Corteselli, S. Chandrasekhar, A. Sierra, X. Liu, P. Winzer, T. Ellermeyer, J. Lutz, R. Schmid, Generation of 224-Gb/s multicarrier offset-QAM using a real-time transmitter, in: Optical Fiber Communication Conference 2012, Paper OM2H.2.
37. Zhao J, Ellis AD. Offset-QAM based coherent WDM for spectral efficiency enhancement. Opt Express. 2011;19:14617–14631.
38. J. Zhao, A.D. Ellis, A novel optical fast OFDM with reduced channel spacing equal to half of the symbol rate per carrier, in: Optical Fiber Communication Conference, 2010, Paper OMR1.
39. Giacoumidis E, Ibrahim SK, Zhao J, Tang TM, Ellis AD, Tomkos I. Experimental and theoretical investigations of intensity-modulation and direct-detection optical fast-OFDM over MMF-links. Photon Technol Lett. 2012;24:52–54.
40. A. Sano et al., 30 × 100-Gb/s all-optical OFDM transmission over 1300 km SMF with 10 ROADM nodes, in: Proceedings of ECOC’07, 2007, PD1.7.
41. Huang Y-K, et al. Transmission of spectral efficient super-channels using all-optical OFDM and digital coherent receiver technologies. IEEE J Lightwave Technol. 2011;29:3838–3844.
42. Hillerkuss D, et al. 26 Tbit-1 line-rate super-channel transmission utilizing all-optical fast Fourier transform processing. Nature Photon. 2011;5:364–371.
43. Chow JS, Tu JC, Cioffi JM. A discrete multitone transceiver system for HDSL applications. IEEE J Sel Areas Commun. 1991;9(6):895–908.
44. A.J. Lowery, L. Du, J. Armstrong, Orthogonal frequency division multiplexing for adaptive dispersion compensation in long haul WDM systems, in: Optical Fiber Communication Conference, Anaheim, CA, 2006, Paper PDP39.
45. Shieh W, Athaudage C. Coherent optical orthogonal frequency division multiplexing. Electron Lett. 2006;42:587–589.
46. Shieh W, Bao H, Tang Y. Coherent optical OFDM: theory and design. Opt Express. 2008;16:841–859.
47. Jansen SL, Morita I, Schenk TC, Tanaka H. Long-haul transmission of 16 × 52.5 Gbits/s polarization-division-multiplexed OFDM enabled by MIMO processing (Invited). J Opt Netw. 2008;7:173–182.
48. Liu X, Chandrasekhar S, Chen X, et al. 1.12-Tb/s 32-QAM-OFDM superchannel with 8.6-b/s/Hz intrachannel spectral efficiency and space-division multiplexed transmission with 60-b/s/Hz aggregate spectral efficiency. Opt Express. 2011;19:B958–B964.
49. Liu X, Buchali F, Tkach RW. Improving the nonlinear tolerance of polarization-division-multiplexed CO-OFDM in long-haul fiber transmission. J Lightwave Technol. 2009;27:3632–3640.
50. P. Winzer, A. Gnauck, A. Konczykowska, F. Jorge, J. Dupuy, Penalties from in-band crosstalk for advanced optical modulation formats, in: 37th European Conference and Exposition on Optical Communications, OSA Technical Digest (CD), Optical Society of America, 2011, Paper Tu.5.B.7.
51. G. Bosco, Spectrally efficient transmission: a comparison between Nyquist-WDM and CO-OFDM approaches, in: 2012 OSA Summer Topical Meeting on Signal Processing in Photonics Communications (SPPCom), Paper SpW3B.1 2012.
52. A. Sano, T. Kobayashi, S. Yamanaka, A. Matsuura, H. Kawakami, Y. Miyamoto, K. Ishihara, H. Masuda, 102.3-Tb/s (224 × 548-Gb/s) C- and Extended L-band All-Raman transmission over 240 km using PDM-64QAM single carrier FDM with digital pilot tone, in: Optical Fiber Communication Conference, OSA Technical Digest, Optical Society of America, 2012, Paper PDP5C.3.
53. Myung HG, Lim J, Goodman DJ. Single carrier FDMA for uplink wireless transmission. IEEE Veh Technol Mag. 2006;1(3):30–38.
54. E. Yamada et al., Novel no-guard-interval PDM CO-OFDM transmission in 4.1 Tb/s (50 × 88.8-Gb/s) DWDM link over 800 km SMF including 50-GHz spaced ROADM nodes, in: Proceedings of OFC’08, 2008, PDP8.
55. R. Kudo, 111 Gb/s no-guard-interval OFDM using low sampling rate analogue-to-digital converter, in: Proceedings of ECOC’09, 2009, Paper P4.09.
56. X. Liu et al., Efficient digital coherent detection of a 1.2-Tb/s 24-carrier no-guard-interval CO-OFDM signal by simultaneously detecting multiple carriers per sampling, in: Proceedings of OFC’10, 2010, OWO2.
57. Youn CJ, Liu X, Chandrasekhar S, et al. Channel estimation and synchronization for polarization-division multiplexed CO-OFDM using subcarrier/polarization interleaved training symbols. Opt Express. 2011;19:16174–16181.
58. Liu X, Buchali F. Intra-symbol frequency-domain averaging based channel estimation for coherent optical OFDM. Opt Express. 2008;16:21944–21957.
59. Tolmachev A, Nazarathy M. Filter-bank based efficient transmission of Reduced-Guard-Interval OFDM. Opt Express. 2011;19:B370–B384.
60. A. Tolmachev, M. Nazarathy, Real-time-realizable filtered-multi-tone (FMT) modulation for layered-FFT Nyquist WDM spectral shaping, in: ECOC 2011, Paper We.10.P1.65.
61. K. Yonenaga et al., 100 Gbit/s all-optical OFDM transmission using 4 × 25 Gbit/s optical duobinary signals with phase-controlled optical sub-carriers, in: Proceedings of OFC’08, 2001, JThA48.
62. J. Yu et al., 30-Tb/s (3 × 12.84-Tb/s) signal transmission over 320 km using PDM 64-QAM modulation, in: OFC 2012, Paper OM2A.4.
63. X. Liu et al., 3 × 485-Gb/s WDM transmission over 4800 km of ULAF and 12 × 100-GHz WSSs using CO-OFDM and single coherent detection with 80-GS/s ADCs, in: OFC’11, 2011, JThA37.
64. X. Liu et al., 1.5-Tb/s Guard-banded superchannel transmission over 56 × 100-km (5600-km) ULAF using 30-Gbaud pilot-free OFDM-16QAM signals with 5.75-b/s/Hz net spectral efficiency, in: ECOC’12, Post-dealine Paper Th.3.C.5.
65. Cho J, Xie C, Winzer PJ. Analysis of soft-decision FEC on non-AWGN channels. Opt Express. 2012;20(7):7915–7928.
66. Bosco G, Curri V, Carena A, Poggiolini P, Forghieri F. On the performance of Nyquist-WDM terabit superchannels based on PM-BPSK, PM-QPSK, PM-8QAM or PM-16QAM subcarriers. J Lightwave Technol. 2011;29(1):53–61.
67. Essiambre RJ, Kramer G, Winzer PJ, Foschini GJ, Goebel B. Capacity limits of optical fiber networks. J Lightwave Technol. 2010;28(4):662–701.
68. A. Splett, C. Kurzke, K. Petermann, Ultimate transmission capacity of amplified optical fiber communication systems taking into account fiber nonlinearities, in: Proceedings of ECOC 1993, 1993, pp. 41–44.
69. Shieh W, Chen X. Information spectral efficiency and launch power density limits due to fiber nonlinearity for coherent optical OFDM system. IEEE Photon J. 2011;3(2):158–173.
70. Chen X, Shieh W. Closed-form expressions for nonlinear transmission performance of densely spaced coherent optical OFDM systems. Opt Express. 2010;18:19039–19054.
71. Vacondio F, Rival O, Simonneau C, et al. On nonlinear distortions of highly dispersive optical coherent systems. Opt Express. 2012;20:1022–1032.
72. Essiambre RJ, Tkach RW. Capacity trends and limits of optical communication networks. Proc IEEE. 2012;100:1035–1055.
73. X. Liu, S. Chandrasekhar, Advanced modulation formats for core networks, in: Proceedings of 2011 OptoElectronics and Communications Conference (OECC), 2011, pp. 399–400.
74. Mitra PP, Stark JB. Nonlinear limits to the information capacity of optical fiber communications. Nature. 2001;411(6841):1027–1030.
75. Essiambre R-J, Foschini GJ, Kramer G, Winzer PJ. Capacity limits of information transport in fiber-optic networks. Phys Rev Lett. 2008;101 Paper 163901.
76. Rafique D, Ellis AD. Impact of signal-ASE four-wave mixing on the effectiveness of digital back-propagation in 112 Gb/s PM-QPSK systems. Opt Express. 2011;19(4):3449–3454.
77. Kartalopoulos SV. Elastic bandwidth. IEEE Circuits Dev Mag. 2002;18:8–13.
78. Kataoka N, Wada N, Sone K, et al. Field trial of data-granularity-flexible reconfigurable OADM with wavelength-packet-selective switch. J Lightwave Technol. 2006;24(1):88–94.
79. Jinno M, Takara H, Kozicki B, Tsukishima Y, Sone Y, Matsuoka S. Spectrum-efficient and scalable elastic optical path network: architecture, benefits, and enabling technologies. IEEE Commun Mag. 2009;47:66–75.
80. S. Chandrasekhar, X. Liu, OFDM based superchannel transmission technology, J. Lightwave Technol., in press.
81. ITU-T G.694.1, Spectral grids for WDM applications: DWDM frequency grid.
82. Frisken S, Poole S, Baxter G. Reconfiguration in transparent agile optical networks. Proc IEEE. 2012;100(5):1056–1064.
83. M. Jinno, H. Takara, Y. Sone, Elastic optical path networking: Enhancing network capacity and disaster survivability toward 1 Tbps era, in: Proceedings of 2011 OptoElectronics and Communications Conference (OECC), 2011, pp. 401–404.
84. S. Thiagarajan, M. Frankel, D. Boertjes, Spectrum efficient super-channels in dynamic flexible grid networks—a blocking analysis, in: OFC/NFOEC 2011, 2011, Paper OTuI6.
85. Shieh W. OFDM for flexible high-speed optical networks. J Lightwave Technol. 2011;29(10):1560–1577.
86. Klekamp A, Gebhard U, Ilchmann F. Energy and cost efficiency of adaptive and mixed-line-rate IP over DWDM networks. J Lightwave Technol. 2012;30(2):215–221.
87. A. Nag, T. Wang, B. Mukherjee, On spectrum-efficient green optical backbone networks, IEEE Global Telecommunications Conference (GLOBECOM 2011), 2011, pp. 1–5.
88. S. Chandrasekhar, X. Liu, Enabling components for future high-speed coherent communication Systems, in: Optical Fiber Communication Conference 2011, 2011, Tutorial talk OMU5.
89. G. Bennett, Superchannels to the rescue!, Lightwave 29 (2) (2012).
90. T. Koch, III–V and silicon photonic integrated circuit technologies, in: OFC/NFOEC 2012, 2012, Tutorial talk OTh4D.
91. Liu X, Gill DM, Chandrasekhar S, et al. Multi-carrier coherent receiver based on a shared optical hybrid and a cyclic AWG array for terabit/s optical transmission. IEEE Photon J. 2010;2(3):330–337.
92. J. Rahn et al., 250 Gb/s real-time PIC-based super-channel transmission over a gridless 6000 km terrestrial link, in: OFC/NFOEC 2012, 2012, Paper PDP5D.5.
93. I. Dedic, High-speed CMOS DSP and data converters, in: Optical Fiber Communication Conference, 2011, Paper OTuN1.
94. Winzer PJ. Optical networking beyond WDM. IEEE Photon J. 2012;4(2):647–651.
95. M.D. Feuer et al., Demonstration of joint DSP receivers for spatial superchannels, Photonics Society Summer Topical, 2012, Paper MC4.2.