Spatial Multiplexing Using Multiple-Input Multiple-Output Signal Processing
Peter J. Winzer, Roland Ryf and Sebastian Randel, Bell Labs, Alcatel-Lucent, Holmdel, NJ 07733, USA
Acknowledgments
We acknowledge valuable discussions with S. Bigo, S. Chandrasekhar, G. Charlet, D. Chizhik, A.R. Chraplyvy, C.R. Doerr, R.-J. Essiambre, N. Fontaine, G.J. Foschini, A.H. Gnauck, X. Liu, H. Kogelnik, S.K. Korotky, G. Raybon, M. Salsi, R.W. Tkach, and C. Xie from Bell Labs, Alcatel-Lucent, D. DiGiovanni, J. Fini, R. Lingle, D. Peckham, T.F. Taunay, and B. Zhu from OFS Labs, and M. Hirano, T. Sasaki, and Y. Yamamoto from Sumitomo Electric.
10.1 Optical Network Capacity Scaling Through Spatial Multiplexing
10.1.1 The capacity crunch
The amount of traffic carried on backbone networks has been growing exponentially over the past two decades, at about 30 to 60% per year (i.e. between 1.1 and 2 dB per year),1 depending on the nature and penetration of services offered by various network operators in different geographic regions [1,2]. The increasing number of applications relying on machine-to-machine traffic and cloud computing could accelerate this growth to levels typical within data centers and high-performance computers [3,4]: According to Amdahl’s rule of thumb [5,6], the interface bandwidth of a balanced computer architecture is proportional to its processing power. Since cloud services are increasingly letting the network take the role of an interface between distributed data processing nodes, the required network bandwidth for such applications may scale with data processing capabilities, at close to 90% (or 2.8 dB) per year [7]. Noncacheable real-time multimedia applications such as high-definition tele-presence and immersive communications [8,9] will further drive the need for more network bandwidth.
For over two decades, the demand for communication bandwidth has been economically met by wavelength-division multiplexed (WDM) optical transmission systems, researched, developed, and abundantly deployed since the early 1990s [10]. At first, WDM capacities increased at around 80% per year, predominantly through improvements in optoelectronic device technologies. By the early 2000s, lasers had reached GHz frequency stabilities, optical filters had bandwidths allowing for 50-GHz WDM channel spacings, and 40-Gb/s optical signals filled up these frequency slots. At this remarkable point in time where “optical and electronic bandwidths met,” optical communications had to shift from physics toward communications engineering to increase spectral efficiencies, i.e. to pack more information into the limited (∼5-THz) bandwidth of single-band optical amplifiers. Consequently, the last decade has seen a vast adoption of concepts from radio-frequency communications, such as advanced modulation formats, coherent detection, sophisticated digital signal processing (DSP), and powerful error correction coding. The associated evolution of experimentally achieved interface rates (per wavelength and polarization), modulation symbol rates, spectral efficiencies, and per-fiber capacities is visualized in Figure 10.1 and reviewed, e.g., in [11] and the references cited therein.

Figure 10.1 (a) Evolution of experimentally achieved single-channel bit rates (single-carrier, single-polarization, electronically multiplexed; green circles), symbol rates in digital coherent detection (purple squares), and aggregate per-fiber capacities (triangles) using wavelength-division multiplexing (WDM; red), polarization-division multiplexing (PDM; blue), and space-division multiplexing (SDM; yellow). (b) Evolution of experimentally achieved per-polarization spectral efficiencies. (Figure reproduced from [11].) (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this book.)
Today’s commercial WDM systems transmit close to 10 Tb/s of traffic at 100 Gb/s per wavelength [12]. In research, interface rates of 320 Gb/s have been demonstrated using quadrature amplitude modulation (QAM) at a symbol rate of 80 GBaud [13], polarization multiplexed to yield a 640-Gb/s single-carrier channel. Interface rates of 1 Tb/s and beyond have been achieved through optical parallelism using multi-carrier [14–16] and orthogonal frequency division multiplexed (OFDM) optical superchannels [17]. Regarding aggregate per-fiber capacities, and as shown in Figure 10.1a, 100-Tb/s transmission over single-mode fiber has been reported [18,19], but capacity increases in WDM research have slowed down to about 20% (0.8 dB) per year since ∼2002, with a similar trend seen in commercial systems with a time delay of about 5 years [1,20]. While spectral efficiencies have been able to keep up with a ∼1-dB annual growth rate, cf. Figure 10.1b, capacities of conventional single-mode fiber systems over meaningful transmission distances are not expected to grow much further.
The evident capacity saturation is explained in recent studies on the nonlinear Shannon capacity of optical networks [21], setting an upper bound on the maximum achievable spectral efficiency for a given transmission distance and fiber type.2 The resulting trade-off between spectral efficiency and system reach (including noise, fiber nonlinearities, as well as current technological shortfalls) is summarized in Figure 10.2. Record experimental results (circles) are shown together with the nonlinear Shannon limit of [21], scaled by a factor of two to represent polarization-division multiplexed (PDM) systems. Both curves trace straight lines on a logarithmic scale for the transmission distance L, since the signal-to-noise ratio (SNR) delivered by the line system to the receiver is inversely proportional to L, and the spectral efficiency is given by [23]
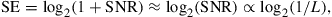 (10.1)
(10.1)
at reasonably high SNR which maximizes the performance of optical transport systems [21]. Importantly, we note that experimental records have approached the nonlinear Shannon limit to within a factor of less than two. The asterisk in Figure 10.2 represents Alcatel-Lucent’s 1830 optical transmission platform, operating at a spectral efficiency of ∼2 b/s/Hz over ∼2000 km of fiber [12] and commercially deployed since mid-2010; the ellipse indicates a range into which commercial systems based on existing technologies and an approximate installed fiber with appropriate SNR margins might fall. At an annual traffic growth rate between 30 and 60%, and over the same, geography-enforced distances, optical transport systems surpassing the Shannon limit would have to be commercially available between 2015 and 2018. This observation leads to the notion of an imminent “optical networks capacity crunch” [24].
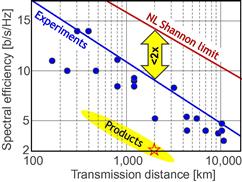
Figure 10.2 Trade-off between dual-polarization spectral efficiency and transmission reach, showing the nonlinear Shannon limit of [21] together with experimentally achieved results (circles). The ellipse indicates a range into which commercial systems might fall, and the asterisk represents an approximate commercially deployed optical transmission platform [12]. (Figure reproduced from [11].)
10.1.2 Spatial multiplexing
Realizing that WDM spectral efficiencies over the required transmission distances are no longer scalable, alternative solutions have to be developed. One option would be to trade spectral efficiency for reach by concatenating several high-spectral-efficiency systems. However, due to the unfavorable scaling of Eq. (10.1), which relates the SE to the logarithm of system reach, a large number of regenerators are needed to achieve a significant gain in SE [23]. For example, taking today’s experimental records as a baseline for system performance, a target spectral efficiency of 20 b/s/Hz over 2000 km would require around 1500 1.3 -km regeneration spans using, e.g., PDM 4096-QAM. Alternatively, a parallel approach may be taken. This requires the use of so far unexploited physical dimensions using multiple optical amplification bands or, likely more scalably, multiple parallel optical paths, referred to as spatial multiplexing or space-division multiplexing (SDM): With just three parallel paths at 7 bits/s/Hz each (e.g., using PDM 32-QAM), the desired aggregate SE is achieved with a total of three transponders per wavelength. The almost-three orders of magnitude difference in transponder count between the two solutions clearly point to SDM as the preferred solution for network capacity growth. A similarly large advantage of parallel transmission solutions over regenerated systems is obtained if not only transponders but also line system components are accounted for [23].
That going parallel in either amplification bands or space are the only capacity scaling options becomes clear from Figure 10.3, showing all known physical dimensions that can be used to construct orthogonal signal spaces for modulation and multiplexing in optical communications [11,25]:
• The time dimension is used for modulation by transmitting one modulation symbol after the other, one per symbol duration  ; the time dimension is used for multiplexing by allocating different time slots to different channels (time-division multiplexing, TDM).
; the time dimension is used for multiplexing by allocating different time slots to different channels (time-division multiplexing, TDM).
• The quadrature dimension, i.e. the real and imaginary parts of the optical field, also referred to as the sine and cosine or the in-phase and quadrature components of this bandpass signal, are used to construct quadrature amplitude modulation (QAM) constellations to convey more than one bit per symbol.
• The polarization dimension is used for polarization-division multiplexing (PDM), allowing for a twofold increase in system capacity.
• The frequency dimension is used for multiplexing wavelength channels in WDM systems or to form optical superchannels or OFDM signals within the context of a single WDM channel. Since commercial WDM systems usually operate in a single amplification band (such as the C-band or the L-band), building multi-band systems would in principle be an option to scale system capacities by up to a factor of ∼10. However, inherent problems associated with efficient and low-noise multi-band amplification as well as the fiber fuse effect, which arises on installed fiber at optical power levels significantly exceeding 1 W [26,27], may limit this option to very modest capacity gains and hence is unlikely to provide a long-term sustainable path forward.
• The space dimension is commonly used to scale short-reach interface rates [3] in a low-power, low-cost, and highly integrated manner. (For example, the 100GBASE-SR10 standard for 100G Ethernet specifies a 100-m interface using 10 × 10.3 Gb/s over a multi-mode 20-fiber ribbon.) Exploiting the space dimension for optical transport networks through SDM holds the promise of getting network capacity growth back onto a 2–2.5-dB/year track, as impressively indicated by the three most recent data points at 112-Tb/s [28,29], 305-Tb/s [30], and 1-Pb/s [31] shown in Figure 10.1a.
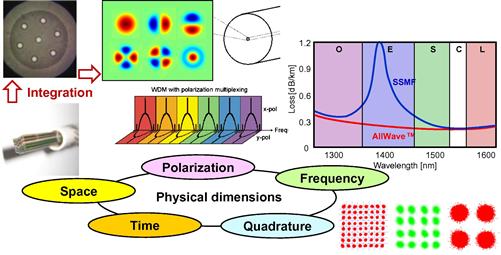
Figure 10.3 Spatial multiplexing exploits the only known physical dimension that has not yet been used in optical transport systems. Implementations include fiber bundles, multi-core, and multi-mode fiber, with increasing levels of integration.
Deploying SDM in its most trivial form by using M parallel optical line systems is a scalable but not yet an economically sustainable path forward, since it still does not reduce the cost or energy per bit compared to today’s systems: M parallel systems carry M times the capacity at M times the cost, energy consumption, and footprint requirements compared to a single system. Commercially successful SDM technologies will be expected to scale capacity with a similar cost, energy, and footprint reduction as WDM (at ∼20% per year [32]), leveraging integration, and sharing of system components among channels. Integration may take place on a system and network level, both from a capital (CAPEX) and operational (OPEX) expenditure point of view. Regarding the latter, Ref. [33] showed that it could be cheaper in certain scenarios to deploy a multi-core system just because of the associated reduced amplifier OPEX, even if sufficient single-mode fiber strands would be available to install M conventional line systems in parallel. Further, integration can take place on a transponder [34] and DSP level, on an optical amplifier level [35,36], and on a fiber level [37,38]. Importantly, apart from being more cost and energy effective than separate individual systems, integrated SDM solutions will have to allow for smooth network upgrades, reusing as much as possible the deployed WDM infrastructure. Initial global efforts in SDM research are reviewed in [39,40].
10.1.3 Crosstalk management in SDM systems
Since integration generally comes at the expense of crosstalk among parallel paths, proper crosstalk management is an important aspect of all SDM systems. Whether a certain level of crosstalk can be treated as a system impairment or needs to be actively compensated for depends on the underlying modulation format [41]: Figure 10.4 shows the crosstalk induced optical SNR (OSNR) penalty at a bit error ratio (BER) of 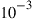 for single-polarization quadrature phase shift keying (QPSK), 16-QAM, and 64-QAM. The solid black curves represent a simple theoretical model, and circles denote measurement results. As the back-to-back implementation penalty in this 21.4-GBaud experiment increases from 0.9 dB (QPSK) to 1.8 dB (16-QAM) and 4.0 dB (64-QAM), the crosstalk tolerance also shrinks compared to theory. For a 0.5-dB crosstalk penalty, QPSK shows a tolerance of about –20 dB, 16-QAM tolerates about –26 dB, and 64-QAM tolerates only about –33 dB of crosstalk. In the context of SDM systems, these crosstalk numbers represent tolerable end-to-end crosstalk requirements, including crosstalk within transponders, optical amplifiers, transmission fibers, splices and connectors, as well as all other optical networking elements such as spatial and spectral optical crossconnects. For example, the 10-km span of 19-core fiber used for 305-Tb/s QPSK transmission in [30] showed a residual crosstalk level as high as –16 dB at the long-wavelength end of the exploited spectrum, revealing the difficulties of building highly scalable low-crosstalk optical components and transmission systems.
for single-polarization quadrature phase shift keying (QPSK), 16-QAM, and 64-QAM. The solid black curves represent a simple theoretical model, and circles denote measurement results. As the back-to-back implementation penalty in this 21.4-GBaud experiment increases from 0.9 dB (QPSK) to 1.8 dB (16-QAM) and 4.0 dB (64-QAM), the crosstalk tolerance also shrinks compared to theory. For a 0.5-dB crosstalk penalty, QPSK shows a tolerance of about –20 dB, 16-QAM tolerates about –26 dB, and 64-QAM tolerates only about –33 dB of crosstalk. In the context of SDM systems, these crosstalk numbers represent tolerable end-to-end crosstalk requirements, including crosstalk within transponders, optical amplifiers, transmission fibers, splices and connectors, as well as all other optical networking elements such as spatial and spectral optical crossconnects. For example, the 10-km span of 19-core fiber used for 305-Tb/s QPSK transmission in [30] showed a residual crosstalk level as high as –16 dB at the long-wavelength end of the exploited spectrum, revealing the difficulties of building highly scalable low-crosstalk optical components and transmission systems.

Figure 10.4 Tolerance of various higher-order modulation formats to in-band crosstalk (solid curves: theory; circles: experiments at 21.4 GBaud [41]). As soon as end-to-end crosstalk exceeds an acceptable system margin, MIMO techniques need to be employed.
Recently, low-crosstalk multi-core fiber for SDM has been reported [29,42,43], and impressive SDM system experiments have been performed, including record per-fiber capacities of 109 Tb/s [28], 112 Tb/s [29], 305 Tb/s [30], and 1 Pb/s [31] over a few tens of km, as shown in Figure 10.1. Recent SDM experiments going beyond the nonlinear Shannon limit of single-mode fiber in terms of aggregate per-fiber spectral efficiency and transmission reach (cf. Figure 10.2) include 19-core transmission at 30.5 b/s/Hz over 10.1 km [30], 12-core transmission at 91.4 b/s/Hz over 52 km [31], as well as 7-core transmission at 15 b/s/Hz over 2688 km [44], at 42.2 b/s/Hz over 845 km [45], and 60 b/s/Hz over 76.8 km [46].
If crosstalk rises to levels where it induces penalties beyond acceptable system margins, multiple-input-multiple-output (MIMO) techniques, originally developed for wireless systems [47], have to be used to accommodate crosstalk by joint coherent detection and digital signal processing. As an example, the two highlighted areas in Figure 10.4 represent the case of 16-QAM with a 0.5-dB margin allocation for crosstalk. As soon as end-to-end crosstalk levels reach –26 dB, MIMO detection and processing is required, independent of the exact crosstalk level in this high-crosstalk regime.
Using MIMO techniques, a reliable (low-outage) capacity gain in a system with M coupled paths (or “modes”) can be obtained, provided that the following key conditions are met [48,49]:
• The transmitter is able to uniquely map signals onto a complete orthonormal set of M (spatial and polarization) modes whose propagation is supported by the transmission fiber. This set of modes does not necessarily have to be the set of true fiber modes but can be any suitable linear combination of modes, as discussed in Section 10.4.
• The transmission fiber performs mostly unitary mode coupling, i.e. rotations of the M signals in mode space, without introducing excessive mode-dependent loss (MDL) or mode-dependent gain (MDG). As we shall see below, unitary transformations can be undone at the receiver without loss of information.
• The receiver is able to coherently detect a suitable complete orthonormal set of M modes. These M signals are then used to reconstruct the transmitted information using MIMO processing, as discussed in Section 10.3.
If the transmission properties of each mode in terms of noise and fiber nonlinearities are comparable to those of a single-mode reference system, an M-fold capacity gain can be achieved. The above requirements distinguish the type of MIMO-SDM described in this chapter from earlier work on mode-division multiplexing or mode-group multiplexing [50–56].
Recently, several impressive experimental demonstrations of coupled-mode MIMO-SDM transport have been reported, including transmission of six coupled spatial and polarization modes over up to 4,200-km microstructured fiber [57] as well as 1200-km few-mode fiber [58], MIMO-SDM using up to 12 modes [59], and discrete [60–62] as well as distributed Raman [63] amplification of few-mode signals.
In the remainder of this chapter, we describe key aspects of MIMO-SDM theory and implementation and highlight some of the challenges associated with this technology.
10.2 Coherent MIMO-SDM with Selective Mode Excitation
10.2.1 Signal orthogonality
Communication signals can be multiplexed onto and can be uniquely demultiplexed from a common transmission channel if they are orthogonal in at least one of the physical dimensions discussed in the context of Figure 10.3.
10.2.1.1 Orthogonality in time and frequency
Orthogonality in time and frequency between two (scalar) waveforms 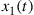 and
and 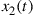 requires their inner product in signal space to vanish [25,64]:
requires their inner product in signal space to vanish [25,64]:
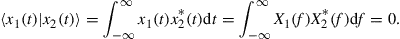 (10.2)
(10.2)
Here, t and f denote time and frequency, 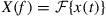 is the Fourier transform of
is the Fourier transform of  , and * denotes the complex conjugate. Important examples for orthogonal waveforms in time and frequency are shown in Figure 10.5. (We will link these considerations to orthogonality in space in Section 10.2.1.2.) In particular, signals that are nonoverlapping either in time (b) or in frequency (c) are orthogonal, irrespective of their shape. Further, as shown in (a),
, and * denotes the complex conjugate. Important examples for orthogonal waveforms in time and frequency are shown in Figure 10.5. (We will link these considerations to orthogonality in space in Section 10.2.1.2.) In particular, signals that are nonoverlapping either in time (b) or in frequency (c) are orthogonal, irrespective of their shape. Further, as shown in (a),  -time-shifted copies of certain temporally overlapping pulses
-time-shifted copies of certain temporally overlapping pulses  are orthogonal if
are orthogonal if 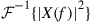 has nulls at integer multiples of the symbol rate
has nulls at integer multiples of the symbol rate 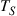 , which follows from Eq. (10.2) with
, which follows from Eq. (10.2) with 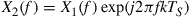 . This condition is equivalent to Nyquist’s criterion for no inter-symbol interference (ISI) [64,65]. An important class of pulse shapes satisfying this criterion are square-root raised cosine pulses. By the same token, using
. This condition is equivalent to Nyquist’s criterion for no inter-symbol interference (ISI) [64,65]. An important class of pulse shapes satisfying this criterion are square-root raised cosine pulses. By the same token, using  in Eq. (10.2) reveals that
in Eq. (10.2) reveals that  -frequency-shifted copies of
-frequency-shifted copies of 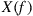 are orthogonal provided that
are orthogonal provided that 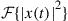 has nulls at integer multiples of
has nulls at integer multiples of 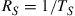 , as illustrated in Figure 10.5(d). This condition is at the heart of pulse shaping in orthogonal frequency division multiplexing (OFDM) [66].
, as illustrated in Figure 10.5(d). This condition is at the heart of pulse shaping in orthogonal frequency division multiplexing (OFDM) [66].
Once a set of orthogonal signals 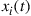 supported by the communication channel is established as an orthonormal basis, multiple transmitters can transmit their information
supported by the communication channel is established as an orthonormal basis, multiple transmitters can transmit their information 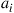 , each by uniquely addressing one of the channel’s basis functions, i.e. by sending
, each by uniquely addressing one of the channel’s basis functions, i.e. by sending 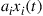 . Provided that the communication channel is able to maintain signal orthogonality, a receiver can demultiplex any such signal by forming the inner product between the aggregate received waveform
. Provided that the communication channel is able to maintain signal orthogonality, a receiver can demultiplex any such signal by forming the inner product between the aggregate received waveform 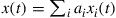 and the respective basis function,
and the respective basis function,
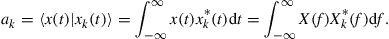 (10.3)
(10.3)
For example, orthogonality in a WDM system is established through spectrally nonoverlapping frequency slots. Each transmitter sends its signal confined to within its frequency slot. Each receiver optically filters the aggregate WDM spectrum to extract the intended frequency slot, which is equivalent to calculating the inner product according to Eq. (10.3). If the transmitted spectrum spills into adjacent frequency slots, and unless frequency orthogonality is established through OFDM techniques, orthogonality is degraded, which is referred to as WDM crosstalk in this context. A degradation of orthogonality in the time domain is usually referred to as ISI.
10.2.1.2 Orthogonality in space and polarization
Orthogonality in space and polarization between a first spatial waveguide mode3 with transverse electric field distribution 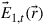 and a second spatial waveguide mode with transverse magnetic field distribution
and a second spatial waveguide mode with transverse magnetic field distribution 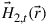 is generally established as [67,68]
is generally established as [67,68]
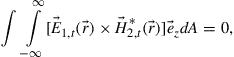 (10.4)
(10.4)
where A denotes the transverse  plane relative to the propagation direction (unit vector
plane relative to the propagation direction (unit vector 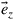 ). Any spatial field distribution can be expanded into a superposition of modes with expansion coefficients given by the integral in Eq. (10.4)[67]. It can further be shown that
). Any spatial field distribution can be expanded into a superposition of modes with expansion coefficients given by the integral in Eq. (10.4)[67]. It can further be shown that
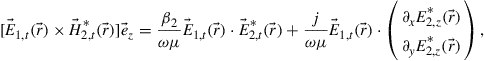 (10.5)
(10.5)
 (10.6)
(10.6)
Here, 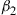 is the propagation constant of mode 2,
is the propagation constant of mode 2, 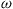 is the optical carrier frequency, and
is the optical carrier frequency, and 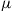 and
and  are permeability and dielectric constant, respectively. The partial derivative with respect to x and y is denoted by ∂x and ∂y, respectively. The second term on the right-hand side of Eq. (10.5) vanishes for transversal electric (TE) modes, while the second term on the right-hand side of Eq. (10.6) vanishes for transversal magnetic (TM) modes. For modes with small z-components of electric or magnetic fields, such as LP pseudo-modes in the weakly guiding approximation of circular dielectric waveguides (i.e. optical fibers), the second terms may be neglected. In all these cases, the orthogonality relation (10.4) can either exactly or approximately be turned into the more familiar spatial overlap integral
are permeability and dielectric constant, respectively. The partial derivative with respect to x and y is denoted by ∂x and ∂y, respectively. The second term on the right-hand side of Eq. (10.5) vanishes for transversal electric (TE) modes, while the second term on the right-hand side of Eq. (10.6) vanishes for transversal magnetic (TM) modes. For modes with small z-components of electric or magnetic fields, such as LP pseudo-modes in the weakly guiding approximation of circular dielectric waveguides (i.e. optical fibers), the second terms may be neglected. In all these cases, the orthogonality relation (10.4) can either exactly or approximately be turned into the more familiar spatial overlap integral
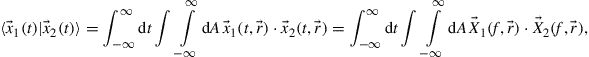 (10.7)
(10.7)
where 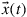 may denote either electric or magnetic field, leading to the unified notion of an “optical field.” Equation (10.7) generalizes the familiar inner product of Eq. (10.2) to the space and polarization dimension. Two optical fields with orthogonal polarizations are hence orthogonal, as are two fields whose spatial profiles don’t overlap, such as the fields of separate optical fibers or the fields that are confined to uncoupled cores of multi-core fibers. In analogy to time and frequency dimensions, and as discussed in the context of Figure 10.5, spatially overlapping optical fields distributions can also be orthogonal, provided that their overlap integral vanishes, which is the case, e.g., between waveguide modes with even and odd symmetries, such as the
may denote either electric or magnetic field, leading to the unified notion of an “optical field.” Equation (10.7) generalizes the familiar inner product of Eq. (10.2) to the space and polarization dimension. Two optical fields with orthogonal polarizations are hence orthogonal, as are two fields whose spatial profiles don’t overlap, such as the fields of separate optical fibers or the fields that are confined to uncoupled cores of multi-core fibers. In analogy to time and frequency dimensions, and as discussed in the context of Figure 10.5, spatially overlapping optical fields distributions can also be orthogonal, provided that their overlap integral vanishes, which is the case, e.g., between waveguide modes with even and odd symmetries, such as the 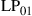 and the
and the  “modes” discussed in Section 10.4.
“modes” discussed in Section 10.4.
As with multiplexing in time and frequency, multiplexing in space and polarization requires the transmitters to selectively address a mode out of an orthogonal set of basis functions. Any spill-over manifests itself as performance degrading modal crosstalk. Similarly, the receiver has to calculate the inner product (i.e. the overlap integral) between the aggregate received field and the modal basis function it wants to receive. Owing to reciprocity considerations, a device that is able to selectively excite a certain waveguide mode at the transmitter will also extract that same mode at the receiver when operated in reverse. Orthogonal mode multiplexers (MMUXs) will be discussed in Section 10.4.
10.2.2 MIMO system capacities and outage
Neglecting inter- and intra-modal fiber nonlinearities, a coupled-mode SDM system in its simplest form can be represented by the linear matrix channel [49]
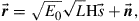 (10.8)
(10.8)
as visualized in Figure 10.6; we use bold print to indicate stochastic processes and random variables. The SDM fiber supports a set of M orthogonal (spatial and polarization) modes. We use the term “mode” in the physical sense (cf. footnote 3 on page 437) to refer to a complete orthogonal set of waveguide modes, in contrast to wireless MIMO literature, which typically uses the term to refer to the eigenmodes of the channel matrix. Upon propagation, the fiber modes may be subject to coupling, differential gain or loss, and differential delay. We assume that the transmitter is able to selectively excite 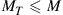 waveguide modes, and that the receiver is able to coherently extract
waveguide modes, and that the receiver is able to coherently extract 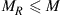 modes. The average signal energy transmitted per symbol period and per channel mode is
modes. The average signal energy transmitted per symbol period and per channel mode is 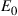 , hence the total transmit energy across all modes is
, hence the total transmit energy across all modes is 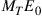 per symbol and
per symbol and 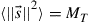 . This definition differs from the constant total power constraint often used in wireless MIMO, where spatial waterfilling may then be used to optimally distribute power among the modes [69]. In an optical SDM system, the total transmit power is neither constrained by battery power nor by regulations pertaining to the use of the radio-frequency spectrum; rather, fiber nonlinearity is likely to set an upper bound on the optical power per mode[70] such that we are faced with a per-mode power constraint as opposed to an overall power constraint across all modes. Circularly symmetric complex Gaussian noise
. This definition differs from the constant total power constraint often used in wireless MIMO, where spatial waterfilling may then be used to optimally distribute power among the modes [69]. In an optical SDM system, the total transmit power is neither constrained by battery power nor by regulations pertaining to the use of the radio-frequency spectrum; rather, fiber nonlinearity is likely to set an upper bound on the optical power per mode[70] such that we are faced with a per-mode power constraint as opposed to an overall power constraint across all modes. Circularly symmetric complex Gaussian noise 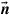 with power spectral density
with power spectral density 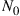 per mode is added at the receiver. (We will discuss the case of distributed noise loading in Section 10.2.2.4.)
per mode is added at the receiver. (We will discuss the case of distributed noise loading in Section 10.2.2.4.)
The SDM waveguide is described by an 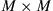 matrix
matrix 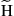 , which we normalize as
, which we normalize as 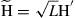 by factoring out the mode-average net propagation loss (or gain) L,
by factoring out the mode-average net propagation loss (or gain) L,
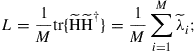 (10.9)
(10.9)
tr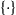 denotes the trace of a matrix,
denotes the trace of a matrix, 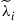 are the M eigenvalues of
are the M eigenvalues of 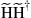 , and
, and 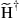 is the conjugate transpose of
is the conjugate transpose of 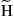 . Apart from noise, the MIMO channel is then given by the
. Apart from noise, the MIMO channel is then given by the 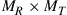 matrix H spanning the subspace of
matrix H spanning the subspace of 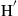 addressed by the transponders.
addressed by the transponders.
We next assume that each individual instantiation H of the ensemble of channel matrices H is known to the receiver (e.g. through appropriate training sequences) but is unknown to the transmitter (since the receiver-to-transmitter feedback delays in optical transport networks are usually much longer than the kHz channel dynamics due to acoustic or thermal variations). Without access to channel state information, the transmitter sends uncorrelated signals of equal power on all transmit modes and at best achieves the open-loop Bell Labs Layered Space Time (BLAST) capacity4[47]
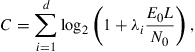 (10.10)
(10.10)
where  are the
are the 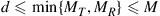 nonzero eigenvalues of
nonzero eigenvalues of  and d is referred to as the rank of the MIMO channel. The term
and d is referred to as the rank of the MIMO channel. The term
 (10.11)
(10.11)
represents the mode-average SNR at the receiver when all M channel modes are excited and detected  or, equivalently, the SNR measured as the ratio of the total received signal power to the total received noise power for equal power launched into all modes. We proceed to discuss capacities of several important optical MIMO-SDM channels [49].
or, equivalently, the SNR measured as the ratio of the total received signal power to the total received noise power for equal power launched into all modes. We proceed to discuss capacities of several important optical MIMO-SDM channels [49].
10.2.2.1 Uncoupled channel
For the special case of M transmitters, M receivers, and M uncoupled channels, H is the M-dimensional identity matrix 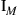 , whose M eigenvalues are unity. Hence, Eq. (10.10) yields the capacity
, whose M eigenvalues are unity. Hence, Eq. (10.10) yields the capacity
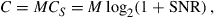 (10.12)
(10.12)
which is M times the corresponding single-mode capacity 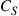 , as expected.
, as expected.
10.2.2.2 Unitary mode coupling channel
Assuming again M transmitters and M receivers, but letting the M-dimensional channel randomly couple the signals in a unitary manner such that H = U (corresponding to a random rotation in mode space), we have 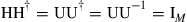 , leading to the same capacity as in the uncoupled case,
, leading to the same capacity as in the uncoupled case,
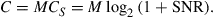 (10.13)
(10.13)
This shows that unitary mode coupling has no effect on the achievable MIMO transmission capacity. A familiar example are PDM systems operating on single-mode fiber. Such systems represent 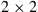 MIMO channels with random polarization rotations. In the linear regime, and without impairments such as polarization-dependent loss (PDL), their capacity is exactly twice the capacity of a single-polarization system. (In the nonlinear propagation regime, their capacity is almost twice that of a single-polarization system, as discussed in Chapter 1 of this book.) Obviously, to recover the data at the receiver, appropriate DSP has to be used to rotate the received mode space back to its original transmit orientation. DSP techniques for M-mode MIMO-SDM will be discussed in Section 10.3.
MIMO channels with random polarization rotations. In the linear regime, and without impairments such as polarization-dependent loss (PDL), their capacity is exactly twice the capacity of a single-polarization system. (In the nonlinear propagation regime, their capacity is almost twice that of a single-polarization system, as discussed in Chapter 1 of this book.) Obviously, to recover the data at the receiver, appropriate DSP has to be used to rotate the received mode space back to its original transmit orientation. DSP techniques for M-mode MIMO-SDM will be discussed in Section 10.3.
10.2.2.3 Under-addressed channel
Another channel of interest [49,71] is the 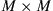 random unitary channel of Figure 10.6, where we only use
random unitary channel of Figure 10.6, where we only use 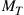 transmitters and
transmitters and  receivers such that
receivers such that 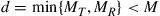 . In contrast to wireless MIMO systems, the assumption of constant per-mode transmit power lets the SDM capacities of this channel be symmetric in
. In contrast to wireless MIMO systems, the assumption of constant per-mode transmit power lets the SDM capacities of this channel be symmetric in 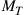 and
and 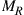 , i.e. an
, i.e. an 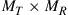 system shows the same performance as an
system shows the same performance as an 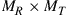 system. If the transmitter is able to address all M modes but the receiver can only detect
system. If the transmitter is able to address all M modes but the receiver can only detect 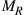 modes, the capacity is given by
modes, the capacity is given by 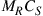 . Conversely, if the transmitter is able to only address
. Conversely, if the transmitter is able to only address 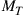 modes but the receiver can detect all M modes, the capacity is given by
modes but the receiver can detect all M modes, the capacity is given by 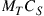 [49].
[49].
In all other cases, capacity loss has to be accepted. To analyze these reduced MIMO capacities due to under-addressing the SDM channel, we first acknowledge that the resulting MIMO capacity will be an inherently random quantity. For example, and with reference to Figure 10.6 for 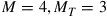 , and
, and 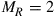 , some random channel instantiation may couple 2 out of the 3 transmit signals to the 2 undetected receive modes, leaving only a single transmit mode for information transmission. At best, the receiver is able to extract 2 modes from the channel. In general, the minimum potential capacity of an under-addressed channel is given by
, some random channel instantiation may couple 2 out of the 3 transmit signals to the 2 undetected receive modes, leaving only a single transmit mode for information transmission. At best, the receiver is able to extract 2 modes from the channel. In general, the minimum potential capacity of an under-addressed channel is given by 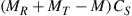 [71], and the maximum potential capacity of an under-addressed channel is given by
[71], and the maximum potential capacity of an under-addressed channel is given by 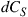 [49], d being the rank of the channel, cf. Eq. (10.10). The statistical distribution of the resulting (random) MIMO capacity
[49], d being the rank of the channel, cf. Eq. (10.10). The statistical distribution of the resulting (random) MIMO capacity  is shown in Figure 10.7a, based on 100,000 random realizations of the
is shown in Figure 10.7a, based on 100,000 random realizations of the  (unitary) channel matrix; the generation of uniform ensembles of M-dimensional unitary matrices is described in [72,49]. Most of the time, capacities approaching
(unitary) channel matrix; the generation of uniform ensembles of M-dimensional unitary matrices is described in [72,49]. Most of the time, capacities approaching  are attained, but sometimes it may happen that the capacity almost drops to
are attained, but sometimes it may happen that the capacity almost drops to 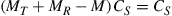 . This worst-case situation may occur very rarely, though, and designing the entire system for the worst case may result in unattractively low SDM capacities. Depending on the nature and dynamics of the channel, one may take one of the following approaches:
. This worst-case situation may occur very rarely, though, and designing the entire system for the worst case may result in unattractively low SDM capacities. Depending on the nature and dynamics of the channel, one may take one of the following approaches:
• Slowly varying frequency-flat channel: Assuming that the channel characteristics are constant across the signal bandwidth and change slowly compared to the burst error correction capability of the underlying code, as visualized in the top row of Figure 10.7b, the transmitter codes for (and transmits at) a certain capacity 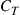 that may occasionally lead to uncorrectable blocks of bits.
that may occasionally lead to uncorrectable blocks of bits. 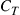 is chosen such that the probability that a random channel instantiation only supports a capacity
is chosen such that the probability that a random channel instantiation only supports a capacity 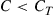 is acceptably small. These rare cases will then inherently lead to system outage. Hence, outage considerations become an integral part of this kind of SDM system design, similar to what is commonly done in the context of polarization-mode dispersion (PMD) [73–75]. The shaded area in Figure 10.7a represents the probability
is acceptably small. These rare cases will then inherently lead to system outage. Hence, outage considerations become an integral part of this kind of SDM system design, similar to what is commonly done in the context of polarization-mode dispersion (PMD) [73–75]. The shaded area in Figure 10.7a represents the probability 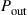 that the channel capacity will fall below
that the channel capacity will fall below  to result in system outage,
to result in system outage,
 (10.14)
(10.14)
where 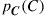 is the probability density function (PDF) of the random channel capacity
is the probability density function (PDF) of the random channel capacity 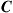 . Note that in contrast to some wireless MIMO systems, fiber-optic transport networks typically require exceptionally low outage probabilities, typically below
. Note that in contrast to some wireless MIMO systems, fiber-optic transport networks typically require exceptionally low outage probabilities, typically below 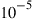 , corresponding to 99.999% (“five nines”) in system availability.
, corresponding to 99.999% (“five nines”) in system availability.
• Rapidly varying frequency-flat channel: As in the above case, channel variations are assumed to be constant across the signal bandwidth, but the channel varies rapidly compared to the burst error correction capabilities of the underlying code. This method is similar to what has been proposed to combat PMD outage in single-mode fiber systems [76,77] and results in a system that supports the average channel capacity 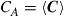 , which is usually larger than the achievable capacity at low outage, cf. Figure 10.7. The method can be implemented at the expense of latency by code design, or at the expense of optical complexity by either introducing dynamic mode scrambling elements into the transmission line, or by switching between different sets of transmit and receive mode sets [49].
, which is usually larger than the achievable capacity at low outage, cf. Figure 10.7. The method can be implemented at the expense of latency by code design, or at the expense of optical complexity by either introducing dynamic mode scrambling elements into the transmission line, or by switching between different sets of transmit and receive mode sets [49].
• Frequency-selective channel: In this case, the channel characteristics vary rapidly across the signal’s bandwidth, as visualized in the bottom row of Figure 10.7b. This situation is encountered, e.g., for channels with significant differential group delay (DGD) between modes, as the number of uncorrelated frequency bins within the signal bandwidth is approximately given by the ratio of the signal bandwidth to the channel’s coherence bandwidth (which is inversely proportional to the channel’s delay spread) [78,79]. If each signal frequency component (e.g. each independent subcarrier of an OFDM signal) experiences a different channel instantiation, the signal ultimately sees the average channel capacity 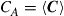 . In the idealized limiting case of a highly frequency selective channel, this average capacity is then guaranteed, i.e. if the transmitter codes for
. In the idealized limiting case of a highly frequency selective channel, this average capacity is then guaranteed, i.e. if the transmitter codes for 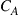 , the receiver will always be able to extract
, the receiver will always be able to extract 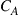 without experiencing outage [49,80].
without experiencing outage [49,80].

Figure 10.7 (a) Histogram of MIMO capacities 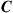 , normalized to the single-mode capacity
, normalized to the single-mode capacity 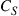 . The shaded area represents the probability that
. The shaded area represents the probability that 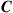 is smaller than
is smaller than 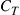 , leading to system outage if the system is designed to code for capacity
, leading to system outage if the system is designed to code for capacity 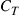 . The dashed line at
. The dashed line at 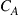 denotes the average capacity that would be obtained on a frequency-selective or rapidly time varying channel. (b) Visualization of slowly-varying temporal capacity evolution over a frequency-flat channel (top) and a strongly frequency-selective channel (bottom); green boxes denote channel capacities above the actually transmitted capacity, while red boxes denote outages. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this book.)
denotes the average capacity that would be obtained on a frequency-selective or rapidly time varying channel. (b) Visualization of slowly-varying temporal capacity evolution over a frequency-flat channel (top) and a strongly frequency-selective channel (bottom); green boxes denote channel capacities above the actually transmitted capacity, while red boxes denote outages. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this book.)
In practice, the above three limiting cases may not be representative of any given real system and a hybrid approach may be necessary.
Figure 10.8 shows the 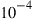 outage capacities
outage capacities  for static flat-fading (a) and the average capacities
for static flat-fading (a) and the average capacities 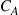 for frequency-selective fading (b) in multiples of the single-mode capacity
for frequency-selective fading (b) in multiples of the single-mode capacity  ; we assume channels supporting M = 4, 8, 16, 32, 64, and 128 modes, and symmetric transponder pairs
; we assume channels supporting M = 4, 8, 16, 32, 64, and 128 modes, and symmetric transponder pairs 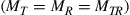 at 20-dB SNR. The dashed line
at 20-dB SNR. The dashed line 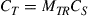 represents crosstalk-free performance as an upper bound to any MIMO system, only to be reached in the unitary MIMO case if the transponders are able to address all channel modes, as shown above. It can be seen that for a given transponder complexity (i.e. for fixed
represents crosstalk-free performance as an upper bound to any MIMO system, only to be reached in the unitary MIMO case if the transponders are able to address all channel modes, as shown above. It can be seen that for a given transponder complexity (i.e. for fixed 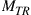 ) it is generally preferable in terms of aggregate SDM capacity to use a waveguide that supports
) it is generally preferable in terms of aggregate SDM capacity to use a waveguide that supports 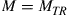 modes. Deploying “future-proof” waveguides whose mode count exceeds current transponder capabilities results in a significant start-up capacity penalty. For example, operating a waveguide supporting
modes. Deploying “future-proof” waveguides whose mode count exceeds current transponder capabilities results in a significant start-up capacity penalty. For example, operating a waveguide supporting 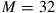 modes with transponders that only address
modes with transponders that only address  modes results in a capacity of around
modes results in a capacity of around 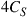 . This capacity can also be achieved using only half the amount of transponders (and consequently much less MIMO signal processing) on a waveguide supporting just 4 modes. Hence, one should always strive to match the number of coupled waveguide modes to the number of modes that the transponders can address and are able to MIMO-process.
. This capacity can also be achieved using only half the amount of transponders (and consequently much less MIMO signal processing) on a waveguide supporting just 4 modes. Hence, one should always strive to match the number of coupled waveguide modes to the number of modes that the transponders can address and are able to MIMO-process.
10.2.2.4 Channel with distributed noise loading
With reference to Figure 10.9a, we now consider an 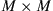 SDM system operating on a matched M-mode waveguide composed of K concatenated segments with segment matrices
SDM system operating on a matched M-mode waveguide composed of K concatenated segments with segment matrices  . Since we only consider the
. Since we only consider the  case here, we have
case here, we have  . Noise power
. Noise power 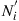 is added at the end of each segment. As before, we factor out the net mode-average gain or loss
is added at the end of each segment. As before, we factor out the net mode-average gain or loss 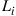 according to Eq. (10.9). In the linear regime covered here, it is immaterial whether the mode-independent gain or loss within a segment physically occurs before or after the mode coupling described by the segment matrix. If a segment is identified with a net transparent amplification span, we have
according to Eq. (10.9). In the linear regime covered here, it is immaterial whether the mode-independent gain or loss within a segment physically occurs before or after the mode coupling described by the segment matrix. If a segment is identified with a net transparent amplification span, we have  , and the physical segment loss is reflected in the amount of noise
, and the physical segment loss is reflected in the amount of noise 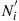 associated with optical amplification to reach per-span transparency.
associated with optical amplification to reach per-span transparency.
We next define an equivalent system according to Figure 10.9b by replacing the individual segment losses by a lumped loss of 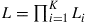 at the input to the channel and adjusting the noise powers at each segment such as to match the actual noise found in the original system, i.e.
at the input to the channel and adjusting the noise powers at each segment such as to match the actual noise found in the original system, i.e. 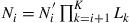 . Note that for an ensemble of random, nonunitary segment matrices, the overall net mode-average loss (or gain)
. Note that for an ensemble of random, nonunitary segment matrices, the overall net mode-average loss (or gain) 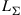 for each instantiation of the concatenated system will generally differ from our lumped loss variable L, with some channel instantiations showing more and some showing less net mode-average loss than L, as discussed in Ref. [49]. However, for most cases of practical interest, the ensemble average of the mode-average loss of the concatenated system is closely approximated by L.
for each instantiation of the concatenated system will generally differ from our lumped loss variable L, with some channel instantiations showing more and some showing less net mode-average loss than L, as discussed in Ref. [49]. However, for most cases of practical interest, the ensemble average of the mode-average loss of the concatenated system is closely approximated by L.
If all noise sources are statistically independent, we find for the noise correlation matrix at the receiver:
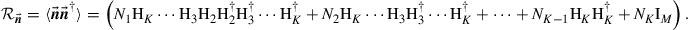 (10.15)
(10.15)
If only modal crosstalk occurs within each fiber segment (i.e. if the segments 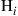 are all unitary), the correlation equals that of spatio-temporally white noise,
are all unitary), the correlation equals that of spatio-temporally white noise,
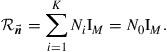 (10.16)
(10.16)
Hence, a concatenation of unitary segments with distributed noise has the same capacity as a unitary channel that is noise-loaded at the receiver by the same amount of noise, 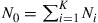 .
.
If the segment matrices are not unitary, the channel can be written as
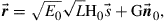 (10.17)
(10.17)
where 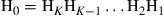 is the overall channel matrix for the signal, and the white noise
is the overall channel matrix for the signal, and the white noise 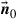 of power density
of power density 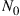 is colored by a matrix G such that
is colored by a matrix G such that 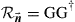 , as shown in Figure 10.9c. Placing the deterministic matrix
, as shown in Figure 10.9c. Placing the deterministic matrix  as a whitening filter inside the receiver leaves the MIMO capacity unchanged but produces the equivalent white-noise MIMO channel
as a whitening filter inside the receiver leaves the MIMO capacity unchanged but produces the equivalent white-noise MIMO channel
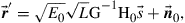 (10.18)
(10.18)
as shown in Figure 10.9c; its open-loop BLAST capacity is given by Eq. (10.10) with 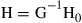 . The matrix G can be found from the measured noise correlation matrix
. The matrix G can be found from the measured noise correlation matrix 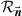 by decomposing
by decomposing 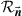 into the form
into the form 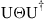 , where U is a unitary matrix and
, where U is a unitary matrix and  is a diagonal matrix containing the eigenvalues
is a diagonal matrix containing the eigenvalues  of
of 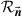 . The matrix G is then given as
. The matrix G is then given as 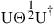 , where
, where  is diagonal with elements
is diagonal with elements 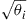 , and
, and 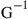 is given as
is given as 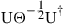 , where
, where 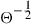 is diagonal with elements
is diagonal with elements  .
.
10.2.2.5 Channel with mode-dependent loss (MDL)
Based on the above results, we next investigate MIMO capacity statistics for a channel with K segments and M modes, all of which can be addressed by transmitter and receiver. Each segment is composed of a random mode coupling element followed by a random MDL element. Without loss of generality, we assume the mode-average optical loss 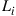 for each individual segment to be unity. Hence, each segment matrix is composed of a random unitary matrix
for each individual segment to be unity. Hence, each segment matrix is composed of a random unitary matrix  , followed by a random diagonal matrix
, followed by a random diagonal matrix  whose M real-valued, positive elements
whose M real-valued, positive elements 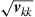 satisfy
satisfy 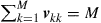 to ensure that
to ensure that  . For each MDL segment matrix
. For each MDL segment matrix  , the numbers
, the numbers 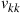 are drawn from a uniform distribution (on a linear scale) such that the ratio of maximum to minimum matrix element equals the pre-specified value for the per segment MDL,
are drawn from a uniform distribution (on a linear scale) such that the ratio of maximum to minimum matrix element equals the pre-specified value for the per segment MDL,
 (10.19)
(10.19)
We assume that all K segments have equal per-segment MDLs (i.e. the intervals from which the above random diagonal matrix elements are chosen are identical for all segments). Both the mode-average loss 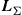 and the MDL of the concatenated system
and the MDL of the concatenated system 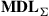 are random variables. The former is given by the trace of
are random variables. The former is given by the trace of 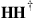 and the latter by the ratio of largest to smallest eigenvalue of
and the latter by the ratio of largest to smallest eigenvalue of 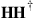 . For the two-mode case, i.e. in the context of polarization-dependent loss (PDL) in single-mode fiber, analytical relations of various sorts have been derived to describe the relationship between mode-average loss and mode-dependent loss as well as their statistical properties (see, e.g., [81–90]). An extension of the statistics of two-mode parameters to M modes is also given, e.g. in [91–94]. Numerically obtained statistics of the concatenated system’s mode-average loss and mode-dependent loss as well as statistics of the concatenated system’s MIMO capacity are given in [49].
. For the two-mode case, i.e. in the context of polarization-dependent loss (PDL) in single-mode fiber, analytical relations of various sorts have been derived to describe the relationship between mode-average loss and mode-dependent loss as well as their statistical properties (see, e.g., [81–90]). An extension of the statistics of two-mode parameters to M modes is also given, e.g. in [91–94]. Numerically obtained statistics of the concatenated system’s mode-average loss and mode-dependent loss as well as statistics of the concatenated system’s MIMO capacity are given in [49].
Evaluating the average MIMO capacity for the frequency-selective channel, normalized to M times the single-mode capacity as a function of the per segment MDL for 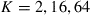 , and 128 segments results in the curves shown in Figure 10.10a for
, and 128 segments results in the curves shown in Figure 10.10a for  modes, both with noise loading at the receiver (red, circles) and with distributed noise loading (blue, squares). The solid red lines and the dashed blue lines give corresponding analytical results [49] using the numerically exact values for mean and standard deviation of
modes, both with noise loading at the receiver (red, circles) and with distributed noise loading (blue, squares). The solid red lines and the dashed blue lines give corresponding analytical results [49] using the numerically exact values for mean and standard deviation of  . As expected, the SDM channel capacity drops with the per segment MDL as well as with the number of segments. For 128 segments, a per segment MDL of 1 dB is tolerable to still achieve over 90% of the ideal channel capacity. Further, we note that distributed noise loading gives slightly better capacities than noise loading at the receiver, which is due to the reduced noise enhancement by receive-side (spatial) equalization. This is in analogy to the better performance of single-mode receivers when noise loading is performed prior to narrow bandpass filtering [20]: If an optical filter is placed after all noise has been added, the filter acts on signal and noise, which lets the receive-side equalizer restore approximately white-noise conditions during signal equalization. On the other hand, an optical filter placed before any noise is added only affects the signal but not the noise, which results in noise enhancement upon signal equalization within the receiver.
. As expected, the SDM channel capacity drops with the per segment MDL as well as with the number of segments. For 128 segments, a per segment MDL of 1 dB is tolerable to still achieve over 90% of the ideal channel capacity. Further, we note that distributed noise loading gives slightly better capacities than noise loading at the receiver, which is due to the reduced noise enhancement by receive-side (spatial) equalization. This is in analogy to the better performance of single-mode receivers when noise loading is performed prior to narrow bandpass filtering [20]: If an optical filter is placed after all noise has been added, the filter acts on signal and noise, which lets the receive-side equalizer restore approximately white-noise conditions during signal equalization. On the other hand, an optical filter placed before any noise is added only affects the signal but not the noise, which results in noise enhancement upon signal equalization within the receiver.
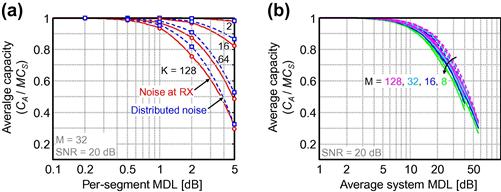
Figure 10.10 Average system capacity as a function of per segment MDL and number of segments K. (a) Systems with 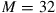 modes and 20 dB SNR. Red circles and blue squares are numerically exact results for receive-side and distributed noise loading, respectively. Solid red and dashed blue lines represent an approximation given in [49]. (b) MDL performance of systems with
modes and 20 dB SNR. Red circles and blue squares are numerically exact results for receive-side and distributed noise loading, respectively. Solid red and dashed blue lines represent an approximation given in [49]. (b) MDL performance of systems with 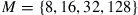 modes and
modes and  segments for 20 dB SNR and distributed noise loading as a function of the aggregate system MDL. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this book.)
segments for 20 dB SNR and distributed noise loading as a function of the aggregate system MDL. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this book.)
To further test the scaling of SDM capacity with K, we plot the average capacity curves for the frequency-selective channel and distributed noise loading as a function of the aggregate average system MDL, 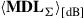 in Figure 10.10b. This lets all curves with equal M essentially collapse, as expected from the scaling relations discussed in [49]. Aggregate average system MDLs of 10 dB are seen to be acceptable for less than a 10% hit in SDM capacity, impressively illustrating the robustness of optical MIMO to MDL effects.
in Figure 10.10b. This lets all curves with equal M essentially collapse, as expected from the scaling relations discussed in [49]. Aggregate average system MDLs of 10 dB are seen to be acceptable for less than a 10% hit in SDM capacity, impressively illustrating the robustness of optical MIMO to MDL effects.
The curves shown in Figure 10.10, which represent the average capacity of a frequency-selective channel, can be compared to the curves in Figures 9 and 10 of [49], which apply to the 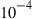 outage capacity of a frequency-flat channel. No significant performance difference in the tolerance to MDL is found between the two cases.
outage capacity of a frequency-flat channel. No significant performance difference in the tolerance to MDL is found between the two cases.
10.3 MIMO DSP
The above analyses of MIMO capacities represent limiting cases of transmission performance that may be approached assuming ideal digital signal processing (DSP) and coding. In this section, we extend the more familiar receiver DSP structure of a PDM system (which represents 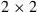 MIMO), to an
MIMO), to an 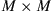 MIMO system of M coupled spatial and polarization modes.
MIMO system of M coupled spatial and polarization modes.
10.3.1 General receiver DSP functional blocks
Figure 10.11 visualizes the general  MIMO-DSP structure of a PDM coherent receiver (see, e.g., [95–97]) with its most basic functional blocks: In-phase (I) and quadrature (Q) components of the received
MIMO-DSP structure of a PDM coherent receiver (see, e.g., [95–97]) with its most basic functional blocks: In-phase (I) and quadrature (Q) components of the received 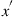 and
and 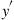 polarizations (in the local oscillator’s x′-y′-coordinate system) are first converted into the digital domain typically through over-sampled analog-to-digital converters (ADCs) and combined into two complex sample streams,
polarizations (in the local oscillator’s x′-y′-coordinate system) are first converted into the digital domain typically through over-sampled analog-to-digital converters (ADCs) and combined into two complex sample streams, 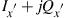 and
and 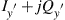 that fully represent the received optical signal field. After applying front-end corrections that compensate for various imperfections of the optoelectronic receiver front-end, such as phase errors of the optical 90° hybrid or sampling skews between the ADCs, chromatic dispersion (CD) of the transmission link is compensated by digitally applying the inverse CD filter function (an allpass filter with quadratic phase [95,98]). Since the transmitter’s x-y coordinate system is randomly rotated by the fiber’s
that fully represent the received optical signal field. After applying front-end corrections that compensate for various imperfections of the optoelectronic receiver front-end, such as phase errors of the optical 90° hybrid or sampling skews between the ADCs, chromatic dispersion (CD) of the transmission link is compensated by digitally applying the inverse CD filter function (an allpass filter with quadratic phase [95,98]). Since the transmitter’s x-y coordinate system is randomly rotated by the fiber’s  Jones matrix relative to the receiver’s
Jones matrix relative to the receiver’s 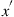 -
- -coordinate system, the DSP next needs to apply the inverse Jones matrix to the vector
-coordinate system, the DSP next needs to apply the inverse Jones matrix to the vector 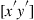 to recover the two signal components multiplexed onto x and y polarizations at the transmitter. This inverse Jones matrix is represented by the shaded butterfly structure in Figure 10.11. In order not only to compensate frequency-independent matrices with scalar elements
to recover the two signal components multiplexed onto x and y polarizations at the transmitter. This inverse Jones matrix is represented by the shaded butterfly structure in Figure 10.11. In order not only to compensate frequency-independent matrices with scalar elements 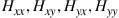 but also to correct for frequency-dependent quasi-unitary polarization rotations due to polarization-mode dispersion (PMD), the matrix elements
but also to correct for frequency-dependent quasi-unitary polarization rotations due to polarization-mode dispersion (PMD), the matrix elements 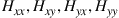 are implemented as individual filters, typically with a few tens of filter taps. The complex filter coefficients are typically found using adaptive algorithms [95–97], such as the blind constant modulus algorithms (CMA), or various forms of blind decision-directed algorithms, such as radius directed multi-modulus algorithm or the least-mean square (LMS) algorithm. Rapid coefficient acquisition can also be obtained with the help of data-aided algorithms that make use of specific training symbols inserted into the transmit data stream [99,100]. At the output of the butterfly filter, the transmitter’s original
are implemented as individual filters, typically with a few tens of filter taps. The complex filter coefficients are typically found using adaptive algorithms [95–97], such as the blind constant modulus algorithms (CMA), or various forms of blind decision-directed algorithms, such as radius directed multi-modulus algorithm or the least-mean square (LMS) algorithm. Rapid coefficient acquisition can also be obtained with the help of data-aided algorithms that make use of specific training symbols inserted into the transmit data stream [99,100]. At the output of the butterfly filter, the transmitter’s original 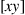 coordinate system is re-established. Subsequent frequency and phase tracking lock the phase of the symbol constellation before hard-decision or soft-decision decoding can take place.
coordinate system is re-established. Subsequent frequency and phase tracking lock the phase of the symbol constellation before hard-decision or soft-decision decoding can take place.

Figure 10.11 Functional blocks of a conventional polarization-diversity intradyne coherent receiver implementing 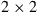 MIMO-DSP.
MIMO-DSP.
Extending this system to an 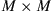 MIMO receiver, we note that the only functional block that changes in this DSP structure is the butterfly equalizer: Instead of undoing the action of a
MIMO receiver, we note that the only functional block that changes in this DSP structure is the butterfly equalizer: Instead of undoing the action of a 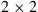 channel, the equalizer now has to deal with an
channel, the equalizer now has to deal with an 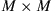 channel based on an appropriate channel estimation or filter adaptation algorithm. In the former case, the channel matrix is estimated and inverted to obtain the equalizer coefficients based on the zero-forcing (ZF) criterion or the minimum-mean-square error (MMSE) criterion. In the latter case, gradient-based coefficient adaptation algorithms are used to directly adapt the filter coefficients to approach the MMSE solution [65].
channel based on an appropriate channel estimation or filter adaptation algorithm. In the former case, the channel matrix is estimated and inverted to obtain the equalizer coefficients based on the zero-forcing (ZF) criterion or the minimum-mean-square error (MMSE) criterion. In the latter case, gradient-based coefficient adaptation algorithms are used to directly adapt the filter coefficients to approach the MMSE solution [65].
10.3.2 Channel estimation
A detailed understanding of the communication channel is essential for the design of efficient equalization and coding schemes. In this context, channel estimation performed in the digital domain can serve as a useful tool that allows to visualize the channel state and to study channel statistics. Channel estimation can also be used to obtain a set of equalizer coefficients from a received training sequence. These coefficients can then be applied to equalize subsequent payload data. In the following, we describe the least-squares (LS) scheme and a stochastic gradient scheme based on the LMS algorithm as two ways to perform channel estimation for the fiber-optic MIMO channel.
10.3.2.1 Least squares channel estimation
Assume an 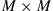 MIMO channel with a linear time invariant (LTI) channel matrix H that we want to estimate from M (possibly oversampled) complex-valued received waveforms, each represented by N consecutive received samples. We can write this received data as an
MIMO channel with a linear time invariant (LTI) channel matrix H that we want to estimate from M (possibly oversampled) complex-valued received waveforms, each represented by N consecutive received samples. We can write this received data as an 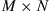 receive matrix
receive matrix
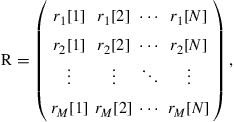 (10.20)
(10.20)
where 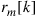 is the sampled waveform at the mth receiver, and
is the sampled waveform at the mth receiver, and  . We next define the channel matrix as
. We next define the channel matrix as
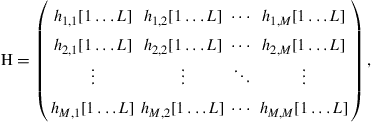 (10.21)
(10.21)
where each matrix element 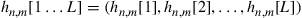 is the L-tap discrete-time impulse response from the nth transmitter to the mth receiver. The size of the channel matrix
is the L-tap discrete-time impulse response from the nth transmitter to the mth receiver. The size of the channel matrix  is
is  . Finally, from the M transmit sequences
. Finally, from the M transmit sequences 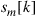 with
with 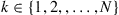 of properly oversampled training symbols, and for a certain pattern delay
of properly oversampled training symbols, and for a certain pattern delay 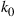 , we can define the
, we can define the 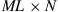 matrix
matrix
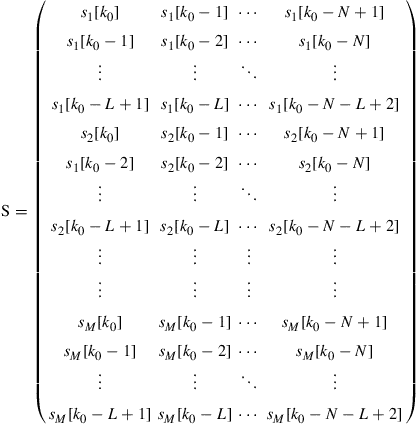 (10.22)
(10.22)
with its Toeplitz submatrices. This allows us to express the action of the MIMO system in compact matrix notation as
 (10.23)
(10.23)
where the 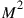 convolutions are now captured by a single matrix multiplication. If the matrices R and S are both known and are properly aligned in time through the parameter
convolutions are now captured by a single matrix multiplication. If the matrices R and S are both known and are properly aligned in time through the parameter  , we can apply the LS method, to obtain the channel estimate
, we can apply the LS method, to obtain the channel estimate
 (10.24)
(10.24)
The matrix 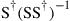 is also referred to as pseudoinverse of
is also referred to as pseudoinverse of 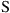 . For a fixed training pattern, the pseudoinverse can be determined ahead of time, stored in memory, and later used for estimating different MIMO channels. Regarding the selection of training patterns, one needs to take care that the training patterns of the M transmitters are uncorrelated. In practice, the LS method provides a very useful tool to analyze the properties of experimental fiber-optic MIMO systems, even though the assumption of an LTI channel is typically not strictly fulfilled in the presence of phase noise introduced by the transmit laser and the local oscillator.
. For a fixed training pattern, the pseudoinverse can be determined ahead of time, stored in memory, and later used for estimating different MIMO channels. Regarding the selection of training patterns, one needs to take care that the training patterns of the M transmitters are uncorrelated. In practice, the LS method provides a very useful tool to analyze the properties of experimental fiber-optic MIMO systems, even though the assumption of an LTI channel is typically not strictly fulfilled in the presence of phase noise introduced by the transmit laser and the local oscillator.
10.3.2.2 Least mean squares channel estimation
Alternatively, the channel matrix can be estimated using the LMS algorithm. In this case the system can be expressed as 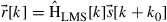 , where
, where  corresponds to the M received waveforms at sampling instant
corresponds to the M received waveforms at sampling instant 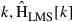 is the estimated channel matrix at time instant k, and
is the estimated channel matrix at time instant k, and  is the time-aligned and properly upsampled vector of transmit data. The LMS algorithm provides an approximation of the MMSE solution by adapting the channel estimate
is the time-aligned and properly upsampled vector of transmit data. The LMS algorithm provides an approximation of the MMSE solution by adapting the channel estimate 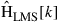 in the direction of the minimum instantaneous squared error
in the direction of the minimum instantaneous squared error
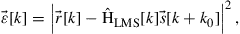 (10.25)
(10.25)
using the update rule
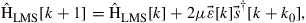 (10.26)
(10.26)
where  is the adaptation gain. A benefit of LMS-based channel estimation is that it can track variations of the channel matrix across the training sequence and that it can even be combined with a phase recovery scheme in order to separate the effect of laser phase noise from the channel matrix. However, LMS-based channel estimation typically results in a reduced accuracy compared to the LS scheme.
is the adaptation gain. A benefit of LMS-based channel estimation is that it can track variations of the channel matrix across the training sequence and that it can even be combined with a phase recovery scheme in order to separate the effect of laser phase noise from the channel matrix. However, LMS-based channel estimation typically results in a reduced accuracy compared to the LS scheme.
10.3.3 Adaptive MIMO equalization
Crosstalk from mode coupling in conjunction with modal delay spread (MDS), defined as the temporal width of the overall system’s 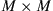 channel matrix H, can set a hard limit on the transmission distance of SDM systems if no means are undertaken to compensate for it. We will show in this section that MIMO equalization can compensate for these impairments to a large extent if the communication channel is designed in a proper way. As we already pointed out above, adaptive
channel matrix H, can set a hard limit on the transmission distance of SDM systems if no means are undertaken to compensate for it. We will show in this section that MIMO equalization can compensate for these impairments to a large extent if the communication channel is designed in a proper way. As we already pointed out above, adaptive  MIMO equalization is already widely used in single-mode optical communications in order to separate the two transmitted polarization-multiplexed data streams. If the SDM transmission link exhibits a sufficiently low level of MDL, the same concept can be extended to few-mode fiber transmission, resulting in a matrix of
MIMO equalization is already widely used in single-mode optical communications in order to separate the two transmitted polarization-multiplexed data streams. If the SDM transmission link exhibits a sufficiently low level of MDL, the same concept can be extended to few-mode fiber transmission, resulting in a matrix of  equalizers.
equalizers.
Extending our discussions on MDL in Section 10.2.2.5, we first introduce the channel matrix in terms of the z transform as  where the
where the 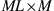 delay matrix has the form
delay matrix has the form
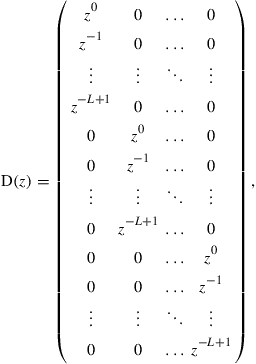
and obtain the frequency dependent channel matrix as 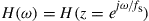 over the frequency interval
over the frequency interval 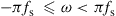 (sampling rate fs). Now, we can derive the MDL of the estimated channel matrix by carrying out a singular value decomposition according to
(sampling rate fs). Now, we can derive the MDL of the estimated channel matrix by carrying out a singular value decomposition according to
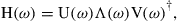 (10.27)
(10.27)
where U(ω) and V(ω) are frequency dependent unitary matrices of sizes 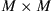 , respectively. The
, respectively. The  diagonal matrix Λ(ω) has the singular values
diagonal matrix Λ(ω) has the singular values 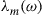 on the main diagonal from which we obtain the MDL as
on the main diagonal from which we obtain the MDL as
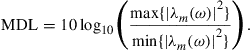 (10.28)
(10.28)
Let us now consider a linear MIMO equalizer that is operating on a twofold oversampled input signal (oversampling ratios different from two are also feasible but require a proper modification of the DSP). This oversampled implementation of the linear equalizer has the advantage that the optimal symbol-spaced sampled MMSE filter can be approximated using a fully digital adaptation scheme [65]. We transmit a sequence of symbols 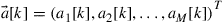 with symbol index
with symbol index  through the MIMO channel, and receive the sequence
through the MIMO channel, and receive the sequence  with sample index
with sample index 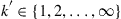 . We further consider a linear equalizer with
. We further consider a linear equalizer with 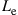 taps at two samples per symbol, whose output
taps at two samples per symbol, whose output 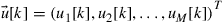 with
with 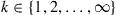 is calculated once for every transmit symbol. We can then obtain the output of the linear equalizer from
is calculated once for every transmit symbol. We can then obtain the output of the linear equalizer from
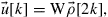 (10.29)
(10.29)
where 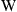 is an
is an 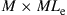 matrix of complex-valued equalizer coefficients and the received samples are expressed by the
matrix of complex-valued equalizer coefficients and the received samples are expressed by the 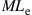 -element vector
-element vector 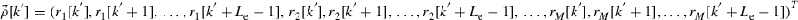 . In the case where the channel has no MDL, the channel matrix H is unitary, i.e.
. In the case where the channel has no MDL, the channel matrix H is unitary, i.e. 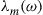 for
for  , and if the noise is white, all mode coupling and inter-symbol interference can be fully compensated using the coefficient matrix
, and if the noise is white, all mode coupling and inter-symbol interference can be fully compensated using the coefficient matrix 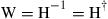 . In the presence of weak or moderate MDL, i.e. less than approximately 10 dB (compare Figure 10.10b), a linear MIMO equalizer is still able to recover the transmitted signal with a small penalty. However, if the channel has strong MDL, linear equalization will lead to considerable noise enhancement and advanced schemes like decision-feedback equalization (DFE) or maximum-likelihood sequence estimation (MLSE) are required in order to recover the transmit signal [65].
. In the presence of weak or moderate MDL, i.e. less than approximately 10 dB (compare Figure 10.10b), a linear MIMO equalizer is still able to recover the transmitted signal with a small penalty. However, if the channel has strong MDL, linear equalization will lead to considerable noise enhancement and advanced schemes like decision-feedback equalization (DFE) or maximum-likelihood sequence estimation (MLSE) are required in order to recover the transmit signal [65].
In analogy to the general MIMO-DSP structure of Figure 10.11, the MIMO equalizer is typically followed by a carrier phase estimation scheme, such as the Viterbi and Viterbi scheme for QPSK constellations [101], that provides an estimate of the carrier phase offset 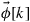 . In MIMO systems an interesting option is to apply a joint phase recovery over all modes in order to improve accuracy [102,103].
. In MIMO systems an interesting option is to apply a joint phase recovery over all modes in order to improve accuracy [102,103].
As the channel is expected to be slowly time-varying compared to the symbol rate, gradient-based adaptive algorithms are attractive in order to adapt the equalizer coefficients. A popular adaptation scheme is the CMA that updates the coefficients based on the error criterion
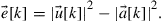 (10.30)
(10.30)
For QPSK modulation, we have  . The equalizer coefficients are updated according to
. The equalizer coefficients are updated according to
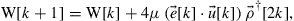 (10.31)
(10.31)
where · denotes element-wise multiplication. A benefit of the CMA algorithm is that it operates fully blindly and that no information about the carrier phase is required. This makes the algorithm attractive for real-time implementation. However, in an  MIMO system, the CMA can mis-converge in a way that different sub-equalizers converge to the same solution, resulting in the same information signal at multiple equalizer outputs while entirely dropping other information signals. Advanced algorithms like the independent component analysis (ICA) can be applied to solve this issue [104,105a] and to achieve fully blind convergence.
MIMO system, the CMA can mis-converge in a way that different sub-equalizers converge to the same solution, resulting in the same information signal at multiple equalizer outputs while entirely dropping other information signals. Advanced algorithms like the independent component analysis (ICA) can be applied to solve this issue [104,105a] and to achieve fully blind convergence.
An alternative to the CMA is the LMS algorithm, where the adaptation error is defined as
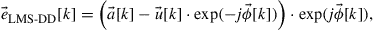 (10.32)
(10.32)
and the coefficients are updated according to
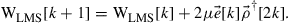 (10.33)
(10.33)
Compared to the CMA, the LMS algorithm requires additional information about the carrier phase offset  and about the transmit symbol
and about the transmit symbol 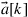 . The former issue can be solved by feeding back the output of the carrier phase estimator to the equalizer adaptation algorithm. This approach, however, can cause difficulties in a high-speed real-time DSP implementation, as the required feedback delay becomes rather long. The problem that information about the transmitted symbol
. The former issue can be solved by feeding back the output of the carrier phase estimator to the equalizer adaptation algorithm. This approach, however, can cause difficulties in a high-speed real-time DSP implementation, as the required feedback delay becomes rather long. The problem that information about the transmitted symbol 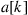 is required at the receiver can be solved by applying hard-decision after the carrier recovery to obtain an estimate of the transmitted symbol. In this so-called decision-directed mode, the LMS algorithm can track variations of the channel blindly. However, the decision-directed LMS algorithm usually fails to converge during the initial coefficient acquisition phase, as the transmit symbol and the carrier phase offset cannot be estimated reliably in the presence of strong ISI. An attractive way to achieve initial coefficient convergence in a reliable way is the use of training symbols that are inserted within the transmit sequence and that are known to the receiver [99,100]. Using this data-aided LMS scheme allows to achieve convergence of the equalizer coefficients after a certain number of training symbols. If we assume a system working at 28 GBaud and a 50,000-symbol training sequence for coefficient acquisition that is inserted once every millisecond, the required overhead is still less than 0.2%.
is required at the receiver can be solved by applying hard-decision after the carrier recovery to obtain an estimate of the transmitted symbol. In this so-called decision-directed mode, the LMS algorithm can track variations of the channel blindly. However, the decision-directed LMS algorithm usually fails to converge during the initial coefficient acquisition phase, as the transmit symbol and the carrier phase offset cannot be estimated reliably in the presence of strong ISI. An attractive way to achieve initial coefficient convergence in a reliable way is the use of training symbols that are inserted within the transmit sequence and that are known to the receiver [99,100]. Using this data-aided LMS scheme allows to achieve convergence of the equalizer coefficients after a certain number of training symbols. If we assume a system working at 28 GBaud and a 50,000-symbol training sequence for coefficient acquisition that is inserted once every millisecond, the required overhead is still less than 0.2%.
10.3.4 MIMO equalizer complexity
In the previous subsection we have shown that a linear MIMO equalizer is able to compensate for mode coupling and MDS in case of weak or moderate MDL. With respect to the practical implementation of MIMO-SDM systems, the overall DSP-complexity is an important constraint. As a reference for the following complexity analysis, we consider an SDM system with 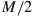 uncoupled single-mode waveguides terminated by receivers of the type shown in Figure 10.11. A
uncoupled single-mode waveguides terminated by receivers of the type shown in Figure 10.11. A 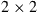 MIMO equalizer is applied for each waveguide in order to uncouple the polarizations and to compensate for polarization-mode dispersion such that the total number of sub-equalizers equals
MIMO equalizer is applied for each waveguide in order to uncouple the polarizations and to compensate for polarization-mode dispersion such that the total number of sub-equalizers equals 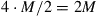 . If we compare this to a MIMO-SDM system with
. If we compare this to a MIMO-SDM system with 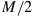 coupled waveguides supporting 2 polarizations each, we require a single
coupled waveguides supporting 2 polarizations each, we require a single 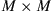 MIMO equalizer of the form shown in Figure 10.12, with a total of
MIMO equalizer of the form shown in Figure 10.12, with a total of  sub-equalizers. A coupled-mode MIMO-SDM system with
sub-equalizers. A coupled-mode MIMO-SDM system with 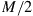 spatial paths thus requires
spatial paths thus requires 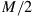 as many sub-equalizers as the corresponding uncoupled SDM system.
as many sub-equalizers as the corresponding uncoupled SDM system.

Figure 10.12 Schematic representation of a  MIMO equalizer followed by carrier recovery and joint decoder. The dashed line represents an optional joint carrier recovery scheme.
MIMO equalizer followed by carrier recovery and joint decoder. The dashed line represents an optional joint carrier recovery scheme.
In addition to the larger number of required equalizers, a MIMO-SDM system will typically need a larger number of taps per sub-equalizer. To roughly estimate the resulting complexity increase for MIMO-SDM systems, we note that in single-mode fiber systems, the required equalizer memory for compensating PMD is on the order of 100 ps, while the required equalizer memory for long-haul MIMO-SDM transmission can grow up to, e.g., 10 ns [57,58], a factor of 100 larger. If the linear equalizer is implemented in the time-domain using a tapped-delay-line structure, the associated complexity is approximately one complex multiplication per sample per equalizer tap. In our example, this would mean that a MIMO-SDM equalizer is about 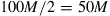 more complex than the equalizer for the equivalent uncoupled SDM receiver. However, a frequency-domain implementation of the sub-equalizers scales much more favorable than a tapped-delay-line structure [105b,106,107a,107b]; a common way to implement the sub-equalizer in an efficient way is the overlap-and-save (or overlap-and-discard) method [108]. In this case, the complexity of a single sub-equalizer is of order
more complex than the equalizer for the equivalent uncoupled SDM receiver. However, a frequency-domain implementation of the sub-equalizers scales much more favorable than a tapped-delay-line structure [105b,106,107a,107b]; a common way to implement the sub-equalizer in an efficient way is the overlap-and-save (or overlap-and-discard) method [108]. In this case, the complexity of a single sub-equalizer is of order
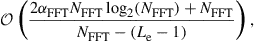 (10.34)
(10.34)
where 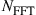 is the FFT-size and
is the FFT-size and 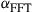 depends on the way the FFT is implemented (e.g.
depends on the way the FFT is implemented (e.g. 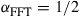 for a radix-2 implementation) [109]. Figure 10.13 shows the relative complexity of different equalizer structures. It becomes clear that the complexity of the overlap-save algorithm grows only slowly as a function of the equalizer length. Albeit this is only a rough estimate (e.g. since the complexity of the adaptation scheme is not taken into account), we note that the complexity of a coupled-mode MIMO-SDM equalizer scales linearly with
for a radix-2 implementation) [109]. Figure 10.13 shows the relative complexity of different equalizer structures. It becomes clear that the complexity of the overlap-save algorithm grows only slowly as a function of the equalizer length. Albeit this is only a rough estimate (e.g. since the complexity of the adaptation scheme is not taken into account), we note that the complexity of a coupled-mode MIMO-SDM equalizer scales linearly with 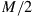 but only slowly as a function of the equalizer memory as compared to the equalizer for an uncoupled SDM system.
but only slowly as a function of the equalizer memory as compared to the equalizer for an uncoupled SDM system.
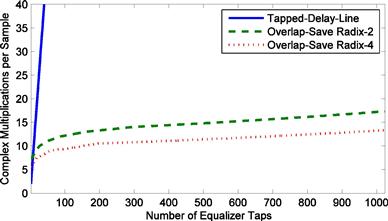
Figure 10.13 Number of complex multiplications per sample for different equalizer implementation schemes versus number of equalizer taps 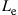 .
.
If the complexity of a full 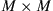 MIMO-SDM system is too large to be handled efficiently, be it due to DSP complexity, due to the required number of on-chip ADCs, or due to purely optical constraints such as the possibility of building optical fibers with reasonably low MDS or optical amplifiers with reasonably small modal gain variations, one can partition an SDM system of multiplicity
MIMO-SDM system is too large to be handled efficiently, be it due to DSP complexity, due to the required number of on-chip ADCs, or due to purely optical constraints such as the possibility of building optical fibers with reasonably low MDS or optical amplifiers with reasonably small modal gain variations, one can partition an SDM system of multiplicity 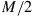 into a set of
into a set of 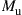 nominally uncoupled optical paths, each supporting
nominally uncoupled optical paths, each supporting 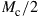 coupled spatial modes. The resulting DSP then consists of
coupled spatial modes. The resulting DSP then consists of  independent
independent 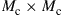 MIMO-DSP engines that could be implemented on separate ASICs if needed, as visualized in Figure 10.14. An example of such a system could be a fiber whose LP “modes” show negligible coupling [59] or a multi-core fiber with
MIMO-DSP engines that could be implemented on separate ASICs if needed, as visualized in Figure 10.14. An example of such a system could be a fiber whose LP “modes” show negligible coupling [59] or a multi-core fiber with 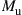 nominally uncoupled cores, each of which supports
nominally uncoupled cores, each of which supports  propagation modes [31,58,110], allowing for a capacity increase by a factor
propagation modes [31,58,110], allowing for a capacity increase by a factor  compared to a single-mode fiber. In a system of this kind, the uncompensated residual crosstalk between the
compared to a single-mode fiber. In a system of this kind, the uncompensated residual crosstalk between the 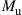 individual MIMO systems becomes a major design criterion, in analogy to the crosstalk considerations for weakly coupled single-mode systems (cf. Figure 10.4).
individual MIMO systems becomes a major design criterion, in analogy to the crosstalk considerations for weakly coupled single-mode systems (cf. Figure 10.4).

Figure 10.14 Schematic representation of three weakly coupled waveguides, each with 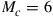 strongly coupled modes. MIMO processing is applied per waveguide.
strongly coupled modes. MIMO processing is applied per waveguide.
In [58] the crosstalk tolerance for a system of 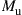 , nominally uncoupled waveguides each supporting 3 spatial modes and performing
, nominally uncoupled waveguides each supporting 3 spatial modes and performing  MIMO equalization, was studied, showing that for QPSK transmission a crosstalk of about –20 dB from the nominally uncoupled waveguides can be tolerated, similar to the single-mode case of Figure 10.4.
MIMO equalization, was studied, showing that for QPSK transmission a crosstalk of about –20 dB from the nominally uncoupled waveguides can be tolerated, similar to the single-mode case of Figure 10.4.
10.4 Mode Multiplexing Components
As described in Section 10.2.2, the ability to selectively excite and extract a complete orthogonal set of fiber modes is a critical requirement for MIMO-SDM performance. This is in complete analogy to a PDM system, where the transmitter needs to be able to couple its two signals distinctly into two orthogonal polarizations and the receiver also needs to be able to coherently extract a pair of orthogonal polarization states. If the transmitter does not couple its two signals into two essentially orthogonal polarization states, some irreversible crosstalk will occur that manifests itself in a performance degradation. Therefore, optical components that selectively couple M single-mode signals into M spatial fiber modes (or into unitary combinations thereof) without much nonunitary crosstalk are essential for MIMO-SDM systems. Devices that achieve this functionality are referred to as mode multiplexers (MMUXs).
10.4.1 Mode multiplexer characteristics
A mode multiplexer is fully characterized by its 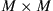 transfer matrix
transfer matrix  (see Fig. 10.6 for channel matrix definitions), where each matrix element can be calculated by the overlap integral defined in Eq. (10.7), evaluated for each of the M optical field distributions generated by the MMUX with respect to each of the M optical field distributions of the fiber modes. (An exemplary calculation is given below.)
(see Fig. 10.6 for channel matrix definitions), where each matrix element can be calculated by the overlap integral defined in Eq. (10.7), evaluated for each of the M optical field distributions generated by the MMUX with respect to each of the M optical field distributions of the fiber modes. (An exemplary calculation is given below.)
The impact of the MMUX on MIMO capacity can be determined using the methods presented in Section 10.2.2. Starting with the 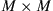 MMUX transfer matrix
MMUX transfer matrix 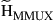 , we first factor out its mode-average loss L according to Eq. (10.9). We call this the MMUX’s mode-average insertion loss. For an MMUX used at the transmitter, its mode-average insertion loss can be compensated for by increasing the transmit power without implications on system performance. Used in-line at amplifiers or other networking elements, its mode-average insertion loss directly impacts the corresponding span loss, and therefore contributes to the system’s noise performance.
, we first factor out its mode-average loss L according to Eq. (10.9). We call this the MMUX’s mode-average insertion loss. For an MMUX used at the transmitter, its mode-average insertion loss can be compensated for by increasing the transmit power without implications on system performance. Used in-line at amplifiers or other networking elements, its mode-average insertion loss directly impacts the corresponding span loss, and therefore contributes to the system’s noise performance.
After factoring out the MMUX’s mode-average insertion loss, we arrive at the normalized MMUX matrix  . If the MIMO-SDM system consists solely of an MMUX and a mode demultiplexing receiver, the matrix
. If the MIMO-SDM system consists solely of an MMUX and a mode demultiplexing receiver, the matrix  by itself represents the MIMO channel. Knowing that a unitary MIMO channel does not degrade system performance, we first acknowledge that a transmit-side MMUX may map its M single-mode inputs onto any unitary transformation of fiber modes without loss of MIMO-SDM system performance. This fact also holds true for any arbitrary (linear) MIMO channel
by itself represents the MIMO channel. Knowing that a unitary MIMO channel does not degrade system performance, we first acknowledge that a transmit-side MMUX may map its M single-mode inputs onto any unitary transformation of fiber modes without loss of MIMO-SDM system performance. This fact also holds true for any arbitrary (linear) MIMO channel  following a unitary MMUX, since the overall MIMO channel capacity is then determined by the eigenvalues of
following a unitary MMUX, since the overall MIMO channel capacity is then determined by the eigenvalues of 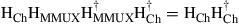 , which are the same as those without a unitary MMUX. Furthermore, we note that the transmit-side MMUX, by definition preceding any noise loading, has no effect on the noise correlation matrix of Eq. (10.15).
, which are the same as those without a unitary MMUX. Furthermore, we note that the transmit-side MMUX, by definition preceding any noise loading, has no effect on the noise correlation matrix of Eq. (10.15).
If the MMUX is nonunitary, i.e. if it exhibits nonunitary crosstalk, at least two of the M eigenvalues 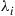 of
of  will differ from unity, resulting in the MDL channel model given by Eq. (10.19). The impact of MDL on MIMO system performance is discussed in Section 10.2.2.5 (Figure 10.10).
will differ from unity, resulting in the MDL channel model given by Eq. (10.19). The impact of MDL on MIMO system performance is discussed in Section 10.2.2.5 (Figure 10.10).
Note that a mode multiplexer is used here as a general term; in particular the same MMUX device can be used both on the transmit side and at the receive side, where it operates in reverse as a mode demultiplexer. When used as a mode demultiplexer at the receiver, the MMUX characteristics are less stringent, as this component will usually appear after all noise has been added to the signal. Hence, as long as the mode demultiplexer’s matrix is invertible, and as long as its MDL is small enough not to lead to other sources of post-demultiplexing receiver noise that suddenly become important (such as thermal noise or quantization noise from signal digitization), its characteristics have no impact on system performance. Mode demultiplexers placed in-line (e.g. at amplifier sites or in connection with other networking elements) will add MDL and loss to the system, just like an equivalent MMUX at those locations.
10.4.2 Mode multiplexer design
A large variety of fibers has been proposed for SDM including few-mode fibers (FMFs), multi-core fibers (MCFs) with single-mode cores, multi-core fibers with few-mode cores, and photonic crystal fibers (PCFs). Each fiber asks for its optimized mode multiplexer. Furthermore, for a given fiber type, multiple strategies to implement mode multiplexers exist, depending on the crosstalk management strategy used in the transmission system: If crosstalk in an SDM system is not actively compensated but is rather treated as an impairment (cf. Figure 10.4), a direct one-to-one correspondence between the input single-mode channels and the fiber’s spatial modes needs to be established in order for the receiver to uniquely detect a mode. This is the case, for example, in MCFs using nominally uncoupled cores, where each signal is uniquely coupled to one of the fiber cores. On the other hand, if MIMO processing is being used, any unitary mode combination may be excited at the transmitter, as discussed above. This offers more degrees of freedom in MMUX design.
Because the modes in a fiber are orthogonal according to Eq. (10.7), it should theoretically be possible to build a loss-less MMUX, in analogy to polarization multiplexing, where a polarizing beam splitter is used to losslessly multiplex two orthogonal polarizations onto a single fiber, or in analogy to WDM, where a diffraction grating may be used to losslessly combine WDM channels into a single fiber. In practice, this is not always possible, however. Generally, we can divide MMUX designs into two main categories:
• Broadcast and select mode shapers: Here, the MMUX shapes M individual spatial mode patterns of the waveguide. If these patterns overlap in space, they need to be passively combined by means of beam combiners before projection onto the waveguide’s end facet. Since the light leaving the unused port of a beam combiner is inherently lost, this class of MMUXs tends to be lossy and scale poorly with M. Operated as mode demultiplexers in reverse, this class of MMUXs first splits the light coming from a SDM fiber into M equal copies and later selectively filters each path by a suitable mode converter. Examples for this architecture are phase-plate based designs [111] discussed in Section 10.4.3.1, Liquid Crystal on Silicon (LCoS)-based designs [112,113], single-stage thin hologram-based designs [114], as well as long-period fiber gratings (LPG) [115–117].
• Mode transformers: Here, the MMUX transforms its M single-mode inputs into M optical field patterns that are individually projected onto the waveguide’s end facet without prior passive combining. Conversely, when operated as a demultiplexer, the light coming from a SDM fiber is mode-selectively split into M single-mode fibers. Depending on whether the mode transformation occurs abruptly or in a distributed fashion, we distinguish between:
– Single-step mode transformers: Here, mode conversion happens abruptly in the waveguide coupling plane. An example is the spot coupler [118] discussed in Section 10.4.3.2. Since the abrupt mode conversion is generally not perfectly matched to the waveguide modes, it may induce loss through the excitation of radiation modes, or it may induce mode dependent loss through nonorthogonal mode mapping.
– Distributed mode transformers: Here, mode conversion happens over a certain length within a volume rather than within a single coupling plane. MMUXs of this kind have the potential of being lossless for arbitrary values of M. Examples for this architecture are photonic lanterns [119] discussed in Section 10.4.3.2, volume holograms [120], and mode sorters [121].
In the following sections we review a selection of promising mode multiplexing components that are relevant for MIMO-SDM transmission systems.
10.4.3 Mode couplers for few-mode fibers
Few-mode fibers (FMFs) are single-core fibers where the refractive index profile of the core is designed to support a specific number of fiber modes (see Chapter 8 in Volume A). Refractive index profiles currently under study are step-index profiles, depressed-cladding index profiles, graded-index profiles, and ring-core profiles.
Mode multiplexers are often making use of symmetry properties of the modes. It is therefore instructive to consider the first 6 modes of a step-index fiber in detail. These modes, which are represented graphically in Figure 10.15, comprise the fundamental 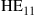 mode (which is twofold degenerate in polarization, resulting in the
mode (which is twofold degenerate in polarization, resulting in the 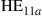 and
and  modes), the
modes), the 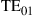 mode, the
mode, the 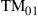 mode, and the
mode, and the  mode (twofold degenerate into
mode (twofold degenerate into  and
and  ). The
). The 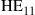 modes are linearly polarized (LP) with a single radial maximum and no angular dependence, which motivates denoting them also as
modes are linearly polarized (LP) with a single radial maximum and no angular dependence, which motivates denoting them also as 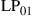 . In the limit of weakly guiding index profiles [122], the three higher-order modes
. In the limit of weakly guiding index profiles [122], the three higher-order modes 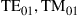 , and
, and 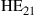 become almost degenerate as well. As shown in Figure 10.15, certain linear combinations of these modes are linearly polarized with one radial intensity maximum and with one set of positive maximum and negative minimum optical field amplitudes (resulting in two angular intensity maxima). This motivates grouping these modes into what is called the
become almost degenerate as well. As shown in Figure 10.15, certain linear combinations of these modes are linearly polarized with one radial intensity maximum and with one set of positive maximum and negative minimum optical field amplitudes (resulting in two angular intensity maxima). This motivates grouping these modes into what is called the 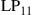 pseudo-mode. (In contrast to a true waveguide mode, whose electric field distribution is invariant with propagation distance, cf. footnote 3 on page 437, all but the
pseudo-mode. (In contrast to a true waveguide mode, whose electric field distribution is invariant with propagation distance, cf. footnote 3 on page 437, all but the 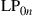 “modes” change their spatial distribution, owing to the small differences in propagation constant
“modes” change their spatial distribution, owing to the small differences in propagation constant 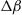 of their true waveguide mode constituents. The resulting beat length
of their true waveguide mode constituents. The resulting beat length  is in the range of a few cm up to meters for typical silica fibers, which causes the three constituent modes to strongly mix during transmission [123]).
is in the range of a few cm up to meters for typical silica fibers, which causes the three constituent modes to strongly mix during transmission [123]).

Figure 10.15 Grayscale intensity representation of the modes and the LP pseudo-modes of a step-index fiber supporting six spatial and polarization modes. The arrows indicate the direction of the electric field. Phase jumps are shown by opposite directions of the electric field vector.
10.4.3.1 Phase-plate based mode multiplexer
Experimentally, it is simpler to generate beams that resemble the LP “modes,” because lasers usually generate linearly polarized light which can be readily phase and amplitude shaped to match an LP profile. In contrast, shaping the true waveguide modes making up 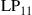 , for example, requires polarization changes across the transversal coordinate (cf. Figure 10.15). Furthermore, LP “modes” have very characteristic phase profiles, consisting of one or more regions with constant phase and a
, for example, requires polarization changes across the transversal coordinate (cf. Figure 10.15). Furthermore, LP “modes” have very characteristic phase profiles, consisting of one or more regions with constant phase and a  -phase jump between these regions. This suggests a simple way to generate LP “modes” by using binary phase plates, whereby the phase plates, introduced in the optical path between the feeding single-mode fiber and the FMF, match the phase profile of the target LP “mode” [124]. Such an MMUX design is shown in Figure 10.16 for a FMF that supports six spatial and polarization modes, equivalent to the first two LP “modes,”
-phase jump between these regions. This suggests a simple way to generate LP “modes” by using binary phase plates, whereby the phase plates, introduced in the optical path between the feeding single-mode fiber and the FMF, match the phase profile of the target LP “mode” [124]. Such an MMUX design is shown in Figure 10.16 for a FMF that supports six spatial and polarization modes, equivalent to the first two LP “modes,” 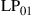 and
and 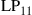 .
.
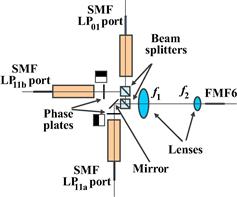
Figure 10.16 Phase-plate based mode multiplexer for a few-mode fiber that supports six spatial and polarization modes.
The strategy of phase-only mode shaping works well for fibers with six spatial and polarization modes (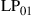 and
and 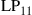 ). For fibers supporting 12 spatial and polarization modes (
). For fibers supporting 12 spatial and polarization modes ( , and
, and 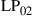 ), the method introduces a crosstalk of 12 dB between the
), the method introduces a crosstalk of 12 dB between the 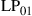 and the
and the  mode. This crosstalk dominates even when more modes are added. It can be reduced if in addition to binary phase plates the intensity profile is shaped as well, for example by using appropriate amplitude plates.
mode. This crosstalk dominates even when more modes are added. It can be reduced if in addition to binary phase plates the intensity profile is shaped as well, for example by using appropriate amplitude plates.
Since each phase plate shapes only a single spatial mode of the fiber, multiple phase plates are required to construct an MMUX. After phase shaping, the generated mode profiles are combined using beam combiners, which introduce significant loss since their second output ports remain unused. The loss scales proportional with the number of spatial modes. The same scaling law applies in general to all single-stage thin hologram-based couplers [125]. For six spatial modes, the combiner loss would amount to about 10 dB, which limits the practical use of phase-plate based MMUXs to a fairly small number of spatial modes.
Regarding the performance characteristics of the MMUX shown in Figure 10.16, we first note that it consists of 3 independent paths containing different phase plates. No phase plate is required for the 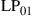 mode of the FMF, since it matches the
mode of the FMF, since it matches the 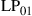 mode of the feeding single-mode fiber (SMF) up to a magnification factor
mode of the feeding single-mode fiber (SMF) up to a magnification factor 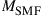 , defined as the magnification between the SMF and FMF end facets. For the
, defined as the magnification between the SMF and FMF end facets. For the 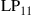 “mode,” the phase plate consists of two half planes with a constant phase difference of
“mode,” the phase plate consists of two half planes with a constant phase difference of 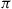 . Rotating the phase plate by 90° produces the second
. Rotating the phase plate by 90° produces the second  “mode” (cf. Figure 10.15). The spatial Fourier transform of the LP “modes” has the interesting property of being self-similar [126], i.e. the field’s phase structure is maintained by focusing/collimating the beam while the intensity profile retains similar characteristics (a spot stays a spot; a ring stays a ring but with changed geometric proportions). Hence, the mode-selecting phase plates can be placed either in the Fourier plane of the related FMF end facet or in the plane of the fiber end facet.
“mode” (cf. Figure 10.15). The spatial Fourier transform of the LP “modes” has the interesting property of being self-similar [126], i.e. the field’s phase structure is maintained by focusing/collimating the beam while the intensity profile retains similar characteristics (a spot stays a spot; a ring stays a ring but with changed geometric proportions). Hence, the mode-selecting phase plates can be placed either in the Fourier plane of the related FMF end facet or in the plane of the fiber end facet.
In order to calculate the elements of the MMUX transfer matrix 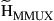 and extract its mode-average insertion loss and MDL, we first evaluate the overlap integrals
and extract its mode-average insertion loss and MDL, we first evaluate the overlap integrals 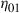 and
and 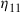 between the
between the 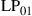 mode of a feeding standard SMF and the
mode of a feeding standard SMF and the 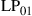 as well as the
as well as the 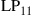 “modes” of a step index FMF with normalized frequency
“modes” of a step index FMF with normalized frequency 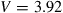 and core diameter d = 17 μm according to Eq. (10.7). These are shown as a function of the magnification factor
and core diameter d = 17 μm according to Eq. (10.7). These are shown as a function of the magnification factor 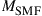 in Figure 10.17 for an MMUX arrangement where the phase plates are placed in the imaging plane. The quantities
in Figure 10.17 for an MMUX arrangement where the phase plates are placed in the imaging plane. The quantities  and
and 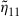 denote the case where the phase plates are located in the Fourier plane of the FMF. The coupling efficiency for coupling into the
denote the case where the phase plates are located in the Fourier plane of the FMF. The coupling efficiency for coupling into the 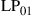 mode is essentially the same for both coupling geometries and shows a maximum coupling very close to 0 dB for a magnification of 1.7. The maximum coupling efficiencies when coupling into the
mode is essentially the same for both coupling geometries and shows a maximum coupling very close to 0 dB for a magnification of 1.7. The maximum coupling efficiencies when coupling into the  mode are –1 dB and –1.1 dB for the phase plates located in the Fourier plane and image plane, respectively, albeit at different magnification factors. The arrangement with phase plates located in the Fourier plane has a slightly lower loss, but the image plane arrangement offers the advantage of being more tolerant toward errors in the magnification factor. By choosing the optimum beam combining ratio, which corrects for the difference in mode conversion loss due to the additional coupling loss for the
mode are –1 dB and –1.1 dB for the phase plates located in the Fourier plane and image plane, respectively, albeit at different magnification factors. The arrangement with phase plates located in the Fourier plane has a slightly lower loss, but the image plane arrangement offers the advantage of being more tolerant toward errors in the magnification factor. By choosing the optimum beam combining ratio, which corrects for the difference in mode conversion loss due to the additional coupling loss for the 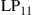 “mode” by phase-only mode shaping, a theoretical minimal loss of 5.5 dB can be obtained. Although smaller losses are desirable, the loss is acceptable considering the simplicity of the optical arrangement.
“mode” by phase-only mode shaping, a theoretical minimal loss of 5.5 dB can be obtained. Although smaller losses are desirable, the loss is acceptable considering the simplicity of the optical arrangement.
In an experimental implementation [111], three identical collimators with a nominal beam diameter of 500 μm were imaged onto the end facet of a FMF by means of two lenses, the first with a focal length of 75 mm and the second, an aspheric lens, with a focal length of 3.9 mm placed in front of the FMF. This resulted in a magnification factor of 2.6. The phase plates were made of 0.5 -mm thick Borosilicate glass, and a photolithographic process was used to create the phase pattern, which was subsequently time etched into the glass, in order to achieve a 1.7 -μm thickness difference. The three beams were combined using two splitters with a non-ideal splitting ratio of 37/63. A coupling loss of 8.3 dB, 10.6 dB, and 9.0 dB was measured for the 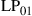 and the two
and the two  modes, respectively. Typically, large mode selectivity of
modes, respectively. Typically, large mode selectivity of 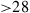 dB can be observed for an MMUX pair connected by a short (few meters long) FMF, which can be exploited not just for SDM transmission, but also as a characterization tool for SDM components.
dB can be observed for an MMUX pair connected by a short (few meters long) FMF, which can be exploited not just for SDM transmission, but also as a characterization tool for SDM components.
10.4.3.2 Spot-based mode multiplexer
A second strategy to build mode multiplexers is based on the spatial sampling of the amplitude, phase, and polarization in different transverse locations on the end facet of a FMF. Ideally, the sampling spots excite orthogonal combinations of propagating fiber modes, described by a unitary mode coupling matrix. The optimum positions of the sampling spots (the “spot configuration”) depend on the symmetry of the fiber modes. As discussed in Section 10.4.1, configurations that provide small MDL are of particular interest.
The intensity distributions of the true waveguide modes in a FMF all show radial symmetry (cf. Figure 10.15), if the appropriate linear combination is chosen for the degenerate modes, and will therefore appear as one or more “rings,” which strongly suggests that the spots of the mode couplers should also be arranged on one or more circles. Also, the numbers of spots to be placed on each circle are preferably chosen according to the symmetry of the modes of the FMF [127].
Figure 10.18 shows practical arrangements for the first few LP modes of a FMF. The spot arrangements are constructed based on circles, were each circle corresponds to a particular radial mode number v of the FMF, starting with the most external circle corresponding to 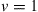 . The spots are then added and distributed on the corresponding circle according to their radial number; a single spot is added for the nondegenerate LP modes, and two spots are added for each twofold degenerate mode, respectively. In the case where there is only one mode with a certain radial mode number, the ring will collapse into a spot. Following this rule, we obtain patterns that fill the fiber cross-section homogeneously. The patterns are not unique, in particular it is possible, for example, to rotate the spots on one ring with respect to a second ring. Note that the obtained patterns differ from the more common hexagonal pattern which is the arrangement with largest packing density.
. The spots are then added and distributed on the corresponding circle according to their radial number; a single spot is added for the nondegenerate LP modes, and two spots are added for each twofold degenerate mode, respectively. In the case where there is only one mode with a certain radial mode number, the ring will collapse into a spot. Following this rule, we obtain patterns that fill the fiber cross-section homogeneously. The patterns are not unique, in particular it is possible, for example, to rotate the spots on one ring with respect to a second ring. Note that the obtained patterns differ from the more common hexagonal pattern which is the arrangement with largest packing density.
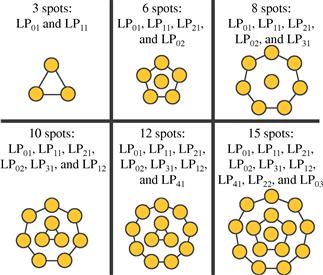
Figure 10.18 Example of different spot arrangements to couple into the modes of a FMF in the sequence they appear by increasing the normalized frequency of the FMF.
In the following we will analyze in detail the three-spot arrangement for a fiber supporting six spatial and polarization modes. The spot configuration consists of a single ring, and the 3 spots are arranged as an equilateral triangle centered with respect to the fiber core. Figure 10.19a shows graphically how the spots are related to the LP “modes” of the fiber.
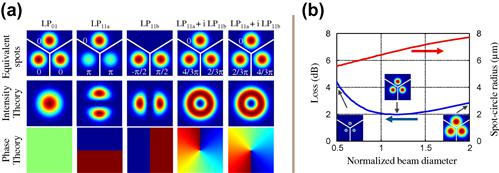
Figure 10.19 (a) Relation between  and
and  modes and 3-spot configurations. The first row shows the spot intensities in false-colors; the spot phases are indicated by labels next to the spots. The intensity and phase profiles of the targeted LP pseudo modes are shown in false-color in rows 2 and 3, respectively. (b) Insertion loss and radius of the circle where the spots are located, as a function of the beam diameter normalized to a standard SMF mode-field diameter. (For interpretation of the color in this figure, the reader is referred to the web version of this book.)
modes and 3-spot configurations. The first row shows the spot intensities in false-colors; the spot phases are indicated by labels next to the spots. The intensity and phase profiles of the targeted LP pseudo modes are shown in false-color in rows 2 and 3, respectively. (b) Insertion loss and radius of the circle where the spots are located, as a function of the beam diameter normalized to a standard SMF mode-field diameter. (For interpretation of the color in this figure, the reader is referred to the web version of this book.)
Further, in the following calculations, the spots are not allowed to spatially overlap, but are clipped into regions corresponding to 120° angular sectors, demarcated by lines in Figure 10.19a. The truncation effect becomes relevant when the width of the spots becomes comparable to the distance between the spots, at which point the clipped light will dominate the MMUX insertion loss. Experimentally this is equivalent, e.g., to the case where the spots are created by combining collimated beams using a reflector with a shape of a pyramid with a triangular base. Alternatively the spots can be brought close together by using clipping mirrors [128] or planar waveguide circuits (PLCs) [129].
Making use of the form for the degenerate 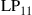 “modes” that has radial symmetry in intensity (
“modes” that has radial symmetry in intensity ( , see also column 4 and 5 of Figure 10.19a), the coupling matrix of the 3-spot coupler that describes the transformation from the 3 individual spots into the fiber modes
, see also column 4 and 5 of Figure 10.19a), the coupling matrix of the 3-spot coupler that describes the transformation from the 3 individual spots into the fiber modes 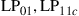 , and
, and 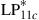 can be written as
can be written as
 (10.35)
(10.35)
and the matrix elements can then be determined by evaluating only two overlap integrals to determine  and
and 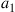 , which correspond to the overlap integral between a single spot and the
, which correspond to the overlap integral between a single spot and the 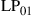 and
and 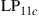 mode, respectively. It can be shown that Eq. (10.35) is unitary up to a constant loss factor, and therefore MDL = 0, if the condition
mode, respectively. It can be shown that Eq. (10.35) is unitary up to a constant loss factor, and therefore MDL = 0, if the condition  is fulfilled. In practice
is fulfilled. In practice  can always be achieved by varying the radius of the circle on which the spots are located. In fact if the radius is made small, more light is coupled into the
can always be achieved by varying the radius of the circle on which the spots are located. In fact if the radius is made small, more light is coupled into the 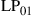 mode and
mode and 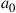 will become dominant, whereas a larger radius will couple more light into the
will become dominant, whereas a larger radius will couple more light into the  mode, and
mode, and 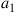 will become larger than
will become larger than 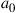 . The theoretical insertion loss for a 3-spot coupler with MDL = 0 is reported in Figure 10.19b as a function of the spot width normalized to the mode size of a SMF. The calculation reported in Figure 10.20b predicts that insertion losses
. The theoretical insertion loss for a 3-spot coupler with MDL = 0 is reported in Figure 10.19b as a function of the spot width normalized to the mode size of a SMF. The calculation reported in Figure 10.20b predicts that insertion losses  are possible, and low-loss 3-spot couplers with MDL = 0 can be realized with a wide range of spot fill-factors, as long as the overall magnification between the fiber modes and the spot pattern is chosen correctly. In practice, insertion losses as low as 4 dB have been reported in [128] using discrete collimators and clipping mirrors, cf. arrangement in Figure 10.20b.
are possible, and low-loss 3-spot couplers with MDL = 0 can be realized with a wide range of spot fill-factors, as long as the overall magnification between the fiber modes and the spot pattern is chosen correctly. In practice, insertion losses as low as 4 dB have been reported in [128] using discrete collimators and clipping mirrors, cf. arrangement in Figure 10.20b.
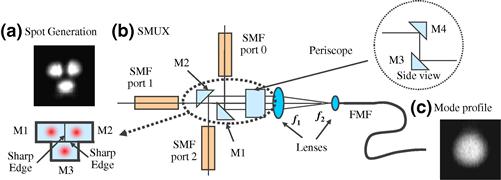
Figure 10.20 (a) Functional arrangement of the mirrors  , and
, and  used to generate 3 spots. (b) Setup for 3-spot coupler. (c) Intensity profile at the end facet of the transmission fiber when 3 spots are launched.
used to generate 3 spots. (b) Setup for 3-spot coupler. (c) Intensity profile at the end facet of the transmission fiber when 3 spots are launched.
For larger numbers of spots, the MDL for the optimum spot arrangement is in general not zero [118]. It also becomes more difficult to implement the coupler using discrete collimators, and integrated technologies like photonic lanterns [119] or PLCs [129] are preferable. The two approaches are shown in Figure 10.21a and b, respectively. The photonic lantern offers the advantage of completely eliminating the MDL by adapting the spot profile to the mode-profile of the FMF by using an adiabatically tapered waveguide structure.
10.4.4 Mode couplers for multi-core fibers
In uncoupled multi-core and coupled-core multi-core fibers, the intensity distributions of the individual core modes are typically well separated, and coupling to the individual cores can be performed using a coupler arrangement based on individual collimators [130], as presented in Figure 10.20, for example, by using integrated optical couplers [34] or tapered couplers [29]. For strongly coupled-core arrangements showing considerable differences between the intensity profile of entire multi-core waveguide structure (the super-modes) as compared to the superposition of the individual core modes, the fiber starts behaving more like a few-mode fiber and similar coupling strategies as presented in Section 10.4.3.2 can be applied, and the super-modes can be directly excited.
10.5 Optical Amplifiers for Coupled-Mode Transmission
As discussed in Section 10.1.2, in order for SDM to be economic and energy efficient, integrated few-mode and multi-core optical amplifiers are a key requirement [35]. In particular, sharing pump power between SDM channels and reducing the number of optical components compared to M parallel single-mode amplifiers is key to reduce system cost and energy consumption. This is in analogy to optical amplification in WDM systems, where the optical pump power as well as the amplifier hardware is shared among all WDM channels.
10.5.1 Optical amplifiers for few-mode fibers
Few-mode fibers offer a significant advantage for optical amplification because of the strong intensity overlap between the modes, which allows to share the pump power across multiple fiber modes in a very effective way. Optical amplification in FMFs has been shown based on the Raman effect in passive FMFs as well as on rare earth doped FMFs. In general, Raman-based few-mode amplification is easier to understand, because it is solely described by pump and signal intensity distributions and does not require taking into account any doping profiles. Hence, algebraic solutions can be derived for practically relevant system configurations. Doped few-mode fiber amplifiers, on the other hand, require complex numerical simulations to arrive at quantitative results.
10.5.1.1 Raman amplification in few-mode fibers
Distributed Raman amplification does not require doped fibers, but utilizes the transmission fiber as an amplifying medium [131]. The Raman process requires in general higher pump powers than needed for doped amplifiers, and the optimal pump wavelength is around 1455 nm for maximum amplification at a signal wavelength of 1550 nm. In few-mode fiber, the pump power can be coupled into different fiber modes just like the transmitted signal, and the net gain experienced by each signal is determined by
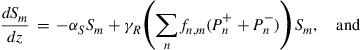 (10.36)
(10.36)
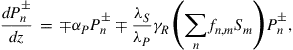 (10.37)
(10.37)
where 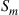 is the signal power present in mode m at position z along the fiber,
is the signal power present in mode m at position z along the fiber,  is the power at the pump wavelength in mode n,
is the power at the pump wavelength in mode n, 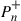 and
and 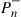 denote co-propagating and counter-propagating pumps, respectively,
denote co-propagating and counter-propagating pumps, respectively, 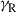 is the Raman gain coefficient, related to the cross-section of spontaneous Raman scattering, and
is the Raman gain coefficient, related to the cross-section of spontaneous Raman scattering, and 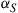 and
and 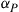 are the absorption coefficients at wavelengths
are the absorption coefficients at wavelengths 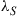 and
and 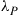 , respectively. The intensity overlap integrals are defined as
, respectively. The intensity overlap integrals are defined as
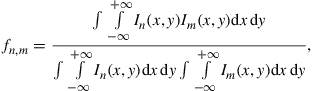 (10.38)
(10.38)
where we assume that the wavelength dependence of the mode profile 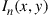 is negligible. Example calculations for intensity overlap integrals are given in Table 10.1.
is negligible. Example calculations for intensity overlap integrals are given in Table 10.1.
Table 10.1
Intensity overlap integrals 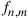 (in
(in  ) for a FMF supporting 12 spatial- and polarization-modes.
) for a FMF supporting 12 spatial- and polarization-modes.
Equations (10.36) and (10.37) can be solved analytically in the undepleted pump approximation [131]. The solution is given by
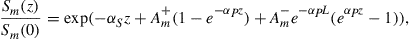 (10.39)
(10.39)
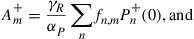 (10.40)
(10.40)
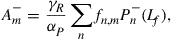 (10.41)
(10.41)
where Lf is the length of the fiber, and the coefficients 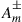 describe the exponential mode-dependent gain (MDG).
describe the exponential mode-dependent gain (MDG).
Low MDG can be obtained by optimizing the pump power distribution across the fiber modes. In order to correctly predict the amplification produced by the pump power in a particular mode, it is important to base the calculation on the true waveguide modes of the fiber, e.g. on  ,
, 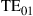 ,
, 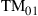 , and
, and  instead of the LP pseudo-modes whenever there is LP degeneracy (cf. Figure 10.15). For example, coupling into the
instead of the LP pseudo-modes whenever there is LP degeneracy (cf. Figure 10.15). For example, coupling into the 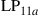 mode with an unpolarized pump laser will equally excite all true waveguide modes forming both
mode with an unpolarized pump laser will equally excite all true waveguide modes forming both 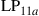 and
and 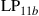 “modes.” Since Raman amplification takes place over fiber lengths considerably exceeding the beat length
“modes.” Since Raman amplification takes place over fiber lengths considerably exceeding the beat length  between the true waveguide modes, the spatial pump pattern within the fiber will change multiple times to provide homogeneous gain for all waveguide modes forming the
between the true waveguide modes, the spatial pump pattern within the fiber will change multiple times to provide homogeneous gain for all waveguide modes forming the 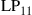 mode. This is especially true for backward pumping. The gain between
mode. This is especially true for backward pumping. The gain between 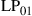 and
and 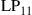 signals can then be equalized by adjusting the relative pump power between
signals can then be equalized by adjusting the relative pump power between  and
and 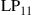 “modes” at the pump wavelength. The exact power ratio can be calculated by evaluating the intensity overlap integrals defined in Eq. (10.38), which are summarized for a weakly guiding step-index FMF with
“modes” at the pump wavelength. The exact power ratio can be calculated by evaluating the intensity overlap integrals defined in Eq. (10.38), which are summarized for a weakly guiding step-index FMF with 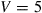 in Table 10.1.
in Table 10.1.
The MDG can then be minimized by varying the pump power configurations 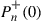 and
and 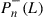 and finding the minimum value for the error function
and finding the minimum value for the error function 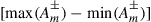 , evaluated over all modes m of interest. In order to minimize the MDG along the whole fiber, the configurations for forward and backward amplification have to be optimized individually. However, the resulting optimum configuration will be the same for both directions.
, evaluated over all modes m of interest. In order to minimize the MDG along the whole fiber, the configurations for forward and backward amplification have to be optimized individually. However, the resulting optimum configuration will be the same for both directions.
For a FMF supporting six spatial and polarization modes (i.e. 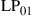 and
and 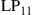 ), the optimal pump power configuration with perfectly equalized gain is obtained when
), the optimal pump power configuration with perfectly equalized gain is obtained when 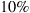 of the pump power is coupled into
of the pump power is coupled into 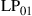 and
and 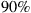 into one of the
into one of the 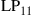 “modes;” this is close to the experimental condition explored in [63], where equalized gain in a depressed cladding FMF was observed by coupling
“modes;” this is close to the experimental condition explored in [63], where equalized gain in a depressed cladding FMF was observed by coupling 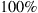 into one of the two degenerate
into one of the two degenerate  “modes.” For a FMF supporting 12 spatial and polarization modes (i.e.
“modes.” For a FMF supporting 12 spatial and polarization modes (i.e. 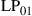 ,
, 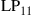 ,
, 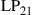 , and
, and 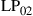 ), the residual MDG can be reduced to 0.13 dB for each 10 dB of Raman gain when
), the residual MDG can be reduced to 0.13 dB for each 10 dB of Raman gain when 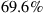 of pump power is launched into
of pump power is launched into 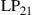 and
and 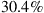 into
into 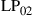 . Note that no power is launched into
. Note that no power is launched into 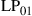 and
and  in this case.
in this case.
Because of the strong intensity overlap between the modes, the pump power is effectively shared between the signal modes, which results in a significant advantage in power efficiency [35]. In order to quantify this advantage, we compare the total pump power required to amplify  SMFs with the same effective area as the
SMFs with the same effective area as the 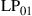 mode of a FMF, where M is the number of spatial and polarization modes used in the FMF. The equivalent multiple SMF system requires 2.1 and 3.2 times the total Raman pump power of the FMF system for
mode of a FMF, where M is the number of spatial and polarization modes used in the FMF. The equivalent multiple SMF system requires 2.1 and 3.2 times the total Raman pump power of the FMF system for  and
and 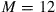 , respectively. This represents a considerable power advantage (which will, however, be reduced with pump depletion).
, respectively. This represents a considerable power advantage (which will, however, be reduced with pump depletion).
Based on this method, low MDG has been demonstrated using Raman amplification in six spatial- and polarization-mode fibers, with gains of up to 10 dB [63]. The experimental results for gain and equivalent noise figure are summarized in Figure 10.22.
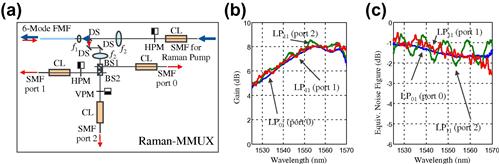
Figure 10.22 (a) Experimental arrangement of a phase-plate based mode multiplexer with backward Raman pump coupler. (b) On–off gain of the Raman amplification. (c) Equivalent noise figure at the FMF end [63].
10.5.1.2 Optical amplification in doped few-mode fiber
Optical amplification in Erbium-doped multimode fibers has been reported in 1991 by Nykolak et al. [132], but a strong mode-dependent gain (MDG) was observed. Minimizing the MDG for in-line amplification is essential to guarantee consistent performance. In contrast to Raman amplification, where the MDG only depends on the intensity overlap integrals, two additional drivers for the MDG are present in doped fibers, namely the transversal doping profile and the nonlinear nature of the optical active inversion in the amplifier. The latter depends on both the pump power and on the modal power content of the signal to be amplified. Detailed studies on MDG in Erbium-doped FMF have been presented in [133,134] (see Figure 10.23[62]).
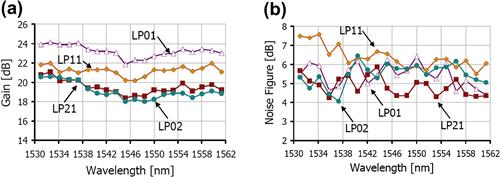
Figure 10.23 (a) Gain and (b) noise figure as a function of wavelength for a few-mode fiber supporting 12 spatial and polarization modes [62].
In order to reduce the MDG in doped fibers, two main strategies have been adopted: The first approach optimizes the pump power distribution across the fiber modes [133], similar to the case of Raman amplification. The second approach is based on optimizing the doping profile [134–136]. The MDG in 6 and 12 spatial- and polarization-mode fibers has recently been brought under control and reduced to  variation across the C-band, by using ring shaped doping profiles, which reduces the gain of the otherwise dominant
variation across the C-band, by using ring shaped doping profiles, which reduces the gain of the otherwise dominant  mode [62,135]. Figure 10.23 shows the experimental result presented in [62] for a 12 spatial- and polarization-mode fiber, where a combination of a ring- and a step-based doping profile is used to equalize the MDG.
mode [62,135]. Figure 10.23 shows the experimental result presented in [62] for a 12 spatial- and polarization-mode fiber, where a combination of a ring- and a step-based doping profile is used to equalize the MDG.
10.5.2 Optical amplifier for multi-core fibers
In uncoupled-core and coupled-core multi-core fibers, optical amplifiers are straight forward to implement by using Raman amplification or multi-core rare earth-doped fibers [137,138]. Investigations have so far focused on integration, size reduction, pumping strategies like cladding pumping [137], and pump distribution schemes [138–140].
10.6 Systems Experiments
Transmission experiments using mode division multiplexing in multi-mode fibers were first conducted in 1982 by Berdague and Facq [50], but due to the large number of modes supported by their fiber and without access to coherent detection and MIMO techniques, experimental results were inherently limited in bit rate and transmission distance. MIMO was first experimentally introduced to optical fiber transmission in 2000 by Stuart [51] to exploit spatial diversity in multi-mode fiber in combination with direct detection. This was followed by numerous studies and experiments to increase the performance of local-area multi-mode fibers through mode group multiplexing [53–56]. Coherent MIMO techniques have also been proposed [141], however the lack of a selective access to all modes of the fiber limited the practicality of this method. The use of few-mode fiber [112,142,143], together with the selective excitation and detection of all fiber modes followed by full coherent MIMO signal processing, was first proposed and experimentally demonstrated by the authors [48,144]. This approach was shown to essentially reach a per-mode transmission performance comparable to that of single-mode fiber. Several impressive MIMO-SDM transmission systems of this kind have since been demonstrated [59,61,63,105a,111].
10.6.1 Single-span MIMO-SDM transmission over few-mode fiber
The first experimental demonstration of  MIMO transmission over few-mode fiber was presented in [144]. The initial single-span transmission distance of 10 km was subsequently increased to 33 and 96 km by improving the coupler alignment [100,111]. The experimental setup is shown in Figure 10.24.
MIMO transmission over few-mode fiber was presented in [144]. The initial single-span transmission distance of 10 km was subsequently increased to 33 and 96 km by improving the coupler alignment [100,111]. The experimental setup is shown in Figure 10.24.
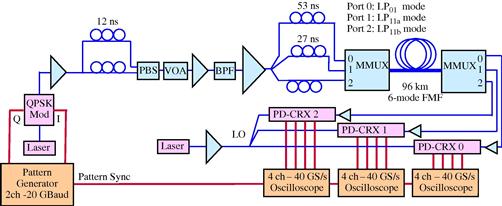
Figure 10.24 Experimental setup of [144]. QPSK-Mod: QPSK Modulator, PBS: Polarization beam splitter, VOA: Variable optical attenuator, BPF: Bandpass filter, LO: Local oscillator, PD-CRX: Polarization-diversity coherent receiver.
The system was based on the phase-plate based MMUXs described in Section 10.4.3.1 and used 10 km of low-DGD depressed cladding few-mode fiber (DC-FMF). The fiber was designed to cut off the  and to minimize the DGD between the
and to minimize the DGD between the 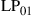 and
and  “modes,” resulting in a DGD
“modes,” resulting in a DGD  ns for a 96-km long fiber over a wavelength range of 1530–1565 nm. In comparison, the DGD of a step-index (SI) profile FMF with similar parameters is more than two orders of magnitude larger. The fiber loss was 0.205 dB/km at 1550 nm for all modes, and the effective areas were 155 and 159 μm2 for the
ns for a 96-km long fiber over a wavelength range of 1530–1565 nm. In comparison, the DGD of a step-index (SI) profile FMF with similar parameters is more than two orders of magnitude larger. The fiber loss was 0.205 dB/km at 1550 nm for all modes, and the effective areas were 155 and 159 μm2 for the 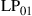 and
and 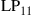 “modes”, respectively. The chromatic dispersion was 18 ps/(nm km) for both
“modes”, respectively. The chromatic dispersion was 18 ps/(nm km) for both 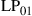 and
and  “modes”.
“modes”.
The transmission performance of this FMF was evaluated by launching three delay-decorrelated PDM-QPSK signals at 20 GBaud, into the three ports of the MMUX. This resulted in a spatial superchannel with a single-wavelength aggregate bit rate of 240 Gb/s. On the receiving end, the FMF was terminated by another MMUX acting as a mode demultiplexer, whose outputs were fed into three polarization-diversity coherent receivers (CRXs), followed by digitization at 40 GS/s using 12 ports of a synchronized high-speed digital oscilloscope system. The off-line DSP algorithms subsequently equalized the 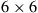 MIMO channel matrix as described in Section 10.3 to recover the 6 independent data streams. Measurements performed on a 96-km span of the same FMF showed a penalty between measurement and theory of
MIMO channel matrix as described in Section 10.3 to recover the 6 independent data streams. Measurements performed on a 96-km span of the same FMF showed a penalty between measurement and theory of 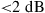 at a BER of
at a BER of 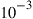 when using 120-tap filters for the MIMO-DSP. This excellent performance shows that mode coupling in 96 km of this FMF can be almost completely compensated with low impact on system performance.
when using 120-tap filters for the MIMO-DSP. This excellent performance shows that mode coupling in 96 km of this FMF can be almost completely compensated with low impact on system performance.
In order to better understand the coupling between the fiber modes, it is instructive to examine the 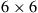 matrix of impulse responses of the MIMO channel using the channel estimation techniques presented in Section 10.3.
matrix of impulse responses of the MIMO channel using the channel estimation techniques presented in Section 10.3.
Figure 10.25 shows the squared magnitudes of the estimated 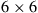 impulse responses as a two-dimensional array corresponding to each combination of input and output of the
impulse responses as a two-dimensional array corresponding to each combination of input and output of the  MIMO channel. In this representation, the columns correspond to the ports of the transmit-side MMUX, and the rows correspond to the ports of the receive-side MMUX, respectively. In order to show the impulse responses only due to mode coupling, the mode-average chromatic dispersion of
MIMO channel. In this representation, the columns correspond to the ports of the transmit-side MMUX, and the rows correspond to the ports of the receive-side MMUX, respectively. In order to show the impulse responses only due to mode coupling, the mode-average chromatic dispersion of 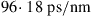 as well as the carrier frequency offset were electronically compensated prior to estimating the impulse response matrix. This results in sharp peaks that clearly identify the main mode coupling locations.
as well as the carrier frequency offset were electronically compensated prior to estimating the impulse response matrix. This results in sharp peaks that clearly identify the main mode coupling locations.
Figure 10.25 can be divided into four regions designated A, B, C, and D: Region A is the 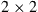 array located in the top left corner that shows the coupling between the two polarizations of the fundamental mode (
array located in the top left corner that shows the coupling between the two polarizations of the fundamental mode (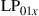 and
and 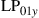 ), as also observed in a single-mode fiber. Region B is formed by the
), as also observed in a single-mode fiber. Region B is formed by the 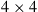 array on the bottom right corner that shows the coupling between the degenerate LP “modes”
array on the bottom right corner that shows the coupling between the degenerate LP “modes”  ,
, 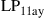 ,
, 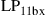 , and
, and 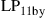 . The two remaining off-diagonal regions C and D describe the crosstalk between
. The two remaining off-diagonal regions C and D describe the crosstalk between 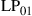 and
and 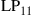 “modes.” We observe sharp and strong coupling peaks within regions A and B, and typically 100 to 1000 times weaker, 2.6-ns wide distributed coupling in regions C and D. The width of the distributed coupling in regions C and D corresponds to the DGD of 96 km of this FMF and represents distributed coupling at various locations along the fiber. If the light travels mostly in the
“modes.” We observe sharp and strong coupling peaks within regions A and B, and typically 100 to 1000 times weaker, 2.6-ns wide distributed coupling in regions C and D. The width of the distributed coupling in regions C and D corresponds to the DGD of 96 km of this FMF and represents distributed coupling at various locations along the fiber. If the light travels mostly in the 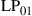 “mode”, it arrives earlier, whereas it arrives delayed by the DGD if it travels mostly in the slower
“mode”, it arrives earlier, whereas it arrives delayed by the DGD if it travels mostly in the slower 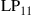 “mode”. Also, regions A and B show weaker distributed coupling next to the strong coupling peaks. This weaker distributed coupling is caused by light that couples back and forth between
“mode”. Also, regions A and B show weaker distributed coupling next to the strong coupling peaks. This weaker distributed coupling is caused by light that couples back and forth between 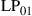 and
and 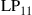 . For
. For 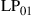 “modes” (region A) the distributed coupling, whose width is also consistent with the DGD of 96 km of FMF, is located on the right of the main pulse, whereas it is located on the left of the main pulse for the
“modes” (region A) the distributed coupling, whose width is also consistent with the DGD of 96 km of FMF, is located on the right of the main pulse, whereas it is located on the left of the main pulse for the  “modes” (region B). Finally, Figure 10.25 also confirms the excellent alignment of the MMUX: Any misalignment in the coupler would create a narrow crosstalk peak either at the beginning or at the end of the distributed coupling in regions C and D. The channel estimation gives a very clear picture of the crosstalk introduced by the MMUX and the propagation through the FMF and allows for a better understanding of the observed performance of the MIMO DSP.
“modes” (region B). Finally, Figure 10.25 also confirms the excellent alignment of the MMUX: Any misalignment in the coupler would create a narrow crosstalk peak either at the beginning or at the end of the distributed coupling in regions C and D. The channel estimation gives a very clear picture of the crosstalk introduced by the MMUX and the propagation through the FMF and allows for a better understanding of the observed performance of the MIMO DSP.
Modal crosstalk can also be directly observed by imaging the end facet of the FMF to an InGaAs camera. The results are shown in Figure 10.26a and b for a fiber length of 96 and 33 km, respectively. The intensity profiles after 33-km FMF are in good agreement with the corresponding theoretical intensity profiles reported in Figure 10.26c, whereas after 96 km the images become “blurry” and coupling between the modes becomes evident. Crosstalk measurements at the MMUX for this kind of FMF of 2-m, 33-km, and 96-km length also confirmed a crosstalk of –18 and –11 dB between  and
and  , for a distance of 33 and 96 km, respectively. The accumulated crosstalk after 96 km is significant, and makes SDM transmission impossible without the use of MIMO-DSP.
, for a distance of 33 and 96 km, respectively. The accumulated crosstalk after 96 km is significant, and makes SDM transmission impossible without the use of MIMO-DSP.
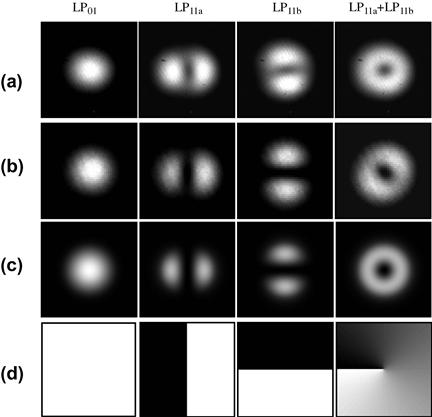
Figure 10.26 Intensity profiles measured after (a) 96 km and (b) 33 km of 6-mode FMF when launching either  or
or 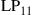 “modes”. (c) Theoretical mode intensity profiles and (d) theoretical phase profile of a 6-mode FMF. (e) Schematic setup of the MMUX.
“modes”. (c) Theoretical mode intensity profiles and (d) theoretical phase profile of a 6-mode FMF. (e) Schematic setup of the MMUX.
Single-span transmission distances have since been considerably increased, up to 209 km in an experiment using backward-pumped distributed Raman amplification [63], by using spot-based couplers [128], and also using a DGD compensated hybrid fiber span [145].
10.6.2 Multi-span MIMO-SDM transmission over few-mode fiber
Within the boundary conditions typical of research environments, FMF transmission beyond a single amplification span is best demonstrated using a re-circulating loop, as shown in Figure 10.27, allowing to emulate tens of amplification spans with the equipment needs of a single span. However, in contrast to single-mode re-circulating loops, a FMF loop requires one set of amplifiers and switches for each supported spatial mode.

Figure 10.27 Experimental setup for MIMO loop transmission experiment. PBS: Polarization beam splitter. Triangles denote EDFAs.
Transmitter and receiver in Figure 10.27 are similar to the setup described in Figure 10.24. The triple re-circulating loop is loaded and closed using three Lithium Niobate switches (LN-SWs). Three Erbium-doped optical amplifiers (EDFAs) and wavelength blockers are used to amplify and gain-equalize the wavelength channels of the individual spatial modes after the MMUX. A critical part of the experimental setup is the exact adjustment of the relative loop lengths to within  (corresponding to
(corresponding to 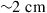 of fiber). In addition, the accumulated DGD in the fiber span, which is the main driver for impulse response broadening, has to be kept small to reduce the number of equalizer taps necessary for the MIMO-DSP. This is achieved by using a DGD compensated span, where multiple GI-FMFs with DGDs of opposite sign are spliced together to form a span with almost no residual DGD.
of fiber). In addition, the accumulated DGD in the fiber span, which is the main driver for impulse response broadening, has to be kept small to reduce the number of equalizer taps necessary for the MIMO-DSP. This is achieved by using a DGD compensated span, where multiple GI-FMFs with DGDs of opposite sign are spliced together to form a span with almost no residual DGD.
The fiber had a loss of 0.24 dB/km, and a dispersion of 18.5 ps/nm/km for both  and
and 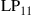 “modes.” The effective areas were 64 μm2 for LP01 and 67 μm2 for LP11 “modes,” respectively. Multiple fiber spools with different lengths were measured with an intensity modulated pulse, as described in [111]. We used two spools with lengths of 25 and 5 km, respectively. One spool was additionally shortened to correct the overall DGD to
“modes.” The effective areas were 64 μm2 for LP01 and 67 μm2 for LP11 “modes,” respectively. Multiple fiber spools with different lengths were measured with an intensity modulated pulse, as described in [111]. We used two spools with lengths of 25 and 5 km, respectively. One spool was additionally shortened to correct the overall DGD to 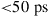 . The segments were then connected using a commercial splicer, where particular care was taken to minimize the crosstalk introduced by splice imperfections. The wavelength dependence of the overall DGD of the composite fiber was
. The segments were then connected using a commercial splicer, where particular care was taken to minimize the crosstalk introduced by splice imperfections. The wavelength dependence of the overall DGD of the composite fiber was  over a wavelength range of 1525–1570 nm, thus providing good performance across the entire C-band.
over a wavelength range of 1525–1570 nm, thus providing good performance across the entire C-band.
Results for  MIMO transmission over the 30-km long span are shown in Figure 10.28 in terms of the Q-factors versus distance for all six spatial modes at different launch powers of –3 dBm, 0 dBm, and 2 dBm per spatial mode. At –3 dBm of launched power, a reach of 1200 km is achieved, assuming a forward-error-correction limit of
MIMO transmission over the 30-km long span are shown in Figure 10.28 in terms of the Q-factors versus distance for all six spatial modes at different launch powers of –3 dBm, 0 dBm, and 2 dBm per spatial mode. At –3 dBm of launched power, a reach of 1200 km is achieved, assuming a forward-error-correction limit of  and an equalizer with 400 taps. For higher launch powers, the transmission distance is limited by the onset of fiber nonlinearity.
and an equalizer with 400 taps. For higher launch powers, the transmission distance is limited by the onset of fiber nonlinearity.

Figure 10.28 Q-factor versus transmission distance for all six modes at three different launch powers per spatial mode [58].
The impulse response of the MIMO channel, shown for various modes and distances in Figure 10.29, shows that DGD compensation is only partially working, because for long transmission distances the crosstalk in the fibers and particularly at the splice points between the individual fiber segments is no more negligible. It can be shown that the major driver for impulse response broadening is the maximal DGD excursion in the span [146], as long as the total accumulated crosstalk is significantly smaller than the power that stays in the mode in which it was originally launched. For even longer distances, the coupling is complete and the impulse response will take on a Gaussian shape whose width is expected to grow with the square root of the distance, as predicted in [92].
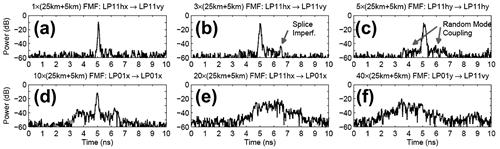
Figure 10.29 Exemplary impulse responses of a phase-plate based transmission experiment using a DGD-compensate few-mode fiber [58].
10.6.3 MIMO-SDM in coupled multi-core fiber
Uncoupled multi-core fibers offer a simple way to implement SDM over an optical fiber [28–46], but the minimum distance between the cores (and hence the spatial information density within the fiber) is limited by crosstalk considerations (cf. Section 10.1.3). If coupling between cores is allowed because MIMO-DSP is being provided, cores can be placed in closer vicinity, allowing for an increased spatial density of the SDM paths within the fiber cross-section. The first demonstration of 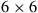 MIMO transmission over 24 km of coupled 3-core fiber (CCF) was reported in [147]. The distance between the cores was 38 μm, which is significantly smaller than what has been demonstrated for uncoupled multi-core fibers. More recently, the distance between the cores of a new 3-core CCF was further reduced to 29.4 μm [148]. The fiber had a length of 60 km, a large effective area of
MIMO transmission over 24 km of coupled 3-core fiber (CCF) was reported in [147]. The distance between the cores was 38 μm, which is significantly smaller than what has been demonstrated for uncoupled multi-core fibers. More recently, the distance between the cores of a new 3-core CCF was further reduced to 29.4 μm [148]. The fiber had a length of 60 km, a large effective area of 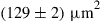 , and an attenuation of 0.181 dB/km for all cores. The coupling between cores was so strong that light launched into a core is almost equally distributed among the cores after 60 km of fiber. The presence of such strong coupling between cores suggests that the modes of the fiber can no longer be considered as simple superpositions of the individual core modes, but the modes of the whole structure, the “supermodes,” have to be considered [149,150].
, and an attenuation of 0.181 dB/km for all cores. The coupling between cores was so strong that light launched into a core is almost equally distributed among the cores after 60 km of fiber. The presence of such strong coupling between cores suggests that the modes of the fiber can no longer be considered as simple superpositions of the individual core modes, but the modes of the whole structure, the “supermodes,” have to be considered [149,150].
A cross-section of the 3-core CCF is shown in Figure 10.30a together with the calculated linearly polarized super-modes (upper row) and their far-fields (bottom row). The modes are named in analogy to the symmetry-equivalent LP modes in a FMF. Including polarization, a total of six independent channels, the same as for the 6-mode FMF, are available.
Figure 10.30 (a) Fiber cross-section of the 3-core CCF. (b) Linearly polarized super-modes (upper row) and corresponding far-fields (bottom row) of the 3-core CCF.
In order to study MIMO transmission over 3-core CCFs, we built a spot-based MMUX consisting of three individual collimators that are projected onto the end facet of the 3-core CCF. This way, low loss 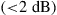 and low crosstalk
and low crosstalk 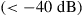 could be obtained. A similar re-circulating loop set up as shown in Figure 10.27 was used for transmission, and the results are reported in Figure 10.31. A maximum transmission distance of 4200 km was obtained for a per-core launch power of –3 dBm at a Q-factor
could be obtained. A similar re-circulating loop set up as shown in Figure 10.27 was used for transmission, and the results are reported in Figure 10.31. A maximum transmission distance of 4200 km was obtained for a per-core launch power of –3 dBm at a Q-factor 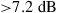 (equal to a BER of 10–2) representing the limit tolerable for state-of-the-art 20% overhead hard-decision FEC. The required number of MIMO-DSP equalizer taps grows as a function of distance, starting with 60 taps after 60 km and growing up to 400 taps at 4200 km. This experiment clearly demonstrates that CCFs represent a promising long-haul transmission technology when MIMO-DSP is being used.
(equal to a BER of 10–2) representing the limit tolerable for state-of-the-art 20% overhead hard-decision FEC. The required number of MIMO-DSP equalizer taps grows as a function of distance, starting with 60 taps after 60 km and growing up to 400 taps at 4200 km. This experiment clearly demonstrates that CCFs represent a promising long-haul transmission technology when MIMO-DSP is being used.
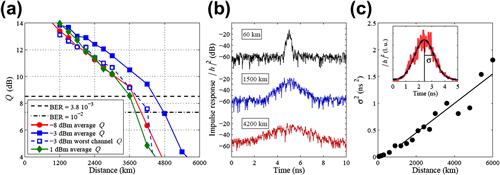
Figure 10.31 (a) Transmission results for  MIMO transmission in 3-core CCF. (b) Impulse response after 60-, 1500-, and 4200-km transmission distance. (c) Variance of the impulse response width as function of distance.
MIMO transmission in 3-core CCF. (b) Impulse response after 60-, 1500-, and 4200-km transmission distance. (c) Variance of the impulse response width as function of distance.
As in the case for a FMF supporting six spatial modes, the impulse responses matrix of the 3-core CCF also consists of a 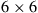 impulse responses (cf. Figure 10.29). However, in contrast to the FMF, where the DGD between the
impulse responses (cf. Figure 10.29). However, in contrast to the FMF, where the DGD between the  and
and  “mode” causes the impulse response of the MIMO channel to exhibit two prominent peaks separated by the DGD, the impulse response of the 3-core CCF after 60-km transmission only shows a single peak with a width of 600 ps. Also, all 36 impulse responses look similar and only one representative impulse response is hence shown in Figure 10.31b, where the squared magnitude of the impulse response h as obtained from LS channel estimation and after digital chromatic dispersion compensation is shown for a selection of transmission distances. Figure 10.31c shows the complete evolution of the variance of the width of
“mode” causes the impulse response of the MIMO channel to exhibit two prominent peaks separated by the DGD, the impulse response of the 3-core CCF after 60-km transmission only shows a single peak with a width of 600 ps. Also, all 36 impulse responses look similar and only one representative impulse response is hence shown in Figure 10.31b, where the squared magnitude of the impulse response h as obtained from LS channel estimation and after digital chromatic dispersion compensation is shown for a selection of transmission distances. Figure 10.31c shows the complete evolution of the variance of the width of  obtained by a Gaussian fit. The linear fit suggests a complete randomization of the time delays between the cores during propagation, as well as a growth of the MDS as a function of the square-root of distance, as predicted for strong coupling in [92].
obtained by a Gaussian fit. The linear fit suggests a complete randomization of the time delays between the cores during propagation, as well as a growth of the MDS as a function of the square-root of distance, as predicted for strong coupling in [92].
10.7 Conclusion
Wavelength-division multiplexing (WDM) has been the workhorse of data networks since the early 1990s, enabling ubiquitous and affordable data services with unabated exponential traffic growth. Today, commercial WDM systems can carry close to 10 Tb/s over a single fiber, and research experiments have reached the 100-Tb/s mark. Over the past few years, however, WDM capacities have approached the nonlinear Shannon limit to within a factor of 2.
In order to further scale network capacities and to avoid a looming “capacity crunch,” space has been identified as the only known physical dimension yet unexploited for optical modulation and multiplexing. Space-division multiplexing (SDM) may use parallel strands of single-mode fiber, uncoupled or coupled cores of multi-core fiber, or individual modes of multi-mode waveguides. In this context, integration at various levels (including optical amplifiers, transponders, networking elements, and transmission fiber CAPEX and OPEX) is essential to continue the reduction in cost and energy consumption per transported information bit that has allowed the Internet to thrive. Integration, however, inherently comes at the expense of crosstalk. If crosstalk rises to levels where it cannot be treated as a transmission impairment any more, multiple-input multiple-output (MIMO) digital signal processing (DSP) techniques have to be used to manage crosstalk in highly integrated SDM systems.
At the beginning of an exciting new era in optical communications, we reviewed fundamentals as well as practical experimental aspects of MIMO-SDM: We discussed the importance of selectively addressing all modes of a coupled-mode SDM channel at transmitter and receiver in order to achieve reliable capacity gains and showed that reasonable levels of mode-dependent loss (MDL) are acceptable without much loss of channel capacity. We then introduced MIMO-DSP techniques as an extension of familiar algorithms used in polarization-division multiplexed (PDM) digital coherent receivers and discussed their functionality and scalability. Finally, we reviewed the design of mode multiplexers (MMUXs) that allow for the mapping of the individual transmission signals onto an orthogonal basis of waveguide modes, and discussed their performance in experimental demonstrations. Although MIMO-SDM has been experimentally proven to be a feasible technique for reliable high-capacity long-haul fiber transmission beyond the nonlinear Shannon limit of single-mode fiber, significant research, development, and standardization efforts have to be invested to enable a smooth upgrade path from today’s single-mode systems to MIMO-SDM based optical communication networks.
References
1. Tkach RW. Scaling optical communications for the next decade and beyond. Bell Labs Tech J. 2010;14(4):3–9.
2. S.K. Korotky, Traffic trends: drivers and measures of cost-effective and energy-efficient technologies and architectures for backbone optical networks, in: Proc. OFC, OM2G.1, 2012.
3. Taubenblatt MA. Optical interconnects for high-performance computing. J Lightwave Technol. 2012;30(4):448–458.
4. Vlasov YA. Silicon CMOS-integrated nano-photonics for computer and data communications beyond 100G. IEEE Commun Mag. 2012;50(2):S67–S72.
5. J. Gray, P. Shenoy, Rules of thumb in data engineering, Microsoft Research Technical Report MS-TR-99-100, 2000.
6. Hennessy JL, Patterson DA. Computer Architectures: A Quantitative Approach. San Francisco, CA: Morgan Kaufmann; 2003.
7. <http://top500.org/lists/2010/06/performance>.
8. Apostolopoulos JG, et al. The road to immersive communication. Proc IEEE. 2012;100(4):974–990.
9. Dou M, et al. Room-sized informal telepresence system. Proc IEEE Virt Real. 2012;15–18.
10. Kogelnik H. On optical communication: Reflections and perspectives. Proc ECOC 2004;Mo1.1.1.
11. Winzer PJ. High-spectral-efficiency optical modulation formats. J Lightwave Technol. 2012;30(24):3824–3835.
12. Alcatel-Lucent 1830 Photonic Service Switch, Brochures and data sheets, <http://www.alcatel-lucent.com>.
13. Raybon G, et al. All-ETDM 80-Gbaud (640-Gb/s) PDM 16-QAM generation and coherent detection. Photon Technol Lett. 2012;24(15):1328–1330.
14. J. Renaudier et al., Spectrally efficient long-haul transmission of 22-Tb/s using 40-Gbaud PDM-16QAM with coherent detection, in: Proc. OFC, OW4C.2, 2012.
15. G. Raybon et al., 1-Tb/s dual-carrier 80-GBaud PDM-16QAM WDM transmission at 5.2 b/s/Hz over 3200 km, in: Proc. IPC, PD1.2, 2012.
16. X. Liu et al., 1.5-Tb/s guard-banded superchannel transmission over 56  100-km (5600-km) ULAF using 30-Gbaud pilot-free OFDM- 16QAM signals with 5.75-b/s/Hz net spectral efficiency, in: Proc. ECOC, Th.3.C.5, 2012.
100-km (5600-km) ULAF using 30-Gbaud pilot-free OFDM- 16QAM signals with 5.75-b/s/Hz net spectral efficiency, in: Proc. ECOC, Th.3.C.5, 2012.
17. Chandrasekhar S, Liu X. OFDM based superchannel transmission technology. J Lightwave Technol. 2012;30(24):3816–3823.
18. D. Qian et al., 101.7-Tb/s (370x294-Gb/s) PDM-128QAM-OFDM transmission over 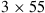 -km SSMF using pilot-based phase noise mitigation, in: Proc. OFC, PDPB5, 2011.
-km SSMF using pilot-based phase noise mitigation, in: Proc. OFC, PDPB5, 2011.
19. A. Sano et al., 102.3-Tb/s (224 × 548-Gb/s) C- and extended L-band all-Raman transmission over 240 km using PDM-64QAM single carrier FDM with digital pilot tone, in: Proc. OFC, PDP5C.3, 2012.
20. Winzer PJ. Beyond 100G Ethernet. IEEE Commun Mag. 2010;48:26–30.
21. Essiambre R-J, et al. Capacity limits of optical fiber networks. J Lightwave Technol. 2010;28(4):662–701.
22. Essiambre R-J, Tkach RW. Capacity trends and limits of optical communication networks. Proc IEEE. 2012;100(5):1035–1055.
23. Winzer PJ. Energy-efficient optical transport capacity scaling through spatial multiplexing. Photon Technol Lett. 2011;23(13):851–853.
24. A.R. Chraplyvy, The coming capacity crunch, ECOC, plenary talk, 2009.
25. Winzer PJ, Essiambre R-J. Advanced optical modulation formats. In: Kaminow I, Li T, Willner A, eds. Optical Fiber Telecommunication V B. NewYork: Academic Press; 2008;23–94. (Chapter 2).
26. T. Morioka, Ultrafast optical technologies for large-capacity TDM/WDM photonic networks, in: IEEE Photonics Society Summer Topical Meetings, 2010, pp. 121–122.
27. IEC Technical Report IEC 61292–4, Optical amplifiers—Part 4: Maximum permissible optical power for the damage-free and safe use of optical amplifiers, including Raman amplifiers, Edition 2.0, 2010.
28. J. Sakaguchi et al., 109-Tb/s ( -Gb/s SDM/WDM/PDM) QPSK transmission through 16.8-km homogeneous multi-core fiber, in: Proc. OFC, PDPB6, 2011.
-Gb/s SDM/WDM/PDM) QPSK transmission through 16.8-km homogeneous multi-core fiber, in: Proc. OFC, PDPB6, 2011.
29. Zhu B, et al. 112-Tb/s Space-division multiplexed DWDM transmission with 14-b/s/Hz aggregate spectral efficiency over a 76.8-km seven-core fiber. Opt Express. 2011;19(17):16665–16671.
30. J. Sakaguchi et al., 19-core fiber transmission of 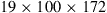 -Gb/s SDM-WDM-PDM-QPSK signals at 305Tb/s, in: Proc. OFC, PDP5C.1, 2012.
-Gb/s SDM-WDM-PDM-QPSK signals at 305Tb/s, in: Proc. OFC, PDP5C.1, 2012.
31. H. Takara et al., 1.01-Pb/s (12 SDM/222 WDM/456 Gb/s) crosstalk-managed transmission with 91.4-b/s/Hz aggregate spectral efficiency, in: Proc. ECOC, Th.3.C.1, 2012.
32. Tucker RS. Green optical communications—part I: Energy limitations in transport. IEEE J Sel Top Quantum Electron. 2011;17(2):245–260.
33. Korotky SK. Price-points for components of multi-core fiber communication systems in backbone optical networks. J Opt Commun Netw. 2012;4(5):425–435.
34. Doerr CR, Taunay TF. Silicon photonics core-, wavelength-, and polarization-diversity receiver. Photon Technol Lett. 2011;23(9):597–599.
35. Krummrich PM. Optical amplification and optical filter based signal processing for cost and energy efficient spatial multiplexing. Opt Express. 2011;19(17):16636–16652.
36. Abedin KS, et al. Amplification and noise properties of an erbium-doped multicore fiber amplifier. Opt Express. 2011;19(17):16715–16721.
37. T. Morioka, New generation optical infrastructure technologies: EXAT initiative towards 2020 and beyond, in: Proc. OECC, FT4, 2009.
38. Kokubun Y, Koshiba M. Novel multi-core fibers for mode division multiplexing: Proposal and design principle. IEICE Electron Expr. 2009;6(8):522–528.
39. Li G, Liu X. Focus issue: Space multiplexed optical transmission. Opt Express. 2011;19(17):16574.
40. Morioka T, et al. Enhancing optical communications with brand new fibers. IEEE Commun Mag. 2012;50:s31.
41. P.J. Winzer et al., Penalties from in-band crosstalk for advanced optical modulation formats, in: Proc. ECOC, Tu.5.B.7, 2011.
42. K. Imamura et al., Trench assisted multi-core fiber with large Aeff over 100 μm2 and low attenuation loss, in: Proc. ECOC, Mo.1.LeCervin.1, 2011.
43. Hayashi T, et al. Design and fabrication of ultra-low crosstalk and low-loss multi-core fiber. Opt Express. 2011;19(17):16576–16592.
44. S. Chandrasekhar et al., WDM/SDM transmission of 10  128-Gb/s PDM-QPSK over 2688-km 7-core fiber with a per-fiber net aggregate spectral-efficiency distance product of 40,320 km b/s/Hz, in: Proc. ECOC, Th.13.C.4, 2011.
128-Gb/s PDM-QPSK over 2688-km 7-core fiber with a per-fiber net aggregate spectral-efficiency distance product of 40,320 km b/s/Hz, in: Proc. ECOC, Th.13.C.4, 2011.
45. A.H. Gnauck et al., WDM transmission of 603-Gb/s superchannels over 845 km of 7-core fiber with 42.2 b/s/Hz spectral efficiency, in: Proc. ECOC, Th.2.C.2, 2012.
46. X. Liu et al., 1.12-Tb/s 32-QAM-OFDM superchannel with 8.6-b/s/Hz intrachannel spectral efficiency and space-division multiplexing with 60-b/s/Hz aggregate spectral efficiency, in: Proc. ECOC, Th.13.B.1, 2011.
47. Foschini GJ. Layered space-time architecture for wireless communication in a fading environment when using multi-element antennas. Bell Labs Tech J. 1996;1:41–59.
48. P.J. Winzer, G.J. Foschini, Outage calculations for spatially multiplexed fiber links, in: Proc. OFC, OThO5, 2011.
49. Winzer PJ, Foschini GJ. MIMO capacities and outage probabilities in spatially multiplexed optical transport systems. Opt Express. 2011;19(17):16680–16696.
50. Berdague S, Facq P. Mode division multiplexing in optical fibers. Appl Opt. 1982;21(11):1950–1955.
51. Stuart HR. Dispersive multiplexing in multimode optical fiber. Science. 2000;289(5477):281–283.
52. Murshid S, et al. Spatial domain multiplexing: a new dimension in fiber optic multiplexing. Opt Laser Technol. 2008;40(8):1030–1036.
53. Tarighat A, et al. Fundamentals and challenges of optical multiple-input-multiple-output multimode fiber links. IEEE Commun Mag. 2007;45(5):57–63.
54. S. Schoellmann et al., Experimental realisation of  MIMO system with mode group diversity multiplexing limited by modal noise, in: Proc. OFC, JWA68, 2008.
MIMO system with mode group diversity multiplexing limited by modal noise, in: Proc. OFC, JWA68, 2008.
55. Nazarathy M, Agmon A. Coherent transmission direct detection MIMO over short-range optical interconnects and passive optical networks. J Lightwave Technol. 2008;26(14):2037–2045.
56. B. Franz et al., High speed OFDM data transmission over 5 km GI-multimode fiber using spatial multiplexing with  MIMO processing, in: Proc. ECOC, Tu.3.C.4, 2010.
MIMO processing, in: Proc. ECOC, Tu.3.C.4, 2010.
57. R. Ryf et al., Space-division multiplexed transmission over 4200 km 3-core microstructured fiber, in: Proc. OFC, PDP5C.2, 2012.
58. S. Randel et al., Mode-multiplexed  -GBd QPSK transmission over 1200-km DGD-compensated few-mode fiber, in: Proc. OFC, PDP5C.5, 2012.
-GBd QPSK transmission over 1200-km DGD-compensated few-mode fiber, in: Proc. OFC, PDP5C.5, 2012.
59. R. Ryf et al.,  MIMO transmission over 130-km few-mode fiber, Proc. Frontiers in Optics, paper FW6C.4, 2012.
MIMO transmission over 130-km few-mode fiber, Proc. Frontiers in Optics, paper FW6C.4, 2012.
60. Y. Yung et al., First demonstration of multimode amplifier for spatial division multiplexed transmission systems, in: Proc. ECOC, Th.13.K.4, 2011.
61. E. Ip et al.,  -Gb/s WDM transmission over 50 km of three-mode fiber with inline few-mode fiber amplifier, in: Proc. ECOC, Th.13.C.2, 2011.
-Gb/s WDM transmission over 50 km of three-mode fiber with inline few-mode fiber amplifier, in: Proc. ECOC, Th.13.C.2, 2011.
62. M. Salsi et al., A six-mode Erbium-doped fiber amplifier, in: Proc. ECOC, Th.3.A.6, 2012.
63. R. Ryf et al., Mode-equalized distributed Raman amplification in 137-km few-mode fiber, in: Proc. ECOC, Th.13.K.5, 2011.
64. Proakis JG, Salehi M. Digital Communications. fifth ed. New York: Mc Graw Hill; 2007.
65. Barry JR, Lee EA, Messerschmitt DG. Digital Communication. third ed. Kluwer Academic Publishers 2004.
66. Tan P, Beaulieu NC. Analysis of the effects of Nyquist pulse-shaping on the performance of OFDM systems with carrier frequency offset. Eur Trans Telecomm. 2009;20:9–22.
67. Kogelnik H. Theory of optical waveguides. In: Fraser N, ed. Guided-Wave Optoelectronics. Springer Verlag 1988.
68. Marcuse D. Light Transmission Optics. Van Nostrand Reinhold Company 1972.
69. Cover TM, Thomas JA. Elements of Information Theory. second ed. New York: John Wiley and Sons; 2006.
70. C. Koebele et al., Nonlinear effects in long-haul transmission over bimodal optical fibre, in: Proc. ECOC, Mo.2.C.6, 2010.
71. Dar R, et al. The underaddressed optical multiple-input, multiple-output channel: capacity and outage. Opt Lett. 2012;37(15):3150–3152.
72. Mezzadri F. How to generate random matrices from the classical compact groups. Notices of the AMS. 2007;54:592–604.
73. Kogelnik H, Nelson LE, Jopson RM. Polarization mode dispersion. In: Kaminow IP, Li T, eds. Optical Fiber Telecommunications IV B. San Diego: Academic Press; 2002;725–861. (Chapter 15).
74. Brodsky M, Frigo NJ, Tur M. Polarization mode dispersion. In: Kaminow IP, Li T, Willner AE, eds. Optical Fiber Telecommunications V A. New York: Academic Press; 2008;605–670. (Chapter 17).
75. C. Xie, Polarization-mode-dispersion impairments in 112-Gb/s PDM-QPSK coherent systems, in: Proc. ECOC, Th.10.E.6, 2010.
76. B. Wedding, C.N. Haslach, Enhanced PMD mitigation by polarization scrambling and forward error correction, in: Proc. OFC, WAA1, 2001.
77. Liu X, et al. Demonstration of broad-band PMD mitigation in the presence of PDL through distributed fast polarization scrambling and forward-error correction. Photon Technol Lett. 2005;17(5):1109–1111.
78. Bölcskei H, et al. On the capacity of OFDM-based spatial multiplexing systems. IEEE Trans Commun. 2002;50(2):225–234.
79. Paulraj AJ, et al. An overview of MIMO communications—A key to Gigabit wireless. Proc IEEE. 2004;92(2):198–218.
80. Ho K-P, Kahn JM. Frequency diversity in mode-division multiplexing systems. J Lightwave Technol. 2011;29(24):3719–3726.
81. Shtaif M. Performance degradation in coherent polarization multiplexed systems as a result of polarization dependent loss. Opt Express. 2008;16(18):13918–13932.
82. Nafta A, et al. Capacity limitations in fiber-optic communications systems as a result of polarization dependent loss. Opt Lett. 2009;34(23):3613–3615.
83. Meron E, et al. Use of space-time coding in coherent polarization-multiplexed systems suffering from polarization dependent loss. Opt Lett. 2010;35(21):3547–3549.
84. Mecozzi A, Shtaif M. The statistics of polarization-dependent loss in optical communication systems. Photon Technol Lett. 2002;14(3):313–315.
85. Fukada Y. Probability density function of polarization dependent loss (PDL) in optical transmission system composed of passive devices and connecting fibers. J Lightwave Technol. 2002;20(6):953–964.
86. Yu M, et al. Statistics of polarization-dependent loss, insertion loss, and signal power in optical communication systems. Photon Technol Lett. 2002;14(12):1695–1697.
87. Mecozzi A, Shtaif M. Signal-to-noise-ratio degradation caused by polarization-dependent loss and the effect of dynamic gain equalization. J Lightwave Technol. 2004;22(8):1856–1871.
88. Nelson LE, et al. Statistics of polarization dependent loss in an installed long-haul WDM system. Opt Express. 2011;19(7):6790–6796.
89. Steinkamp A, et al. Polarization mode dispersion and polarization dependent loss in optical fiber systems. Proc SPIE. 2004;5596:243–254.
90. El Amari A, et al. Statistical prediction and experimental verification of concatenations of fiber optic components with polarization dependent loss. J Lightwave Technol. 1998;16(3):332–339.
91. Antonelli C, et al. Stokes-space analysis of modal dispersion in fibers with multiple mode transmission. Opt Express. 2012;20(11):11718–11733.
92. Ho KP, Kahn JM. Statistics of group delays in multimode fiber with strong mode coupling. J Lightwave Technol. 2011;29(21):3119–3128.
93. Ho K-P, Kahn JM. Mode-dependent loss and gain: statistics and effect on mode-division multiplexing. Opt Express. 2011;19(17):16612–16635.
94. S. Warm, K. Petermann, Outage capacity for spliced mode multiplexed multi-mode fiber links, in: Proc. OFC, JW2A.39, 2012.
95. Savory SJ. Digital filters for coherent optical receivers. Opt Express. 2008;16(2):804–817.
96. M.G. Taylor, Algorithms for coherent detection, in: Proc. OFC, OThL4, 2010.
97. Savory SJ. Digital coherent optical receivers: Algorithms and subsystems. J Sel Top Quant Electron. 2010;16(5):1164–1179.
98. Agrawal G. Nonlinear Fiber Optics. fourth edition San Diego, CA: Elsevier; 2006.
99. Kuschnerov M, et al. Data-aided versus blind single-carrier coherent receivers. IEEE Photon J. 2010;2(3):387–403.
100. Randel S, et al. 6  56-Gb/s mode-division multiplexed transmission over 33-km few-mode fiber enabled by 6
56-Gb/s mode-division multiplexed transmission over 33-km few-mode fiber enabled by 6  6 MIMO equalization. Opt Express. 2011;19(17):16697–16707.
6 MIMO equalization. Opt Express. 2011;19(17):16697–16707.
101. Ip E, Kahn JM. Feedforward carrier recovery for coherent optical communications. J Lightwave Technol. 2007;25(9):2675–2692 and Addendum to Feedforward carrier recovery for coherent optical communications, J. Lightwave Technol. 25 (13) (2009) 2552–2553.
102. Bai N, et al. Mode-division multiplexed transmission with inline few-mode fiber amplifier. Opt Express. 2012;20(3):2668–2680.
103. M.D. Feuer et al., Demonstration of joint DSP receivers for spatial superchannels, in: IEEE Photonics Society Summer Topical Meetings, MC4.2, 2012.
104. Papadias CB. Globally convergent blind source separation based on a multiuser kurtosis maximization criterion. IEEE Trans Signal Proc. 2000;48(12):3508–3519.
105. (a) V.A.J.M. Sleiffer et al., 73.7 Tb/s ( -Gb/s) mode-division multiplexed DP-16QAM transmission with inline MM-EDFA, in: Proc. ECOC, Th.3.C.4, 2012.
-Gb/s) mode-division multiplexed DP-16QAM transmission with inline MM-EDFA, in: Proc. ECOC, Th.3.C.4, 2012.
105. (b) Shynk JJ. Frequency-domain and multirate adaptive filtering. IEEE Signal Proc Mag. 1992;9(1):14–37.
106. J. Kahn, K.P. Ho, Mode coupling effects in mode-division-multiplexed systems, in: IEEE Photonics Society Summer Topical Meetings, TuC 3.4, 2012.
107. (a) B. Inan et al., DSP requirements for MIMO spatial multiplexed receivers, in: IEEE Photonics Society Summer Topical Meetings, MC 4.4, 2012.
107. (b) Bai N, et al. Adaptive frequency-domain equalization for the transmission of the fundamental mode in a fewmode fiber. Opt Express. 2012;20(21):24010–24017.
108. Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in C. Cambridge: New York; 1992.
109. J. Leibrich, W. Rosenkranz, Frequency domain equalization with minimum complexity in coherent optical transmission, in: Proc. OFC, OWV1, 2010.
110. Xia C. Hole-assisted few-mode multi-core fiber for high density space division multiplexing. Photon Technol Lett. 2012;24(21):1914–1917.
111. Ryf R, et al. Mode-division multiplexing over 96 km of few-mode fiber using coherent  MIMO processing. J Lightwave Technol. 2012;30(4):521–531.
MIMO processing. J Lightwave Technol. 2012;30(4):521–531.
112. M. Salsi et al., Transmission at  Gb/s, over two modes of 40 km-long prototype few-mode fiber, using LCOS based mode multiplexer and demultiplexer, in: Proc. OFC, PDPB9, 2011.
Gb/s, over two modes of 40 km-long prototype few-mode fiber, using LCOS based mode multiplexer and demultiplexer, in: Proc. OFC, PDPB9, 2011.
113. J. Carpenter, T.D. Wilkinson, All optical degenerate mode-group multiplexing using a mode selective switch, in: IEEE Photonics Society Summer Topical Meetings, 2012, pp. 236–237.
114. R. Ryf et al., Optical coupling components for spatial multiplexing in multi-mode fibers, in: Proc ECOC, Th.12.B.1, 2011.
115. Poole CD, et al. Optical fiber-based dispersion compensation using higher order modes near cutoff. J Lightwave Technol. 1994;12(10):1746–1758.
116. Giles I. Fiber LPG mode converters and mode selection technique for multimode SDM. Photon Technol Lett. 2012;24(21):1922–1925.
117. L. Grüner-Nielsen, J.W. Nicholson, Stable mode converter for conversion between LP01 and LP11 using a thermally induced long period grating, in: IEEE Photonics Society Summer Topical Meetings, WC1.2, 2012.
118. R. Ryf, Spot-based mode coupler for mode-multiplexed transmission in few mode fiber, in: IEEE Photonics Society Summer Topical Meetings, 2012, pp. 199–200.
119. N.K. Fontaine et al., Evaluation of photonic lanterns for lossless mode-multiplexing, in: Proc. ECOC, Th.2.D.6, 2012.
120. Case SK, Han MK. Multi-mode holographic waveguide coupler. Opt Commun. 1975;15(2):306–307.
121. Berkhout GCG, et al. Efficient sorting of orbital angular momentum states of light. Phys Rev Lett. 2010;105:153601.
122. Gloge D. Weakly guiding fibers. Appl Opt. 1971;10(10):2252–2258.
123. Kogelnik H, Winzer PJ. Modal birefringence in weakly guiding fibers. J Lightwave Technol. 2012;30(14):2240–2245.
124. Thornburg WQ, et al. Selective launching of higher-order modes into an optical fiber with an optical phase shifter. Opt Lett. 1994;19(7):454–456.
125. J. Carpenter, T.D. Wilkinson, Holographic mode generation for mode division multiplexing, in: Proc. OFC, JW2A.42, 2012.
126. Soifer VA, Golub MA. Laser Beam Mode Selection by Computer Generated Holograms. CRC Press 1994.
127. Black RJ, Gagnon L. Optical Waveguide Modes: Polarization. McGraw-Hill Professional: Coupling and Symmetry; 2009.
128. R. Ryf et al., Low-loss mode coupler for mode-multiplexed transmission in few-mode fiber, in: Proc. OFC, PDP5B.5, 2012.
129. N.K. Fontaine et al., Space-division multiplexing and all optical MIMO demultiplexing using a photonic integrated circuit, in: Proc. OFC, PDP5B.1, 2012.
130. W. Klaus, Free-space coupling optics for multi-core fibers, in: IEEE Photonics Society Summer Topical Meetings, WC3.3, 2012.
131. Bromage J. Raman amplification for fiber communications systems. J Lightwave Technol. 2004;22(1):79–93.
132. Nykolak G, et al. An Erbium-doped multimode optical fiber amplifier. Photon Technol Lett. 1991;3(12):1079–1081.
133. Bai N, et al. Multimode fiber amplifier with tunable modal gain using a reconfigurable multimode pump. Opt Express. 2011;19(17):16601–16611.
134. E. Ip, Gain equalization for few-mode fiber amplifiers with more than two propagating mode groups, in: IEEE Photonics Society Summer Topical Meetings, 2012, pp. 224–225.
135. S. Alam, Modal gain equalization in a few moded erbium-doped fiber amplifier, in: IEEE Photonics Society Summer Topical Meetings, 2012, pp. 218–219.
136. D. Askarov, J.M. Kahn, Design of multi-mode erbium-doped fiber amplifiers for low mode-dependent gain, in: IEEE Photonics Society Summer Topical Meetings, 2012, pp. 220–221.
137. Abedin KS, et al. Cladding-pumped erbium-doped multicore fiber amplifier. Opt Express. 2012;20(18):20191–20200.
138. H. Takahashi et al., First demonstration of MC-EDFA-repeatered SDM transmission of 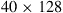 -Gbit/s PDM-QPSK signals per core over 6,160-km 7-core MCF, in: Proc. ECOC, Th.3.C.3, 2012.
-Gbit/s PDM-QPSK signals per core over 6,160-km 7-core MCF, in: Proc. ECOC, Th.3.C.3, 2012.
139. K. Tsujikawa, Optical fiber amplifier employing a bundle of reduced cladding erbium-doped fibers for multi-core fiber transmission, in: IEEE Photonics Society Summer Topical Meetings, 2012, pp. 228–229.
140. Y. Yamauchi, A highly-efficient remotely-pumped multi-core EDFA transmission system with a novel hybrid wavelength/space-division multiplexing scheme, in: Proc. OECC, 2012, pp. 479–480.
141. Shah AR, et al. Coherent optical MIMO (COMIMO). J Lightwave Technol. 2005;23(8):2410–2419.
142. A. Li et al., Reception of mode and polarization multiplexed 107Gb/s CO-OFDM signal over a two-mode fiber, in: Proc. OFC, PDPB8, 2011.
143. N. Hanzawa et al., Demonstration of mode-division multiplexing transmission over 10 km two-mode fiber with mode coupler, in: Proc. OFC, OWA4, 2011.
144. R. Ryf et al., Space division multiplexing over 10 km of three-mode fiber using coherent  MIMO processing, in: Proc. OFC, PDPB10, 2011.
MIMO processing, in: Proc. OFC, PDPB10, 2011.
145. Ryf R, et al. Spot based mode couplers for mode multiplexed transmission in few mode fiber. Photon Technol Lett. 2012;24(21):1973–1976.
146. Ryf R, et al. Mode-multiplexed transmission over a 209-km dgd-compensated hybrid few-mode fiber span. Photon Technol Lett. 2012;24(21):1965–1968.
147. Ryf R, et al. MIMO-based crosstalk suppression in spatially multiplexed  -Gb/s PDM-QPSK signals for strongly-coupled 3-core fiber. Photon Technol Lett. 2011;23(20):1469–1471.
-Gb/s PDM-QPSK signals for strongly-coupled 3-core fiber. Photon Technol Lett. 2011;23(20):1469–1471.
148. R. Ryf et al., Coherent 1200-km  MIMO mode-multiplexed transmission over 3-core microstructured fiber, in: Proc. ECOC, Th.13.C.1, 2011.
MIMO mode-multiplexed transmission over 3-core microstructured fiber, in: Proc. ECOC, Th.13.C.1, 2011.
149. Xia C, et al. Supermodes for optical transmission. Opt Express. 2011;19(17):16653–16664.
150. R. Ryf et al., Impulse response analysis of coupled-core 3-core fibers, in: Proc. ECOC, Mo.1.F.4, 2012.
1Following [1], we conveniently express traffic growth in decibels, i.e. a 30% growth corresponds to a growth of 10 log 10(1.3) = 1.14 dB.
2Advances in low-loss or low-nonlinearity fiber will not be able to change this picture significantly [22].
3A waveguide mode is an electromagnetic field distribution that, apart from a scalar multiplication factor, does not change its shape upon transmission along the waveguide [67,68].
4As is common in MIMO literature, we use the term “capacity” in this context to refer to the “capacity per channel use,” which equals the “spectral efficiency” for signals using minimum-bandwidth Nyquist pulses. The overall fiber transmission capacity is obtained by multiplying this quantity by the employed optical bandwidth.
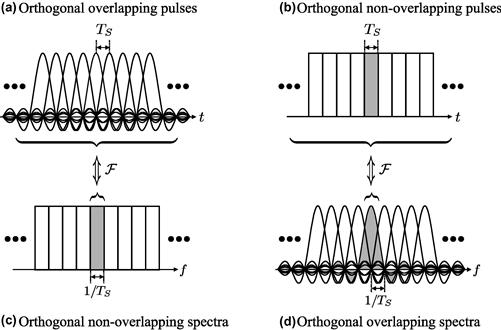
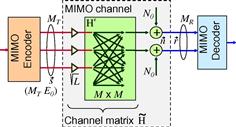
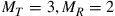 , and
, and 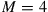 .
.
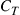 relative to the single-mode capacity
relative to the single-mode capacity 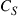 at
at 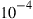 outage (a) and average capacity
outage (a) and average capacity 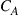 (b), both at 20 dB SNR, as a function of the number of modes
(b), both at 20 dB SNR, as a function of the number of modes  processed by a fixed mode set transponder. The number of modes M supported by the waveguide parameterizes the curves.
processed by a fixed mode set transponder. The number of modes M supported by the waveguide parameterizes the curves.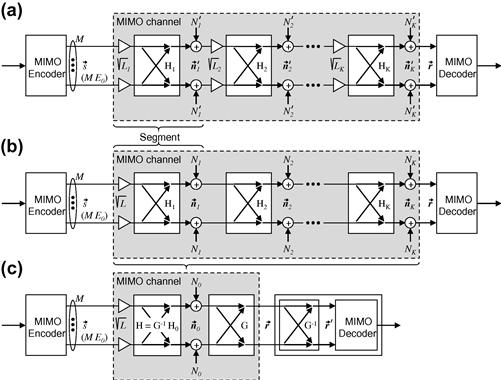
 impulse responses for 96 km of 6-mode FMF.
impulse responses for 96 km of 6-mode FMF.