Chapter 10
Getting into Shapes with Geometry
IN THIS CHAPTER
 Getting straight with lines and angles
Getting straight with lines and angles
 Working with polygons
Working with polygons
 Taking on triangles and quadrilaterals
Taking on triangles and quadrilaterals
 Circumnavigating circles
Circumnavigating circles
 Working with 3-D shapes
Working with 3-D shapes
Geometry is all about shapes: lines, angles, triangles, rectangles, squares, circles, cubes, and more. This chapter introduces you to the many basic shapes you’re likely to encounter on the GRE along with the strategies and equations that you’ll need to answer the questions. You also get hands-on practice answering a few example questions.
Exploring Lines and Angles
The main parts of most of these shapes are lines and angles, so start with these.
Lines
You’ve probably heard the term straight line, but in geometry, that’s redundant. By definition, a line is straight. If it curves, it’s not a line. Once in a while the GRE splits lines — er, hairs — and forces you to consider whether the line goes on forever in both directions, is a line segment, or has one endpoint and an arrow at the other end, making it a ray that goes on in one direction. But most of the time, don’t worry about it: You can usually solve the problem without worrying about how far the line goes.
Parallel lines don’t cross and are represented by the symbol 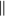 . Perpendicular lines cross at right angles and are represented by the symbol
. Perpendicular lines cross at right angles and are represented by the symbol 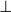 . A perpendicular bisector is a line that both passes through the midpoint of a line segment and is perpendicular to it.
. A perpendicular bisector is a line that both passes through the midpoint of a line segment and is perpendicular to it.
Angles
Angles are a common part of GRE geometry problems. An angle is the space between two lines or segments that cross or share an endpoint. Fortunately, there’s not much to understanding angles when you know the different types of angles and a few key concepts.
Finding an angle is usually a matter of simple addition or subtraction. Besides the rules in the following sections, these three rules apply to the angles on the GRE:
- Angles can’t be negative.
- Angles can’t be 0 degrees or 180 degrees.
- Fractional angles, such as
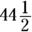 degrees or 179.5 degrees, are rare on the GRE. Angles are typically whole numbers, rounded to be easy to work with. If you’re plugging in a number for an angle, plug in a whole number, such as 30, 45, or 90.
degrees or 179.5 degrees, are rare on the GRE. Angles are typically whole numbers, rounded to be easy to work with. If you’re plugging in a number for an angle, plug in a whole number, such as 30, 45, or 90.
Right angle
Right angles equal 90 degrees and are represented by perpendicular lines with a small box where the two lines meet.

© John Wiley & Sons, Inc.
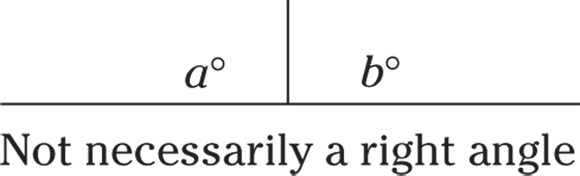
© John Wiley & Sons, Inc.
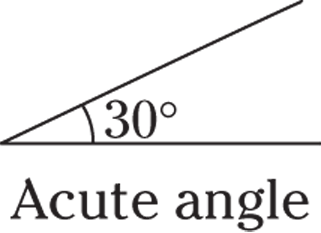
Acute angle
An acute angle is any angle greater than 0 degrees but less than 90 degrees.
© John Wiley & Sons, Inc.
Obtuse angle
An obtuse angle is any angle greater than 90 degrees but less than 180 degrees.

© John Wiley & Sons, Inc.
Complementary angles
Together, complementary angles form a right angle: 90 degrees.

© John Wiley & Sons, Inc.
Supplementary angles
Together, supplementary angles form a straight line: 180 degrees.
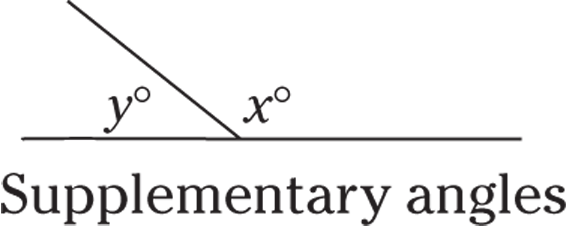
© John Wiley & Sons, Inc.
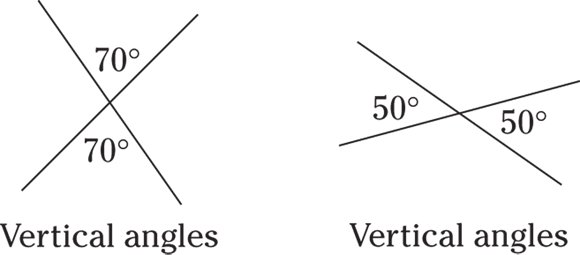
Vertical angles
Vertical angles are formed when two lines cross, and they always have equal measures.
© John Wiley & Sons, Inc.
Bisectors
A bisector, or line that bisects, cuts directly down the middle, and this is a term that you need to know. Yes, more vocab. If a line (or segment) bisects an angle, it divides that angle into two equal angles; if a first segment bisects a second segment, the first one cuts the second one perfectly in half. And if the first segment bisects the second segment at 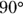 , then it is a perpendicular bisector as mentioned previously, and yes, the GRE will expect you to know what that is. Don’t worry though — there will almost always be a drawing.
, then it is a perpendicular bisector as mentioned previously, and yes, the GRE will expect you to know what that is. Don’t worry though — there will almost always be a drawing.
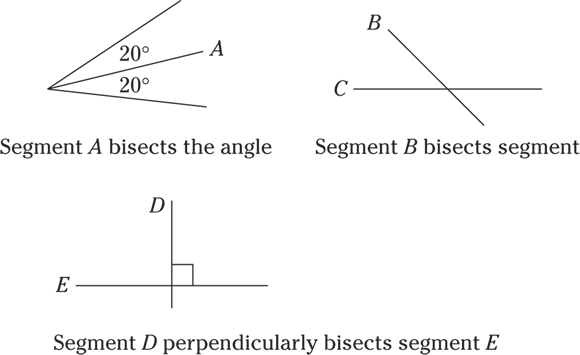
© John Wiley & Sons, Inc.
Other key points
Angles around a point total 360 degrees, just as in a circle.

© John Wiley & Sons, Inc.
A line that cuts through two parallel lines forms two sets of four equal angles. In this drawing, all the x’s are the same, and all the y’s are the same.
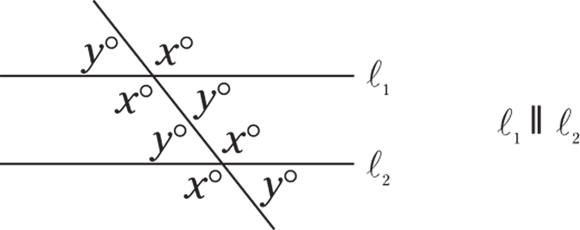
© John Wiley & Sons, Inc.
Recognizing Polygons
A polygon is any closed shape consisting of line segments, which includes everything from a triangle (three sides) to a dodecagon (a dozen sides) and beyond. The polygons you’re most likely going to encounter on the GRE are triangles and quadrilaterals (with four sides). Table 10-1 lists the names of polygons you may bump into, but don’t get caught up with the names — these problems almost always include a drawing, so you can count the sides.
TABLE 10-1 Polygons
|
Number of Sides |
Name |
|
3 |
Triangle |
|
4 |
Quadrilateral (including the square, rectangle, trapezoid, and parallelogram) |
|
5 |
Pentagon |
|
6 |
Hexagon (think of x in six and x in hex) |
|
7 |
Heptagon |
|
8 |
Octagon |
|
9 |
Nonagon |
|
10 |
Decagon |
If two polygons are congruent, they’re identical. If they’re similar, they have identical angles but are different sizes. The following explains what you need to know about polygons for the GRE.
Determining total interior angle measure
Because you may be asked to find the total interior angle measure of a particular polygon, keep this formula in mind (where n stands for the number of sides):
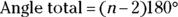
For example, here are the sums of the interior angles of the following polygons:
- Triangle:
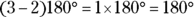
- Quadrilateral:
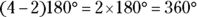
- Pentagon:
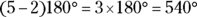
- Hexagon:
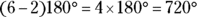
- Heptagon:
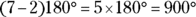
- Octagon:
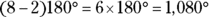
- Nonagon:
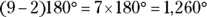
- Decagon:
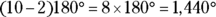
Finding one interior angle
I’ve seen GRE problems asking for the measure of one interior angle of a regular polygon. If you see one of these problems, here’s what you do:
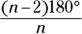
Remember that n stands for the number of sides (which is the same as the number of angles), so here’s how to find a single angle measure of a regular pentagon:
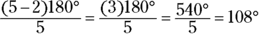
Understanding Triangles
Comprised of three sides, the triangle is a key figure in geometry, especially on the GRE. Understanding how triangles work helps understand other polygons. The following sections introduce you to certain common triangles and explain how to do the related math.
Recognizing triangle types
You need to know three types of triangles for the GRE: equilateral, isosceles, and right, as described in the following sections.
Equilateral triangle
An equilateral triangle has three equal sides and three equal angles. Though technically also a regular or equiangular triangle, it’s referred to as equilateral on the GRE.
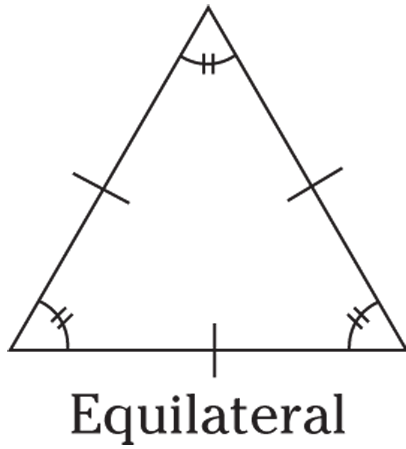
© John Wiley & Sons, Inc.
In these figures, the curved lines with the double lines through them inside the triangle indicate that the angles are equal. The short lines through the sides of the triangle indicate that the sides are equal.
Isosceles triangle
An isosceles triangle has two equal sides and two equal angles.
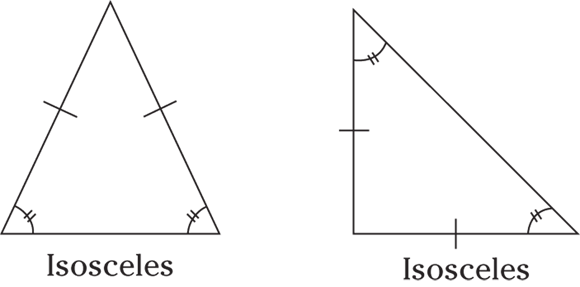
© John Wiley & Sons, Inc.
Right triangle
A right triangle has one 90-degree angle.
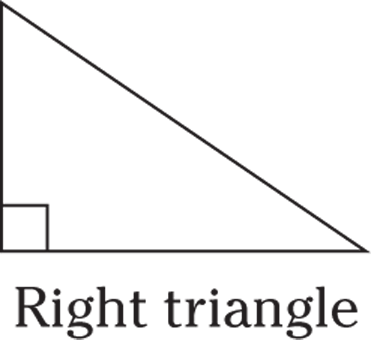
© John Wiley & Sons, Inc.
The little box in the lower-left corner of the triangle indicates that the angle is 90 degrees. If the box isn’t shown and the question doesn’t state that you’re looking at a right triangle, then don’t assume you are.
Noting key characteristics
Triangles have some notable characteristics that help you field some of the geometry questions on the exam. The following points bring you up to speed:
- The largest angle is opposite the longest side. Conversely, the smallest angle is opposite the shortest side.
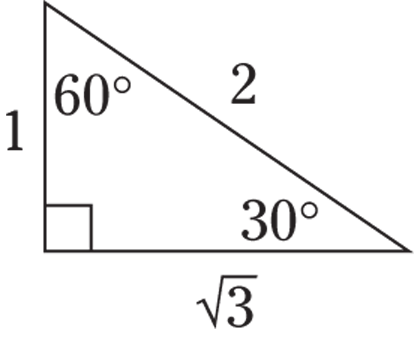
© John Wiley & Sons, Inc.
- The sum of any two sides must be greater than the length of the remaining side. This idea can be written as
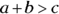 , where a, b, and c are the sides of the triangle.
, where a, b, and c are the sides of the triangle.
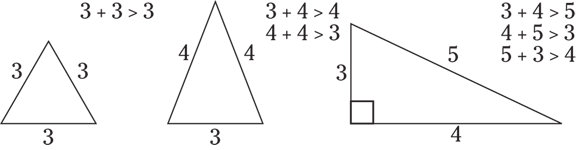
© John Wiley & Sons, Inc.
- The sum of the interior angles is always 180 degrees. No matter what the triangle looks like, or how big it is, the angle total is 180 degrees.

© John Wiley & Sons, Inc.
- Any exterior angle is equal to the sum of the two other interior angles. Follow the logic. The sum of supplementary angles is
 , and the
, and the 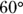 angle (inside the triangle, lower right) and the
angle (inside the triangle, lower right) and the 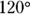 angle (outside the triangle) are supplementary, so
angle (outside the triangle) are supplementary, so 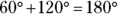 . The sum of the angles inside any triangle is
. The sum of the angles inside any triangle is 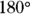 , so in this case
, so in this case 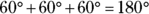 . The two angles on the left (
. The two angles on the left (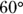 and
and 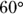 ) add to the angle outside the triangle,
) add to the angle outside the triangle, 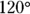 .
.
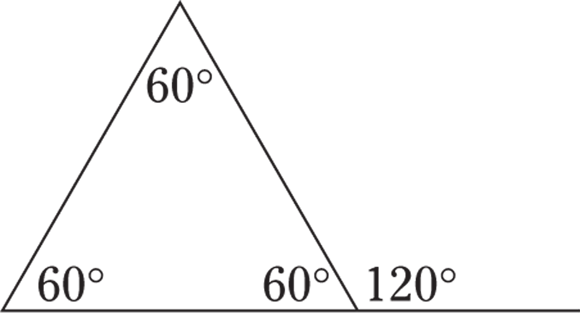
© John Wiley & Sons, Inc.
Calculating perimeter and area
You may encounter at least one question on the exam that asks for the perimeter or area of a triangle. The following sections can help you clear that hurdle.
Calculating perimeter
Perimeter is the distance around a triangle, so add up the lengths of the sides.
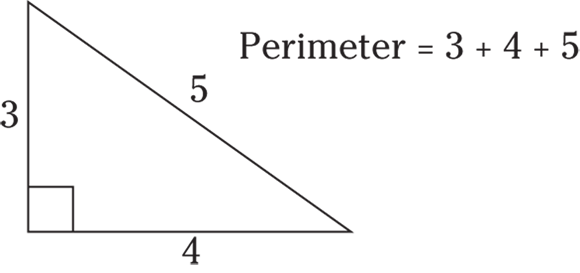
© John Wiley & Sons, Inc.
Calculating area
The area of a triangle is 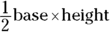 . The height is a line perpendicular to the base, and in a right triangle it’s one of the sides.
. The height is a line perpendicular to the base, and in a right triangle it’s one of the sides.
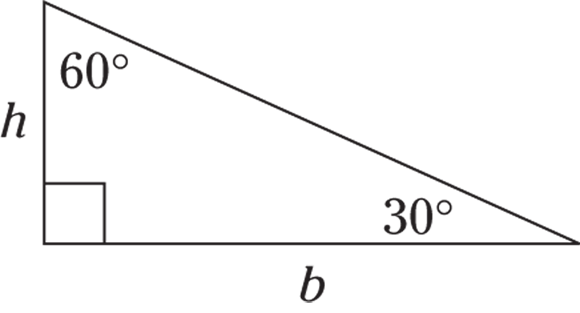
© John Wiley & Sons, Inc.
The height may be inside the triangle, represented by a dashed line and a 90-degree box.

© John Wiley & Sons, Inc.
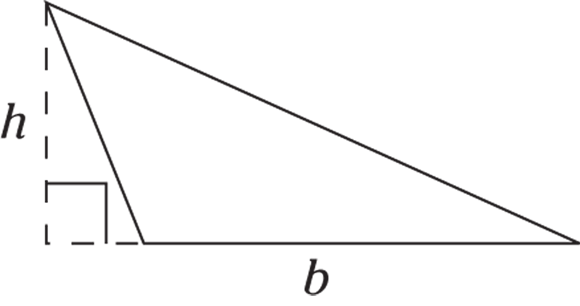
© John Wiley & Sons, Inc.
Understanding the Pythagorean theorem
The Pythagorean theorem only works on a right triangle. It states that the sum of the squares of the two shorter sides is equal to the square of the hypotenuse. If you know the lengths of any two sides, you can find the length of the third side with this formula:
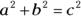
Here, a and b are the legs of the triangle, and c is the hypotenuse. The hypotenuse is always opposite the 90-degree angle and is always the longest side of the triangle.
© John Wiley & Sons, Inc.

© John Wiley & Sons, Inc.
To find the unknown length of the third side, start with the Pythagorean Theorem:
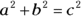
In this case you know the a and the c, but you’re missing the b. Plug in the side lengths that you have and solve for the missing side:
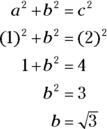
Or, say you’re asked for the length of the hypotenuse of this triangle:

© John Wiley & Sons, Inc.
Here are the calculations:
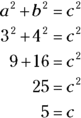
Identifying common right triangles
The two preceding triangles are examples of common right triangles. With a common right triangle, you don’t need to work the Pythagorean theorem every time the question asks for a third side length. These next sections show you four common right triangles that make things a whole lot easier.
3:4:5
If one side of a right triangle is 3 and the other is 4, then the hypotenuse must be 5. Likewise, if the hypotenuse is 5 and the length of one side is 4, the other side must be 3. I proved this relationship with the Pythagorean theorem in the preceding section.
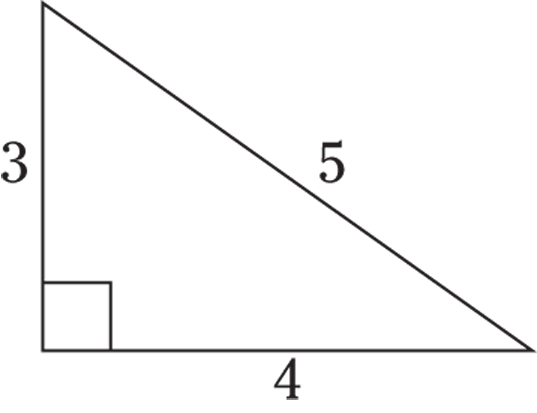
© John Wiley & Sons, Inc.
5:12:13
If one side of a right triangle is 5 and another side is 12, then the hypotenuse must be 13. Likewise, if you know the hypotenuse is 13 and one of the sides is 5, then the other side must be 12. You don’t need the Pythagorean theorem. This triangle is not nearly as common as the 3:4:5 described in the preceding section, and it almost never appears in multiples such as  .
.

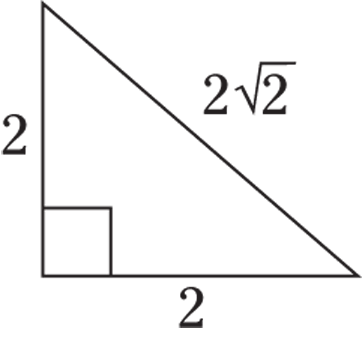
© John Wiley & Sons, Inc.
This ratio is for an isosceles right triangle (containing 45-45-90-degree angles), and s stands for side. If one side is 2 and a second side is also 2, then the hypotenuse is 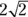 .
.
© John Wiley & Sons, Inc.
If you’re given the length of the hypotenuse of an isosceles right triangle and need to find the length of the other two sides, use this formula, where h is the hypotenuse:
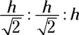
 If the diagonal of a square is 5, what is the area of the square?
If the diagonal of a square is 5, what is the area of the square?

© John Wiley & Sons, Inc.
To find the area, first you need the length of a side. If the diagonal is 5, then right away you know the side length is 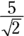 , and the side-length ratio of the triangle is this:
, and the side-length ratio of the triangle is this:
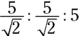
The hypotenuse is 5, and the length of any side of the square is 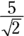 . The area of the square is then
. The area of the square is then 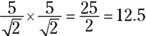 square units.
square units.
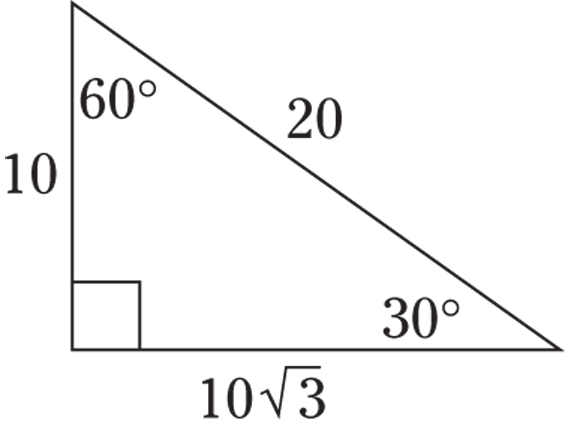
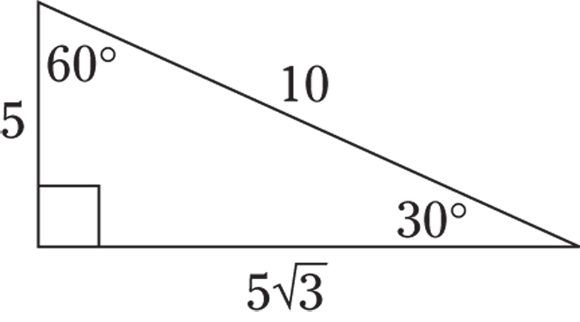
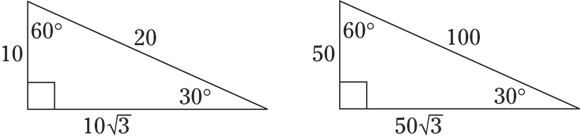
This is a special ratio for the sides of a 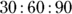 triangle, which has angles measuring 30, 60, and 90 degrees. S is the length of the short side (opposite the 30-degree angle),
triangle, which has angles measuring 30, 60, and 90 degrees. S is the length of the short side (opposite the 30-degree angle), 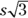 is the longer side, and 2s is the hypotenuse.
is the longer side, and 2s is the hypotenuse.
© John Wiley & Sons, Inc.
This type of triangle is a favorite of the test-makers. The important fact to keep in mind here is that the hypotenuse is twice the length of the short side (opposite the 30-degree angle). If you encounter a word problem that says, “Given a 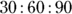 triangle with a hypotenuse of 20, find the area,” or “Given a 30:60:90 triangle with a hypotenuse of 100, find the perimeter,” you can do so because you can quickly find the lengths of the other sides.
triangle with a hypotenuse of 20, find the area,” or “Given a 30:60:90 triangle with a hypotenuse of 100, find the perimeter,” you can do so because you can quickly find the lengths of the other sides.
© John Wiley & Sons, Inc.
Knowing Quadrilaterals
Any four-sided shape is a quadrilateral. The interior angles of any quadrilateral total 360 degrees, and you can cut any quadrilateral into two triangles, each of which has total interior angles of 180 degrees. Specific quadrilaterals include squares, parallelograms, trapezoids, and other shapes. The following sections present everything you need to know about quadrilaterals for the GRE.

© John Wiley & Sons, Inc.
- Square: The simplest quadrilateral is the square — a quadrilateral with four equal sides and four right angles. The area of a square is
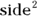 (that is,
(that is, 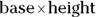 ), or
), or 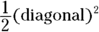 .
.
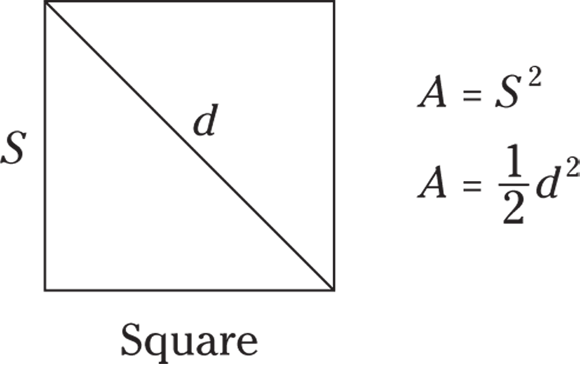
© John Wiley & Sons, Inc.
- Rhombus: A rhombus is a quadrilateral with four equal sides and angles that aren’t right angles. A rhombus looks like a diamond, except that it can be sideways. The area of a rhombus is
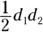 , or
, or 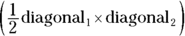 .
.
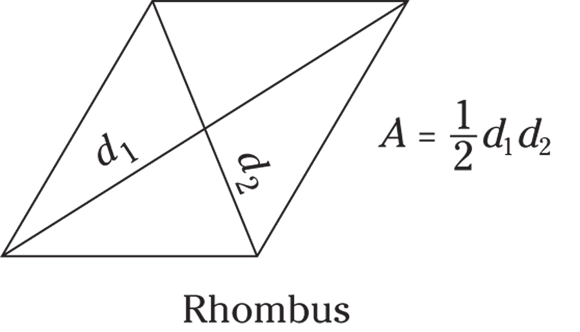
© John Wiley & Sons, Inc.
- Rectangle: A rectangle is a quadrilateral that has four right angles and opposite sides that are equal. (Rectangle means “right angle.”) The area of a rectangle is
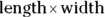 (which is the same as
(which is the same as 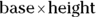 ).
).
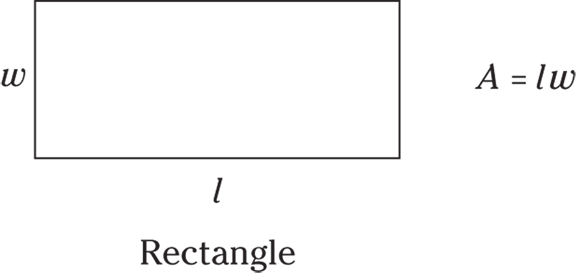
© John Wiley & Sons, Inc.
- Parallelogram: A parallelogram is a quadrilateral where the opposite sides are equal but the angles aren’t necessarily right angles. The area of a parallelogram is
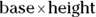 , and the height is the distance between the two bases. The height is represented by a perpendicular dashed line from the tallest point of the figure down to the base.
, and the height is the distance between the two bases. The height is represented by a perpendicular dashed line from the tallest point of the figure down to the base.
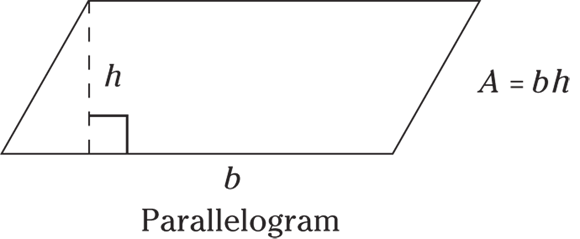
© John Wiley & Sons, Inc.
 A square is a specific rectangle, and a rectangle is a specific parallelogram.
A square is a specific rectangle, and a rectangle is a specific parallelogram. - Trapezoid: A trapezoid is a quadrilateral that has only two parallel sides, while the other two opposite sides are not parallel. The area of a trapezoid is
 . It doesn’t matter which base is base1 or base2, because you’re adding them together anyway. Just be sure to add them before you multiply by
. It doesn’t matter which base is base1 or base2, because you’re adding them together anyway. Just be sure to add them before you multiply by 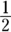 .
.
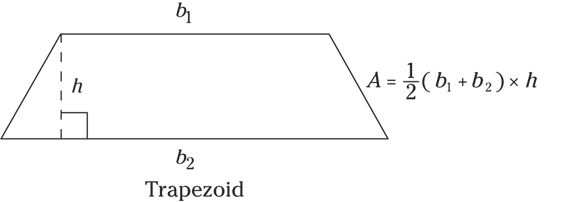
© John Wiley & Sons, Inc.
- Other quadrilaterals: Some quadrilaterals don’t have nice, neat shapes or special names.

© John Wiley & Sons, Inc.
 Don’t immediately decide that you can’t find the area of a strange shape. You may be able to divide the quadrilateral into two triangles and find the area of each triangle.
Don’t immediately decide that you can’t find the area of a strange shape. You may be able to divide the quadrilateral into two triangles and find the area of each triangle.
Working with Circles
Determining a circle’s circumference (distance around the circle) or area using its radius (the distance from the center of the circle to its edge) is easy if you know the formulas and the features of the circle. The following sections cover the characteristics and the formulas you need to solve problems related to circles.
Recognizing a circle’s features
Circles have several unique features. You need to know these to decipher the terminology used on the test.
- Center: The center is right in the middle of the circle. If a question refers to the circle by a capital letter, that’s both the circle’s center and its name.

© John Wiley & Sons, Inc.
- Diameter: The diameter is the length of a line segment that passes through the center of the circle and touches the opposite sides. The diameter is equal to twice the radius.

© John Wiley & Sons, Inc.
- Circumference: The circumference is the distance, or perimeter, around the circle.

© John Wiley & Sons, Inc.
 , or pi: Pronounced “pie,”
, or pi: Pronounced “pie,”  is the ratio of the circumference of a circle to the diameter of a circle. It equals approximately 3.14, but usually circle-based questions have answer choices in terms of
is the ratio of the circumference of a circle to the diameter of a circle. It equals approximately 3.14, but usually circle-based questions have answer choices in terms of  , such as
, such as 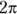 , rather than 6.28.
, rather than 6.28.- Radius: The radius is the distance from the center of the circle to the edge of the circle. The radius of a circle is half the diameter.
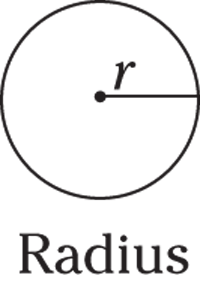
© John Wiley & Sons, Inc.
- Tangent: A tangent is a line outside a circle that touches the circle at one point.
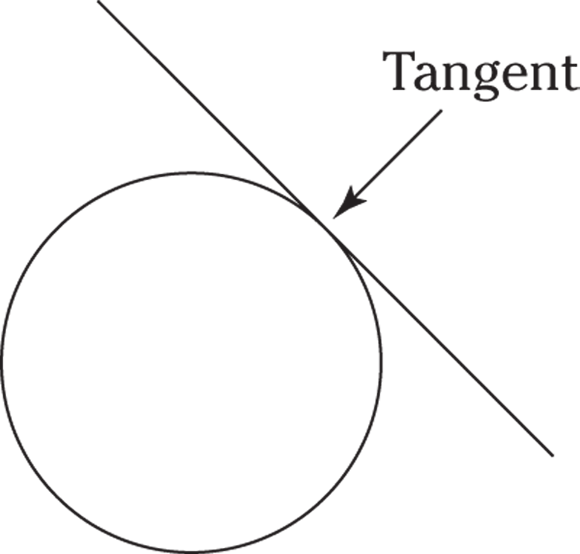
© John Wiley & Sons, Inc.
- Chord: A chord is a line segment that crosses through the circle and connects it on two points. The longest chord in a circle is the diameter.
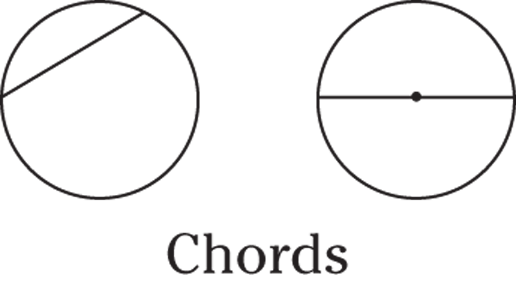
© John Wiley & Sons, Inc.

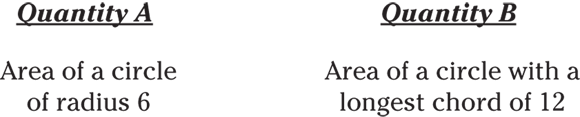
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
The longest chord of a circle is the diameter. Because the diameter is twice the radius, a circle with diameter 12 has a radius of 6. In other words, the circles are the same size and have the same area. (Don’t worry about solving for that area; you know the two circles are the same.) The correct answer is Choice (C).


 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
A chord connects any two points on a circle, but you don’t know whether this particular chord is the diameter. Quantity B doesn’t specify the longest chord. If it did, the quantities would be equal, but it doesn’t, so you don’t know the size of the circle in Quantity B. The correct answer is Choice (D).
Mastering essential formulas
Solving circle problems is all about knowing formulas and how to use them. The following sections reveal the formulas and provide guidance on solving problems, complete with sample questions.
Circumference: 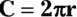 or
or 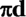
Circumference is a fancy word for perimeter — the distance around a circle. The formula is 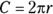 (where C is the circumference and r is radius). Because diameter is twice the radius, you may also use the equation
(where C is the circumference and r is radius). Because diameter is twice the radius, you may also use the equation 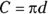 (where d is the diameter).
(where d is the diameter).

© John Wiley & Sons, Inc.
For example, the circumference of a circle with a radius of 3 is
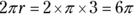
 A wagon has a wheel radius of 6 inches. If the wagon wheel travels 100 revolutions, approximately how many feet has the wagon rolled?
A wagon has a wheel radius of 6 inches. If the wagon wheel travels 100 revolutions, approximately how many feet has the wagon rolled?
 325
325
 314
314
 255
255
 201
201
 It cannot be determined from the information given.
It cannot be determined from the information given.
The question gives the radius in inches, but the answer choices are all in feet, so the first order of business is to convert inches into feet: 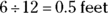 . One revolution of the wheel carries the wagon a distance of one circumference of the wheel, so start by finding the circumference of the circle in feet:
. One revolution of the wheel carries the wagon a distance of one circumference of the wheel, so start by finding the circumference of the circle in feet:
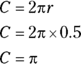
Then multiply by the number of revolutions:
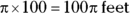
Now look at the answer choices. They’re in real numbers, so replace  with 3.14 and multiply:
with 3.14 and multiply:
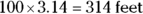
Choice (E) is definitely not the answer. If you have a radius, you can solve for nearly anything having to do with circles. The correct answer is Choice (B).
Area: 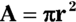
Area is the space inside the circle. The formula is 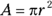 , so if a circle has a radius of 4, you can find the area like this:
, so if a circle has a radius of 4, you can find the area like this:
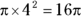
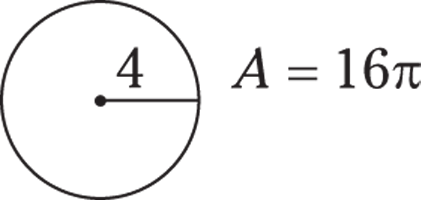
© John Wiley & Sons, Inc.
Arcs and angles inside a circle
An arc is a part of the circumference of a circle. This is typically formed by either a central angle or an inscribed angle:
- Central angle: A central angle has its vertex at the center of a circle and its endpoints on the circumference. The degree measure of a central angle is the same as the degree measure of its minor arc (the smaller arc formed by the two points where the angle’s lines touch the circle).
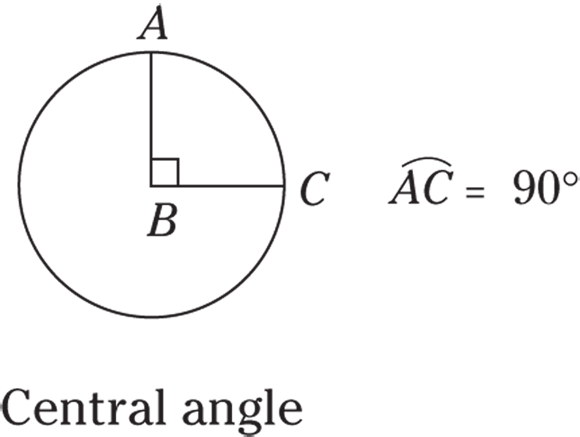
© John Wiley & Sons, Inc.
- Inscribed angle: An inscribed angle has both its vertex and endpoints on the circumference. The degree measure of an inscribed angle is half the degree measure of its intercepted arc, as shown in the following figure. The intercepted arc is 80 degrees, and the inscribed angle is half of that, at 40 degrees.
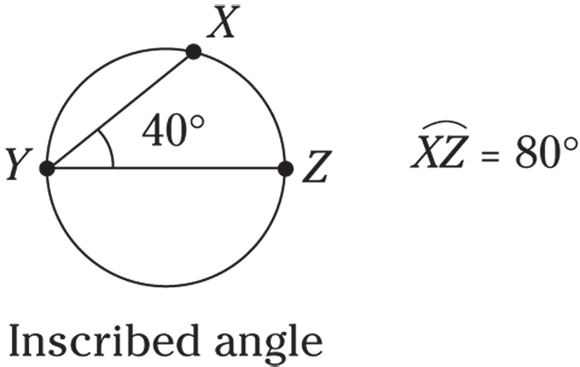
© John Wiley & Sons, Inc.
Even a drawing that looks like a dream-catcher, with lines all over, isn’t so bad if you know how the vertices, arcs, and angles work.
 In this figure, if minor arc
In this figure, if minor arc 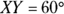 , what is the sum of the degree measures of angles
, what is the sum of the degree measures of angles 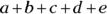 ?
?
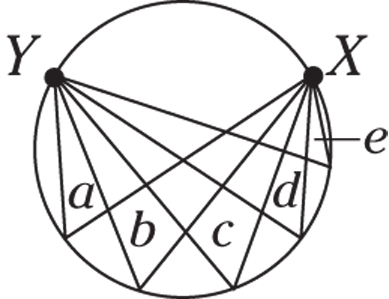
© John Wiley & Sons, Inc.
 60
60
 90
90
 120
120
 150
150
 180
180
The angles a, b, c, d, and e are inscribed angles, meaning each angle has half the degree measure of its intercepted arc. You know from the drawing that the endpoints of each angle are X and Y, and the problem tells you that arc XY measures 60 degrees. This means that each angle is 30 degrees, for a total of  . The correct answer is Choice (D).
. The correct answer is Choice (D).
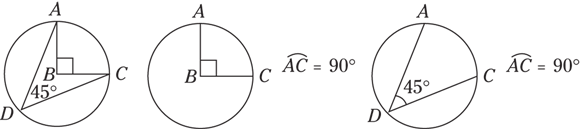
© John Wiley & Sons, Inc.
To find the length of an arc when you have its degree measure, follow these steps:
- Find the circumference of the entire circle.
- Put the degree measure of the arc over 360 and reduce the fraction.
- Multiply the circumference by the fraction.
 Find the length of minor arc AC.
Find the length of minor arc AC.
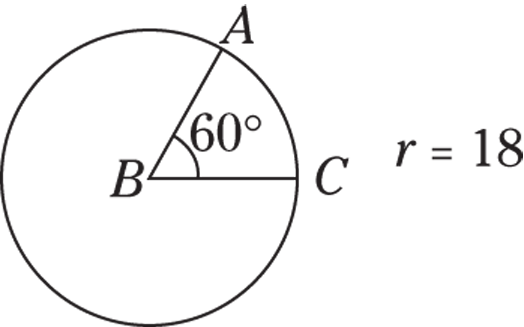
© John Wiley & Sons, Inc.

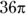

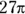

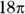

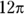

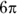
Take the steps one at a time:
- Find the circumference of the entire circle:
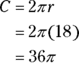
Don’t multiply
 out; the answer choices are in terms of
out; the answer choices are in terms of  .
. -
Put the degree measure of the arc over 360 and reduce the fraction.
The degree measure of the arc is the same as its central angle, 60 degrees:
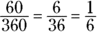
- Multiply the circumference by the fraction:
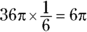
The correct answer is Choice (E).
Try another one. Make it intuitive.
 Find the length of minor arc RS in this figure.
Find the length of minor arc RS in this figure.
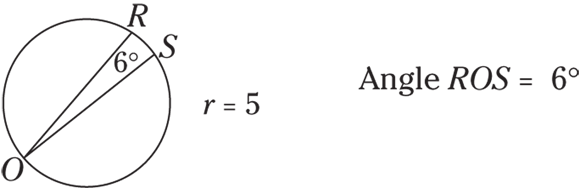
© John Wiley & Sons, Inc.

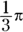



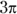

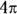
 12
12
- Find the circumference of the entire circle:
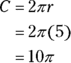
-
Put the degree measure of the arc over 360 and reduce the fraction.
Here, the inscribed angle is 6 degrees. Because the intercepted arc has twice the degree measure of the inscribed angle, the arc is 12 degrees:
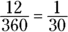
- Multiply the circumference by the fraction:
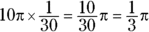
The correct answer is Choice (A).
Sectors
A sector is part of the area of a circle that comes from a central angle. The degree measure of a sector is the same as the degree measure of the central angle. You won’t see a sector from an inscribed angle.
To find the area of a sector, do the following:
- Find the area of the entire circle.
- Put the degree measure of the sector over 360 and reduce the fraction.
- Multiply the area by the fraction.
Finding the area of a sector is similar to finding the length of an arc. The only difference is in the first step: You find the circle’s area, not circumference. With this in mind, try out a few sample sector problems:
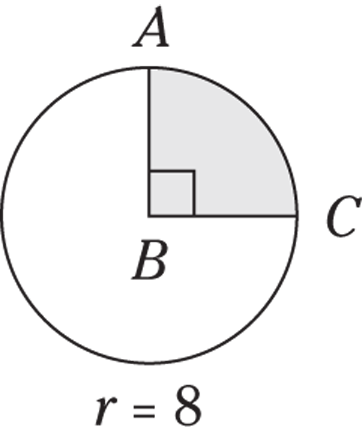
 Find the area of minor sector ABC.
Find the area of minor sector ABC.
© John Wiley & Sons, Inc.

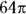

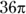

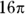

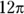


Use the steps listed previously:
- Find the area of the entire circle.
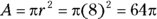
-
Put the degree measure of the sector over 360 and reduce the fraction.
The sector is 90 degrees, the same as its central angle:
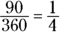
- Multiply the area by the fraction.
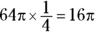
The correct answer is Choice (C).
 Find the area of minor sector XYZ in this figure.
Find the area of minor sector XYZ in this figure.
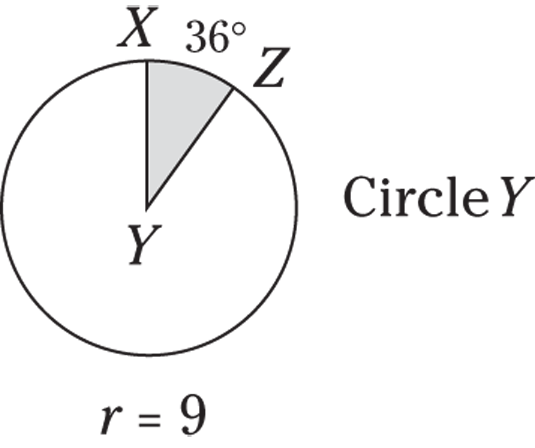
© John Wiley & Sons, Inc.

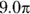

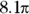

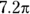

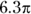

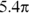
- Find the area of the entire circle.
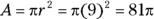
-
Put the degree measure of the sector over 360 and reduce the fraction.
A sector has the same degree measure as its intercepted arc:
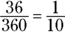
- Multiply the area by the fraction.
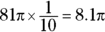
The correct answer is Choice (B).
Tackling shaded-area problems
A shaded-area problem presents two shapes with one overlapping the other but not completely covering it. The visible part of the shape underneath is the shaded area. Your job is to calculate the total shaded area. Fortunately, you don’t always have to find an exact number.
 A circle of radius 4 inches is centered over an 8-inch square. Find the total shaded area.
A circle of radius 4 inches is centered over an 8-inch square. Find the total shaded area.

© John Wiley & Sons, Inc.
This is just a basic shape that’s partly covered up. Here’s how to calculate the area of the shaded part:
-
Calculate the total area of the outside shape.
Each side of the square is 8 inches:
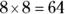
- Calculate the area of the inside shape.
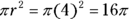
-
Subtract the area of the inside shape from the area of the outside shape.
The difference between the two shapes is the shaded area.
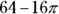
And that’s the answer!
You don’t have to get an exact number. Try one like it:

© John Wiley & Sons, Inc.
 In the preceding drawing, exactly half the circle overlaps the square. If the square has a side length of 4 and the circle has a radius of 2, what is the area of the shaded region?
In the preceding drawing, exactly half the circle overlaps the square. If the square has a side length of 4 and the circle has a radius of 2, what is the area of the shaded region?

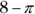

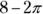

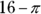

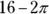

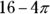
The key here is that half the circle overlaps the square, so you need to calculate the area of the sector to subtract from the area of the square. The circle has a radius of 2, so its area is 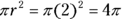 . Only half the circle overlaps the square, so the area that you subtract is half the circle:
. Only half the circle overlaps the square, so the area that you subtract is half the circle: 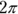 . The square has an area of 16, so the difference between the two shapes is
. The square has an area of 16, so the difference between the two shapes is 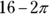 : The correct answer is Choice (D).
: The correct answer is Choice (D).

© John Wiley & Sons, Inc.
 The preceding drawing shows a circular rock garden surrounded by a sidewalk. If the rock garden has a diameter of 8 and the sidewalk is exactly 2 feet wide, what is the area of the sidewalk?
The preceding drawing shows a circular rock garden surrounded by a sidewalk. If the rock garden has a diameter of 8 and the sidewalk is exactly 2 feet wide, what is the area of the sidewalk?

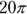

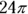

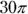

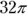

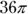
This one is exactly the same as the others, only you’re subtracting two circles. The small circle has a diameter of 8, so its radius is 4. The visible part of the large circle has a width of 2, so combined with the small circle’s radius of 4, it has a total radius of 6. Now find the areas so you can subtract them. The large circle has an area of 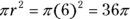 , while the small circle has an area of
, while the small circle has an area of 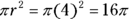 . Subtract them for a sidewalk area of
. Subtract them for a sidewalk area of 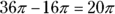 . The correct answer is Choice (A).
. The correct answer is Choice (A).
Turning 3-D Shapes
There are only two 3-D shapes that you may encounter on the GRE: the rectangular solid (which includes the cube) and the cylinder. In the following sections, I provide all you need to answer any GRE question based on these shapes.
Calculating volume
Volume is the space inside a three-dimensional object. When the GRE asks you the volume of a rectangular solid, think of how much water goes into a fish aquarium (a rectangular aquarium, not a round or curved one). The following sections explain how to calculate the volumes of the 3-D shapes you encounter on the GRE — a cube, a rectangular solid, and a cylinder.
Volume of a cylinder 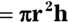
The GRE calls its cylinders right circular cylinders, meaning that the top and bottom circles are the same and that the sides go straight up and down. A cylinder is basically a can of soup. The base of the cylinder, as a circle, has an area of 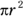 . Multiply that by the cylinder’s height to get its volume:
. Multiply that by the cylinder’s height to get its volume: 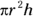 .
.
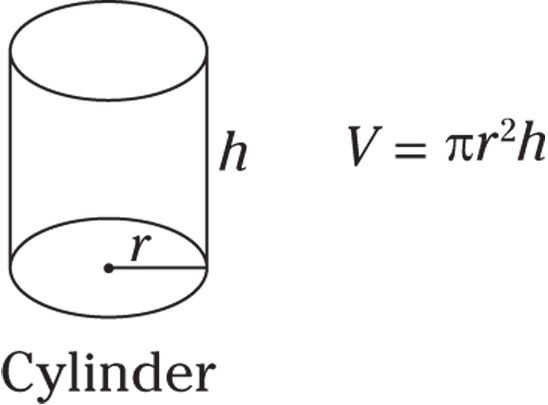
© John Wiley & Sons, Inc.
 What is the volume of a right circular cylinder having a radius of 3 and a height of 5?
What is the volume of a right circular cylinder having a radius of 3 and a height of 5?

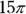

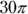

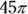

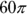

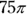
The volume of a cylinder is found with the area of its circle times its height, or 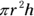 . Just plug in the radius and height, and you have the volume:
. Just plug in the radius and height, and you have the volume:
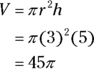
The correct answer is Choice (C).
 What is the height of a right circular cylinder having a volume of
What is the height of a right circular cylinder having a volume of 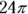 and a radius of
and a radius of 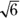 ?
?
 2
2
 3
3
 4
4
 5
5
 6
6
If this question seems to laugh at you, you can laugh right back. Just place the volume and radius into the formula and solve for the height:
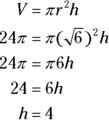
The correct answer is choice (C).
Rectangular solid volume 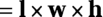
A rectangular solid on the GRE has six sides that are rectangles. It’s basically a shoebox. The base is a rectangle, which has an area of 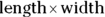 . Multiply that by the box’s height to find its volume:
. Multiply that by the box’s height to find its volume: 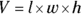 .
.
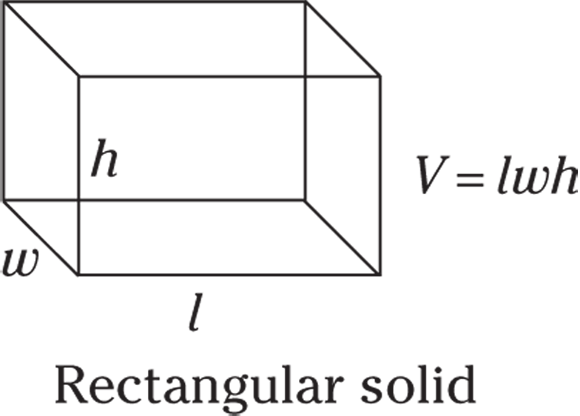
© John W iley & Sons, Inc.
 What is the volume of a rectangular shoebox having a length of 6, a width of 3, and a depth of 4?
What is the volume of a rectangular shoebox having a length of 6, a width of 3, and a depth of 4?
 72
72
 60
60
 48
48
 36
36
 24
24
This one is just practice. Multiply out the dimensions for the answer: 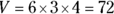 .
.
The correct answer is Choice (A).
 If a rectangular salt-water aquarium has a volume of 14,400 cubic inches, and the surface area of each end is 120 square inches, what is its length, in feet?
If a rectangular salt-water aquarium has a volume of 14,400 cubic inches, and the surface area of each end is 120 square inches, what is its length, in feet?
 10
10
 12
12
 15
15
 18
18
 20
20
You know that the volume of a rectangular solid is 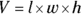 and in this case is 14,400. You don’t actually get the width and height, but you get their product (result from multiplying), which is 120. That’s okay, because you multiply them anyway in the formula. First find the length in inches, then convert it to feet:
and in this case is 14,400. You don’t actually get the width and height, but you get their product (result from multiplying), which is 120. That’s okay, because you multiply them anyway in the formula. First find the length in inches, then convert it to feet:
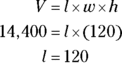
Good thing you get an on-screen calculator. Anyway, if the length is 120 inches, then it’s 10 feet, because there are 12 inches in one foot. The correct answer is Choice (A).
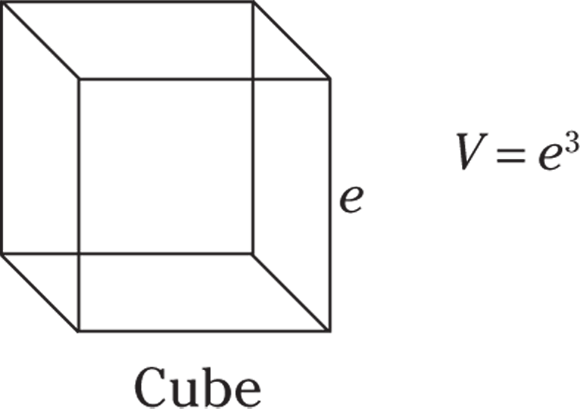
Cube volume 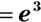
A cube is a three-dimensional square. Think of a six-sided die (one of a pair of dice). The cube’s dimensions, length, width, and height, are the same, so they’re called edges and are all represented by the letter e. The volume of a cube is thus 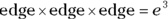 .
.
© John Wiley & Sons, Inc.
 What is the volume of a cube having an edge length of 4?
What is the volume of a cube having an edge length of 4?
 16
16
 24
24
 32
32
 48
48
 64
64
Consider this question to be your hors d’oeuvre, or appetizer, for the true cube questions coming up. You have the edge length, so plug that into the formula:
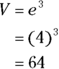
The correct answer is Choice (E).
Calculating surface area
Surface area is the outside of an object. If you were to wrap the object as a gift, it would be how much wrapping paper you’d need. The cube is typically the only shape for which the GRE asks you to calculate the surface area. In fact, it’ll give you the cube’s volume, and you back-solve to find the surface area — or vice versa. This next section provides the formula for calculating the surface area of the cube and back-solving it to get the edge.
Cube surface area 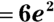
A cube has six identical faces, and each face is a square. The area of a square is 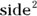 . On the cube, because you call each side an edge, the area of a face is
. On the cube, because you call each side an edge, the area of a face is 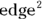 . Because the cube has six faces, the surface area is
. Because the cube has six faces, the surface area is 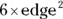 , or
, or 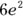 .
.
© John Wiley & Sons, Inc.
 What is the surface area of a cube having an edge length of 3?
What is the surface area of a cube having an edge length of 3?
 18
18
 27
27
 36
36
 45
45
 54
54
Another hors d’oeuvre. You have the edge length, so plug that in: =
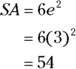
The correct answer is Choice (E).
 If a cube has a volume of 8, what is its surface area?
If a cube has a volume of 8, what is its surface area?
 8
8
 12
12
 16
16
 24
24
 32
32
Now, this is more like it. First back-solve with the volume formula to find the edge length:
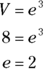
Now plug that into the surface area formula:
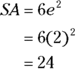
The correct answer is Choice (D).
 If a cube has a surface area of 600, what is its volume?
If a cube has a surface area of 600, what is its volume?
 10
10
 60
60
 100
100
 600
600
 1,000
1,000
First, back-solve with the surface area formula to find the edge length:
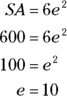
Now plug that puppy right back into the volume formula:
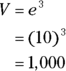
The correct answer is Choice (E).
 Other than the words “right angle” and “bisect,” you will probably not see the following terms, so don’t worry about memorizing words such as “obtuse” or “supplementary.” But, review the definitions so that you understand how the angles work, because that’s the key to solving almost any GRE angle problem.
Other than the words “right angle” and “bisect,” you will probably not see the following terms, so don’t worry about memorizing words such as “obtuse” or “supplementary.” But, review the definitions so that you understand how the angles work, because that’s the key to solving almost any GRE angle problem. 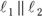 indicates that the two lines are parallel.
indicates that the two lines are parallel.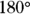 , and add 180 for each additional side.
, and add 180 for each additional side.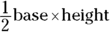 .
. 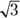 , take a quick glance at the answer choices — they will almost always be in terms of the radical. This is an example of where the calculator is not always your friend: If you are all set with an answer of 1.732, and you have to choose from the answer choices
, take a quick glance at the answer choices — they will almost always be in terms of the radical. This is an example of where the calculator is not always your friend: If you are all set with an answer of 1.732, and you have to choose from the answer choices 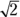 ,
, 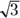 , and
, and 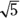 , you’ll have to start over.
, you’ll have to start over.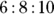 (multiplied by 2),
(multiplied by 2), 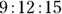 (multiplied by 3), or
(multiplied by 3), or 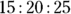 (multiplied by 5).
(multiplied by 5).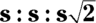
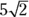 , because a square’s diagonal cuts the square into two isosceles right triangles This is true regardless of the size of the square: If a side length is 64, you know right away that the hypotenuse is
, because a square’s diagonal cuts the square into two isosceles right triangles This is true regardless of the size of the square: If a side length is 64, you know right away that the hypotenuse is 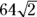 . If the side length is
. If the side length is 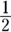 , you know right away that the hypotenuse is
, you know right away that the hypotenuse is 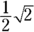 .
.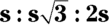
 , so in this example, you’d select
, so in this example, you’d select 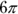 . If you do encounter a problem with the answer choices in regular numbers, such as, “How far did a wheel with a 3-inch radius travel if it rolled 6 times,” just replace the
. If you do encounter a problem with the answer choices in regular numbers, such as, “How far did a wheel with a 3-inch radius travel if it rolled 6 times,” just replace the  with 3.14 in your answer. But first, look at the answer choices.
with 3.14 in your answer. But first, look at the answer choices. in it. If you picked Choice (E), 12, you found the degree measure of the arc rather than its length.
in it. If you picked Choice (E), 12, you found the degree measure of the arc rather than its length.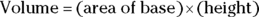 . Keep that in mind to help you remember the formulas for cubes, rectangular solids, and cylinders. You simply calculate the area of the base as you normally do and then multiply by the object’s height.
. Keep that in mind to help you remember the formulas for cubes, rectangular solids, and cylinders. You simply calculate the area of the base as you normally do and then multiply by the object’s height.