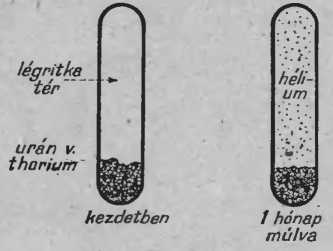
37. ábra. Így mutatható ki az, hogy az uránból vagy tóriumból új elem keletkezik : a hélium
Ezeket a részecskéket α (alfa) részeknek nevezzük.
ÚJ ELEM SZÜLETÉSE
Az a kérdés, hogy mi is tulajdonképpen ez az α-rész. Mivel atomsúlyát 4-nek találták, és a hélium atomsúlya is 4, tehát könnyen felötlött az a gondolat, hogy az uránból és a tóriumból héliumatomok repülnek ki.
De ez a gondolat ellenkezett a fizikusok addigi természet-szemléletével — hiszen ők az elem állandóságának és változhatatlanságának elvét vallották. Most viszont felbukkant egy olyan jelenség, amely arra mutatott, hogy az egyik elemből egy másik elem keletkezhetik: vagyis az elem nem állandó, hanem átalakulhat.
Ez annyira forradalmi jellegű gondolat volt, hogy ebben a kérdésben feltétlen bizonyosságot kellett szerezni. Az a kérdés, hogyan járnánk el mi, ha ránk bíznák a kérdés vizsgálatát.
Először is vásárolnánk egy gázharisnyát. Előző kísérletünk azt mutatta, hogy a gázharisnya α-részeket sugároz. Az a gyanúnk, hogy ezek a részek a héliumgáz atomjai. Tehát össze fogjuk gyűjteni az alfa-részeket és azután megvizsgáljuk, vajon az összegyűlt anyag valóban a héliumgáz tulajdonságait mutatja-e. Valóban, így végezték el a kísérletet (37. ábra).

37. ábra. Így mutatható ki az, hogy az uránból vagy tóriumból új elem keletkezik : a hélium
A sugárzó anyagot egy üvegedénybe zárták. A levegőt eltávolították az edényből. Így az edényben pl. uránon kívül nem volt semmi. Néhány hónap múlva megvizsgálták az edény tartalmát. Megjegyezzük, hogy az ú. n. színkép-elemző készülék segítségével meg tudjuk mondani, hogy egy üvegedényben milyen gáz van és ehhez az edényt fel sem kell nyitnunk.
A színképelemző azt mutatta, hogy a csőben héliumgáz van. Ezt a kísérletet 1903-ban végezte el két kutató (Ramsay és Soddy). Kétségtelenül kiderült, hogy az uránból, vagy a tóriumból héliumgáz keletkezik, más szóval: az egyik elemből egy másik elem keletkezhetik.
A felvillanások segítségével könnyű megszámlálni, hogy 1 gr urán vagy 1 gr tórium 1 mp alatt hány α-részt bocsát ki.
GYÁRTSUNK héliumot
Azt találták, hogy 1 gr uránt tartalmazó szurokérc mp-ként 100 000 α-részt sugároz ki magából. 1 gr sokáig álló tórium pedig 27 000 részt. Ezek szerint egy hosszú gázharisnya (tórium-tartalma 3/4 gr) mintegy 21 000 α-részt sugároz mp-ként.
Ha tehát a gázharisnya fölé olyan üvegburát húznánk, amelynek belső falát felvillanó festékkel vontuk be és így valamennyi α-rész kijönne a harisnyából, akkor másodpercenként 21000 felvillanást figyelhetnénk meg.
Feladat. Számítsuk ki, mennyi hélium fejlődik 1 kg gázharisnyaporból egy év alatt. — Ezt a kis számítást azért végezzük el, hogy fogalmunk legyen az új elem keletkezésének gyorsaságáról.

38. ábra. A gázlámpákból jól ismert hosszú gázharisnya mintegy 3/4 gramm tóriumot tartalmaz. Aligha tudtuk idáig, hogy ez a gázharisnya valóságos héliumgyár. Ugyanis másodpercenként kb. 21000 héliumatomot (helyesebben
atommagot) sugároz ki. Ezek az úgynevezett alfa-részek, okozzák a világítófesték felvillanását.
1 évben kb. 31 millió mp van — 1 kg tórium 1 mp alatt 27 000 * 1000 = 27 millió α-részt sugároz. Tehát egy év alatt 31 milliószor 27 millió = 837 billió = 837 • 1012 héliumatom keletkezik.

30. ábra. A tóriumból rádióaktív sugárzással héliumgáz keletkezik. Jóllehet 1 gramm tórium 1 másodperc alatt kb. 30 000 héliummagol sugároz ki magából, mégis 33 000 kg tóriumot kellene felhalmoznunk, hogy belőle radioaktív bomlással 1 köbcentiméter héliumgáz keletkezzék 1 év alatt.
Azt már tudjuk, hogy 4 gr hélium 22,4 liter teret foglal el. De azt is tudjuk, hogy 4 gr héliumban 6 * 1023 atom van.
A kérdést tehát így fogalmazhatjuk: ha 6 • 1023 atom 22,4 liter teret tölt be, akkor 837 • 1012 atom mekkora teret foglal el? Ez egyszerű következtetési feladat. A számítás eredménye az, hogy 837 • 1012 atomnyi hélium térfogata 3 század köbmilliméter, azaz 1 kg tóriumból kb. 33 éven át keletkeznék rádióaktív sugárzás folytán 1 köbmilliméter térfogatú héliumgáz. Ennek a gázmennyiségnek súlya a gramm százmilliomod részének fele. Tehát gázharisnyánk súlya a sugárzás következtében 33 év alatt a gramm százmilliomod részének felével csökkenne. Ez roppant kicsiny súlyveszteség. Úgy látszott, hogy nehéz lesz az anyagok sugárzása miatt bekövetkező súlycsökkenést kimutatni. Mégis csak sikerült.
Foglaljuk tehát össze még egyszer azt a jelenséget, amely szemünk előtt játszódik le és amelyről könnyű kísérletekkel szerezhetünk szinte kézzelfogható bizonyságot: a sugárzó (rádióaktív) anyagok 13 000—21 000 km/mp sebességű, 4 atomsúlynyi részecskéket lövellnek ki. Ezek a részecskék az ú. n. α-részek, a hélium-elem atomjainak bizonyulnak. Tehát a rádióaktivitás első nagy tudományos meglepetése az volt, hogy megdöntötte az elemek állandóságának reakciós és tudománytalan tanát.
Az elem nem változhatatlan, hanem az egyik elem másik elemmé alakulhat át.
EGY FELEJTHETETLEN TŰZIJÁTÉK
Az α-részecskék záporozása és az elemátalakulás, a héliumkeletkezés jelensége ott játszódik le ébresztő óránk, vagy karóránk világító mutatójában. Könnyen megfigyelhetjük a kilövellő α-részek okozta felvillanások százait.

40. ábra. Helyezzünk a tanulómikroszkóp lencséje alá egy üveg (papír) lapra tett önmagától világító óramutatót. Másodpercenként többszáz, sőt ezer különálló felvillanást látunk hol itt, hol ott. A felvillanásokat a világítófestékbe kevert rádióaktív anyagból kirepülő héliummagok ütközése okozza. — Amint egy előző kísérlet bizonyítja: a héliummagok a levegőbe is százszámra kirepülnek
Az órákon úgynevezett önmagától világító festék van. A közönséges festék csupán akkor világít, ha előzőleg megvilágítottuk. Az önmagától világító festék is ilyen közönséges világítófesték, csakhogy parányi, erősen rádióaktív anyag van belekeverve, Az önmagától világító festék akkor is világít, ha előzőleg nem világítottuk meg. Akár évekig is sötétben lehet, mégis állandóan világít. Világítását a sugárzó anyagból kirepülő α-részek okozta felvillanásoknak köszönheti. Ha ez így van, akkor a felvillanásoknak nagyítóval egyenként láthatóknak kell lenniük.
Kísérlet. Legcélszerűbb ezt a kísérletet este végezni, amikor szemünk már hozzászokott a sötétséghez. A világító órát legalább egy órán át tartsuk előzőleg sötétségben. Szemünk pedig legalább 10—15 percig alkalmazkodjék a sötétséghez. Ha ezután egy 10—50-szeresen nagyító lencsén át nézzük az óra világító festékét, akkor itt-ott szabálytalan összevisszaságban felvillanó fénypontok százait-ezreit látjuk mp-ként. Egy közepesen jó óramutatóban napként mintegy ezer-kettőezer felvillanás jelentkezik.
Világító órák festékjében tehát állandóan szemünk előtt folyik a rádióaktív sugárzás és az elemátalakulás. Egy ébresztőóra számlapja és mutatói mp-ként sok hélium-atomot termelnek. Ezek az atomok ott maradnak az óralap és az üveg között. Tehát valóságos héliumgyárunk működik. Eddig talán nem is tudtunk róla.
Bizonyára sokszor hallottunk már a héliumgázról, amelyet először a Nap színképében fedeztek fel, azután megtalálták a földgázban. Végül pedig a rádióaktív α-sugárzás termékének bizonyult. Azt hittük, hogy ez a héliumgáz valami tőlünk idegen, anyag. De íme, most kiderült, hogy ott keletkezik óránk világító számlapján és így nagyszámú héliumatom gyűlik össze az óraüveg alatt.
A TISZTA ELEKTRON-SUGÁRZÁS MINT KÖZÖNSÉGES JELENSÉG
Előző kísérleteinkben kétféle rádióaktív sugárzást mutattunk ki. Könnyű, egyszerű kísérletekkel bizonyítottuk be, hogy óránk lapjának önmagától világító festéke vagy a gázharisnya, röntgensugárzást és héliumatomokból álló sugárzást bocsát ki.
A rádióaktivitás felfedezése után néhány évvel észrevették, hogy a rádióaktív anyagok még egy harmadik sugárzást is kibocsátanak. Ez a harmadik fajta sugárzás elektronokból áll, vagyis az elektromosság atomjaiból.
Ez megint meglepő tény. Mert emlékezzünk vissza: a katódsugárban is elektronok repülnek. De mennyi tudás, mennyi készülék és mennyi költség kell ahhoz, hogy ezt az elektronsugárzást a katódcsőben létrehozzuk. És íme: azt állítjuk, hogy a szurokérc, a gázharisnya, a világító óramutató csakúgy ontja magából — ráadásul önmagától, egészen természetes úton — ezeket az elektronokat. A γ sugárzást a fényképezőlemezzel nehézség nélkül tudtuk mutatni Becquerel módszerével. Az α sugarak kimutatása is könnyen sikerült a felvillanások segítségével. Egy cseppet sem nehezebb, bár némileg több előkészületet kíván az elektronsugárzás kimutatása.
Kísérlet. Szükséges hozzá egy kb. 4 cm hosszú, rézből vagy ólomból készült cső, egy kevés sugárzó anyag (gázharisnyapor vagy világító óramutató), patkómágnes és fényképezőlemez. A cső egyik végét elzárjuk a ráragasztott két-három írópapírlappal. Föléje teszünk egy 1 cm hosszú csövet.
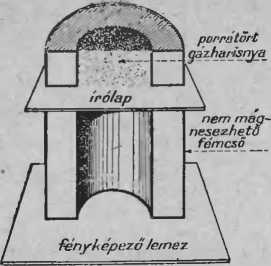
41. ábra. Ez a kép keresztmetszetben ábrázolja azt a csövet, amit a gázharisnyaporból kiinduló harmadik fajta sugárzás (az elektronsugárzás) kimutatására készítünk
Ezt a kis csövet megtöltjük gázharisnyaporral (vagy pedig a papírlap fölé egy világító óramutatót helyezünk, úgy, hogy sugárzása a papíron át az alsó cső nyílásába jusson). Azután a csövet vastagabb papírral lefödjük. (A csövet oldalt is körültekerhetjük ragasztó papirossal, hogy a két csőrész szét ne váljék.) Két ilyen eszközt készítünk.
A két csövet szabad nyílásával lefelé fordítva ráhelyezzük a fényképezőlemez érzékeny oldalára (természetesen vörös lámpa fényénél, de a lemezt nem burkoljuk papirosba). A lemezre egy patkómágnest is ráteszünk. Az egyik cső a patkómágnes sarkai között álljon, tehát erős mágneses térben, a másik cső pedig a patkó görbületében, ahol igen gyenge a mágnesesség. A második csövet a mágnestől távolabbra is tehetjük. Azután az egészet sötét helyre tesszük. (A szerző dobozba zárta ezt a szerkezetet, azután egy sötét szekrénybe tette). Mintegy két hét múlva előhívhatjuk a lemezt. Azt tapasztaljuk, hogy a két cső alatt köralakban megfeketedett a lemez. Hasonlítsuk össze a két feketedést. Azt látjuk, hogy a mágnes sarkai közé helyezett csőnek nyílása alatt kisebb mértékű a feketedés.

42. ábra. Két egyforma csövet készítünk, azután burkolatlan fényképezőlemez érzékeny oldalára állítjuk őket úgy, hogy az egyik egy erős mágnes mágneses terében álljon, a másik pedig ne legyen mágneses térben. — A mágneses térben álló cső alatt kisebb mértékű a fényképezőlemez feketedése. Kevesebb sugárzás érte a lemezt
Hogy nagy árnyalatkülönbséget mutató képet kapjunk, el kell találnunk azt az időt, ameddig a csöveket a lemezen kell hagyni. Jó kép készítéséhez több próba szükséges.

43. ábra. Mi történik a mágneses térben álló cső sugárzásával? Az alfasugárzást felfogja a papírlap. — A papírlapon átjutó sugárzás egy részét eltéríti a mágneses tér. Ez az eltérített sugárzás nem, lehet gamma-sugár, mert arra nem hat a mágnes. Tehát csak egy harmadik féle sugárzás lehet!
Mi annak az oka, hogy a patkómágnes sarkai közé helyezett cső aljára gyengébb sugárzás jutott, mint a mágnes nélküli cső aljára. (43. ábra.)
A cső felső részét megtöltő sugárzó anyagból — amint már tudjuk — γ és α-sugárzás indul ki. A γ-sugárzás könnyen áthalad a papírlapon és a cső belsején keresztül a fényképezőlemezre jut és megfeketíti. Az α-sugárzást a papírréteg teljesen visszatartja.
A röntgen- illetve γ-sugárzást a mágnes nem téríti el. Ezt kísérletekkel megállapították. Ha tehát a köralakú feketedés csak a γ-sugárzástól eredne, akkor mind a két cső alatt ugyanakkora fokúnak kellene lennie a feketedésnek, akár van ott mágnes, akár nincsen.
De mivel a mágneses térbe helyezett cső aljára gyengébb sugárzás ért, mint a mágnes nélküli cső aljára, ebből az következik, hogy a sugárzó anyagból jövő sugárzásnak egy része nem tudott a mágneses téren át a cső aljához, a lemezhez jutni, hanem közben eltérítődött.
Ha a cső oldalara lyukakat fúrnánk és a csövet fényérzékeny filmmel tekernénk körül, akkor az elhajlított sugárzás keresztüljutna a lyukakon és megfeketítené a filmet. Ebből megállapíthatnék, milyen irányban tér el a sugárzás a mágneses térben. Az ilyen kísérletek azt mutatják, hogy a sugár úgy tér el, mintha negatív elektromosság repülne benne.
Kísérlet. Az előző kísérletnek első része igen könnyen és biztosan elvégezhető. A következő kísérlet az új sugárzásnak e nagyon fontos tulajdonságát mutatja meg. Mondtuk, hogy az eltérített új sugárzás a cső két oldalán fúrt lyukakon át kijön a szabadba. Tegyünk a sugárzás útjába cinkszulfidporral bekent átlátszó lemezt és nézzük meg a sötétben nagyítóval. A gyakorlott és tökéletesen kipihent szem különálló, apró felvillanásokat észlel. E felvillanások sokkal gyengébbek azoknál a felvillanásoknál, amelyeket az α-részek okoznak és csak nehezen figyelhetők meg.
De az új sugárzástól okozott egyes felvillanások azt bizonyítják, hogy ez az új sugárzás is különálló részecskékből áll. Tehát ilyen elvileg egyszerű kísérlettel megállapíthatjuk, hogy az új sugárzásban negatív töltésű részecskék repülnek.
Hasonló kísérletekkel most már nem nehéz a részecskék töltésének nagyságát is meghatározni. Ebben a harmadik fajta sugárzásban repülő részecskék töltése is, tömege is akkora, mint az elektroné. Tehát ez a harmadik fajta sugárzás elektron-sugárzás.
Sikerült az elektronok sebességét is megmérni. Mint tudjuk, a leggyorsabb α-részeknek sebessége akkora (13 000—21 000 km/mp), hogy 1 mp alatt az északi sarktól a déli sarokig repülnének. A β-sugárban repülő elektronok sebessége még ennél is sokkalta nagyobb. A legsebesebb β-részck sebessége megközelíti a fény sebességét, tehát egy ilyen részecske 1 mp alatt hétszer tudná megkerülni a Földet a legnagyobb délkör mentén.
SZÉDÍTŐ MÉRETEK
Érdemes egy kissé megállni és körülnézni. Gondoljuk csak meg, hogy minden tudásunk felhasználásával sem sikerült nagyobb sebességet adni az anyagnak, csak másodpercenként kb. 1 km-nyit. Ekkora sebességgel repül ugyanis fegyvereink lövedéke. A természetben működő erők pedig 10—20-ezerszer nagyobb sebességre bírják az α-részecskét és 100-ezerszer nagyobbra a β-részecskét.
Tudjuk, hogy az α-részecskék héliumatomok. Ha ritkított terű csövet héliumgázzal töltünk meg, a részecskéket akár 20 000 km-re is felgyorsíthatjuk mp-ként. Csakhogy ekkor kb. 4 millió volt feszültségnek kellene lennie a csőbe forrasztott két elektród között. Ezt azonban még a mai technika sem tudja egyszerű eszközökkel megoldani.

44. ábra. Az eddig ismertetett egyszerű kísérletekben kitünően megfigyelhető alfa-részek sebessége mintegy 14—21 000 mp-ként. Ha mesterségesen akarnák a részecskéket ilyen sebességre gyorsítani, akkor kb. 4 000 000 volt feszültséget kellene alkalmazni!
Így aztán elképzelhetjük, milyen szörnyű nagy energiáknak kell dolgozniuk az urán-, illetőleg a tórium-atomban, hogy az α-részeknek ekkora sebességet adjon.
Ha fegyverlövedék acélba vagy falba ütközik, összenyomódik; energiájának nagyrésze meleggé változik. Láttuk, hogy az α-részek már egy papírlapon sem tudnak áthaladni — a papír elnyeli őket. A β-sugarak áthatolóképessége már nagyobb, de egy kb. 100-szor vastagabb réteg azokat is elnyeli. Még 100-szor vastagabb rétegen pedig már a γ-sugarak legnagyobb része sem tud áthatolni. A rádióaktív anyag belsejéből is indulnak ki ilyen sugarak. Ezek nem tudnak átjutni az anyagon, elnyelődnek a rádióaktív anyagban és felmelegítik azt. Tehát a sugárzó anyagoknak állandóan melegebbnek kell lenniük a környezetüknél.
Curie-ék a rádium felfedezése után észlelték, hogy a rádium állandóan meleget termel. Ezt a meleget meg is mérték. Azt találták, hogy 1 gramm rádium a vele egyenlő tömegű 0-fokú vizet 43 perc alatt forralná fel. Ez már az első pillanatra is hatalmas hőfejlődésre mutat. De még nagyobbnak látszik, ha meggondoljuk, hogy a rádium, változatlan sugárzás mellett 2280 évig tudná termelni ezt az energiát.
Feladat. Számítsuk ki: 1 gramm rádium sugárzása hányszor annyi meleget termel mint 1 gramm szén elégetése.
1 gramm jóminőségű, 6000 kalóriás szén elégetésekor annyi meleg szabadul fel, amennyi 60 gramm 0-fokú hideg vizet felforralna. 1 gramm rádium kisugárzása pedig, tudjuk, 1 gramm vizet 43 perc alatt forral fel. Tehát 60 gramm vizet 60 • 43 perc = 43 óra alatt forral fel.
De a rádium ekkor még nem adta ki energiáját: ezt a teljesítményét 2280 éven át meg tudná tartani. 2280 év a 43 óránál kereken 465 000-szer több. Ezért mondhatjuk, hogy a rádium sugárzása 465-ezerszer több meleget fejleszt annál a melegnél, amennyi ugyanakkora súlyú jóminőségű szén elégésekor szabadul fel.
Ugyanez áll a többi sugárzó anyagra (urán, tórium, gázharisnya, világító óramutató) is, amint ezt a következő újabb kis számítás igazolja.

A hosszú gázharisnyában kb. 0,75 gramm tórium van. A tórium 24 ezermillió évig tudna változatlan erősséggel sugározni, míg végre megszűnnék sugárzóképessége. Pontos mérésekkel megállapították, hogy mennyi meleget fejleszt 1 gramm tórium 1 óra alatt. Ennek alapján kiszámíthatjuk, hogy 1 gramm tórium — annyi idő alatt; ameddig a sugárzóképessége tart — 940 000-szer annyi energiát termel sugárzással, mint amennyi energia 1 gramm szén elégésekor szabadul fel.
Tehát a mi gázharisnyánkban levő 3/4 gr tóriumnak energiája 940 000-szer ennyi súlyú szén fűtőértékének felel meg. Ezért 3/4 gr tórium 705 000 gr = 705 kg szénnel egyenlő értékű.
Gondoltuk-e valamikor, amidőn a könnyű gázharisnyát zsebünkbe tettük, avagy a harisnya ott ízzott a gázlángon, hogy zsebünkben hét mázsa szénnek megfelelő energiát viszünk? Ez a rádióaktív sugárzó energia (atomenergia) olcsó energia is, hiszen 7 mázsa szén energiáját egy gázharisnya áráért vásárolhatjuk meg.
Bárhol emelünk fel egy földrögöt vagy kődarabot, bennük is mindig találunk uránt és tóriumot. Bárhol emelünk ki 1 m3 földet, benne átlagosan 16 gr uránra és 54 gr tóriumra bukkanunk. Mivel 1 gr uránban 860 kg szén fűtőértéke rejtőzik, 1 gr tóriumban pedig 705 kg szén fűtőértéke, azért 1 m3 földben található urán és tórium az idők folyamán annyi meleget fejleszt, mint 38 tonna szén.
Gondoltuk volna, hogy az 1 m3 földben, falban vagy kövezetben rejlő rádióaktív anyagok annyi meleget adnak, mint 38 tonna szén elégése?
KÍSÉRLETEZETT MÁR EMANÁCIÓGÁZZAL?
Sokszor lehet hallani e nevet: emanációgáz (radon). Az emanáció valóban a legérdekesebb gázok közé tartozik. Először is atomjai nehezebbek az ólom atomjainál, mégis gáz. Másodszor pedig ez a gáz rádióaktív és sugározza az α-részecskéket. Nem látott még ilyen gázt? Ott van körülöttünk a levegőben. Jelen van mindenütt.
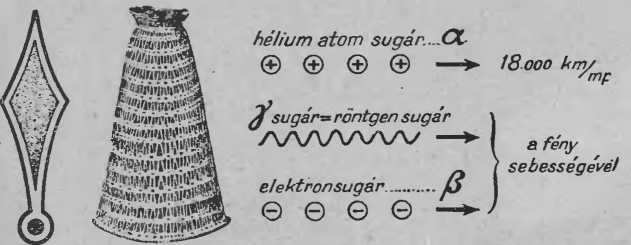
46. ábra. Önmagától világító óramutatónkból, avagy a közismert gázharisnyából ez a háromféle rádióaktív sugárzás lövell ki szünet nélkül.
Az emanációgázt már két évvel a rádium előállítása után felfedezték. Valóban nehéz lett volna fel nem fedezni. A gázharisnyából, világító óramutatókról állandóan száll ez a gáz. Órai apunk és óraüvegünk között nemcsak héliumgáz van, hanem emanáció-gáz is. Azt állítjuk tehát, hogy világító óramutatónkból, gázharisnyánkból nemcsak α-, β-, γ-sugárzás indul ki, hanem egy érdekes radioaktív gáz: az emanációgáz is kiszáll a levegőbe. Ezt kísérlettel könnyen be is bizonyíthatjuk. Egy kis világító óramutatón egymilliomod gramm rádium századrésze sugárzásával felérő hatású radioaktív anyag van. Kimutathatjuk, hogy belőle radioaktív emanációgáz keletkezik.
Kísérlet. Tegyünk kis üvegfiolába egy világító óramutatót A fiolát kapcsoljuk gumicsővel egy másik fiolához. A második fiola belső falának egy részére ragasszunk felvillanóport. A két fiola közötti gumicsövet csőszorítóval szorítsuk össze, úgy hogy a mutatós csőből semmiféle gázmolekula ne juthasson át az üres csőbe. (47. ábra.)
Hagyjuk a készüléket így pihenni 1 óráig. Ha ezután sötétben egy nagyítóval megfigyeljük az üres fiola felvillanó ernyőjét (felvillanóporral bekent oldalát), nem látunk felvillanásokat. — Távolítsuk el a szorítót a gumicsőről. Néhány pillanat múlva egyre szaporodó felvillanásokat figyelhetünk meg az üvegcső falán. — Szorítsuk újra össze a csövet, a felvillanások száma fogy.

47. ábra. Ilyen egyszerűen mutatjuk ki azt, hogy önmagától világító óramutatónkból ugyancsak radioaktív emanációgáz száll ki. A jobboldali zárt üvegcső falára világítóport (cinkszulfidpor) ragasztunk. Ha a gumicsövet összenyomjuk, a felvillanások száma fogy.
Ha a csőben egy világító óramutató, vagy gázharisnya van, akkor a cső elzárása után 1 perc múlva felére fogy a felvillanások száma. Ha rádium volna benne, akkor a felvillanások száma csak 4 nap múlva csökkenne felére, mert ennyi a rádiumemanáció felezési ideje. Ha óramutató van a csőben, akkor a felvillanások száma először rohamosan fogy, utána napokig lassan csökken. Ez azt bizonyítja, hogy a világító óramutatón tórium is, rádium is van. (Ha valaki egy világító óramutatót adna nekünk azzal, hogy állapítsuk meg, mi van a világítófestékbe keverve: tórium-e, vagy rádium, de kikötné, hogy nem szabad a világító anyaghoz nyúlnunk — ezt a nagyon nehéznek látszó feladatot az előző eljárás alapján egyszerű kísérlettel meg tudjuk oldani.)
A kísérletünkben leírt jelenségnek az a magyarázata, hogy a cső megnyitásakor a baloldali edénykéből rádióaktív gázatomok áramlottak át a jobboldali edénykébe. A felvillanások pedig azt bizonyítják, hogy ez a gáz is α-részeket sugároz. A felvillanások számának csökkenése pedig arról tájékoztat bennünket, milyen gyorsan fogynak az emanációgáz atomjai; ha t. i. egy emanáció-atom kisugárzott egy α-részt, akkor többé már nem emanációgáz. A kísérlet tanúsága szerint a rádiumemanáció atomjainak fele négy nap alatt már nem él, nem sugárzik. A tórium emanáció-atomjainak fele pedig 1 perc alatt hal meg.
Minden radioaktív elem sugárzása idővel csökken. Mert ha pl. egy rádiumatom kisugároz egy alfa-részt, akkor a rádiumatomok száma eggyel fogy. — Kiszámítható, hogy a rádiumatomok fele 1580 év alatt változik át más atommá az α-rész kisugárzása miatt. Azt mondjuk, hogy a rádium felezési ideje 1580 év.
Előbbi kísérleteink szerint a rádiumemanáció felezési ideje kb. 4 nap, a tórium-emanáció felezési ideje kb. 1 perc. — A felezési idő minden sugárzó elemre nézve más-más, azért nagyon fontos, hogy ismerjük a sugárzó anyagok felezési idejét. Táblázatunkban a rádióaktív anyagokra jellemző adatok között a felezési időt is megtalálhatjuk.
Azt már tudjuk, hogy az uránból és a tóriumból héliumgáz keletkezik. Ebben a kísérletben pedig azt láttuk, hogy a sugárzó anyagokból egy másik fajta elem: emanációgáz is keletkezik. Megfigyelhettük ennek a gáznak születését és halálát. (Keressük meg atomsúly-táblázatunkban az emanáció-elemet.)
Rutherford angol tudós az emanációból annyit gyűjtött össze, hogy atomsúlyát meg tudta mérni. A gáz atomsúlyát 222-nek találta. De a rádium atomsúlya 226. — Most már világos a kettő közötti kapcsolat. (48. ábra.)
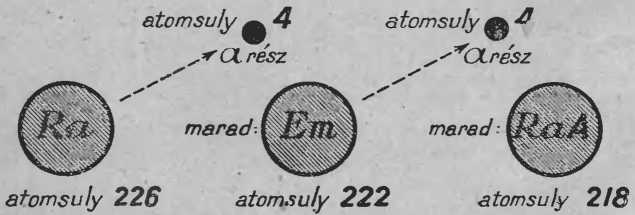
48. ábra. Miközben a sugárzó elem atomja egy alfa-részt kilök magából, alomsúlya 4-gyel kevesebb lesz és a megmaradt atom egy új elem atomja.
A 226-os rádium 4 atomsúlyú α-részt sugároz ki. Marad a 222 atomsúlyú emanációgáz. A gondolatmenetet kísérletünk alapján Rutherford nélkül is tovább tudjuk folytatni. Kísérletünkben láttuk, hogy az emanáció szintén α-részt sugároz. Mivel az α-rész atomsúlya 4, ezért az emanáció atomsúlya 4-gyel csökken, az α-rész kisugárzása miatt. A keletkező új elem atomsúlya: 222—4 = 218. Ez az új elem már nem gáz, tehát benne marad a jobboldali edényben és ott kimutathatónak kell lennie.
Könnyen ki is mutathatjuk. Vegyük le jobboldali üvegedényünket a gumicsőről és fújjuk ki belőle az emanációgázt. Azután figyeljük az edénynek a világítófestékkel bevont oldalát. Felvillanásokat veszünk észre, pedig már nincsen emanációgáz az edényben. A felvillanások száma rohamosan fogy. Ez azt mutatja, hogy a rádiumemanációból származó új elem, amely az edény falára rakódott le, szintén α-részt sugároz és rövidéletű.
Ezt az új elemet is sikerült meghatározni. Atomsúlya 4-gyel kisebb a rádiumemanáció atomsúlyánál, azaz 222 —4 = 218. Felezési ideje 3 perc. Neve: rádium A.
A 218 atomsúlyú rádium A (Polónium) megint α-részt sugároz. Így egy további 4-gyel kisebb atomsúlyú új elem keletkezik. Ez az elem a rádium B (ólom), atomsúlya 218—4 = 214. A rádium B megint sugárzó, csakhogy nem α-részt sugároz, hanem csupán elektront.
Foglaljuk össze a nyomon követett átalakulásokat egy kis táblázatban.

De az átalakulások sora itt még nem áll meg, hanem tovább folyik.
TÍZ SUGÁRZÓ ELEM A GÁZHARISNYÁBAN
Minthogy a gázharisnya közönségesen ismert sugárzó anyag, azért most a táblázat nyomán a gázharisnya tóriumából kialakult elemeket fogjuk figyelemmel kísérni. A szöveg olvasása közben nézzük a táblázatot.
A tórium atomsúlya 232. — Miközben egy felvillanást
okozó α-részt kisugároz, atomsúlya 4-gyel csökken és 228 atomsúlyú új elem keletkezik, a mezotórium 1. A tórium-atomok fele 13 400 millió év alatt alakul át.
A mezotórium 1. nagyon jó ismerősünk, mert ezt keverik bele az önmaguktól világító festékekbe. Ilyen festékkel van bekenve világító mutatójú, számlapú óránk is. A mezotórium 1. abban tér el a tóriumtól, hogy nem sugároz α-részt, hanem csak elektront. Ezért a keletkező új elem a mezotórium 2. atomsúlya ugyanannyi marad, mint a mezotórium l. atomsúlya, vagyis 228. A mezotórium 1. atomjainak fele 6,7 év alatt átalakul.

Az uránból keletkező sugárzó elemek
A rádium sorozat
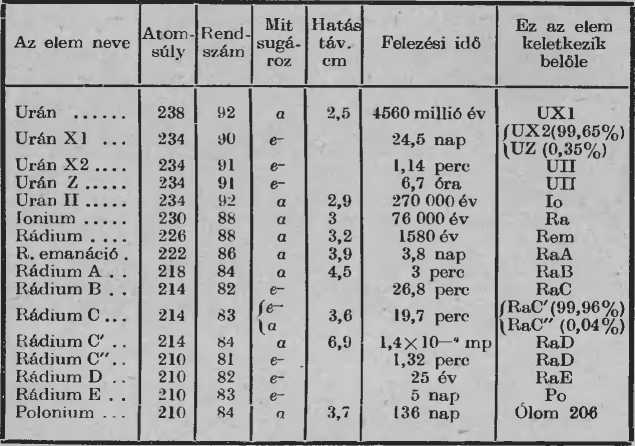
A 228 atomsúlyú mezotórium 2. atomjainak fele 6 óra alatt β- és γ-sugárzás közben új elemmé, rádiótóriummá alakul át.
A rádiótórium α-részecskéket sugároz, azért 4-gyel kevesebb atomsúlyú, 228 —4 = 224 atomsúlyú új elem, a tórium X keletkezik belőle. Felezési ideje 3,6 nap.
A tórium X-ből α-sugárzás közben tóriumemanáció keletkezik. Ezt a jelenséget figyeltük meg kísérletünkben. És így tovább keletkeznek a táblázat szerint az újabb elemek, míg végül a 208-as atomsúlyú ólom marad meg, mint az átalakulás végső terméke. Ez az ú. n. tóriumólom már nem sugárzik. (Az uránsorozatban található 206-os atomsúlyú ólom a rádiumólom.)
Ma már mintegy 40-féle természetesen sugárzó anyagot ismerünk. Közülük 23 sugároz α-részeket. Természetesen hosszas kutató munkára és több mint egy évtizedre volt szükség, amíg lassanként felfedezték a sorozat egyes tagjait és végre 1913-ban megtalálták közöttük azt az összefüggést, amelyet a mi táblázataink feltüntetnek.
MIÍRT FÉNYLIK GYENGÉBBEN A RÉGI ÓRAMUTATÓ?
Az óramutató világító festékébe mezotórium 1-et kevernek, felezési ideje 6,7 év. Ezért a mutatóban megfigyelhető felvillanások száma 7 év múlva felére, 14 év múlva negyedére csökken. Ezért megérthetjük, hogy idővel veszítenek fényértékükből az önmaguktól világító festékek. De mivel 10—14 évnél nem szokott hosszabb lenni az órák átlagos életideje, ezért felesleges a mutatóba rádiumot tenni. Ha a mutatóban rádium volna, akkor a világítása csak 1600 év múlva csökkenne a felére, de csak elméletileg. A felvillanó kristályszemecskéket ugyanis a levegő nedvessége már előbb tönkretenné.
Ha a mutató világítása végleg megszűnik, akkor ezt nem a benne levő sugárzó anyag végkimerülése okozza, hanem az, hogy a cinkszulfid nem hajlandó többé fölvillanni. A sugárzó anyag tudvalevően még több ezer év múlva is lök ki α-részeket, mert az óramutatón levő mezotóriumban kb. 20% rádium van.
Miért van rádium is a mezotóriumban és ha van benne, miért nem választják ki belőle. A tórium-tartalmú ásványok mindig tartalmaznak uránt is, az uránból pedig rádium keletkezik. A mezotórium és a keletkező rádium szétválasztása igen nehéz volna és többe kerülne a kiválasztott rádium értékénél.
ÚJ TITKOK NYOMÁBAN
Honnan ered a radióaktív anyagoknak ez a roppant energiája, amely többszázezerszer akkora, mint a szén égési energiája ? Ezt a kérdést vetették fel a tudósok. A választ a rádium felfedezői is keresték, de helytelen úton haladtak. Azt hitték, hogy a sugárzó anyagok atomjaiban valami különös képesség van, hogy a világűrből idesugárzó energiát összegyűjtsék, azután újra kisugározzák. Ma már tudjuk, honnan ered ez az energia.
Annyi bizonyos, hogy valami történik az anyag belsejében, az atomokban. Az atom belsejében lezajló folyamat közben repülnek ki az atomokból az irtózatos sebességű α-részek, valamint a még sebesebb elektronok és a legkeményebb röntgensugárzásnál is áthatolóbb γ-sugarak. Ez a háromféle sugárzás hordozza az égéskor felszabaduló energiánál mintegy milliószor nagyobb sugárzási energiát.
Már a katódsugarak és az elektromosság egyéb jelenségei is azt mutatták, hogy minden anyagban elektronok vannak. Hol és hogyan vannak ezek az elektronok az anyagban? Íme alig 4—5 esztendő múlt csak el a rádióaktivitás felfedezése óta, de már izgalmas kérdések egész sora vár arra, hogy megfejtse a gondolkodó és kutató ember.
Az új kérdések megfejtéséhez új megfigyelésekre, új tényekre van szükség. Ezek mutatják azt az utat, amelyen elindulhatunk. Az előzőkben tárgyaltakból azt láttuk, hogy az egyszerű kérdések tisztázása még egy-két évszázaddal ezelőtt is évtizedeken át húzódott. Ma már sokkal nehezebb problémákat is megoldunk évek alatt. Nemcsak azért, mert ma hasonlíthatatlanul pontosabb megfigyelő eszközökkel dolgozunk (Galilei még szívverését használta időmérőnek), hanem, mert régebben csak egy-két gondolkodó, ma pedig a. kutatók százai, ezrei dolgoznak a kérdések megoldásán, az elért eredmények pedig napok alatt közismertté lesznek. A mai kutatók sokkalta előnyösebb helyzetben vannak a régieknél; így hát a fizika ugrásszerű fejlődése, amelynek éppen az utolsó félszázadban voltunk tanúi, egészen természetes.
Hogy a fizika tudománya az utolsó évtizedek alatt mekkora változáson ment át, az különösen akkor szembetűnő, ha a 40—50 évvel ezelőtt megjelent természettani könyveket forgatjuk. Így pl. egy 1903-ban kiadott 960 lapos fizikai tankönyvben fél lap (az is apróbetűs) foglalkozik a rádióaktivitással és a sugárzást úgy magyarázza, hogy a 226 atomsúlyú rádiumatomban mintegy negyed-félmillió elektron van összesűrítve (1) „természetes — mondja — hogy ezek roppant erővel lökik ki egymást az atomokból
Sejtették, hogy a sugárzás forrásának magában az atomban kell lennie, mert hiszen a rádiumot bármilyen vegyi átalakulásnak vetették is alá, bármilyen vegyületben volt is lekötve, akár kloridban, akár bromidban, vagy szulfátban — sugárzóképessége változatlan maradt. Fizikai hatásokkal is megpróbálták a rádióaktív anyagok sugárzóképességét megváltoztatni. De pl. hiába tették a gázharisnyát az ívfény hőségébe (4000 fok), vagy hűtötték le az abszolút 0 fokhoz (—273°) közeli hőmérsékletre, sugárzóképessége változatlan maradt.
EGY KÜLÖNÖS CÉLLÖVÖLDE
Igazán élvezetes és vonzó tudományos foglalkozás a felvillanásokat okozó α-lövedékekkel kísérletezni. Ezekhez fogható tüzérségi lövedék nincsen. Ez az α-részekkel való foglalkozás, a felvillanások megfigyelése vezetett rá bennünket a kérdés nyitjára: ez adott legelőször közelítő képet az atom szerkezetéről.
Lássunk néhány tapasztalati tényt az α-részecskékre.

49. ábra. Így bizonyítjuk be kísérlettel azt, hogy az alfa-részek egyenes irányban repülnek.
Kísérlet. Bebizonyítjuk, hogy a részecskék egyenes irányban repülnek. Állítsunk az α-részecskék útjába keskeny rést. A rés mögé helyezzünk felvillanó ernyőt. Figyeljük meg a felvillanásokat. A felvillanások pontosan a rés képének helyén jelennek meg. Tehát az α-részek valóban egyirányban repülnek. (49. ábra.)
Kísérlet. Az α-részek áthatolóképességének megállapítása. Fedjük le a rést vékony lemezekkel, pl. alumínium lemezzel (szaloncukorkát csomagolnak bele). Legyen egy ilyen közönséges alumínium lemez vastagsága 0,010 mm = 10 μ. A lemez mögött felvillanásokat mutat az ernyő. Tehát ilyen vékony lemezen könnyen áthatolnak az α-részek. Ha a rést 2, 3, 4 lemezzel fedjük be, észrevesszük, hogy egyre kevesebb részecske tud csak átjutni (csupán a nagy sebességűek). Ha a lemez vastagsága több 0,041 mm-nél, akkor már egyetlen részecske sem tud átjutni.
Hát csak ilyen vékony rétegen tudnak áthatolni ezek az irtózatos sebességű α-részecskék? Tévedünk, amikor ezt a vastagságot kicsinek tartjuk. Később látni fogjuk, hogyan lehet meghatározni az α-részek átmérőjét. Ehhez képest az átütött lemez szinte elképzelhetetlenül vastag.
Mit szólnánk ahhoz a fegyverhez, amelynek 1 cm hosszú lövedéke 50 ezer km vastag acéllemezt, vagy 100 ezer km vastag alumínium lemezt tudna, átütni? A Föld átmérője kb. 12 700 km. Négy földgolyót kellene egymás mellé tenni, hogy együttes vastagságuk 50 000 km legyen. Ha tehát a, fegyvergolyó képes lenne arra, amire az a részecske, akkor négy egymás mellett lévő acélból készült földgolyót kellene átütnie a legvastagabb részen.
Erre a teljesítményre azt kellene mondanunk, hogy lehetetlen. Lehetetlen olyan acélgolyót elképzelni, amelyik csak tíz méter vastag acélfalon is áthalad, hiszen a lövedék már jóval előbb szétlapul, darabokra szakad. De íme, kísérletünk szerint mégis van olyan atomlövedék, amely az előbbi hihetetlen teljesítményt elvégzi. Kiszámítható, hogy az alfarészecskék mintegy százezer atomot szelnek át. Utána azonban még mindig akkora a sebességük, hogy felvillanásokat okoznak.
Hogyan lehetséges ez a kétségtelen tapasztalati tény?
Csakis úgy, hogy miközben a α-lövedék áthatol a százezer atomon, közben nem ütközik neki semminek. Tehát az a kísérletünk, hogy az alfarészecske a saját vastagságához képest elképzelhetetlenül széles szilárd anyagrétegen tud átrepülni, arra utal, hogy az atom belsejében az anyag nem oszlik el egyenletesen, vannak olyan részek, ahol az ellenállás rendkívül kicsi. Ez a felismerés abban az időben roppant meglepő volt.
Az atomot t. i. addig tökéletesen rugalmas golyó alakúnak képzelték, amelynek terét az anyag egyenletesen tölti ki. De lám, most egy egyszerű jelenség azt bizonyítja, hogy ez nem így van.
De akkor milyen az atom belső szerkezete? Hiszen az kétségtelen, hogy az atomoknak jól mérhető tömege van. Azt is kérdezhetjük tovább, hogy hol van az atomban az elektron? Hisz minden anyagról elektronokat tudunk leválasztani.
Ezek előtt a kérdések előtt állott a tudományos világ 1900 és 1910 között. Leírunk egy nagy fontosságú kísérletet, amely a kérdés megoldásához közelebb visz.
MEGTALÁLJUK AZ ATOMMAGOT
Kísérlet. Szükségünk van egy parányi rádiumra, egy alumínium lapra, egy felvillanó ernyőre és egy nagyítóra. (50. ábra.)
A rádiumból alfa-sugarak lövellnek ki. A sugarak útjába helyezzünk alumínium lemezt. Ha a lemez vékony, akkor lesznek olyan α-részecskék, amelyek átszelik a lemezt és még a lemez mögött is okoznának felvillanásokat. De most a felvillanó ernyőt ne a lemez mögé tegyük, hanem az ábra szerint oldalt a lemez elé. A felvillanó ernyő és a sugárzó anyag közé helyezzünk egy olyan lapot, amely az α-sugarak számára áthatolhatatlan. Láthatjuk, hogy a rádiumból közvetlenül nem juthat α-rész az ernyőre. Tehát felvillanást semmiképpen sem észlelhetünk. De a kísérlet eredményt mutat: néha-néha felvillan az ernyő.
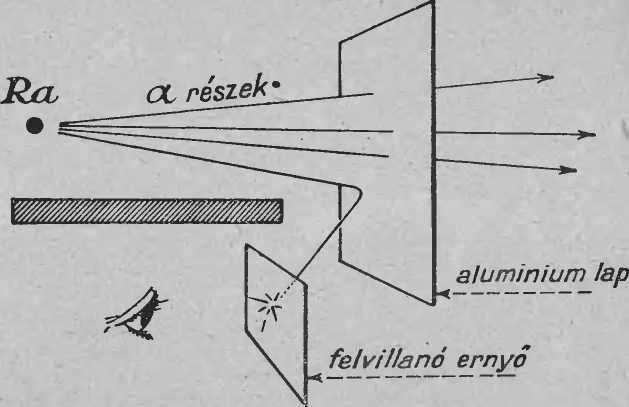
60. ábra. Ez a kísérlet bizonyítja az atommag létezését. Tízezer alfa-rész közül. mintegy 9999 áthatol az összefüggő anyagrétegen, de átlag 1 részecske, visszaverődik.
Hogyan lehet ez ? Bizonyára az alumínium lemezről α-részecske verődött vissza.
Hasonló eljárással azt is ki lehet mutatni, hogy a lemezen áthatoló α-részek közül is meggörbül néhánynak a pályája, mintha valamilyen erő eltérítené azokat egyenes útjukból. Fárasztó kísérletek azt mutatták, hogy kb. tízezer α-részecskére jut egy erősen eltérített részecske.
Kell tehát valaminek lennie az atom terében, ami nagy ritkán eltérít egy-egy lövedéket az útjából.
Tudvalevőleg a repülő alfa-rész töltése pozitív. Az eltérítés és a visszaverődés azonnal érthető lesz, mihelyt az eltérítő valamit is pozitív töltésűnek képzeljük.
Mivel tízezer részecske közül csak egy találkozik ezzel a valamivel, sőt ez az egy is csupán akkor, ha az atomok tízezrein repül át, ebből a tényből egyszerűen ki tudjuk számítani, hogy ennek az eltérítő valaminek — nevezzük atommagnak — nagysága az atomhoz képest elenyészően kicsi.

51. ábra. Az előző ábrán látható kísérletnek ez a magyarázata. Az alfa-részecske pozitív elektromos töltésű, annak a valaminek, ami visszaverte (az atommagnak) szintén pozitív töltésűnek kell lennie (egynemű elektromosságok taszítják
egymást)
Ilyen kísérleteken alapuló számítások azt bizonyítják, hogy az atommag térfogata kb. csak billiomod része az atom térfogatának. — Összefoglaljuk : kétségbevonhatatlan és könnyen megismételhető kísérletek azt mutatják, hogy az atom terét az anyag nem egyenletesen tölti ki, az atom térfogatának billiomod részét foglalja el egy pozitív elektromosságú valami: az atommag,
amely az α-részecskéket eltéríti irányukból és amely az atom tömegének legnagyobb részét képviseli.
Az eltérítő kísérletekből meg lehet határozni az atommag pozitív elektromos töltésének nagyságát is. Vegyük egységül az elektron töltését. Azt találjuk, hogy a hidrogén atommag töltése 1 pozitív töltés egység, a hélium atommag töltése 2 egység, az alumínium atommagé 27. Nézzük meg az elemek periódusos rendszerében az említett elemek rendszámát (vagy másnéven sorszámát). Meglepődve győződünk meg arról, hogy ahányadik helyen áll az elem a periódusos rendszerben, annyi az elem atommagjának töltése is.
Ez megint nem feltételezés, hanem kísérleti tény.
Most már két nagyon érdekes törvényszerűséget érthetünk meg a rádióaktív elemek táblázatában. Figyeljük csak meg, hogy ha egy elem α-részt sugároz ki, akkor a keletkező elem rendszáma 2-vel alacsonyabb lesz. Pl. a 88. rendszámú rádiumból α-sugárzás révén a 86. rendszámú emanációgáz keletkezik. (52. ábra.) Miért?
A magyarázat egyszerű: az α-részecskének két pozitív magtöltése van. Tehát az α-rész kisugárzása után 2-vel csökkennie kell a hátramaradó mag töltésének. De mondottuk, hogy az elem rendszáma éppen a magtöltések számával egyezik.

52. ábra. Ha egy elem atomja alfa-részt (hélium mag) sugároz ki, akkor olyan új elem keletkezik, amelynek magtöltése 2-vel csökken, mert két töltésegység távozott el. Tehát a keletkező új elem rendszáma is 2-vel kisebb. Atomsúlya pedig 4-gyel csökken.
A másik kérdés, amire most már szintén felelni tudunk, a következő: keressünk ki a természetesen sugárzó elemek táblázatában egy olyan elemet, amely elektront (e—) sugároz. Azt látjuk, hogy a belőle keletkező elem rendszáma 1-gyel nagyobb tesz. Pl. a 83. rendszámú rádium E-ből egy elektron kisugárzása után a 84. rendszámú polónium lesz. Miért?
Azért, mert ha a magból eltávozik egy negatív töltés, akkor a magban eggyel több pozitív töltés érvényesül — tehát 1-gyel nő a rendszám is.
MILYEN AZ ATOM?
1911
Az atomban van elektron is. Hol vannak ezek az elektronok? — Erre megint a tapasztalati tények alapján kell megfelelnünk. Tapasztalati tény az, hogy az anyag vagy az atom közönséges állapotban nem mutat elektromos töltést. Hogyan lehetséges ez, amikor az atom magjának kétségtelenül pozitív töltése van?
Ezeknek a kísérleti tényeknek alapján 1911-ben az atomról a következőt állapították meg :
Az atom pozitív töltésű atommagból és a negatív töltésű elektronokból áll. Az atommag tartalmazza az atomnak majdnem egész tömegét, de az atommag mérete az atom méreteihez képest igen kicsi.
A mag és az elektronok ellentétes töltései vonzzák egymást. Ezért az elektronok beleesnének a magba. Minthogy ez mégsem történik meg, tehát az elektronoknak keringeniük kell a mag körül.
Ennek alapján lássuk a legegyszerűbb elem, a H-atomszerkezetét. A H-atom az egységnyi pozitív töltésű hidrogén atommagból és egy körülötte keringő elektronból áll.

53. ábra. A hidrogénatom szerkezete. Középen van az 1,8 * 10-13 cm sugarú atommag. — A magtól 0,532 * 10-8 cm távolságban kering a hidrogénatommaggal kb. egyenlő nagyságú (de 1840 szer kisebb tömegű) elektron.
A tudomány mai állása szerint a hidrogén atommag sugara R = 1,8 - 10-13 cm, az egyik legnagyobb atomsúlyú elem, a tórium magjának sugara kb. 6,2-szer akkora, mint a hidrogénatom sugara.
Az elemek atomjainak átmérője pedig 10-7 — 10-8 cm nagyságrendűnek bizonyul.
Később majd megértjük, miért nem lehet az atom átmérőre is olyan határozott számot megállapítani, mint a mag átmérőjére.
A hidrogénatom szerkezetének nagysági viszonyait a Napból és a Földből álló rendszerben szemléltethetjük. Képzeljük el, hogy a Nap az atom magja, a Föld pedig a keringő elektron. A Nap meg a Föld mai távolsága nem felel meg az atom arányainak. A Földet még háromszázszor messzebb kellene elhelyezni a Naptól, mint most van, hogy aránylag olyan távol legyenek egymástól, amilyen messze a keringő elektron van az atommagtól. (Megjegyezzük, hogy a legtávolabbi bolygó, a Plutó csak 40-szer van messzebb a Naptól, mint a Pöld.)

54. ábra. A Földet a Naptól 300-szor olyan messzire kellene vinni, mint jelenleg van, hogy aránylag olyan messze legyen a Naptól, mint a hidrogénatomban az elektron van a magtól.
Amit eddig tanultunk az még semmit sem mond arra nézve, hogy a hidrogénnél nagyobb súlyú elemek magja miből van összetéve? Pl. a hélium atomsúlya 4. Miből áll a hélium magja? Azt sem mondja meg, hogy az elektron vagy az elektronok hogyan, milyen pályán avagy pályákon keringenek az atommag körül.
Köztudomású, hogy a higany 13,6-szor, az ólom 11,3-szor, az arany 19,2-szer sűrűbb, súlyosabb a víznél. Mekkora lehet az atom magjának sűrűsége? Hogyan, hát még ezt is ki tudjuk számítani? — Természetesen, mégpedig minden különös nehézség nélkül. Hiszen említettük, hogy a mag térfogata mintegy billiószor kisebb az atom térfogatánál. Ezért az atom anyaga mintegy billiószor kisebb térben van összesűrítve, mint az atom. Az atom magjának tehát billiószor sűrűbbnek kell lennie a víznél és a legsűrűbb földi anyagoknál is.
Ez megint kétségbevonhatatlan valóság. De próbáljuk szemléletesen elképzelni, mit is mond ez a tény : gondoljunk egy 50 vagonból álló, vagononként 30 tonnás olyan tehervonatra, amelyet száz tonnás mozdony húz. A tehervonat egész súlya 1600 tonna. — Kérdésünk: ha ennek a tehervonatnak atommagjait szorosan
egymás mellé sikerülne csomagolni, mekkora helyet foglalna el az egész szerelvény? Aki nem hiszi el, próbálja kiszámítani a közölt adatok alapján: ez a tehervonat beleférne egy gombostű fejének 10-ed részébe. (Ha a gombostűfej térfogatát 1 mm3-nek gondoljuk.) Tehát a hatalmas tehervonat egy alig látható porszemben elférne. — De ez a porszem aztán 1600 tormát nyomna!
Nem tévedünk? Lehetséges ez? Mutat a világmindenségben más jelenség is ilyen irtózatos sűrűségeket? Nagyon érdekes, de már jóval azelőtt, hogy az atom szerkezetéről ez a képünk meg lett volna, a csillagászok különös dolgot figyeltek meg. A távoli csillagok tömegét és térfogatát ki tudják számítani.. Ebből a két adatból megállapítható a sűrűségük is. A csillagászok találtak olyan égitesteket, melyeknek sűrűsége 50 ezernek, sőt 300 ezernek mutatkozott. (Az úgynevezett fehéren izzó törpe csillagok, pl. a Sirius kísérője.) Ebből pedig az következett volna, hogy vannak a világűrben olyan anyagok, amelyek á földi anyagoknál 10 ezerszer, 100 ezerszer sűrűbbek. Abban az időben ezt nem tudták elképzelni. De ma már önként adódik a magyarázat: az illető égitestekben uralkodó hatalmas nyomás úgy összepréseli az anyagokat, hogy az atomok magjai sokkal közelebb jutnak egymáshoz, mint a földi körülmények között. Ma már tudjuk, hogy nem lehetetlen a földi anyagoknál milliószor sűrűbb anyagok létezése.
Most pedig gondoljuk meg, milyen érdekes következtetést vonhatunk le ebből a mutató világítását okozó α-részecskékre, amelyek egy része a mi világító óramutatónkból ki is sugárzik. Ezeknek a lövedékeknek alig elképzelhető 20 ezer km/mp-es sebességét már megcsodáltuk. Most pedig tanulmányozzuk a sűrűséget. Tudjuk, hogy az α-rész a héliumatom magja. Ezért az α-rész legalább billiószor sűrűbb a földi anyagoknál. — Ha egy 5 köbcentiméter térfogatú gyűszűt megtöltenénk α-részecskékkel mekkora lenne ennek a súlya? Rövid számítás azt mutatja, hogy az α-részecskékkel telt gyűszű súlya legkevesebb 50 millió mázsa lenne.
Valahányszor óramutatónkra nézünk, gondoljunk arra, milyen meglepő sebességű, de talán még meglepőbb sűrűségű lövedékek okozzák benne a felvillanásokat és repülnek ki belőle.
ÖSSZEFOGLALÁS
A természetes sugárzásoknak eddig ismertetett jelenségei alig 15 év alatt fizikai tudásunk hatalmas fejlődését idézték elő. A fejlődés főbb pontjait a következőkben jelölhetjük meg :
1. Megdöntötték az elemek állandóságának elvét. Hiszen szemünk előtt, a legközönségesebb körülmények között folyik le az elemek egész sorának átalakulása egymásba : a gázharisnyában és a világító óramutatóban.
2. A rádióaktivitás felfedte az ember előtt a kémiai energiánál milliószor hatalmasabb atomenergiát.
3. A rádióaktivitás segítségével bepillantottunk az atom szerkezetébe. Felfedeztük az atommagot.