Chapter 6

How to teach anyone to calculate:
Strategies for Mathematics

TAP THIS TO SEE THE VIDEOS

‘In mathematics you don’t understand things.
You just get used to them.’ (1)

John von Neumann

In this chapter

One day, we were discussing a strategy a little boy used to prepare for his SATs test in Mathematics. The school Kate had visited was one of the few schools in the UK where all the staff are trained in NLP. The little boy explained to his teacher how he went into his very own maths room in his mind and all the answers to the maths questions were on the walls of this room. His teacher said to the whole class, ‘let’s all have a maths room so maths is easy’ and set about teaching each child how to have a room in their minds too. Richard began to laugh as he explained that when he had elicited the strategy of a genius mathematician some years before, he had discovered that the mathematician had a maths room where all the equations were calculating automatically on the walls. Both this child and the mathematical genius had mathematical minds!

The poor literacy level in the USA and the UK (Chapter 4) are nothing in comparison to the percentage of people who have difficulty with numeracy and mathematics. Up to 40% of people in the UK are functionally innumerate, nearly one in three adults in the USA have only low level numeracy skills, and in some ways, being no good at maths has almost become a badge of honour (2) . Often, the primary emotion associated with mathematics is fear. This is the opposite of the feelings we want to associate with numbers – the feelings of comfort and certainty.

Many people think of maths as complex and difficult. Sadly, the unpleasant feelings that adults have about maths directly affect children. When mothers express to their daughters that they are no good at maths, their daughters’ grades go down(3) . We want to reduce the process to the simplest and easiest way of doing maths, so that everyone feels great about making it simple.

When a group of students complained to their teacher that they couldn’t do maths, the teacher responded by saying ‘that’s OK, neither can I, so I’m going to show you the tricks to get around it’ . He was telling the truth, because the solutions to mathematical problems are processes and procedures which resolve problems or puzzles in the simplest way possible; they are the tricks of the trade!

Learning maths in a sequence and making sure all the pieces are in place will ensure people are confident and enjoy maths. Missing a few steps along the way often leads to the confusion that makes people move away from maths rather than towards the fun of solving puzzles and problems. So to be great at maths and to enjoy learning it’s helpful to begin at the beginning and make sure each stage of learning connects to the next stage, and that the steps at each point are explicit in that they clearly show the learner what to do on the outside and what to do on the inside of their mind.

We want to do even more than this though. We want to create a Mathematical Mind . When you learn to have a mathematical mind, it is full of numbers that are pleasing and comfortable to have in your head. The numbers move by themselves, automatically finding simple and easy solutions and the quickest way to find answers to all kinds of problems. A mind that enjoys the magic of maths is filled with numbers and patterns, so that a problem reduces logically to the simplest and easiest level, so maths becomes natural and comfortable.

It may be that you want to teach a small child to begin learning maths, or you want to help an adult to improve and enjoy Mathematics. Either way, the key stages to building a mathematical mind are Counting, Addition, and Subtraction. Later you may want to teach fractions and percentages, or ratio and proportion, or statistics. However, each of these disciplines requires the fundamentals of counting, addition and subtraction, so let’s start with these. Here are some approaches to Mathematics that are based on how the brain works, so you can start to adapt and create your own strategies based on sound neurological principles and NLP.

When we learn to ride a bicycle or a scooter we don’t just learn to ride. We learn to balance, steer, and push with our feet on the pedals. The activity becomes ingrained or encoded. So much so that, even after years of not riding a bike, it comes straight back to you at that magical moment when you sit on the saddle; the foundations are laid in just the right way and with just the right state attached to the learning. We want to encode Mathematics in the same way.

As with other strategies such as reading and spelling, you know that if you are to remember something visually in your mind, it is best if it is big and bold. It is the same with numbers. When children start at school, numbers are made bright, bold and big. As they progress through school, more and more numbers appear on the page, they get smaller and smaller and are usually reduced to black and white. Fortunately, the inside of your mind is not limited in this way. We want the look and feel of numbers to be interesting and engaging. Have a go at this exercise for yourself to discover how you can change the submodalities of numbers so they are pleasing to you. Once you have this experience for yourself, it will be easy to create comfort and fun around numbers for your learners.

Think of a number you are certain about. Look at it in your mind and know it is right. See it in a certain place, a certain size or colour. The bigger it is in your mind, the easier it is to be sure of, so make it at least 20 centimetres tall. Make it just the right size so it feels comfortable. Now move on to another number and do the same thing. Is it a different colour? Is it in a different place? How big is this number? There are only nine numbers plus a zero - so there are not that many to remember and not that many to make every one of them special, developing a great feeling of certainty and comfort with each number.

Whether you are starting to teach little people or helping adults with numeracy, this is a good place to start, because if you are going to fill your head with numbers, it’s a good idea that you enjoy having them inside your mind!

Counting
We have a vast heritage of counting songs and the internet offers endless animated versions of these songs. Songs that count up and count down help to encode the sequence with feelings of fun and laughter, laying the foundations of a mathematical mind filled with number certainty, pleasure and comfort. Do you remember singing ‘1, 2, 3, 4, 5 once I caught a fish alive’ , or ‘10 green bottles hanging on the wall’ , and ‘there were 10 in a bed and the little one said ‘roll over, roll over’ ? Were you singing along as you read those phrases? Combining the internal visual representation of the numbers with the auditory sound of the numbers and the good feelings associated with the activity are the foundations of enjoyable numeracy and magical maths .

The unconscious mind repeats this learning over and over and very quickly encodes the learning. So whatever the age of your learners ensure that you count up and down, not just to 10, but on and on to higher and higher numbers, running the sequence over and over. Unlike the monotony of rote learning, this is best done as fast as possible, so make it a race. The brain learns quickly and the patterns form effectively when it happens all at once. Think of the metaphor of the little books with one picture on each page, which you flip with your thumb to make a little movie. You are encoding numbers in the same way!

Skip Counting
Once a person can add any combination of numbers together and race through them up and down, all the combinations they need become encoded and automated. Counting leads to addition. When someone can add up numbers they can easily learn to subtract, and are ready to learn to multiply and divide.

The next step to learning to add numbers is to count and add at the same time - sometimes called Skip Counting . The more fun the counting game is, the better it feels. Einstein and other great mathematicians paid more attention to how the numbers made them feel than focusing on just the visual images.

Start with sequences that are easy for the learner. Often, small children will find counting in 2s easiest, but older learners and adults will often find 5s and 10s easier. Ask your learners which sequences are easiest for them and remind them of the feelings of certainty and comfort about the numbers they have in their mind before you begin. Beginning with the easiest sequence enhances these feelings, so you can build the belief that all the other sequences are easy too.

Now the game to play here is to see how quickly you can count in sequence. Have a competition to see who can get to 100 or to another specified number first. Your learners may not know all the numbers to start with, so have them write out the sequence in a long list to start with, so they are not burdened with trying to remember the numbers and they have all the information to keep up with the game. Very quickly, the learners will stop using the list as the number sequence becomes easy to remember.

Some people may think this is an odd thing to do, as you are giving the answers to the learner. But remember - we want the learner to have certainty, and this certainty feeling is connected to what will quickly and easily be memorised – the sequence of numbers.

As an example, start with counting-up and down in 2s: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 … all the way to 100 and then count back down again.

Or in 10s:
10, 20, 30, 40, 50, 60, 70, 80, 90, 100 and then count back down again.

Now move to 3s: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 all the way to 102 and back again.

Repeat this with each set of numbers so you have the complete set of sequences up to and including 10s, which will be so easy for your learners now.

Each time the learner succeeds, ensure that you reinforce how easy this is and how fast they are getting. Remind them that the bigger the number they are counting with, the fewer numbers are in the sequence and the less there is to remember; the bigger the numbers, the easier it gets! Whether you use this strategy for yourself or with your learners, the more you repeat this process, the more your unconscious will identify the patterns emerging in your mind.

The wonder of the human brain is its plasticity. Children find this so easy and so much fun. Adults are surrounded by numbers and sequences - phone numbers that just pop into your mind, email addresses, money and change. Just those 10 digits that match your fingers and toes create exquisite patterns in your learner’s mind.

Once you have had fun running each sequence in order, continue to play this game by mixing up the number sequences. For example, do 4s followed by 7s followed by 3s and 5s and 8s etc. It’s not about being able to understand mathematics, but about being able to take the steps to build a more organised and more numbered mind.

These games encode the number sequences so quickly that you will see rapid improvements when you begin to teach addition and subtraction, multiplication and division. These are great games for the car or on school trips and can involve, ‘let’s get to 100 before the next petrol station’ , or ‘can we do the 6s before we get home?’

Moving to addition
Once your learners are confident and comfortable with skip counting, you can move on to a range of skills to make addition fun and easy. You can experiment with these:

double-up
Once your learners can count and skip count, they already have some addition skills. Now they can easily move on to how to double up numbers:
Double two: 2+2 is 4
Double six: 6+6 is 12
When they have all the double numbers encoded the next step is easy!

double plus 1
This strategy uses the information they already know and builds on it.
Take 5+6 - the learner already knows 5+5 = 10, so add 1 more and the answer is 11.
Continue with each of the doubles and add one more.

counting-up
 The first step is to add two numbers together. Look at the two numbers in the sum and choose the biggest one. So in the sum 4 + 3; the biggest number is 4.
Start with the number 4 and count up the same number of times as the smallest number – in this case 3 times.
4 (count up 3 times): 5 - 6 - 7
Now the learner knows 4 + 3 =7 and 3 + 4 = 7
Move on to bigger numbers such as 8 + 5.
8 is the biggest number, so count up from 8, five times
8 (count up 5 times) 9-10-11-12-13
Now the learner knows 8+5 = 13 and 5+8 = 13
Continue practising with other sums, counting up from the big number by the small number so that all the sequences become familiar. Very soon the learner will automatically remember the sequences and see the patterns in the numbers.

getting to 10
Remind the student of all the nice pictures and feelings they have about the numbers, then begin to use the counting-up strategy to work out all the numbers that make 10. Begin with the biggest ones: 9 +1=10, 8+2 =10, 7+3=10, 6+4=10, 7+3=10, 6+4=10, and look - now 5+5=10 and so does 4+6! So, once they see the pattern they realise they already know the rest! Once your students know ‘getting to 10’, all the other additions become easy with this next game.

building a number counter
 Now it’s time to learn to manipulate much bigger numbers whilst realising that there are really only 10 digits to deal with in any number, however big it gets. The problem with larger numbers is that learners try to hold too many numbers in their mind. What we want them to learn to do is just hold the last and biggest number in their mind, so it is clear and easy to remember.

The strategy for doing this is to build a number counter in the learner’s mind that is big, bold and clear. So now take a number such as 24 and see it in your mind as big and colourful and clear so it looks something like this:

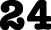
Now add 2 to each of the numbers starting with the number on the right.
4 + 2 = 6 make a click sound, and see the counter move from 4 to the number 6.
Now take the number next to it on the left: 2 + 2 = 4, make the click sound and move counter from 2 to 4.
Now this is the only number to have in your mind. A really big colourful number:

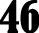A useful representation to have here is a digital meter, or digital calendar, where the numbers automatically go back to zero after 9. As they roll around, add a ‘click’ sound to the movement, you know it has moved on.

So now the only number we have in our mind is 46. Add 2 to each number and hear the click each time the number rolls around: 6 + 2 (click) the counter moves to 8. 4 + 2 (click) the counter moves to 6. Now the new number is 68 and this is the only number in your mind, big, bold and clear:

Move on, adding 3 to the number and then 4 to the number until the machine inside your head is working by itself.
Move on to adding a number to a 3-digit counter such as 423, so the meter gets bigger and bigger.
Keep going until the meter has as many numbers as you want it to have. Keep playing the game, (remember the ‘click’ each time) until the counter is encoded in your student’s mind and they are ready to move on to the real addition strategy.
Remember, we are building a head full of numbers to be manipulated and played with for fun!
Now there comes a point where the numbers added together are 10 or more. So now it’s time to talk about real addition.

real addition
 Once the digital meter is working all by itself, the next step is to adjust the numbers every time the number goes around the clock past zero. So start with the big number 99 and add 11 to it:

The 9 moves up to 0 and the next 9 goes to 0 plus 1 and a new column appears with 1 in it, so the new number is 110 and this is the only number in your mind:

110

Move on to even more interesting numbers! Have 626 as big and bold at the top an`d underneath have the number 333, still clear but a little smaller. Like this:

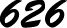
Now add the top right number (6) and the bottom right number (3) and turn the number on the meter to 9. Next do the same (remember the click) with the top middle number (2) and the bottom middle number (3) and turn the top number to 5. Now do the same with the left hand numbers 6 plus 3 and turn the top number to 9. Now you have a new big number at the top:

Carry on adding 333 to this number. This time, when the number goes past 0 click the big number up one -so 3 plus 9 is 2, and the 5 clicks to 6. 3 plus 6 is 9. So the left hand numbers are 3 plus 9 so this number clicks to 2 and a new number appears in a new column 1292 and this is the only number in your mind:

It doesn’t matter how big the numbers get, it’s just as simple as adding one column and moving to the next using just the numbers 1 to 9 plus 0.

When learning maths, children are instructed to ‘show your working out’. With this process there is nothing to show on the outside - it’s all happening on the inside. Showing how the answer has been achieved is often for the teacher’s benefit so that they can be sure the child has gone through the process of carrying numbers and number placement. This is not the purpose here. We are building machines inside our learners so that the basics of mathematics happen automatically. With these strategies installed inside young minds, multiplication, division, algebra, and geometry become easier processes and maths is fun!

Subtraction
Once we have the machine in our heads to add numbers, the same machine can subtract numbers. So all the same games can be played in reverse to build a subtraction machine. Start with the counting game, but this time the counting counts back from 100. Move on to the take away game, which is the same as the addition game, but this time with the question ‘who can get to zero first?’

Doubling up becomes halving, getting to 10 becomes getting to 0, and the addition game becomes the subtraction game. Starting with two numbers and take off 2 at a time, move on to 3 or 4 first and then make the big number at the top drop down one rather than adding a number on.

Maths is about finding the simple solutions and the easy way to do things. Adding 4+4+4+4 may seem quite a bit of work, but if your mind sees that it is the same as 2 lots of 8 and double 8 is 16, it’s easy. It doesn’t matter how big the number is, it is always made up of smaller numbers.

Humans are neurologically wired for the decimal system. We have 10 fingers and 10 toes. Discomfort with numbers is often because we haven’t found the right voice and the right place to have the good feeling; when we find the most comfortable place you can find the solutions and strategies for your students to have inside their minds.

summary

In this chapter you have discovered strategies that work on the inside to build mathematical machines. You have learned that maths isn’t just a process of manipulating numbers on a piece of paper, but creating a mind full of numbers and strategies that make manipulating numbers and solving problems easy. You have built the basis of a mathematical mind with counting, addition and subtraction - and next we explore how the fun multiplies.

references

1 Reply, according to Dr. Felix T. Smith to a physicist friend who had said “I’m afraid I don’t understand the method of characteristics,” as quoted in The Dancing Wu Li Masters: (1979) by Gary Zukav, Bantam Books,

2. Skilled for life? Key Findings from the Survey of Adult Skills Ref http://skills.oecd.org/documents/SkillsOutlook_2013_KeyFindings.pdf

3. Gunderson E, Ramirez G, Levine S. C, Bellock S.L, 2011The Role of Parents and Teachers in the Development of Gender-Related Math, Published online

activities

The digital meter in your head Install the digital meter to learn addition and subtraction. Practise adding bigger and bigger numbers to each other as above.

The BIG counter
Using a smart board, create a BIG counter on the screen and play the counting games with the whole class

Elicit excellent strategies
 Elicit strategies from 2 different people for subtracting large numbers. Find out what they do inside their minds to make it easy. Try them on and see which one works best for you.

The meter method
 Teach someone who is convinced they are no good at maths to add numbers using the meter method outlined in this chapter. Simplify your language so concepts are really easy to connect to the learner’s previous experience and create states of certainty and comfort in the learner.

Extension activity
How could you utilise this method for teaching decimals and negative numbers?

This eBook is licensed to Dominic Luzi, dluzi@managementalchemy.com on 10/18/2018